More reliable inference for the dissimilarity index of segregation

Summary

The most widely used measure of segregation is the so‐called dissimilarity index. It is now well understood that this measure also reflects randomness in the allocation of individuals to units (i.e. it measures deviations from evenness, not deviations from randomness). This leads to potentially large values of the segregation index when unit sizes and/or minority proportions are small, even if there is no underlying systematic segregation. Our response to this is to produce adjustments to the index, based on an underlying statistical model. We specify the assignment problem in a very general way, with differences in conditional assignment probabilities underlying the resulting segregation. From this, we derive a likelihood ratio test for the presence of any systematic segregation, and bias adjustments to the dissimilarity index. We further develop the asymptotic distribution theory for testing hypotheses concerning the magnitude of the segregation index and show that the use of bootstrap methods can improve the size and power properties of test procedures considerably. We illustrate these methods by comparing dissimilarity indices across school districts in England to measure social segregation.

1. INTRODUCTION

Segregation remains a major topic of research in a number of contexts, such as neighbourhoods, workplaces and schools. Researchers study segregation by poverty status, by sex and by ethnicity, among other characteristics. Almost always, these studies are comparative in some way; for example, arguing that ethnic segregation in neighbourhoods is higher in one city than another, or that segregation by sex in some occupation has changed over time. There is often also an implicit or explicit causal model in mind, and the difference in segregation is associated with some behavioural process. However, the inferential framework for segregation indices is underdeveloped, a fact that limits the progress that can be made. In this paper, we propose an approach to strengthen this framework.

It is central to our approach to think of segregation as the outcome of a process of assignment. This includes the assignment of people to neighbourhoods, workers to jobs, or pupils to schools. In general, this allocation is likely to be the result of the interlocking decisions of different agents rather than of a dictator. This perspective offers a number of advantages. First, it ties the outcome to a set of processes that can be analysed and estimated. Second, it makes it clear that the observed outcome is one of a set of possible outcomes, and so naturally leads on to a framework for statistical inference. Third, the connection with the underlying processes makes explicit that it is this systematic or behaviour‐based segregation that is the object of interest in terms of analysing the causes of segregation.

There is a large body of literature concerning the measurement of segregation, with a number of indices in use, all with differing properties. The most widely used measure of segregation is the dissimilarity index, D, defined below; see Duncan and Duncan (1955). It is now widely understood that this measure also reflects randomness in the allocation of individuals to units (i.e. it measures deviations from evenness, not systematic segregation). Furthermore, the impact of randomness on D depends on the nature of the context (made precise below). This makes one of the prime tasks in the measurement of segregation difficult, namely making statements on true differences in segregation between cities, school districts, industries or time periods. For example, the overall proportion of the minority group influences this because a very small minority group is more likely to be unevenly distributed across units by chance, compared to a larger minority group. This problem is particularly acute with small unit sizes. This is easy to see in the following example. Consider a large population, half male and half female. Suppose they are assigned to work in two very large firms. A random assignment process would produce an outcome close to a 50 : 50 male–female split in each firm and an estimated D of about zero. However, if they were allocated to many firms of size 2, then a random assignment procedure would lead to many all‐female firms, many all‐male firms and many mixed firms, and a high value for D. The high value reflects a strong deviation from evenness despite pure randomness. Others have noted the problem of small unit size in the measurement of segregation; see, e.g. Carrington and Troske (1997). They proposed an adjustment to segregation indices that has since been used by researchers measuring workplace segregation where small units are particularly likely (e.g. Hellerstein and Neumark, 2008) and measuring school segregation (e.g. Söderström and Uusitalo, 2010).

In comparing segregation across areas or time, small unit bias should be of concern to researchers for two reasons. First, the size of the bias will differ across comparison areas, potentially leading to an incorrect ranking of levels of segregation across areas. Second, the presence of small unit bias makes a correlation between measured segregation index values and a potentially causal variable, say X, difficult to interpret. It will impact on the estimated effect of X on measured segregation, even if the parameters of the problem (unit size, minority fraction and population) do not vary across areas. In addition, it is likely that the bias as a function of these parameters will be correlated with X, making the true relationship between X and D difficult to identify.

The variable X could, for example, be income differentials. If one were to investigate racial segregation in schools in an area, then one explanation of racial segregation, as indicated by a high value of D, could be income inequality between the two groups. Income inequality could be the cause of neighbourhood and hence school segregation. If there is no income inequality between the two groups in the area, then this could be indicative of behaviour due to other preferences.

In this paper, we propose an inferential framework for the canonical segregation measure, D, based on an underlying statistical model. This set‐up is related to, but different from, that used by Ransom (2000). He derives (asymptotic) inference procedures for D by specifying the sampling variation of a multinomial distribution. In Section 2., we specify the assignment problem in a very general way, and set out the difference in assignment probabilities that underlies the resulting segregation. From this, we derive bias adjustments to D in Section 3., and a likelihood ratio test for the presence of any systematic segregation in Section 4.. One of our bias adjustments is based on a simple bootstrap bias correction; other adjustments use the asymptotic normal distribution of the observed frequencies. Following Ransom (2000), in Sections 5. and 6., we further develop the asymptotic distribution theory for testing hypotheses concerning the magnitude of the segregation index and we show that use of bootstrap methods can improve the size and power properties of test procedures considerably. As in Ransom (2000), our asymptotic distribution theory relies on the number of units being fixed, with unit sizes going to infinity. Our results indicate that our methods work well in settings such as our analysis of social segregation in English schools, where the average number of units (schools) in the local authorities are about 55, with the average number of pupils per school equal to 38.

Rathelot (2012) recently proposed a Beta‐Binomial mixture model to describe segregation and has shown that it performs well in a setting with many small units (i.e. under asymptotics where the number of units goes to infinity); see also d'Haultfœuille and Rathelot (2011). In Section 7., we present a brief discussion of the measure proposed by Rathelot (2012) and also the one proposed by Carrington and Troske (1997). In Section 8., we illustrate our methods in an example of social segregation in schools in England. We conclude in Section 9..

2. STATISTICAL FRAMEWORK

Underlying an assignment of individuals to units is an allocation process. This might be purely random, or it may be influenced by the actions of agents, including those whose allocation we are studying, as well as others. This systematic allocation process will, in general, reflect the preferences and constraints of both the individual (such as preferences for racial composition of neighbourhood or ability to pay for houses in a particular neighbourhood) and of the unit to match with particular individuals (such as a firm's desire for highly educated workers or school admissions procedures that favour children of parents of a particular religious denomination). Typically, the research question is about characterizing segregation arising from this behaviour.

Our notation is as follows. There are units $j=1,...,J$, nested within an area. Individuals $i=1,...,n$ either have or do not have a characteristic measurable on a dichotomous scale, $c=\{0,1\}$. This could be black ethnicity, female sex or poverty status. The number of individuals in the area of status c is denoted $n^c$. Individuals are assigned to units and we observe the resulting allocations, $n_j^c$ individuals in unit j having status c. The total number of individuals in unit j is $n_j=n_j^1+n_j^0$.

There are many indices used to measure segregation; see Duncan and Duncan (1955), Massey and Denton (1988), and White (1986) for an overview. The formula for each provides an implicit definition of segregation. Massey and Denton (1988) characterize segregation along five dimensions: evenness (dissimilarity), exposure (isolation), concentration (the amount of physical space occupied by the minority group), clustering (the extent to which minority neighbourhoods abut one another) and centralization (proximity to the centre of the city). Throughout this paper, we use the index of dissimilarity (denoted D), the most popular unevenness index in the literature. However, our analysis can be extended to other unevenness segregation indices.

The formula for the index of dissimilarity D in the area, which is bounded by 0 (no segregation) and 1, is given by Duncan and Duncan (1955) as¹

$$D=\frac{1}{2}\sum _{j=1}^J\left|\frac{n_j^1}{n^1}-\frac{n_j^0}{n^0}\right|.$$ (2.1)

The basis for an allocation procedure is a set of probabilities $p_j^c$, which specify the probability that an individual is assigned to unit j, $j=1,...,J$, conditional on the individual being of status c. We define systematic segregation as being present when there exists j such that $p_j^1\ne p_j^0$. We can see the relationship between D and the probabilities of the underlying allocation process by noting that the fractions $n_j^c/n^c$, $c=0,1$, are estimates of these probabilities. With ${\widehat{p}}_j^c=n_j^c/n^c$, the index of dissimilarity (2.1) is just one half of ${\sum }_{j=1}^J|{\widehat{p}}_j^1-{\widehat{p}}_j^0|$.

Formally, the allocation process is as follows. An area population of n individuals, with a given proportion $p=n^1/n$ with status $c=1$, is allocated to J units, according to the probabilities $p_j^c$. Each individual is allocated independently of the others. All implicit dependences of group formations are captured by the allocation probabilities $p_j^c$. The outcomes of this process are the allocations $n_j^1$ and $n_j^0$. Clearly, unit sizes are not fixed in this set‐up as they are equal to $n_j=n_j^1+n_j^0$ and are therefore determined by the stochastic allocation. The expected unit sizes are given by $E\left[n_j\right]=n^1{p}_j^1+n^0{p}_j^0$.

We can now interpret the index of dissimilarity as an estimator for the population quantity:

$$D_{\mathrm{pop}}=\frac{1}{2}\sum _{j=1}^J\left|p_j^1-p_j^0\right|.$$

It is clear that $D_{\mathrm{pop}}=0$ if and only if $p_j^1=p_j^0$ for all $j=1,...,J$.

From the allocation process described above, we can estimate the conditional probabilities by maximum likelihood. As the allocations are two independent multinomial distributions, the log‐likelihood function, given the observed allocations, is given by

$$logL=log\left(\frac{n^1!}{n_1^1!...n_J^1!}\right)+log\left(\frac{n^0!}{n_1^0!...n_J^0!}\right)+\sum _{j=1}^J{n}_j^{1}log{p}_j^1+\sum _{j=1}^J{n}_j^{0}log{p}_j^0.$$ (2.2)

Clearly, the maximum likelihood estimates are given by ${\widehat{p}}_j^1=n_j^1/n^1$ and ${\widehat{p}}_j^0=n_j^0/n^0$, $j=1,...,J$, exactly the same as the estimates that appear in D.

Ransom (2000) proposed the following statistical model for a random sample of size n:

$$Pr(n_1^0,n_2^0,...,n_J^0,n_1^1,n_2^1,...,n_J^1;{\pi }_{jc})=n!\prod _{j=1}^J\prod _{c=0}^1\frac{{\left({\pi }_{jc}\right)}^{n_j^c}}{n_j^c!},$$

where ${\pi }_{jc}$ is the joint probability of observing an individual with status c and in unit j in the sample. Mora and Ruiz‐Castillo (2007), and references therein, consider a similar set‐up for an information index of multigroup segregation. Ransom (2000, p. 458) notes that this model is not appropriate when the population is observed, because then ${\pi }_{jc}$ are known. The parameters ${\pi }_{jc}$ are not those that enter the segregation index D _pop, which are the conditional probabilities $p_j^c=Pr(\mathrm{unit}=j|c)={\pi }_{jc}/{\sum }_{s=1}^J{\pi }_{sc}$.

Our model is applicable even when we observe the complete, finite population, because randomness is achieved by the random allocation process to units. Our statistical model is for a finite population of fixed size $n=n^0+n^1$, with parameters $p_j^c$, $j=1,...,J$, $c=0,1$, and is given by

$$Pr(n_1^0,n_2^0,...,n_J^0,n_1^1,n_2^1,...,n_J^1;n^0,n^1;p_j^c)=\prod _{c=0}^1{n}^c!\prod _{j=1}^J\frac{{\left(p_j^c\right)}^{n_j^c}}{n_j^c!}.$$

The logarithm of this expression is just the log‐likelihood (2.2). In the remainder of the paper, we focus on this particular model.

Our design is particularly well suited for our analysis of social segregation in schools in England. The provision of education in England is organized at the district, or local authority (LA), level. Pupils within an LA have to choose a school within that district with certain limitations due, for example, to catchment area requirements. School (cohort) sizes vary substantially within an LA and school cohort sizes vary over time owing to changing demand and size of the cohort population.

A different model would apply if the unit sizes $n_j$ are assumed fixed, as well as the population size n and minority fraction $p=n^1/n$. In this case, the allocation mechanism is determined by the probability that an individual has status c conditional on being in unit j instead of the other way round. However, no matter whether unit sizes are random or fixed, D is still an estimator of D _pop if, instead of the full population, we obtain a random sample drawn from it.

2.1. Bias

As D is an estimator of D _pop, we define the bias of D as $E\left[D\right]-D_{\mathrm{pop}}$, where the expectation is taken over the independent multinomial distributions with probabilities $p_j^c$, $j=1,...,J$, $c=0,1$. For given population size n and minority proportion p, we have

$$E\left[D\right]=\frac{1}{2}\sum _{\{n_1^0,\cdots ,n_J^0\}}\sum _{\{n_1^1,\cdots ,n_J^1\}}\left[\left(\sum _{j=1}^J\left|\frac{n_j^1}{n^1}-\frac{n_j^0}{n^0}\right|\right)\prod _{c=0}^1{n}^c!\prod _{j=1}^J\frac{{\left(p_j^c\right)}^{n_j^c}}{n_j^c!}\right].$$

The value of $E\left[D\right]$ is a function of the underlying conditional probabilities, summarized by D _pop, and of unevenness generated by the randomness of the allocation process. As has been well documented in the literature, see for instance Carrington and Troske (1997), D can be severely upward biased when unit sizes are small and there is no systematic segregation, that is, $p_j^1=p_j^0$ for all j and $D_{\mathrm{pop}}=0$. Intuitively, this bias arises because D is the sum of the absolute value of differences between the minority and majority proportions in a unit. Suppose that in unit j, $p_j^1=p_j^0$. Sampling variation in the estimated proportions will almost surely lead to non‐zero estimated differences, especially if unit sizes are small. Because the dissimilarity index sums the absolute values of these differences, this will lead to an upward bias in the index.

For a small number of units J and small unit sizes, we can calculate the expected value of D analytically. Figure 1 graphs the bias $E\left[D\right]-D_{\mathrm{pop}}$ for $J=4$, $n=\{20,40,60\}$, $p=0.1$, and for various values of D _pop. These values of D _pop are obtained by setting $p_j^c$ according to a scheme discussed in Section 3.. The expected unit sizes are the same for the four units (i.e. 5 when $n=20$, 10 when $n=40$ and 15 when $n=60$). The small‐unit bias is apparent in the figure. When expected unit sizes are equal to 5, $E\left[D\right]$ is equal to 0.56 when $D_{\mathrm{pop}}=0$. The graph also shows that the bias is a decreasing function of increasing systematic segregation (D _pop) and a decreasing function of expected unit size.

Figure 1.

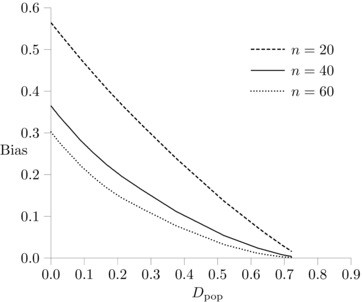
Bias $E\left[D\right]-D_{\mathrm{pop}}$, $J=4$, $p=0.1$, equal expected unit sizes.

3. BIAS CORRECTION

The purpose of a bias correction to D is to reduce the upward bias of the estimate of D _pop, as highlighted in Figure 1. We first consider a bootstrap bias correction, as described by Hall (1992) and Davison and Hinkley (1997) among many others. Given an observed allocation, a new sample is generated with the same sample size n and minority proportion p, but using the observed conditional probabilities ${\widehat{p}}_j^1=n_j^1/n^1$ and ${\widehat{p}}_j^0=n_j^0/n^0$ for the allocation process. Note that none of the bootstrap data‐generating processes used in this paper involves resampling. The value for D in this bootstrap sample is denoted $D_b$. Repeating this B times, we can calculate

$${\overline{D}}_b=\frac{1}{B}\sum _{b=1}^B{D}_b.$$ (3.1)

The population value of the segregation measure in the bootstrap sample is D itself, and so a measure of the bias of D is given by ${\overline{D}}_b-D$. A bootstrap bias‐corrected estimate of D _pop is then obtained as

$$D_{\mathrm{bc}}=D-({\overline{D}}_b-D)=2D-{\overline{D}}_b.$$ (3.2)

This type of bias correction works well if the bias is constant for different values of D _pop. This is clearly not the case here, because the biases as displayed in Figure 1 are much larger for smaller values of D. This bias correction is therefore not expected to work well for small unit sizes combined with small values of D _pop.

What turns out to be a more effective way of reducing the bias is a modified maximum‐likelihood approach. As $n^c\to \infty$ with J fixed, ${\widehat{p}}_j^c\to p_j^c$ almost surely, and the limiting distribution of $\sqrt{n^c}({\widehat{p}}_j^c-p_j^c)$ is normal with expectation 0 and variance $p_j^c(1-p_j^c)$. It follows that D is consistent for D _pop, and that it is asymptotically normal with an asymptotic variance that can be computed using the delta method, as pursued in Section 5.. For bias reduction, rather than working with the full log‐likelihood (2.2), we proceed as though ${\widehat{p}}_j^c$, $c=1,2$, $j=1,...,J$ were actually distributed according to their asymptotic normal distribution.

However, the asymptotic normality of D is not of the usual kind where the limiting distribution of $\sqrt{n}(D-D_{\mathrm{pop}})$ would be normal with expectation zero. We have seen that $D={\sum }_{j=1}^J|{\widehat{p}}_j^1-{\widehat{p}}_j^0|/2$. The fact that D depends on the absolute values of the differences means that the expectation of the limiting distribution is not zero whenever the true value of D _pop is either zero or is such that $D_{\mathrm{pop}}=O\left(n^{-1/2}\right)$ as $n\to \infty$. This implies that asymptotic inference of the usual sort is not valid, because the non‐zero expectation acts like a non‐centrality parameter. However, we can still use the asymptotic normal distribution of ${\widehat{p}}_j^c$ as an approximation in computing the asymptotic bias. The finite‐sample bias is given by

$$E\left[D\right]-D_{\mathrm{pop}}=\frac{1}{2}\sum _{j=1}^J\left(E|{\widehat{p}}_j^1-{\widehat{p}}_j^0|-|p_j^1-p_j^0|\right),$$

where, in each term of the sum, the random variables ${\widehat{p}}_j^1$ and ${\widehat{p}}_j^0$ are independent.

Let $X\sim N(\mu ,{\sigma }^2)$. The distribution of $Z=\left|X\right|/\sigma$ is the so‐called folded normal distribution; see Leone et al. (1961). Let θ denote $\left|\mu \right|/\sigma$. Then, the density of Z is given by

$$f\left(z\right)=\phi (z-\theta )+\phi (z+\theta ).$$ (3.3)

Here, ϕ is the standard normal density. In order to derive the bias of D, we replace Z by ${\widehat{\theta }}_j=|{\widehat{p}}_j^1-{\widehat{p}}_j^0|/{\widehat{\sigma }}_j$, where ${\widehat{p}}_j^1-{\widehat{p}}_j^0\sim N(p_j^1-p_j^0,{\sigma }_j^2)$ approximately, with

$${\sigma }_j^2=p_j^1(1-p_j^1)/n^1+p_j^0(1-p_j^0)/n^0\text{and}{\widehat{\sigma }}_j^2={\widehat{p}}_j^1(1-{\widehat{p}}_j^1)/n^1+{\widehat{p}}_j^0(1-{\widehat{p}}_j^0)/n^0.$$

The asymptotic approximation to the density of ${\widehat{\theta }}_j$ is then $\phi ({\widehat{\theta }}_j-{\theta }_j)+\phi ({\widehat{\theta }}_j+{\theta }_j)$, where ${\theta }_j=|p_j^1-p^0|/{\sigma }_j$, the ‘true’ value of θ. Thus, asymptotically, the data‐dependent quantity ${\widehat{\theta }}_j$ is sufficient for ${\theta }_j$, and so an approximate maximum‐likelihood estimate of ${\theta }_j$ is the value of ${\theta }_j$ that maximizes the approximate density.

It can be shown that, for ${\widehat{\theta }}_j\le 1$, the maximum occurs at ${\theta }_j=0$, and that the maximizing ${\theta }_j$ tends to ${\widehat{\theta }}_j$ as ${\widehat{\theta }}_j\to \infty$. Let the maximizing ${\theta }_j$ be denoted by $n\left({\widehat{\theta }}_j\right)$. The cut‐off imposed by the function n is at ${\widehat{\theta }}_j=1$. Because $|{\widehat{p}}_j^1-{\widehat{p}}_j^0|={\widehat{\sigma }}_j{\widehat{\theta }}_j$, we can define another estimator of D _pop,

$$D_{\mathrm{dc}}=\frac{1}{2}\sum _{j=1}^J{\widehat{\sigma }}_{j}n\left({\widehat{\theta }}_j\right),$$ (3.4)

where the notation ‘dc’ stands for density‐corrected.

We show in the next sections that the proposed bias‐correction procedures reduce enough of the bias to make reasonable inferences about levels of segregation, provided unit sizes are not too small. Where unit sizes are very small, we show in Section 4. that the observed level of segregation can rarely statistically be distinguished from evenness. Thus, we suggest that in these cases the data are inappropriate for making inferences about segregation.

In the Appendix, we consider two other plausible methods of bias reduction, but simulations (not presented here) show that they are less effective than the density‐correction method.

3.1. Monte Carlo simulations

In this section, we evaluate the performance of the bias adjustments for estimating levels of segregation. To do this, we follow the Duncan and Duncan (1955) approach of generating a level of unevenness between no segregation and complete segregation using a single parameter, $0\le q<1$. This parameter maps to a set of parabolic segregation curves via the formula:²

$$Pr(\mathrm{unit}\le j|c=1)=\frac{(1-q)Pr(\mathrm{unit}\le j|c=0)}{1-q·Pr(\mathrm{unit}\le j|c=0)}.$$

This formula, combined with the constraint of equal expected unit sizes, fixes the conditional allocation probabilities for both groups. An allocation is then generated by assigning n ¹ and n ⁰ individuals to the J units using these calculated conditional probabilities.

This process is repeated 5,000 times for each n, p and D _pop combinations over the following parameter space:

• 1.number of units, J, is fixed at 50;
• 2.unit sizes $n_j$ are equal in expectation, with expected unit size 10, 30 or 50;
• 3.proportion of $c=1$ individuals, p, equal to 0.05, 0.2 or 0.35;
• 4.systematic segregation generator, q, varies such that the values of D _pop are equal to 0, 0.056, 0.127, 0.225, 0.382 or 0.634.

For the bootstrap bias correction, ${\overline{D}}_b$ is calculated from (3.1) using 250 bootstrap samples. Tables 1(a), 1(b), 1(c) present the bias and root mean squared error (rmse) of D and D _bc from (3.2), and D _dc from (3.4). The tables show that, where the minority proportion is very small, $p=0.05$, unit sizes are small (e.g. $E\left[n_j\right]=10$) and systematic segregation is very low (e.g. $D_{\mathrm{pop}}=0.056$), observed segregation incorrectly suggests that a highly segregating process underlies the allocation, with $D=0.606$. The bias corrections, although reducing the bias, cannot fully get rid of it, the smallest bias being obtained with the density‐corrected estimator, $D_{\mathrm{dc}}=0.406$. At the other extreme, where the minority proportion is large (e.g. $p=0.35$), unit sizes are large (e.g. $n=50$) and systematic segregation is high (e.g. $D_{\mathrm{pop}}=0.634$), no correction is needed, because the mean value of observed segregation is only slightly different from D _pop. However, in much social science data, the phenomenon of interest tends to have moderate (D _pop around 0.1–0.4) rather than very high levels of segregation. In this range, the bias corrections tend to work well and are necessary, provided that p and $E\left[n_j\right]$ are not both simultaneously very small. For example, when the minority proportion is 10% and unit sizes are expected to be 30, if underlying segregation is 0.225, the observed index of segregation would be upward biased by 0.093, whereas the density‐corrected estimator would successfully reduce this bias to just 0.005.

Table 1(a).

Bias and rmse of D and bias‐corrected estimators for $J=50$, $E\left[n_j\right]=10$ and combinations of p and D _pop

	D pop
	0		0.056		0.127		0.225		0.382		0.634
$E\left[n_j\right]=10$	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse
$p=0.05$
D	0.60	0.61	0.55	0.55	0.48	0.49	0.40	0.40	0.29	0.29	0.15	0.15
D bc	0.48	0.49	0.43	0.43	0.37	0.37	0.29	0.30	0.20	0.20	0.097	0.11
D dc	0.40	0.41	0.35	0.35	0.29	0.29	0.21	0.22	0.13	0.14	0.058	0.086
$p=0.10$
D	0.41	0.42	0.36	0.36	0.30	0.30	0.23	0.24	0.15	0.16	0.071	0.084
D bc	0.26	0.27	0.21	0.22	0.15	0.17	0.097	0.12	0.043	0.077	0.009	0.058
D dc	0.26	0.27	0.21	0.22	0.15	0.16	0.094	0.11	0.040	0.072	0.011	0.056
$p=0.20$
D	0.31	0.31	0.26	0.26	0.20	0.21	0.15	0.15	0.089	0.097	0.039	0.053
D bc	0.19	0.20	0.14	0.15	0.090	0.11	0.046	0.067	0.011	0.051	−0.002	0.044
D dc	0.17	0.18	0.12	0.13	0.070	0.082	0.024	0.052	−0.009	0.050	−0.015	0.047
$p=0.35$
D	0.26	0.26	0.21	0.21	0.16	0.16	0.11	0.11	0.063	0.072	0.026	0.042
D bc	0.16	0.16	0.11	0.12	0.063	0.074	0.027	0.050	0.004	0.043	−0.002	0.038
D dc	0.15	0.15	0.095	0.10	0.048	0.060	0.009	0.041	−0.013	0.045	−0.012	0.040

Bias and rmse reported for 5,000 replications. Number of bootstrap repetitions 250.

Table 1(b).

Bias and rmse of D and bias‐corrected estimators for $J=50$, $E\left[n_j\right]=30$ and combinations of p and D _pop

	D pop
	0		0.056		0.127		0.225		0.382		0.634
$E\left[n_j\right]=30$	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse
$p=0.05$
D	0.33	0.34	0.28	0.28	0.22	0.23	0.16	0.17	0.099	0.11	0.044	0.057
D bc	0.21	0.21	0.16	0.16	0.10	0.11	0.055	0.074	0.015	0.054	−0.003	0.046
D dc	0.18	0.18	0.13	0.13	0.072	0.084	0.024	0.054	−0.009	0.053	−0.015	0.049
$p=0.10$
D	0.24	0.24	0.19	0.19	0.14	0.14	0.093	0.098	0.052	0.061	0.022	0.036
D bc	0.14	0.15	0.095	0.10	0.051	0.063	0.019	0.043	0.000	0.040	−0.003	0.034
D dc	0.13	0.14	0.084	0.089	0.038	0.051	0.005	0.038	−0.010	0.041	−0.008	0.035
$p=0.20$
D	0.18	0.18	0.13	0.13	0.088	0.090	0.054	0.059	0.029	0.039	0.012	0.026
D bc	0.11	0.11	0.060	0.065	0.024	0.038	0.005	0.031	−0.001	0.031	−0.001	0.025
D dc	0.099	0.10	0.051	0.056	0.014	0.030	−0.006	0.031	−0.008	0.032	−0.004	0.026
$p=0.35$
D	0.15	0.15	0.10	0.11	0.065	0.068	0.038	0.044	0.020	0.030	0.008	0.021
D bc	0.090	0.092	0.045	0.050	0.014	0.029	0.002	0.027	−0.001	0.026	−0.000	0.021
D dc	0.083	0.086	0.038	0.043	0.005	0.024	−0.007	0.027	−0.006	0.027	−0.003	0.021

Bias and rmse reported for 5,000 replications. Number of bootstrap repetitions 250.

Table 1(c).

Bias and rmse of D and bias‐corrected estimators for $J=50$, $E\left[n_j\right]=50$ and combinations of p and D _pop

	D pop
	0		0.056		0.127		0.225		0.382		0.634
$E\left[n_j\right]=50$	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse
$p=0.05$
D	0.26	0.26	0.21	0.21	0.15	0.16	0.11	0.11	0.060	0.069	0.026	0.040
D bc	0.15	0.16	0.11	0.11	0.061	0.072	0.024	0.048	0.003	0.042	−0.003	0.035
D dc	0.15	0.15	0.098	0.10	0.052	0.063	0.016	0.042	−0.003	0.041	−0.005	0.035
$p=0.10$
D	0.19	0.19	0.14	0.14	0.093	0.096	0.058	0.063	0.031	0.041	0.013	0.027
D bc	0.11	0.11	0.064	0.070	0.027	0.040	0.007	0.032	−0.001	0.031	−0.001	0.026
D dc	0.10	0.11	0.056	0.061	0.017	0.032	−0.003	0.031	−0.007	0.032	−0.004	0.027
$p=0.20$
D	0.14	0.14	0.093	0.094	0.057	0.060	0.033	0.038	0.017	0.027	0.008	0.020
D bc	0.082	0.085	0.039	0.044	0.011	0.026	0.001	0.024	−0.001	0.023	0.000	0.020
D dc	0.076	0.078	0.032	0.037	0.003	0.023	−0.006	0.025	−0.005	0.024	−0.002	0.020
$p=0.35$
D	0.12	0.12	0.072	0.073	0.041	0.044	0.023	0.029	0.012	0.022	0.005	0.016
D bc	0.069	0.071	0.027	0.032	0.005	0.021	−0.000	0.020	−0.000	0.020	−0.000	0.017
D dc	0.064	0.066	0.021	0.027	−0.002	0.020	−0.006	0.022	−0.003	0.020	−0.001	0.017

Bias and rmse reported for 5,000 replications. Number of bootstrap repetitions 250.

The bias‐corrected estimator D _bc is dominated in both bias and rmse by the density‐corrected estimator D _dc in almost all experiments, except for the cases of high D _pop values and larger minority proportions, in which the bias and rmse of both corrected estimates are small.

4. TESTS OF NO SYSTEMATIC SEGREGATION

To complement the bias‐corrected estimators of D, we provide a test for no systematic segregation. We consider two alternative methods to test whether we can reject the hypothesis that the level of segregation observed was generated by randomness alone, $D_{\mathrm{pop}}=0$. It is common in the literature to run a randomization procedure to generate the distribution of D under the null of no systematic segregation – see, e.g., Boisso et al. (1994) – and D is compared to this distribution. Here, we generate the distribution of D under the null of no systematic segregation by creating B samples generated using the restricted conditional probabilities ${\widehat{p}}_j^0={\widehat{p}}_j^1={\widehat{p}}_j=(n_j^0+n_j^1)/n$ and calculating D in each sample, which we denote $D^{*}$. The null hypothesis $H_0:D_{\mathrm{pop}}=0$ is then rejected at level α if $1/B{\sum }_{b=1}^B\mathrm{I}(D_b^{*}>D)<\alpha$, where I(.) is the indicator function.

Alternatively, following the statistical model developed in Section 2., we can employ a likelihood ratio test for the hypothesis

$$H_0:p_j^0=p_j^1=p_j\forall j,$$

with test statistic

$$\mathit{LR}=2\sum _{j=1}^J\left(n_j^{0}log{\widehat{p}}_j^0+n_j^{1}log{\widehat{p}}_j^1-n_{j}log{\widehat{p}}_j\right),$$

which follows an asymptotic ${\chi }_{J-1}^2$ distribution. This asymptotic distribution is for large n and fixed J, and therefore for large unit sizes. For large J and/or small unit sizes, the asymptotic approximation can be expected to be poor, as we originally found in our simulation results discussed below. Therefore, we also utilize a bootstrap procedure to improve the size properties of the test. Let $L{R}^{*}$ be the value of the likelihood ratio test in a sample generated from ${\widehat{p}}_j^0={\widehat{p}}_j^1={\widehat{p}}_j=(n_j^0+n_j^1)/n$. Then the null hypothesis of no systematic segregation is rejected at level α if $1/B{\sum }_{b=1}^B\mathrm{I}(L{R}_b^{*}>LR)<\alpha$.

Table 2 presents the test results for $J=50$ and $E\left[n_j\right]=10$ and $E\left[n_j\right]=30$, for various values of D _pop and minority proportions p. The number of Monte Carlo replications was 10,000 with 599 bootstrap samples. The size and power properties of the two tests are virtually identical. They have good size properties for all minority proportions p, with overall $LR$ dominating the randomization test. The tests fail to reject the null for small values of D _pop combined with small minority proportions p, exactly the circumstances in which the bias corrections do not remove much of the bias of D. Clearly, any calculation of D and the bias‐corrected estimators should be accompanied by $D^{*}$ and/or bootstrapped $LR$ tests. If these tests fail to reject, no further inference should be pursued.

Table 2.

Rejection frequencies of D randomization and likelihood ratio tests, for $J=50$, level $\alpha =0.05$

		D pop
p	Test	0	0.056	0.127	0.225	0.382	0.634
$E\left[n_j\right]=10$
0.05	$D^{*}$	0.096	0.104	0.131	0.237	0.619	0.998
	$LR$	0.066	0.074	0.098	0.194	0.594	0.999
0.10	$D^{*}$	0.056	0.069	0.112	0.307	0.878	1.000
	$LR$	0.069	0.083	0.132	0.362	0.919	1.000
0.20	$D^{*}$	0.067	0.086	0.192	0.618	0.999	1.000
	$LR$	0.062	0.080	0.183	0.606	0.998	1.000
0.35	$D^{*}$	0.065	0.090	0.269	0.827	1.000	1.000
	$LR$	0.053	0.077	0.232	0.791	1.000	1.000
$E\left[n_j\right]=30$
0.05	$D^{*}$	0.060	0.071	0.165	0.534	0.992	1.000
	$LR$	0.051	0.067	0.160	0.546	0.995	1.000
0.10	$D^{*}$	0.056	0.086	0.285	0.882	1.000	1.000
	$LR$	0.054	0.080	0.275	0.877	1.000	1.000
0.20	$D^{*}$	0.057	0.117	0.553	0.997	1.000	1.000
	$LR$	0.050	0.108	0.537	0.997	1.000	1.000
0.35	$D^{*}$	0.055	0.147	0.775	1.000	1.000	1.000
	$LR$	0.050	0.138	0.777	1.000	1.000	1.000

Rejection frequencies reported for 10,000 replications. Number of bootstrap repetitions 599.

5. INFERENCE ON D

Having established that the bias corrections work well for a large part of the parameter space, we next develop reliable inference procedures such as 95% confidence intervals and Wald test statistics for equivalence of segregation in different areas. Inference based on a bias‐corrected estimator is, of course, expected to work well only in that part of the parameter space where the bias corrections work well (i.e. where the tests of no systematic segregation reject the null strongly, as indicated in Table 2). We start by deriving the asymptotic distribution of D given our statistical framework, following the procedures as developed in Ransom (2000).

Under the data‐generating process as described in Section 2., for $0<p_j^c<1$, with $c=0,1$; $j=1,...,J$; ${\sum }_j{p}_j^c=1$, the estimated conditional probabilities ${\widehat{p}}_j^c$, are asymptotically normally distributed, as

$$\sqrt{n^c}\left[\begin{array}{c}{p}_1^c-p_1^c\\ p_2^c-p_2^c\\ ⋮\\ p_J^c-p_J^c\end{array}\right]=N\left(\mathbf{0},\left[\begin{array}{cccc}\hfill p_1^c(1-p_1^c)& \hfill -p_1^c{p}_2^c& \hfill ...& -p_1^c{p}_J^c\\ \hfill -p_1^c{p}_2^c& \hfill p_2^c(1-p_2^c)& \hfill ...& -p_2^c{p}_J^c\\ \hfill ⋮& \hfill ⋮& \hfill \ddots & ⋮\\ \hfill -p_1^c{p}_J^c& \hfill -p_2^c{p}_J^c& \hfill ...& p_J^c(1-p_J^c)\end{array}\right]\right)\equiv N(\mathbf{0},{\mathit{\Omega }}^c).$$

As $n^1=pn$ and $n^0=(1-p)n$, the limiting distribution of D can then be obtained via the delta method:

$$\sqrt{n}(D-D_{\mathrm{pop}})\stackrel{d}{\to }N\left(0,{\lambda }^{\top }(p^{-1}{\mathit{\Omega }}^1+{(1-p)}^{-1}{\mathit{\Omega }}^0)\lambda \right),$$

where $\lambda$ is a J‐vector with rth element ${\lambda }_r=\mathrm{sign}(p_r^1-p_r^0)/2$, where p sign$\left(q\right)=1$ if $q>0$ and $\mathrm{sign}\left(q\right)=-1$ if $q<0$.³ This follows from

$$\frac{\partial D_{\mathrm{pop}}}{\partial p_r^1}=\frac{\partial }{\partial p_r^1}\frac{1}{2}\sum _{j=1}^J|p_j^1-p_j^0|=\mathrm{sign}(p_r^1-p_r^0)/2,$$ (5.1)

and

$$\frac{\partial D_{\mathrm{pop}}}{\partial p_r^0}=\frac{\partial }{\partial p_r^0}\frac{1}{2}\sum _{j=1}^J|p_j^1-p_j^0|=-\mathrm{sign}(p_r^1-p_r^0)/2.$$ (5.2)

Clearly, this derivation is valid only when $|p_r^1-p_r^0|$ is not in a root‐n neighbourhood of zero, as discussed in Section 3.. The asymptotic distribution of D is then approximated by

$$D\stackrel{a}{\sim }N\left(D_{\mathrm{pop}},n^{-1}{\lambda }^{\top }(p^{-1}{\mathit{\Omega }}^1+{(1-p)}^{-1}{\mathit{\Omega }}^0)\lambda \right),$$

or, equivalently,

$$D\stackrel{a}{\sim }N\left(D_{\mathrm{pop}},{\lambda }^{\top }({\mathit{\Omega }}^1/n^1+{\mathit{\Omega }}^0/n^0)\lambda \right),$$

which can form the basis for constructing confidence intervals and Wald test statistics for hypotheses of the form $H_0:D_{\mathrm{pop}}=\delta$. If we denote by $\widehat{\lambda }$ and ${\widehat{\mathit{\Omega }}}^c$ the estimated counterparts of $\lambda$ and ${\mathit{\Omega }}^c$, and substitute the observed fractions ${\widehat{p}}_j^c$ for $p_j^c$, the Wald test is then computed as

$$W=\frac{{(D-\delta )}^2}{{\widehat{\lambda }}^{\top }({\widehat{\mathit{\Omega }}}^1/n^1+{\widehat{\mathit{\Omega }}}^0/n^0)\widehat{\lambda }},$$ (5.3)

and converges in distribution to the ${\chi }_1^2$ distribution under the null.

Clearly, we do not expect this approximation to work well when δ, group sizes and/or minority proportions are small, if only on account of the upward bias of D as established in the previous sections. However, the Wald test statistic W is asymptotically pivotal in the sense that its limiting distribution is not a function of nuisance parameters. We can therefore use bootstrap P‐values, which may result in an improvement in the finite‐sample behaviour of the test; see, e.g., Hall (1992), Davison and Hinkley (1997), Davidson and MacKinnon (2000), and Davidson (2009). If we denote the Wald statistic in the bth bootstrap sample as $W_b$, calculated as

$$W_b=\frac{{(D_b-D)}^2}{{\widehat{\lambda }}_b^{\top }({\widehat{\mathit{\Omega }}}_b^1/n^1+{\widehat{\mathit{\Omega }}}_b^0/n^0){\widehat{\lambda }}_b},$$ (5.4)

then the bootstrap P‐value is given by $1/B{\sum }_{b=1}^B\mathrm{I}(W_b>W)$. This bootstrap procedure is equivalent to a symmetric two‐tailed test for the t‐statistic.

Let τ denote the t‐statistic that is the signed square root of the Wald statistic (5.3). Let ${\tau }_b$ denote the signed square root of (5.4). Then, a test that does not assume symmetry can be based on the equal‐tail bootstrap P‐value

$$2min\left[\frac{1}{B}\sum _{b=1}^B\mathrm{I}({\tau }_b<\tau ),\frac{1}{B}\sum _{b=1}^B\mathrm{I}({\tau }_b>\tau )\right].$$

Alternatively, we can base the inference directly on any of the bias‐corrected estimators of D _pop. In order to estimate the variance of the bias‐corrected estimators, we again perform a bootstrap procedure. For example, denoting the bootstrap estimate of the variance of D _dc by ${\widehat{\mathrm{Var}}}_b\left(D_{\mathrm{dc}}\right)$, the Wald test based on D _dc is then calculated as

$$W_{\mathrm{dc}}=\frac{{(D_{\mathrm{dc}}-\delta )}^2}{{\widehat{\mathrm{Var}}}_b\left(D_{\mathrm{dc}}\right)},$$

and this is again compared to the ${\chi }_1^2$ distribution.

Figure 2 shows P‐value plots for testing the true hypothesis $H_0:D_{\mathrm{pop}}=0.292$, for $E\left[n_j\right]=30$, $J=50$ and $p=0.3$. The Wald test that is based on the asymptotic normal distribution of D and uses ${\chi }_1^2$ critical values is denoted W, whereas the Wald test that uses the bootstrap critical values is denoted W _pb. The test based on the equal‐tail bootstrap P‐value for the t‐test is denoted T _pb. The Wald statistic that uses the density‐corrected estimator and its bootstrap variance estimate is denoted W _dc. The results shown are for 10,000 Monte Carlo replications. Note that 599 bootstrap samples per replication are drawn for the calculation of the variances and the bootstrap distribution of the Wald test.

Figure 2.

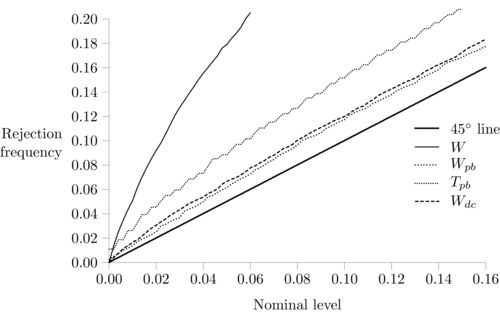
P‐value plot, $H_0:D_{\mathrm{pop}}=0.292$, $E\left[n_j\right]=30$, $J=50$, $p=0.30$.

The first column of numbers in Table 3 presents the bias and rmse for the various estimates. There is an 11% upward bias in D, but D _bc is unbiased. D _dc has a small downward bias of 2.8%. As is clear from Figure 2, the asymptotic Wald test based on W using the ${\chi }_1^2$ critical values does not have good size properties. It rejects the true null too often (e.g. at 5% nominal size, it rejects the null in 18.6% of the replications). In contrast, using the P‐values from the bootstrap distribution of the Wald statistic improves the size behaviour considerably. At the 5% level, the rejection frequency is now reduced to 6.9%. Using the equal‐tailed bootstrap P‐values for the t‐test also improves on the size performance of the asymptotic Wald statistic, but it performs less well than W _pb. W _dc has the same size properties as W _pb.

Table 3.

Bias and rmse of D and bias‐corrected estimators

	$D_{\mathrm{pop}}=0.292$		$D_{\mathrm{pop}}=0.292$		$D_{\mathrm{pop}}=0.382$
	$E\left[n_j\right]=30,p=0.30$		$E\left[n_j\right]=20,p=0.10$		$E\left[n_j\right]=30,p=0.30$
	bias	rmse	bias	rmse	bias	rmse
D	0.031	0.038	0.106	0.111	0.022	0.032
D bc	−0.000	0.027	0.020	0.051	−0.001	0.026
D dc	−0.008	0.029	−0.000	0.046	−0.007	0.028

$J=50$ in all designs. Results from 10,000 Monte Carlo replications.

Figure 3 shows the P‐value plot for a similar design, but now for smaller expected group sizes $E\left[n_j\right]=20$ and a smaller minority proportion, $p=0.10$. The bias of D in this case is 0.106, or 36%, that of D _bc is around 0.020, or 6.5%, while D _dc is unbiased.

Figure 3.

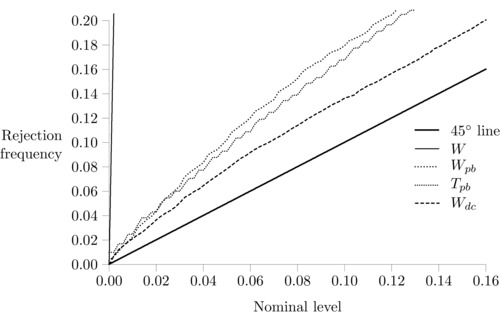
P‐value plot, $H_0:D_{\mathrm{pop}}=0.292$, $E\left[n_j\right]=20$, $J=50$, $p=0.10$.

The size distortions of the test statistics are now more severe. The asymptotic Wald test is severely size distorted, with a 68% rejection rate at the 5% level. The Wald and asymmetric t‐tests using the bootstrap P‐values behave much better, with T _pb behaving somewhat better. At the 5% level, the rejection frequencies for these tests are 10% and 9.0%, respectively. Here, W _dc has the best size performance of all tests; it rejects the true null 7.0% of the time at the 5% level and is the only test where the size properties remain the same as those seen in Figure 2.

There is a one‐to‐one correspondence between the P‐value plots as depicted in Figures 2 and 3 and the coverage properties of the confidence intervals associated with the particular test statistics. Using the normal approximation, $(1-\alpha )$% confidence intervals associated with the asymptotic Wald and W _bc tests are constructed as

$$D-z_{1-\alpha /2}\sqrt{\widehat{\mathrm{Var}}\left(D\right)}<D_{\mathrm{pop}}<D+z_{1-\alpha /2}\sqrt{\widehat{\mathrm{Var}}\left(D\right)}$$

and

$$D_{\mathrm{bc}}-z_{1-\alpha /2}\sqrt{{\widehat{\mathrm{Var}}}_b\left(D_{\mathrm{bc}}\right)}<D_{\mathrm{pop}}<D_{\mathrm{bc}}+z_{1-\alpha /2}\sqrt{{\widehat{\mathrm{Var}}}_b\left(D_{\mathrm{bc}}\right)}$$

respectively, where $z_{1-\alpha /2}$ is the $(1-\alpha /2)$ quantile of the standard normal distribution.

For the bootstrap Wald test, the associated confidence interval is given by

$$D-\sqrt{w_{1-\alpha }^{*}\widehat{\mathrm{Var}}\left(D\right)}<D_{\mathrm{pop}}<D+\sqrt{w_{1-\alpha }^{*}\widehat{\mathrm{Var}}\left(D\right)},$$

where $w_{1-\alpha }^{*}$ is the $1-\alpha$ quantile of the distribution of the bootstrap repetitions $W_b$. The equal‐tailed bootstrap t‐test has the corresponding confidence interval given by

$$D-{\tau }_{1-\alpha /2}^{*}\sqrt{\widehat{\mathrm{Var}}\left(D\right)}<D_{\mathrm{pop}}<D-{\tau }_{\alpha /2}^{*}\sqrt{\widehat{\mathrm{Var}}\left(D\right)},$$

where ${\tau }_{1-\alpha /2}^{*}$ and ${\tau }_{\alpha /2}^{*}$ are, respectively, the $1-\alpha /2$ and $\alpha /2$ quantiles of the distribution of the bootstrap repetitions ${\tau }_b$.

For the example with $E\left[n_j\right]=20$ and $p=0.10$ as described above, the observed rejection frequencies of 68%, 9.8%, 9.0% and 7.0% for the W, W _pb, T _pb and W _dc tests, respectively, translate into coverage probabilities of 32%, 90.2%, 91% and 93% of the associated 95% confidence intervals. Given the upward bias of D, this leads to an interesting observation concerning the confidence interval based on the bootstrap Wald test W _pb. As the size and associated coverage properties of this test are reasonably good, but as the confidence interval is symmetric around the upward biased D, this suggests that the Wpb‐based confidence interval will be quite large. Table 4 shows the averages of the lower and upper limits and lengths of the 95% confidence intervals associated with W _pb, T _pb, and W _dc respectively. This confirms that the W _pb‐based confidence interval is, on average, much wider than those based on W _dc and T _pb. Whereas the lower limit is quite similar to those of the other two confidence intervals, its upper limit is much higher, as expected owing to the symmetry around the upward biased D. Clearly, W _pb can therefore have poor power properties when D has substantial bias.

Table 4.

Average lower limit, upper limit and length of 95% confidence intervals

Test	Lower limit	Upper limit	Length
W pb	0.228	0.568	0.340
T pb	0.212	0.378	0.166
W dc	0.209	0.374	0.167

$D_{\mathrm{pop}}=0.292$, $E\left[n_j\right]=20$, $J=50$, $p=0.10$.

In principle, a likelihood ratio test of the hypothesis $D_{\mathrm{pop}}=\delta$ is possible. In practice, obtaining the maximized log‐likelihood under that constraint is a largely intractable problem, because the constraint is not differentiable with respect to $p_j^0$ and $p_j^1$ when they are equal.

The test results presented here show that inference can be based on the W _pb, T _pb and W _dc tests when the sample size, the value of D _pop and the minority proportion are such that the bias corrections work reasonably well, although, as Figures 2 and 3 show, some size distortions occur also for these tests. We next consider the case where $D_{\mathrm{pop}}=0.127$, $E\left[n_j\right]=10$ and $p=0.10$. From Tables 1(a)– (c), it is clear that the bias‐corrected estimators remain biased in this case, with D _dc having a bias of 0.15. Table 2 also shows that the tests for no systematic segregation only reject the null around 12% of the time. The rejection frequencies at the 5% level for the W, W _pb, T _pb and W _dc tests are 100%, 42%, 26% and 80%, respectively, indicating that W _dc in this case is severely oversized, as expected, whereas T _pb performs best, but is still oversized substantially. When we increase $E\left[n_j\right]$ to 30, the bias of D _dc is reduced to 0.038, and the tests reject the null of no systematic segregation around 28% of the time. The rejection frequencies at the 5% level for W, W _pb, T _pb and W _dc are now 99%, 35%, 25% and 16%, respectively, showing a substantial improvement of the performance of W _dc, whereas the performance of T _pb is similar to before. At the other end of the scale, when we set $D_{\mathrm{pop}}=0.634$, $E\left[n_j\right]=30$ and $p=0.35$, all tests work well with rejection frequencies at the 5% level of 6.6%, 5.2%, 6.5% and 5.2% for W, W _pb, T _pb and W _dc, respectively.

6. TESTS FOR EQUALITY OF SEGREGATION

A researcher may well be interested in determining whether segregation has changed significantly within an area over time, or whether segregation in one area is significantly different from that in another similar, or perhaps neighbouring, area. We consider the performances of the test statistics for comparing the two hypothetical areas for which the results were simulated above. Area 1 has $J=50$, $E\left[n_j\right]=30$ and $p=0.30$, whereas Area 2 has $J=50$, $E\left[n_j\right]=20$ and $p=0.10$. To study the size properties of the tests for the null hypothesis

$$H_0:D_{\mathrm{pop},1}=D_{\mathrm{pop},2},$$

we set the two area population segregation measures $D_{\mathrm{pop},1}=D_{\mathrm{pop},2}=0.292$ as before. Given the area‐specific conditional allocation probabilities, the allocations in the areas are determined independently and therefore the Wald test

$$W=\frac{{(D_1-D_2)}^2}{\widehat{\mathrm{Var}}\left(D_1\right)+\widehat{\mathrm{Var}}\left(D_2\right)}$$

is asymptotically ${\chi }_1^2$ distributed. The Wald test based on, e.g., the density‐corrected estimates is defined as

$$W_{\mathrm{bc}}=\frac{{(D_{\mathrm{dc},1}-D_{\mathrm{dc},2})}^2}{{\widehat{\mathrm{Var}}}_b\left(D_{\mathrm{dc},1}\right)+{\widehat{\mathrm{Var}}}_b\left(D_{\mathrm{dc},2}\right)},$$

whereas the bootstrap P‐values for the W _pb test are based on the distribution of the bootstrap repetitions of

$$W_b=\frac{{\left(D_{b,1}-D_{b,2}-(D_1-D_2)\right)}^2}{\widehat{\mathrm{Var}}\left(D_{b,1}\right)+\widehat{\mathrm{Var}}\left(D_{b,2}\right)},$$

where $D_{b,1}$ and $D_{b,2}$ are calculated from independent bootstrap repetitions. The bootstrap P‐values for the T _pb test are obtained in an equivalent way.

As an example, the bias of $D_1-D_2$ as an estimate for $D_{\mathrm{pop},1}-D_{\mathrm{pop},2}$ can be obtained from the results as presented in Table 3 and is equal to −0.075. As the covariance between D ₁ and D ₂ is equal to zero, the rmse can be calculated as ${({\left(\mathrm{rmse}\left(D_1\right)\right)}^2+{\left(\mathrm{rmse}\left(D_2\right)\right)}^2-2\mathrm{bias}\left(D_1\right)\mathrm{bias}\left(D_2\right))}^{1/2}=0.085$. The equivalent numbers for $D_{\mathrm{dc},1}-D_{\mathrm{dc},2}$ are −0.007 and 0.054 for the bias and rmse, respectively. Note that this rmse calculation is not exact, because the Monte Carlo sample covariance between the two area segregation measures is not exactly equal to zero, but this difference is negligible.

Figure 4 depicts the P‐value plots for the true null of equal population segregation measures D _pop in the two areas. The asymptotic Wald test again over‐rejects substantially, 28.2% at the 5% level. The W _dc test displays the best size properties in this case, rejecting 8.6% of the time at the 5% level, followed by T _pb and then W _pb. The rejection probabilities for these latter tests at the 5% level are 11.3% and 13.4%, respectively.

Figure 4.

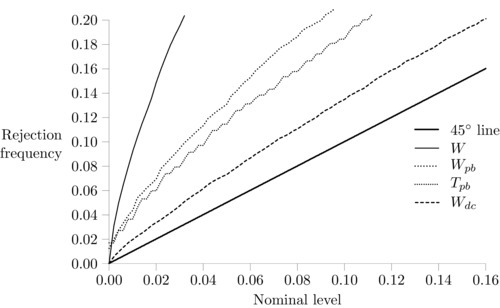
P‐value plot, $H_0:D_{\mathrm{pop},1}=D_{\mathrm{pop},1}$, size properties.

We next turn to the power properties of these tests when the two population segregation measures D _{pop, 1} and D _{pop, 2} are not equal. We keep D _{pop, 2} equal to 0.292, but increase D _{pop, 1} to 0.382. The estimation results for this design are presented in the third column of Table 3. As discussed above, because D ₂ is substantially biased upwards, we expect the W _pb test to have low power. This is confirmed by the P‐value plots in Figure 5. The standard Wald test has power below nominal size, but the bootstrap‐based Wald test W _pb completely fails to reject the null of equal segregation. In contrast, the Wald tests based on the bias‐corrected estimator and T _pb show reasonable power properties, with T _pb having the most power to detect this deviation from the null, although it has not been size‐adjusted. The P‐value plots, not shown here, for the true null that $D_{\mathrm{pop},1}-D_{\mathrm{pop},2}=0.0897$ are very similar to those in Figure 4. Clearly, these results combined show that for simple hypothesis testing, W _dc and T _pb are the test procedures with reasonably good size and power properties in the settings we have considered.

Figure 5.

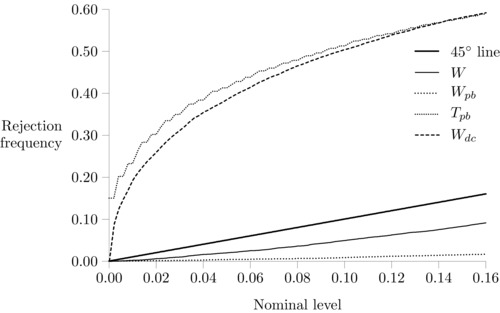
P‐value plot, $H_0:D_{\mathrm{pop},1}=D_{\mathrm{pop},1}$, power properties.

7. DISCUSSION

Recently, Rathelot (2012) and d'Haultfœuille and Rathelot (2011) have also considered the problem of measuring segregation when units are small. In their set‐up, the number of individuals in units is small at around 5 or 10, whereas the number of units is large. Indeed, the methods in these papers rely on large‐number‐of‐units asymptotics. Both papers show that the parametric method proposed by Rathelot (2012) performs well in the estimation of the dissimilarity index and other measures of inequality, such as the Gini and the Theil indices. In this set‐up, the number of individuals in unit j, $n_j$, is drawn from a given, unknown distribution. Then, the number of individuals in unit j having status c, $n_j^c$, is distributed as Binomial$(n_j,{\pi }_j^c)$, and ${\widehat{\pi }}_j^c=n_j^c/n_j$ is an unbiased estimate of ${\pi }_j^c$. The parametric method of Rathelot (2012) is then to assume that ${\pi }_j^c$ is distributed as a mixture of Beta distributions, leading to the Beta‐Binomial model. In the simulations in Rathelot (2012), it is shown that estimates of the dissimilarity index from this Beta‐Binomial model have better properties in terms of smaller bias than the bootstrap bias correction in the setting of a large number of small units. We have tried to analyse the behaviour of this estimator in our set‐up, but found in the simulations of our design of Section 3.1. that the Beta‐Binomial estimation procedure often did not converge, making it difficult to compare the performance of this estimator with the others in our set‐up.⁴ For larger minority fractions and values of D _pop, convergence of the ML estimator is easier to obtain in our design. Table 5 shows the estimation results for D _beta1, which is the Beta‐Binomial estimator with a one‐component Beta distribution, for $E\left[n_j\right]=30$, $J=50$, $p=0.20$, where we obtained valid Monte Carlo results for $D_{\mathrm{pop}}=0.127$ and larger. The results show that in this design, D _beta1 behaves similarly to D _dc for $D_{\mathrm{pop}}=0.127$, but has a substantially larger bias and/or rmse for larger values of D _pop. For this design, increasing the number of mixtures of beta distributions to two does not change the results, because in almost all cases this model converges to the one‐component model. The Beta‐Binomial estimator is not consistent for a fixed number of units and unit sizes going to infinity. For example, when we increase the expected sample size to $E\left[n_j\right]=100$, the bias and rmse of D _beta1 increases to −0.042 and 0.044, respectively, when $D_{\mathrm{pop}}=0.382$. The bias and rmse of D itself in that case are 0.009 and 0.018, respectively.

Table 5.

Bias and rmse of D _beta1 and D _ct

	D pop
	0		0.056		0.127		0.225		0.382		0.634
	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse	bias	rmse
D	0.180	0.180	0.130	0.130	0.088	0.090	0.054	0.059	0.029	0.039	0.012	0.026
D dc	0.099	0.100	0.051	0.056	0.014	0.030	−0.006	0.031	−0.008	0.032	−0.004	0.026
D beta1					−0.012	0.037	−0.020	0.037	−0.033	0.042	−0.054	0.060
D ct	−0.032	0.075	−0.067	0.089	−0.085	0.091	−0.100	0.110	−0.099	0.100	−0.064	0.085

$E\left[n_j\right]=30$, $J=50$, $p=0.20$. No results reported for D _beta1 in first two columns owing to the convergence problems of the estimator.

Another bias‐corrected measure is the one proposed by Carrington and Troske (1997), which has been widely used in school segregation (Söderström and Uusitalo, 2010) and occupational segregation (Hellerstein and Neumark, 2008) research. Carrington and Troske (1997) argue that segregation indices can be modified to take into account the underlying value under no systematic segregation, when $p_j^1=p_j^0$, $j=1,...,J$. They propose a modified segregation index that measures the (economic) extent to which a sample deviates from the expected value of D under no systematic segregation, denoted $D^{*}=E{\left[D\right]}_{p_j^1=p_j^0}$, which can be calculated as in Section 4.. They argue that their new index of systematic dissimilarity does not depend on the margins in the area and is therefore a better means of comparing the extent to which systematic segregation exists. Their measure, denoted D _ct here, is defined as

$$D_{\mathrm{ct}}=\frac{D-D^{*}}{1-D^{*}}\text{if}D\ge D^{*};D_{\mathrm{ct}}=\frac{D-D^{*}}{D^{*}}\text{if}D<D^{*},$$

and hence $D_{\mathrm{ct}}\in [-1,1]$. D _ct can be interpreted as the extent to which the area is more dissimilar than random allocation would imply, expressed as a fraction of the maximum amount of such excess dissimilarity that could possibly occur. $D_{\mathrm{ct}}=0$ implies that the allocation of individuals in the area is equivalent to no systematic segregation. It is worth noting that D _ct is almost identical to the index proposed by Winship (1977), which was criticized by Falk et al. (1978) and then partially withdrawn by Winship (1978). The problem with D _ct is that it is not entirely clear what it is intended to achieve. D _ct is always lower than D _pop, but tends to D _pop for large unit sizes. In our simulations, for many values of the parameters, D _ct underestimates D _pop by a larger amount than D itself overestimates D _pop. As an illustration of this, Table 5 presents simulation results for $E\left[n_j\right]=30$, $J=50$ and $p=0.20$. The problem with D _ct is that decomposition of a segregation index into one part produced by systematic segregation and another part produced by randomness cannot be done additively.

In the previous Monte Carlo designs, all unit sizes were equal in expectation. We next perform the simulations with designs like those of the first two columns in Table 3, but for unequal expected unit sizes. In the first design, labelled Design 1 in Table 6, we split the 50 units into half with a smaller expected group size and half with a larger expected group size. For the example containing 1500 individuals, these sizes are approximately 10 and 50; for the second example of 1000 individuals, these are approximately 7 and 33. In the second design, labelled Design 2 in the table, all expected unit sizes are different, within the aforementioned ranges in steps of just under one individual. Tables 6 and 7 present the estimation and testing results. The results are all very similar to those with equal expected unit sizes, as presented in Sections 5. and 6..

Table 6.

Results for designs with unequal expected unit sizes

	$n=1500$, $p=0.3$		$n=1000$, $p=0.1$
	bias	rmse	bias	rmse
Design 1
D	0.022	0.032	0.083	0.091
D bc	−0.003	0.027	0.018	0.050
D dc	−0.010	0.029	0.009	0.047
Design 2
D	0.027	0.035	0.094	0.100
D bc	−0.002	0.027	0.016	0.049
D dc	−0.009	0.028	0.005	0.045
Rejection frequencies for tests of $H_0:D_{\mathrm{pop}}=0.292$
Nominal size	0.10	0.05	0.10	0.05
Design 1
W	0.192	0.116	0.596	0.457
W pb	0.106	0.056	0.200	0.119
T pb	0.162	0.100	0.175	0.100
W dc	0.135	0.078	0.127	0.071
Design 2
W	0.246	0.154	0.726	0.596
W pb	0.115	0.064	0.167	0.096
T pb	0.161	0.095	0.167	0.095
W dc	0.134	0.075	0.134	0.076

$J=50$, $D_{\mathrm{pop}}=0.292$; 10,000 Monte Carlo replications, 599 bootstrap repetitions.

Table 7.

Test results for $H_0:D_{\mathrm{pop},1}=D_{\mathrm{pop},2}$

	Design 1				Design 2
Size	W	W pb	T pb	W dc	W	W pb	T pb	W dc
0.10	0.293	0.221	0.193	0.139	0.352	0.208	0.186	0.138
0.05	0.184	0.140	0.119	0.079	0.234	0.125	0.118	0.081

See Table 6.

8. SOCIAL SEGREGATION IN SCHOOLS

In this section, we illustrate our inference procedures with an empirical application relating to social segregation in primary schools in England. The dichotomous measure is an indicator of poverty based on eligibility for free school meals (FSMs). This context is useful as it naturally produces small unit sizes, and shows a range of minority proportions and overall populations across different LAs. We use administrative data collected by the Department for Children, Families and Schools, and made available to researchers as part of the National Pupil Database on pupils aged 10/11 in English primary schools in 2006. Measurement of school segregation using this data set has been carried out by many researchers; see Allen and Vignoles (2008), Burgess et al. (2006), and Gibbons and Telhaj (2006). Using the tools developed above, we can assess whether the small unit sizes and/or small minority populations lead to incorrect inferences about differences in segregation across areas. We provide two cases. First, we compare two similar pairs of LAs, showing that quite small differences in their characteristics imply different outcomes of inference; these are North‐East Lincolnshire and North Lincolnshire, and Blackburn and Oldham. Second, we compare all the different LAs in inner‐city London, and consider which pairwise comparisons yield significant differences. Table 8 shows the descriptive statistics and the dissimilarity indices of the LAs. North‐East Lincolnshire and North Lincolnshire have almost the same number of pupils, 2005 and 2011 respectively, but differ in the number of schools, 46 and 57 respectively, and consequently also average cohort size. They also differ in the percentages of children eligible for FSMs, 21% and 13% respectively. The dissimilarity index for North‐East Lincolnshire is 0.43, higher than that of North Lincolnshire, which has an index of 0.36. Blackburn and Oldham differ rather more in size, but have closer average unit sizes, and slightly higher percentages of children eligible for FSMs.

Table 8.

Key parameters of primary schools across English LAs

	Number	Number	Average	%
LA name	of pupils	of schools	cohort size	FSM	D
North‐East Lincolnshire	2005	46	44	21	0.43
North Lincolnshire	2011	57	35	13	0.36
Blackburn	2105	51	41	26	0.34
Oldham	2990	86	35	21	0.47
Camden	1394	41	34	42	0.23
Greenwich	2666	66	40	36	0.29
Hackney	2194	54	41	43	0.22
Hammersmith and Fulham	1177	39	30	45	0.30
Islington	1845	48	38	41	0.26
Kensington and Chelsea	881	27	33	36	0.32
Lambeth	2428	60	40	40	0.24
Lewisham	2833	70	40	29	0.30
Southwark	2929	72	41	36	0.21
Tower Hamlets	2703	68	40	61	0.20
Wandsworth	2124	60	35	27	0.29
Westminster	1336	39	34	39	0.33

Are the school allocations in North‐East Lincolnshire more segregated than those in North Lincolnshire? Table 9 shows that the observed D marginally overstates the level of segregation in each LA, but the bias‐corrected estimates of D _pop do not alter the ranking. Table 9 further presents the various test procedures and confidence intervals as described in the previous section. Here, we generate 999 bootstrap samples. The LR test for no systematic segregation clearly rejects for both LAs, with both bootstrap P‐values equal to 0. The rejection of the null of equal segregation in North‐East Lincolnshire and North Lincolnshire depends on the test statistics employed. Using the test statistics W _dc and T _pb, we reject the null of equal segregation in the two LAs at the 5% and 1% levels, respectively.

Table 9.

Bias‐corrected dissimilarity indices, confidence intervals and test statistics for North‐East and North Lincolnshire

	North‐East Lincolnshire	North Lincolnshire
D	0.433	0.364
D bc	0.420	0.322
D dc	0.416	0.334
LR‐test, bootstrap P‐value	0	0
CI‐W	[0.386–0.481]	[0.306–0.421]
CI‐W pb	[0.380–0.487]	[0.275–0.452]
CI‐T pb	[0.371–0.466]	[0.265–0.371]
CI‐W dc	[0.367–0.465]	[0.278–0.390]
	$H_0:D_{\mathrm{pop},\mathrm{NEL}}=D_{\mathrm{pop},\mathrm{NL}}$, P‐values
W	0.067
W pb	0.114
T pb	0.000
W dc	0.032

CI are 95% confidence intervals. Number of bootstrap repetitions 999.

Table 10 shows test statistics for Blackburn and Oldham. In this example, we can reject, with a high degree of confidence, the null of equal segregation in these areas. This greater confidence than in the Lincolnshire example is possible, despite similar segregation levels, because the LAs are slightly larger and the minority proportions are higher.

Table 10.

Bias‐corrected dissimilarity indices, confidence intervals and test statistics for Blackburn and Oldham

	Blackburn	Oldham
D	0.342	0.472
$D_{dc}$	0.306	0.446
LR test, bootstrap P‐value	0	0
CI‐$T_{pb}$	[0.288–0.362]	[0.420–0.485]
CI‐$W_{dc}$	[0.263–0.348]	[0.410–0.483]
	$H_0:D_{\mathrm{pop},\mathrm{Blackburn}}=D_{\mathrm{pop},\mathrm{Oldham}}$, P‐values
T pb	0.000
W dc	0.000

CI are 95% confidence intervals. Number of bootstrap repetitions 999.

For our second illustration, Table 11 compares observed and density‐corrected segregation levels across the 12 LAs in Inner London. The density correction makes little differences to the ranking of segregation levels, with just Wandsworth and Greenwich switching positions. Results for the tests of equivalence of D _pop in Table 12 show that the LAs can be approximately divided into three groups, with possible multiple membership, where the tests do not reject the null of equal segregation. These groups are: Tower Hamlets, Southwark and Hackney, with the lowest level of segregation; Hackney, Camden and Lambeth, with medium level of segregation; Wandsworth, Greenwich, Hammersmith and Fulham, Lewisham, Kensington and Chelsea, and Westminster with the highest level of segregation. Islington is a medium‐segregation LA with some overlap with the group of highest‐segregation LAs.

Table 11.

Bias‐corrected dissimilarity indices and confidence intervals for Inner London

	D	D dc	LR(P)	CI–W dc	CI–T pb
Tower Hamlets	0.197	0.162	0	[0.126–0.192]	[0.125–0.198]
Southwark	0.206	0.165	0	[0.137–0.201]	[0.128–0.202]
Hackney	0.219	0.184	0	[0.154–0.225]	[0.142–0.226]
Camden	0.231	0.188	0	[0.153–0.236]	[0.140–0.237]
Lambeth	0.240	0.209	0	[0.172–0.241]	[0.170–0.248]
Islington	0.257	0.231	0	[0.183–0.258]	[0.188–0.273]
Wandsworth	0.290	0.243	0	[0.219–0.292]	[0.200–0.286]
Greenwich	0.286	0.251	0	[0.226–0.291]	[0.213–0.288]
Hammersmith and Fulham	0.303	0.264	0	[0.226–0.323]	[0.208–0.319]
Lewisham	0.304	0.274	0	[0.244–0.312]	[0.235–0.312]
Kensington and Chelsea	0.317	0.296	0	[0.231–0.347]	[0.230–0.361]
Westminster	0.328	0.302	0	[0.257–0.347]	[0.252–0.352]

CI are 95% confidence intervals. Number of bootstrap repetitions 999.

Table 12.

P‐values for tests of equivalence of D _pop for Inner London

	Sou	Hac	Cam	Lam	Isl	Wan	Gre	Ham	Lew	Ken	Wes
Tower	0.725	0.202	0.176	0.040	0.014	0.003	0.000	0.001	0.000	0.000	0.000
Hamlets	0.899	0.426	0.389	0.081	0.016	0.005	0.001	0.003	0.000	0.000	0.000
Southwark		0.368	0.310	0.094	0.030	0.000	0.000	0.000	0.000	0.000	0.000
		0.502	0.454	0.107	0.022	0.007	0.001	0.004	0.000	0.001	0.000
Hackney			0.875	0.466	0.234	0.016	0.000	0.006	0.000	0.002	0.000
			0.897	0.388	0.123	0.054	0.019	0.024	0.002	0.005	0.000
Camden				0.631	0.338	0.020	0.016	0.008	0.002	0.004	0.000
				0.511	0.195	0.098	0.045	0.044	0.007	0.009	0.001
Lambeth					0.555	0.046	0.034	0.028	0.002	0.014	0.002
					0.457	0.250	0.128	0.111	0.020	0.025	0.004
Islington						0.214	0.126	0.098	0.038	0.064	0.008
						0.690	0.489	0.351	0.142	0.101	0.033
Wandsworth							0.853	0.587	0.376	0.314	0.124
							0.795	0.561	0.300	0.187	0.081
Greenwich								0.655	0.494	0.350	0.150
								0.696	0.398	0.239	0.106
Hammersmith									0.911	0.653	0.396
and Fulham									0.776	0.467	0.318
Lewisham										0.663	0.388
										0.571	0.382
Kensington											0.779
and Chelsea											0.880

Top and bottom rows are for T _pb and W _dc, respectively. Number of bootstrap repetitions 999.

9. CONCLUSIONS

To make statements about the true underlying degree of segregation, or to understand the processes causing segregation, it is desirable to measure the level of systematic segregation. However, where minority proportions and unit sizes are small, the level of segregation observed by researchers in their data is known to be significantly greater than systematic segregation. Furthermore, because the size of the bias of observed segregation over systematic segregation is known to be a function of minority proportion, unit sizes and systematic segregation, differences in any of these parameters between areas or over time may lead to incorrect inferences.

In this paper, we have proposed and tested procedures for adjusting the dissimilarity index of segregation for this bias. Our corrections work well, provided both the minority proportion and unit size are not very small. Where very small minority proportions and unit sizes render our corrections useless, we show that levels of segregation are often not statistically distinguishable from zero. We have developed and tested our statistical framework using the index of dissimilarity, D, but it can, in principle, be extended to other segregation indices.

From our statistical framework, we have developed tests for a null of no systematic segregation and a null of equal segregation in two areas, and we have established confidence intervals for levels of systematic segregation. In tests using unit sizes, minority proportions and underlying segregation levels similar to those encountered by social scientists, the Wald statistics using the bootstrap variance estimate for the bias‐corrected estimators and the test based on the equal‐tail bootstrap P‐value for the t‐test (T _pb) are found to perform best. The methods proposed in this paper provide a framework for more reliable inference as to levels of segregation, which will aid the further investigation of the causes of segregation.

Supporting information

Replication Files

Appendix 1.

1.1.

In this Appendix, we consider two methods of bias correction, which, although somewhat effective, turn out not to be as effective as the density‐correction method of Section 3..

The expectation of the folded normal variable Z of which the density is given by (3.3) is easily seen to be $E\left[Z\right]=2\phi \left(\theta \right)+\theta \left(2\Phi \right(\theta )-1)\equiv m\left(\theta \right)$. If we think of Z as an estimator of θ, then the bias is

$$b\left(\theta \right)=m\left(\theta \right)-\theta =2\left(\phi \right(\theta )+\theta (\Phi \left(\theta \right)-1\left)\right).$$

The bias function $b\left(\theta \right)$ is shown in Figure A.1. It decreases monotonically from its value of ${(2/\pi )}^{1/2}$ at $\theta =0$, which corresponds to $\mu =0$, and tends rapidly to 0 for values of θ greater than around 2.5.

Figure A.1.

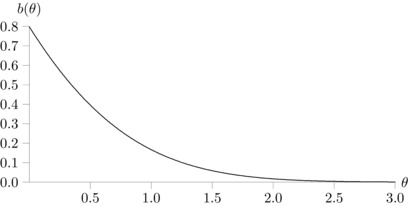
Bias function $b\left({\theta }_j\right)$.

Recall that ${\widehat{\theta }}_j=|{\widehat{p}}_j^1-{\widehat{p}}_j^0|/{\widehat{\sigma }}_j$. Using the function $b\left(\theta \right)$ to estimate the bias of ${\widehat{\theta }}_j$ leads to a bias‐corrected estimator of D _pop:

$$D_{\mathrm{bc},1}=D-\frac{1}{2}\sum _{j=1}^J{\widehat{\sigma }}_{j}b\left({\widehat{\theta }}_j\right),$$

As with the bootstrap bias correction, because of the shape of $b\left(\theta \right)$, we do not expect this correction to work well with small unit sizes combined with small values for D _pop.

Another approach pretends that ${\tilde{\theta }}_j$ really has expectation $m\left({\theta }_j\right)$:

$$E[{\tilde{\theta }}_j-m\left({\theta }_j\right)]=0.$$

We can treat this relation as an estimating equation for ${\theta }_j$, thereby defining a new estimator ${\widehat{\theta }}_j^{bc}$ as

$${\widehat{\theta }}_j^{bc}=m^{-1}\left({\tilde{\theta }}_j\right).$$

Because, in practice, we must estimate ${\sigma }_j$, we end up with the bias‐corrected estimator

$$D_{\mathrm{bc},2}=\frac{1}{2}\sum _{j=1}^J{\widehat{\sigma }}_j{m}^{-1}\left(\max [{(2/\pi )}^{1/2},{\widehat{\theta }}_{\mathrm{j}}]\right).$$

The inverse function $m^{-1}$ cannot be expressed analytically in closed form, but it is easy to compute. Its argument must not be smaller than ${(2/\pi )}^{1/2}$, because that is the smallest value of $m\left({\theta }_j\right)$. Thus, any ${\widehat{\theta }}_j$ smaller than this cut‐off leads to a zero contribution to $D_{bc,2}$.

It is clear that the new estimator D _{bc, 2} is still biased, for two reasons. First, m is a non‐linear function and, second, the random quantities ${\widehat{\sigma }}_j$ appear in the denominator of the argument of $m^{-1}$.