A Bayesian framework to account for uncertainty due to missing binary outcome data in pairwise meta‐analysis

Abstract

Missing outcome data are a common threat to the validity of the results from randomised controlled trials (RCTs), which, if not analysed appropriately, can lead to misleading treatment effect estimates. Studies with missing outcome data also threaten the validity of any meta‐analysis that includes them. A conceptually simple Bayesian framework is proposed, to account for uncertainty due to missing binary outcome data in meta‐analysis. A pattern‐mixture model is fitted, which allows the incorporation of prior information on a parameter describing the missingness mechanism. We describe several alternative parameterisations, with the simplest being a prior on the probability of an event in the missing individuals. We describe a series of structural assumptions that can be made concerning the missingness parameters. We use some artificial data scenarios to demonstrate the ability of the model to produce a bias‐adjusted estimate of treatment effect that accounts for uncertainty. A meta‐analysis of haloperidol versus placebo for schizophrenia is used to illustrate the model. We end with a discussion of elicitation of priors, issues with poor reporting and potential extensions of the framework. Our framework allows one to make the best use of evidence produced from RCTs with missing outcome data in a meta‐analysis, accounts for any uncertainty induced by missing data and fits easily into a wider evidence synthesis framework for medical decision making. © 2015 The Authors. Statistics in MedicinePublished by John Wiley & Sons Ltd.

1. Introduction

Systematic reviews identify, appraise and synthesise all information relevant to a specific research question 1and are increasingly used to guide healthcare policy and clinical decisions 2. The results from randomised controlled trials (RCTs) identified in a systematic review may be summarised by pooling them in a meta‐analysis to obtain a single estimate of treatment effect that reflects uncertainty based on the existing RCT evidence 3. Whilst RCTs are considered the highest quality evidence to inform relative treatment effect estimates, they may still be subject to bias 4, and any bias in an individual RCT will also be present in any meta‐analysis that includes it 5. One common threat to the validity of a trial is missing outcome data, which can lead to biased relative effect estimates 6. In some cases, it may be appropriate to assume the outcomes are missing at random (MAR), meaning that missingness is dependent on observed data (e.g. covariates), but not dependent on the unobserved data. Under MAR, an analysis that restricts to the observed data only (complete case analysis) provides an unbiased central estimate of the treatment effect, and there is increased uncertainty due to the smaller numbers included. However, the existence of incomplete outcome data brings with it additional uncertainty concerning treatment effectiveness, which is not reflected in a complete case analysis 6and which can lead to misleadingly precise estimates. If the MAR assumption does not hold, then a complete case analysis will produce biased, as well as overly precise estimates.

The Cochrane Collaboration 1and National Institute for Health and Care Excellence 7, 8provide recommendations on how missing data should be handled within a meta‐analysis in an attempt to account for this potential bias and uncertainty around treatment estimates induced by missing data. The first recommendation is that a judgement on the level of risk of bias due to missing data in each individual trial be made. The next recommendation is to explore the impact of this potential bias. Finally, it is suggested that a number of sensitivity analyses are carried out making different assumptions about the missing outcomes. For example, for binary outcomes, where we are measuring whether treatment is a success or a failure, first carry out the meta‐analysis assuming that all of the missing outcomes in the data are treatment failures, that is, non‐events (an ‘all failures’ analysis) and then repeat the analysis assuming that all missing outcomes are treatment successes, that is, events. Another option is to carry out treatment arm‐specific sensitivity analyses; a ‘worst‐case’ meta‐analysis assumes that all missing data in the intervention arms of trials are treatment failures, but the missing outcomes in the control arms are successes. Conversely, a ‘best‐case’ meta‐analysis makes the opposite assumption; that is, missing data in the intervention arms are treated as successes, whilst the missing data in the control arms are assumed to be failures 1. These approaches are useful to put limits on how extreme the effects of missing outcome data may be; however, they focus mainly around data manipulation to provide (deterministic) sensitivity analyses to assumptions about the distribution of events and non‐events in missing participants, which are unlikely to be realistic in practise. For decision making, what is required is a single credible estimate of treatment effect, together with an estimate of its uncertainty accounting for the strength of evidence and missing data, which can be used as an input to a decision model.

In this paper, we present a statistical model to account for the bias and quantify uncertainty in treatment effect estimates induced by missing data 1. We take a decision‐making perspective, so that the quantity (estimand) we are interested in estimating is the effect that we would expect to see in the population of all patients that were randomised, which is attributable to the treatment they were initially randomised to. This focus on effectiveness, rather than efficacy, is termed a de factohypothesis in the literature on longitudinal RCTs 9, 10, 11, and our estimand of interest corresponds to estimand 6 described by Mallinckrodt et al. 10.

A Bayesian statistical approach naturally allows for uncertainty due to missing data in the meta‐analysis through the use of suitable prior distributions 12, 13. A two‐stage Bayesian approach to account for uncertainty due to missing binary outcomes has previously been proposed 5that firstly adjusts study‐specific estimates of treatment effect and its associated variance using prior beliefs on the missingness mechanism (using the informative missingness odds ratio (IMOR); see Section 3.3.2), and then pools these adjusted estimates in a meta‐analysis 5. A key disadvantage of taking such a two‐stage approach is that the adjustment is ‘fixed’, and there is no potential for the observed data to inform the missingness parameter estimates nor to borrow strength across studies. Other limitations of this approach include that it makes an a priori assumption that the IMOR is independent of the amount of missingness and of other parameters, and it requires arbitrary ‘fixes’ when cell counts are zero. Furthermore, a one‐stage approach that simultaneously incorporates prior beliefs and pools evidence across trials is conceptually simpler and allows the methods to be extended to more complex situations, for example, network meta‐analysis 14. A one‐stage Bayesian approach has previously been proposed that puts a hierarchical model on the IMORs and attempts to estimate them from the observed data for both pairwise 15and network meta‐analyses 16; however, this approach is complex to apply, is very computationally intensive and is found to have limited ability to identify the IMORs from the observed data 15, 16.

To date, the work on incorporating uncertainty due to missingness in binary outcomes in meta‐analysis has focussed on the IMOR 5, 15. However, there may be other missingness parameters on which we have prior information. In particular, if we have no prior information at all on the missingness mechanism, the most natural way to reflect this is through a flat prior on the probability of an event conditional on being missing. This will directly propagate the prior uncertainty in the true value of the missing outcomes into the analysis.

The aim of this paper is to present a general framework to reflect the uncertainty arising from missing binary outcome data in RCTs included in the meta‐analysis. We present a conceptually simple one‐stage Bayesian approach that allows priors (including minimally informative priors) to be given for parameters describing the missingness mechanism in a variety of ways, including the probability of success given a subject was missing, the IMOR 17, probability success ratio and the response probability ratio 18.

The paper is structured as follows. In Section 2, we introduce a motivating example meta‐analysis of haloperidol versus placebo for schizophrenia with missing binary outcome data 19. In Section 3, we begin by presenting the standard pairwise meta‐analysis model for binary data and common deterministic sensitivity analyses that are conducted. We then present our general framework to account for uncertainty due to missing binary outcome data in meta‐analysis when no prior information on the missingness mechanism is available and outline how to apply the framework for some common missingness parameters for which prior information may be available or elicited. In Section 4, we explore the ability of the model to learn about the missingness parameters using artificial data scenarios. We then present the results from the motivating example in Section 5and end with a discussion.

2. Motivating example: haloperidol versus placebo for treatment of schizophrenia

We illustrate our framework using a meta‐analysis of 17 RCTs comparing haloperidol with placebo in the treatment of schizophrenia 17. Trials involving schizophrenic patients often report high levels of missing data because of treatment side effects, poor treatment compliance and strict execution of the RCT protocols. For each study, i, we have for each arm, k, the number of observed events (defined as the number of patients ‘improved’), r _i,k, the total number of individuals randomised in each arm, n _i,k, and the number of missing individuals, m _i,k, where k= 1 indicates the placebo arm and k= 2 the haloperidol arm. The number of individuals in each arm for whom an outcome was actually observed (the complete cases) is therefore c _i,k=n _i,k−m _i,k (Table 1). In this dataset, six of the 17 RCTs contained no missing data, and overall, there was proportionately more missing data in the control group, possibly because of lack of efficacy 16.

Table 1.

Data from a meta‐analysis of 17 trials comparing haloperidol with placebo for the treatment of schizophrenia 19.

Trial	Placebo				Haloperidol
	No. of events	No. missing	No. of complete cases	Total no. randomised	No. of events	No. missing	No. of complete cases	Total no. randomised
i	r i,1	m i,1	c i,1	n i,1	r i,2	m i,2	c i,2	n i,2
i	r i,1	m i,1	c i,1	n i,1	r i,2	m i,2	c i,2	n i,2
1	18	0 (0%)	51	51	25	2 (4%)	50	52
2	20	34 (50%)	34	68	29	22 (32%)	47	69
3	2	1 (3%)	30	31	12	1 (3%)	29	30
4	0	0 (0%)	12	12	3	0 (0%)	12	12
5	3	0 (0%)	22	22	10	0 (0%)	21	21
6	1	0 (0%)	15	15	11	0 (0%)	19	19
7	4	1 (4%)	25	26	7	1 (4%)	25	26
8	3	0 (0%)	13	13	8	0 (0%)	17	17
9	14	2 (3%)	64	66	19	2 (3%)	64	66
10	0	0 (0%)	10	10	1	1 (10%)	9	10
11	0	0 (0%)	13	13	11	3 (8%)	34	37
12	2	0 (0%)	11	11	20	0 (0%)	29	29
13	7	18 (62%)	11	29	17	11 (38%)	18	29
14	0	1 (7%)	13	14	4	0 (0%)	14	14
15	0	1 (13%)	7	8	2	0 (0%)	16	16
16	1	0 (0%)	12	12	11	0 (0%)	12	12
17	0	1 (3%)	29	30	9	1 (3%)	29	30

3. Methods

3.1. Pairwise meta‐analysis in the absence of missing data

In the absence of missing outcome data, the pairwise meta‐analysis model for binary outcomes 14, 20, 21is as follows. The number of events in study iarm k, r _i,k, is assumed to have a binomial likelihood determined by the total number of individuals randomised to that arm, n _i,k, and the probability of an event occurring in all randomised individuals, ${\pi }_{i,k}^{\text{all}}$:

$$r_{i,k}\sim \text{Binomial}\left({\pi }_{i,k}^{\text{all}},n_{i,k}\right)$$ (1)

The logit link function is used to model ${\pi }_{i,k}^{\text{all}}$ to ensure that the probabilities lie on (0,1) as follows:

$$\text{logit}\left({\pi }_{i,k}^{\text{all}}\right)=\left\{\begin{array}{ll}{\mu }_i& k=1\\ {\mu }_i+{\delta }_i& k=2\end{array}\right.$$ (2)

where μ _i are the study‐specific log‐odds of the outcome on treatment 1 (the control) and are treated as unrelated nuisance parameters.

For a fixed effects model, we assume each study ito be estimating the same underlying treatment effect. For a random effects model, we instead assume that the study‐specific treatment effects, δ _i, are exchangeable and come from a common normal population of treatment effects. Thus,

$$\begin{array}{ll}{\delta }_i\sim N(d,{\sigma }^2)& \text{Random effects model}\\ {\delta }_i=d& \text{Fixed effects model}\end{array}$$ (3)

where dis the pooled log‐odds ratio and σ is the between studies standard deviation.

3.2. Sensitivity analyses in the presence of missing data

When data are missing, different analyses can be carried out to assess the sensitivity of results to varying assumptions on the missing outcomes. A complete case analysis can be carried out using the standard pairwise meta‐analysis model (Equations (1), (2), (3)) where the denominator n _i,kin Equation (1)is replaced by the number of complete cases c _i,k. Similarly, best‐case and worst‐case scenarios can be obtained by replacing r _i,kin Equation (1)by

$$r_{i,k}^{\text{best}}=\left\{\begin{array}{ll}{r}_{i,k}& \text{if}k=1\\ r_{i,k}+m_{i,k}& \text{if}k=2\\ \end{array}\right.\text{and}{r}_{i,k}^{\text{worst}}=\left\{\begin{array}{ll}{r}_{i,k}+m_{i,k}& \text{if}k=1\\ r_{i,k}& \text{if}k=2\end{array}\right.$$

Finally, an analysis where all missing data are assumed to be failures (non‐events) can be obtained using Equations (1), (2), (3)directly.

3.3. General framework to account for missing data

We extend the standard meta‐analysis model described earlier to account for the uncertainty introduced by missing outcome data. We propose a pattern‐mixture model where the outcome is modelled conditional on whether or not it is missing 22. The approach assumes that the data are MAR with non‐ignorable missingness 23. Our general model is illustrated in a directed acyclic graph in Figure 1. We assume that m _i,k, the number of missing observations in arm kof study i, has a binomial likelihood:

$$m_{i,k}\sim \text{Binomial}\left(q_{i,k},n_{i,k}\right)$$ (4)

where q _i,k is the probability of being missing. Then, conditional on being observed, the number of events, r _i,k, are assumed to have a binomial likelihood with the total number of patients observed, c _i,k, as the denominator:

$$r_{i,k}\sim \text{Binomial}\left({\pi }_{i,k}^{\text{obs}},c_{i,k}\right)$$ (5)

where ${\pi }_{i,k}^{\text{obs}}$ is the probability of an event conditional on an individual being observed.

Figure 1.

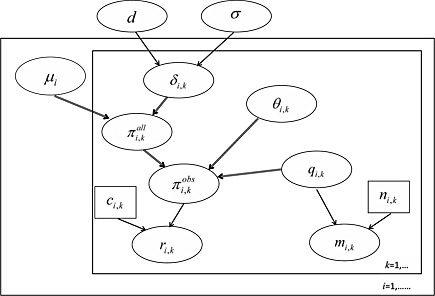
Directed acyclic graph (DAG) of our missing data framework: μ _i,kis the study‐specific log‐odds of the outcome in treatment 1 (the control), δ _i,kis the log‐odds ratio, ${\pi }_{i,k}^{\text{all}}=\text{p(success)}$, ${\pi }_{i,k}^{\text{obs}}=\text{p(success | observed)}$, r _i,kis the number of observed events, c _i,kis the number of observed outcomes, θ _i,kis the missing data parameter, q _i,k=p(missing), m _i,kis the number of missing outcomes and n _i,kis total number randomised. Ellipses denote stochastic parameters or observed data. Small boxes denote constants. The two large boxed (‘plates’) represent indexing of studies iand treatments k. Single line arrows denote stochastic relationships, and double‐line arrows denote logical relationships. Note that c _i,k=n _i,k−m _i,k; however, we omit the logical relationship between these parameters in the DAG, as c _i,kis constant conditional on the observed number of missing outcomes.

The model for the probability of an event for the population of all individuals (whether observed or missing) in arm kof trial i, ${\pi }_{i,k}^{\text{all}}$, is as set out in Equation (1). Our challenge is therefore to link the parameters we can estimate from the observed data, $\left\{{\pi }_{i,k}^{\text{obs}},q_{i,k}\right\}$, to the key parameter of interest, ${\pi }_{i,k}^{\text{all}}$. This is achieved by defining a ‘missingness’ parameter θ _i,k, which describes our belief about the missingness process and allows us to write ${\pi }_{i,k}^{\text{obs}}$as a function of $\left\{{\pi }_{i,k}^{\text{all}},q_{i,k}\text{and}{\theta }_{i,k}\right\}$ (Figure 1), so that the observed data can be used to estimate ${\pi }_{i,k}^{\text{all}}$, the key parameter of interest.

Various options for the missingness parameter θ _i,k have been proposed 15, 17. If we have no prior information on the missingness process, then the most straightforward option is to set ${\theta }_{i,k}={\pi }_{i,k}^{\text{miss}}$ the probability of an event in the individuals with missing outcomes, which can be given a flat prior to reflect the uncertainty in this probability. If we do have prior information on the missingness process (e.g. from experts), then it may be easier to use other missingness parameters that allow beliefs to be expressed on the likelihood of an event in the missing individuals relativeto the observed individuals. We first describe our approach for the case where ${\theta }_{i,k}={\pi }_{i,k}^{\text{miss}}$. We then describe how the framework can also incorporate alternative definitions for θ _i,k in which we may have, or be able to elicit, prior information and show how to link ${\pi }_{i,k}^{\text{obs}}$to $\left\{{\pi }_{i,k}^{\text{all}},q_{i,k}\text{and}{\theta }_{i,k}\right\}$for some specific definitions of θ _i,k that have been used in the literature.

3.3.1. Probability of success given missing, ${\pi }_{i,k}^{\text{miss}}$

When ${\theta }_{i,k}={\pi }_{i,k}^{\text{miss}}$, we can write the probability of an event in all individuals as a weighted average of an event in the missing and observed individuals:

$${\pi }_{i,k}^{\text{all}}=q_{\mathrm{ik}}{\pi }_{i,k}^{\text{miss}}+(1-q_{i,k}){\pi }_{i,k}^{\text{obs}}$$

Rearranging this formula gives us the following linking equation:

$${\pi }_{i,k}^{\text{obs}}=\frac{{\pi }_{i,k}^{\text{all}}-{\pi }_{i,k}^{\text{miss}}{q}_{i,k}}{(1-q_{i,k})}$$ (6)

Equations (2), (3), [Link], (4), (5), [Link], (6), with either a fixed or random effects model for the δ _i, determine the model.

Beta priors are a natural choice for probability parameters, such as ${\pi }_{i,k}^{\text{miss}}$, because they are constrained to (0,1). When no prior information is available, (unrelated) Beta(1,1) priors for each ${\pi }_{i,k}^{\text{miss}}$will appropriately reflect the uncertainty in the probability of an event in the missing individuals.

If the observed data do not provide any information on the missingness mechanism, then the uncertainty in the prior will be propagated to the treatment effect estimate. In this case, values for θ _i,kare simulated ‘forward’ from their prior (as in probabilistic sensitivity analysis commonly used in economic evaluation), as opposed to the deterministic sensitivity analyses where values for θ _i,kare assumed fixed at a particular value. However, in some cases, the information available on the relative treatment effects from studies where few or no data are missing, will allow the prior distribution for ${\pi }_{i,k}^{\text{miss}}$to be updated, so that we ‘learn’ about the missingness mechanism from the data. This approach means that trials with no missing values will have relatively more influence on the estimated treatment effect than those with large amounts of missing data.

3.3.2. Alternative definitions of the missingness parameter, θ _i,k

Although ${\theta }_{i,k}={\pi }_{i,k}^{\text{miss}}$ is a natural parameter on which to place an uninformative prior, it is not a natural parameter on which to elicit informative priors, because it is an absolute, rather than relative measure. If prior information is available on the missingness process, then it may be easier to elicit that information using an alternative definition for the missingness parameter. In this section, we describe some alternative missingness parameters and give the linking equation to replace Equation (6), in our general framework.

3.3.3. θ _i,k= Informative missingness odds ratio

The IMOR 5, 15is defined as the ratio of the odds of the outcome among participants for whom the outcome is missing to the odds of the outcome among observed participants:

$${\mathit{\text{IMOR}}}_{i,k}={\varphi }_{i,k}=\frac{\left({\pi }_{i,k}^{\text{miss}}/\left(1-{\pi }_{i,k}^{\text{miss}}\right)\right)}{\left({\pi }_{i,k}^{\text{obs}}/\left(1-{\pi }_{i,k}^{\text{obs}}\right)\right)}$$

Appendix A shows that the linking equation can be written as

$${\pi }_{i,k}^{\text{obs}}=\frac{-\left(\left(q_{i,k}-{\pi }_{i,k}^{\text{all}}\right)(1-{\varphi }_{i,k})-1\right)-\sqrt{{\left(\left(q_{i,k}-{\pi }_{i,k}^{\text{all}}\right)(1-{\varphi }_{i,k})-1\right)}^2-4{\pi }_{i,k}^{\text{all}}(1-q_{i,k})(1-{\varphi }_{i,k})}}{2(1-q_{i,k})(1-{\varphi }_{i,k})}$$ (7)

Equations (2), (3), [Link], (4), (5)and (7), with either a fixed or random effect model for δ _i, determine the model. Normal priors on log(IMOR _i,k) are a natural choice; however, sensible and informative priors are required for robust results to be obtained.

3.3.4. θ _i,k= Response probability ratio

Defining ω _i,kas the response probability ratio (RPR) 18, we obtain

$${\mathit{\text{RPR}}}_{i,k}={\omega }_{i,k}=\frac{p\left(\text{observed| success}\right)}{p\left(\text{observed| failure}\right)}$$

Applying Bayes' rule and rearranging, we obtain the linkage function:

$${\pi }_{i,k}^{\text{obs}}=\frac{{\omega }_{i,k}\left({\pi }_{i,k}^{\text{all}}/1-{\pi }_{i,k}^{\text{all}}\right)}{1+{\omega }_{i,k}\left({\pi }_{i,k}^{\text{all}}/1-{\pi }_{i,k}^{\text{all}}\right)}$$ (8)

Equations (2), (3), [Link], (4), (5), [Link], (6)and (8), with either a fixed or random effect model for δ _i, determine the model. Normal priors on log(ω _i,k) are a natural choice.

3.3.5. θ _ik= Success probability ratio

Another option could be to instead define θ _i,k=ρ _i,k as the ratio of the probability of success given a subject was missing to the probability of success given a subject was observed

$${\rho }_{i,k}=\frac{{\pi }_{i,k}^{\text{miss}}}{{\pi }_{i,k}^{\text{obs}}}$$

Substituting into Equation (6)and rearranging, we obtain the linkage function:

$${\pi }_{i,k}^{\text{obs}}=\frac{{\pi }_{i,k}^{\text{all}}}{1-q_{i,k}(1-{\rho }_{i,k})}$$ (9)

Equations (2), (3), [Link], (4), (5), [Link], (6)and (9), with either a fixed or random effect model for δ _i, determine the likelihood. Normal priors on log(ρ _i,k) are a natural choice.

3.3.6. More structured models for the missingness parameter

Earlier, we have assumed independent but identical priors for θ _i,kacross studies and arms. These can be modelled in a variety of more structured ways. Here, we give some suggested structural assumptions that could be made, but note that these should be informed by expert opinion, and different sets of assumptions will be appropriate in different applications. Prior distributions could be (i) the same across trial arms but different between trials, (ii) different between trial arms but the same between studies or (iii) different between arms and studies. Furthermore, these different prior distributions across arm and study may be independent, hierarchical or common across trials/arms.

Estimates of treatment effect will be affected by the structure of the missingness model, including prior distributions, as this will determine how much can be ‘learnt’ about the missingness parameters. The stronger the assumptions made in the priors, the more potential for learning, but the validity of the results relies on the validity of the assumptions. Therefore, the choice of model structure should be an informed one and be a part of any elicitation exercise to obtain priors for the missingness parameters 24. For example, if from clinical experience, those who drop out of an active treatment arm are expected to have stopped taking the medication (non‐compliers); it may be considered reasonable to use a model structure where there is an arm‐specific missingness parameter, but that the missingness parameter on the active arm is set equal (or similar) to that for observedoutcomes in a placebo arm 25.

3.4. Priors and implementation

For all models, we assign a Uniform(0,1) prior distribution to the probability of being missing q _i,k, and a Normal(0,100²) prior distribution for the trial‐specific baselines μ _i. In random effects models, we give a Uniform(0,5) prior for the between studies standard deviation, σ. However, it is well documented that results can be sensitive to the form of prior assumed for random effects variances 26. We therefore explored the sensitivity of the results to the prior for σ using the alternative priors: Uniform(0,2) distribution for σand also an informative log Normal(−2.34, 1.62²) prior distribution for σ ², as suggested for a meta‐analysis of a pharmacological treatment versus placebo/control where the outcome is subjective (as is the case here) by Turner et al. 27. Possible priors for the missingness parameters, θ _i,k, have already been indicated in Section 3.3; the specific priors that are used in the applications are described in Sections 4and 5, and we return to consider prior specification further in the discussion.

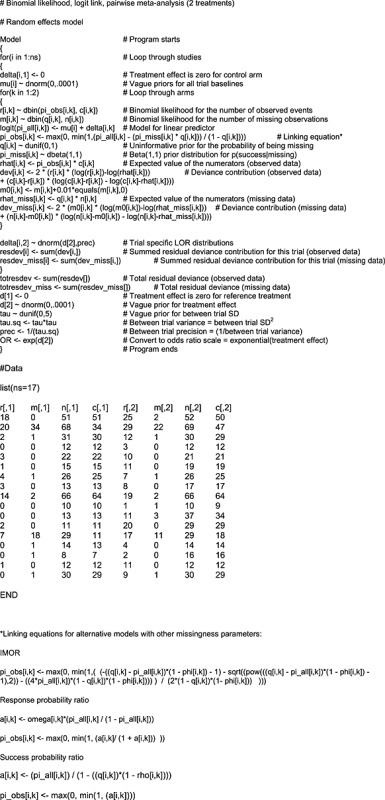
We estimated the model using Markov Chain Monte Carlo simulation implemented in WinBUGS 1.4.3 28. The WinBUGS code to fit our missing data models for each of the proposed definitions of the missingness parameter can be found in Appendix B. The stability of the parameter estimates, Brooks–Gelman–Rubin statistics, auto‐correlation and level of Monte Carlo (MC) error was assessed for each model to determine convergence and the simulation sample size for inference 21.

3.5. Model fit and comparison

To assess the fit of an individual model, we calculated the posterior mean of the residual deviance, ${\overline{D}}_{\text{res}}$. We sum over data points (conditional on being observed) in the calculation of residual deviance, so that models with ${\overline{D}}_{\text{res}}$ close to the number of observed independent data points (conditional on being observed) can be considered an adequate fit to the observed data, whereas models with ${\overline{D}}_{\text{res}}$much bigger than this indicate a lack of fit 3, 14, 21, 29.

4. Exploring uncertainty and learning

We explored the effect of different proportions of missing data and distribution of missing data across trial arms on the resulting estimates of ${\pi }_{i,k}^{\text{miss}}$ using two fictitious data scenarios. We chose an illustrative meta‐analysis of 11 trials with a binary outcome (mortality) 30for which a fixed effect model is known to be appropriate 30and manipulated the data in two ways. In the first scenario, we investigate the effect of fitting our model to a dataset where missing outcomes were not associated with the outcome or treatment arm. We therefore removed 20% of outcomes evenly across arms for eight of the 11 trials.

In the second scenario, we investigate the effect of fitting our model to a dataset where missing outcomes were associated with outcome and treatment arm, but only some trials had missing data. We expect that there is more scope for learning about the treatment effect in this scenario because (i) the missing data depends on outcome and arm, and (ii) there are more trials with complete data to help identify the missingness parameters. We removed 20% of outcomes from each arm of some of the trials (trials 2, 5, 6, 8, 9 and 11), but the proportion of events missing differed between arms for some studies. See Appendix C for the data used in these scenarios.

4.1. Models

We carried out a fixed effects meta‐analysis on each of our two scenarios listed in Section 4. For each scenario, a complete case model was run and the results compared with those obtained for our missing data model (Equations (2), (3), [Link], (4), (5), [Link], (6)), where we put priors on the probability of an event, given missing, ${\pi }_{i,k}^{\text{miss}}\sim \text{beta}(1,1)$.

4.2. Results from artificial data scenarios

4.2.1. Scenario 1: Missingness not associated with outcome or treatment arm

According to the posterior mean residual deviance, there is little difference between the model fit of the complete case model and the Beta(1,1) missing data model (Table 2). In terms of treatment effect, the odds ratio is the same in the two models (median OR 0.80 in both the complete case analysis and in the missing data model), as we would expect because data were assumed MAR. However, the CIs around the treatment effect estimate from the missing data model are wider (Table 2), reflecting the uncertainty induced by missing data. Figure C.1in Appendix C shows the posterior mean and 95% CIs for the probability of missing, q _i,k, which is close to 0 in studies with no missing data (studies 1, 4 and 10), and approximately 0.2 in the other studies, as expected because missingness was introduced by removing approximately 20% of the observed outcomes evenly across arms. Figure 2shows box‐plots of the estimated posterior distribution for ${\pi }_{i,k}^{\text{miss}}$. It can be seen that whilst there is a large degree of uncertainty in these parameters, in some cases, the posterior distribution has moved away from the prior (Beta(1,1) centred on 0.5), showing that the model has ‘learnt’ about the p(success | missing) parameter (Figure 2), albeit only weakly.

Table 2.

Results from artificial data scenarios.

		Posterior mean a	Posterior median odds
Scenario	Model	residual deviance	ratio (95% CI)
Scenario 1: Missingness not	Complete case analysis	19.7	0.80 (0.62, 1.04)
associated with outcome	Missing data framework, prior:	19.4	0.80 (0.50, 1.23)
or treatment arm	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(1,1)$
Scenario 2: Missingness	Complete case analysis	26.0	0.74 (0.58, 0.95)
associated with arm and outcome	Missing data framework, prior:	18.5	0.80 (0.57, 1.11)
	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(1,1)$

^aCompare with 22 data points. Values larger than this are indicative of lack of fit.

Figure 2.

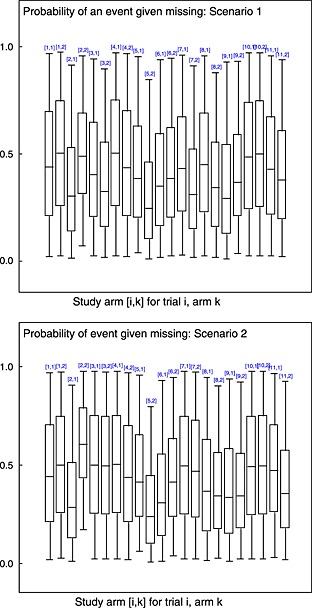
Box‐plots of posterior distribution for ${\pi }_{i,k}^{\text{miss}}$for each study arm [i,k] for trial i, arm k. Plotted for scenarios 1 and 2, respectively. Boxes represent inter‐quartile range, the whiskers represent the 95% CI and line within the box represents the median.

4.2.2. Scenario 2: Missingness associated with arm and outcome

According to the posterior mean residual deviance, the missing data model is a better fit than the complete case model (Table 2). In terms of treatment effect, the odds ratio is different between the two models (median OR 0.74 in the complete case analysis and 0.80 in the missing data model), which together with the model fit results, suggests that the missing data model allows a bias adjustment that explains the lack of fit seen in the complete case model. As in scenario 1, the CI around the treatment effect estimate is wider in the missing data model, reflecting the uncertainty induced by missing data. As with scenario 1, the proportion of missing data is well estimated (Figure C.1in Appendix C). It can be seen from the box‐plots of the estimated posterior distributions for ${\pi }_{i,k}^{\text{miss}}$shown in Figure 2that although there is a large degree of uncertainty in these parameters, there are some study arms where the posterior has moved away from the prior. This suggests that the model has ‘learnt’ about the ${\pi }_{i,k}^{\text{miss}}$ parameters, producing a bias‐adjusted estimated of treatment effect that accounts for the uncertainty introduced by missing data.

5. Application to schizophrenia example

5.1. Prior distributions for ${\pi }_{i,k}^{\text{miss}}$

We begin by considering the case where there is no prior information on the missingness pattern, and so we use independent Beta(1,1) priors for each ${\pi }_{i,k}^{\text{miss}}$as the base case. We then illustrate the impact of using more informative priors. The priors chosen are just illustrative; however, in practise, they would be based on clinical expert opinion. We first explore the impact of increasing the certainty in the prior to Beta(5,5), and then of changing the central estimate by using a Beta(3,7). We then look at the case where there are two different priors for the different arms Beta(3,7) for arm 1 (placebo) and Beta(5,5) for arm 2 (haloperidol). Finally, we use an informative N(0,1) prior on the log(I M O R), to illustrate the impact of a prior belief of MAR (log(I M O R) = 0). For comparison, we also present the standard sensitivity analyses proposed for missing data: complete case, best‐case and worst‐case scenarios and assuming all missing data are failures.

All other prior distributions are as described in Section 3.4.

5.2. Results

For each model, we used at least a 20 000 iteration burn‐in period with at least 60 000 sampling iterations. The posterior mean residual deviance 29, 31suggests that a random effects model is a better fit to the data than a fixed effects model in all cases (Table 3). Within the different fixed effects models, all of the missing data models seem to be a better fit than the standard complete case analysis (Table 3). Trial 2, which is one of the trials with the highest proportion of missing data, has the greatest improvement in model fit, with each arm contributing about 4 to the residual deviance in the complete case model, and only about 1 in the missing data model. Table 1shows that the majority of the trials have only a small amount of missing data. This is likely to be the reason why the estimate of treatment effect is so similar between the complete case model and the Beta(1,1) missing data model (Table 4). The box‐plot of the posterior distribution for p(success | missing) for trial 2 with a high amount of missingness illustrates that the model is ‘learning’ about p(success | missing) as the posterior differs from the Beta(1,1) prior (Figure 3). The missing data model is providing a bias‐adjusted estimate, but because of the small amount of missing data, this estimate is very similar to that produced by the complete case analysis.

Table 3.

Model fit results from applying the standard models and our missing data model to the schizophrenia meta‐analysis example.

		Fixed effect models		Random effects models
		Posterior mean		Posterior mean
		residual deviance		residual deviance
		Event data	Number	Event data	Number
		(given observed)a	missinga	(given observed)a	missinga
Standard models	Complete cases	62.9	NA	32.6	NA
	All missing are failures	60.4	NA	33.5	NA
	Best‐case scenario	66.1	NA	32.3	NA
	Worst‐case scenario	115.4	NA	33.0	NA
	${\pi }_{i,k}^{\text{miss}}=0$	57.7	48.9	33.5	46.8
Missing data	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(1,1)$	46.8	49.4	30.7	46.2
framework	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(5,5)$	50.6	49.5	30.4	46.1
models priors	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(3,7)$	53.0	49.1	31.2	46.3
	${\pi }_{i,1}^{\text{miss}}\sim \text{Beta}(3,7)$and ${\pi }_{i,2}^{\text{miss}}\sim \text{Beta}(5,5)$	52.7	47.8	31.1	45.9
	log(IMOR i,k)= log(ϕ i,k) ∼ Normal(0,1)	56.5	48.0	32.7	47.6

^aCompare with 34 data points. Values larger than this are indicative of lack of fit.

Table 4.

Treatment effect estimates results from applying the standard models and our missing data model to the schizophrenia meta‐analysis example.

		Fixed effect models	Random effects models
		Posterior median	Posterior median
		(95%CI)	(95%CI)
				Between studies
		Odds ratio	Odds ratio	standard deviation
Standard models	Complete cases	3.75 (2.66, 5.37)	8.51 (3.63, 30.66)	1.41 (0.70, 2.80)
	All missing are failures	3.65 (2.65, 5.09)	7.60 (3.48, 26.80)	1.27 (0.58, 2.66)
	Best‐case scenario	6.16 (4.40, 8.74)	12.92 (5.42, 48.38)	1.44 (0.72, 2.86)
	Worst‐case scenario	1.69 (1.26, 2.29)	4.39 (1.60, 14.96)	1.81 (1.11, 3.15)
	${\pi }_{i,k}^{\text{miss}}=0$	3.59 (2.63, 4.97)	7.06 (3.38, 21.63)	1.19 (0.56, 2.41)
Missing data	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(1,1)$	3.76 (2.67, 5.37)	5.80 (2.96, 15.34)	1.01 (0.37, 2.12)
framework	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(5,5)$	3.35 (2.44, 4.62)	5.41 (2.83, 14.05)	1.05 (0.46, 2.12)
models priors	${\pi }_{i,k}^{\text{miss}}\sim \text{Beta}(3,7)$	3.46 (2.52, 4.77)	5.92 (3.02, 15.71)	1.08 (0.50, 2.15)
	${\pi }_{i,1}^{\text{miss}}\sim \text{Beta}(3,7)\text{and}{\pi }_{i,2}^{\text{miss}}\sim \text{Beta}(5,5)$	3.89 (2.83, 5.37)	6.53 (3.37, 17.64)	1.05 (0.48, 2.16)
	log(I M O R i,k)= log(ϕ i,k) ∼ Normal(0,1)	4.09 (2.86, 5.90)	8.60 (3.64, 35.41)	1.39 (0.66, 3.00)

Figure 3.

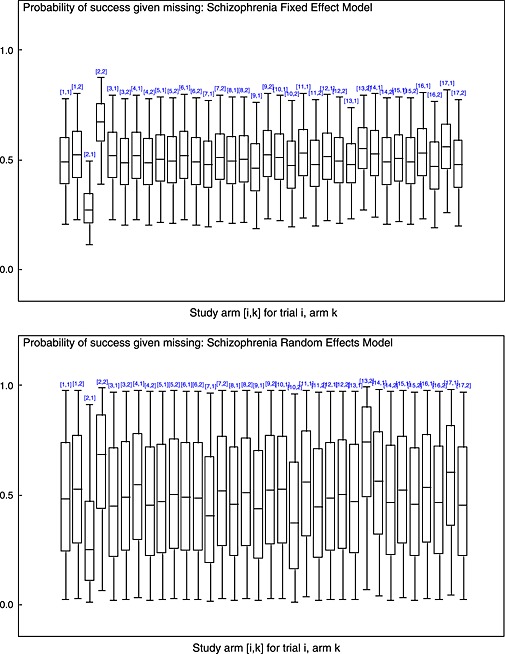
Box‐plots of posterior distribution for ${\pi }_{i,k}^{\text{miss}}$for each study arm [i,k] for trial i, arm kin the schizophrenia meta‐analysis 19. Plotted for fixed and random effect models where a missing data model is used with Beta(1,1) priors for ${\pi }_{i,k}^{\text{miss}}$. Boxes represent inter‐quartile range, the whiskers represent the 95% CI and line within the box represents the median.

Within the random effects models, there is little difference in fit between any of the models (Table 3). These results were expected as random effects models are flexible models that generally fit very well. However, in the random effects missing data models, the between‐study heterogeneity estimates are reduced compared with the standard models, with the exception of the log(I M O R) model (Table 4). There are two possible explanations for this. Firstly, increased uncertainty in the study‐specific treatment effect estimates is consistent with lower heterogeneity, and secondly, adjusting for the missingness mechanism allows for some of the heterogeneity to be explained. In the random effects missing data models, there was also a reduction in the estimate of treatment effect, with the exception of the log(I M O R) model (Table 4). These results are likely because there is only a small amount of missing data, but proportionately, there was more missing data in the control arms of the trials. Increasing the certainty in the prior, by using a Beta(5,5) distribution, resulted in a reduction in the estimate of treatment effect in both the fixed and random effects models. Similarly, changing the central estimate of the prior, using a Beta(3,7) distribution, reduced the estimate of treatment effect (Table 4). The log(I M O R) prior we used was informative and compatible with a belief of MAR. The results from this prior are therefore in line with those from a complete case analysis (Table 4). The meta‐analysis results were sensitive to the choice of prior placed on the heterogeneity parameter; however, the same pattern in the results was found between the complete case and missing data models (results not shown).

Setting ${\pi }_{i,k}^{\text{miss}}$ equal to zero with no uncertainty makes the missing data model similar to an ‘all missing are failures’ analysis. These two models make the same underlying assumption but are not exactly the same. One fixes the observations, stating that all missing outcomes were failures, whereas the other fixes the parameter that generates the data stating that the probability of success in the missing individuals is zero. The two models produce similar results, although the between‐trial standard deviation is reduced when accounting for the missingness parameter in the missing data model.

6. Discussion

We have proposed and illustrated a conceptually and computationally simple Bayesian framework for handling missing binary outcome data in pairwise meta‐analysis. Our model provides an estimate of treatment effect that accounts for uncertainty due to missing outcomes, to provide information for clinicians and local and national health policy makers. The missingness parameter can be parameterised in a variety of formats, including the IMOR, and can be viewed as a one‐stage version of the model presented by White et al. 5. This differs from the model presented in White et al., 12which is a one‐stage, hierarchical selection model, rather than the pattern‐mixture model proposed here.

Our framework does, however, require prior information on the missingness parameter. In the absence of any such prior information, we recommend using a Beta(1,1) prior on the probability of an event given missingness. Note that by using such a flat prior, the missingness parameters may only be weakly identified. However, in the absence of prior information, the uncertainty introduced by missing data will be reflected in the relative effect estimate. If prior information is available, we recommend that it is used. In particular, if the outcome is a rare event, then implicitly, there is prior information that the probability of an event is low regardless of whether the outcome is missing or not, and this information should be incorporated.

A difficulty that arises in all methods that utilise informative prior beliefs is how these beliefs should be obtained 32. If the aim is to simply reflect the uncertainty around missingness, then a flat, uninformative prior will achieve this. One option for eliciting informative prior distributions for unknown outcome parameters is to ask experts to assign a total weight of 100 over several categories of potential options for the unknown parameter and then to model this distribution of weights 12. A similar approach was used by Turner et al.to elicit priors based on asking experts to mark a range of believable values on a scale 33, whilst Mavridis et al.suggest a method based on eliciting the lowest and highest values an expert would conceivably expect 34. White et al. 5suggest that a more realistic prior about the missingness might be obtained by providing an expert with a plausible estimate for the probability of success given a subject was observed (perhaps based on a previous study) and from that, asking their opinion on the probability of success given a subject was missing. From this, the IMOR can then be calculated 5. Other potential options for θ _i,kin our framework (i.e. probability success ratio and probability success difference) could also be elicited this way. Ideally, prior beliefs about unknown parameters should be elicited from experts within the appropriate field. It could be argued that in this context, the investigators of each individual trial may be in the best position to inform the prior distributions required for our models; however, priors elicited from individuals who were involved in the design, running or analysis of the trials may not be objective. It may be more appropriate to elicit prior distributions based on the beliefs of the clinical members of the meta‐analysis team who were not involved personally with any of the trials being used in the analysis. To date, the only study we are aware of that has elicited priors to inform missingness parameters in a meta‐analysis is the work of White et al. 9, although there is work on eliciting opinion for individual trials 12, 35, 36. There is clearly a need for further empirical elicitation studies, to explore the value of this approach in different clinical areas (where reasons for missingness may be very different) and where the proportion of missingness varies (there may be less value in elicitation if there is high power within the meta‐analysis to estimate the missingness pattern). The papers identified in the systematic review may describe methods to adjust for missing data, which may indicate whether there is likely to be informative missingness, and the potential direction of any bias and thus providing further prior information. A recent review of how missing data was handled  in RCTs published in top medical journals 37noted that about 86% of the included studies stated a reason for missingness, with some RCTs reporting specific explanations for missingness. These may be useful to inform priors. Note that, as the posterior distribution for θ _i,kwill in many cases be heavily dependent on the prior assigned to it, it is essential that sensitivity analyses are carried out varying this prior distribution. In addition, the ability of the model to learn about the missingness parameter will diminish with increasing heterogeneity, although the missingness mechanism may potentially explain heterogeneity, as seen in the artificial example.

Another issue that can occur in all meta‐analyses is poor reporting of trials. Trials may not specifically mention missing data, but this does not necessarily mean that outcomes were observed for all participants; there may just have been poor reporting. In some cases, even after close inspection of the text, tables and CONSORT diagram, it may still be unclear whether there are missing data. Because we estimate the probability of a subject being missing, q _i,k, for all studies, our model will estimate q _i,k as non‐zero even when there are no missing data in that trial, and there will be uncertainty in this estimate (Figure C.1in Appendix C). In some applications, this may be appropriate, as some trials may not report missing observations when there are in fact some. Again, clinical input can be helpful to assess whether there are likely to be unreported missing observations. The Cochrane risk of bias tool 1includes an assessment of risk of bias due to missing data. In theory, these assessments could be incorporated into the modelling framework either as covariates or to inform priors; however, this is a notoriously difficult dimension of risk of bias to assess.

The Bayesian approach we have taken is essential in order to be able to specify prior distributions for the missingness parameters and also has the advantage of easy extension from pairwise to network meta‐analysis 14. In network meta‐analysis, because of the consistency assumption, there is the potential to be able to estimate the missingness parameter with more certainty, although the power to do so may still be low 16, 38. This power could be increased by making some of the structural assumptions set out in Table 5. This is an area for further work. The Bayesian approach also allows for the results from the meta‐analysis to be easily integrated into decision models 39, 40. In cost‐effectiveness analyses, estimating the uncertainty in the optimal decision is vital to inform policy decisions. Our framework provides a treatment effect estimate that reflects the uncertainty introduced by missing data, can correct for bias induced by the missing data and can be viewed as a probabilistic sensitivity analysis.

Table 5.

Examples of prior structures for the missingness parameter.

	Model structure for
	θ i,k	Arm‐specific	Trial‐specific	Example
1	Independent	No	No	θ i,k∼f(·)
2	Independent	Yes	No	θ i,k∼f k(·)
3	Independent	No	Yes	θ i,k∼f i(·)
4	Independent	Yes	Yes	θ i,k∼f i,k(·)
5	Hierarchical	No	No	θ i,k∼f(η),η∼ g(·)
6	Hierarchical	Yes	No	θ i,k∼f(η k),η k∼g k(·)
7	Hierarchical	No	Yes	θ i,k∼f(η i),η i∼g i(·)
8	Identical	No	No	θ i,k=η,η∼ f(·)
9	Identical	Yes	No	θ i,k=η k,η k∼f k(·)
10	Identical	No	Yes	θ i,k=η i,η i∼f i(·)
11	Identical	Yes	Yes	θ i,k=η i,k,η i,k∼f i,k(·)

Given prior information on the missingness mechanisms, combinations of these prior structures can be chosen for subsets of the trials included in the meta‐analysis.

fand grepresent generic distributions with given parameters values or depending on a vector of parameters ηor scalar η.

This paper has restricted to the case where the outcome of interest is binary. Dealing with missing data where there are continuous outcome measures is more complex. Different studies may report results using different imputation methods (e.g. last observation carried forwards, baseline observation carried forwards or multiple imputation techniques), which raise challenges for evidence synthesis. Recent work 41has extended the concept of the IMOR to continuous outcomes, defining the informative missingness difference of means and the informative missingness ratio of means, and proposed a pattern‐mixture model for pairwise and network meta‐analysis, using a two‐stage estimation procedure. Extending our framework together with the ideas from Mavridis et al. 41is an exciting area for further work.

In conclusion, the framework outlined here provides a simple method for the best utilisation of evidence produced from RCTs that accounts for any uncertainty induced by missing data, allows for the incorporation of prior information on a variety of different missingness metrics and fits easily into the wider evidence synthesis model for medical decision making 42.

Appendix A. The linking equation when the missingness parameter is the IMOR

A.1.

By definition 17, the IMOR, which we shall denote ϕ _i,k, is

$${\mathit{\text{IMOR}}}_{i,k}={\varphi }_{i,k}=\frac{\left({\pi }_{i,k}^{\text{miss}}/\left(1-{\pi }_{i,k}^{\text{miss}}\right)\right)}{\left({\pi }_{i,k}^{\text{obs}}/\left(1-{\pi }_{i,k}^{\text{obs}}\right)\right)}$$ (A.1)

If ϕ _i,k=1, then ${\pi }_{i,k}^{\text{obs}}={\pi }_{i,k}^{\text{miss}}$, so that Equation (6)gives the linking equation ${\pi }_{i,k}^{\text{obs}}={\pi }_{i,k}^{\text{all}}$. Otherwise, for ϕ _i,k≠1, rearranging (A.1)and substituting into Equation (6)gives the linking equation:

$${\pi }_{i,k}^{\text{obs}}=\frac{-\left(\left(q_{i,k}-{\pi }_{i,k}^{\text{all}}\right)(1-{\varphi }_{i,k})-1\right)\pm \sqrt{{\left(\left(q_{i,k}-{\pi }_{i,k}^{\text{all}}\right)(1-{\varphi }_{i,k})-1\right)}^2-4{\pi }_{i,k}^{\text{all}}(1-q_{i,k})(1-{\varphi }_{i,k})}}{2(1-q_{i,k})(1-{\varphi }_{i,k})}$$ (A11)

However, we need to identify which is the correct root to take. If we define (dropping the iksubscript for convenience)

$$\begin{array}{l}A=1-({\pi }^{\text{all}}-q)\left(\varphi -1\right)\\ B=2\left(1-q\right)\left(1-\varphi \right)\\ \text{so that}\\ {\pi }^{\text{obs}}=\frac{A\sqrt{A^2-2B{\pi }^{\text{all}}}}{B}\end{array}$$ (A.2)

then very careful consideration of the following scenarios shows that:

1. If A< 0 and ϕ< 1 then π ^all<0, which is impossible.

2. If A> 0 and ϕ< 1 then the negative root lies on the interval [0,1], whereas the positive root is always greater than 1. π ^obsmust lie between 0 and 1, and so we take the negative root.

3. If A< 0, ϕ> 1(⇒B< 0), then the negative root lies on the interval [0,1], whereas the positive root is always less than 0. We therefore take the negative root.

4. If A> 0, ϕ _ik>1(⇒B< 0), then the negative root lies on the interval [0,1], whereas the positive root is always less than 0. We therefore take the negative root.

In all cases, we therefore take the negative root, giving the linking equation:

$${\pi }_{i,k}^{\text{obs}}=\frac{-\left(\left(q_{i,k}-{\pi }_{i,k}^{\text{all}}\right)(1-{\varphi }_{i,k})-1\right)-\sqrt{{\left(\left(q_{i,k}-{\pi }_{i,k}^{\text{all}}\right)(1-{\varphi }_{i,k})-1\right)}^2-4{\pi }_{i,k}^{\text{all}}(1-q_{i,k})(1-{\varphi }_{i,k})}}{2(1-q_{i,k})(1-{\varphi }_{i,k})}$$ (A13)

Appendix B. WinBUGS code

B.1.

Appendix C. Artificial data scenarios

C.1.

Original dataset

Trial	Arm 1		Arm 2
	No. of events	Total no. randomised	No. of events	Total no. randomised
i	ri , 1(%)	ni , 1	ri , 2(%)	ni , 2
1	3 (5.5%)	55	1 (1.8%)	55
2	10 (10.6%)	94	3 (3.2%)	95
3	40 (7.0%)	573	32 (5.7%)	565
4	2 (3.3%)	61	3 (4.8%)	62
5	16 (3.8%)	419	20 (4.8%)	421
6	5 (7.2%)	69	3 (4.2%)	71
7	5 (6.7%)	75	5 (6.7%)	75
8	59 (7.5%)	782	52 (6.6%)	790
9	5 (6.2%)	81	2 (2.5%)	81
10	16 (7.1%)	226	12 (5.3%)	225
11	8 (12.1%)	66	6 (8.5%)	71

Scenario 1 dataset: Missingness not associated with outcome or treatment arm

	Arm1						Arm2
		No.	No. of	Total no.	%	%	No. of	No.	No. of	Total no.	%	%
Trial	No. of	missing	complete	randomised	events	events	events	missing	complete	randomised	events	events
	events ri , 1	mi , 1	cases ci , 1	ni , 1	in obs	in miss	ri ,2	mi ,2	cases ci ,2	ni ,2	in obs	in miss
1	3	0	55	55	5.5		1	0	55	55	1.8
2	8	19	75	94	10.7	10.5	2	19	76	95	2.6	5.3
3	32	115	458	573	7.0	7.0	26	113	452	565	5.8	5.3
4	2	0	61	61	3.3		3	0	62	62	4.8
5	13	84	335	419	3.9	3.6	16	84	337	421	4.7	4.8
6	4	14	55	69	7.3	7.1	2	14	57	71	3.5	7.1

Scenario 2 dataset: Missingness associated with arm and outcome

	Arm1						Arm2
		No.	No. of	Total no.	%	%	No. of	No.	No. of	Total no.	%	%
Trial	No. of	missing	complete	randomised	events	events	events	missing	complete	randomised	events	events
	events ri , 1	mi , 1	cases ci , 1	ni , 1	in obs	in miss	ri ,2	mi ,2	cases ci ,2	ni ,2	in obs	in miss
7	4	15	60	75	6.7	6.7	4	15	60	75	6. 7	6. 7
8	47	156	626	782	7.5	7.7	42	158	632	790	6.6	6.3
9	4	16	65	81	6.2	6.3	1	16	65	81	1.5	6.3
10	16	0	226	226	7.1		12	0	225	225	5.3
11	6	13	53	66	11.3	15.4	5	14	57	71	8.8	7.1
1	3	0	55	55	5.5		1	0	55	55	1.8
2	10	19	75	94	13.3	0	1	19	76	95	1.3	10.5
3	40	0	573	573	7.0		32	0	565	565	5. 7
4	2	0	61	61	3.3		3	0	62	62	4.8
5	10	84	335	419	3.0	7.1	16	84	337	421	4.7	4.8
6	4	14	55	69	7.3	7.1	1	14	57	71	1.8	14.3
7	5	0	75	75	6. 7		5	0	75	75	6. 7
8	59	156	626	782	9.4	0	42	158	632	790	6.6	6.3
9	4	16	65	81	6.2	6.3	2	16	65	81	3.1	0
10	16	0	226	226	7.1		12	0	225	225	5.3
11	6	13	53	66	11.3	15.4	6	14	57	71	10.5	0

Figure C.1.

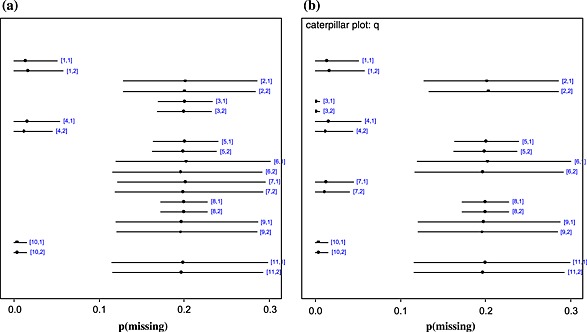
Caterpillar plots showing posterior mean (dot) and 95% CIs (line) of p(missing) for each trial arm in the artificial data scenarios. Indices [i,k] represent arm k(k= 1=placebo;k= 2=active treatment) of trial i. (a) Scenario 1 – trials 2, 3, 5, 6, 7, 8, 9 and 11 had 20% of outcomes removed (from the observed events) from each arm. (b) Scenario 2 – trials 2, 5, 6, 8, 9 and 11 had 20% of outcomes removed from each arm.

Turner, N. L. , Dias, S. , Ades, A. E. , and Welton, N. J. (2015), A Bayesian framework to account for uncertainty due to missing binary outcome data in pairwise meta‐analysis. Statist. Med., 34, 2062–2080. doi: 10.1002/sim.6475.