Mastering variation: variance components and personalised medicine

Abstract

Various sources of variation in observed response in clinical trials and clinical practice are considered, and ways in which the corresponding components of variation might be estimated are discussed. Although the issues have been generally well‐covered in the statistical literature, they seem to be poorly understood in the medical literature and even the statistical literature occasionally shows some confusion. To increase understanding and communication, some simple graphical approaches to illustrating issues are proposed. It is also suggested that reducing variation in medical practice might make as big a contribution to improving health outcome as personalising its delivery according to the patient. It is concluded that the common belief that there is a strong personal element in response to treatment is not based on sound statistical evidence. © 2015 The Authors. Statistics in Medicine published by John Wiley & Sons Ltd.

1. Introduction

Tout le monde y croit cependant, me disait un jour M. Lippmann, car les expérimentateurs s'imaginent que c'est un théorème de mathématiques, et les mathématiciens que c'est un fait expérimental. Henri Poincaré (p. 171)(Nevertheless everyone believes in it, as Lippmann once told me, since the experimental scientists assume it is a mathematical theorem and the mathematicians that it is an empirical fact.)

The quotation from Henri Poincaré 1 concerns the normal distribution, but in my view, a similar situation has arisen regarding variation in response to pharmaceuticals: the trialists have assumed that genetics has shown such variation to be inevitable and the geneticists that clinical trials demonstrate it. However, clinical trials are rarely designed to find it, or at least not in any sense that implies a deep causal structure. Observed variation is, of course, a commonplace, but repeatable variation is quite another matter, and it is here that the problems arise.

It is a simple lesson taught in introductory statistical courses on the design and analysis of experiments that the key to studying interaction is replication. Many analysis of variance courses have proceeded through a set of increasingly complicated designs starting with the completely randomised design, moving on to the randomised block design and then to the randomised block design with replication. Only for the latter is it possible to study treatment‐by‐block interaction, the key to this being that the replication of treatments within blocks permits the separation of the interaction term from the within‐block error, with which it would otherwise be confounded.

In the context of clinical trials, a consequence of this is that the identification of differential response to treatment requires replication at the level at which differential response is claimed 2, 3. Such replication is only achievable with great difficulty at the level of the patient, involving as it would repeated period cross‐over designs or equivalently designs in which a number of patients were given so‐called n‐of‐1 protocols 4, 5, 6.

It is from one point of view surprising, therefore, that the literature of drug development is full of claims from persons of influence and authority that variation in response to treatment is important and known to be so. For example, a recent report 7 (excellent in many ways) of the Food and Drug Administration (FDA) of America provided a list of proportions of non‐responders by disease category, ranging from 38% for depression to 75% for cancer via, for example, 48% for migraine and 52% for osteoporosis. These figures are surprisingly precise, but it is far from clear what they could mean. For example, testicular cancer is one that can be treated with great success, but lung cancer is one with poor prognosis. (Cancer Research UK 8 cites 98% 10‐year survival rates for the former and 5% for the latter.) In this sense, there clearly is a difference in success rates. However, if we therefore classify all lung cancer patients as non‐responders and most testicular cancer patients as responders is this what most understand by personal variation in response? I assume not. Turning to migraine, in the context of that disease, what exactly does non‐response mean?

No further explanation of the figures on non‐response is given by the FDA apart from referring the reader to a paper by Spear et al. 9, in which a table, similar to that given by the FDA, but classifying diseases in terms of responder as opposed to non‐responder rates appears. (I take it as indicative of the problems of identifying such responder rates that the FDA can only cite a single publication, published 12 years earlier as evidence.) Spear et al. themselves give little explanation as to how these figures were calculated beyond stating ‘We have analyzed the efficacy of major drugs in several important diseases, based on published data’ (p. 201). A footnote to the table gives the published source in question, and it turns out to be the 54th edition of The Physicians' Desk Reference 10, a secondary source, which would only be capable of delivering information on responders to treatment if the scientific studies to identify them were widely conducted, which they are not.

The current situation strikes me as being very unsatisfactory, and this paper is conceived as a contribution to increasing communication of the issues, in particular the statistical issues, to non‐statisticians. Accordingly, the emphasis will be on graphical presentations and verbal explanations that can be used to try and make the statistical points as simply as possible. What originality the paper has is mainly in terms of presentation and argument rather than statistical theory. However, there is some evidence that even statisticians can be confused about these matters. For instance, in connection with meta‐analysis, the term ‘random effects’ has been used in two quite different ways in this journal, with the consequences that authors have sometimes talked at cross‐purposes about variation 11.

Two further matters will also be addressed. One has to do with interactions, additivity and clinical relevance; the other has to do with a generally neglected source of variation in the system, namely, physicians. In fact, a personal inspiration for the paper was hearing Brent James give the Deming lecture at the Joint Statistical Meeting in Vancouver in 2010. The lecture was very much concerned with controlling unwanted variation in the healthcare system. One of Deming's important lessons to managers was that they had to understand the origins of variation in a system in order to be able to intervene effectively to improve its quality 12.

The plan of this paper is as follows. The next part briefly reviews components of variation and their influence on observed outcomes in clinical trials. Part three shows how these points may be conveyed using various types of graph. The fourth section considers a technical point of some importance: good statistical models use scales that stabilise variances and minimise interactions, but this does not mean (to the extent that this goal is achieved) that interactions are not important on the clinically relevant scale. The fifth section considers the additional variation in the healthcare system because of variations in physician practice. The sixth section provides a brief discussion.

I am conscious that this is a rather mixed bag of issues, but the unifying theme is that variation in observed outcome can have many different sources and that an effective approach to personalising medicine requires that these be understood.

2. Components of variation

Table 1 is based on Senn, 2001 2 and gives sources of variation in observed outcome in a clinical trial. The meaning of the labels is slightly different depending on the inferential framework used. For example, even sticking within frequentist statistics, one could employ a strict randomisation framework or one could instead use a linear model framework. Within a linear model framework, there are choices as to which effects are fixed and random. Within a Bayesian framework, everything is random, but it depends on what factors are treated hierarchically. This will be touched on briefly having discussed types of trial that might be used to estimate these sources of variation.

Table 1.

Sources of variation in a clinical trial.

	Type of variation	Definition
A	Between treatments	The variation between treatments averaged over all patients
B	Between patients	The variation between patients given the same treatments
C	Patient‐by‐treatment interaction	The extent to which the effects of treatments vary from patient to patient
D	Within patients	Variation from occasion to occasion when the same patient is given the same treatment

Table 2 gives sources of variation that are identifiable according to type of trial. The list of type of trial is not exhaustive. For example, it does not include cluster randomised trials 13, for which the three terms B, C and D are confounded with a further term ‘between‐cluster variation’. In fact almost all parallel group trials are multi‐centre trials. Variation between centres is also identifiable in such trials and hence can be eliminated from the error term. Furthermore, because the patients provide replication at the level of centre, then patient‐by‐centre interaction can also be identified, a subject that has spawned a huge literature in its own right 14, 15, 16, 17, 18, 19. Also not included are so‐called n‐of‐1 trials 4. These are trials in which a single patient is taken as the context for experimentation and is studied in a number of periods being randomised to one or other treatment in a given period. However, if a series of such trials is run 20, then the data for the trials as a whole resemble those that would be obtained from a repeated period cross‐over.

Table 2.

Identifiable sources of variation according to trial design.

Type of trial	Description	Identifiable components of variation	‘Error’ term
Parallel group	Patients are randomised to a course of one of the treatments being compared, which they then follow for the period of the trial.	A	B + C + D
Classical cross‐over	Patients are randomised to sequences of treatments (to be taken in different periods) with the purpose of studying differences between treatments. Each treatment being compared is studied in one period.	A, B	C + D
Repeated period cross‐over	Patients are randomised to sequences in which they are treated by each treatment in more than one period.	A, B, C	D

As mentioned earlier, the meaning of the terms depends somewhat on inferential framework. For example, one might notionally envisage a population of patients who might have been recruited into the trial of which the patients one has are representative. This population might (rather naively) be supposed to be the target population to whom the treatments being compared might be applied or (rather hypothetically) some infinite similar population of which these could be considered to be a suitable sample. Or it might be that any population envisaged is the population of all possible randomisations of patients to treatment, of which, in a two armed trial comparing N patients randomised in equal numbers to each there would be N !/[(N/2) ! (N/2) !] such randomisations. Even for a small trial with only 24 patients in total, there are more than 2.5 million possible allocations. For further discussion of randomisation (and other arguments), see the classic text by David Cox 21 and the more recent one by Rosenberger and Lachin 22.

Given suitable assumptions, then in a modelling framework, it may in fact be possible to identify some interaction even using more simple designs. For an example, one possible interpretation of an increase of variance in the experimental group compared with the control group might be a variation in response to treatment by patients in the experimental group. For an early recognition of this, see Fisher's letter to Daniels 23 (pp. 63–64) of 18 February 1938 in which he has in mind, however, the context of agricultural experiments.

However, this is not the only possible explanation of such an increase in variance. Consider, for example, the comparison of an oral form of a drug with an intravenous form. Absorption may well vary from patient to patient, and this would be a source of interaction. It is also possible, however, that absorption might vary from occasion to occasion for a given patient, and this would thus lead to heteroscedasticity of the within‐patient variances.

Yet another sign of variation at the patient level is a treatment‐by‐subgroup interaction. Here, the members of a subgroup in a trial form the means of providing replication. Also, even if a parallel group trial is run, repeated measures, given strong modelling assumptions, can provide additional degrees of freedom and thus help identify interaction. Finally, cross‐over trials with more than two periods, even if no treatments are repeated, have more degrees of freedom for ‘error’ once treatment, period and patient effects are fitted, and so, some limited identification of response is possible. Preece 24 in a careful re‐analysis of the Cushny and Peebles 25, 26 data quoted by Student 27 gives an example. The strongest form of evidence, however, is given by cross‐over trials, in which at least one of the treatments is repeated. An example in Parkinsonism is given by Senn, Rolfe and Julious 28.

A practical problem is that for many indications cross‐over trials, let alone repeated cross‐over trials, cannot be undertaken. Because replication is the key to identifying interaction, identification of interaction must thus be accepted as only being possible at the group level. For example, it is clearly possible in principle to identify sex‐by‐treatment interaction in any clinical trial provided only that adequate numbers of each sex can be studied.

A further issue that a referee raises is the possibility that if and when we have truly ‘individualised’ treatment, conventional clinical trials may become impossible because there will be so many versions of the treatment. For example, suppose that the treatment itself is derived from the patient's own cells as a sort of personalised vaccine 29. Clearly it is, in a sense, unique. In that case, no repetitions of the treatment are possible. However, repetitions of the technique of personalisation are possible, and it is this that would have to be compared with some alternative strategy, for example, giving all the patients a standard therapy. In that case, the strategy of personalisation as a whole could be assessed. A recent editorial in Nature 30 draws attention to this possibility; although, the claims it makes for proportions of non‐responders in conventional clinical trials are based on highly questionable interpretations of number needed to treat.

Thus, I am not claiming that elements of individual response can hardly ever be identified. I am claiming that the effort necessary, whether in design or analysis, is rarely made and that labelling patients as ‘responders’ and ‘non‐responders’ according to some largely arbitrary dichotomy 31, 32 is not a sensible way to investigate personal response.

3. Some simple graphical lessons

In the section, I present some simple graphs that can be used to teach some lessons about treatment effects. The examples are simulated, and details of the simulations are given in the Appendix.

Figure 1 shows some simulated data from a placebo‐controlled parallel group trial in asthma with 24 patients. The X axis gives the outcome measured in litres of forced expiratory volume in 1 s (FEV₁). High values are ‘good’. The Y axis provides a means of plotting the result patient by patient. The left‐hand panel shows a counterfactual situation in which the values that each patient would have, were he or she treated by placebo or active treatment, as the case might be, are given. It can be seen that the difference patient by patient of the value under active treatment to that under placebo is nearly constant and that no patient does worse under the active treatment than under placebo.

Figure 1.

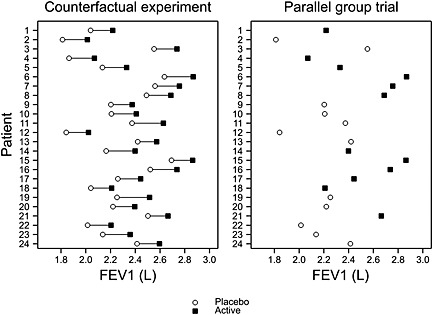
A parallel group trial in asthma with outcome measured in litres of FEV₁. The left‐hand panel shows a theoretical situation that could never be observed, whereby each patient provides an outcome for each treatment. The right‐hand panel shows what would be observed in practice. FEV₁, forced expiratory volume in 1 s.

However, such a trial can never be run. Even a cross‐over trial is not a true counter‐factual experiment because some conditions will have changed once we come to treat the patient again. In a parallel group trial, what we do is randomly choose which patient obtains placebo and which obtains the active treatment. This has been performed in the right‐hand panel of Figure 1 in which one of more than 2.5 million possible allocations, mentioned previously, and splitting 24 patients evenly between the two arms has been chosen.

We can see that the black squares, representing the treatment results, are generally to the right of the open circles for placebo. However, it is by no means the case that all the highest values are under treatment and that all the lowest are under placebo. A common error is to assume that this implies that not all patients benefitted from the treatment. In this case, provided that benefit is measured as the difference in FEV₁, between one treatment and another, the left‐hand panel shows that the benefit was nearly constant from patient to patient. Of course, we are not entitled to assume that this is the case if we only see the right‐hand panel, which corresponds to the sort of parallel group trial we could actually run, but the key point is that nothing entitles us to assume that this is not the case.

What could we do to identify such response? The answer is to carry out, as suggested in Table 2, a repeated cross‐over design 33. Suppose that we carry out such a design in asthma, comparing an active treatment with a placebo, and using the sequences proposed in Table 3. Then in each pair of periods, we can calculate the difference for the patient between the active treatment and placebo. To avoid complications, let us assume that the secular period differences are zero, although in fact by estimating overall period effects and calculating treatment‐centred residuals such complications can easily be dealt with 34. Then in that case, we can plot, patient by patient, on the Y axis the observed difference active − placebo for periods 3 and 4 against the corresponding difference for periods 1 and 2.

Table 3.

Possible sequences for a double cross‐over design.

	Period
Sequence	1	2	3	4
I	Placebo	Active	Placebo	Active
II	Active	Placebo	Active	Placebo
III	Placebo	Active	Active	Placebo
IV	Active	Placebo	Placebo	Active

Such a trial has been simulated for 1000 patients, and the results are show in Figure 2 in the following. An arbitrary threshold for response has been set to 0.3 L, and the dashed lines show these boundaries for the first and second cross‐over trials. The solid lines show the mean difference specified in setting up the simulation, and this is 0.5 here.

Figure 2.

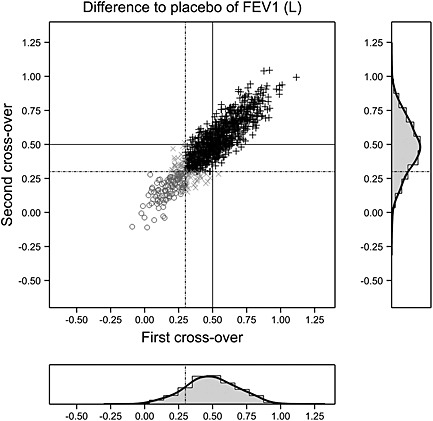
A double cross‐over trial in asthma with difference treatment – placebo calculated for each of two pairs of periods. The difference for the second pair is plotted against that for the first. The solid lines show the mean difference of 0.5 L; the dashed lines represent an arbitrary threshold for ‘response’ at 0.3 L. Black plus signs: responded on both occasions. Open circles: responded on neither occasion. A patient who responded on one occasion only is plotted as an x. The correlation between differences is 0.9. Marginal distributions are also shown as histograms and a smoothed density. FEV₁, forced expiratory volume in 1 s.

Patients can be classified as to whether they responded, by this arbitrary definition, on both occasions. The frequencies are given in Table 4 from which it can be seen that of the 846 patients who responded in the first cross‐over, 806 responded in the second, a proportion of 806/846 = 0.95. However, it is also interesting to note that of the 154 who did not respond in the first cross‐over, 31 responded in the second, a proportion of 31/154 = 0.2. However, it seems clear here that ‘response’ in the first cross‐over is highly predictive of ‘response’ in the second so that one may indeed speak of ‘responders’ and ‘non‐responders’ (even if on an individual basis they cannot be perfectly identified).

Table 4.

Patients in a double cross‐over in asthma classified by response in each cross‐over for a case in which there is a strong element of personal response.

		Second cross‐over
		Responder
First cross‐over		Yes	No	Total
Responder	Yes	806	40	846
	No	31	123	154
	Total	837	163	1000

A very different picture, however, is given in Figure 3. Here, there appears to be no relationship between response in the first pair of periods and response in the second.

Figure 3.

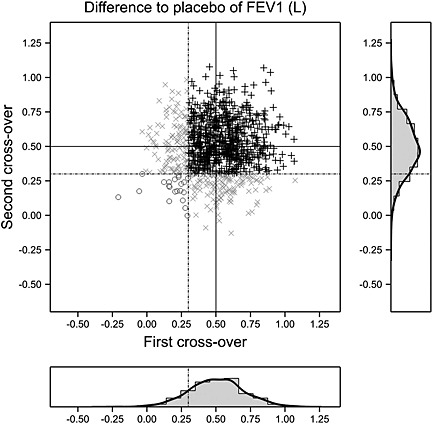
A double cross‐over trial in asthma with difference treatment – placebo calculated for each of two pairs of periods. The difference for the second pair is plotted against that for the first. The solid lines show the mean difference of 0.5 L; the dashed lines represent an arbitrary threshold for ‘response’ at 0.3 L. Black plus signs: responded on both occasions. Open circles: responded on neither occasion. A patient who responded on one occasion only is plotted as an x. The correlation between differences is 0.02. Marginal distributions are also shown as histograms and a smoothed density. FEV₁, forced expiratory volume in 1 s.

This is confirmed by Table 5 where, although the marginal probabilities of response are approximately 85% just as was the case before, the conditional probability of response given previous non‐response is 116/137 = 0.85 and thus no different from that given previous response, which is 736/863 = 0.85. In other words, this is a situation in which 100% of the patients respond 85% of the time rather than being one in which 85% of the patients respond most of the time.

Table 5.

Patients in a double cross‐over in asthma classified by response in each cross‐over for a case in which there is no element of personal response.

		Second cross‐over
		Responder
First cross‐over		Yes	No	Total
Responder	Yes	736	127	863
	No	116	21	137
	Total	852	148	1000

The marginal distributions are plotted both as histograms and kernel density estimates in Figures 2 and 3. The important point to note is that had we only run one cross‐over trial, that is to say only using periods 1 and 2 and not 3 and 4, we could not have drawn a scatter plot of response (if this is defined as the difference between treatment with an active treatment and treatment with placebo). All we could have drawn is a marginal distribution. However, the marginal distributions on the X axis in Figures 2 and 3 are indistinguishable or at least, given either you could not tell which of the two cases it represented. The key to identifiablity of interaction is adequate replication.

4. Interaction

In their careful discussion of interaction 35, Amy Berrington de Gonzalez and David Cox (BG & C) following an earlier paper by Cox 36 distinguish between primary factors and intrinsic factors. In the context here, the treatment given in a clinical trial, and hence by extension in clinical practice, is a primary factor, and covariates that vary from individual to individual are intrinsic factors. An interaction between a treatment and a covariate is an indication that, on the scale on which it is observed, the effect of treatment (primary) varies according to the level of the covariate (intrinsic).

As BG & C show, provided that the cumulative distribution of response under one treatment does not cross the distribution for the other as a covariate (or function of covariates) varies, then in principle, a transformation (which may be complicated) can be found, which makes the differences between the treatments constant on the scale chosen, so that an additive 37 model may be used. Of course, David Cox's famous paper with George Box illustrates a flexible approach to finding a suitable transformation 38. Such scales can simplify the model that has to be fitted and thereby increases the precision of predictions.

BG & C suggest that transformations that are hard to interpret should be avoided. However, although this is very much in the spirit of much practice in medical statistics, it is very much against almost everything that is carried out in bioinformatics, where the willingness to ‘black box’ predictive algorithms is pretty much unrestrained. (As an example, see Lone et al. 39, where extremely complex classifiers for diagnosing Parkinsonism were developed, without really revealing a portable scoring method for others to use, the whole being based on 49 patients and 41 controls!) In my view, the issue is rather one of how modelling results may be used, and sacrificing additivity in the name of interpretability of the effect scale means that the covariate scale will have to become part of the definition of the treatment effect anyway 37. Thus, a complicated story cannot be avoided. My own preference is to use the scale that leads to a simpler model whether or not this is the scale that is easier to understand. A very useful reference on turning models into predictions is the paper by Lane and Nelder 40.

Of course, there may be then some necessary work to translate from the additive scale to the clinically relevant one. For example, empirical work has shown that the log‐odds ratio scale exhibits less heterogeneity in meta‐analysis than the risk difference scale 41, 42, and there are good reasons for expecting this to be so for most cases (although one can think of exceptions).

However decision‐making requires calculation on the probability scale. Thus, a combination of modelling on the log‐odds scale and prediction on the probability scale (using estimates of background risk) can be a powerful way of translating from clinical trials to personal decision‐making. A very nice illustration of this approach was given 20 years ago in a simple article in the British Medical Journal by Glasziou and Irwig 43. Consider a case where the risk of side effect cannot be distinguished amongst patients, who thus can do no better than assume that the average risk applies to them. On the other hand, benefit is assumed constant on the log‐odds scale, and this means that rational choice of treatment depends on background risk. This also shows, however, that there is a sense in which the variability that the statistician removes by transformation has not gone away: it still has important clinical consequence.

As BG & C point out, a very different type of interaction is one that is truly qualitative and cannot be removed by transformation. A key paper is that of Rothman, Greenland and Walker 44 who draw a careful distinction between statistical and biologic interaction. See also Sjolander et al. for bounds on ‘causal’ interaction 45. A spectacular example of such an interaction was given by Pearson et al. in the New England Journal of Medicine 46 in which they showed that 44 out of 49 diabetic patients with a Kir6.2 mutation could cease insulin treatment when given sulfonylureas, for which there was a very plausible biological explanation. This is the sort of interaction that is purely qualitative and, in fact, has a monogenic origin. Where responses to treatment are modulated in this on–off way, then estimation approaches such as the sure outcome of random events approach proposed in this journal by Bouckaert and Mouchart 47 might be useful. However, it is, of course, one thing for such qualitative interactions to be present and another to be able to identify them.

Thus, to sum up this section, there are different sorts of interactions. A lack of a statistical interaction on a given scale may, nonetheless translate into what Rothman et al.44 call an interaction in individual decision‐making. Conversely, interactions on a default statistical scale, let alone a clinically relevant scale do not prove that there is a biologic interaction. Careful thought about what one is looking for and what one wishes to claim is important but understanding the components of variation involved is also key.

5. Variation in a healthcare system

Figure 4 presents data on tonsillectomy rates in those aged under 15 years by local authority in England for the years 2009–2011 using data collected by The Unit of Health Care Epidemiology of the University of Oxford 48. The local authorities have been sorted by order of rate from highest to lowest.

Figure 4.

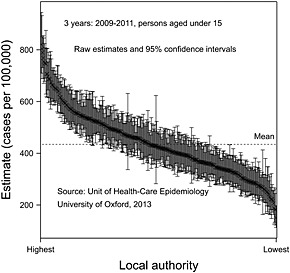
Tonsillectomy rates for persons under 15 years of age for 3 years (2009–2011) by local authority, together with 95% confidence limits.

Of course, some of the differences could be random and so, respecting the message of this paper, it is important not to overreact to observed differences. However, the confidence intervals permit, of course, standard errors to be calculated, and so it is possible to carry out a conventional random effects meta‐analysis and hence shrink the results. This has been carried out in Figure 5 from which it can be seen that most of the variation is not pure statistical error but represents some true underlying variation. The ratio in ‘true’ rates, highest to lowest, is nearly 4.7, and this is something that would be hard to explain in terms of case‐mix, although, of course, a formal investigation of this would be useful to establish exactly how much can be explained in terms of patient differences. Be that as it may, it seems plausible that either the population is being over‐treated in some authorities or under‐treated in others. It is hard to believe that every policy in every authority is correct.

Figure 5.

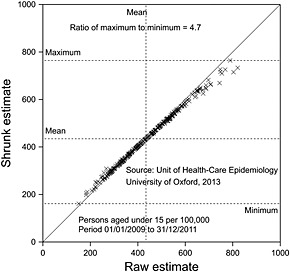
Shrunk tonsillectomy rates for persons under 15 years of age for 3 years (2009–2011) by local authority plotted against raw rate by local authority given in Figure 4. The diagonal solid line is a line of equality of shrunk and original effects. Dashed horizontal lines indicate minimum, mean and maximum shrunk values. A dashed vertical line gives the mean original value.

Of course, the example is an extreme one, but there are surely many others in which there is considerable variation in medical practice that is hard to justify in terms of case‐mix. For example, Wennberg and Thomson 49 claim that ‘US and UK data show that much of the variation in use of healthcare is accounted for by the willingness and ability of doctors to offer treatment rather than differences in illness or patient preference’ and that in the US, ‘… regions with high rates of use of supply sensitive care do not have better overall outcomes as measured by mortality and indicators of the quality of care…’ It thus seems that a further source of variation can be added to the four listed in Table 1, namely, variation between ‘providers’.

Managers (or other with decision‐making capabilities) who intervene in a system without understanding it adequately was what Deming identified as being an important adverse influence on quality 12. This problem has been taken seriously by Brent James and colleagues at Intermountain Health who have implemented a vigorous policy of addressing unwanted variation by getting practice to converge to an agreed policy 50. Of course, such convergence is only valuable if the agreed policy has a ‘correct’ specification in the first place, and it is towards establishing what such policies should be that the efforts of evidence‐based medicine have been developed. There is a considerable danger, however, that an obsession with personalising medicine before a reasonable average policy has been established may actually introduce harmful variations into the system. Again understanding components of variation is key.

6. Discussion

The purpose of this paper is not to dispute that there is a potential for personalising treatment. In fact, the history of medical progress has clearly involved personalisation at every stage. For example, classifying diabetes as being two different diseases and hence treating them differently is a form of personalisation, and in this context, the work of Pearson et al.46, already cited, can be seen as a further development of this process and, indeed, one that relied on genetics.

However, it is also useful to be hard‐headed about this. There are many difficulties in personalising medicine. One of the problems in doing so using genetic information is what might be called the phenotypic squeeze: any strategy based on genetics will be more complicated than a ‘one size fits all’ approach but likely to be less precise than one based on the phenotype. (See chapter 25 of Statistical Issues in Drug Development for a discussion 51.) A good example of this is given by Jack James who makes the point that in many cases, genetics adds little and (again concerning diabetes) says: ‘One explanation of this poor performance is that known clinical risk factors such as obesity and elevated glucose levels are themselves substantially inherited’ 52 (p. 386).

Many encouraging examples of personalisation of medicine are given in the FDA document I have already criticised. Nevertheless, it is disturbing that that document can do no better than cite some statistics that cannot be checked and which are themselves derived from a secondary source. If the FDA's belief that the personal component is well founded, the agency ought to be able to better than this to justify it. Elsewhere, in epidemiology and psychology, there has been a long history of using twin studies and other approaches based on research in families to establish how much variation is genetic. This is hardly a secret. A much‐cited paper 53 by Lichtenstein et al., combining data from 44,788 pairs of twins from Danish, Finnish and Swedish twin registries were able to assess the relative importance of heritability and environment for cancer at 11 sites. By comparing monozygotic and dizygotic twins, they were able to estimate the proportion of variation that was genetic. (They make the point that this depends, of course, on the degree of variation that the environment offers.) The highest proportion they estimated was 42% for prostate cancer. (This figure may also seem rather precise, but unlike the FDA, they also quote confidence limits, which for this site are 29% and 50%.) However, the interesting bonus that the study delivered was that for some cancers they were nevertheless able to establish that this variation exceeded that that was known from single‐gene mutations. Thus careful study of components of variation yields the dividend of a better idea as to what there might be to find. In fact, Kalow et al. have proposed cross‐over trials as the trialist's equivalent of the twin study 6, and such designs seem to be currently underexploited for the purpose of understanding sources of variation 2.

George Davy Smith 54, whose discussion of Lichtenstein et al., first brought their paper to my attention, has also suggested that despite the large amount of variation that remains inexplicable, it is not entirely a ‘Gloomy Prospect’ that faces epidemiologists and, in particular, that allele scoring approaches may help to classify risk. Nevertheless, it should be understood that whether the source is environment or genetics, the sorts of variation that Lichtenstein et al. examine are (potential) contributions to the source of variation labelled B in Table 1. They are main effects, whereas what personalised medicine targets is the interactive effect labelled C in the table. Such interactive effects are usually less important.

In short, the business of personalising medicine is likely to be difficult. We already know that it has turned out to be much more difficult than many thought it would be. A contribution that statisticians can make is to remind their colleagues of the importance of understanding sources of variation.

Appendix: Details of the simulation

For figure 1, 24 values under placebo were simulated from a normal distribution with a mean of 2.3 L and a variance of 0.07 L². To these placebo values, a constant difference of 0.2 L was added to create the value under active treatment. Twenty‐four random effects were then simulated from a normal distribution with mean 0 and variance 0.001 L². The resulting 24 values were divided in 2 and subtracted from the corresponding placebo value and added to the corresponding active values and the results plotted in the left‐hand panel. For the right‐hand panel, 12 pairs of values chosen at random had the active member of the pair removed, and for the remaining 12, the placebo member of the pair was removed.

For figure 2, 1000 pairs of differences active – placebo were generated from a bivariate normal distribution with means 0.5 L, variances 0.04 L² and a correlation coefficient of 0.9.

For figure 3, 1000 pairs of differences active – placebo were generated from a bivariate normal distribution with means 0.5 L, variances 0.04 L² and a correlation coefficient of 0.02.

Senn, S. (2016) Mastering variation: variance components and personalised medicine. Statist. Med., 35: 966–977. doi: 10.1002/sim.6739.