Analytical gradients for MP2, double hybrid functionals, and TD‐DFT with polarizable embedding described by fluctuating charges

Abstract

A polarizable quantum mechanics (QM)/ molecular mechanics (MM) approach recently developed for Hartree–Fock (HF) and Kohn–Sham (KS) methods has been extended to energies and analytical gradients for MP2, double hybrid functionals, and TD‐DFT models, thus allowing the computation of equilibrium structures for excited electronic states together with more accurate results for ground electronic states. After a detailed presentation of the theoretical background and of some implementation details, a number of test cases are analyzed to show that the polarizable embedding model based on fluctuating charges (FQ) is remarkably more accurate than the corresponding electronic embedding based on a fixed charge (FX) description. In particular, a set of electronegativities and hardnesses has been optimized for interactions between QM and FQ regions together with new repulsion–dispersion parameters. After validation of both the numerical implementation and of the new parameters, absorption electronic spectra have been computed for representative model systems including vibronic effects. The results show remarkable agreement with full QM computations and significant improvement with respect to the corresponding FX results. The last part of the article provides some hints about computation of solvatochromic effects on absorption spectra in aqueous solution as a function of the number of FQ water molecules and on the use of FX external shells to improve the convergence of the results. © 2015 The Authors. Journal of Computational Chemistry Published by Wiley Periodicals, Inc.

Introduction

Hybrid quantum mechanics (QM) molecular mechanics (MM) approaches (QM/MM) have become key ingredients of the so‐called multiscale computational strategies.1, 2, 3, 4, 5, 6, 7 The idea behind those approaches is to treat accurately, by QM methods, a small but critical part of the overall system under investigation, while resorting to less accurate, but much cheaper MM methods for the remaining part. These approaches are, of course, far more efficient than the corresponding full QM model, thus allowing the study of phenomena localized on some dozens of atoms, but tuned by the effect of thousands of more distant atoms. QM/MM models have provided interesting results for a variety of chemical systems and/or physical chemical properties in the fields of catalysis,8, 9 spectroscopy,10, 11, 12, 13 reaction mechanisms,14 and drug discovery.15, 16 In addition to those fields, QM/MM approaches are particularly suited to deal with solvation phenomena provided that boundary conditions are taken into the proper account.11, 17, 18, 19, 20 As a matter of fact, full QM approaches become in this case not only unfeasible unless resorting to oversimplified (e.g., semiempirical) methods, but also quite illogical, whenever the interest is not to reach a detailed description of the whole solvent, but, rather, of the tuning of solute structure and/or properties by the solvent. For this reason, focused models, that is, strategies paying privileged attention to the solute, seem the methods of choice and several reports suggest that, among different alternatives, QM/MM models are especially effective.11, 21, 22 Solvent effects on the solute structure and/or properties are tuned by a subtle interplay of short‐ and long‐range contributions. The latter effects are described with sufficient accuracy by mean‐field approaches, like the polarizable continuum model23 (PCM), whose latest implementations couple reliability and negligible computational cost in very robust algorithms also for analytical derivatives with respect to geometrical parameters and electromagnetic field.24, 25, 26 However, when short‐range interactions play a leading role (e.g., for polar moieties in hydrogen bonding solvents) a continuum description of the solvent is no more fully adequate and explicit strategies are required to ensure an accurate description of the so‐called cybotactic region (roughly corresponding to the first solvation shell).27 In most applications of QM/MM methodologies to solvation phenomena, the combination of a QM description of the solute with a fixed charge (FX) description of solvent molecules (together with repulsion–dispersion contributions from a purposely tailored force field28, 29) is sufficient to yield accurate results. However, in some cases the QM region needs to be enlarged with a few solvent molecules,30 thus introducing some ambiguity in the selection of those molecules, together with technical difficulties for a fully dynamical treatment due to possible exchanges between QM and MM solvent molecules.31, 32 It is, therefore, interesting to develop improved classical descriptions including (at least) polarization effects to completely avoid the use of QM solvent molecules. Such an approach is also more consistent with the use of boundary conditions based on the PCM, which includes by construction polarization. Several methods have been proposed to include polarization into QM/MM models, a concept pioneered in the seminal paper by Warshel and Levitt.1 Among the different possibilities we have selected the so‐called fluctuating charge (FQ) approach,33, 34 which avoids computation of electric fields and is more consistent with both density functional theory (DFT) and PCM descriptions. From the one side, fluctuating charges are obtained by the so‐called electronegativity equalization principle,35, 36 which can be regarded as a simplified second‐order approximation to DFT. From the other side, endowing each atom with an effective charge depending on its environment is strongly reminiscent of the effective charges generated on the finite elements describing the surface of the cavity embedding the solute in the PCM. The recent extension of the QM/FQ model to analytical first and second derivatives for Hartree–Fock (HF) and Kohn–Sham (KS) methods37 and to the corresponding response equations for various internal and external perturbations38, 39 makes this model particularly suitable for the evaluation of molecular properties and spectroscopic parameters. Use of polarizable QM/MM models (hereafter referred to as polarizable embedding [PE]) becomes even more significant for excited electronic states and has been considered by several groups39, 40, 41, 42, 43 since the pioneering work by Luzhkow and Warshel exploiting the Langevin dipole solvent model.44 However, to the best of our knowledge, those studies have been limited to excitation energies or excitation energy transfers, whereas excited state structures have never been addressed so far, not to speak about vibronic contributions.45, 46 In this work, we present, for the first time, the theory and implementation of a PE based on FQ's to excited state structures and properties, through the definition of effective algorithms to compute TD‐DFT analytical gradients. The machinery developed for this purpose is closely related to that needed for other nonvariational methods and, in particular, for second order many body perturbation theory (e.g., MP2). Apart from its intrinsic interest, MP2 enters as a contribution in the so‐called double hybrid (DH) functionals, which are able to deliver very accurate results for structures, thermodynamic, and spectroscopic properties.47, 48, 49, 50, 51, 52, 53, 54 We have, therefore, implemented energies and analytical gradients also for MP2/FQ and DH/FQ models.

The article is organized as follows. In the next section, the theoretical background is presented together with some details about our implementation in the Gaussian package.55 After a brief description of the computational segments of this work, the implementation is validated by comparison with finite difference results. Next, electronegativities, hardnesses, and dispersion‐repulsion parameters have been optimized for the interaction of water molecules with a number of basic chromophores (acetone, formamide, pyridine, pyrimidine) in their ground electronic states. Without introducing any further parameter, absorption spectra have been computed including vibronic effects for adducts of the same chromophores with one or two water molecules. Finally, the solvatochromic shift of the $n\to {\pi }^{*}$ transition of pyridine in aqueous solution has been investigated using increasing numbers of FQ water molecules together with different nonperiodic boundary conditions. As a last remark, we point out that in this work, the discussion will be restricted to noncovalent interactions between QM and MM regions: extension to covalent bond breaking is straightforward in the framework of the ONIOM approach,56 but requires a detailed tuning of computational parameters, which will be dealt with in a forthcoming study.

Theory

In this section, we extend the QM/FQ approach to the evaluation of time dependent DFT (TD‐DFT) excited state gradients and ground state gradients for MP2 and DFT DH functionals. The discussion starts with a brief summary of the QM/FQ approach and of the related quantities/equations, together with a brief presentation of analytical geometrical derivatives and response equations. Then, TD‐DFT excited state gradients are treated, as well as the extension to the Z‐vector formalism. All the implementations have been done on a development version of the Gaussian code.55

The QM/FQ model

Given a large molecular system, one common approach is to treat the most important region at an high level of theory, usually based on QM methods, and the remaining part at a lower level of theory, usually based on MM methods. In the standard QM/MM formalism,34, 39, 57, 58, 59 the total energy of the system reads

$$E_{\text{tot}}=E^{\text{QM}}+E^{\text{MM}}+E^{\text{int}},$$ (1)

where the functional form of E ^QM depends on the specific choice of the QM method used for the treatment of the high‐level region, while E ^MM contains all the intra‐ and intermolecular terms of the MM force field of the low‐level region. When the QM and MM subsystems are not covalently bonded and charge transfer effects are neglected, the interaction energy term E ^int can be partitioned into electrostatic, polarization, repulsion, and dispersion contributions

$$E^{\text{int}}=E^{\text{el}}+E^{\text{pol}}+E^{\text{rep}}+E^{\text{disp}}.$$ (2)

In this work, repulsion and dispersion contributions will be approximated by simple Lennard–Jones (LJ) functions

$$E^{\text{rep}}+E^{\text{disp}}\simeq E^{\text{LJ}}=\sum _{l\in \text{MM}k\in \text{QM}}{s}_{kl}^{\text{LJ}}4{\mathrm{ϵ}}_{kl}\left[{\left(\frac{{\sigma }_{kl}}{R_{kl}}\right)}^{12}-{\left(\frac{{\sigma }_{kl}}{R_{kl}}\right)}^6\right],$$ (3)

where ϵ_kl and σ_kl are two empirical parameters, $R_{kl}=|{\overrightarrow{R}}_k-{\overrightarrow{R}}_l|,\hspace{0.17em}{\overrightarrow{R}}_k$ and ${\overrightarrow{R}}_l$ are the atomic coordinates, and $s_{kl}^{\text{LJ}}$ is a scaling factor (or, in principle, even a continuous function), which takes into account the fact that in the most popular force fields 1–2, 1–3, and, even, 1–4 interactions are either screened or completely removed. The electrostatic term of eq. (2), E ^el, is the interaction energy between the QM ( $n(\overrightarrow{r})$) and the MM ( $\rho (\overrightarrow{r})$) charge densities

$$E^{\text{el}}={\displaystyle \int d}\overrightarrow{r}d\overrightarrow{r}\hspace{0.17em}\prime \frac{n(\overrightarrow{r})\rho (\overrightarrow{r}\hspace{0.17em}\prime )}{|\overrightarrow{r}-\overrightarrow{r}\hspace{0.17em}\prime |},$$ (4)

where $\rho (\overrightarrow{r})$ is considered as a distribution of N point‐like charges $q_k\hspace{0.17em}(k=1,\mathrm{2...},N)$ located at ${\overrightarrow{R}}_k$

$$\rho (\overrightarrow{r})={\displaystyle \sum _{k\in \text{MM}}{q}_k}\delta (\overrightarrow{r}-{\overrightarrow{R}}_k).$$ (5)

Equation (4) can be evaluated using different approaches of various sophistication and physical meaning (see Refs. 57, 58, 59 and references therein). The simplest one is to resort to the so‐called mechanical embedding (ME) scheme, where the electrostatic interaction energy is treated by assigning a set of point charges to the QM atoms, which interact with the MM charges via a Coulomb kernel

$$E^{\text{ME}}={\displaystyle \sum _{l\in \text{MM}k\in \text{QM}}{s}_{kl}^{\text{el}}}\frac{q_k{q}_l}{R_{kl}}.$$ (6)

In this formula, $s_{kl}^{\text{el}}$ is a scaling factor, analogous to $s_{kl}^{\text{LJ}}$ of eq. (3). An alternative approach is the so‐called electronic embedding (EE) scheme, where the electrostatic interaction is included in the QM Hamiltonian59 and E ^el is evaluated from the “true” QM electrostatic potential (i.e., without making any approximation on the QM charge distribution, besides the ones intrinsic to the current QM method)

$$E^{\text{EE}}={\displaystyle \sum _{k\in \text{MM}}{\displaystyle \int d}}\overrightarrow{r}\frac{n(\overrightarrow{r})q_k}{|\overrightarrow{r}-{\overrightarrow{R}}_k|}.$$ (7)

Finally, the polarization energy accounts for the mutual polarization of the QM density and the MM charge distribution, and is the basis of the so‐called PE schemes. Among the several methods proposed for the inclusion of polarization effects on the total QM/MM energy,34, 39, 60, 61, 62, 63, 64, 65, 66 in our approach,34, 39 we will exploit the fluctuating charges (FQ)33, 34, 35, 36, 37, 38, 39, 67 scheme. In such a model, the polarization effects are treated by endowing each MM atom with a charge, which depends on the atomic electronegativity and hardness.34 The equilibrium between the charge interactions and the differences in the atomic electronegativities represents the physical basis of the electronegativity equalization principle,33, 35, 36 which defines, in turn, the FQ model. The QM/FQ model has recently been extended by some of the present authors to the evaluation of analytical first and second derivatives,37 response equations,39 magnetic perturbations with gauge independent atomic orbitals (GIAO)38 and excitation energies at the equation of motion coupled cluster singles and doubles (EOM‐CCSD) level,43 and has been shown to give remarkable agreement with experimental findings in various applications in the field of computational spectroscopy.11, 21, 22 In the polarizable QM/FQ approach, the interaction energy is analogous to eq. (7), with the FQ classical charge distribution ( $\stackrel{\sim }{\rho }(\overrightarrow{r})$) written in terms of a set of polarizable charges $\stackrel{\sim }{\mathbf{q}}$

$$\stackrel{\sim }{\rho }(\overrightarrow{r})={\displaystyle \sum _{k\in \text{MM}}{\stackrel{\sim }{q}}_k}\delta (\overrightarrow{r}-{\overrightarrow{R}}_k),$$ (8)

and the electrostatic interaction with the QM density reads

$$E^{\text{PE}}={\displaystyle \sum _{k\in \text{MM}}{\displaystyle \int d}}\overrightarrow{r}\frac{n(\overrightarrow{r}){\stackrel{\sim }{q}}_k}{|\overrightarrow{r}-{\overrightarrow{R}}_k|}.$$ (9)

The QM charge density can be then expanded in the molecular orbital (MO) basis

$$n(\overrightarrow{r})={\displaystyle \sum _{A\in \text{QM}}{Z}_A}\delta (\overrightarrow{r}-{\overrightarrow{R}}_A)-{\displaystyle \sum _{pq\sigma }^{\text{MO}}{D}_{pq\sigma }}{\varphi }_{p\sigma }(\overrightarrow{r}){\varphi }_{q\sigma }(\overrightarrow{r}),$$ (10)

where Z_A is the atomic number of the A nucleus, D the ground‐state density matrix, p, q indexes run over the set of MO orbitals ( ${\varphi }_{p\sigma }(\overrightarrow{r})$), σ is the spin label. Then, the electrostatic potential at point $\overrightarrow{R_k}$ associated to such a density ( $\mathbf{V}[\mathbf{D}]$) is

$$V_k[\mathbf{D}]={\displaystyle \sum _{A\in \text{QM}}{Z}_A}(A|k)-{\displaystyle \sum _{pq\sigma }^{\text{MO}}{D}_{pq\sigma }}(pq\sigma |k),$$ (11)

where the integrals are defined as

$$(pq\sigma |k)={\displaystyle \int d}\overrightarrow{r}d\overrightarrow{r}\hspace{0.17em}\prime \hspace{0.17em}\frac{{\varphi }_{p\sigma }(\overrightarrow{r}){\varphi }_{q\sigma }(\overrightarrow{r})\delta (\overrightarrow{r}\hspace{0.17em}\prime -\overrightarrow{R_k})}{|\overrightarrow{r}-\overrightarrow{r}\hspace{0.17em}\prime |}=V_{pq\sigma ,k}$$ (12)

$$(A|k)={\displaystyle \int d}\overrightarrow{r}d\overrightarrow{r}\hspace{0.17em}\prime \hspace{0.17em}\frac{\delta (\overrightarrow{r}-\overrightarrow{R_A})\delta (\overrightarrow{r}\hspace{0.17em}\prime -\overrightarrow{R_k})}{|\overrightarrow{r}-\overrightarrow{r}\hspace{0.17em}\prime |},$$ (13)

and eq. (9) can then be written in matrix formalism

$$E^{\text{PE}}=V\stackrel{\sim }{\mathbf{q}}.$$ (14)

The vector $\stackrel{\sim }{\mathbf{q}}$ is obtained by variationally minimizing the total energy of the FQ subsystem34, 39 ( $\mathcal{E}$) with respect to the charges, in the presence of the QM electrostatic potential

$$\mathcal{E}={\displaystyle \sum _{\alpha i}{q}_{\alpha i}}{\chi }_{\alpha i}+\frac{1}{2}{\displaystyle \sum _{\alpha i}{\displaystyle \sum _{\beta j}{q}_{\alpha i}}}{\eta }_{\alpha i,\beta j}{q}_{\beta j}+{\displaystyle \sum _{\alpha }{\lambda }_{\alpha }}{\displaystyle \sum _i(q_{\alpha i}-Q_{\alpha })}+V\stackrel{\sim }{\mathbf{q}},$$ (15)

where the α and β indices run over the molecules, i and j indicate the atoms of each molecule, $Q_{\alpha }$ is the total charge of the molecule α, ${\chi }_{\alpha i}$ is the electronegativity of the atom αi and ${\eta }_{\alpha i,\beta j}$ the charge–charge interaction kernel. The FQ equations can be solved for the charges by exploiting either matrix inversion or iterative procedures: in the following, we will refer to matrix inversion, for which the following relation holds

$$\stackrel{\sim }{\mathbf{q}}[\mathbf{D}]={\mathbf{J}}^{-1}(-{\mathbf{C}}_{\mathbf{Q}}-\mathbf{V}[\mathbf{D}]),$$ (16)

where J is the matrix including the charge–charge interaction kernel and charge constraints, while ${\mathbf{C}}_{\mathbf{Q}}$ includes the electronegativities and the $Q_{\alpha }$s, as reported in detail in the previous works.34, 39 Please note that the J matrix of this work corresponds to the D matrix of the previous works, and we have slightly changed the notation here since the D symbol has been used for the ground‐state density matrix. Then, at each SCF step, V is evaluated from the current QM density and the FQ charges are computed with eq. (16). The ground‐state total energy of the QM/MM system, E _tot, is variationally optimized with respect to $n(\overrightarrow{r})$ and $\stackrel{\sim }{\mathbf{q}}$. Please refer to the original works34, 39 for a detailed presentation of the method and implementation.

As mentioned above, the physics behind the electrostatic embedding with fixed charges and the PE with the FQ model is different, since different energy contributions are involved in the two models. As a matter of fact, the EE based on fixed charges can be used for the treatment of bulk environmental effects, whereas the PE can be used to treat the QM/MM interface. For this reason, both approaches can be simultaneously used in the calculations for solvated systems, resulting in the solvent molecules far from the solute and belonging to the bulk to act as a polarization effect on the solute, without being affected by the solute charge density, whereas the solvent molecules near to the solute are polarized by the QM charge density. The present implementation of the QM/FQ approach permits the coexistence of fluctuating and fixed charges in the MM subsystem, and each set of charges is properly treated. When the QM/FQ scheme is used in conjunction with fixed charges, the total energy of eq. (1) becomes

$$E_{\text{tot}}=E^{\text{QM}}+E^{\text{MM}}+E^{\text{PE}}+E^{\text{EE}}+E^{\text{LJ}},$$ (17)

where E ^PE and E ^EE depend on FQ and fixed charges, respectively. Several implementations of E ^MM and E ^LJ together with analytical first and second derivatives are already available also for FQ force fields,^[34,37] and enter without modifications also the new developments. For this reason, in the following, we will only focus on quantities connected to the PE and EE terms in eq. (17).

Some useful FQ quantities

In this section, we recall some quantities related to the QM/FQ model, entering the expressions of analytic energy derivatives and linear response properties of eq. (17). For practical purposes, it is useful to introduce a reference effective ground state Hamiltonian, which includes all terms explicitly depending on the QM density

$$E_0=〈\Psi \left|{\mathcal{H}}_{\text{eff}}\right|\Psi 〉=E^{\text{QM}}+E^{\text{PE}}+E^{\text{EE}}.$$ (18)

In this article, we will be concerned with HF, KS ,and MP2 models together with their combinations (e.g., hybrid and double‐hybrid functionals). It is, therefore, convenient to express E ^QM in a form general enough to include all these approaches47, 48, 49, 50

$$\begin{array}{cc}& E^{\text{QM}}=V_{NN}+h+J+a_x{E}_x^{\text{HF}}+a_{xc}{E}^{\text{XC}}+a_c{E}_c^{\text{PT}2}\\ & E^{\text{XC}}=(1-a_x)E_x^{\text{GGA}}+(1-a_c)E_c^{\text{GGA}}\\ & E_c^{\text{PT}2}=\frac{1}{4}{\displaystyle \sum _{ia,jb}{t}_{ab}^{ij}}(ia||jb)\\ & t_{ab}^{ij}=\frac{(ia||jb)}{{\epsilon }_i+{\epsilon }_j-{\epsilon }_a-{\epsilon }_b}.\end{array}$$ (19)

In the last equation, $E_x^{\text{HF}}$ is the HF exchange energy, J is the classical Coulomb energy, E ^XC is the pure DFT exchange‐correlation energy, $E_c^{\text{PT}2}$ is the correction for the MP2 correlation treatment, the $i,j,\mathrm{...}$ indexes run over the occupied spin‐orbitals, $a,b,\mathrm{...}$ over the virtual spin‐orbitals, and ${\epsilon }_i$ is the orbital energy of the ith spin‐orbital and $(ia||jb)$ is the common notation for the Coulomb and exchange integrals. a_x is the mixing parameter introduced by Becke,68, 69 which allows to continuously pass from a pure functional (a_x = 0) to a full HF theory ( $a_x=1,a_{xc}=a_c=0$) (hybrid functionals), while a_c accounts for a further generalization of the treatment of the correlation, from a pure local (GGA) form (a_c = 0) to the pure PT2 form (a_c = 1). Then, the pure GGA is recovered by choosing $a_x=a_c=0$, the pure HF by $a_x=1,a_c=a_{xc}=0$, and the MP2 method by $a_x=a_c=1,a_{xc}=0$. In the B2PLYP DH functional,47, 48, 49, 50 $a_x=0.53,a_c=0.27$, with X=B88,70 and C=LYP.71 More recent spin‐scaled approaches can be also used splitting the last term of eq. (19) into parallel and opposite spin contributions with different percentages.72, 73

The energy in eq. (18) can be rewritten by separating out the SCF and PT2 contributions

$$E_0=E^{\text{SCF}}+a_c{E}^{\text{PT}2},$$ (20)

where the PE and EE interaction energies have been included in the SCF term. Consequently, the generic Fock matrix element in the MO basis is

$$F_{pq\sigma }=h_{pq\sigma }+{\displaystyle \sum _{i\tau }[(pq\sigma |ii\tau )-a_x{\delta }_{\sigma \tau }(pi\sigma |iq\sigma )]}+v_{pq\sigma }^{\text{XC}}+v_{pq\sigma }^{\text{PE}}+v_{pq\sigma }^{\text{EE}},$$ (21)

where $\sigma ,\tau$ are spin indexes with values α, β, and the PE contribution ( $v_{pq\sigma }^{\text{PE}}$) is the derivative of E ^PE with respect to the generic $D_{pq\sigma }$ density matrix element

$$v_{pq\sigma }^{\text{PE}}=\frac{\partial E^{\text{PE}}}{\partial D_{pq\sigma }}=-{\displaystyle \sum _{k\in \text{MM}}{V}_{pq\sigma ,k}}{\stackrel{\sim }{q}}_k=-{\mathbf{V}}_{pq\sigma }\stackrel{\sim }{\mathbf{q}}.$$ (22)

By analogy with the previous equation, $v_{pq\sigma }^{\text{EE}}$ can be obtained in a similar way by using the set of fixed charges q and the potential as evaluated at the proper coordinates.

The Fock operator derivative with respect to the $D_{rs\tau }$ matrix element (the so‐called coupling matrix)74, 75, 76 is required to define TD‐DFT and coupled perturbed hartree fock (CPHF) procedures

$${\mathbb{K}}_{pq\sigma ,rs\tau }=\frac{\partial F_{pq\sigma }}{\partial D_{rs\tau }}=(pq\sigma |rs\tau )-a_x{\delta }_{\sigma \tau }(pr\sigma |sq\sigma )+f_{pq\sigma ,rs\tau }^{\text{XC}}+f_{pq\sigma ,rs\tau }^{\text{PE}}.$$ (23)

A major difference between PE and EE approaches is that the FQ charges $\stackrel{\sim }{\mathbf{q}}$ depend on the QM density, and therefore, an explicit FQ term appears in eq. (23), which is instead not present in the EE scheme. The kernel of the FQ interaction ( $f_{pq\sigma ,rs\tau }^{\text{PE}}$), then reads

$$f_{pq\sigma ,rs\tau }^{\text{PE}}=\frac{\partial v_{pq\sigma }^{\text{PE}}}{\partial D_{rs\tau }}=-{\displaystyle \sum _{kl\in \text{MM}}{\displaystyle \int d}}\overrightarrow{r}d\overrightarrow{r}\hspace{0.17em}\prime \hspace{0.17em}\frac{{\varphi }_{p\sigma }(\overrightarrow{r}){\varphi }_{q\sigma }(\overrightarrow{r})}{|\overrightarrow{r}-{\overrightarrow{R}}_k|}{J}_{kl}^{-1}\frac{{\varphi }_{r\tau }(\overrightarrow{r}\hspace{0.17em}\prime ){\varphi }_{s\tau }(\overrightarrow{r}\hspace{0.17em}\prime )}{|\overrightarrow{r}\hspace{0.17em}\prime -{\overrightarrow{R}}_l|},$$ (24)

and analogously to the $f_{pq\sigma ,rs\tau }^{\text{XC}}$ term, for real orbitals is symmetric under the $r\to s$ exchange. The previous equation can be rewritten in a more compact matrix form

$$f_{pq\sigma ,rs\tau }^{\text{PE}}=-{\displaystyle \sum _{kl\in \text{MM}}{V}_{pq\sigma ,k}}{J}_{kl}^{-1}{V}_{rs\tau ,l}=-{\mathbf{V}}_{pq\sigma }{\mathbf{J}}^{-1}{\mathbf{V}}_{rs\tau },$$ (25)

in analogy with the expression obtained by some of us by means of time dependent perturbation theory.39

Although TD‐DFT is always formulated in the MO formalism, in practical implementations, it is generally recast into the atomic orbital (AO) basis. By expanding the density in the AO basis, the PE energy, Fock and coupling matrix elements read

$$E^{\text{PE}}={\displaystyle \sum _{A\in \text{QM},k\in \text{MM}}{Z}_A}(A|k){\stackrel{\sim }{q}}_k-{\displaystyle \sum _{\mu \nu \sigma ,k\in \text{MM}}{D}_{\mu \nu \sigma }}(\mu \nu |k){\stackrel{\sim }{q}}_k,$$ (26)

$$v_{\mu \nu \sigma }^{\text{PE}}=-{\displaystyle \sum _{k\in \text{MM}}(\mu \nu |k)}{\stackrel{\sim }{q}}_k$$ (27)

and

$$f_{\mu \nu \sigma ,\kappa \lambda \tau }^{\text{PE}}=-{\displaystyle \sum _{kl\in \text{MM}}(\mu \nu |k)J_{kl}^{-1}(l|\kappa \lambda )},$$ (28)

where the Greek indices have been used for the AO basis functions, $D_{\mu \nu \sigma }$ is the generic AO density matrix element, and the $(\mu \nu |k)$ integrals are the analogous of the ones defined in eq. (12) in the MO basis.

Analytical derivatives

The derivation of the ground‐state energy gradient within the EE‐QM/MM framework, including also issues related to the link atom approach, has been presented in several papers,57, 58, 59, 77 and in a recent work, the extension to the FQ model has also been reported.37 In case of nuclear coordinate perturbations, the analytical gradient of the QM/MM energy in eq. (17) involves different contributions on the basis of which atom the perturbation is referred to. As mentioned in The QM/FQ Model section, the gradients of E ^MM and E ^LJ are already available and have not been modified in this work. Regarding the other contributions, following previous works on this topic,37, 77 the gradient of the energy in eq. (20) with respect to a QM atomic coordinates reads

$$E_0^x=E^{\text{SCF},x}+a_c{E}^{\text{PT}2,x},$$ (29)

where the SCF term reads77

$$E^{\text{SCF},x}=〈{\mathbf{h}}^x\mathbf{D}〉+\frac{1}{2}〈{\mathbf{G}}^{(x)}(\mathbf{D})\mathbf{D}〉+\stackrel{\sim }{\mathbf{q}}{\mathbf{V}}^{(x)}(\mathbf{D})-〈\mathbf{W}{\mathbf{S}}_{oo}^x〉,$$ (30)

where $〈\hspace{1em}〉$ denotes the usual trace operation. In the previous equation, h and G are the one‐ and two‐electron Fock matrices, S is the AO overlap and W the SCF energy‐weighted density matrix. If the derivative refers to a fixed‐charge atom, $\stackrel{\sim }{\mathbf{q}}{\mathbf{V}}^{(x)}$ is replaced by $\mathbf{q}{\mathbf{V}}^{(x)}$. The evaluation of the PT2 part in eq. (29) is more complex, because it is a nonvariational contribution and involves the derivatives of the spin‐orbitals rotation coefficients, which require the solution of a set of ${(3N)}^n$ CPHF equations. In the Z‐vector approach,78 such a set is reduced to one single set of equations independent of the perturbation, so that once the Lagrangian (L) and the response operator ( $\mathbf{R}[{\mathbf{P}}^{\Delta }]$) are built, orbital rotations are obtained as the occupied‐virtual (ov) blocks of the ${\mathbf{P}}^{\Delta }$ matrix49

$$({\epsilon }_{a\sigma }-{\epsilon }_{i\sigma })P_{ai\sigma }^{\Delta }+R_{ai\sigma }[{\mathbf{P}}^{\Delta }]=L_{ai\sigma }.$$ (31)

The response operator associated to the Fock operator in eq. (21) is

$$R_{pq\sigma }[{\mathbf{P}}^{\Delta }]={\displaystyle \sum _{rs\tau }{P}_{rs\tau }^{\Delta }}[2(pq\sigma |rs\tau )+2f_{pq\sigma ,rs\tau }^{\text{XC}}+2f_{pq\sigma ,rs\tau }^{\text{PE}}-c_x{\delta }_{\sigma \tau }[(ps\sigma |rq\sigma )+(pr\sigma |sq\sigma )]],$$ (32)

and can be also expressed in terms of the coupling matrix $\mathbb{K}$ as

$$R_{pq\sigma }[{\mathbf{P}}^{\Delta }]={\displaystyle \sum _{rs\tau }{P}_{rs\tau }^{\Delta }}\left[{\mathbb{K}}_{pq\sigma ,rs\tau }+{\mathbb{K}}_{pq\sigma ,sr\tau }\right].$$ (33)

As previously discussed in Some Useful FQ Quantities section, being the PE scheme quadratically dependent on the QM density matrix, one contribution related to eq. (22) is explicitly included in eq. (31).

The solution of eq. (31) allows to build the one particle relaxed difference density matrix (1PDM) ${\mathbf{P}}^{\Delta }$ (ov blocks), the energy weighted difference density matrix ( ${\mathbf{W}}^{\text{PT}2}$), and the two particle density matrix ( ${\mathbf{\Gamma }}^{\text{PT}2}$), and the final form of the gradient can then be assembled from such quantities49, 79

$$E_0^x=〈{\mathbf{h}}^x\mathbf{D}〉+〈{\mathbf{W}}^{\text{PT}2}{\mathbf{S}}^x〉+{\displaystyle \sum _{\mu \nu \kappa \lambda }{\Gamma }_{\mu \nu \kappa \lambda }^{\text{PT}2}}{(\mu \nu |\kappa \lambda )}^x+E^{\text{XC},x}({\mathbf{P}}^{\Delta },\mathbf{D})+〈v^{\text{PE},x}{\mathbf{P}}^{\Delta }〉.$$ (34)

The PE term can be computed from the derivative of the AO Fock matrix operator

$$v_{\mu \nu \sigma }^{\text{PE},x}=-{\displaystyle \sum _{k\in \text{MM}}{(\mu \nu |k)}^x}{\stackrel{\sim }{q}}_k[\mathbf{D}]-{\displaystyle \sum _{k\in \text{MM}}(\mu \nu |k)}{\stackrel{\sim }{q}}_k^x[\mathbf{D}]$$ (35)

and contraction with the 1PDM

$$\begin{array}{cc}〈v^{\text{PE},x}{\mathbf{P}}^{\Delta }〉=& -{\displaystyle \sum _{\mu \nu \sigma ,k\in \text{MM}}{P}_{\mu \nu \sigma }^{\Delta }}{(\mu \nu |k)}^x{\stackrel{\sim }{q}}_k[\mathbf{D}]-{\displaystyle \sum _{kl\in \text{MM}}{\stackrel{\sim }{q}}_k}[{\mathbf{P}}^{\Delta }]J_{kl}^x{\stackrel{\sim }{q}}_l[\mathbf{D}]\\ & +{\displaystyle \sum _{\mu \nu \sigma ,k\in \text{MM}}{D}_{\mu \nu \sigma }}{(\mu \nu |k)}^x{\stackrel{\sim }{q}}_k[{\mathbf{P}}^{\Delta }]-{\displaystyle \sum _{A,k\in \text{MM}}{Z}_A}{(A|k)}^x{\stackrel{\sim }{q}}_k[{\mathbf{P}}^{\Delta }].\end{array}$$ (36)

In the last equation, the set of charges $\stackrel{\sim }{\mathbf{q}}[{\mathbf{P}}^{\Delta }]$ has been obtained in analogy with eq. (16)

$$\stackrel{\sim }{\mathbf{q}}[{\mathbf{P}}^{\Delta }]=-{\mathbf{J}}^{-1}\mathbf{V}[{\mathbf{P}}^{\Delta }],$$ (37)

where the electrostatic potential generated by the ${\mathbf{P}}^{\Delta }$ charge distribution is defined as

$$V_k[{\mathbf{P}}^{\Delta }]=-{\displaystyle \sum _{\mu \nu \sigma }{P}_{\mu \nu \sigma }^{\Delta }}(\mu \nu |k).$$ (38)

It is worth noting that in case also a set of fixed charges is included in the calculation, another gradient contribution is present, accounting for the FQ‐fixed charge interaction. Such a term has a shape similar to the last term of the previous equation, where the nuclear charges Z_A are substituted with the set of fixed charges q_i.

Linear response theory

When the linear response approach74, 75, 76, 80, 81 is applied to the QM/FQ model, in principle both the QM and the FQ charge distributions should respond to the perturbation. However, in case, the interest is focused to the chromophore, which is assumed to be fully included in the model system, linear response theory is applied only to the QM Hamiltonian of the model system. Here, we briefly recall the main aspects of the TD‐DFT equations applied to the SCF energy of eq. (20), and we will formulate the method in terms of a variational functional, which is convenient when analytic derivatives are to be computed.80, 81, 82, 83, 84

By following Furche et al.,80, 81 the vertical excitation energies Ω are the stationary points of the functional

$$G[X,Y,\Omega ]=〈X,Y\left|\Lambda \right|X,Y〉-\Omega (〈X,Y|\Delta |X,Y〉-1),$$ (39)

where

$$|X,Y〉=\left(\begin{array}{c}\mathbf{X}\\ \mathbf{Y}\end{array}\right)$$ (40)

and

$$\Lambda =\left(\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{B}& \mathbf{A}\end{array}\right),\hspace{1em}\hspace{1em}\Delta =\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).$$ (41)

X and Y are the amplitudes for the single particle excitation and de‐excitation, respectively, and the response matrices A and B are defined in terms of derivatives of the ov blocks of the Fock matrix in the MO basis

$$\begin{array}{cc}& A_{ai\sigma ,bj\tau }={\delta }_{\sigma \tau }{\delta }_{ab}{\delta }_{ij}({\epsilon }_{a\sigma }-{\epsilon }_{i\sigma })+{\mathbb{K}}_{ai\sigma ,bj\tau }\\ & B_{ai\sigma ,bj\tau }={\mathbb{K}}_{ai\sigma ,jb\tau }.\end{array}$$ (42)

The functional in eq. (39) is variational in sense that by imposing the derivative of G with respect to $〈X,Y|$ to be zero, the Casida equations follow,74, 75 while the zeroth derivative with respect to Ω includes orthonormality conditions on the amplitudes $〈X,Y|$. This is equivalent to minimize the energy

$$\Omega =〈X,Y\left|\Lambda \right|X,Y〉$$ (43)

under the constraint

$$〈X,Y|\Delta |X,Y〉=1.$$ (44)

In the following, the linear combinations of A and B matrices rather than the single matrices will be required81

$$\begin{array}{cc}& {(\mathbf{A}+\mathbf{B})}_{ia\sigma ,jb\tau }={\delta }_{\sigma \tau }{\delta }_{ab}{\delta }_{ij}({\epsilon }_{a\sigma }-{\epsilon }_{i\sigma })+2(ia\sigma |jb\tau )+2f_{ia\sigma ,jb\tau }^{\text{XC}}-a_x[(ja\sigma |ib\sigma )+(ab\sigma |ij\sigma )]+2f_{ia\sigma ,jb\tau }^{\text{PE}}\\ & {(\mathbf{A}-\mathbf{B})}_{ia\sigma ,jb\tau }={\delta }_{\sigma \tau }{\delta }_{ab}{\delta }_{ij}({\epsilon }_{a\sigma }-{\epsilon }_{i\sigma })+a_x[(ja\sigma |ib\sigma )-(ab\sigma |ij\sigma )].\end{array}$$ (45)

The FQ interaction kernel is symmetric under the spin exchange, so that it only appears in the $(\mathbf{A}+\mathbf{B})$ combination, whereas it cancels out in the $(\mathbf{A}-\mathbf{B})$ combination.85 In practical implementations, TD‐DFT equations are solved in AO basis with standard techniques as76, 85, 86, 87, 88

$${(\mathbf{A}-\mathbf{B})}^{1/2}(\mathbf{A}+\mathbf{B})|X+Y〉={\omega }^2{(\mathbf{A}-\mathbf{B})}^{-1/2}|X+Y〉.$$ (46)

TD‐DFT excited state gradient

In a time‐dependent framework, the energy of the nth excited state is expressed as the sum of the ground‐state energy and the vertical transition energy, so that the generalized excited state gradient is given by the sum of two separate contributions

$$E_n^x=E_0^{\text{SCF},x}+{\omega }_{0\to n}^x.$$ (47)

The evaluation of the ground state contribution, $E_0^{\text{SCF},x}$, has already been discussed in Analytical Derivatives section, while ${\omega }_{0\to n}^x$ is the derivative of the excitation energy calculated by applying the linear response theory to eq. (18) (see Linear Response Theory section), and by neglecting the PT2 contribution. Then, ${\omega }_{0\to n}^x$ can in principle be calculated as the derivative of the G functional

$${\Omega }^x=〈X,Y\left|{\Lambda }^x\right|X,Y〉,$$ (48)

where the derivatives of the transition amplitudes $|X,Y〉$ are not required in virtue of the variational character of G, whereas the derivatives of the molecular orbital coefficients are involved for the evaluation of ${\Lambda }^x$. This leads to a high‐computational cost and complex expressions for excited state gradients.81 In the practice, it is more convenient to recast the derivatives in a Lagrangian formulation,81 by making use of the Z‐vector method78

$${\Omega }^x=G^{(x)}[X,Y,\Omega ]+{\displaystyle \sum _{ia\sigma }{Z}_{ia\sigma }}{F}_{ia\sigma }^{(x)}+{\displaystyle \sum _{pq\sigma ,p\le q}{W}_{pq\sigma }}{S}_{pq\sigma }^{(x)}.$$ (49)

In eq. (49), the contribution arising from the MO relaxation is dropped out from G^x (which becomes $G^{(x)}$, using a well‐known formalism77), and is included in the Lagrange multipliers $Z_{ia\sigma }$ and $W_{pq\sigma }$, contracted with the derivatives of the Fock and overlap matrices, respectively.

FQ contribution to the Z‐vector equations

The procedure for the determination of Z and W has been reported in the literature81, 85; here, we will focus on FQ contributions. The unrelaxed difference density matrix T is built once the eigenvectors X and Y are found from the solution of the TD‐DFT equations81

$$\begin{array}{cc}& T_{ab\sigma }=\frac{1}{2}{\displaystyle \sum _i\left[{(X+Y)}_{ia\sigma }{(X+Y)}_{ib\sigma }+{(X-Y)}_{ia\sigma }{(X-Y)}_{ib\sigma }\right]}\\ & T_{ij\sigma }=-\frac{1}{2}{\displaystyle \sum _a\left[{(X+Y)}_{ia\sigma }{(X+Y)}_{ja\sigma }+{(X-Y)}_{ia\sigma }{(X-Y)}_{ja\sigma }\right]}\\ & T_{ia\sigma }=T_{ai\sigma }=0.\end{array}$$ (50)

The T matrix includes contributions of the SCF spin‐orbitals to the excited state density, without accounting for any relaxation. Therefore, the effect of the FQ embedding is included in T through the X and Y vectors. The relaxation of the spin‐orbitals due to the perturbation is included in the ov blocks of Z (which has zero oo and vv blocks), which is determined by solving the Z‐vector equations [see eq. (31)], where the response operator is $R[\mathbf{Z}]$ and the Lagrangian on the right‐hand side is now expressed in terms of X and Y. All such matrices are affected by the FQ embedding, as well as Z. Once Z is computed, 1PDM is assembled as

$${\mathbf{P}}^{\Delta }=\mathbf{T}+\mathbf{Z},$$ (51)

and corresponds to the effective excited state contribution to the total generalized density matrix.

It is worth noting that the fixed charges used in the standard EE scheme do not depend on the QM density matrix, so that there is not any explicit contribution arising from the EE in eq. (45). Furthermore, by comparing the last expression with the analogous one related to the PT2 derivatives, we note that in the latter case, the 1PDM was obtained only as the ov blocks of Z, whereas in the present case contributions arising from the oo and vv blocks are included through the T matrix. After the Z‐vector equations are solved, the energy‐weighted difference density matrix W is assembled.

TD‐DFT gradients working equations

Once eq. (31) is solved and all the quantities introduced in FQ Contribution to the Z‐Vector Equations section have been assembled, eq. (49) can be written as

$$\begin{array}{cc}{\omega }^x=& 〈{\mathbf{h}}^x{\mathbf{P}}^{\Delta }〉-〈{\mathbf{S}}^x{\mathbf{W}}^{\Delta }〉+〈v^{\text{XC},(x)}{\mathbf{P}}^{\Delta }〉+〈〈{(\mu \nu |\kappa \lambda )}^x\mathbf{\Gamma }〉〉\\ & +〈〈(\mathbf{X}+\mathbf{Y})f^{\text{XC},(x)}(\mathbf{X}+\mathbf{Y})〉〉+{\omega }^{\text{PE},x}\end{array}$$ (52)

where $〈\hspace{1em}〉$ denotes the trace operation on $\mu \nu$ indexes, $〈〈\hspace{1em}〉〉$ denotes the double trace operation on the $\mu \nu$ and $\kappa \lambda$ indexes, and $\mathbf{\Gamma }$ is the two‐particle difference density matrix (2PDM). ${\omega }^{\text{PE},x}$ is the explicit FQ contribution

$${\omega }^{\text{PE},x}=〈v^{\text{PE},x}{\mathbf{P}}^{\Delta }〉+〈(\mathbf{X}+\mathbf{Y})f^{\text{PE},x}(\mathbf{X}+\mathbf{Y})〉.$$ (53)

The first term of eq. (53) is analogous to the PT2 one, already treated in Analytical Derivatives section. The derivatives of the FQ kernel can be evaluated from eq. (28)

$$\begin{array}{c}{f}_{\mu \nu \sigma ,\kappa \lambda \tau }^{\text{PE},x}=-{\displaystyle \sum _{kl\in \text{MM}}{(\mu \nu |k)}^x}{J}_{kl}^{-1}(l|\kappa \lambda )-{\displaystyle \sum _{kl\in \text{MM}}(\mu \nu |k){(J_{kl}^{-1})}^x}(l|\kappa \lambda )\\ -{\displaystyle \sum _{kl\in \text{MM}}(\mu \nu |k)J_{kl}^{-1}{(l|\kappa \lambda )}^x},\end{array}$$ (54)

and the contraction with $(\mathbf{X}+\mathbf{Y})$ gives

$$〈(\mathbf{X}+\mathbf{Y})f^{\text{PE},x}(\mathbf{X}+\mathbf{Y})〉=-2{\displaystyle \sum _{\mu \nu \sigma ,k\in \text{MM}}{(\mathbf{X}+\mathbf{Y})}_{\mu \nu \sigma }}{(\mu \nu |k)}^x{\stackrel{\sim }{q}}_k[\mathbf{X}+\mathbf{Y}]-{\displaystyle \sum _{kl\in \text{MM}}{\stackrel{\sim }{q}}_k}[\mathbf{X}+\mathbf{Y}]J_{kl}^x{\stackrel{\sim }{q}}_l[\mathbf{X}+\mathbf{Y}],$$ (55)

where the set of charges $\stackrel{\sim }{\mathbf{q}}[\mathbf{X}+\mathbf{Y}]$ are evaluated from the $(\mathbf{X}+\mathbf{Y})$ matrix in analogy with eqs. (37) and (38).

In summary, the evaluation of TD‐DFT gradients within the QM/FQ approach requires to:

1. Given any AO density matrix (say $\mathbf{x}=\mathbf{D},{\mathbf{P}}^{\Delta },(\mathbf{X}+\mathbf{Y})$), calculate the electrostatic potential $\mathbf{V}[\mathbf{x}]$;

2. Assemble the FQ interaction kernel J;

3. Calculate the FQ charges $\stackrel{\sim }{\mathbf{q}}[\mathbf{x}]$ by inverting the J matrix and applying either eq. (16) or (37);

4. Contract the charges with the different quantities involving the derivatives.

Computational Details

In the following, the results obtained with QM/MM methods using EE and PE schemes will be compared with full DFT calculations. The B3LYP68 functional has been used for most of the full DFT calculations and the QM part of the QM/MM schemes. The full DFT calculations will be referred to as B3LYP in the following, while the polarizable and nonpolarizable QM/MM methods will be referred to as B3LYP/FQ and B3LYP/FX, respectively. The B2PLYP47, 48, 49, 50 DH functional and the MP2 method89 have also been used: the related schemes will be referred to as B2PLYP, B2PLYP/FQ, B2PLYP/FX and MP2, MP2/FQ, MP2/FX, with an analogous notation as that exploited for B3LYP‐based approaches. All the calculations have been performed using the 6‐31+G* basis set except for some specific tests (see Vertical Excitation Energies section).

In the fixed charge B3LYP/FX method, the flexible TIP3P model,90 as implemented in the Gaussian code,55 is used to describe water. A 1/R‐Coulomb interaction kernel with the exclusion of 1–2 and 1–3 interactions is exploited while the dispersion–repulsion terms are based on LJ potentials, using the arithmetic averages of the σ and ϵ atomic parameters, excluding 1–2 and 1–3 interactions and scaling by 0.5, the 1–4 interactions. For QM atoms, the parameters proposed by Freindorf et al.28 have been used. The stretching and bending parameters of water have been reoptimized to reproduce the B3LYP/6‐31+G* harmonic frequencies and geometries.

Moving to the polarizable B3LYP/FQ scheme, the electrostatics is treated with the 1/R Coulomb kernel for all interactions except intramolecular FQ–FQ ones, which are described by the Ohno interaction kernel67 without any exclusion (or scaling) for 1–2, 1–3, and 1–4 interactions. The dispersion–repulsion interactions are used with the same form as for the B3LYP/FX method. All the details of the parametrization procedure used for the FQ electrostatics and the LJ interactions are given in The QM/FQ Model section.

The complete force field used for the B3LYP/FQ and B3LYP/FX models is reported in Table 1, together with atomic charges, geometries, and frequencies obtained for a single isolated water molecule. Notice that the discrepancy between the QM and the FQ or FX frequencies is due to the use of a simple diagonal force field lacking stretching–stretching and stretching–bending off–diagonal terms.

Table 1.

Parameters employed for the water force field with the B3LYP/FQ and B3LYP/FX models used in this work.

Parameter	Atomtype(s)	B3LYP	B3LYP/FX	B3LYP/FQ
Electrostatics
χ (a.u.)	OW			0.189194a
χ (a.u.)	OW(HQM)			0.185500a
η (a.u.)	OW			0.623700a
q (a.u.)	OW	−0.659b	−0.83490	−0.659c
χ (a.u.)	HW			0.012767a
χ (a.u.)	HW(OQM)			0.022500a
χ (a.u.)	HW(NQM)			0.042000a
η (a.u.)	HW			0.637512a
q (a.u.)	HW	0.329b	0.41790	0.329
Lennard–Jones
$\sigma /2$ (Å)	OW		1.768390	1.58991
ϵ (kcal/mol)	OW		0.152090	0.155991
$\sigma /2$ (Å)	OQM		1.66528	2.030a
ϵ (kcal/mol)	OQM		0.1928	0.19a
$\sigma /2$ (Å)	NQM		1.9328	2.180a
ϵ (kcal/mol)	NQM		0.1328	0.13a
Bonded
r 0 (Å)	OW–HW		0.9689a	0.9904a
Kr (kcal mol−1 Å−2)	OW–HW		580.0a	580.0a
θ 0 (degree)	HW–OW–HW		105.5a	102.5a
$K_{\theta }$ (kcal mol−1 degree−2)	HW–OW–HW		51.5a	57.7a
Gas phase water
qgas (a.u.)	OW	−0.659b	−0.83490	−0.659
qbulk (a.u.)	OW		−0.83490	−0.848d
r (Å)	OW–HW	0.9689	0.9689	0.9689
θ (degree)	HW–OW–HW	105.5	105.5	105.5
νA (cm−1)	OW–HW	3860	3828	3827
νS (cm−1)	OW–HW	3736	3770	3771
${\nu }_{\delta }$ (cm−1)	HW–OW–HW	1663	1661	1663
Dimer (FQ acceptor)		Distance (Å)	full FQ
q (a.u.)	HW(OQM)	1.881	0.384	0.384
q (a.u.)	OW		−0.692	−0.687
q (a.u.)	HW		0.308	0.303
Dimer (FQ donor)
q (a.u.)	HW	1.889	0.352	0.353
q (a.u.)	OW(HQM)		−0.689	−0.689
q (a.u.)	HW		0.337	0.336

The 6‐31+G* basis set is always used.

^aAdjusted in this work.

^bCM5 population analysis.

^cAt B3LYP geometry.

^dAverage over eight configurations (see The QM/FQ model section)

Results and Discussion

The four molecular complexes shown in Figure 1—formamide–water (Fm–W), pyridine–water (Py–W), pyrimidine–water (Pm–W2), and acetone–water (Ac–W2)—were chosen as test cases to study the reliability of the QM/MM schemes when compared with full QM calculations. Such complexes are representative of four common configurations of hydrogen‐bonded complexes, that is, one water molecule bonded to one acceptor bond (Py–W and Pm–W2), two water molecules bonded to one acceptor bond (Ac–W2) and a bridge configuration, where the water molecule is bonded to both a donor and an acceptor site (Fm–W). The B3LYP/FX and B3LYP/FQ models in which the organic molecules are treated at the B3LYP level, whereas the water molecules are treated at the MM level will be compared to full B3LYP results.

Figure 1.

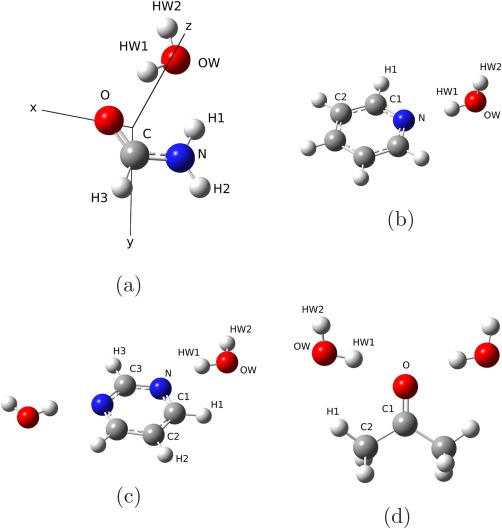
a) Formamide–water (Fm–W), b) pyridine–water (Py‐W), c) pyrimidine–water (Pm‐W2), and d) acetone–water (Ac‐W2) complexes with atom labelling. The axes in (a) are related to the force components of Table 5.

Parametrization and model systems

The electrostatics of the FQ model was first adjusted by fitting the FQ parameters of water (η _OW, η _HW, χ _OW, and χ _HW) so to reproduce a target set of charges, representative of the charge distribution of one gas (i) and bulk (ii) phase water molecule, as well as of one water molecule interacting with a QM density (iii).

The reference charges for the isolated water molecule (i) were obtained using the CM592 population analysis, at the B3LYP/6‐31+G* level. Such a choice is supported by the fact that the value of the dipole moment provided by the CM5 charges at such level of theory for the gas‐phase water is very close to the corresponding experimental value.

For the water molecules in bulk solution (ii), a training set of seven configurations was extracted from a molecular dynamics (MD) simulation with NPT conditions, using the TIP3P‐FB91 model at fixed geometry for the water molecules. Each configuration was composed by a central water molecule (the target molecule for parameterization purposes), and a first and second shell of surrounding molecules. The water molecules comprised in the first shell had at least one oxygen–hydrogen pair with the central water being at distance shorter than 2.5 Å; the second shell is a 10‐Å‐wide sphere centered on the central water. On average, the total number of water molecules considered in each snapshot was between 110 and 120, depending on the specific configuration. In such configurations, the central water molecule and the molecules of the first solvation shell were endowed with FQ charges, whereas the fixed TIP3P‐FB charges were assigned to the outer molecules. Finally, one additional configuration was added to the reference set, corresponding to one water molecule surrounded by four hydrogen bonded water molecules at the B3LYP/6‐31+G* geometry (Fig. 2).

Figure 2.

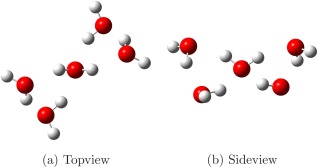
One water molecule embedded in its first tetrahedral solvation shell, optimized at the B3LYP/6‐31+G* level. These clusters were used in the optimization procedure of the FQ parameters.

This procedure yielded nine configurations, corresponding to a gas‐phase water molecule, seven snapshots, and one solvation pentamer. Then, a merit function was defined as the absolute error between the FQ charges of the central water molecule in all such configurations and the CM5 (for the gas‐phase water) and TIP3P‐FB charges (for the bulk models), respectively. Such a merit function was then minimized by means of a nonlinear optimization algorithm, implemented on purpose. A weight of 8.0 was given to the gas‐phase configuration in the merit function, to balance the eight configurations which were included for the bulk water.

The parameters obtained through such a fitting procedure are reported in Table 1, and provide FQ charges of −0.659 for the OW atom in gas‐phase water at the B3LYP geometry, and values of about −0.8 for the bulk models. In particular, by averaging out the values of the atomic charge on OW over the eight bulk configurations used by the fitting procedure, a value of −0.848 is obtained (Table 1).

Finally, the interaction with a QM charge distribution (iii) was tuned. Since the QM atomic charges are strongly dependent on the specific method used for the population analysis, on the specific combination of functional/basis set, and, especially when considering interacting fragments, on the magnitude of the charge transfer effects and BSSE, we used a simple approach for the tuning of the QM–FQ parameters independently of the QM methods used. The main difference between the FQ/FX and QM charge densities is that the former are described as point charge distributions by means of Dirac delta functions [see eqs. (5) and (8)], while in the latter, the charge distribution decays smoothly, due to the tails of the QM electronic density. Generally speaking, the electrostatic potential experienced by the FQ atoms closest to the QM charge density is different from the one experienced by the other MM atoms. By neglecting second‐order effects on the atomic hardnesses, this can be rationalized in terms of a first‐order effect, thus applying a scaling factor either on the in situ electronegativiy or on the electrostatic potential related to such atoms. For practical purposes, in this work, we chose the first strategy and we, therefore, modified the electronegativity of the FQ atoms closest to the QM charge distribution. Starting from the geometry of the pentamer (Fig. 2), we extracted one dimer in which the OW atom of the central molecule acts as hydrogen bonding donor and one dimer in which one HW atom of the central molecule acts as hydrogen bonding acceptor (the two other possible dimers are equivalent for symmetry reasons). Then, we adjusted the electronegativity of the OW donor and HW acceptor atoms by imposing that, for both dimers, the FQ charges are the same when both molecules of the dimer are treated at the full FQ level or when the central one is treated at the FQ level and the other one at the B3LYP level. The modified electronegativities together with the FQ charges of the dimers are shown in Table 1.

Once the FQ electrostatic interactions were adjusted, the stretching and bending parameters related to the HW–OW distance and the HW–OW–HW angle were tuned to reproduce the gas‐phase geometry and the harmonic frequencies at the B3LYP/6‐31+G* level. The stretching constant (K_r) and r ₀ were adjusted to reproduce the symmetric (ν_S) and antisymmetric (ν_A) stretching frequencies and the OW–HW bond length (r), and analogously the HW–OW–HW bending constant ( $K_{\theta }$) and θ ₀ were fixed to reproduce the harmonic frequency of the water bending mode ( ${\nu }_{\delta }$) and the correct angle (θ). In Table 1, the bonded parameters optimized for the FQ models are reported, together with the equilibrium charges and geometries obtained after geometry optimization.

Finally, the intermolecular dispersion–repulsion interactions based on the LJ potentials of eq. (3) were adjusted. To treat the dispersion–repulsion term consistently with the electrostatic interactions, a flexible functional form should be developed to go smoothly from the interaction with the QM charge distribution to the bulk limit. Such a model is under development and will be the topic of a future work. At this stage, we used a simplified approach based on eq. (3), where the OW parameters were taken from the TIP3P‐FB model91 and reproduce the bulk phase limit, while corrections for the interaction with the QM part were included in the LJ parameters of the QM atoms.

In a previous work, Freindorf et al.28 have faced a similar problem in finding the optimal set of LJ parameters for reproducing the hydrogen bond distances in QM/MM computations by employing the fixed charge approach. In their case, an extended set of organic molecules was chosen, and treated at the B3LYP/6‐31+G* level, while the TIP3P90 model was exploited for water. Then, the QM/MM hydrogen bonding distances were fitted to their B3LYP values by adjusting the LJ parameters of the QM atoms, while the parameters for water were constrained to the TIP3P values. Here, we started from the results of such a study, and we used these parameters for the QM atoms and the TIP3P ones for the water molecules. The LJ parameters of water in the TIP3P model are defined only for OW, therefore, the different treatment of the electrostatic terms between the TIP3P and the FQ model does not affect the results for water, whereas it affects the QM‐FQ interactions. Let us assume that only the QM atom(s) directly bonded to the water molecule requires different LJ parameters for FQ and FX models. Then, we slightly adjusted the σ parameters of the LJ potentials of the N and O atoms of the QM molecules, to reproduce the hydrogen bonding distance at the B3LYP/6‐31+G* level.

Ground state SCF geometries

In Table 2, the water atomic charges are reported for the four complexes under study, together with the main geometrical parameters, at the B3LYP, B3LYP/FX, and B3LYP/FQ level of theory (the atom labelling refers to Fig. 1). It can be observed that in all the molecular systems, the values of the charge on the hydrogen bond acceptor atom (HW1) predicted by the FQ model are slightly lower than the TIP3P90 values. Also the FQ charge on the OW atom (about 0.7) is lower than the TIP3P one (0.83), and closer to the CM5 values. This is a consequence of our fitting procedure. In fact, the FQ charges are close to the CM5 values both in the gas‐phase water molecule (Table 1) and for the molecular complexes. It is worth noting that while the overall polarization of the water molecules reproduced by the FQ model is consistent with the B3LYP results, some discrepancy is found in the value of the charges of the two hydrogens HW1 and HW2 in the complexes. In fact, in all the molecular complexes (Table 2), the CM5 charges of HW1 are slightly lower than HW2, while in the FQ model such a trend is reversed. This is due to charge transfer effects occurring in the full QM treatment, which cannot be included in the QM/MM model, where the total charge of the two subsystems must be retained. Such an effect has been found to be strongly dependent on the model used for performing the charge population analysis. In fact, the Mulliken or NBO population analyses yield different values of the total charge transfer and of the polarization between the two water hydrogen atoms. Indeed, this suggests that the charge transfer in such molecular complexes is a subtle effect, which strongly depend on the computational approach used for the calculations. An accurate analysis of such effects is well beyond the purpose of this work. Here, we will assume that the charge transfer effects in the molecular complexes under study are small enough to be effectively enclosed in the optimized parameters, and that the electrostatic effects play the major role in the molecular properties, as will be discussed in the following. Regarding the ground state geometries, a remarkable aspect is that the B3LYP/FQ intermolecular bonds in all the proposed systems are closer to the B3LYP values than the corresponding B3LYP/FX ones. In particular, the bond lengths related to the O–HW1 (Fm–W), N–HW1 (Py–W), N–HW1 (Pm–W2), and O–HW1 (Ac–W2) are underestimated by about 0.10, 0.06, 0.08, and 0.18 Å, respectively, by the B3LYP/FX method, while the errors related to the B3LYP/FQ approach are one order of magnitude smaller.

Table 2.

Atomic charges (a.u.), bond distances (Å) and angle (degrees) of the water complexes of Figure 1.

Method	q ${}_{HW1}$	qOW	q ${}_{HW2}$	Bond lengths							Water angle
Fm–W				OW–H1	C–O	C–N	N–H1	O–HW1	HW1–OW	OW–HW2	HW1–OW–HW2
B3LYP/FX	0.417	−0.834	0.417	2.075	1.230	1.351	1.022	1.798	0.988	0.969	103.1
B3LYP/FQ	0.333	−0.728	0.394	2.158	1.227	1.353	1.020	1.988	0.976	0.967	104.8
B3LYP	0.303	−0.654	0.327	2.040	1.231	1.350	1.021	1.910	0.984	0.968	106.9
Py–W						N–C1	C1–C2	N–HW1	HW1–OW	OW–HW2	HW1–OW–HW2
B3LYP/FX	0.417	−0.834	0.417			1.341	1.397	1.891	0.985	0.967	103.0
B3LYP/FQ	0.292	−0.700	0.408			1.341	1.397	1.949	0.976	0.970	104.5
B3LYP	0.285	−0.694	0.312			1.341	1.396	1.949	0.983	0.968	105.4
Pm–W2					N–C3	N–C1	C1–C2	N–HW1	HW1–OW	OW–HW2	HW1–OW–HW2
B3LYP/FX	0.417	−0.834	0.417		1.337	1.342	1.394	1.910	0.983	0.967	103.9
B3LYP/FQ	0.387	−0.691	0.304		1.337	1.341	1.394	1.987	0.975	0.969	104.9
B3LYP	0.291	−0.686	0.318		1.337	1.342	1.394	1.990	0.980	0.968	106.2
Ac–W					C1–O	C1–C2	C2–H1	O–HW1	HW1–OW	OW–HW2	HW1–OW–HW2
B3LYP/FX	0.417	−0.834	0.417		1.232	1.510	1.093	1.750	0.984	0.968	103.6
B3LYP/FQ	0.384	−0.701	0.317		1.229	1.512	1.093	1.929	0.975	0.969	104.8
B3LYP	0.290	−0.676	0.321		1.231	1.510	1.092	1.928	0.978	0.968	106.4

Vertical excitation energies

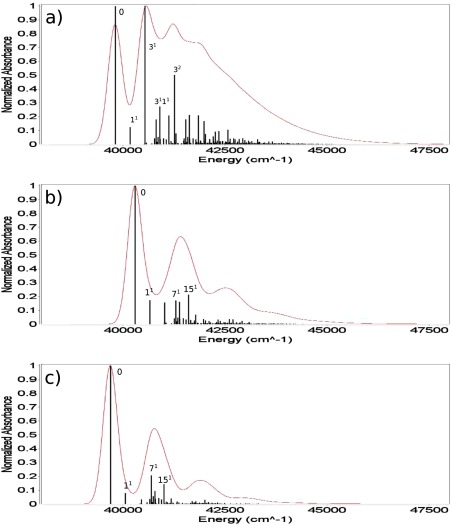
In Table 3, the vertical excitation energies of the $n\to {\pi }^{*}$ transition of the four complexes are reported, as computed in the gas phase (B3LYP level, without any water molecule), with single point calculations on the complexes constrained at the B3LYP geometries, and after optimization at each level of theory. It is apparent that in all cases, the vertical energy provided by the B3LYP/FQ method is closer to the corresponding B3LYP value than the B3LYP/FX one. This can be due to the improved treatment of the electrostatic interactions, since the FQ model predicts a polarization of the atomic charges in close agreement with the B3LYP CM5 charges. When the geometry relaxation effects are considered, the good agreement between the B3LYP/FQ and B3LYP results is retained. The geometry optimization leads to an increase of the excitation energy of about 0.01 eV for the B3LYP/FQ method for the cases of Py–W, Pm–W, and Fm–W complexes, and of about 0.04 eV, in the case of Ac‐W2. In comparison, such an effect is sensibly larger (0.05–0.1 eV) for the B3LYP/FX method. This is mainly due to the fact that the B3LYP/FQ geometry is closer to the B3LYP one, than the B3LYP/FX geometry.

Table 3.

Vertical excitation energies (eV) of the first $n\to {\pi }^{*}$ electronic transition and atomic charges (a.u.) of the complexes shown in Figure 1 at the B3LYP geometry and after optimization.

		(at B3LYP geometry)				Absolute	${\omega }_{n\to \pi *}$
System	Method	q ${}_{HW1}$	qOW	q ${}_{HW2}$	${\omega }_{n\to \pi *}$	error	(after optimization)
Fm	B3LYP				5.6388 (0.0009)
Fm–W	B3LYP	0.303	−0.654	0.327	5.7964 (0.0011)		5.7964 (0.0011)
Fm–W	B3LYP/FQ	0.406	−0.726	0.320	5.8136 (0.0008)	0.0172	5.8129 (0.0009)
Fm–W	B3LYP/FX	0.417	−0.834	0.417	5.8089 (0.0009)	0.0125	5.8733 (0.0009)
Py	B3LYP				4.8358 (0.0043)
Py–W	B3LYP	0.285	−0.694	0.312	5.0330 (0.0033)		5.0330 (0.0033)
Py–W	B3LYP/FQ	0.356	−0.660	0.304	5.0806 (0.0046)	0.0476	5.1378 (0.0047)
Py–W	B3LYP/FX	0.417	−0.834	0.417	5.1188 (0.0046)	0.0858	5.1552 (0.0046)
Pm	B3LYP				4.3090 (0.0053)
Pm–W2	B3LYP	0.291	−0.686	0.318	4.5344 (0.0041)		4.5344 (0.0041)
Pm–W2	B3LYP/FQ	0.338	−0.656	0.318	4.5305 (0.0056)	0.0040	4.5935 (0.0056)
Pm–W2	B3LYP/FX	0.417	−0.834	0.417	4.5947 (0.0056)	0.0602	4.6435 (0.0057)
Ac	B3LYP				4.3978 (0.0000)
Ac–W2	B3LYP	0.290	−0.676	0.321	4.6477 (0.0000)		4.6477 (0.0000)
Ac–W2	B3LYP/FQ	0.387	−0.699	0.312	4.6540 (0.0000)	0.0063	4.6864 (0.0000)
Ac–W2	B3LYP/FX	0.417	−0.834	0.417	4.6619 (0.0000)	0.0142	4.7870 (0.0000)

The 6‐31+G* basis set has been used in all cases. The Mean Absolute Error averaged over the four complexes of B3LYP/FQ (B3LYP/FX) is 0.0188 (0.0432) eV

Although a detailed study of the effect of the basis set is beyond the aim of this work, we performed a comparison of several basis sets (6‐31+G*, 6‐31++G**, 6‐311++G**, cc‐pVTZ, and aug‐cc‐pVTZ) for the Fm–W complex. In Table 4, charges and excitation energies are shown for the aforementioned basis sets, and it can be observed that the charges are quite stable, the variations being only on the third decimal digit. Regarding the excitation energies, while obviously the overall magnitude of the energies depends on the size of the basis, the difference between the values in the gas phase and for the water complex are quite similar. As a matter of fact, the 6‐31+G* basis set provides results very similar to those delivered by larger basis sets, suggesting that once the diffuse functions are added the effects induced on the environment do not vary so much with the basis size.

Table 4.

Vertical excitation energies (eV) of the first $n\to {\pi }^{*}$ electronic transition and atomic charges (a.u.) of the Fm–W complex shown in Figure 1 at the B3LYP/6‐31+G* geometry.

		${\omega }_{n\to \pi *}$	${\omega }_{n\to \pi *}$	$\Delta {\omega }_{n\to \pi *}$
	qOW	(gas phase)	(water complex)
cc‐pVTZ	−0.723	5.5312	5.7816	0.2504
6‐31+G*	−0.726	5.5517	5.8136	0.2619
6‐311++G**	−0.726	5.4526	5.7163	0.2637
aug‐cc‐pVTZ	−0.730	5.4184	5.6946	0.2762

The effect of the basis set at fixed geometry on the charge and excitation energies is shown

TD‐DFT analytical gradients for excited states

In Table 5, the comparison between analytical and numeric derivatives for the Fm–W complex, at the TD‐B3LYP/FQ and B2PLYP/FQ levels is shown, to demonstrate the reliability of our implementation. Using tight convergence criteria for the SCF (10⁻¹¹ a.u.), numerical evaluation of integrals over DFT grids (10⁻¹²), CPHF (10⁻⁹), and Davidson diagonalization procedures^[88] for the TD‐DFT equations (10⁻⁹), the maximum discrepancies between analytical and numerical forces are of the order of 10⁻⁸ a.u. This value is much lower than the thresholds usually used in the geometry optimization algorithms, and is only related to numerical fluctuations.

Table 5.

Comparison between analytical and numerical forces (a.u.) for the Formamide–Water complex, computed for the B3LYP/6‐31+G* equilibrium geometry.

	Analytic			Numeric
Atoms	x‐comp	y‐comp	z‐comp	x‐comp	y‐comp	z‐comp
TD‐B3LYP/FQ
C	−0.064662163	0.146337317	−0.030789285	−0.064662114	0.146337323	−0.030789281
H	0.009247938	−0.010031637	0.002242626	0.009247943	−0.010031635	0.002242618
O	0.098527562	−0.105630706	0.023396645	0.098527555	−0.105630734	0.023396652
N	−0.043791024	−0.026063875	0.004134635	−0.043791029	−0.026063889	0.004134623
H	0.004953252	−0.003285285	0.000762794	0.004953251	−0.003285259	0.000762799
H	−0.002206063	0.005865218	−0.001177980	−0.002206067	0.005865207	−0.001177972
OW	−0.000788163	−0.002201577	0.000391206	−0.000788188	−0.002201594	0.000391190
HW	−0.000717674	−0.005376463	0.001127487	−0.000717635	−0.005376466	0.001127493
HW	−0.000563665	0.000387007	−0.000088130	−0.000563666	0.000386963	−0.000088149
B2PLYP/FQ
C	−0.002959734	0.005558747	−0.001173929	−0.002959733	0.005558749	−0.001173932
H	−0.000488653	−0.001723402	0.000317073	−0.000488656	−0.001723403	0.000317071
O	0.003410427	−0.003708308	0.000846802	0.003410429	−0.003708311	0.000846796
N	−0.001151459	−0.000232885	−0.000029289	−0.001151455	−0.000232881	−0.000029294
H	0.000830283	−0.000692713	0.000164568	0.000830282	−0.000692715	0.000164569
H	0.000391927	0.000701231	−0.000075504	0.000391922	0.000701234	−0.000075499
OW	0.000027634	0.000111627	−0.000047147	0.000027636	0.000111624	−0.000047142
HW	−0.000061537	−0.000009129	−0.000004089	−0.000061538	−0.000009135	−0.000004088
HW	0.000001110	−0.000005167	0.000001514	0.000001109	−0.000005171	0.000001512
MP2/FQ
C	−0.007895800	0.011603102	−0.002499396	−0.007895815	0.011603106	−0.002499397
H	−0.000202653	−0.001386633	0.000255970	−0.000202661	−0.001386627	0.000255971
O	0.009168345	−0.009790195	0.002200098	0.009168350	−0.009790187	0.002200099
N	−0.001093861	−0.000183241	−0.000036583	−0.001093861	−0.000183227	−0.000036588
H	0.000101851	0.000418741	−0.000075773	0.000101857	0.000418734	−0.000075787
H	−0.000038435	−0.000840722	0.000223471	−0.000038435	−0.000840720	0.000223468
OW	0.000042998	0.000147207	−0.000054897	0.000042987	0.000147233	−0.000054886
HW	−0.000068893	0.000035101	−0.000013776	−0.000068873	0.000035107	−0.000013783
HW	−0.000013553	−0.000003361	0.000000887	−0.000013555	−0.000003350	0.000000898

The basis set is 6‐31+G* in every case, the x‐, y‐ and z‐components are projected on the axes shown in Figure 1a

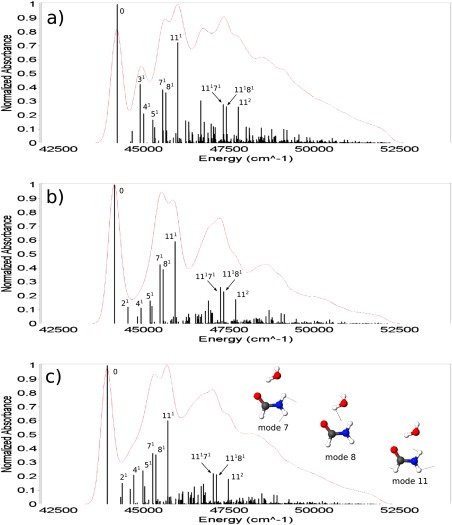
Finally the post‐SCF gradients were used to evaluate different properties of the complexes shown in Figure 1. The TD‐DFT analytical forces were used for the calculation of UV–Vis spectra including vibronic contributions in the vertical gradient (VG) approximation (see Ref. 93 and references therein), that is, by assuming that the vibrational frequencies and normal modes of the excited state are the same as those of the ground state and by estimating geometry relaxation in terms of the excited state gradient at the ground‐state equilibrium geometry. Such computations were performed for the Py–W, Pm–W2, and Fm–W complexes. Since our aim is to evaluate the reliability of excited state results delivered by the TD‐B3LYP/FQ and TD‐B3LYP/FX methods, we used the B3LYP ground‐state Hessian in all cases, so that the differences between the spectra are only due to the differences in the excited‐state computations, being the ground‐state frequencies the same for all the methods. In Figures 3, 5, 6, the VG spectra of the three complexes are shown, as computed with the three methods. Temperature effects on the electronic spectra have been neglected, so that the 0–0 transition is the lowest energy one, and its position depends on the value of the vertical energies computed with the different methods. In all three cases, the band positions given by the B3LYP/FQ method are in closer agreement with the B3LYP reference than the ones predicted with the B3LYP/FX scheme, due to the higher accuracy of the excitation energies (see Table 3 and the discussion above). In the case of the Fm–W complex (Fig. 3), the spectral shape is very complex, being due to many features spread over about 10,000 cm⁻¹, and the analysis is quite difficult. From the assignments shown in the Figure, it is possible to evaluate the agreement among the transitions predicted with all the three proposed levels of theory, the different peaks being due to the same transitions in all the spectral regions. Nevertheless, it is evident that the B3LYP/FQ spectrum shows an higher accuracy than the B3LYP/FX one in the region below 45,000 cm⁻¹. This could be due to a better treatment of the modes of water, such as the bending at 1682 cm⁻¹, and the ones in the low frequency zone (674 and 439 cm⁻¹). In the small inset on the last spectrum, the displacement vectors of the three most significant modes are visualized, while in Figure 4, the shift vector for the normal modes of the Fm–W complex is shown. In the cases of the Py–W and Pm–W2 complexes (Figs. 5 and 6), the spectral lineshape at the B3LYP/FQ level closely resembles the one at the B3LYP level. In particular, it is worth noting that the shoulder at about 35,000 cm⁻¹, which appears in the B3LYP spectrum of Figure 6, is visible in the B3LYP/FQ spectrum, while it does not appear in the B3LYP/FX one.

Figure 3.

VG spectra of the Fm–W complex (FWHM = 200 cm⁻¹). Ground state Hessians at the B3LYP level, excited state gradients at the B3LYP/FX (a), B3LYP/FQ (b), and B3LYP (c) levels; The 6‐31+G* basis set has been used in every case. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 5.

VG spectra of the Py–W complex (FWHM = 200 cm⁻¹). Ground state Hessians at the B3LYP level, excited state gradients at the B3LYP/FX (a), B3LYP/FQ (b), and B3LYP (c) levels; The 6‐31+G* basis set has been used in every case. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 6.

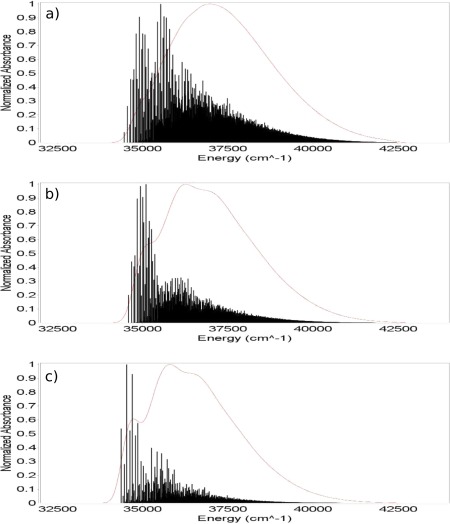
VG spectra of the Pm–W2 complex (FWHM = 200 cm⁻¹). Ground state Hessians at the B3LYP level, excited state gradients at the B3LYP/FX (a), B3LYP/FQ (b), and B3LYP (c) levels; The 6‐31+G* basis set has been used in every case. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 4.

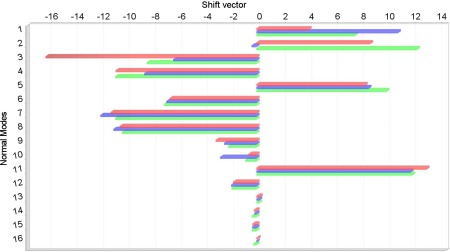
Shift vector (a.u.) for the Fm–W complex. Red, blue, and green bars refer to B3LYP/FX, B3LYP/FQ, and B3LYP computations, respectively; with 6‐31+G* basis set in every case. Mode 2: water ip torsion, 439 cm⁻¹. Mode 4: water oop torsion, 774 cm⁻¹. Mode 10: water bending, 1682 cm⁻¹. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

TD‐DFT, MP2 and B2PLYP analytical gradients for geometry optimizations

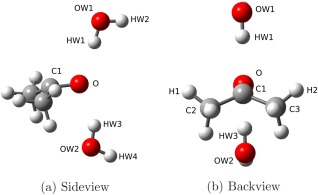
The Ac–W2 complex is quite challenging from a computational point of view, due to the presence of the two methyl groups and to a large flexibility of the water molecules. Furthermore, the low energy electronic transitions can break the symmetry reflection plane defined by the O, C1, and C2 atoms in the ground state (Fig. 1d), showing a typical umbrella configuration (Fig. 7) in the excited state. Thus, such a complex is a nontrivial test case for validating our QM/MM models for excited‐state computations.

Figure 7.

First excited state geometry of the acetone–water complex (Ac‐W2). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In Table 6, the excited‐state geometries obtained with the TD‐B3LYP/FQ and TD‐B3LYP/FX models are compared with the full TD‐B3LYP ones. In the ground state, the O–HW1 and O–HW3 bonds are equivalent, and their bond length is 1.928 Å at the B3LYP level. In the excited state, the two water molecules are not equivalent, due to the geometry rearrangement. The O–HW1 and O–HW3 bonds are stretched by about 0.04 and 0.08 Å, at the B3LYP level, and this shift is correctly reproduced at the B3LYP/FQ and B3LYP/FX levels. Furthermore, in all the three models, the distortion of the excited state from planarity is consistently predicted. In fact, the dihedral angle $\phi$ (C2–O–C1–C3) is 180° in the ground state, while it is lower in the first excited state where the C2 and C3 atoms are closer to each other. Such a shift is of about 35° at the B3LYP level, and it is correctly reproduced by both the B3LYP/FQ and B3LYP/FX methods.

Table 6.

Atomic charges (a.u.), adiabatic excitation energy (eV), bond distances (Å) and angle (degrees) of the Ac‐W2 complex.

Methoda	q ${}_{HW1}$	qOW	q ${}_{HW2}$	C1–O	C1–C2	C2–H1	O–HW1	HW1–OW	OW–HW2	HW1–OW–HW2
Ground state
B2PLYP/FX	0.417	−0.834	0.417	1.236	1.507	1.091	1.749	0.984	0.968	103.6
B2PLYP/FQ	0.387	−0.703	0.316	1.234	1.509	1.091	1.929	0.975	0.969	104.8
B2PLYP	0.298	−0.686	0.326	1.235	1.508	1.090	1.932	0.977	0.967	106.4
MP2/FX	0.417	−0.834	0.417	1.242	1.504	1.092	1.749	0.984	0.968	103.7
MP2/FQ	0.376	−0.693	0.317	1.240	1.505	1.092	1.927	0.975	0.969	104.8
MP2	0.305	−0.694	0.330	1.241	1.505	1.091	1.951	0.979	0.970	106.2
First excited state
TD‐B3LYP/FX				1.331	1.509	1.095	1.799	0.980	0.967	104.0
TD‐B3LYP/FQ				1.325	1.512	1.095	2.004	0.973	0.969	104.8
TD‐B3LYP				1.327	1.511	1.095	1.972	0.975	0.968	105.7
…continue				ωad	$\Delta {\phi }^a$	O–C1–C2	O–HW3	HW3–OW	OW–HW4	HW3–OW–HW4
TD‐B3LYP/FX				4.086	−36.17	113.8	1.814	0.980	0.968	104.2
TD‐B3LYP/FQ				4.049	−37.52	113.9	2.068	0.974	0.968	105.0
TD‐B3LYP				4.031	−34.93	114.3	2.009	0.976	0.968	106.4

The ground state geometry and atom labelling refer to Figure 1 and 7 for the ground and excited states, respectively. The 6‐31+G* basis set has been used in all cases.

^aGiven $\phi$ the dihedral angle formed by the C2–O–C1–C3 atoms, which is 180° in the ground state, $\Delta {\phi }^a$ is the variation in the excited state geometry

Also geometry optimizations of the Ac–W2 ground state at the MP2 and B2PLYP levels have been performed, and the results are shown in the same table. Although both the QM/MM force fields have been optimized for B3LYP calculations, a remarkable agreement is found for the geometric parameters with respect to full B2PLYP and MP2 calculations. Generally speaking, the accuracy of the ground‐state geometries is analogous to the corresponding results discussed for the B3LYP methods in the previous section. This is encouraging us toward the development of QM/MM methods for accurate frequency computations of large systems using the B2PLYP functional.

Multilayered solvation schemes

We discuss here how multiscale QM/MM schemes can be used for the calculation of excited‐state properties of large systems. In our previous works,21, 22, 34, 37, 39 the QM/FQ approach was presented as a part of a more extended embedding approach, which includes also an outer PCM layer, while in this work, we have introduced also the fixed charges (FX). In this last paragraph, we will discuss the effects of the nature of the different layers (QM, FQ, FX) on the QM wavefunction and on the MM charge distribution using the pyridine molecule in water as test case.

The structure of pyridine surrounded by explicit water molecules was obtained from a MD simulation. Pyridine was modeled by means of a flexible force field, whose intramolecular part was tailored on DFT‐level vibrational data by the Joyce29, 94 program. Intermolecular interactions were modeled using LJ potentials, with parameters taken from optimized potentials for liquid simulations (OPLS)95 and charges obtained from a CM5 analysis performed on the DFT/PCM electronic structure of pyridine in water solution. The charge on the Nitrogen atom (−0.42 e) was placed on a virtual site lying at 0.35 Å from the nucleus. The simulation was performed in the NPT ensemble (300 K, 1 atm) with the GROMACS4.696 package, using a box of 3197 equilibrated TIP3P‐FB91 water molecules and exploiting periodic boundary conditions. A random snapshot was extracted for the analysis, and several spheres of explicit solvent molecules were cut at increasing radii, R ₀, and center on the nitrogen atom (Fig. 8). The largest sphere has a radius $R_0=22.0$ Å including 1396 water molecules and will be referred to as System 8 (Fig. 8h). Then, smaller models were cut, using values of R ₀ of 19.0, 16.0, 12.5, and 8.5 Å (Systems 7–4 in Fig. 8). Finally, the smallest models were obtained by selecting the 8 and 2 water molecules closest to the nitrogen (Systems 2 and 3, respectively). System 1 only consists of the isolated Pyridine in the MD geometry. Systems 1–8 can, therefore, be viewed as a hierarchical set of models, which can be used to test the convergence of the electrostatic properties in multilayered calculations, by applying the QM, FQ, and FX schemes in different combinations. In particular, two aspects will be studied: the physical reliability of the FQ charge distribution of the MM layer, and of the vertical electronic excitation energies in the QM part.

Figure 8.

Solvation shells of pyridine taken from one snapshot of an MD simulation. In Figures (d)–(h) spheres of different radii R ₀ centered on the Nitrogen have been cut from the snapshot. N is the number of water molecules included in the systems. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In Figure 9, the FQ charges on the water oxygen have been plotted as a function of the distance from the nitrogen for System 5, with two computational models. When the pyridine is treated at the QM level, and all the water molecules are treated with the FQ model (the QM/FQ approach), we observe that the FQ charges have a value of about −0.75 in the vicinity of the nitrogen, while the average charge decreases to about −0.6 for the farthest ones. In the FQ model, the polarization depends not only on the intrinsic parameters, but also on the electrostatic potential at the position of the FQ atoms. Such a potential in turn depends on how many molecules (i.e., the sources of electrostatic potential) are located in the nearby of the FQ water molecule, and how strong such sources are. Therefore, we can reasonably assume that the polarization of an FQ water molecule depends on two main factors, namely the charges and the number of surrounding molecules. Then, the trend of the polarization in the QM/FQ scheme can be explained by recalling that in the parametrization procedure used for extracting the FQ parameters, we fitted the FQ charges so to reproduce the CM5 charges at the B3LYP/6‐31+G* level for the gas phase water; such charges are about −0.66 and about −0.84 for the bulk phase (Table 1). In System 5, the inner water molecules have an higher coordination number than the outer ones, so that the latter show a lower polarization (i.e., the oxygen atoms are less negative) than the former ones approaching the gas‐phase limit. The average values of the charges as a function of the distance from the QM system have been interpolated with a line with a slope of about +0.015, which can be considered a rough estimation of the depolarization rate of the FQ charges as a function of the distance from the QM atoms. The QM/FQ model appears to mimic a molecule at the center of a droplet in vacuo, rather than a molecule in solution, since the outer FQ charges approach the gas‐phase limit rather than the bulk solvent. Certainly one good question is what we consider to be the bulk limit of the water charges, and what we expect to be the trend of the charge distribution at large distances from the solute. Some helpful hints to answer to this question could be that the dipole moment of the isolated pyridine at the B3LYP/6‐31+G* level at the current geometry (System 1 in Fig. 8a) is 2.31 Debye, while the one of an isolated gas‐phase water molecule at the same level of theory is 2.25 Debye. Furthermore, the CM5 charge on the nitrogen of a pyridine is −0.388, much lower than the corresponding charge on the water oxygen, which is −0.659. For comparison, the corresponding Mulliken charges are −0.179 and −0.928 for the pyridine nitrogen and water oxygen, respectively. Then, we expect that the electrostatic potential generated by the pyridine molecule is lower than the potential generated by the water molecule, due to a lower polarization of the charge distribution (they have similar dipole moments but the pyridine is much larger than water). Furthermore, pyridine has a larger steric hindrance than water, so that we can assume that a water molecule in the bulk phase coordinates more molecule than a water molecule in the vicinity of the pyridine molecule. Following these arguments, we expect the FQ charges of the water molecules in the bulk phase to be slightly higher than the ones of the water in the nearby of Pyridine. This trend cannot be reproduced by a simple QM/FQ model, because the outer water molecules have low coordination numbers due to the unphysical truncation of the sphere.

Figure 9.

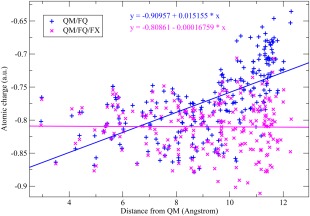
Charges (1/R kernel) on the oxygen atoms of the FQ water molecules surrounding pyridine in System 5 (Figure 8e). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

To ensure that the charge distribution approaches a reasonable bulk solvent limit at long distances, an outer layer of water molecules with fixed charges can be used to embed the FQ charge distribution. In particular, System 6 (Fig. 8f) has been used, treating the water molecules included in the sphere of radius $R_0=12.5$ Å (i.e., System 5) at the FQ level, while the outer molecules included in the shell between $R_0=12.5$ and 16.0 Å ere endowed with fixed TIP3P‐FB92 charges. The FQ charge distribution is referred to as the QM/FQ/FX method in Figure 9, and shows a (slightly) negative slope of the average charge in different shells. In fact, in this model, the FQ charges belonging to the outer layer respond to the electrostatic potential of the FX charges, approaching a value of −0.85 in the bulk limit. In Fig. 10, the results of QM/FQ and the QM/FQ/FX approaches are sketched for System 7 (Fig. 8g), to show that the results are independent on the specific molecular system used, confirming the same conclusions presented above for System 5.

Figure 10.

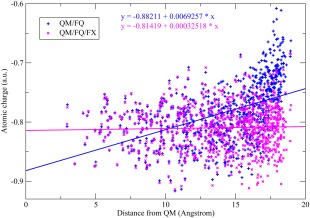
Charges (1/R kernel) on the oxygen atoms of the FQ water molecules surrounding pyridine in System 7 (Figure 8g). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Finally, in Figure 11, the solvatochromic shift of the first ( $n\to {\pi }^{*}$) vertical excitation energy of the pyridine molecule is shown, to study the effect of the embedding on a significant QM property. The solvatochromic shifts for Systems 2–8 of Figure 8 are reported, as computed using the QM/FQ, QM/FX, and the QM/FQ/FX models. The QM/FQ and QM/FX shifts have similar trends, showing a good convergence to the largest systems. Indeed, both curves have a very fast increase for the smaller systems (2–4) and then the trend becomes smoother. In both cases, the solvatochromic shifts of System 6 ( $R_0=16.0$ Å) are very close to the values of System 8 ( $R_0=21.0$ Å), so that they can be considered at convergence. Obviously, due to larger charges, the QM/FX model converges to values of the solvatochromic shifts larger than the QM/FQ model, in agreement with the results collected in Table 3 for the small complexes. The QM/FQ/FX model, which was found to provide the correct FQ charge distribution is also shown for Systems 3–8. It can be observed that for Systems 3, 5, 6, 7, and 8, the values predicted by the QM/FQ/FX model are very close to the ones at the QM/FQ level, suggesting that only the charges of the water molecules close to the QM region have a significant effect on the QM properties. For System 4, at $R_0=8.5$ Å, the differences between the QM/FQ/FX and QM/FQ models are slightly larger. This is mainly due to the fact that for such a system the outer FX layer is spherical, but this is not case for the inner FQ one (corresponding to System 3), so that the QM charge density interacts with both FQ and FX charges, leading to a solvatochromic shift comparable with the QM/FX one.

Figure 11.

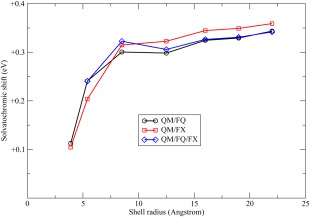
Solvatochromic shift of the vertical excitation energies (eV) of pyridine in water for different solvation models. The shell radius on the x‐axis refers to the R ₀ values of the systems shown in Figure 8. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Conclusions

The polarizable QM/MM scheme based on the FQ model developed in the past years for the calculation of ground‐state properties and vertical excitation energies has been extended to the computation of post‐SCF gradients. Excited state properties, as well as geometry optimizations at B2PLYP and MP2 levels are now available in our code, allowing a wide choice of methods for the study of large systems.

The parameters of the FQ model have been optimized to tune the QM–FQ interaction and the dispersion–repulsion parameters have been consequently adjusted to perform geometry optimization consistently with the FQ electrostatics.

From the comparison between QM/MM approaches based on fixed and polarizable charges, it is apparent that the FQ model provides two main advantages with respect to fixed charge approaches. The first one is that it becomes possible to find a unique set of parameters which provides charges for the ground‐state QM density, excited‐state QM density and interaction with other MM/PCM layers. This allows to perform calculations using a unique model for different properties. On the contrary, the fixed charge models require different parametrizations for gas phase, solvent, ground‐state and excited‐state calculations.

The second advantage is that the FQ model allows to predict the properties of both the QM and MM subsystems, providing good charge distributions on the MM atoms, especially when multilayered models like QM/FQ/PCM and/or QM/FQ/FX are used. This is a significant improvement of the QM/MM method especially whenever static calculations are combined with dynamic approaches, where the time evolution of the systems is studied with classical MD simulations.

The promising results obtained in this work for both the QM side (VG spectra of the QM subsystem embedded in the FQ layer) and the MM side (the FQ charge distributions) are encouraging and pave the route toward the development of robust and reliable QM/MM protocols able to accurately model large molecular systems.

How to cite this article: Carnimeo I., Cappelli C., Barone V.. J. Comput. Chem. 2015, 36, 2271–2290. DOI: 10.1002/jcc.24195