REDUCING CSF PARTIAL VOLUME EFFECTS TO ENHANCE DIFFUSION TENSOR IMAGING METRICS OF BRAIN MICROSTRUCTURE

Abstract

Technological advances over recent decades now allow for in vivo observation of human brain tissue through the use of neuroimaging methods. While this field originated with techniques capable of capturing macrostructural details of brain anatomy, modern methods such as diffusion tensor imaging (DTI) that are now regularly implemented in research protocols have the ability to characterize brain microstructure. DTI has been used to reveal subtle micro-anatomical abnormalities in the prodromal phase ofº various diseases and also to delineate “normal” age-related changes in brain tissue across the lifespan. Nevertheless, imaging artifact in DTI remains a significant limitation for identifying true neural signatures of disease and brain-behavior relationships. Cerebrospinal fluid (CSF) contamination of brain voxels is a main source of error on DTI scans that causes partial volume effects and reduces the accuracy of tissue characterization. Several methods have been proposed to correct for CSF artifact though many of these methods introduce new limitations that may preclude certain applications. The purpose of this review is to discuss the complexity of signal acquisition as it relates to CSF artifact on DTI scans and review methods of CSF suppression in DTI. We will then discuss a technique that has been recently shown to effectively suppress the CSF signal in DTI data, resulting in fewer errors and improved measurement of brain tissue. This approach and related techniques have the potential to significantly improve our understanding of “normal” brain aging and neuropsychiatric and neurodegenerative diseases. Considerations for next-level applications are discussed.

INTRODUCTION

Advances in radiology over the past several decades have drastically increased the ability to examine the living human brain in detail. The introduction of computed tomography (CT) allowed for low-resolution three-dimensional reconstruction of brain tissue and represented a landmark improvement in medical care potential (37). The subsequent technique of magnetic resonance imaging (MRI) has continued to expand the potential of in vivo imaging technology (45). Clinical MRI is now commonly performed using MR systems operating at a1.5 Tesla (T) field strength, with 3T and higher fields becoming ever increasingly common for both clinical and research applications (58,86). High-field imaging provides an invaluable tool for identification of various brain disorders with the goal of informing therapeutic methods and eventual cures.

In conjunction with the notable potential of these technologies to answer important questions about brain health, key technical components merit attention to optimize analytical procedures in both clinical and research settings. Examples of these components include the MR pulse sequence parameters, traditional methods of maximizing spatial accuracy of resulting images, and modern advances that exploit patterns of molecular movements within tissues to illustrate cellular integrity in greater detail, with particular regard to diffusion tensor imaging (DTI). This review will discuss foundational elements of MRI technology as it relates to diffusion MRI, explore potential sources of error when using traditional methods (e.g., cerebrospinal fluid (CSF) contamination), and propose an acquisition and post-processing approach to better manage artifacts associated with this phenomenon.

SOURCES OF VARIANCE IN THE MR SIGNAL

Structural imaging techniques are based on the nuclear spin of a hydrogen nucleus composed of a single charged proton. Viewing this phenomenon classically, the combination of nuclear spin and electrical charge can be considered to generate a “magnetic moment” that aligns with the external magnetic field (B₀). Because of these nuclear moments, a large ensemble of nuclear spins (e.g., water) generates a net magnetization. In a constant magnetic field, the net magnetization is a vector that has points along the z axis that runs parallel to B₀ (i.e., the longitudinal direction) and a transverse component that lies in the x-y plane that is perpendicular to B₀. In MRI, this net magnetization is detected by tipping the net magnetization vector from the longitudinal direction into the x-y plane (i.e., transverse plane), where the MRI scanner can detect it independent of the main magnetic field (B₀). The magnetization is tipped by applying a radiofrequency (RF) pulse that has a time-varying field that oscillates in the x-y plane. The RF pulse is applied at the characteristic frequency (Larmor frequency) of the hydrogen nucleus. The Larmor frequency changes in proportion to changes in magnetic field strength. A 90° RF pulse tips the magnetization entirely into the transverse (x-y) plane. The longitudinal magnetization is zero after the 90° pulse. Typical pulse sequences utilize a 90° RF pulse to maximize signal detection. Once the RF pulse is turned off, the longitudinal magnetization begins to grow back through a process called longitudinal relaxation (T₁ relaxation). At the same time, the transverse magnetization vector rotates in the transverse plane at the Larmor frequency, and the transverse vector magnitude (length) decays to zero by a faster process called transverse relaxation (T₂ relaxation) (14,29,86).

There are different physical mechanisms that influence T₁ and T₂ relaxation times (14). Pertinent to this review, relaxation times for both T₁ and T₂ vary by tissue composition according to the surrounding chemical environment of water protons (91). Water nuclei in fat and water have similar Larmor frequencies; therefore, fat is visible on MR images. However, due to the different physical environments between fat and water, fat has a short T₁ and T₂ (i.e., fast longitudinal and transverse relaxation). By contrast, brain gray matter and white matter have an intermediate T₁ and T₂, while pure water and CSF have a long T₁ and T₂ due to intrinsic biophysical factors (13,41,80,91).

Image Formation and Contrast

Image formation relies on the spatial encoding of the signal generated by the net transverse magnetic vector rotating in the transverse plane (91). The MRI signal is detected by an RF receiver coil that is similar to the RF coil used to tip the net magnetization (RF transmit coil). The RF receiver coil simply “listens” to the transverse magnetization vector after the RF transmit coil is turned off. Each time the transverse magnetization rotates 360° in the transverse plane, a peak voltage is generated in the receiver coil and then digitized. The MR signal then becomes an oscillating voltage that has a frequency equal to the Larmor frequency but contains no information indicating the location of signal generation in the brain. The signal is spatially encoded by applying external magnetic field gradients across the brain that alter the strength of B₀ in a predictable pattern that causes a change in the resonance Larmor frequency according to position. As a result, the transverse magnetization rotates at different frequencies at different positions across the brain. The variations in signal frequency are transmitted through the RF receiver coil and distinguished as spatial frequencies using a Fourier Transform (FT). A similar second spatial encoding is completed in the perpendicular direction across the brain. The signals are digitized and stored as raw data points on a two-dimensional grid (“k-space”) and then reconstructed by the FT to produce an image. Each discrete data point in the reconstructed image is called a pixel (i.e., a picture element). The brightness of each pixel corresponds to the sum of the MRI signals in the corresponding small rectangular volume of tissue called a voxel (i.e., the volume element). At each point in the image, the brightness is proportional to the signal intensity generated by the total transverse magnetization in that corresponding voxel of the brain. Thus, the image intensity depends on the number (density) of hydrogen nuclei and the T₁ and T₂ in a specific area of brain tissue (29,91).

Differences in relaxation times between tissues (e.g., gray and white matter, CSF) produce different signal intensity contrasts in the image. The degree to which an MRI scan is sensitive to differences in T₁ or T₂ is controlled by the operator of the scanner. Most images are created using a “spin-echo,” which is a basic pulse sequence that consists of operator-modifiable parameters such as echo time (TE) and repetition time (TR). TE is the time between the initial RF pulse and the peak of the signal, whereas TR is the time between consecutive RF pulses. A pulse sequence with short TR and TE is sensitive to differences in T₁, and the resulting image is called a T₁-weighted image. In such an image, tissues with a long T₁ (e.g., CSF) appear dark. A pulse sequence with long TR and TE produces a T₂-weighted image, in which tissues with a long T₂ (e.g., CSF) appear bright (14,54,91). Thus, selecting the correct pulse sequence setting is critical for determining the relative visibility of certain brain structures and neuropathology.

Diffusion-weighted imaging (DWI) is an alternative approach to capture tissue contrast that depends on the random microscopic movements of water molecules (i.e., diffusion) in brain tissue (26,46,84 92). In DWI, strong magnetic field gradients are applied during a T₂-weighted spin-echo pulse sequence to make the sequence sensitive to water diffusion. After applying the RF pulse to tip the net magnetization into the transverse plane, a diffusion-encoding gradient is applied along one direction, such that the B₀ field is higher in one direction and lower in the opposite direction. As water molecules begin to move around randomly in the tissue, some molecules will move to areas with higher resonant frequencies, and others will move to areas with lower resonant frequencies. The net result is a direct interference in the MR signal that causes signal loss. Signal loss is more severe if diffusion is faster and the diffusion gradients are stronger.

Adjusting the strength of the diffusion-encoding gradient adjusts the strength of the diffusion weighting (i.e., b value). Higher b values indicate stronger diffusion sensitivity, up to a b value given by b D = 1, where D is the diffusion coefficient or “diffusivity” (D ~ 10⁻³ mm²/s in brain tissue). Thus, a b value of 1000 s/mm² is typically used in DWI. A higher b value will reduce the signal intensities and produce a darker image at that tissue location (18,26). Because DWI is also T₂-weighted, “T₂-shine through” effects can occur from the bright signal intensities of free-water. These T₂ effects can be eliminated by calculating the diffusion coefficient (D) from images with two different b values (typically from a T₂-weighted image with b~0 and a DWI) (70). Because the diffusion coefficient depends on complex factors in tissue, it is sometimes referred to as the apparent diffusion coefficient (ADC). Thus, the observed D in tissues represents the effective rate of diffusion in an image voxel. To measure D, DWI sequences sometimes utilize at least two different b-values to plot the best-fit D using the log of the signal intensity measured in a specific tissue (26).

Diffusion encoding gradients can be applied along three orthogonal axes to produce three different DWI contrasts that provide information regarding the directionality of water motion. Water molecules that diffuse in tissues composed of fibers (e.g., white matter) move rapidly along the fiber, but slowly across the fiber due to fiber walls that act as barriers (80). In these tissues, water diffusion is anisotropic (i.e., varies along different directions). Water molecules in pure water do not encounter barriers and travel quickly and equally in all directions (isotropic diffusion). For tissue that is generally isotropic (e.g., gray matter and CSF), water molecules follow a random pattern of motion, and the signal loss is not dependent on the direction of the diffusion-encoding gradient. In these tissues, a single scalar D is sufficient to characterize diffusion (26). By contrast, the signal loss in anisotropic tissue (e.g., white matter) strongly depends on the direction of white matter fibers and the diffusion-encoding gradients, which complicate interpretation of DWI contrast. Thus, the directionally-averaged D (or mean diffusivity (MD) image) is often calculated in clinical practice, which is the average of the computed D images obtained from the orthogonal encoding directions. Sometimes the average DWI or isotropic DWI (DWI_iso) is also shown, which is the geometric mean of the corresponding DWIs. In both MD and DWI_iso, the effects of white matter fiber direction have been removed. For a more complete description of the directional motion of water molecules in anisotropic tissues, a diffusion tensor is required (9,10,19).

DIFFUSION TENSOR IMAGING

Derivation of the diffusion tensor from the DWIs allows for the quantification of water diffusion in living brain tissue, thus providing information about the underlying tissue microstructure. The diffusion tensor characterizes the three-dimensional spread of diffusing water molecules from a point source using three-dimensional ellipsoids. Various biological factors influence the shape of the diffusion ellipsoid, including the microstructural composition of human brain tissue. DTI scan protocols require the application of at least six non-collinear diffusion-encoding gradients and a reference image (typically a b~0 image) to capture the full extent of directional water mobility in anisotropic tissue voxels (an anisotropic tissue voxel is a voxel that is, for example, 2×2×5mm in dimensions) (19,63). Modern research scan protocols tend to utilize many more directions (up to 64) to increase the sensitivity of the signal and improve measurement accuracy (35).

The majority of work utilizing DTI has focused on white matter integrity, as changes in white matter microstructure can be readily delineated using DTI metrics. White matter primarily consists of myelinated and unmyelinated axon fibers that restrict water movement in directions perpendicular to the fibers, thus increasing anisotropy (56). Damage to axons and/or the myelin sheath reduces anisotropy and increases the rate of diffusion in directions perpendicular to the fibers, which is a common result of aging and disease (4,56,82). DTI can also be used to evaluate changes in gray matter microstructure, though the biological interpretation of gray matter diffusion is less clear than in white matter due to the high level of isotropic diffusion that is evident in normal-appearing gray matter (4,28). Increases in gray matter diffusion have been reported in previous studies of aging (59,68,75,76), yet the mechanisms underlying these changes have not been fully delineated.

Fractional anisotropy (FA) and MD are traditional DTI scalar metrics that measure diffusion processes by quantifying the degree of directionality of water diffusion and the directionally-averaged rate of water movement within an image voxel, respectively (15). Damage to cellular microstructure (e.g., axon degeneration, myelin loss, etc.) alters the movements of water molecules and typically results in increased MD and decreased FA (3). Axial diffusivity (AD) and radial diffusivity (RD) are additional DTI metrics that measure water diffusion that occurs parallel and perpendicular to axon fibers (60). Increased RD and decreased AD are believed to reflect reduced integrity as a result of demyelination, axon damage, fiber rarefaction, and/or gliosis (11).

TECHNICAL LIMITATIONS OF DTI

Numerous factors influence accuracy and precision of DTI data, including imperfections in scanner hardware (e.g., RF coil, magnetic field gradients), selection of operator controlled parameters (e.g., pulse sequence, number of acquisitions, number of diffusion-encoding gradients), and patient variables (e.g., motion) (55). As a result, quality control (QC) of imaging data is critical for obtaining accurate DTI measurements. Various QC procedures can be implemented to minimize errors from multiple sources, and these procedures are often selected according to the research question of interest. Despite these efforts, certain image artifacts remain after correction, and the presence of these artifacts significantly limits research investigations utilizing diffusion indices. Below, we review partial volume effects as a key limitation to DTI applications, specifically in the use of DTI to understand normal and abnormal brain conditions.

Partial Volume Effects

Because the voxel signal is a sum of all tissue signals within the voxel (i.e., all transverse magnetization vectors), finite image resolution inevitably causes a mixture of signals at the interface of two tissues. Qualitatively, this partial volume effect (PVE) can cause loss of edge contrast between tissues occupying the same voxel and can even obscure small lesions near the interface between tissues (72). Quantitatively, PVEs can cause errors in volumetric measurements using structural MRI or region-of-interest (ROI) measurements using DTI. The PVE is more severe when the signal difference between the two tissues is greater, and when the tissue interface makes a shallow angle with respect to the edge of the voxel. Such effects are particularly strong when using a slice thickness that is larger than the in-plane voxel dimensions (87) (e.g., non-isotropic voxel dimensions).

A main source of PVEs is CSF contamination of gray matter on the surface of the cortical ribbon (42). The CSF-gray matter PVE is particularly strong due to the high contrast between CSF and gray matter on T₁ and T₂-weighted images, and because of the undulations of the cortical ribbon that lead to unpredictably shallow interface angles. Further, CSF-gray matter PVEs manifest as errors in gray matter volumetric measurements and ROIs that are proportional to the ratio of surface area to volume of a measured tissue, which is higher for gray matter. These artifacts are of greater concern in studies of abnormal brain integrity in normal aging and age-related disorders, as tissue atrophy increases the magnitude of the PVE (12,88). Thus, DTI examinations of clinical populations may yield variable conclusions across studies as a result of latent CSF PVEs. Further, voxels containing more than one type of tissue will exhibit heterogeneous diffusion properties and produce biased measurements. Signal contamination causes an overestimation of MD and underestimation of FA (78) and represents a major limitation for studies investigating brain microstructure. Specifically, CSF PVEs have been shown to reduce the biological approximation of DTI parameters by as much as 15–60% in previous studies (6,7,44).

Voxel and pixel size are important operator-controlled parameters that influence PVEs. Larger voxels are more likely to include multiple brain structures and therefore have a greater propensity for CSF contamination (2). This effect is often observed in gray matter, where larger voxels are sometimes used to enhance signal intensity of subcortical nuclei, though the effect may also be observed in deep white matter regions. Reducing the size of the image voxels will reduce PVEs, yet this comes at a cost to the signal-to-noise ratio (SNR) (78,95). Since these factors have the potential to alter imaging analytical approaches, an investigation into methods that can mitigate CSF PVEs is warranted.

STRATEGIES TO REDUCE CSF CONTAMINATION

Initial attempts to control CSF PVEs relied on fluid attenuated inversion recovery (FLAIR) (27). The FLAIR sequence consists of an inversion pulse at the beginning of the pulse sequence that tips the net longitudinal magnetization 180° into the z plane. The longitudinal magnetization then undergoes T₁ relaxation to become positive. After the inversion time (TI), signal is generated using a 90° RF pulse (described earlier in this review). The TI interval is chosen so that the CSF longitudinal magnetization recovers exactly at the time of the 90° RF pulse, which ensures that the signal is not generated from CSF. Because CSF has a longer T₁ than gray or white matter, the longitudinal magnetization of brain tissues recovers to a positive value prior to the 90° pulse, thus generating the signal. FLAIR also utilizes a long TE to produce T₂-hyperintense signals in fluid-filled lesions near the ventricles (21,27). However, recovery of longitudinal magnetization in brain tissue is incomplete and therefore reduces SNR.

The FLAIR approach can also be used to suppress CSF signals in DTI by preparing the magnetization with a 180° RF pulse prior to the conventional DTI pulse sequence (44,64). While several studies have reported that FLAIR increases the accuracy of DTI and DTI-based tractography measurements (17,64), it also reduces SNR, reduces the number of slices, increases scan time, and has limited utility at higher magnetic field strengths (e.g., > 3T) (8,53). Further, this technique is seldom utilized clinically, as FLAIR-prepared DTI sequences require cardiac gating to avoid motion artifact from cardiac pulsations (53).

Sub-Voxel Modeling as a Solution to CSF PVEs

Other previous efforts to resolve the problem of CSF PVEs have relied on fitting a tissue tensor and a CSF tensor (or CSF diffusion coefficient) to the DWI data to account for mixed diffusion signals within a voxel (53,65,66,69). The most common approach is referred to as the “free water elimination” (FWE) method of Pasternak et al. (65). This approach assumes that there are two subregions within a voxel that demonstrate characteristic tensor signals for brain tissue and free-water. By calculating separate tensors for CSF versus brain tissue, the CSF contamination can be controlled. This FWE method uses a single b value for diffusion weighting, and thus can be used to analyze existing data acquired with typical research DTI scan protocols. A variant of the FWE method was also developed to give better estimates of the free water component by acquiring and fitting multiple “shells” of DWI data, with each shell providing tensor information and having a different b value (66). This method also uses a different neighboring voxel regularization scheme. While effective (53), this multi-shell approach increases scan time significantly (66).

FWE imposes constraints to a regularization bitensor model fitting to yield continuity between tissue tensors of adjacent voxels. It has been stated that these FWE methods enable estimation of the free water fraction and the distinction between water from CSF versus water from vasogenic edema (66). Because the latter source of water signal is a result of physiologic changes (e.g., aging, stroke, etc.) rather than partial volume artifact, this method was thought to be suited to removing CSF signal in brain scans of older individuals who may have pathologic sources of tissue water. Technically, the FWE approaches are limited by smoothing constraints that reduce sensitivity to subtle microstructural abnormalities (47) and therefore may not be ideal for certain research questions examining brain changes in the early stages of disease.

A significant aspect of the sub-voxel modeling approaches described above is the modeling of free water and tissue signal components, and the assumption that each component signals a non-monoexponential pattern of signal decay (57). The exponentiality of signal decay likely depends on the range of b values used and the dependence of tissue and CSF signal on the b value (22,33,52,57). One view postulates that true diffusion decay of brain parenchymal tissue is in fact non-monoexponential (34,51,52), independent of the CSF signal. A potential limitation of these approaches that is not commonly discussed is that CSF in sulci and ventricles often exhibits bulk flow and pulsatile motion (49) and therefore may have a more complex signal decay behavior compared to stationary water in a container. Gaussian diffusion, in which molecular water displacements have a Gaussian distribution, forms the basis for the ellipsoid model of diffusion. Several techniques have been developed to measure non-Gaussian diffusion, such as q-space imaging (5), diffusion kurtosis imaging (34), and diffusion spectrum imaging (90). While each of these approaches has provided new insights into image analysis and our understanding of neurophysiology, the theory of diffusion-weighted signal decay in brain tissue has not gained categorical acceptance, possibly due to variations in the intra- and extracellular volume fractions used across methods (52).

Alternative Techniques to Suppress the CSF Signal

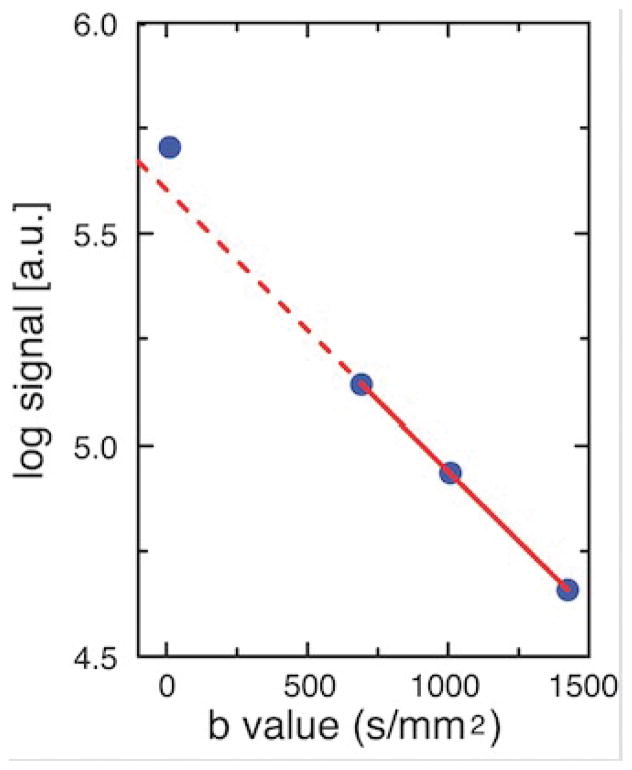
As an alternative to modeling the CSF signal component in the voxel, the CSF signal can be suppressed using the diffusion-encoding gradients (as opposed to using FLAIR). In developing such a model-independent approach, our group recently examined CSF suppression and multiexponential decay in the gray matter of older individuals (75). We analyzed DWI_iso images (computed as the geometric means of the DWIs) efficiently acquired at 4 b values based on the following pulse sequence: 5 acquisitions at b~0, 3 perpendicular directions at b = 680 s/mm², 24 intermediate directions at b = 996 s/mm², and 4 tetrahedral directions at b = 1412 s/mm² (75). To assess the potential effect of CSF PVEs on the decay curve and the exponential nature of the signal decay, signal intensities were graphed as a function of b values for several bilateral ROIs, including perisulcal gray matter (e.g., superior temporal gray matter), periventricular gray matter (e.g., caudate), and gray matter distant from CSF (e.g., putamen). Semilog plots of the DWI_iso signal intensity (geometric means) versus b value in perisylvian gray matter revealed that the b~0 signal was above the straight-line fit of the three b ≥ 680 s/mm² points (Figure 1). Further, the b ≥ 680 s/mm² points were observed to follow a straight line, indicating that CSF contamination is a source of non-monoexponential decay in gray matter that can be suppressed with the removal of the b~0 data. Importantly, this result also indicates that the remaining data points from b ≥ 680 to 1412 s/mm² followed a monoexponential pattern of decay, demonstrating that a tensor can be accurately fit to this range of b values without including b~0 data.

Figure 1.

Diffusion-weighted signal decay curve for right superior temporal gray matter (GM) in one subject from the study by Salminen et al. (25). The isotropic DWI (DWI_iso) image was computed from the geometric mean of the DWIs at each of the four b values (b~0 and b= 680, 996, and 1412 s/mm²). The DWI_iso signal intensity was measured from the geometric mean images using a ROI in superior temporal GM. The log of the DWI_iso is graphed versus b value so that the monoexponentiality of signal decay can be assessed by the fit of the data to a straight line. The solid red line is fit to the three b ≥ 680 s/mm² data points. The graph shows that the b~0 data point is artifactually above the dashed red line that is extrapolated from the fit to the other three data points. The DWI_iso images at b~0 showed bright CSF signal, while the three DWI_iso images with b ≥ 680 had absent CSF signal (not shown). Thus, the deviation in the b~0 data point indicates partial volume averaging with CSF in the adjacent sulci and Sylvian fissure. The observation that the three data points with b ≥ 680 fall on a straight line indicates monoexponential decay of gray matter after removing CSF effects. The artifactual deviation in the b~0 data due to CSF effects is somewhat muted by the large ROI, which contains some voxels that are not adjacent to CSF (for voxels adjacent to CSF spaces, the effect is stronger). The log of the ventricular CSF signal deviated from linearity at all data points (not shown), indicating a more complex signal behavior in CSF. The signal intensity and its log are in arbitraty units [a.u.].

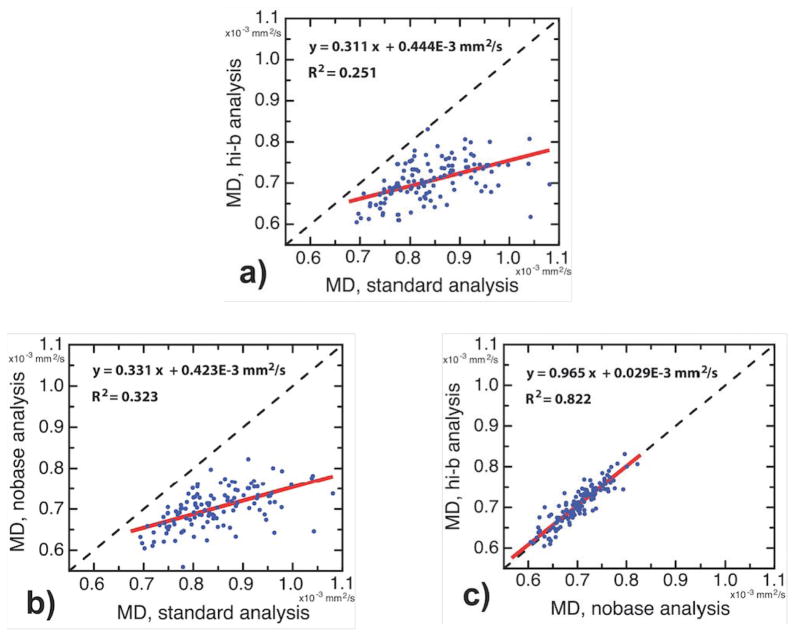
CSF suppression and tissue exponential decay were further tested by comparing MD that was calculated from the results of three separate tensor-fitting schemes: 1) the standard scheme in which all four b values were included; 2) the nobase scheme in which only b~0 data were eliminated; and 3) the high-b scheme in which only the two highest b values were included. The results for the different schemes are compared in Figure 2. First, MD measured by the standard method was compared to MD from the nobase method in the right superior temporal gray matter (Figure 2a). Each data point in the scatterplot represents a different subject. The deviation from the line of identity is due to the CSF effect. A similar deviation occurred for the standard versus high-b methods (Figure 2b). In contrast, the nobase and high-b results fell on the line of identity (Figure 2c), which indicates that the CSF effect was eliminated and that the b values between 680–1412 s/mm² sample the same exponential decay curve. The smallest difference across the three different fitting schemes was observed for the putamen (1%, d < .4), which was expected given its distal location to CSF areas. Moderate differences were observed in the caudate between standard and nobase, and between standard and high-b methods (11%, d < .75). Even larger differences were observed in sulcal gray matter areas (15%, d > 1.0). Differences between nobase and high-b were negligible for nearly all brain regions (1–2%), and these minor differences were likely a result of the additional random noise caused by the narrower range of b values in the high-b analyses (note that all CSF correction methods have increased SNR). For example, the left putamen demonstrated a subtle negative percent change between nobase and high-b (−1.8%). Further study is needed to determine whether this very small difference is due to a subtle effect of CSF-like signals (e.g., Virchow-Robin spaces).

Figure 2.

Scatterplots demonstrating the difference between mean diffusivity (MD) measurements in superior temporal gray matter of the right hemisphere (rh.superiortemporal) using the three different schemes: standard (all four b values), nobase (no b~0 data), and high b (no b~0 data and no b ≥ 680 s/mm² data). The diagonal black dashed lines are lines of identity. Figures 2a and 2b show that the standard MD is overestimated with respect to the other measures. The agreement between nobase and high-b in Figure 2c indicates that nobase effectively corrects for CSF PVEs. In Figure 2c, the slope is 0.965 +/− 0.041, and the y-intercept is 0.0293 × 10-3 +/− 0.0505 × 10-3 (+/− 1.0 standard error in each case), indicating agreement in the nobase and hi-b measures. Note that MD values are in units of mm²/s. Each data point represents a ROI measurement for one participant in the study. Linear regression lines are shown (solid red), with regression equations and R² statistics given as text.

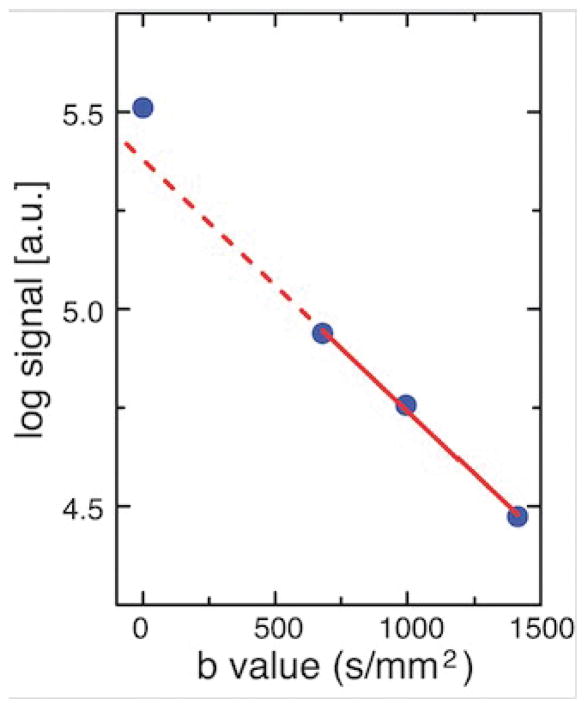
Similar phenomena can occur in white matter. A semilog graph of the isotropic DWI signal versus b value in white matter anterior to the temporal horns of the lateral ventricle (Figure 3) shows deviation of the b~0 data point, while the b ≥ 680 s/mm² data points fall on a straight line. This effect is indicative of a CSF PVE in this white matter region and monoexponential decay in the underlying white matter parenchyma over the range of b values from 680 – 1412 s/mm². This monoexponentiality is important because it enables accurate tensor measurement over a subset of b values that exclude the b~0 data. It also enables tensor fitting using a reduced number of encoding directions at each b value, thus shortening the scan time.

Figure 3.

Semilog graph of the isotropic DWI signal (DWI_iso) versus b value in white matter. Measurement, analysis, and graphical display as described in Figure 1, except that the ROI in Figure 3 is in white matter posterior to the left temporal pole. Partial volume averaging with CSF is evident by the upward deviation of the b~0 data point relative to the dashed black line, due to the adjacent temporal horn of the lateral ventricle. Like the gray matter ROI in Figure 1, the three data points with b ≥ 680 s/mm² fall on the straight solid red line, suggesting monoexponential decay over the b value range of 680–1412 s/mm².

Recently, Baron and Beaulieu (8) independently reported a similar approach to improve the accuracy of DTI tractography using a non-zero b-minimum (b_min = 425 s/mm²) and a relatively short TR (TR = 3.0 s). This study compared the effects of both parameters on fiber tracking. Specifically, they determined the effects on pathway volume and diffusion scalar metrics in pathways vulnerable to CSF PVEs (such as the fornix) and also tracts that are less sensitive to CSF (such as the superior longitudinal fasciculus, SLF). The combination of a short TR and b_min = 425 s/mm² resulted in more than a 50% increase in pathway volume for the crura and body of the fornix, and a 14% increase in SLF volume. As a result, 30% higher FA and 36% lower MD were observed in the crura. These results are consistent with the trends that would be expected if CSF contamination of tissue voxels were reduced. Percentage increases were not reported using a non-zero b-minimum alone without a short TR. DTI accuracy was also improved for the body of the fornix and the SLF, though these improvements were less robust. Interestingly, using a non-zero b-minimum without adjusting TR produced nearly equivalent volumetric increases as the combined model in both tracts. Furthermore, reducing TR alone did not significantly impact SLF measurements, suggesting a greater effect of b~0 data on CSF PVEs in white matter.

The significance of the above two methods that omit the acquisition or analysis of b~0 is very high. CSF contamination significantly reduces the accuracy of DTI measurements and DTI-based tractography. Artificially low FA values in voxels adjacent to CSF can bias DTI measurements or cause tractography to fail in these regions due to FA falling below the tracking threshold (8). DTI measurements and tractography of white matter fiber bundles, such as the fornix, cingulum, uncinate fasciculus, and corpus callosum, may be particularly sensitive to CSF PVEs given their anatomical proximity to CSF spaces. Abnormalities in each of these structures have been identified in normal aging and in various neurological conditions (e.g., dementia, multiple sclerosis, schizophrenia, etc.) (31,43,96), and accurate DTI measurements are critical for understanding the implications of these structural alterations. The fornix is of particular interest in studies of neurodegenerative and neuropsychiatric disease, as it is a major white matter projection from the hippocampus that directly passes through the ventricles. As such, it is highly susceptible to CSF contamination and requires a corrective technique to remove CSF signal. Few studies of the fornix have employed such a method, however, which is likely due to limited recognition of CSF PVEs and the limitations of prior corrective techniques in DTI. The outcomes reported by Baron and Beaulieu (8) indicate that CSF suppression using a non-zero b-minimum and shorter TR causes fewer voxels to be missed during tractography, translating to greater accuracy of diffusion measurements. Our study (75) also reveals that removal of b~0 data from the analysis results in more sensitive detection of age effects in gray matter of the right temporal lobe (Figure 2), and removes CSF effects from white matter regions adjacent to CSF spaces (Figure 3).

To date, there has been limited research on water diffusion in gray matter using CSF suppression techniques. Interpretation of diffusion measurements in gray matter is less straightforward compared to interpretations of white matter measurements due to greater isotropic diffusion and cellular heterogeneity inherent in gray matter. Deep gray matter areas are also occupied by fluid-filled Virchow-Robin spaces (VRSs) that contribute relatively high signal intensity on b~0 images and may alter overall voxel diffusion measurements. The results of our study offer resolution to CSF contamination of gray matter through the removal of b~0 data and tensor fitting of data ranging in b values from 680 to 1412 s/mm² (75). We also postulate that our technique may be effective at suppressing water-like signal in VRSs in addition to CSF. Enlarged VRSs (>2mm) are commonly observed in the basal ganglia of older adults (97). In our opinion, it is still preferred to acquire b~0 data (at little cost in scan time) because it can be included in the analysis of regions not affected by CSF-like PVEs, thus increasing SNR. Collectively, the two methods described by Salminen et al. (75) and Baron and Beaulieu (8) can be considered no-b-zero (NBZ) approaches to CSF suppression. Unlike the previously discussed methods, NBZ methods do not depend on a model of CSF or tissue signal (i.e., are model-independent), and CSF is suppressed regardless of CSF flow pattern or T₁ value.

The observation that CSF contamination was evident in both NBZ studies suggests that outcomes of earlier investigations utilizing DTI have likely been impacted to some degree by CSF PVEs in certain brain regions. This is particularly true in studies of older individuals in whom age-related physiologic factors (e.g., ventricular enlargement, sulcal expansion) increase the propensity for CSF PVEs. The CSF suppression techniques proposed by our group (75) and Baron and Beauleiu (8) offer promising alternatives to former correction methods by robustly reducing the CSF signal to negligible levels in both gray and white matter, thereby improving the biological approximation of the DTI measurements. As such, there are several implications for using this technique in conjunction with numerous imaging modalities and data processing schemes. For the remainder of this review, we will discuss potential uses of CSF-suppressed DTI in general, and the NBZ approaches in particular.

NEW APPLICATIONS OF CSF-SUPPRESSED DTI AND FUTURE INNOVATION

To date, CSF-suppressed DTI using a model-free NBZ approach has been utilized in only two studies (8,75), both of which focused on older adults without neurologic disease. The potential for CSF suppression to improve the accuracy of DTI metrics in neurological populations represents an important direction for future research. Small vessel ischemic disease is common among older individuals and is related to poorer cognitive performance in otherwise healthy adults, which may progress to vascular dementia in some individuals (61). Further, vascular disease has been hypothesized to represent a risk factor for the subsequent development of Alzheimer’s disease (AD) (36,50). CSF-suppressed DTI, particularly using a NBZ approach, may help identify key mechanisms of neurological dysfunction in these clinical conditions. Similarly, while standard DTI has been utilized to examine multiple sclerosis and HIV-associated brain dysfunction, the neuroimaging signatures associated with these conditions are significantly complicated by acute inflammatory fluctuations (16,71,74), resulting in variable outcomes across studies. Application of CSF-suppressed DTI has the potential to more accurately characterize tissue microstructure in these conditions to improve clinical assessment and patient care strategies.

Multimodal MR Imaging

An additional opportunity for future applications of CSF-suppressed DTI includes multimodal imaging. The neuroimaging field is evolving towards the integration of multiple forms of imaging outcomes from various modalities. Multimodal imaging capitalizes on the strengths of different modalities that are uniquely valuable at detecting abnormalities in brain tissue across multiple neural systems. While many studies have applied different MR imaging sequences in parallel within a population (e.g., anatomical MRI, DTI, magnetic resonance spectroscopy (MRS), and resting state functional MRI (rs-fMRI)) (25,30,32,79,81,94), integration of outcomes from different MRI modalities into a unified and meaningful explanatory model of brain structure/function represents a future innovation in brain imaging.

Ajilore et al. (1) revealed the relative power of multimodal MR imaging compared to single modality imaging by integrating rs-fMRI with DTI to create a functional-by-structural hierarchical (FSH) map. This study revealed clinically relevant brain abnormalities that were not evident when either DTI or rs-fMRI outcomes were analyzed separately. These results demonstrate enhanced sensitivity of multimodal imaging to detect alterations in the brain connectome over single modality imaging. Implementing CSF-suppressed DTI has the potential to enhance FSH mapping by removing CSF contamination from voxels along white matter track lines that are adjacent to CSF spaces, resulting in a more accurate depiction of tract anatomy and more accurate measurement of tract metrics, such as tract anisotropy and mean fiber bundle length.

Machine Learning

Another area of innovation involves machine learning approaches. Machine learning is an area of artificial intelligence that can detect spatially distributed patterns within a group (48). Earlier imaging studies utilized machine learning techniques such as support vector machine (SVM) analysis to classify patterns of brain activation across individuals (62,67,85). New applications of machine learning include pattern recognition through high-level, multidimensional clustering. The advantage of this technique is that it automatically detects regularities in imaging data across disparate datasets (77). These regularities can be used to generate predictions for ascribing cognitive states to patterns of brain activity. As such, machine learning allows for automated pattern recognition that can be used as a diagnostic tool for complex diseases (62). SVM has been used to facilitate differential diagnoses of complex diseases (38,40), distinguish mild forms of AD from aging, distinguish individuals with clinically asymptomatic conditions from normal controls (39,73), define behavioral subtypes of clinical conditions (24), and reliably fit functional activity signals to genetic networks (20,89,93).

Machine learning is not without limitations. Specifically, while machine learning is designed to manage complex and heterogeneous data, the method becomes less reliable when there are image artifacts or variations in imaging acquisition procedures (23,83). Machine learning also requires large data sets, often acquired at multiple project centers. CSF-suppressed DTI may be one solution for reducing the variance of multicenter DTI data, as some of the variance could be a result of CSF PVEs and inconsistent CSF-correction strategies. Studies are needed to confirm whether CSF-suppressed DTI effectively stabilizes the variance of DTI metrics and improves the accuracy of future prediction models.

CONCLUSIONS

In the midst of remarkable technological advancement and innovation, our ability to improve health and the human condition has increased dramatically, but the human brain remains the greatest mystery in medical science. While advances in medical oncology, pathobiology, immunology, and microbiology provide demonstrable benchmarks toward the understanding and treatment of diseases such as cancer, diabetes, HIV, ebola, etc., the understanding and treatment of many brain disorders remain elusive. Noninvasive neuroimaging is one of the most powerful tools in our arsenal to reveal biological signatures of human brain pathology. CSF-suppressed DTI, and in particular the NBZ approaches, offer a new frontier of imaging research that may yield measurements of increased biological value. By reducing signal artifact and measurement bias, we can remove more barriers of uncertainty, which will allow us to unveil the dynamic physiological and microstructural mechanisms of the normal and disordered brain. Pushing the conventions of neuroimaging technology will continue to boost the value of data it yields and help solve the mysteries of this remarkably complex organ.