Laboratory measurements and astronomical search for the HSO radical

Abstract

Context

Despite the fact that many sulfur-bearing molecules, ranging from simple diatomic species up to astronomical complex molecules, have been detected in the interstellar medium, the sulfur chemistry in space is largely unknown and a depletion in the abundance of S-containing species has been observed in the cold, dense interstellar medium (ISM). The chemical form of the missing sulfur has yet to be identified.

Aims

For these reasons, in view of the fact that there is a large abundance of triatomic species harbouring sulfur, oxygen, and hydrogen, we decided to investigate the HSO radical in the laboratory to try its astronomical detection.

Methods

High-resolution measurements of the rotational spectrum of the HSO radical were carried out within a frequency range well up into the THz region. Subsequently, a rigorous search for HSO in the two most studied high-mass star-forming regions, Orion KL and Sagittarius (Sgr) B2, and in the cold dark cloud Barnard 1 (B1-b) was performed.

Results

The frequency coverage and the spectral resolution of our measurements allowed us to improve and extend the existing dataset of spectroscopic parameters, thus enabling accurate frequency predictions up to the THz range. These were used to derive the synthetic spectrum of HSO, by means of the MADEX code, according to the physical parameters of the astronomical source under consideration. For all sources investigated, the lack of HSO lines above the confusion limit of the data is evident.

Conclusions

The derived upper limit to the abundance of HSO clearly indicates that this molecule does not achieve significant abundances in either the gas phase or in the ice mantles of dust grains.

1. Introduction

Many sulfur-bearing molecules, ranging from simple diatomic species up to astronomical complex molecules such as ethyl mercaptan (CH₃CH₂SH), have been detected in interstellar gas clouds and circumstellar outflows (see, for example, Müller et al. 2005; Kolesniková et al. 2014). These observations comprise a wide variety of astronomical sources in our local Galaxy and at greater distance, and include the detection of di- and triatomic atom sulfur species in the intermediate redshift environment. Nevertheless, sulfur chemistry in space is still largely unknown: sulfur exists in the gas phase in the diffuse ISM with almost no depletion compared to its solar abundance (Savage & Sembach 1996), while in the cold, dense ISM much lower abundances of sulfur are observed (Joseph et al. 1986). This depletion is thought to be due to the accretion of sulfur onto solid dust grains, even if the form of sulfur on, or in, these grains remains unknown. The presence of hydrogen sulfide on dust grains has been proposed, and laboratory results from Garozzo et al. (2010) suggest that mixtures of CO and H₂S when exposed to ion irradiation form other sulfur-bearing species including OCS and SO₂. These are the only sulfur-bearing species that have been detected so far on grains (Palumbo et al. 1997; Zasowski et al. 2009). As of now, none of these species has been found to compensate for the lack of sulfur detected. The location and the chemical form of the missing sulfur have yet to be identified. For these reasons, we decided to investigate the HSO radical, aiming to detect it astronomically. Since accurate rest frequencies are needed for searches in the ISM, this work starts with a laboratory study of the rotational spectrum of HSO up to the THz region. The large abundance in space of triatomic species harbouring sulfur, oxygen, and hydrogen such as H₂O, H₂S, OCS, SO₂, HCO⁺, and HCS⁺ especially in high-mass star-forming regions (see, e.g., Li et al. 2015; Goicoechea et al. 2015; Crockett et al. 2014; Belloche et al. 2013; Esplugues et al. 2013; Marseille et al. 2010; Tercero et al. 2010; Matthews et al. 1987) and also in cold dark clouds (Liu et al. 2013; Caselli et al. 2012; Cernicharo et al. 2011; Kaifu et al. 2004; Minh et al. 1989; Irvine et al. 1983) is well known. Therefore, a triatomic species containing these three atoms, such as HSO, can be expected to exist and to be identified in these astronomical objects. Furthermore, HSO is one of the key intermediates in the atmospheric oxidation of H₂S to sulfuric acid (H₂SO₄), and it has also been proposed to play a predominant role in catalytic cycles that cause stratospheric ozone depletion (Tyndal et al. 1991).

The HSO radical has already been the subject of a few experimental and theoretical investigations. The first experimental evidence of HSO was provided by Schurath et al. (1977), based on the observation of low-resolution chemiluminescence spectra in the visible region by using a reaction of atomic oxygen with H₂S and O₃ for the generation of HSO. A few years later, Endo et al. (1981) provided the first high-resolution spectral characterisation of the radical and of its deuterated substituted species, DSO, by means of microwave spectroscopy in the millimiter-wave region, thereby employing a glow discharge cell and a mixture of H₂S (D₂S for DSO) and O₂. Endo and co-authors also determined the hydrogen hyperfine-coupling constants of HSO, and clarified that the electronic ground state of the radical is of A″ symmetry. In subsequent work Webster et al. (1982) measured the electric dipole moment along the a- axis for the ground electronic state (µ_a = 2.20±0.08 D) and for the òA′ excited electronic state (µ_a = 1.25±0.08 D) of HSO.

In this work, we report laboratory high-resolution rotational spectra of the HSO radical within a frequency range well up into the THz region, thus improving and enlarging the existing dataset of spectroscopic parameters. To guide the high-frequency measurements, we also carried out state-of-the-art quantum-chemical calculations. Based on the spectroscopic results of this work that allow us to provide accurate frequency predictions up to the THz range, we have carried out a rigorous search for the HSO radical in the interstellar gas. The manuscript is organized as follows. In the next three sections, the laboratory experiments, the spectral analysis, and the computational details are described, while in the fourth section the spectroscopic results are reported and the astronomical search is thoroughly discussed.

2. Experiment

Measurements were carried out with a frequency-modulated, computer-controlled spectrometer (65 GHz - 1.6 THz) (Cazzoli & Puzzarini 2006; Puzzarini et al. 2012a; Cazzoli & Puzzarini 2013), with the 194 GHz – 1.2 THz range actually considered. The millimeter-/submillimeter-wave sources employed, phase-locked to a rubidium frequency standard, are frequency multipliers driven by Gunn diode oscillators. The frequency modulation was obtained by sine-wave modulating the 72 MHz local oscillator of the synchronisation loop at 16.66 kHz, with the modulation depth varied from 200 kHz to 1.8 MHz according to the transition frequency under consideration. Liquid-He-cooled InSb and Schottky diode detectors were used and their output processed by means of a lock-in amplifier tuned to twice the modulation frequency (second harmonic detection). Measurements were carried out with a single-path arrangement using a free-space cell that consists of a glass tube ~3 m long.

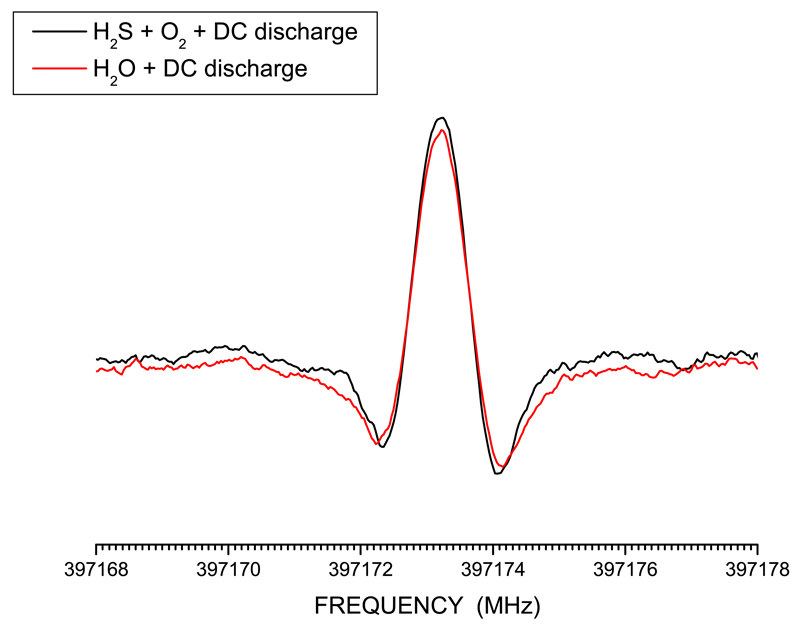
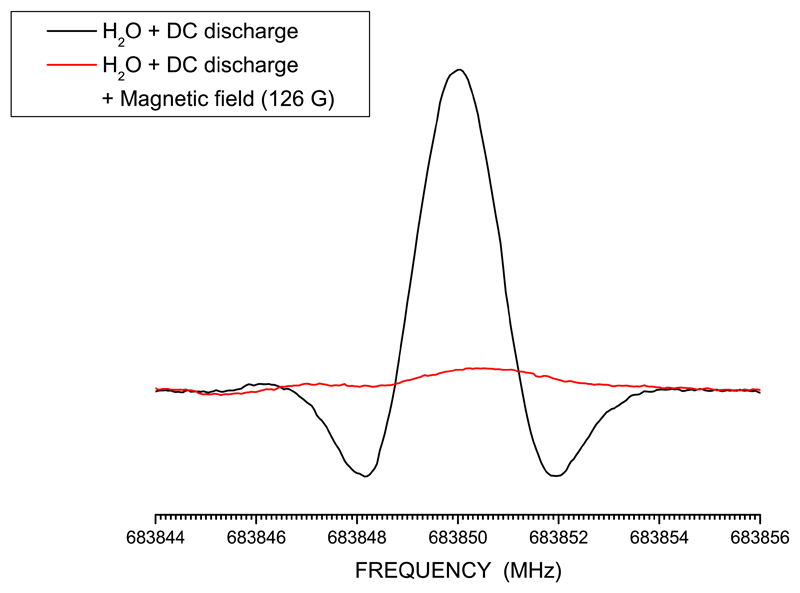
Samples of HSO were prepared directly inside the absorption cell starting from a suitable mixture of gases and by applying a DC discharge of tens of mA (~10-40 mA). The best signals were obtained with a 1:2 mixture of H₂S and O₂, with starting pressures of about 3 to 10 mTorr of H₂S. Measurements were performed in a continuous flow of gas, maintained by a diffusion pump, to constantly provide fresh precursor gases. The use of H₂S and of other sulfur-bearing chemicals in previous unrelated experiments led to sulfur being adsorbed on cell walls and thus allowed us to achieve good signals of HSO employing only a flow of ~35-50 mTorr of H₂O and a DC discharge of 50-60 mA. One advantage of using only water instead of a mixture of H₂S and O₂ is the limited production of S -bearing species other than HSO. In Figure 1 the comparison of two recordings of the N = 10_6,4(5) - 9_6,3(4) transition is depicted; in one case, HSO is produced by employing a mixture of H₂S and O₂, while in the other case only H₂O has been used in the discharge. It is noted that the signal-to-noise (S/N) ratio is very similar for the two spectra, with the signal being marginally more intense when H₂S is employed. These and all other measurements were carried out at room temperature. For each transition, a magnetic field of several Gauss, parallel to the radiation source, was used to confirm that the recorded feature belongs to a free-radical. This is shown in Figure 2: by applying a magnetic field to the N = 17_1,16 - 16_1,15 transition at ~683.8 GHz, due to Zeeman effect, its intensity is strongly reduced and its frequency is shifted.

Fig. 1.

The N = 10_6,4(5) - 9_6,3(4) transition at ~397.2 GHz. In black, the signal when a mixture of H₂S and O₂ is employed in the discharge for producing HSO. In red, the recording when the radical is produced by using H₂O only and sulfur adsorbed on cell walls.

Fig. 2.

The N = 17_1,16 - 16_1,15 transition at ~683.8 GHz. In black, the signal obtained by HSO produced by discharging (current = 55 mA) 43 mTorr of H₂O only and employing a modulation depth of 1.6 MHz. In red we show the signal when a magnetic field of 126 G has been applied to the previous conditions.

The accuracy of our measurements ranges from 70 kHz to 150 kHz and it has been based on the standard deviations of the averages of sets of measurements, the transition intensities, and the S/N ratio (Cazzoli et al. 2004; Landman et al. 1982). The largest uncertainties affect the weak features recorded in the THz region that show a limited S/N ratio.

3. Analysis

HSO is a prolate asymmetric-top radical species, with a ²A″ electronic ground state. The rotational angular momentum N, the electronic spin momentum S, and the nuclear spin angular momentum I (of hydrogen) couple according to Hund’s case b:

$$\mathbf{\text{J}}=\mathbf{\text{N}}+\mathbf{\text{S}}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{F}}=\mathbf{\text{J}}+\mathbf{\text{I}}.$$ (1)

The effective Hamiltonian operator is given by the sum of three terms:

$$H=H_{rot}+H_{S-N}+H_{hfs},$$ (2)

where H_rot is the rotational Hamiltonian that also includes the centrifugal-distortion terms. H_S–N describes the electron spin-rotation interaction (through the electron spin-rotation tensor ∈) and also accounts for the centrifugal-distortion dependence of the electron spin-rotation constants. Finally, H_hfs is the part of the Hamiltonian that describes the nuclear hyperfine interactions and consists of the isotropic (Fermi-contact interaction) and anisotropic parts of the electron spin-nuclear spin coupling (through the a_F constant and T tensor, respectively) as well as the nuclear spin-rotation interaction constant (through the C tensor). The only nucleus contributing to the H_hfs Hamiltonian is hydrogen, which is the only one with a non-zero nuclear spin (I = 1/2). For explicit expressions of the three Hamiltonians mentioned above, the reader is referred for instance to Endo et al. (1981).

4. Computations

Quantum-chemical calculations of the spectroscopic parameters involved in the Hamiltonians above were carried out using the coupled-cluster (CC) theory (Shavitt & Bartlett 2009), unless otherwise noted, within the CC singles and doubles (CCSD) approach augmented by a perturbative treatment of triple excitations, CCSD(T) (Raghavachari et al. 1989), together with correlation-consistent (aug-)cc-p(C)VnZ (n = T-5) basis sets (Dunning 1989; Kendall et al. 1992; Woon & Dunning 1995; Peterson et al. 2002). Computations were performed with the quantum-chemical program package CFour (2012).

While for a detailed account of the computational procedures, the reader is referred to the literature (Puzzarini et al. 2010b; Puzzarini 2013), we briefly summarize the details of interest to the present investigation. For the determination of the rotational constants, a highly accurate equilibrium structure (straightforwardly providing equilibrium rotational constants) was obtained by resorting to a composite scheme that accounts for extrapolation to the complete basis-set limit (CBS; using n = 5,6), core correlation (CV; cc-pCV5Z) and the full treatment of triple (fT; cc-pVTZ) and quadruple (fQ; cc-pVDZ) excitations (CBS+CV+fT+fQ) (Heckert et al. 2005, 2006). Vibrational ground-state rotational constants were then derived by including the vibrational corrections obtained from the evaluation of a cubic force field followed by a second-order vibrational perturbation theory (VPT2) analysis (Mills 1972; Stanton et al. 1998) at the CCSD(T)/cc-pCVQZ level. As a byproduct of the latter analysis, the quartic and sextic centrifugal-distortion constants were also obtained (Mills 1972; Puzzarini et al. 2012b). The CBS+CV+fT+fQ structure was subsequently used in the evaluation of the equilibrium values of the electron spin-rotation tensor and the hyperfine parameters.

The electron spin-rotation tensor ∈ was calculated in a perturbative manner as second derivative of the energy with respect to the electron spin and rotational angular momentum as perturbations, as described in Tarczay et al. (2010). The reduced off-diagonal ${\tilde{\in }}_{ab}$ term was determined according to Brown & Sears (1979) using the theoretical vibrational ground-state rotational constants mentioned above. The evaluation of the isotropic and anisotropic hyperfine coupling constants (hfcc) required the calculation of the spin density at the nucleus for the former and the corresponding dipole-dipole contributions for the latter (see, for example, Perera et al. (1994)). Finally, the nuclear spin-rotation tensor was computed as the second derivative of the electronic energy with respect to the rotational angular momentum and the nuclear spin in conjunction with the so-called rotational London orbitals (Gauss et al. 1996) as explained in Gauss & Stanton (1996) and Gauss & Sundholm (1997). For all these properties, the equilibrium-value computations were carried out at the CCSD(T)/cc-pCV5Z level with all electrons correlated. For the hfccs, due to the importance of the effect of diffuse functions on the neighboring atoms (see, for example, Perera et al. (1994); Puzzarini et al. (2010a)), CCSD(T) computations with the aug-cc-pCV5Z basis sets were performed. Vibrational corrections (at the CCSD(T)/cc-pVTZ level, within the frozen-core approximation) were evaluated in all cases using the VPT2 approach (Mills 1972; Auer et al. 2003).

5. Results and Discussion

5.1. Spectroscopic Parameters

The transition frequencies retrieved from the present measurements together with those reported in Endo et al. (1981) were fitted using Pickett’s SPFIT program Pickett (1991), with each transition weighted proportionally to the inverse square of its experimental uncertainty. The complete set of data consists of transitions in the 79-161 GHz range from Endo et al. (1981) and in the 194 GHz - 1.2 THz interval from the present study. A total of 205 distinct frequency lines (of which 153 are newly detected) were included in the fit, and led to the determination of 25 independent spectroscopic parameters with a root mean square (RMS) deviation of 78 kHz and a dimensionless RMS error of 0.88. The results of the fit are collected in Table 1, while the list of frequencies is available in the supplementary material, which also contains the set of spectroscopic constants obtained in the SPFIT format (in order to facilitate their inclusion in spectroscopic databases). Our present results are compared to those by Endo et al. (1981) and to the theoretical predictions obtained as explained in the previous section. We note that, in addition to the improvement of the available spectroscopic parameters, new constants have been determined. This allowed us to improve the rest frequency determinations in terms of accuracy as well as to extend their availability to the THz region. To give an example, for the N = 9_1,9 - 8_0,8 transition at ~606 GHz the uncertainty of about 600 kHz predicted based on the parameters given by Endo et al. (1981) reduces to less than 50 kHz when the present spectroscopic constants are used. Furthermore, the corresponding fine components change in frequency by about 2 MHz, that is, more than three times the given uncertainty. To provide another example at lower frequency, we can consider the N = 8_6,2(3) - 7_6,1(2) transition at ~318.8 GHz; for this transition, we note that the uncertainty reduces from 1.4 MHz to about 32 kHz, with a change in the transition frequency of about 4 MHz.

Table 1.

Spectroscopic parameters^a of HSO.

Parameter	This work		Endo et al. (1981)b
	Experimentc	Theoryd
A0 / MHz	299483.90(12)	300316.2	299484.68(14)
B0 / MHz	20502.7847(10)	20527.6	20502.7823(83)
C0 / MHz	19135.6989(10)	19160.0	19135.7168(83)
DN / kHz	29.4675(13)	28.61	29.64(11)
DNK / kHz	904.18(11)	882.33	903.41(40)
DK / MHz	26.24(11)	25.99	[27.2]
d1 / kHz	-2.02504(43)	-1.86	-1.926(65)
d2 / kHz	-0.35187(30)	-0.29	-0.527(52)
HN / mHz	-28.42(75)	-29.07
HNK / Hz	2.779(88)	2.28
HKN / Hz	144.7(43)	126.26
HK / kHz	[6.43]	6.43
h1 ×102 / mHz	[-8.32]	-8.32
h2 / mHz	[3.69]	3.69
h3 / mHz	1.10(22)	0.725
LJK / mHz	-11.4(32)
∈aa / MHz	-10366.15(10)	-10979.0(-10940.5)	-10366.17(16)
∈bb / MHz	-426.633(17)	-439.4(-438.9)	-426.683(31)
∈cc / MHz	0.191(21)	2.82(3.29)	0.210(48)
${\tilde{\in }}_{ab}/\text{MHz}$	377.971(16)	404.8(403.3)	377.81(80)
${\in }_{\mathrm{aa}}^{NK}$e / MHz			0.047(12)
${\in }_{\mathrm{aa}}^{NK}$e / MHz	2.979(10)		3.023(35)
${\in }_{\mathrm{bb}}^{NK}$e / MHz	-0.001676(32)
${\in }_{\mathrm{bb}}^{NK}$e / MHz	0.0638(36)
${\in }_{\mathrm{cc}}^{NK}$e / MHz	-0.114(30)
aF(H) / MHz	-35.72(50)	-35.94(-34.58)	-35.98(42)
Taa(H) / MHz	-11.932(86)	-12.38(-13.25)	-11.883(71)
Tbb(H) / MHz	10.45(14)	10.71(11.25)	10.41(11)
Tab(H) / MHz	[-7.53] f	-7.56(-7.53)	[-7.8] f
Caa(H) / kHz		-20.18(-21.56)
Cbb(H) / kHz		2.51(2.51)
Ccc(H) / kHz		-1.52(-1.59)

^aWatson S -reduction. Uncertainties (1σ) are in units of the last significant digit.

^bWatson S -reduction parameters obtained by re-fitting the frequency values reported in (Endo et al. 1981).

^cValues given in square brackets are kept fixed at the computed values.

^dEquilibrium rotational constants at the CBS+CV+fT+fQ level augmented by vibrational corrections at the CCSD(T)/cc-pCVQZ level. Quartic and sextic centrifugal-distortion constants at the CCSD(T)/cc-pCVQZ level. Hyperfine parameters - equilibrium values (given in parentheses): electronic and nuclear SR constants at the CCSD(T)/cc-pCV5Z level, isotropic and anisotropic hyperfine coupling constants at the aug-cc-pCV5Z level. Equilibrium values augmented by vibrational corrections at the CCSD(T)/cc-pVTZ level.

^eCentrifugal-distortion dependence of the electron spin-rotation constants, as given in (Endo et al. 1981).

^fThe negative sign means the sign of T_ab is opposite to that of 1/2(∈ab + ∈ba).

Table 1 also collects the computational results. For all parameters, a good agreement is observed between the theoretical predictions and the experimentally determined parameters. In this context we note that vibrational corrections turn out to be essential for a quantitative prediction of the isotropic and anisotropic hyperfine coupling constants, while they are more or less negligible for the electron spin-rotation tensor. It is worthwhile to mention that the computed sextic centrifugal-distortion constants were used in conjunction with the spectroscopic parameters by Endo et al. (1981) to predict the transition frequencies in the submillimeter-wave region.

5.2. Radioastronomical Observations

Using the improved frequency predictions provided by this paper, we carried out a rigorous search for HSO in space. We focused on the two most studied high-mass star-forming regions, Orion KL and Sagittarius (Sgr) B2, and on the cold dark cloud Barnard 1 (B1-b). We used the MADEX code (Cernicharo 2012) to exploit the spectroscopic parameters presented in this work and to derive the synthetic spectrum of this species (assuming LTE) according to the physical parameters of the source (see below) collected in Table 2. The column density was the only free parameter for these models. Corrections for beam dilution were applied to each line depending on their frequency.

Table 2.

Physical parameters of the considered cloud cores.

Source	Coordinates J2000.0	HPBW† (″)	Frequencies†† GHz	vLSR (km s−1)	ΔvFWHM (km s−1)	dsou (″)	Trot (K)	N(HSO) ×1014 (cm−2)
Orion KL (IRAM 30m)	$\begin{array}{l}\alpha =5^{\text{h}}{35}^{\text{m}}{14}_{.}^{\text{s}}5\\ \delta =-{05}^{\circ }{22}^{\prime }{30}_{.}^{″}0\end{array}$	30-8	80-307	8	3	5	150	≤(2.0±0.6)
Orion KL (ALMA SV) Hot core	$\begin{array}{l}\alpha ={05}^{\text{h}}{35}^{\text{m}}{14}_{.}^{\text{s}}5\\ \delta =-{05}^{\circ }{22}^{\prime }{32}_{.}^{″}5\end{array}$	~1.9×1.4	213.7-246.7	8	3	3	150	≤(4±1)
Orion KL (ALMA SV) Compact ridge	$\begin{array}{l}\alpha ={05}^{\text{h}}{35}^{\text{m}}{14}_{.}^{\text{s}}1\\ \delta =-{05}^{\circ }{22}^{\prime }{36}_{.}^{″}9\end{array}$	~1.9×1.4	213.7-246.7	7.5	2	3	100	≤(1.0±0.3)
Orion KL (ALMA SV) MM4	$\begin{array}{l}\alpha ={05}^{\text{h}}{35}^{\text{m}}{14}_{.}^{\text{s}}2\\ \delta =-{05}^{\circ }{22}^{\prime }{31}_{.}^{″}1\end{array}$	~1.9×1.4	213.7-246.7	3 5	3 8	3 3	150 150	≤(1.0±0.3) ≤(1.0±0.3)
Sgr B2(N) Cold gas	(IRAM 30m) $\begin{array}{l}\alpha ={17}^{\text{h}}{47}^{\text{m}}{20}_{.}^{\text{s}}0\\ \delta =-{28}^{\circ }{22}^{\prime }{19}_{.}^{″}0\end{array}$	30-21	80-115.5	64 75	9 12	60 60	14 14	≤(1.0±0.3) ≤(1.0±0.3)
	(GBT 100m) $\begin{array}{l}\alpha ={17}^{\text{h}}{47}^{\text{m}}{19}_{.}^{\text{s}}8\\ \delta =-{28}^{\circ }{22}^{\prime }{17}_{.}^{″}0\end{array}$	80-15	7-50
Sgr B2(N) (IRAM 30m) Hot gas	$\begin{array}{l}\alpha ={17}^{\text{h}}{47}^{\text{m}}{20}_{.}^{\text{s}}0\\ \delta =-{28}^{\circ }{22}^{\prime }{19}_{.}^{″}0\end{array}$	30-21	80-115.5	64 73 52	8 8 14	3 3 3	150 150 150	≤(700±200) ≤(100±30) ≤(100±300)
B1-b (IRAM 30m)	$\begin{array}{l}\alpha ={03}^{\text{h}}{33}^{\text{m}}{20}_{.}^{\text{s}}0\\ \delta =-{31}^{\circ }{07}^{\prime }{34}_{.}^{″}0\end{array}$	30-21	80-115.5	6.7	0.7	60	12	≤(0.010±0.003)

^†HPBW (half power beam width) for observations with the IRAM 30m telescope and synthetic beam for the ALMA SV observations.

^††Range of frequencies considered in the analysis. Nevertheless, between 7–50 GHz and 80–115.5 GHz only three lines of HSO (39.532, 81.364, and 81.368 GHz) with large intensities are expected (a-type transitions, S_ij≥1, and E_up between 0 and 200 K).

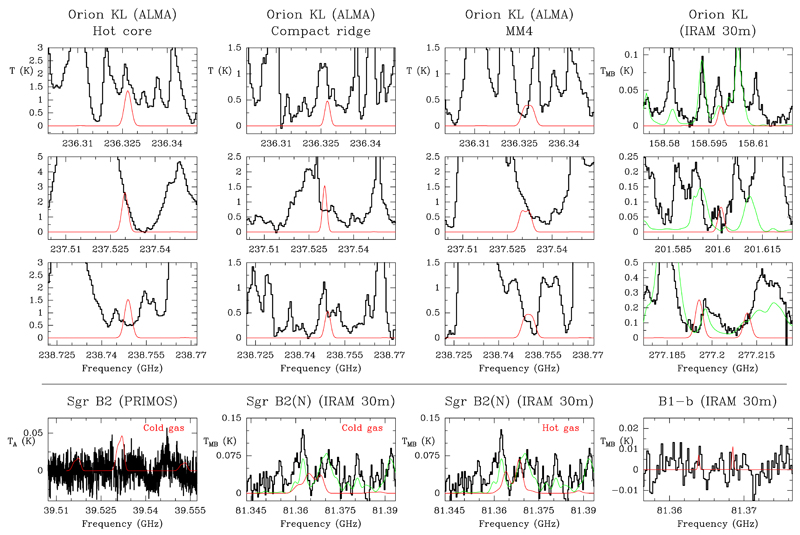
Orion KL: Data from the ALMA interferometer (ALMA Science Verification, SV) and the IRAM 30m telescope (Tercero et al. 2010, 2015) have been explored to search for HSO. The ALMA SV data allow us to obtain the spectrum between 213.7 and 246.7 GHz for different positions within the source characterized by a different chemistry and physical parameters (see e.g., Gong et al. 2015 and references therein). We distinguished (i) the hot core, a position in the middle of the hot core clumpy structure (Favre et al. 2011a) where the emission peaks of ethylene glycol (OHCH₂CH₂OH, Brouillet et al. 2015), acetic acid (CH₃COOH, López et al. in preparation), and methyl isocyanate (CH₃NCO, Cernicharo et al. 2016) are located; (ii) the compact ridge, located at the emission peak of methyl formate (CH₃OCHO, Favre et al. 2011b), dimethyl ether (CH₃OCH₃, Brouillet et al. 2013), and ethyl methyl ether (CH₃CH₂OCH₃, Tercero et al. 2015); and the MM4 source (see Wu et al. 2014), a clump which concentrates a large fraction of the emission of methyl isocyanate (Cernicharo et al. 2016) and acetone (CH₃COCH₃, Peng et al. 2013; Cernicharo et al. 2016) in the region. In addition, the IRAM 30m data provide a very wide frequency band (80–307 GHz) of the average spectrum of the region inside the telescope beam. To model the HSO emission in these components, we have adopted physical parameters according to those derived by Cernicharo et al. (2016) and Tercero et al. (2015). These clumps, related to high-mass star formation, are characterized by warm temperatures. Figure 3 shows selected frequencies and positions of these data together with the model derived by MADEX that demonstrates the lack of HSO lines above the confusion limit of these data. Above the limit established by these models, we see that most of the HSO lines are missing.

Fig. 3.

Observed data of Orion KL, Sgr B2, and B1-b taken with different instruments (histogram black spectrum) together with the synthetic spectra obtained using the column densities given as upper limits in Table 2 (thin red curve). The synthetic total model for the 30m data of Sgr B2(N) (see Belloche et al. 2013) and Orion KL (see Cernicharo et al. 2016) is overlaid in green. A v_LSR of +9.0 km s⁻¹, +64.0 km s⁻¹, and +6.7 km s⁻¹ is assumed for Orion KL, Sgr B2, and B1-b, respectively.

Sagittarius B2: We also searched for HSO in public data available for Sgr B2. The 100m Green Bank Telescope (GBT) PRebiotic Interstellar MOlecule Survey (PRIMOS) (Neill et al. 2012) covers a frequency band between 7 and 50 GHz¹. Only one a-type transition with high line strength (S_ij≥1) and low energy of the upper level (E_up≃2 K) could be detected in this frequency coverage at 39.532 GHz. We did not find this line in the PRIMOS data as shown in Fig. 3. We also found that only two lines (at 81.364 and 81.368 GHz) are expected in the 3 mm data of Belloche et al. (2013). We could only derive an upper limit to the HSO column density (see Fig. 3 and Table 2) according to these data and adopting the physical parameters for the cold gas in the region given by Brünken et al. (2010). Since SO and SO₂ seem to have a hot core component in Sgr B2(N) (see Belloche et al. 2013), we also provided an upper limit to the HSO column density in the compact and warm components derived for SO by Belloche et al. (2013). Nevertheless, we noted that only the same two lines as above at 81.364 and 81.368 GHz (E_up = 19 K) are expected in the warm gas at 3 mm. Transitions with E_up between 80 and 300 K are b-type transitions or have S_ij<0.2. Therefore, the upper limit provided to the hot and compact components in Sgr B2 is very little constrained.

Barnard 1: Barnard 1 is a low-mass star-forming region located in the Perseus molecular cloud at the first evolutionary stages (see, e.g., Gerin et al. 2015). We derived an upper limit to the HSO column density in B1-b (see Fig. 3 and Table 2) to constrain the chemistry of this object using the IRAM 30m data and the physical properties of the cloud shown in Cernicharo et al. (2012).

In Table 3 we provide lower limit column density ratios in order to compare the derived HSO column density to those reported in the literature for other Sulfur-bearing molecules. Nevertheless, these ratios should be taken with caution due to the different methods and physical properties used to obtain the column densities and to the little constrained values we obtained for the upper limits to the HSO column density in Sgr B2(N) and B1-b based on only two or three expected lines at the frequency range covered by these data.

Table 3.

Column density ratios

Source	N(H2CS)/ N(HSO)	N(CH3SH)/ N(HSO)	N(H2S)/ N(HSO)	N(SO)/ N(HSO)	N(SO2)/ N(HSO)	N(CS)/ N(HSO)	N(OCS) /N(HSO)
Orion KL (IRAM 30m)	≥10(a)	≥50(b)	≥5000(c)	≥100(d)	≥1500(d)	≥100(a)	≥250(a)
Sgr B2(N) (Hot gas; ~64 km s−1 comp.)	≥4(e)	≥0.5(f)	≥10(g)	≥10(e)	≥10(e)	≥4(g)	≥3(f)
Sgr B2(N) (Hot gas; ~73 km s−1 comp.)	≥40(e)	≥2(f)	…	≥35(e)	≥100(e)	…	≥8(f)
Sgr B2(N) (Hot gas; ~52 km s−1 comp.)	…	…	≥6(g)	≥20(g)	≥60(e)	…	…
Sgr B2(N) (Cold gas; ~64 km s−1 comp.)	…	…	…	≥30(h)	≥16(h)	…	…
B1-b	≥12(i)	≥1.6(j)	…	…	…	…	…

^(a)Hot core component (d_sou = 10″, v_FWHM = 10 km s⁻¹) column densities derived by Tercero et al. (2010).

^(b)Hot core component (d_sou = 10″, v_FWHM = 7 km s⁻¹) column density derived by Kolesniková et al. (2014).

^(c)Hot core component (d_sou = 6″, v_FWHM = 8.6 km s⁻¹) column density derived by Crockett et al. (2014).

^(d)Hot core component (d_sou = 10″, v_FWHM = 10 km s⁻¹) column densities derived by Esplugues et al. (2013).

^(e)Hot component (d_sou = 2-3″, v_FWHM = 7-10 km s⁻¹) column densities derived by Belloche et al. (2013).

^(f)Warm (60 K) component (d_sou = 5-8″, v_FWHM = 6-8 km s⁻¹) column densities derived by Belloche et al. (2013).

^(g)Hot component (d_sou = 3-5″, v_FWHM = 12-15 km s⁻¹) column densities derived by Belloche et al. (2013).

^(h)Cold component (d_sou = 30″, v_FWHM = 12-14 km s⁻¹) column densities derived by Belloche et al. (2013).

⁽ⁱ⁾Marcelino et al. (2005).

^(j)Cernicharo et al. (2012).

The formation of HSO in molecular clouds has not been addressed in chemical models so far. The reaction of ${\text{H}}_3^{+}$ with SO produces HSO⁺ while with SO₂ the main channel product is ${\text{HSO}}_2^{+}.$ The dissociative recombination of these ions produces mainly SO and SO₂ (UMIST database, McElroy et al. 2013). To our knowledge, the reactivity of HSO⁺ with other species, in particular with H₂, is poorly known. The only reactions of HSO⁺ in the UMIST database are those involving electrons, while for ${\text{HSO}}_2^{+}$ electrons and H₂O do participate in the destruction of this species. In none of these reactions the ion H₂SO⁺ is formed which could lead to HSO. The reaction of methyl mercaptan (CH₃SH) with atomic oxygen, an abundant element in molecular clouds, could produce HSO (Slagle et al. 1978). CH₃SH has a modest abundance in hot cores of ~10⁻⁹ (see e.g., Kolesniková et al. 2014). Hence, the yield of HSO could be too low to produce a significant abundance for this molecule and to allow detection through its rotational spectrum. HSO could be formed in high-temperature regions through the reaction of H₂S and SH with O or O₂ (Goumri et al. 1995), or perhaps through other neutral-neutral or neutral-radical reactions with modest activation barriers (Friedl et al. 1985; Lovejoy et al. 1987). However, these reactions involve molecules with moderate abundance and hence the yield of HSO will be rather low. Therefore, our upper limit to the abundance of HSO indicates that this moleculedoes not achieve significant abundances either in the gas phase or in the ice mantles of dust grains.