Numerosity but not Texture-Density Discrimination Correlates With Math Ability in Children

Abstract

Considerable recent work suggests that mathematical abilities in children correlate with the ability to estimate numerosity. Does math correlate only with numerosity estimation, or also with other similar tasks? We measured discrimination thresholds of school-age (6- to 12.5-years-old) children in 3 tasks: numerosity of patterns of relatively sparse, segregatable items (24 dots); numerosity of very dense textured patterns (250 dots); and discrimination of direction of motion. Thresholds in all tasks improved with age, but at different rates, implying the action of different mechanisms: In particular, in young children, thresholds were lower for sparse than textured patterns (the opposite of adults), suggesting earlier maturation of numerosity mechanisms. Importantly, numerosity thresholds for sparse stimuli correlated strongly with math skills, even after controlling for the influence of age, gender and nonverbal IQ. However, neither motion-direction discrimination nor numerosity discrimination of texture patterns showed a significant correlation with math abilities. These results provide further evidence that numerosity and texture-density are perceived by independent neural mechanisms, which develop at different rates; and importantly, only numerosity mechanisms are related to math. As developmental dyscalculia is characterized by a profound deficit in discriminating numerosity, it is fundamental to understand the mechanism behind the discrimination.

Although humans are the only species with a linguistically mediated code for numbers, we share with other animals an approximate, nonverbal representation of quantity (Dehaene, 2011). This cognitive system has been called the “Approximate Number System” (ANS) and has obvious evolutionary advantages in allowing quick and effortless estimates of zones with more food, and fewer competitors or predators. In humans, ANS sensitivity is typically measured by asking participants to choose the more numerous of two briefly presented ensembles. The inverse of the discrimination threshold—the minimal detectable change in numerosity— gives a measure of the system sensitivity.

An influential theory has proposed that the ANS acts as an early neurocognitive “start-up tool” on which later and more sophisticated language-based mathematical skills are built (Piazza, 2010). Some support for this theory comes from the fact that numerosity discrimination thresholds are significant, even if sometimes weak, predictors of current and future math ability (Anobile, Stievano, & Burr, 2013; Chen & Li, 2014; Feigenson, Libertus, & Halberda, 2013; Halberda, Mazzocco, & Feigenson, 2008; Libertus, Feigenson, & Halberda, 2011; Libertus, Feigenson, & Halberda, 2013; Pinheiro-Chagas et al., 2014). It is worth noting that null relationships between ANS and formal math have also been reported, both with school and preschool children (Lyons, Price, Vaessen, Blomert, & Ansari, 2014; Sasanguie, Defever, Maertens, & Reynvoet, 2014). Definitive proof of the link between numerosity perception and formal math skills is still missing.

The mechanisms behind numerosity perception have been highly debated. Several researchers have suggested that numerosity is not sensed directly, but indirectly as a product of texture-density and area (Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011; Durgin, 1995, 2008; Morgan, Raphael, Tibber, & Dakin, 2014; Tibber, Greenwood, & Dakin, 2012). On the other hand, much evidence points to direct coding of numerosity, independently of density, especially for relatively sparse patterns (Anobile, Cicchini, & Burr, 2014; Arrighi, Togoli, & Burr, 2014; Burr & Ross, 2008; Cicchini, Anobile, & Burr, in press; Ross & Burr, 2010; Stoianov & Zorzi, 2012).

Recently, we suggested that two processes may be operating: a numerosity mechanism (ANS) for low element densities, and texture density mechanisms for higher densities (Anobile et al., 2014; Anobile, Turi, Cicchini, & Burr, 2015; for a review see Anobile, Cicchini, & Burr, 2016). It is commonly accepted that one of the main signatures of the ANS is that it obeys Weber Laws (numerosity discrimination thresholds scales linearly with the intensity of the stimulus), and that Weber Fractions (the minimal detectable change in numerosity, normalized by the perceived stimulus magnitude) are constant across numerosity. However, we have shown that Weber fractions for numerosity discrimination are constant up to a certain numerosity/density value, but after a critical point, they decrease with the square root of numerosity (Anobile et al., 2014). The departure from Weber Law, at higher numerosities/densities, was interpreted as signifying the action of another perceptual system, encoding texture-density. Evidence against the idea of two separate systems for numerosity and density perception comes from the fact that both features are overestimated when the items are presented in a larger area (Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011). Interestingly, we recently replicated this effect but found that it completely vanished for low numerosity/density (Anobile et al., 2016).

In brief, we advanced the idea that the ANS operates only while the items are sparse enough to permit object segmentation. When numerosity increases and objects merge together, the texture-density system will cut in. Taking advantage of the fact that the ANS acuity has often been seen to correlate with math abilities, we advance here a clear prediction: Children’s numerosity discrimination thresholds for sparse stimuli (exciting numerosity mechanisms, ANS) but not for dense stimuli (exciting texture-density mechanisms) should correlate with formal math skills. In order to test this hypothesis we measured numerosity discrimination thresholds for sparse (0.3 items/deg²) and dense (3 items/deg²) ensembles, and correlated the thresholds with formal math skills in a group of 63 school-age children (mean age 9 years). As predicted, we found a strong correlation with math skills for sparse but not dense patterns.

Method

Participants

A total of 83 subjects participated in the study (see Table 1): 73 children, aged 6 to 12.5 years (from Grades 1 to 5, mean age 8.9 years), and 10 adults (mean age 28 years). Children were recruited from local schools, and only those who returned a signed consent from parents were included. None had a diagnosis of learning or attention disorders, and all the nonverbal intelligence scores were within the normal range, as measured by Raven matrices (Belacchi, Scalisi, Cannoni, & Cornoldi, 2008). The entire group of children completed all the perceptual tasks and the nonverbal reasoning level test (Raven matrices), except for the first grade children who were not tested for math skills (because the tests included high numbers with three to six digits, not taught in first grade), resulting in a sample size of 63. Adults were tested only on the visual numerosity discrimination tasks (they would have obtained maximum scores on the math task).

Table 1.

Participants’ Descriptive Statistics and Children Math Scores

Children
Descriptive statistics			Math scores
1°, 2°, 3°, 4° and 5° grades			1°, 2°, 3°, 4° and 5° grades
Age (years)	Raven’s matrices Percentile	Gender	Number of errors	Speed (min)
Mean: 8.92	Mean: 68	Males (N): 43	—	—
Max: 12.5	Max: 99	Female (N): 30
Min: 6	Min: 25
StDev: 1.64	StDev: 23
Nsubj: 73	Nsubj: 73
2°, 3°, 4° and 5° grades			2°, 3°, 4° and 5° grades
Mean: 9.26	Mean: 65	Males (N): 38	Mean: 2.19	Mean: 2.75
Max: 12.5	Max: 99	Female (N): 25	Max: 7	Max: 7.41
Min: 6.3	Min: 20		Min: 0	Min: 1.25
StDev: 1.64	StDev: 24		StDev: 2.27	StDev: 1.16
Nsubj: 63	Nsubj: 63		Nsubj: 63	Nsubj: 63
Adults
Mean: 28	—	Males (N): 8	—	—
Max: 40		Female (N): 2
Min: 23
StDev: 5.3
Nsubj: 10

General Procedures

All visual stimuli were presented in a dimly lit room on a 17-inch LG touch screen monitor with 1,280 × 1,024 resolution at refresh rate of 60 Hz, viewed binocularly from 57 cm. In the perceptual tasks, to minimize finger errors, children were asked to respond by pointing toward the side of the screen containing more dots, or to indicate the direction of motion. The experimenter recorded the responses by appropriate key-press. Stimuli were generated and presented under Matlab 7.6 using PsychToolbox routines (Brainard, 1997). Data were analyzed with both Matlab 7.6 and SPSS 20.0. Numerosity discrimination tasks order was randomized between subjects (half started from N24 the other half from N250). Motion-direction discrimination was the third task, and formal math skills and nonverbal reasoning tasks were administered in the end of each session. Average thresholds, with standard deviations, for both adults and children are reported in Table 2.

Table 2.

Perceptual Task’s Summary Statistics

	Numerosity discrimination		Motion direction discrimination
Task Measure	Coefficient of variation N24	Coefficient of variation N250	Threshold (°s−1)
1°, 2°, 3°, 4° and 5° grades	Mean: .325	Mean: .387	—
	StDev: 1.71	StDev: 1.89
	Nsubj: 73	Nsubj: 73
2°, 3°, 4° and 5° grades	Mean: .315	Mean: .366	Mean: .179
	StDev: 1.684	StDev: 1.866	StDev: 2.063
	Nsubj: 63	Nsubj: 63	Nsubj: 62
Adults	Mean: .219	Mean: .111	—
	StDev: 1.425	StDev: 1.419
	Nsubj: 10	Nsubj: 10

Note. Geometric means and standard deviations are reported.

Numerosity Discrimination

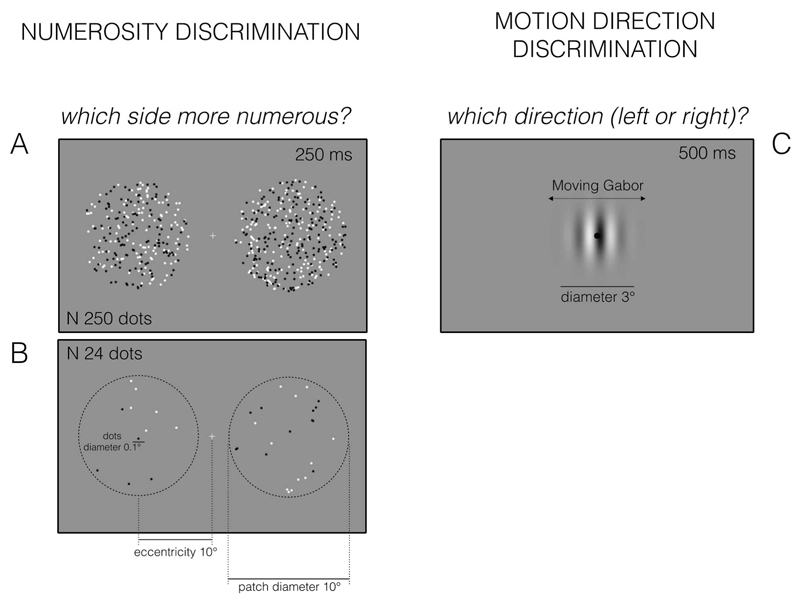
Two patches of dots were briefly (250 ms) presented simultaneously on either side of central fixation, at an eccentricity of 10° of visual angle (see Figure 1). Participants indicated the side of the screen with more dots, guessing if unsure. The numerosity of the test (randomly left or right) was fixed at 24 (sparse) or 250 dots (dense), in separate sessions, while the probe had variable number, adaptively changing from trial to trial, depending on the response of the participant, following the QUEST algorithm (Watson & Pelli, 1983). All stimuli comprised a number of 0.1° diameter dots, half white and half black, constrained to fall within a virtual circle of 10° diameter of visual angle (0.3 and 3.1 dots/deg for N24 and N250, respectively). Each test numerosity was tested separately within a single session of 45 trials (half the participants started with test numerosity 24 and the other half with 250). The proportion of “test greater” trials was plotted against the difference between test and probe, and fitted with cumulative Gaussian “error” functions. The 50% point estimates the point of subjective equality (PSE), and the difference in numerosity between the 50% and 75% points gives the just notable difference (Jnd) which, when normalized by test numerosity, estimates the coefficient of variation (CoV).

Figure 1.

Examples of stimuli and procedures used in the experiments. A and B) Numerosity discrimination task: two circular clouds of dots were briefly (250 ms) presented side by side around a fixation point. Subjects were asked to indicate which side of the screen contained more dots. The two levels of numerosity (A: 250; B: 24) were tested in separate blocks. C) Motion direction discrimination task: a moving Gabor patch was briefly (500 ms) presented around a fixation point. Subjects were asked to indicate the direction of motion (left or right).

Motion Direction Discrimination

Test stimuli were Gaussian-windowed sinusoidal gratings, modulated in luminance on a gray background (carrier frequency 1 cycles/deg, Gaussian space constant 1°, contrast 0.9). On each trial a fixation point was presented for 1 s, followed by a grating-patch presented around the middle of the screen for 500 ms. The test gratings drifted at variable speed, and the subject indicated whether they appeared to drift leftward or rightward (by key-press). The speed of the test on each trial was varied by the adaptive Quest algorithm (Watson & Pelli, 1983), which homed in on the point where the grating appeared to be stationary. The QUEST estimate was jittered by adding to it a speed drawn from a Gaussian distribution of standard deviation 0.5 deg/sec. Every subject performed a single session of 45 trials. The proportion of trials in which the stimulus appeared to drift rightward was plotted against the different velocity of the grating and fitted with a cumulative Gaussian function where the 50% point provided an estimate of the point of subjective stationarity (PSS). The velocity change needed to pass from 50% to 75% responses gave the discrimination threshold.

Math Skills

We tested formal math ability with three separate paper-and-pencil tests (Biancardi & Nicoletti, 2004), consisting of either choosing the largest numbers in a set, or deciding where a number should be placed among others. We administered three separate subtests: (a) 14 trials requiring the child to choose and mark the largest number among a set of three vertically arranged Arabic numbers (one to four digits; e.g., 9, 7, 2; 18, 21, 20; 102, 111, 109; 1,029, 1,106, 1,010); (b) eight additional trials asking the child to chose the largest number but now using numbers with two to six digits; and (c) 12 trials where the child has to position a number (one to four digits) in one of four possible positions among three other numbers. These tasks are believed to tap the semantic component of numeracy (Biancardi & Nicoletti, 2004; Dehaene, Piazza, Pinel, & Cohen, 2003). As the actual experiment was not designed to disentangle between the different links relating ANS and math components, we choose tasks that, according to the literature, had the best probability of stimulating the ANS. In a previous experiment we found that the math tasks that best correlated with ANS were those requiring the encoding and manipulation of the numerical values associated with the digits (Anobile et al., 2013). Importantly, these tasks—but not those more related to transcoding, memory and automatized procedures—specifically related to numerosity discrimination thresholds. Interestingly, this pattern of result is in line with a commonly accepted model of numerical cognition (Dehaene et al., 2003), and replicates those previously found with dyscalculic children (Piazza et al., 2010), although it is conceivable that the results of the present experiment might not generalize to all possible math tasks.

Both accuracy and speed were measured (as the sum of errors and time in minutes required to complete the three tasks). Because speed and accuracy positively correlated with each other, and showed a similarly relationship with numerosity thresholds (see Table 3), we minimized the number of variables by constructing a summary “math ability index,” by averaging the z-scores measured separately for speed and accuracy, giving equal weight to accuracy and speed.

Table 3.

Full Correlation Matrix

Task	1	2	3	4	5	6	7	8
1. Raven’s matrices	1	−.172° (.174)	−.328° (.008)	−.117° (.356)	−.082 (.521)	−.316 (.011)	.121 (.342)	.136 (.288)
2. Age		1	−.247° (.033)	−.315° (.006)	−.267 (.032)	−.304 (.015)	−.581* (.000)	.504* (.000)
3. Numerosity CVN 24			1	.367° (.001)	.360 (.004)	.447* (.000)	.338 (.006)	−.432* (.000)
4. Numerosity CVN 250				1	.135 (.291)	.277 (.027)	.167 (.188)	−.200 (.116)
5. Motion Threshold (°s−1)					1	.177 (.165)	.155 (.224)	−.212 (.094)
6. Mat errors						1	.370 (.003)	.813* (.000)
7. Mat speed							1	.813* (.000)
8. Math ability index								1

Note. Analyses are carried out considering only children. Bivariate Pearson correlation coefficients. Significant correlations highlighted in bold. Bonferroni corrected alpha level = .001 (.05/29).

^°N subjects 73 (N 63 all the others correlations).

^*p < .001.

Data Analysis

Discrimination thresholds were separately measured for each participant and experimental condition. Differences in developmental rate as a function of age, as well as mean group differences were tested by bootstrap sign-tests. The relationships between perceptual as well as cognitive variables were measured by bivariate correlations and hierarchical regressions (see supplementary material for a detailed description of the procedures).

Results

Numerosity and Texture-Density Developmental Trajectories

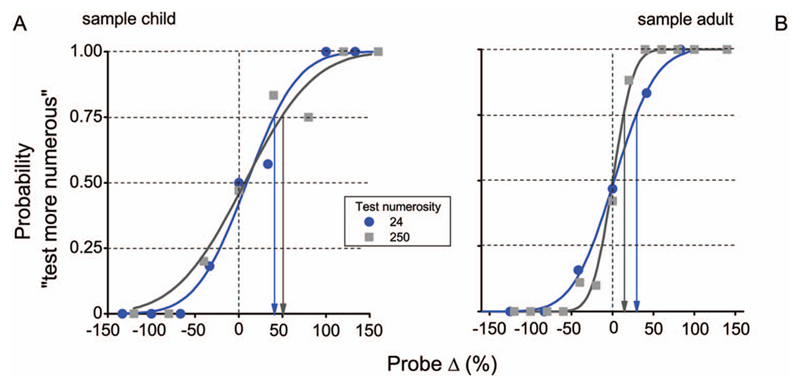
All children were able to perform all tasks well, producing well-ordered psychometric functions. Figure 2 shows examples for a representative child (A) and adult (B), for the two numerosity levels (N24 and N250). In both cases the data are well fit by cumulative Gaussian functions, whose median gives the point of subjective equality (near zero, showing no systematic bias), and difference in numerosity between 50% to 75% responses the just noticeable difference (Jnd). For the adult, the curves are much steeper for the higher numerosity, corresponding to lower normalized thresholds (coefficients of variation): 0.11 compared with 0.20 (similar to the difference reported previously: Anobile et al., 2014). For the child, however, the thresholds were higher than for the adults, and similar to each other.

Figure 2.

Sample psychometric functions in the numerosity discrimination task for a sample child (A) and adult (B), for two levels of numerosity (N 24 and N 250 dots). Data show the probability of judging the test stimulus as more numerous then the probe, as a function of the difference between test and probe. Discrimination thresholds were measured as coefficient of variations = just notable difference/test numerosity. Just notable difference (Jnd) here is defined as the increase in dots to pass from 50% to 75% “greater” responses (black and blue arrows).

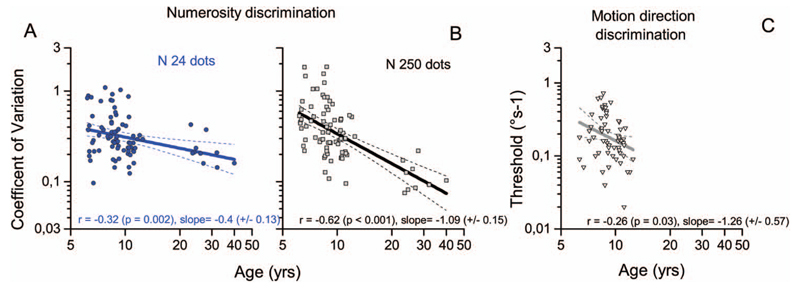
Figure 3A and B show results for all participants, plotting numerosity discrimination thresholds for sparse (A: N24) and dense (B: N250) stimuli against age. As may be expected, both thresholds improve with age, but faster for the dense than for the sparse stimuli (slopes: −0.40 ± 0.13 and −1.09 ± 0.15 for N24 and N250, respectively). The difference in slopes is significant on bootstrap sign-test (p < .0001). Although not statistically significant, the same trend was present even after eliminating adults from the analysis (slopes: −0.6 ± 0.25 and −1.1 ± 0.26 for N24 and N250, respectively; bootstrap sign-test p = .09).

Figure 3.

Individual thresholds in the three visual discrimination tasks (numerosity A and B, motion direction in panel C) as a function of chronological age. Lines are best-fitting regressions considering children and adults (for correlations excluding adults see Table 3).

Numerosity and Texture-Density in Adults and Children, Group Analysis

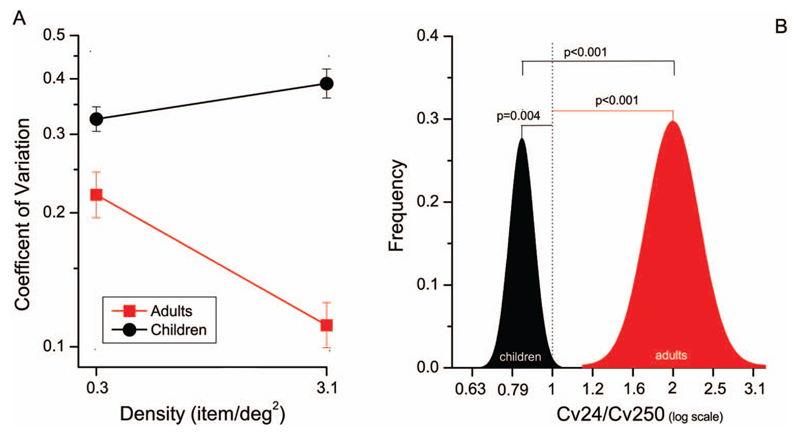
The individual subjects of Figure 2 suggest that while for adults discrimination thresholds at high densities are greater than at low (confirming previous studies), this was not the case for children. Figure 4A examines this difference more quantitatively, plotting CoVs, averaged over all subjects, against density: the adult thresholds clearly decrease with density, while the child thresholds increase slightly. Figure 4B shows the distributions of threshold ratios (low divided by high) after bootstrapping all the data (see methods). By sign-test, the ratio is clearly less than one for the children (p = .004), and greater than one for the adults (p < .001).

Figure 4.

A) Geometric mean of coefficient of variations as a function of density (0.3 dots/deg² for numerosity 24 and 3.1 dots/deg² for numerosity N250) divided in the two groups of participants (children, black circles—adults, red squares). Error bars indicate ± 1 SEM. B) Bootstrap frequency distributions (10,000 reiterations) of ratios between coefficients of variations for N24 and N250 (log scale) separated for the two groups of participants (children-black, adults-red). p value refers to bootstrap sign-tests.

Relationship Between Mathematical Skills, Numerosity, and Texture-Density Thresholds

As a first level of analysis we calculated Pearson’s bivariate correlations between formal math skills and visual discrimination thresholds, keeping math accuracy (number of errors) and speed (time required to complete math exercises) as separate predictors. Table 3 shows that only numerosity thresholds discrimination for sparse (N24) stimuli strongly correlate with math accuracy (r = .447, p < .001, Bonferroni corrected alpha level = 0.001), and tended to approach the significant statistical level for math speed (r = .438, p = .006, Bonferroni corrected alpha level = 0.001). These positive correlations indicated that less precise numerosity discrimination was associated with more errors and slower math performance. Interestingly, discrimination thresholds for dense (N250) stimuli and motion direction are largely independent of math achievements (see Table 3).

It is theoretically possible that the lack of correlation between N250 thresholds and math skills could result from poor reliability of the N250 task. To test this possibility, we developed a test of task reliability appropriate for psychophysical measurements. As splitting the data set in half would leave too few points to estimate thresholds, we used a the “sample-with-replacement” bootstrap technique common in psychophysics (Efron & Tibshirani, 1993). For each child, we calculated two separate thresholds in a given condition (N250 or N24), using a random sample of the data (45 trials, sampled with replacement), and then computed the correlation between those two measures, across subjects. The process was reiterated 1,000 times. We found that mean correlation for N24 and N250 were very similar (Pearson’s r = .54 ± 0.14 and 0.55 ± 0.17, respectively, not statistically different, bootstrap sign-test p = .48). This rules out the possibility that the lack of correlation between dense stimuli and math could be due to lower task reliability in case of denser pattern.

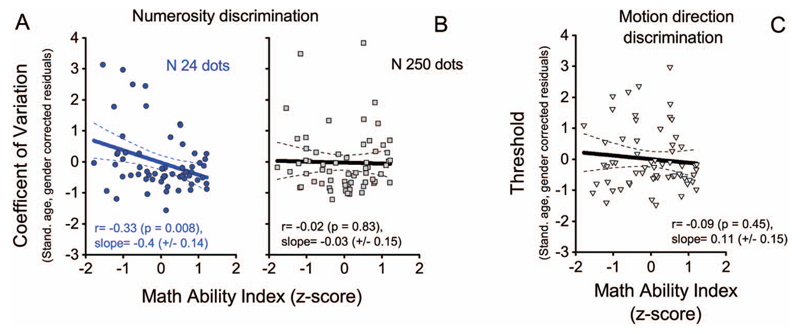
Our simple correlational approach may risk being too conservative, as the high number of comparison variables (29) led to a very conservative Bonferroni corrected alpha level of 0.001, and says little about the degree of specificity of the detected correlations. We therefore performed a multiple regression analysis considering simultaneously chronological age, nonverbal-IQ, gender and the three visual discrimination thresholds (N24, N250, and motion direction) as predictor variables, and the math-ability-index (the average of accuracy and speed z-scores) as the dependent variable. Table 4 shows that the model, overall, is able to account for a significant proportion of variance in math skills, R² = 0.426, F(6, 55) = 6.817, p < .001, and, most importantly for the purpose of this study, that numerosity threshold discrimination for sparse stimuli (N24) was the only statistical significant predictor (β = −0.387, t = −2.976, p = .004) other than age. In order to test further the specificity of this relationship we performed a series of hierarchical multiple regressions (see Table 5) with the three visual thresholds discrimination (numerosity N24, N250, and motion direction) as predictors and the math-ability index as the dependent variable. Each predictor was tested in a separate model and the controlling variables were entered each time together as a block (see methods and Table 5). Controlling for age and gender, numerosity threshold discrimination for sparse stimuli (N24) continued to explain a significant proportion of math ability variance (R change = 12%, F change (1, 59) = 11.828, p = .001). Figure 5 shows standardized discrimination thresholds residuals after that the effects of age and gender were regressed out (higher values indicate higher thresholds), as a function of standardized math ability index (higher values indicate better performance). Figure 5A and B show that for sparse but not highly crowded stimuli, better mathematical achievements correspond to lower thresholds: Pearson’s r = −0.33 and −0.02 (p = .008 and p = .83) for sparse and dense stimuli respectively. Importantly, the control visual discrimination task (motion direction), also did not correlate with math skills (Figure 5C). Furthermore, simultaneously controlling for chorological age, gender and nonverbal IQ did not eliminate the correlation between low numerosity thresholds and math (R change = 7.6%, F change (1, 58) = 7.452, p = .008). All the other predictors were not significant (all p > .05, see Table 5).

Table 4.

Multiple Regressions—Dependent Variable: Mathematical Ability Index

				Beta IC 95%
Predictor	Beta	t	p	Lower limit	Upper limit
Age	.588	4.721	.000***	.016	.040
Nonverbal IQ	.146	1.288	.203	−.003	.013
Gender	.181	1.546	.128	−.090	.695
Numerosity N24	−.387	−2.976	.004**	−2.405	−.469
Numerosity N250	.171	1.369	.176	−.197	1.049
Jnd Motion	.044	.388	.700	−.924	1.368

Note. Analyses are carried out considering only children. R² = .426, F(6,55) = 6.817 (p < .001). Significant predictor highlighted in bold.

^**p < .01.

^***p < .001.

Table 5.

Hierarchical Multiple Regressions—Dependent Variable: Mathematical Ability Index

Controlling variables—Age and gender
Model	Predictor	R2	R2 change	Fchange	df	p
First step	Age and gender	.269	—	11.031	60	.000
Model 1	Numerosity N24	.391	.122	11.828	59	.001**
Model 2	Numerosity N250	.271	.002	.159	59	.691
Model 3	Jnd motion	.278	.009	.709	58	.403
Controlling variables—Age, gender and nonverbal IQ
First step	Age, gender, and IQ	.330	—	9.681	59	.000
Model 1	Numerosity N24	.406	.076	7.452	58	.008**
Model 2	Numerosity N250	.330	.000	.008	58	.931
Model 3	Jnd motion	.334	.004	.325	57	.571

Note. Predictors were tested in separate regressions models (Model 1, 2, 3), controlling variables were entered as a block in the first step. Significant predictor highlighted in bold.

** p < .01.

Figure 5.

A and B) individual coefficient of variations (age and gender corrected) in the numerosity discrimination task for the two measured numerosities (N 24 in panel A; N 250 in panel B), plotted as a function of standardized math skills level (higher number correspond to better math performance). C) Motion discrimination thresholds (age and gender corrected) as a function of math skills. Lines represent best-fitting regressions.

Discussion

Two main results emerge from this study: the first is that sensitivity for sparse and dense patterns develop at different rates, reinforcing the suggestion that the two are processed by different mechanisms. Interestingly, the mechanisms responsible for discriminating numerosity of sparse patterns appear to develop before those for dense patterns, as children show a slight superiority for sparse patterns, where adults show a clear superiority for dense, textured patterns.

The second and more important finding is that only sensitivity to sparse patterns correlates with math ability. The correlation was quite specific, remaining highly significant even when the influence of age, gender, and nonverbal IQ were factored out. Furthermore, we found that discrimination thresholds in a control visual task—motion direction discrimination, also processed through the dorsal stream—were completely unrelated to math performance, further confirmation that higher math skills were not simply linked to higher visual functions in general.

This result finds support in the adult literature. Tibber et al. (2013) tested a large sample of participants on both numerosity and density tasks, and found that numerosity, but not density thresholds, predict math scores:

Particularly puzzling is the lack of an association between mathematical performance and density thresholds since we have previously demonstrated an intimate link between numerosity and density judgments (Tibber, Greenwood, & Dakin, 2012) and provided a relatively simple model of their completion based on a common filtering stage. (Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011)

Our results are very consistent with their finding and, considered in the light of two mechanisms operating for numerosity and density, are less puzzling. Indeed, it is a direct prediction.

Both sets of results add weight to the growing body of data showing that numerosity is related to math performance, reinforcing the idea that numerosity estimation may be a precursor, or “start-up tool” for acquisition of mathematical concepts (Piazza, 2010). A large amount of evidence from neuroimaging experiments points to the IPS as a key area for numerical reasoning, digit encoding as well as numerosity perception (Bugden, Price, McLean, & Ansari, 2012; Bulthe, De Smedt, & Op de Beeck, 2014; Eger, Michel, Thirion, Amadon, Dehaene, & Kleinschmidt, 2009; Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003; Harvey, Klein, Petridou, & Dumoulin, 2013; Lyons, Ansari, & Beilock, 2015; Piazza & Eger, 2015; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004; Piazza, Pinel, Le Bihan, & Dehaene, 2007; Pinel, Dehaene, Riviere, & LeBihan, 2001). This area is unaffected by changes in low-level stimulus features: neural responses are specific for number of items irrespective of area, item size, total circumference or density, supporting the idea that number perception is an independent and primary sensory attribute that might not simply be inferred by a combination of other image’s properties (Harvey, Klein, Petridou, & Dumoulin, 2013). Developmental changes show that IPS is selectively involved in nonsymbolic numerosity discrimination from a very early age, and that good functioning of this region probably sets the stage for the mapping between approximate numbers with their symbolic counterpart (Vogel, Goffin, & Ansari, 2015). Castelli, Glaser, and Butterworth (2006) found that IPS is involved in representing discrete, countable quantities rather than continuous uncountable features and, as previously reported, that the parietal sulcus plays an important role in segmenting the visual scene into objects, by detecting the points of phase congruency (Castaldi, Frijia, Montanaro, Tosetti, & Morrone, 2013; Perna, Tosetti, Montanaro, & Morrone, 2008). Hence, as suggested by Castelli, Glaser, and Butterworth (2006), neural populations along the intra parietal sulcus begin to analyze the image by segmenting the visual scene into objects, then numerosity mechanisms enumerate the segregated objects.

Many studies suggest that numerosity mechanisms act on segregated objects rather than continuous surfaces. Perhaps the clearest evidence is that simply connecting objects by lines greatly reduces their apparent numerosity (Franconeri, Bemis, & Alvarez, 2009; He, Zhang, Zhou, & Chen, 2009; Kirjakovski & Matsumoto, 2016), as well as their selectivity to BOLD repetition suppression (He, Zhou, Zhou, He, & Chen, 2015) and psychophysical adaptation (Fornaciai, Cicchini, & Burr, 2016; He, Zhou, Zhou, He, & Chen, 2015). Anobile, Cicchini, Pomè, and Burr (2016) have shown that the connectedness effect reduces perceived numerosity only at low, not high densities. This, and a vast amount of other evidence (for a review see Anobile et al., 2016) suggests that the ANS operates only at low to moderate densities, where objects can be segregated. That we find a correlation between math skill and discrimination of low-but not high-density patterns suggests that it is the functioning of the ANS that predicts math performance. This does not preclude the possibility that discrimination of continuous variables may also be important, but the evidence there is less clear. Indeed, several studies found that discrimination of continuous quantities (e.g., space, time, size) do not relate to math (Agrillo, Piffer, & Adriano, 2013; Cappelletti, Freeman, & Butterworth, 2011; Piazza, Pica, Izard, Spelke, & Dehaene, 2013), on the other hand, others found significant correlations (Hurks & van Loosbroek, 2014; Vicario, Rappo, Pepi, Pavan, & Martino, 2012) showing also that the pattern of relationships between quantities could change during development (Starr & Brannon, 2015).

Another hint to the dissociation between number and textures comes from the developmental trend. We found that the rate of threshold improvement during development (from 6 to 40 years) was much faster for dense stimuli. Moreover, while adults have significantly lower thresholds for dense stimuli (mean CVs 0.21 and 0.11 for N24 and N250, respectively, p < .05), children show the opposite trend (mean CVs of 0.32 and 0.39 for N24 and N250, respectively, p < .05). We have previously suggested that texture-density mechanisms come into play as density increases, evidenced by a different psychophysical regime, with discrimination thresholds beginning to decrease with numbers/density, rather than remaining constant (Weber’s law) as for the lower densities (Anobile et al., 2014; Anobile et al., 2015). The present results show that for children younger than 8-years-old, this is not true.

Why are thresholds for children worse for the high than for the low densities? We believe that at this age (8 years) the texture-density mechanisms that deal with high numbers are still highly immature, consistent with the idea that number and texture are analyzed by independent mechanisms. However, other explanations are possible. For example, the cause may be a more cognitive, resulting form higher exposure and more practice in dealing with small rather than large numbers at an early age. Nevertheless, the separate developmental rates does fit neatly with the model of separate mechanisms for number and density. One other possibility comes from possible parametric differences within the same mechanism. This evidence should therefore be interpreted with caution and need further investigations.

Understanding the mechanisms of numerosity perception, in particular whether it derives from other perceptual features such as texture-density, is important for understanding the development of math skills in both typically developing and dyscalculic children. Children with developmental dyscalculia often show a profound deficit in numerosity tasks (Butterworth, 2010), with far higher thresholds for numerosity discrimination than age-matched controls (Mazzocco, Feigenson, & Halberda, 2011; Piazza et al., 2010)—but see also Rousselle and Noel (2007) for a different account. Similarly, numerosity perception has recently been found to be impaired in children with developmental coordination disorder (Gomez et al., 2015), in autism spectrum disorder (Turi et al., 2015) and in children born preterm (Hellgren, Halberda, Forsman, Aden, & Libertus, 2013; for different results see Tinelli et al., 2015). Furthermore, many intervention protocols for the treatment of developmental dyscalculia are built on exercises tapping the ANS (Callaway, 2013; for a review see De Smedt, Noël, Gilmore, & Ansari, 2013). Similarly, in the classroom, teachers often use quantity manipulation to teach formal math concepts, and exposure to formal math teaching has been found to enhance ANS sensitivity (Piazza, Pica, Izard, Spelke, & Dehaene, 2013). Our data suggesting that numerosity is sensed directly, independently of texture-density, and correlated with formal math (while texture discrimination is not). Our data should be considered in future research and intervention of dyscalculia.

Conclusions

The data of this study support our main hypothesis: Sensitivity to nonsymbolic numerosities is intimately linked to formal math skills in children, but only when objects composing the stimuli are sufficiently segmented. For crowded textures of unsegmented stimuli, different mechanisms come into play, which develop to yield higher sensitivity to texture in adults. Schoolchildren, however, have lower sensitivity to dense patterns. Importantly, numerosity acuity remains correlated with math skills even when several potential moderator variables are controlled for. We found that math skills were largely independent of motion direction discrimination thresholds—another feature perceived through the dorsal stream—ruling out the suggestion that higher math skills unspecifically relate to higher visual functioning.

Supplementary Material

Supplemental materials: http://dx.doi.org/10.1037/dev0000155.supp