Direct Investigation of Slow Correlated Dynamics in Proteins via Dipolar Interactions

Abstract

The synchronization of native state motions as they transition between microstates influences catalysis kinetics, mediates allosteric interactions and reduces the conformational entropy of proteins. However, it has proven difficult to describe native microstates because they are usually minimally frustrated and may interconvert on the μs-ms time scale. Direct observation of concerted equilibrium fluctuations would therefore be an important tool for describing protein native states. Here we propose a strategy that relates NMR cross-correlated relaxation (CCR) rates between dipolar interactions to residual dipolar couplings (RDCs) of individual consecutive H^N–N and H^α–C^α bonds, which act as a proxy for the peptide planes and the side chains respectively. Using Xplor-NIH ensemble structure calculations restrained with the RDC and CCR data we observe collective motions on time scales slower than nanoseconds in the backbone for GB3. To directly access the correlations from CCR we develop a structure-free data analysis. The resulting dynamic correlation map is consistent with the ensemble-restrained simulations and reveals a complex network. In general we find that the bond motions are on average slightly correlated, and that the local environment dominates many observations. Despite this, some patterns are typical over entire secondary structure elements. In the β-sheet, nearly all bonds are weakly correlated and there is an approximately binary alternation in correlation intensity corresponding to the solvent exposure/shielding alternation of the side chains. For α-helices there is also a weak correlation in the H^N-N bonds and the degree of correlation involving H^α-C^α bonds is directly affected by side-chain fluctuations, while loops show complex and non-uniform behavior.

Introduction

While protein folding is governed by a funneled energy landscape, native state motions constitute an ensemble of interconverting substates at the bottom of the funnel.^1-3 These inherent motions are part of the evolutionary selection criteria and therefore play a key role in protein function. The synchronization of these motions influences the kinetics of catalysis and is a mediator of allosteric interactions. It also impacts the thermodynamic stability of the protein through reduction of its conformational entropy.^4-7 While energy landscape theories have been successfully applied to understand protein folding, the native states are more difficult to model and are therefore less well understood.² Because they are usually minimally frustrated, it has proven difficult to adapt energy landscape theories to the description of native states and molecular dynamics simulations are usually limited to time scales shorter than many biologically relevant conformational changes.⁸ Thus, experimental observation of equilibrium fluctuations in proteins are very much needed in order to further our understanding of protein dynamics and its role in stability and function.⁹

Nuclear magnetic resonance (NMR) is one of the few techniques that can provide such information since each atom may serve as a reporter on dynamics.^10-12 State-of-the-art NMR methods provide very powerful tools for assessing local bond motions, typically those of H^N-N bonds and methyl group symmetry axes.^13-15 However, these motions alone are not sufficient to understand the whole of protein dynamics and conformational entropy. In addition to measuring the magnitude and direction of individual atomic motions, the degree to which they are synchronized to each other must also be quantified. Novel NMR approaches have recently been proposed to achieve this goal. The first such method involves the analysis of the covariation of motional NMR parameters among a set of mutants.¹⁶ Much attention has been dedicated to another approach, the calculation of ensembles of structures whose back-predicted averaged NMR parameters are in better agreement with experiments than those from single conformations.^17-23 Experimental input parameters are mostly nuclear Overhauser enhancement rates (NOEs), residual dipolar couplings (RDCs) and scalar couplings, and recently we have proposed the use of exact NOEs (eNOEs).²⁴ If different conformational states can be distinguished within the ensemble it may indicate modes of collective motions, however the deconvolution of the motional time scales from these ensembles is difficult. The biological insights that such ensembles offer have recently been reviewed.²⁵ Both approaches (covariance and ensemble), however, reveal concerted motions in an indirect manner. Despite this, these methods have been used to great success to measure the degrees of correlated motions like the crankshaft motions of the peptide plane, which occur on the time scale faster than the molecular tumbling time (sub-τ_c),²⁶ and correlated motions on timescales slower than τ_c (supra-τ_c) like the β-lever motion.^21,27

One direct observation of correlation between two events is offered by cross-correlated chemical shift modulation (CSM).^28,29 However, it is difficult to translate the modulation into a physical picture because it ultimately depends on the electron environment of the spins. A second direct observation can be made using cross-correlated dipolar relaxation rates (dipolar CCR rates) that depend on the relative orientation of two dipole-dipole interaction axes, although a careful analysis must be undertaken to bracket errors arising from approximations.^30,31 These are related to nucleus positions in a straight-forward manner within the molecular frame. There is no fundamental restriction as to how far they may be apart as long as one spin of each interaction is involved in the same coherence. Importantly, CCR rates are sensitive to motion on all time scales.^32-34 Thus, multiple-quantum coherences are attractive for the study of the interplay between spatially separated bonds³⁵ and numerous CCR experiments have been designed to determine the angles between H^N-N, H^α-C^α, H^N-C', N-C' and/or C'-C^α bonds.^32,35-42

Internal motion modifies the CCR rate expected for a rigid molecule and can be quantified by a CCR order parameter S²_CCR which is obtained from the ratio of the experimental and the predicted rigid-molecule rate. The order parameters between consecutive H^N-N bonds in globular proteins have been shown to be ca. 0.75 on average and smaller than those obtained in autorelaxation rates.^32,43 Averaged heuristic order parameters estimated from consecutive H^α-C^α and H^N-N/H^α-C^α CCR rates cover a large range of 0.75-1.^36-40,42,44 Recently, dipolar CCR rates have also been used as a selection criterion for realistic NOE- and RDC-restrained molecular dynamics ensembles of ubiquitin.²⁷ Previous studies have used the CCR rates to identify slow correlated motions in a model-free manner because it has been theoretically shown that only correlation of slow bond motions (supra-τ_c) has a significant influence on the measured CCR rates for the pairs of bonds involved.^33,34,45 In one such case, a slow motion (ns - ms) CCR order parameter S²_CCR,slow was defined as S²_CCR/(S_i,fastS_i+1,fast) and extracted by using relaxation H^N-N order parameters for S_fast.⁴³ The value of S²_CCR,slow can be used to detect the presence of slow motion, however, the degree of correlation is not encoded. An improved interpretation of the CCR order parameter requires both order parameters of the individual bond vectors which are sensitive to the supra-τ_c time-scale and in many cases a fully anisotropic description of molecluar tumbling. It is clear that insufficient experimental and structural accuracy would prevent reliable interpretation of the CCR order parameters.

Here, strategies to overcome all these caveats are employed to reliably extract from CCR rates a dense correlation network of H^N-N/H^N-N, H^α-C^α/H^α-C^α and H^N-N/H^α-C^α bonds in the third immunoglobulin binding domain of protein G, GB3 (Fig. 1).⁴⁶ To verify the accuracy of the measured CCR rate the following four points are crucial. 1) All CCR rates were measured with at least two methods that are as different as possible in order to obtain insight into systematic errors in addition to random errors inherent to each method. 2) Non-negligible corrections to the CCRs have been calculated from a full relaxation-matrix analysis.⁴⁷ 3) The orientations of the H^N-N and H^α-C^α bond vectors that have been used, were previously determined to an accuracy of ca. 3 degrees from RDCs measured under multiple alignment conditions.^48,49 4) CCR rates were back-calculated from structures using anisotropic overall tumbling.^34,50

Fig. 1.

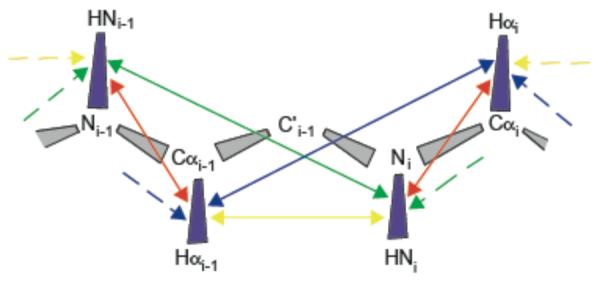
Cartoon representation of the CCR network and the RDC order parameters used in this study. Protein backbone bonds are shown in perspective rectangles. Purple rectangles indicate bond vectors whose RDC order parameters have previously been determined from multiple alignment conditions. Arrows connect bond vectors of the dipolar interactions between which CCRs are measured.

To a good approximation there are two major angular contributions to the general order parameter S². These have been defined by Bruschweiler as short-range collective motion, which is associated with adjacent dihedral angles, and long-range collective motions that lead to angular fluctuations of largly rigid protein segments.⁵¹ Bending and twisting of α-helicies, β-sheets, as well as more complex motions of loops, and turns can produce both short- and long-range collective motions.

Here we report the combined analysis of RDCs and CCRs for GB3 from both ensemble structure calculations and a novel structure free analysis of the same data. Because both CCRs and RDCs are also sensitive to motion on the ns-ms time scale, it is possible to characterize the degree and range of correlated motion exclusively on the supra-τ_c time scale. The degree and type of correlations on this timescale are not well charaterized in the literature, however they are predicted to be distinct from those like the peptide plane crankshaft motion, which is observed on the ps-ns time scale. By using the H^N-N bond vector as a proxy for the peptide plane and the H^α-C^α bond vector as a proxy for the sidechain motion we are able to probe the correlated motions of neighbouring peptide planes and side chains as well as their interactions throughout the protein. Using the structure-free method with the two sets of previously determined RDC order parameters of the individual bonds as previously proposed,^52,53 our analysis of GB3 CCR data produces a highly complex correlation map for slow collective motions whose interpretation invokes not only secondary-structure dependent geometry but also side chain dynamics.

Theory and simulations

The cross-correlated relaxation rate between two dipolar interactions A and B (Γ_A/B) comprised of two spin pairs (A1, A2) and (B1, B2) is

$${\Gamma }_{A∕B}={\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{{\gamma }_{A1}{\gamma }_{A2}{\gamma }_{B1}{\gamma }_{B2}{\mathrm{h}}^2}{10{\pi }^2}\frac{1}{{{\mathit{r}}_{\mathrm{A}}}^3{{\mathit{r}}_{\mathrm{B}}}^3}{J}_{A∕B}$$ (1)

γ_X is the gyromagnetic ratio of nucleus X, r_X is the effective distance between nuclei X1 and X2,⁵⁴ μ₀ is the permeability of free space and h is Planck’s constant. The spectral density function J_A/B depends on the orientation and dynamics of the vectors describing A and B. If the molecule undergoes anisotropic tumbling, five effective overall tumbling times τ_k must be considered.^34,52

It has been shown that J_A/B is virtually independent of the time scale of internal motions as long as it is one order of magnitude faster or slower than τ_c (3.5 - 4 ns for GB3) and only the type of summation over the angular terms is altered when going from fast to slow motion.^34,45 When this condition is met, J_A/B can be factorized into components G_k that depend on the orientation of only A, Ω_A, or only B, Ω_B:

$$J_{A∕B}=\sum _{k=-2}^2{\tau }_k\langle G_k\left({\Omega }_{\mathrm{B}}\right)G_k\left({\Omega }_{\mathrm{A}}\right)\rangle$$ (2)

The averaging is carried out over an ensemble that samples all conformations present over a time longer than τ_c. If correlated slow motion between A and B is absent (but possibly all other types present: fast correlated, fast or slow uncorrelated), then the averaging can also be factorized:

$$J_{A∕B}=\sum _{k=-2}^2{\tau }_k\langle G_k\left({\Omega }_{\mathrm{B}}\right)\rangle \langle G_k\left({\Omega }_{\mathrm{A}}\right)\rangle$$ (3)

This is possible because the fast-scale correlation is lost after a short time (much less than the overall molecular tumbling time) and the integral over the correlation function is nearly identical to one without any correlation at all.⁴⁵

The correlation functions that do not decay over τ_c (slow motions), however, require averaging of their integrals over many molecules. Therefore, such an averaging causes a dependence of the observed CCR rate on the extent of correlation of slow motion. This opens a way to detect correlated slow motion if the CCR rates and the individual G_k factors (averaged over the slow time scale) can be assessed. This is indeed possible with the measurement of the individual RDC order parameters of A and B. Then eq. 3 may be written as

$$J_{A∕B}=S_{\mathrm{A}}^{\mathrm{RDC}}{S}_{\mathrm{B}}^{\mathrm{RDC}}{J_{A∕B}}^{\text{rigid}}$$ (4)

if the A and B motions are sufficiently symmetric. J_A/B^rigid is the spectral density function of a hypothetically rigid molecule. Deviation from eq. 4 is then indicative of slow correlated motion between A and B. We introduce a correlation factor F_corr defined by the ratio of the experimental Γ_A/B^exp and predicted CCR rates Γ_A/B^rigid divided by the RDC order parameters. For all relevant cases the following relationship is valid:

$$F_{\text{corr,A/B}}\equiv \frac{{\Gamma }_{A∕B}^{\text{exp}}}{S_{\mathrm{A}}^{\mathrm{RDC}}{S}_{\mathrm{B}}^{\mathrm{RDC}}{\Gamma }_{A∕B}^{\text{rigid}}}=\frac{J_{A∕B}}{S_{\mathrm{A}}^{\mathrm{RDC}}{S}_{\mathrm{B}}^{\mathrm{RDC}}{J}_{A∕B}^{\text{rigid}}}\{\begin{array}{c}\hfill =1\to \mathit{non}-\mathit{correlated}\hfill \\ \hfill >1\to \mathit{syn}-\mathit{correlated}\hfill \\ \hfill <1\to \mathit{anti}-\mathit{correlated}\hfill \end{array}\phantom{\}}$$ (5)

To restrain the CCRs during ensemble simulations we have implemented an ensemble CCR restraint for isotropically tumbling molecules in Xplor-NIH.⁵⁵ In practice, the following sum of CCR rates is measured

$${\Gamma }_{A∕B}^{\text{iso}}={\Gamma }_{A1,A2∕B1,B2}^{\text{iso}}+{\Gamma }_{A1,B2∕B1,A2}^{\text{iso}}$$ (6)

where the rate ${\Gamma }_{A1,A2∕B1,B2}^{\text{iso}}$ accounts for the dipole interaction between A1-A2 and B1-B2 and depends on the ensemble averaged angle between the two vectors A and B and their respective bond lengths as

$${\Gamma }_{A1,A2∕B1,B2}^{\text{iso}}={\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{{\gamma }_{A1}{\gamma }_{A2}{\gamma }_{B1}{\gamma }_{B2}{\mathrm{h}}^2}{10{\pi }^2}\frac{2{\tau }_c}{5}\langle \frac{3{\cos }^2{\theta }_{A1,A2∕B1,B2}-1}{r_{A1,A2}^3{r}_{B1,B2}^3}\rangle .$$ (7)

The second rate ${\Gamma }_{A1,B2∕B1,A2}^{\text{iso}}$ in equation 7 accounts for the contribution from dipoles A1-B2 and B1-A2 as

$${\Gamma }_{A1,B2∕B1,A2}^{\text{iso}}={\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{{\gamma }_{A1}{\gamma }_{A2}{\gamma }_{B1}{\gamma }_{B2}{\mathrm{h}}^2}{10{\pi }^2}\frac{2{\tau }_c}{5}\langle \frac{3{\cos }^2{\theta }_{A1,B2∕B1,A2}-1}{r_{A1,B2}^3{r}_{B1,A2}^3}\rangle$$ (8)

In most cases, this second contribution is so small that it can safely be neglected, and when the average structure is known this additional contribution can be factored out to a large extent. Given that this contribution cannot be removed experimentally, we have opted to correct the restrained CCR rates for this contribution to the rate and also the effect of anisotropic diffusion. The restrained CCRs were calculated as

$${\Gamma }_{A1,A2∕B1,B2}^{\text{restrained}}={\Gamma }_{A∕B}^{\text{expt}}+\left\{{\Gamma }_{A∕B}^{\text{calc,iso}}-{\Gamma }_{A∕B}^{\text{calc,aniso}}-{\Gamma }_{A1,B2∕B1,A2}^{\text{calc,iso}}\right\}$$ (9)

where the calculated isotropic and anisotropic CCRs were derived from the average structure of GB3.^48,49,56 Note that such a correction for anisotropy is only justified for small deviations. In the case of GB3, the maximum corrections are ca. 5%, but the majority is much smaller. These CCR rates were restrained using a harmonic restraint

$$E_{\mathrm{CCR}}=w_{\mathrm{CCR}}{\left({\Gamma }_{A1,A2∕B1,B2}^{\mathit{calc}}-{\Gamma }_{A1,A2∕B1,B2}^{\mathit{restrained}}\right)}^2$$ (10)

where w_CCR is the weighting factor for the potential term. The weights w_CCR were set to 0.4, 0.8, 0.8, and 2.0 kcal/mol·s² for Γ_{HNiNi/HNi+1Ni+1}, Γ_HNiNi/HAiCAi, Γ_{HNiNi/Hαi-1Cαi-1}, and Γ_{HαiCαi/Hαi-1Cαi-1}, respectively. In the context of the current work the value of ${\Gamma }_{A1,A2∕B1,B2}^{\text{calc}}$ given as a slightly modified version of equation 7 as

$${\Gamma }_{A1,A2∕B1,B2}^{\text{calc}}=\left\{{\left(\frac{{\mu }_0}{4\pi }\right)}^2\frac{{\gamma }_{A1}{\gamma }_{A2}{\gamma }_{B1}{\gamma }_{B2}{\mathrm{h}}^2}{10{\pi }^2}\frac{2{\tau }_c}{5}\frac{1}{r_{A1,A2}^3{r}_{B1,B2}^3}\right\}\langle 3{\cos }^2{\theta }_{A1,A2∕B1,B2}-1\rangle$$ (11)

where the region in curly braces is a constant. This expression substantially simplifies the calcuations of derivatives during structure calculation.

Results

We have recorded 30 data sets in total that encompass H^N-N/H^N-N, H^α-C^α/H^α-C^α, and both intra-residual and sequential H^N-N/H^α-C^α CCR rates. These four pairs of interactions describe the motions of the bond vectors in the backbone (see Figure 1).

We employed as diverse methods as possible but replicated each experiment at least twice. Based on extensive statistical analysis we finally selected 21 sets to obtain the best averaged values and reliable errors for this study (see Tables S1-S4 in the Supporting Information).⁵⁷ The errors are exceptionally small as they fall between 1.5 and 3 % of the observed ranges of the rates. Typically, they are twice as large as the propagated random errors obtained from repetition of individual experiment types (H^α-C^α/H^α-C^α) or similar to them (all others CCR rates).

Agreement of static and dynamic structures with CCRs

As an initial assessment of the structural and dynamic information contained in the CCRs we compared the average solution structures of GB3 and the previously determined dynamic ensemble of GB3 to the CCRs.²² In table 1 the rmsd agreement between the experimental and back-calculated CCRs using Eqn. 1 is given. Focusing first on the average solution structures for H^N N/H^N-N CCRs, the rmsd of 1.12 s⁻¹ for the RDC refined average solution structure (2OED) is larger than the experimental error of 0.19 s⁻¹. A similar rmsd (1.03 s⁻¹) was obtained for a newly refined structure with ³J couplings and RDCs. For the H^α-C^α/H^α-C^α CCRs, the average structure refined with RDCs has an rmsd of 4.71 s⁻¹, compared to the experimental error of 1.37 s⁻¹, while the structure refined with ³J couplings shows improved agreement to the CCRs with an rmsd of 4.10 s⁻¹. Similarly, the agreement of the intraresidual and sequential H^N-N/H^α-C^α CCRs with experimental errors of 0.20 and 0.26 s⁻¹, respectively, ranges from 1.4 to 1.9 s⁻¹. A uniform scaling factor relating the experimental to the predicted CCR rates may be viewed as an ‘average’ CCR order parameter S²_CCR. For the first 2oed structure in table 1, it is 0.81, 0.88, 0.86 and 0.85 when individually calculated for H^N-N/H^N-N, H^α-C^α/H^α-C^α, and intraresidual H^N-N/H^α-C^α and sequential H^α-C^α/H^N-N (see Table S9 in the Supporting Information), which is in fair agreement with previous less quantitative studies.^{32,37-40,42,44} Note that the values decrease to 0.72, 0.76, 0.75 and 0.74 when the bond lengths are not corrected for libration motion. Finally, we have calculated single structure refined with both CCRs and RDCs called Ccr1. These single structures show some improved agreement with the CCRs, compared to the 2OED structures, however agreement with 3J couplings was similar. Therefore, we choose to use the original 2OED structures as the representation of the average structure in solution.

Table 1.

Validation of ensembles and single structures with CCR and ³J coupling data

	CCR rmsd (s−1) a				3J coupling rmsd (s−1) b
	HNN/HNN	CαHα/CαHα	HNN/CαHα	CαHα/HNN	HNHα	C’C’	HNC’	HNCβ
Expt. Err	0.19	1.37	0.20	0.26	0.14	0.03	0.10	0.07
	Single structures
2oed c	1.12	4.71	1.68	1.67	0.98	0.41	0.44	1.07
2oed d	1.03	4.10	1.91	1.42	0.99	0.39	0.42	1.04
Ccr1 e,h	0.65	4.11	0.98	1.23	0.87	0.62	0.63	1.12
	Ensembles
Ens8 e,f	0.78	3.99	1.61	1.28	0.75	0.33	0.40	1.02
Ens16 e,g	0.55	3.74	1.16	1.04	0.71	0.24	0.43	0.68
Ccr16 e, h	0.15	2.02	0.25	0.29	0.55	0.25	0.39	0.72

^abond lengths of 1.041 and 1.117 Å were used to calculate CCRs from structures to account for libration motions that are not present in static structures

^bKarplus parameters used were those for the fits to Ace-Ala-NMe ,⁶⁸ experimental data ^69,70

^cCoordinates from RDC-refined X-ray structure ⁵⁶ whose H^N and H^a proton positions were subsequently optimized with RDCs ^48,49

^dCoordinates re-refined with ³J couplings ⁷¹

^eAverage values calculated from 20 ensembles

^fPreviously determined dynamic ensemble ²²

^gEnsemble generated using the same data as CCR16 except with exclusion of CCR data

^hEnsemble generated using the CCR data and both 6 sets of H^N -N and H^a-C^a RDCs; J couplings are only used for independent validation

Comparison of the CCR rmsd values of the refined average structures to those for dynamic ensemble of GB3 determined by Clore et al. shows better agreement with all four sets of CCRs when compared to the RDC refined average structures.²² In table 1 we also present the independent validation of the average structures with ³J couplings for the backbone (H^N-H^α, C’-C’, H^N-C’ and H^N-C^β). The agreement with the ³J couplings for both structures refined with RDCs is very similar. The independent validation of the ensembles with ³J couplings shows that the ensemble description of structure and dynamics leads to a superior agreement with the experimental data. For all of the structures and ensembles the Pearson correlation coefficients are very similar (data not shown), indicating that the relative scaling of the dynamic contributions is the major cause of the variation in rmsd.

Generation of CCR-restrained ensemble CCR16

Motivated by the poor agreement of the experimental CCRs with the average structures and the improvement observed for the ensemble representation we undertook to generate an ensemble restrained with the experimental CCRs. We used ensemble structure calculations of GB3 restraining both six sets of RDCs for H^N-N and H^α-C^α bond vectors and the four sets of CCR measurements converted to their approximate isotropic values using the average structure. The ensemble was determined using Xplor-NIH with the same general protocol used by Clore et al.²² The angular CCR restraint for isotropic overall tumbling was added and ensembles of varying sizes between 2 and 64 members obtained with 20 replicate ensembles for each size. The optimum ensemble size of 16 members was determined through independent validation with ³J couplings that like CCRs and RDCs are sensitive to fast and slow motions of the backbone. In figure 2a we show the impact of ensemble size on the ability to minimize the disagreement between the experimental and back-calculated RDCs and (anisotropic) CCRs. We also show the agreement with the CCRs after correction for anisotropy.

Fig. 2.

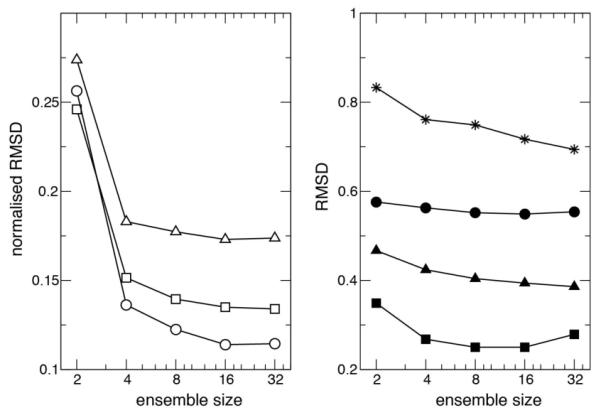
Ensemble restrained data and independent validation of various ensemble sizes. Normalized rmsd for restrained data are shown in the left panel: RDCs (open circles), and experimental CCR rates corrected for anisotropy (open squares), and indirectly restrained anisotropic CCRs (open triangles). Rmsd for unrestrained ³J scalar couplings H^N-H^α (filled circles), C’-C’ (filled squares), H^N-C’ (filled triangles), and H^N-C^β (stars) are shown in the right panel.

In figure 2 we also show the independent validation of the optimum ensemble size using H^N-H^α, C’-C’, H^N-C’ and H^N-C^{β 3}J couplings. It can be seen that no further improvement is obtained in increasing the size of the ensemble from 16 to 32 members. In table 1 we present the validation of ensembles of 16 members with (Ccr16) and without CCR (Ens16) restraints.

For the 16 member ensembles restrained with RDCs and CCRs the agreement with the CCRs approach the experimental error of the CCRs. As a control, we repeated the 16-member ensemble without restraining the CCRs, but keeping the rest of the restraints and simulation parameters the same. This ensemble had good agreement with the experimental data and validated better than the single structures and the previous dynamic ensemble for GB3 (see table 1). However the independent validation for the H^N-H^α and H^N-C’ ³J couplings is better for the CCR restrained ensembles than for the CCR unrestrained ensemble. The slightly poorer agreement for the H^N-C^β couplings is likely related to the inability of the Karplus parameters to accurately account for the influence of different side chain substituents. The correlation plots for the four sets of CCRs for the single structure and ensembles generated in this work are shown in figure 3. We also conducted cross validation by systematically leaving out each set of CCRs from the calculation (see table S10), these results show that even though the backbone is not over-determined by the four sets of CCRs similar results are obtained in most cases. Also revealing in table S10 is that the H^N-H^{α 3}J coupling fit is sensitive to the presence of the intraresidual H^N-N/H^α-C^α CCR data, both of which are sensitive to the backbone φ angle.

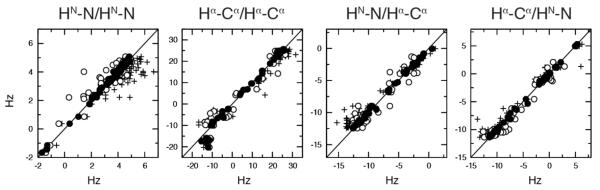
Fig. 3.

Comparison of experimental and back-calculated anisotropic CCR rates. The rates are calculated for the single average RDC-refined X-ray structure ⁵⁶ whose H^N and H^α proton positions were subsequently optimized with RDCs ^48,49 (plus), the RDC restrained ensemble with 16 replicas (open circles), and the RDC and CCR restrained ensemble with 16 replicas (filled circles).

Average correlation from predicted CCR rates

The average F_corr calculated over the entire protein indicates the average degree of correlation throughout the protein. In table 2 the average F_corr values for each pair of bond vectors is presented. The average F_corr values calculated from the back-calculated order parameters and CCR rates from the CCR-restrained ensemble are also presented.

Table 2.

Average F_corr from experimental S² and CCR rates

	Fcorr a
	HNN/HNN	CαHα/CαHα	HNN/CαHα	CαHα/HNN
iterative DIDC b	1.01	1.05	1.10	1.02
ORIUM b	1.24	1.28	1.39	1.29
Ccr16 c	1.10	1.14	1.14	1.04

^aBond lengths of 1.041 and 1.117 Å were used to calculate CCRs from structures to account for libration motions that are not present in static structures

^bCoordinates from RDC-refined X-ray structure ⁵⁶ whose H^N and H^a proton positions were subsequently optimized with RDCs ^48,49

^cAverage values calculated from 20 ensembles.

The average F_corr for the H^N-N/H^N-N bond vectors quantifies the average correlation between neighboring peptide planes and is that closest to one and indicates that the average degree of correlation between these probes is the weakest. The correlation between the side chains probed via the H^α-C^α/H^α-C^α CCR rates are of intermediate strength as is the correlation between side chain and its i+1 peptide plane (sequential H^N-N/H^α-C^α). The intraresidue H^N-N/H^α-C^α correlation has the most correlated behavior of all probes. Despite the uniformity across different CCR types, there is considerable variation between individual bond pairs.

Accuracy of model-free F_corr

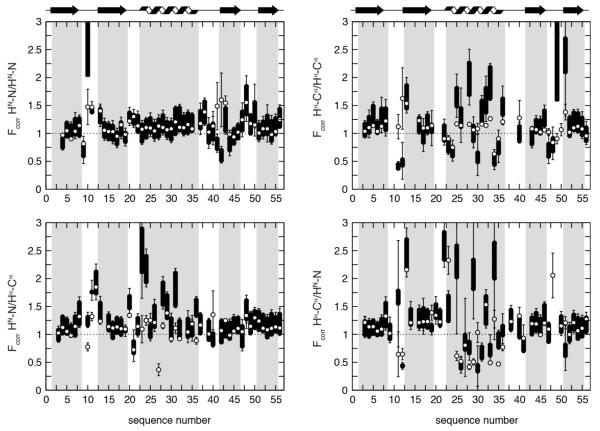
For a detailed quantification of motional correlation, the F_corr value is calculated for each CCR rate (listed in Tables S5 to S8 in the Supporting Information). In Fig. 4, F_corr is plotted versus the residue number. It is crucial for the current study to establish the reliability of F_corr. A realistic error is obtained from error propagation of the well defined errors of the experimental CCR rates and the RDC order parameters. A negligibly small error is assumed for the predicted CCR rate of the rigid GB3 model (see Supporting Information for details). The resulting error bars mostly lie above or below 1. This suggests that correlated motion (both syn and anti) can be deduced from individual CCR rates (see eq. 5). In addition to the error propagated from the RDCs there is also a model error which can impact on the determined order parameters. Here we use the order parameters derived from both the iterative DIDC (iDIDC) and the ORIUM methods,^48,53,58 which essentially correspond to upper and lower limits for the real order parameters. The ORIUM order parameters are shifted toward lower values (Figure S2 in the Supporting Information; for a residue specific comparison see Figure 4 in reference 53), however the two models result in a similar sequence-specific pattern (Figure 4). In this way the F_corr derived from the ORIUM order parameters is an upper estimate, while the F_corr derived from the iDIDC is a lower estimate. In Figure 4 we show the range of correlations as a result of changing the RDC analysis model. It is clear that changing the model shifts the values of F_corr but conserves the sequence-specific pattern.

Fig. 4. Residue specific F_corr values for GB3.

Motional correlation between and among H^N–N and H^α–C^α bonds in GB3. F_corr versus residue numbers are shown for H^N_i–N_i/H^α_i–C^α_i and H^N_i–N_i/H^α_i-1–C^α_i-1 on the left top and bottom, respectively, and for H^N_i–N_i/H^N_i+1–N_i+1 and H^α_i–C^α_i/H^α_i-1–C^α_i-1 on the right top and bottom. Black thick bars connect the lower F_corr estimate from the iDIDC order parameters with the higher estimate from the ORIUM order parameters. The error bars indicate the propagated error from the CCRs and order parameters. If a value or an error is not available from a specific CCR rate or S^RDC data set the bar is calculated as outlined in the Supporting Information. The white points indicate the F_corr calculated from the ensemble that was restrained with the CCR and RDC data. Errors for this F_corr are the RMSD for the F_corr from 20 independent ensembles.

Comparison of the dynamic ensemble and F_corr from the model-free approach

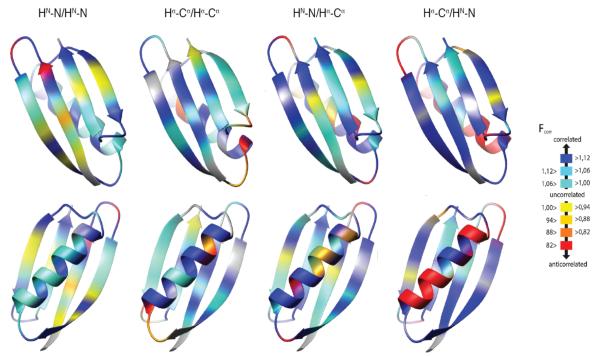
To determine to what extent the dynamic ensemble agrees with the F_corr calculated directly from the experiential data (see below), we calculated the F_corr from the back-calculated CCRs and S² values from the restrained ensemble and its averaged coordinates. In Figure 4 we plot the values of the ensemble F_corr values compared with those from the experimental data. We observe good agreement between the ensemble determined F_corr and the experimental F_corr values. In Figure 5 we show the distribution of the F_corr value on the average structure of GB3 to indicate which parts of the structure undergo concerted motions. The F_corr calculated from the CCR-ensemble restrained structure calculations usually gives values that are intermediate between those for the ORIUM and iDIDC order parameter calculations. The largest exceptions are found for the loops and are mostly associated with large experimental errors. Large errors are typically obtained for small measured CCR rates. For example, intraresidue H^N-N/H^α-C^α F_corr of residue 27 obtained from the DIDC and the ORIUM analysis is −0.04 and −0.06, respectively (see Table S7 in the Supporting Information). Because the measured CCR rate is only 0.96 s⁻¹, the error propagated into F_corr is 0.36 and 0.48 s⁻¹. Therefore, these values are not in contradiction with F_corr obtained from the ensemble, which is 0.37 s⁻¹. All other exceptions are obtained for the helix, typically with small deviations from the structure-free F_corr values. As already inferred from the average F_corr values in Table 2, the bond motions are on average slightly syn-correlated. However, the per residue variation in the F_corr values is highly complex (see Fig. 4) and while many correlations are dominated by the specific local environment, some patterns are typical for entire secondary structure elements.

Fig. 5. Residue specific F_corr values for GB3 from structure calculations.

H^N–N/H^N–N, H^α–C^α/H^α–C^α, and intraresidual and sequential H^N–N/H^α–C^α F_corr are mapped on 3D ribbon representations of GB3. The β-sheet is in the front in the top row, and the α helix in the bottom row. The plots were prepared with the program MolMol.⁷²

For example the H^N-N/H^N-N F_corr ~1 for residue 4, which reports on the correlation of the amide bond vector of Tyr3 with that of the amide bond vector of residue Lys4 in the molecular frame. The side chain between these two residues (Tyr3) is buried in the core of the protein, while the neighboring side chains project out into the solvent. In contrast, the F_corr>1 for residue Leu5, which reports on the correlation between the amide bond vectors of Leu5 and Lys4, where the side chain between these two vectors (Lys4) is exposed to the solvent. This alternating pattern of F_corr repeats along the length of the strand with the F_corr for residue Val6 having an F_corr < 1, and residue Ile7 having a value > 1. The same zig-zag type pattern is observed across the entire set of strands of GB3 as can be seen by the yellow strips that are present on the strands in Figure 5. This regular behavior of the strands contrasts with the irregular correlation pattern for the H^N-N/H^N-N F_corr in the loops. The H^N-N/H^N-N F_corr >1 throughout the helix. However, the F_corr on the interior surfaces of the helix that are packed against the hydrophobic core of GB3 have slightly higher F_corr values. In the case of the H^α-C^α/H^α-C^α vectors, the F_corr >1 in the strands with the only exception being the C-terminal residue. The behavior in the helix is more complex, and the majority of residues show F_corr > 1. For four residue pairs, 22/23, 23/24, 33/34, 34/35, at the ends of the helices however the vectors are negatively correlated. For the intraresidue H^N-N/H^α-C^α F_corr, the majority of the bond vectors are positively correlated. These vectors span the shortest distance that we have measured here and are only separated by a single bond. In the strands the F_corr for residue Val6 is < 1, as are the values for Trp43 and Thr44. These residues do not directly contact one another, but the side chains of Thr53 is positioned between their side chains on the surface of the protein. The residues with F_corr < 1 in the helix are 27, 30, 32, and 36. Residues 32 and 36 are hydrogen bonded in the helix. Finally, the sequential H^N-N/H^α-C^α F_corr is > 1.0 for all residues in the strands with the exception of the H^α-C^α vector of Thr44 with the H^N-N vector of Tyr45, which is very close to 1.0. In contrast the helix has F_corr values predominantly < 1.0 indicative of negative correlations in this secondary element. The residues with values of F_corr > 1 in the helix are close to the center of the helix.

In general, when both bonds are located in residues with solvent-exposed side chains, strong syn-correlation is present. However, anti-correlation is more common if at least one side chain is anchored in the protein core. The loops show highly non-uniform behavior. A specific bond may be in strong anti-correlation with one bond but in syn-correlation with another.

Large-scale correlations

In addition to local correlations that are encoded in the input data, the high information density also offers insight into fluctuation of large segments of GB3. In the following, we investigate collective motions of the β-sheet and the α-helix as well as the motion of the helix relative to the sheet.

To quantify the bending of the α helix bending, we choose to fit ideal helices to the segments on either end of the helix comprising residues 23-26 and 32-35, and calculate the angle between those. The ensembles have average angles of 14.0 ± 0.5° with r.m.s. deviations of 6.2 ± 0.7°. The consistency of these numbers indicate that the extent of bending is reproducible with the ensemble. The bend per residue is 1.6°. The results are very similar when the CCR rates are omitted in the structure calculation with 13.9 ± 0.6° and 5.5 ± 0.7°, but the bending reduces to 8.0 ± 1.2° with a slightly smaller r.m.s.d. of 3.3 ± 0.6°.

For analysis of the β sheet, we fitted a catenoid shape described by the inclined angle of β-strands and minimal radius,⁵⁹ to the β-sheet.⁶⁰ The average inclined angle for the CCR+RDC ensemble is very similar to that of the RDC ensemble (42.7 ± 0.3° and 42.6 ± 0.3°), while the average angle was marginally larger in the control simulation (45.7 ± 0.6°). The r.m.s. deviation that represents the structural heterogeneity in the ensemble is 1.6 ± 0.3° for both the CCR+RDC and RDC ensembles, however the control ensemble is less heterogenous with an r.m.s. deviation of 1.1 ± 0.2°. The minimal radius of the catenoid is inversely related to the twisting of the β-sheet .⁵⁹ For the control simulation the average radius is 12.83 ± 0.19 Å, and reduces to 11.56 ± 0.19 Å for the RDC ensemble and 11.51 ± 0.15 Å for the CCR+RDC ensemble. This indicates that the β-sheet of the RDC and RDC+CCR ensembles are on average more twisted that the control simulation. The r.m.s. deviation of the minimal catenoid radius for the control, the RDC and the CCR+RDC ensembles are 0.48 ± 0.08 Å, 0.56 ± 0.12 Å and 0.65 ± 0.11 Å, respectively. Thus we observe a broader distribution of minimal catenoid radii for the CCR+RDC ensemble. This increased heterogeneity indicates that the CCR+RDC ensemble samples a broader range of twists than the other ensembles.

Discussion

The zig-zag trend of the strong syn-correlated motions along the β-sheet sequence observed in all CCR types may be related to the fact that every other residue has a solvent-exposed side chain. Moreover, neighbouring peptide planes in the helix have hydrogen bonds that are approximately opposite one another, thus the observed anti-correlation of the sequential H^N–N/H^α–C^α CCRs may be related to the slow bending mode of helices.⁶¹ The apparent coupling between the side chains and the backbone results from the H^α-C^α-C^β group acting as a hinge that propagates motions of the side chain to the neighbouring peptide planes. Consequently, the degree of backbone correlation is affected by side-chain fluctuations, as revealed by stronger syn-correlated or anti-correlated motions. Indeed, backbone motion slower than the overall tumbling has previously been observed for solvent exposed residues in Ubiquitin.⁶² The highly non-uniform behavior in the loops is caused by larger-amplitude and possibly multiple-mode fluctuations.

What we learn from the restrained ensemble structure calculations is that much of the correlations that we observe are not encoded in the forcefield alone and that the inclusion of the additional experimental data leads to improved agreement of the resulting ensemble. In a previous analysis, Clore and Schwieters generated an ensemble of GB3 structures restrained by RDCs, J couplings and relaxation order parameters, from which they indirectly obtained correlation functions among and between H^N-N and H^α-C^α bonds (see Supproting Information for details on the calculation).¹⁹ Although relaxation order parameters are only sensitive to sub-nanosecond motion, and their model does not distinguish between syn- and anti-correlation, we compare their findings to our correlation measure F_corr, that can distinguish between syn- and anti-correlations. Most strikingly, the patterns involving an H^α-C^α bond are less uniform than H^N-N/H^N-N. Residue 11 has also the most pronounced F_corr for H^N-N/H^N-N and those of residues 11 and 40 deviate strongly from 1 for H^α-C^α/H^α-C^α, and intraresidual and sequential H^N-N/H^α-C^α. More generally, the loops exhibit stronger deviation from 1, in particular loops β1/β2 (residues 9-12) and β3/α(37-41). One region where our analysis gives different results is the helix, where the F_corr values are not more pronounced for the N-terminal than in the C-terminal segment. The remarkable agreement for ensemble calculations is not unprecedented as other studies have also shown that experimental restraints often improve the quality of the underlying force field.⁶³ Comparison of our GB3 ensemble and the structure-free method indicates that the correlations are present in the backbone and can be detected using either the direct correlation via the calculation of F_corr or through the use of ensemble restrained simulations with RDCs and CCR meausrements.

In numerous studies of GB3, a crankshaft motion has been described.^19,22,24,64 Such anti-correlated fluctuations of the backbone φ_i and ψ_i–1 angles is equivalent to tilting of the peptide plane around the C^α-C^α axis. In the CCR-restrained ensemble we observe two short-range correlated motions, the crankshaft and β-lever correlations are observed (see figure S3 in the Supporting Information). However on the longer timescales the long-range collective motions are predicted to dominate motions and hence the F_corr.⁵¹ Consistent with this idea of angular fluctuations of largely rigid protein segments, we have observed a dominance of syn-correlated rather than anti-correlated motion.

Bouvignies et al. used the three-dimensional Gaussian model with a large set of RDCs to determine the motional amplitudes (but not the degree of correlation).⁶⁴ Despite this the correlated motion of the β-sheet on the ns-ms time scale was observed to improve the agreement with experimentally measured hydrogen bond ³J scalar couplings. In a related study, comparison of RDC and relaxation order parameters to those from Accelerated Molecular Dynamics (AMD) simulations indicated the existence of μs-ms motion in the loops and the β-sheet but not in the α-helix.²³ Also in the AMD study, an alternation of large and small motional amplitudes was observed in the strands β1, β3 and β4, pointing to motions coupled across the β-sheet. Interestingly, the pattern matches the alternation of strongly hydrophobic side chains buried in the protein core observed here and may be related to the weak zig-zag pattern observed in this study.⁶³ Recently, we used exact NOEs to calculate an ensemble of structures.²⁴ Again, correlated motion across the β-sheet and within the loops was revealed. This is in line with the present observation, where CCR rates involving H^α-C^α bonds indicate correlations to neighboring backbone bonds.

In the biological context of GB3 the N-terminal segment of strand β2 is a site of interaction with the Fc immunoglobulin region.⁵⁶ This region is often observed to exhibit increased H^N-N bond mobility in experiments that probe dynamic fluctuations.^{19,21,48,64,65} The current study suggests that this additional mobility is organized in a correlated fashion. From the ensemble we see indications that the sheet is twisting and that the helix is bending. Despite the consistencies with other data, the CCR data does not strictly probe the same aspect of motion. It is rather a complement to other NMR measures, both in terms of time scale and spatial dependence. In conclusion, we introduced a method which quantifies the correlation of protein native state motion. In principle, the method can be extended to include other protein sidechain bonds and also to study nucleic acids. Ultimately, we hope that the methods presented here that allow the determination of local disorder and correlated motions will open an avenue to refine local entropy calculations in biomolecules.

Materials and Methods

Sample expression and purification

GB3 was expressed and purified as described previously.⁶⁶ The ¹³C,¹⁵N- and ²H,¹³C,¹⁵N-labeled NMR samples contained 350 μl and 500 μl of 4 mM and 2 mM protein solution, respectively, in 97%/3% and 95%/5% H₂O/D₂O, 50 mM potassium phosphate buffer, pH 6.5 and 7.0, and 0.5 mg/mL sodium azide.

NMR spectroscopy

All experiments were performed on a BRUKER DRX600 MHz spectrometer, equipped with a z-axis gradient cryogenic probe, respectively, at 298 K. All spectra were processed and analyzed using the software package NMRPipe.⁶⁷

Γ_{HNiNi/HNi+1Ni+1} + Γ_{HNiNi+1/HNi+1Ni} were obtained from the triple labeled sample and 'reference' and 'trans' spectra of 3D ct-¹³C’-HN(CA)CON [ct-¹³C^α-HNCA(CO)N] experiments (derived from a 2D version)⁴⁵ recorded with 36(N, t₁) × 40(C’, t₂)[20(C^α, t₂)] × 512(H^N, t₃) complex points, t_1max = 18.0 ms, t_2max = 26.4[6.6] ms, t_3max = 51.2 ms, an interscan delay of 1 s, τ_MQ = 43 ms, and typically 16[32] scans per increment resulting in a measurement time of 1[2] day. Because the 'trans' spectra are considerably less sensitive they were typically recorded twice and added up thereby effectively doubling the number of scans. The time domain data were multiplied with a square cosine function in the direct dimension and cosine functions in the indirect dimensions and zero-filled to 256 × 128 × 2048 complex points. Spectra with ¹³C’ and with ¹³C^α evolution were recorded twice and three times, respectively, such that averaged CCR rates with associated random errors could be obtained.

Γ_{HαiCαi/Hαi-1Cαi-1} + Γ_{HαiCαi-1/Hαi-1Cαi} were obtained from 'reference' and 'trans' spectra of the 2D HNCA(CA) experiment previously put forward,³⁷ and a 3D ¹³C^α-HNCA(CO)CA experiment recorded with 64(N, t₁) × 512(H^N, t₂) and 36(N, t₁) × 24(C^α, t₂) × 512(H^N, t₃) complex points, t_1max = 32.0 ms, t_2max = 51.2 ms and t_1max = 18.0 ms, t_2max = 7.92 ms, t_3max = 51.2 ms, an interscan delay of 1 s, τ_MQ = 28 ms, and typically 256 and 32 per increment resulting in measurement times of 0.5 and 2 days, respectively. Because the 'trans' spectra are considerably less sensitive than the 'reference' spectra they were typically recorded twice and added up thereby effectively doubling the number of scans. The time domain data were multiplied with a square cosine function in the direct dimension and cosine functions in the indirect dimensions and zero-filled to 1024 × 4096 and 256 × 128 × 2048 complex points. All spectra were recorded twice so that average CCR rates and associated random errors could be obtained.

Γ_{HNiNi/HαiCαi} + Γ_{HαiNi/HNiCαi} were obtained from three experiments. The two experiments used previously were repeated.⁵² The first approach relies on the ACE (all component evolution) method⁵² realized in a 3D ct-HNCA experiment, where all components of the quadruplets of the multi-quantum coherences are resolved. In the second approach, the DIAI (double inphase/antiphase interconversion) method is realized with a pair of 3D HNCA pulse sequences ('reference' and 'trans') in 2 days.³⁸ In addition, a 3D ct-HNCA MMQ (mixed multi-quantum, where zero- and double-quantum coherence evolution is averaged) experiment was used. The ZQ and DQ coherences are superimposed resulting in four components to be evaluated.⁴⁴ The spectrum was recorded twice with τ_MQ = 31.0 ms or τ_MQ = 33.5 ms, 50(MQ[N,C^α], t₁) or 55(MQ[N,C^α], t₁) × 36(N, t₂) × 512(H^N, t₃) complex points, t_1max = 25.0 ms or t_1max = 27.5 ms, t_2max = 18.0 ms, t_3max = 63.28 ms, interscan delays of 1 s or 0.92 s and 16 or 24 scans per increment resulting in measurement times of 1.5 or 2 days. The time domain data were multiplied with a square cosine function in the direct dimension and cosine functions in the indirect dimensions and zero-filled to 256 × 128 × 2048 complex points.

Γ_{HNiNi/Hαi-1Cαi-1} + Γ_{Hαi-1Ni/HNi-1Cαi-1} were obtained by repetition of three previously used experiments.⁵² The first approach relies on ACE realized in a 3D ct-HN(CO)CA experiment. In the second and third approach, the DIAI method is realized with two types of 2D HN(CO)CA experiments.^36,38

Corrections to the apparent CCR rates were calculated with a full matrix analysis as outlined in reference.⁴⁷

Prediction of CCR rates

In order to obtain reliable predicted CCR rates and thus F_corr, the average positions of the H^N and H^α protons are of particular importance. Highly accurate RDCs have been used to orient H^N–N and H^α-C^α bond vectors in the NMR-optimized X-ray structure with pdb entry 2OED.^48,49,66 The impact of angular fluctuation is removed by scaling the H^N–N and H^α-C^α bond lengths to 1.041 and 1.117 Å, respectively.⁵⁴ For the prediction of the CCR rates expected for uncorrelated motion of the two vectors the previously published RDC order parameters were used (Table S11 in the Supporting Information).^48,49,53 Note that structural inconsistencies between the different mutants were identified for residues 19 and 41 for the H^N-N and residues 11, 25, 30 and 40 for the H^α-C^α bonds, four of which are sites of mutations or immediate neighbors.⁴⁸ The errors may be larger than reported and accordingly propagated into F_corr. The CCR rates predicted for the rigid and dynamic models are shown in Tables S5 to S8 in the Supporting Information.