Abstract
Objective
We investigated whether inclusion of simple measures of calcified plaque distribution might improve the ability of the traditional Agatston coronary artery calcium (CAC) score to predict cardiovascular events.
Background
Agatston CAC scoring does not include information on the location and distributional pattern of detectable calcified plaque.
Methods
We studied 3,262 (50%) individuals with baseline CAC >0 from the Multi-Ethnic Study of Atherosclerosis (MESA). Multi-vessel CAC was defined by the number of coronary vessels with CAC (scored 1 to 4, including the left main). The “diffusivity index” was calculated as 1 – (CAC in most affected vessel/total CAC), and was used to group participants into concentrated and diffuse CAC patterns. Multivariable Cox proportional hazards regression, area under the curve (AUC), and net reclassification improvement (NRI) analyses were performed for both coronary heart disease (CHD) and cardiovascular disease (CVD) events to assess whether measures of regional CAC distribution add to the traditional Agatston CAC score.
Results
Mean age of the population was 66 ± 10 years, with 42% women. Median follow-up was 10.0 (9.5 – 10.7) years and there were 368 CHD and 493 CVD events during follow-up. Considerable heterogeneity existed between CAC score group and number of vessels with CAC (p<0.01). Addition of number of vessels with CAC significantly improved capacity to predict CHD and CVD events in survival analysis (HR 1.9-3.5 for 4-vessel vs. 1-vessel CAC), AUC analysis (C-statistic improvement of 0.01-0.033), and NRI analysis (category-less NRI 0.10-0.45) analyses. While a diffuse CAC pattern was associated with worse outcomes in participants with ≥2 vessels with CAC (HR 1.33-1.41, p<0.05), adding this variable to the Agatston CAC score and number of vessels with CAC did not further improve global risk prediction.
Conclusion
The number of coronary arteries with calcified plaque, indicating increasingly “diffuse” multi-vessel subclinical atherosclerosis, adds significantly to the traditional Agatston CAC score for the prediction of CHD and CVD events.
Keywords: risk prediction, risk stratification, cardiac CT
Introduction
Coronary artery calcium (CAC) scores derived from non-contrast cardiac computed tomography (CT) are one of the strongest individual predictors of adverse cardiovascular events1. The association of CAC with cardiovascular disease (CVD) is thought to be driven by the strong correlation between detectable subintimal coronary calcium and total coronary atherosclerosis burden1. Indeed, several studies have suggested a direct relationship between the quantity of calcium and the total amount of coronary atherosclerotic plaque2,3.
CAC is usually scored by the method of Agatston et al4. The Agatston score is calculated as a summed product of the within-slice area of calcium multiplied by a weighting factor derived from the maximal CT attenuation of individual calcified lesions. While elegant and simple, the Agatston score and other current CAC scoring algorithms5-7 do not account for the distribution of CAC within the coronary tree. Therefore, two patients with the same CAC score may have significantly different patterns of CAC involvement8. The implication of the heterogeneity in coronary atherosclerosis distribution within patients with similar CAC scores is not well known. Given the large body of evidence supporting worse prognosis with diffuse coronary artery disease9, we hypothesized that measures of diffuse CAC distribution might be associated with worse prognosis compared to identical CAC scores with a more concentrated pattern. To test this hypothesis, we sought to study the potential incremental prognostic value of adding simple measures of CAC distribution to the traditional Agatston score in a multi-ethnic population free of baseline CVD.
Methods
Study Design and Population
The Multi-Ethnic Study of Atherosclerosis (MESA) is a multi-center population-based prospective cohort study aimed at describing the prevalence, progression, and clinical significance of subclinical atherosclerosis. In brief, MESA includes 6,814 men and women aged 45 to 84 years from different ethnic origins (white, black, Hispanic, and Chinese) with no known baseline clinical cardiovascular at the time or enrollment. Full details of the MESA study design and methods have been previously published10. The study protocol was approved by each institutional review board, and all participants provided written informed consent.
Study Covariates
As part of the baseline examination, staff members at each of the 6 centers collected information about cardiovascular risk factors, including medical history, smoking history, blood pressure measurement, anthropometric measurements, and laboratory data, as previously described10. A central laboratory (University of Vermont, Burlington, Vermont) measured plasma glucose and high-sensitivity C-reactive protein, and levels of total and high-density lipoprotein cholesterol and triglycerides were measured after a 12-hour fast at the Collaborative Studies Clinical Laboratory at Fairview-University Medical Center (Minneapolis, MN).
Event Ascertainment (Follow-up)
Participants were followed for a median of 10.0 years (interquartile range 9.5 – 10.7) for the first occurrence of a coronary heart disease (CHD) or cardiovascular disease (CVD) event. At intervals of 9 to 12 months, an interviewer contacted each participant or family member by telephone to inquire about interim revascularization, hospital admission, or death. To verify self-reported diagnoses, MESA obtained medical records for approximately 98% of hospital events and 95% of outpatient diagnoses. Two physicians from the MESA mortality and morbidity review committee independently classified events.
A CHD event was defined as myocardial infarction, death from coronary heart disease, resuscitated cardiac arrest definite angina, or revascularization if there was adjudicated preceding or concurrent angina. A CVD event was defined as a CHD event or stroke (not transient ischemic attack), cardiovascular death, or other atherosclerotic death. Full details of the MESA follow-up methods are available at the MESA website (http://www.mesa-nhlbi-org).
CT Protocol
All MESA study participants underwent baseline measurement of CAC using non-contrast cardiac computed tomography. Participants were scanned twice, and the score was reported as the average of the two scans. CAC scores was reported as the Agatston score, which is a single summary score reflecting the summed product of the within-slice calcified plaque area and a density weighting factor representing the peak CT attenuation within the individual calcified plaque4. Regional distribution of CAC is not a factor in traditional Agatston CAC scoring. Subjects were told after the baseline visit (2000 to 2002) whether they had no, less than average, average, or greater than average CAC and were encouraged to discuss the results with their physicians.
Definition of CAC Parameters
Vessel-specific CAC measurements were performed in 6,540 MESA participants (96%). A total of 3,262 (50%) of individuals had baseline CAC>0 and form the population for this analysis. We tested two approaches to accounting for the regional distribution of CAC. The number of vessels with CAC, a measure of multi-vessel disease, was calculated as an ordinal variable (1-4) indicating CAC involvement of the left main, left anterior descending, left circumflex, and right coronary arteries11.
In participants with CAC in ≥2 vessels, we calculated a “diffusivity index” representing the degree of dispersion of CAC within the coronary tree. A higher diffusivity index represents a more diffuse pattern of CAC, while a smaller diffusivity index represents a great percentage of the total CAC in a single artery. The diffusivity index was calculated as a continuous variable by dividing the CAC score of the most affected vessel (the single vessel with the highest individual CAC score) by the total Agatston CAC score, and subtracting this quantity from 1 (equation: 1 – CAC in most affected vessel/total CAC). For example, for an individual with 3-vessel CAC and a total score of 300 with 200 in the left anterior descending, 50 in the left circumflex, and 50 in the right coronary artery, the diffusivity index would be (1- [200/300]) = 0.33. If the same individual with total CAC score of 300 had 100 in the left anterior descending, 100 in the left circumflex, and 100 in the right coronary artery the diffusivity index would be (1 – [100/300]) = 0.67.
A categorical variable representing CAC pattern was calculated using thresholds of the diffusivity index. Concentrated CAC pattern was considered to be present when the diffusivity index was <25th percentile for a given number of vessels with CAC. Diffuse CAC pattern was defined as a diffusivity index >75th percentile for a given number of vessels with CAC.
Statistical Methods
Baseline characteristics are presented according to the number of vessels with CAC. Frequencies and proportions were calculated for categorical variables, and either means with standard deviations or medians with interquartile ranges calculated for continuous variables. Differences between the groups were calculated using the Chi-square test, one-way analysis of variance, or non-parametric testing where appropriate.
Absolute CHD and CVD event rates were calculated by dividing the total number of events by the total number of person-years at risk (expressed per 1000 person-years). These rates were displayed both graphically and in tabular form across both increasing number of vessels with CAC and across concentrated vs. intermediate vs. diffuse CAC distribution pattern in those with ≥2 vessels with CAC.
Cox proportional hazards regression was used to model time-to-first CHD or CVD event. The proportionality assumption was confirmed graphically using both the log–log plot and by comparison of Kaplan–Meier and predicted survival plots. The overall analytical goal was to test whether measures of CAC distribution add to the traditional Agatston CAC score for event prediction. First, measures of CAC distribution were added to a model including age, gender, race, and the total Agatston CAC score. Baseline total Agatston CAC was modeled in 3 ways: 1) by CAC score group (1-100, 101-300, >300); 2) as a continuous variable; and 3) as a log transformed variable (ln [CAC + 1])12. Additional models were then conducted adding adjustment for cardiovascular risk factors including body mass index (BMI), cigarette smoking status, diabetes, systolic blood pressure, anti-hypertensive medication use, total cholesterol, HDL cholesterol, and lipid-lowering medication use.
The incremental predictive value of regional CAC measures beyond the traditional total Agatston CAC score was tested using area under the receiver operating curve (AUC) and net reclassification index (NRI) analyses. Incremental AUC analyses were calculated from logistic regression models, and were conducted for each of the described baseline total CAC definitions in unadjusted, age/gender/race-adjusted, and fully adjusted models. The NRI was calculated in fully adjusted models as the category-less continuous NRIc13. Continuous NRIc was selected because the thresholds, size, and interpretation of conventional risk categories vary by old and new risk assessment guidelines and therefore by the use of CHD or CVD as the primary outcome.
The incremental value of identifying which particular coronary artery is afflicted with CAC was also modeled. For this analysis, individual coronary artery involvement was modeled with binary variables (yes/no) and with exact CAC scores. Cox proportional hazards regression models were used entering terms for involvement in each coronary artery after controlling for the total CAC score and the percentage of the total CAC score in the individual coronary arteries.
All statistical analyses were conducted using STATA 13 (Stata Corp, College Station, TX). A two-tailed p-value of <0.05 was considered significant.
Results
The mean age of the study population was 66 ± 10 years with 58% men. Approximately 43% were White, 12% Chinese, 24% African-American, and 20% Hispanic. In general, with increasing number of vessels with CAC, there were a greater number of cardiovascular risk factors present and with greater risk factor severity (Table 1).
Table 1.
Baseline Characteristics and CAC Results
| Total Population N=3261 | Number of Vessels=1 N=1077 | Number of Vessels=2 N=824 | Number of Vessels=3 N=978 | Number of Vessels=4 N=382 | P-value | |
|---|---|---|---|---|---|---|
| Age | 66.3 ± 9.5 | 63.3 ± 9.9 | 66.4 ± 9.2 | 68.3 ± 9.0 | 69.9 ± 8.1 | <0.001 |
| Gender | <0.001 | |||||
| • Male | 1897, 58.2% | 552, 51.3% | 452, 54.9% | 619, 63.3% | 274, 71.7% | |
| • Female | 1364, 41.8% | 525, 48.8% | 372, 45.2% | 359, 36.7% | 108, 28.3% | |
| Race | 0.001 | |||||
| • White | 1413, 43.3% | 425, 39.5% | 343, 41.6% | 444, 45.4% | 201, 52.6% | |
| • Chinese | 397, 12.2% | 153, 14.2% | 106, 12.9% | 110, 11.25% | 28, 7.3% | |
| • Black | 783, 24.0% | 273, 34.9% | 206, 25.0% | 226, 23.1% | 78, 20.4% | |
| • Hispanic | 668, 20.5% | 226, 21.0% | 169, 20.5% | 198, 20.3% | 75, 19.6% | |
| Smoking Status | <0.001 | |||||
| • Never | 1457, 44.8% | 525, 48.8% | 386, 47.0% | 399, 40.9% | 147, 38.5% | |
| • Former | 1378, 42.3% | 406, 37.8% | 346, 42.1% | 439, 45.0% | 187, 49.0% | |
| • Current | 420, 12.9% | 144, 13.4% | 90, 11.0% | 138, 14.1% | 48, 12.6% | |
| BMI (kg/m2) | 28.3 ± 5.2 | 28.0 ± 5.4 | 28.3 ± 5.0 | 28.5 ± 5.2 | 28.8 ± 5.2 | 0.031 |
| Completed High School | 2642, 81.2% | 882, 82.1% | 643, 78.2% | 800, 82.0% | 317, 83.0% | 0.088 |
| Hypertension | 1773, 54.4% | 498, 46.2% | 435, 52.8% | 583, 59.6% | 257, 67.3% | <0.001 |
| Diabetes | 514, 15.8% | 113, 10.50% | 129, 15.7% | 189, 19.4% | 83, 21.9% | <0.001 |
| Systolic Blood Pressure | 134.3 ± 20 | 130.1 ± 20 | 133.7 ± 19 | 137.1 ± 20 | 140.1 ± 19 | <0.001 |
| Diastolic Blood Pressure | 74.90 ± 9.5 | 74.12 ± 9.9 | 74.55 ± 9.3 | 75.53 ± 9.5 | 76.19 ± 8.6 | <0.001 |
| Cholesterol (mg/dL) | 202.79 ± 36 | 202.27 ± 35 | 201.85 ± 36 | 203.26 ± 36 | 205.10 ± 34 | 0.5399 |
| HDL-C (mg/dL) | 49.4 ± 14 | 50.7 ± 15 | 49.2 ± 14 | 48.6 ± 14 | 48.3 ± 14 | 0.0011 |
| LDL-C (mg/dL) | 118.4 ± 32 | 119.2 ± 33 | 117.5 ±32 | 118.3 ± 32 | 118.6 ± 33 | 0.727 |
| Anti-hypertensive Medication | 1480, 45.4% | 402, 37.4% | 363, 44.05% | 491, 50.2% | 224, 58.6% | <0.001 |
| Lipid-lowering Medication | 706, 21.7% | 184, 17.1% | 172, 20.9% | 238, 24.3% | 112, 29.3% | <0.001 |
| Mean CAC Score | 291.4 ± 555 | 34.5 ± 54 | 117.3 ± 154 | 494.6 ± 637 | 870.9 ± 917 | <0.001 |
| Mean Log (CAC+1) | 4.39 ± 1.8 | 2.83 ± 1.2 | 4.15 ± 1.2 | 5.58 ± 1.2 | 6.30 ± 1.0 | <0.001 |
| Median CAC Score (IQR) | 86.5 (22 – 294) | 15.6 (5.5-40) | 67.5 (27 – 149) | 270.5 (121 – 591) | 530.4 (280 – 1158) | <0.001 |
| Diffusivity Index (%) | 23.0 ± 21 | 0 | 24.3 ± 15 | 38.2 ± 15 | 46.0 ± 13 | <0.001 |
| • Concentrated CAC pattern* | - | - | 5.50 ± 3 | 17.7 ± 7 | 27.6 ± 9 | |
| • Diffuse CAC pattern* | - | - | 44.0 ± 4 | 56.1 ± 4 | 61.2 ± 4 |
Concentrated CAC pattern was considered to be present when the diffusivity index was <25th percentile for a given number of vessels with CAC. Diffuse CAC pattern was defined as a diffusivity index >75th percentile for a given number of vessels with CAC.
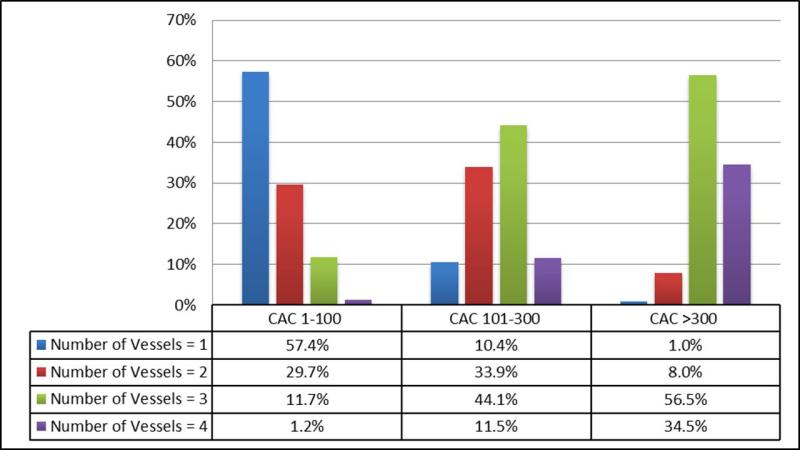
The mean CAC score of the population was 291 ± 555 Agatston Units, with a median and interquartile range of 86 (22 – 294). The mean number of vessels with CAC was 2.2 ± 1.0. The mean diffusivity index (% of CAC in the most affected vessel) was 24% ± 15 for 2-vessel CAC, 38% ± 15 for 3-vessel CAC, and 46% ± 13 for 4-vessel CAC. By definition, 25% of participants in each group (2-vessel, 3-vessel, and 4-vessel) were assigned to the diffuse CAC pattern. Complete CAC characteristics of the population are shown in Table 1 and Supplemental Tables 1 and 2. There was considerable heterogeneity between conventional CAC groups and number of vessels with CAC (Figure 1). Heterogeneity was predominantly noted in the intermediate CAC score 1-300 range. In contrast, the majority of individuals with CAC>300 had at least 3-vessel CAC (91%).
Figure 1. Heterogeneity Between CAC Score Groups and the Number of Vessels with CAC.
There is heterogeneity between CAC score group and the number of vessels with CAC, particularly when CAC is intermediate (1-300). Nearly all participants with CAC>300 have at least 3 vessel CAC.
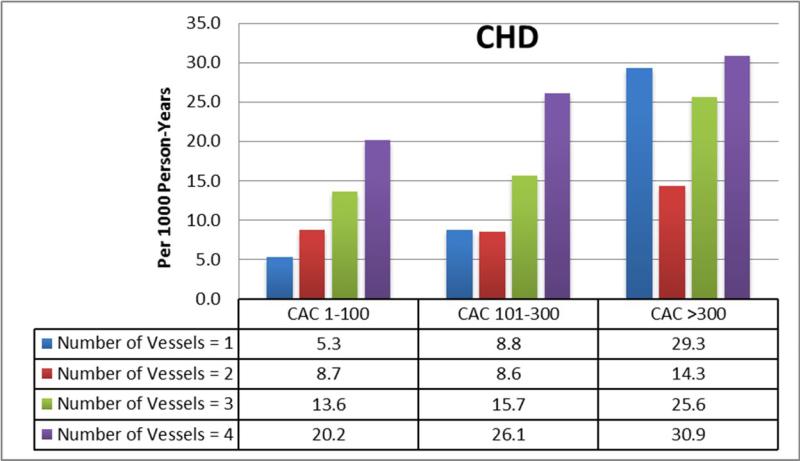
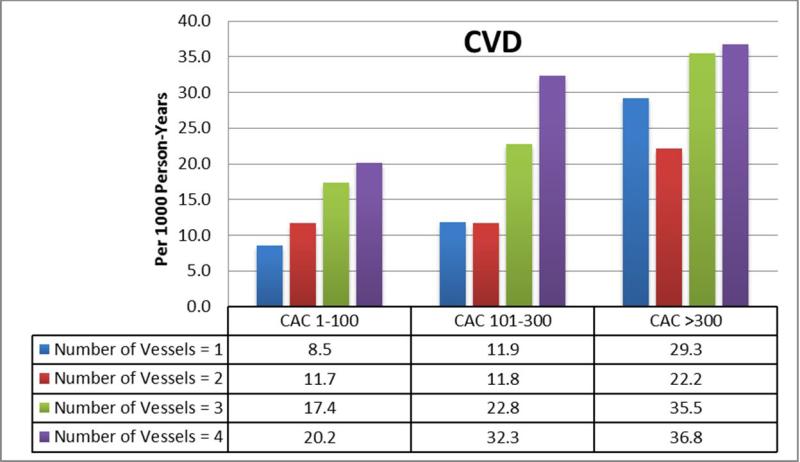
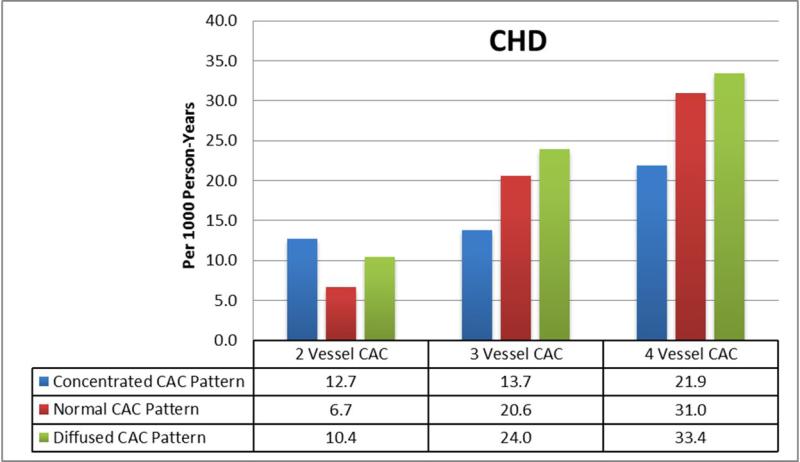
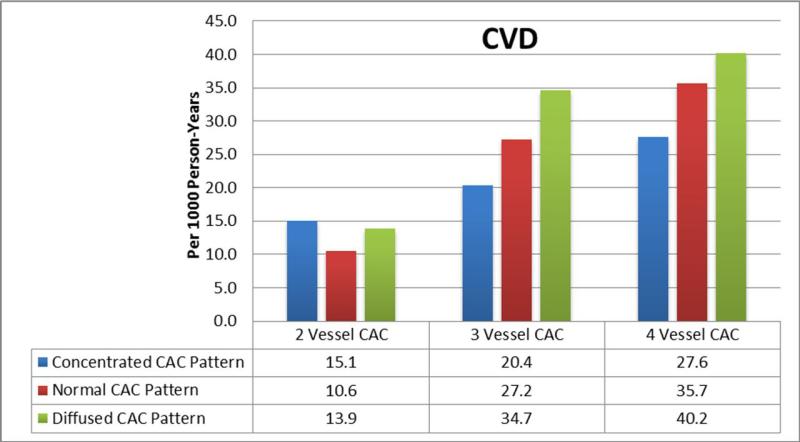
There were a total of 368 CHD and 493 CVD events during follow-up, of which 154 were myocardial infarctions, 19 were resuscitated cardiac arrests, 65 were CHD deaths, 130 were revascularizations with angina, 89 were strokes, and 36 with other cardiovascular/other atherosclerotic deaths. Figures 2A and B show the absolute CHD and CVD event rates across increasing number of vessels with CAC after stratifying by traditional total Agatston CAC score groups. Event rates increased with an increasing number of vessels with CAC. Within subpopulations defined by the number of vessels with CAC, event rates were lowest in those with a concentrated CAC pattern, and progressively higher with an intermediate and diffuse pattern (Figures 2C and D).
Figure 2. Relationship Between a More Diffuse CAC Pattern and CHD and CVD Events.
(A,B): Within each CAC score group, there is a graded increase in CHD and CVD event rates with increasing number of vessels with CAC. (C, D) Within each CAC score group, there is a graded increase in CHD and CVD event rates progressing from a concentrated to a diffuse pattern of CAC distribution.
Table 2 shows the results of the Cox proportional hazards models for both CHD and CVD adding number of vessels with CAC to the total traditional Agatston CAC score. In models adjusted for age, gender, and race, there was 2.5 – 3.5 fold increase in CHD risk and a 2 – 2.5 fold increase in CVD risk with 4-vessel CAC compared to 1-vessel CAC across models adjusting for CAC as a categorical variable, continuous variable, and as a log-transformed variable (all p<0.05). Improvement in risk stratification adding the number of vessels with CAC was only noted in the intermediate CAC score range (1-300) (Supplemental Table 3). With CAC scores >300, where there was little heterogeneity between CAC score group and regional CAC distribution (Figure 1), the number of vessels with CAC provided no added prognostic value. Interaction of number of vessels with CAC and CAC score group is shown in Supplemental Table 4.
Table 2.
Adjusted Hazard Ratios Adding Number of Vessels with CAC to the Traditional Agatston CAC Score
| Hazard Ratio* (95% CI) | ||||||
|---|---|---|---|---|---|---|
| CAC Score Groups** | CAC (Continuous) | Log (CAC + 1) | ||||
| CHD | CVD | CHD | CVD | CHD | CVD | |
| Number of Vessels=1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Number of Vessels=2 | 1.40 (0.97, 2.02) | 1.18 (0.90, 1.56) | 1.47 (1.03, 2.10) | 1.25 (0.93, 1.68) | 1.23 (0.85, 1.79) | 1.05 (0.77, 1.43) |
| Number of Vessels=3 | 2.32 (1.59, 3.40) | 1.95 (1.42, 2.68) | 2.73 (1.99, 3.74) | 2.29 (1.76, 2.97) | 2.03 (1.38, 3.01) | 1.72 (1.24, 2.38) |
| Number of Vessels=4 | 2.93 (1.90, 4.52) | 2.11 (1.46, 3.07) | 3.48 (2.40, 5.03) | 2.47 (1.80, 2.97) | 2.57 (1.63, 4.05) | 1.86 (1.26, 2.74) |
Adjusted for Age, Gender, and Race beyond inclusion of the Agatston CAC score definition in the model.
CAC score groups are CAC=0, CAC 1-100, CAC 101-300, CAC>300
There were a total of 368 CHD and 493 CVD events during follow-up.
In incremental AUC analysis (Table 3), addition of number of vessels with CAC to the total traditional Agatston CAC score resulted in a statistically significant improvement in risk discrimination for both CHD (improvement in C-statistic of 0.016 – 0.030) and CVD (improvement in C-statistic of 0.010 – 0.022) in unadjusted models. The results were attenuated, but generally remained statistically significant, after complete risk factor adjustment. The magnitude of improvement in the C-statistic was largest when CAC was intermediate (CHD: 0.036, CVD: 0.024-0.025), however the improvements in this smaller subset (N=2,458) no longer reached statistical significance after complete risk factor adjustment (supplemental table 5).
Table 3.
Incremental AUC and NRI Adding Number of Vessels with CAC to the Traditional Agatston CAC Score
| CAC Score Groups | CAC (Continuous) | Log (CAC + 1) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Unadjusted | Model 1* | Model 2** | Unadjusted | Model 1* | Model 2** | Unadjusted | Model 1* | Model 2** | |
| CHD | |||||||||
| Agatston CAC Score | 0.644 | 0.669 | 0.697 | 0.661 | 0.652 | 0.684 | 0.661 | 0.671 | 0.697 |
| With # of Vessels | 0.674 | 0.6855 | 0.707 | 0.678 | 0.685 | 0.706 | 0.677 | 0.685 | 0.706 |
| AUC Difference | 0.030 | 0.0165 | 0.010 | 0.017 | 0.033 | 0.022 | 0.016 | 0.014 | 0.009 |
| P-value | 0.0001 | 0.02 | 0.0495 | 0.02 | 0.002 | 0.008 | 0.009 | 0.020 | 0.049 |
| Continuous NRI | 0.194 | 0.194 | 0.197 | 0.454 | 0.415 | 0.376 | 0.180 | 0.190 | 0.170 |
| P-value | 0.0004 | 0.0004 | 0.0004 | <0.0001 | <0.0001 | < 0.0001 | 0.0012 | 0.0006 | 0.0021 |
| CVD | |||||||||
| Agatston CAC Score | 0.637 | 0.667 | 0.701 | 0.654 | 0.655 | 0.692 | 0.654 | 0.667 | 0.700 |
| With # of Vessels | 0.659 | 0.679 | 0.708 | 0.665 | 0.679 | 0.707 | 0.664 | 0.677 | 0.706 |
| AUC Difference | 0.022 | 0.012 | 0.007 | 0.011 | 0.024 | 0.015 | 0.010 | 0.010 | 0.006 |
| P-value | 0.0005 | 0.014 | 0.0675 | 0.04 | 0.003 | 0.0115 | 0.0195 | 0.020 | 0.038 |
| Continuous NRI | 0.135 | 0.135 | 0.143 | 0.384 | 0.359 | 0.298 | 0.101 | 0.1200 | 0.118 |
| P-value | 0.0057 | 0.0057 | 0.0036 | <0.0001 | <0.0001 | < 0.0001 | 0.0392 | 0.0145 | 0.0158 |
Model 1: Adjusted for Age, Gender, and Race beyond inclusion of the Agatston CAC score definition in the model.
Model 2: Adjusted for Age, Gender, Race, BMI, Systolic Blood Pressure, Hypertension Meds, Diabetes, Smoking Status, Cholesterol, HDL-C, Lipid Lowering Meds beyond inclusion of the Agatston CAC score definition in the model.
Table 3 also shows the results of the NRIc analysis adding number of vessels with CAC to the total CAC score. In age, gender, and race adjusted models, addition of number of vessels with CAC led to an NRIc of between 0.14 to 0.41 for CHD and of between 0.11 and 0.35 for CVD (p<0.05). The NRIc values were mildly attenuated in the fully adjusted model, but remained statistically significant. Supplemental Table 5 shows that NRIc values were higher when CAC was in the intermediate 1-300 range (log [CAC +1] model).
Table 4 shows the results of the Cox proportional hazards model adding the diffusivity index and the categorical measure of CAC pattern to the total traditional Agatston CAC score in participants with ≥2 vessels with CAC. In all models, the diffusivity index was positively associated with cardiovascular outcomes (HR 1.01 [CI 1.00 – 1.02] per 1% change), suggesting higher risk with an increasingly diffuse CAC pattern. In addition, there was a graded increase in the risk of both CVD and CHD with advancement from a concentrated to an intermediate to a diffuse CAC pattern. However, addition of the diffusivity index and the CAC pattern to the total traditional Agatston CAC score and the number of vessels with CAC did not lead to further improvement in the C-statistic (Supplemental tables 6 and 7).
Table 4.
Adjusted Hazard Ratios Adding CAC Pattern to the Traditional Agatston CAC Score in Participants with ≥ 2 Vessels with CAC
| Hazard Ratio* (95% CI) | ||||||
|---|---|---|---|---|---|---|
| CHD | CVD | |||||
| CAC Score Groups | CAC (Continuous) | Log (CAC+1) | CAC Score Groups | CAC (Continuous) | Log (CAC+1) | |
| Diffusivity Index, per 1% (Continuous) | 1.01 (1.00, 1.02) | 1.01 (1.00, 1.02) | 1.01 (1.00, 1.02) | 1.01 (1.00, 1.02) | 1.01 (1.00, 1.02) | 1.01 (1.00, 1.02) |
| Concentrated CAC Pattern (<25th Percentile Diffusivity Index) | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| Intermediate CAC Pattern (25th-75th Percentile Diffusivity Index) | 1.14 (0.85, 1.51) | 1.10 (0.85, 1.74) | 1.12 (0.84, 1.49) | 1.14 (0.89, 1.47) | 1.10 (0.85, 1.41) | 1.12 (0.87, 1.44) |
| Diffused CAC Pattern (>75th Percentile Diffusivity Index) | 1.39 (1.02, 1.911) | 1.33 (1.01, 1.75) | 1.37 (1.00, 1.88) | 1.41 (1.07, 1.85) | 1.33 (1.01,1.75) | 1.37 (1.04, 1.81) |
Adjusted for: Age, Gender, Race, BMI, Systolic Blood Pressure, Hypertension Meds, Diabetes, Smoking Status, Cholesterol, HDL-C, Lipid Lowering Meds beyond inclusion of the Agatston CAC score definition in the model.
There were a total of 368 CHD and 493 CVD events during follow-up.
Table 5 shows the results of the analysis testing the prognostic significance associated with which specific coronary artery is afflicted with CAC. In models adjusting for the total Agatston CAC score and the percent of the total CAC score in the coronary arteries, only presence of CAC in the right coronary artery remained a significant predictor of CHD and CVD (HR 2.10 [CI 1.51 – 2.90] for CHD and HR 1.62 [CI 1.24 – 2.14] for CVD). For the left main coronary artery, the point estimate signaled an increase in events, however this did not reach statistical significance. Modeling the exact CAC score in the individual coronary arteries did not change the overall conclusions. Addition of involvement of individual coronary arteries, or just the right coronary artery, to the Agatston score did not improve the AUC for CHD or CVD events (data not shown).
Table 5.
Hazard Ratios for Identity of Coronary Vessel Involvement Adjusted for Traditional Agatston CAC Score and Distribution
| Event Type | CAC Definition Adjusted for | Left Main | LAD | RCA | Circumflex |
|---|---|---|---|---|---|
| CHD | CAC Score Groups | 1.31 (0.98, 1.74) | 1.33 (0.78, 2.24) | 2.21 (1.59, 3.07) | 1.23 (0.87, 1.74) |
| Log (CAC+1) | 1.29 (0.97, 1.71) | 1.09 (0.63, 1.86) | 2.10 (1.51, 2.90) | 1.14 (0.81, 1.62) | |
| CVD | CAC Score Groups | 1.19 (0.92, 1.52) | 1.23 (0.79, 1.92) | 1.71 (1.30, 2.26) | 1.23 (0.91, 1.66) |
| Log (CAC+1) | 1.16 (0.91, 1.49) | 1.00 (0.63, 1.57) | 1.63 (1.24, 2.15) | 1.13 (0.84, 1.52) |
All models Contain CAC and terms for the % involvement of individual vessels, therefore terms should be interpreted as yes/no involvement of individual vessels with CAC.
*Adjusted for: Age Gender Race BMI Systolic Blood Pressure Hypertension Meds Diabetes Smoking Status Cholesterol HDL Lipid Lowering Meds beyond inclusion of the Agatston CAC score definition in the model.
There were a total of 368 CHD and 493 CVD events during follow-up.
Discussion
In our study of a well-defined multi-ethnic cohort free of baseline CVD, we have shown that measures of diffuse CAC distribution add predictive value to the Agatston CAC score, particularly when traditional CAC scores are in the intermediate range (1-300). This incremental predictive value is of similar magnitude to that commonly attributed to adding novel serum biomarkers to traditional risk factors in intermediate risk patients14.
The most important finding is that simple addition of the number of vessels with CAC to the traditional Agatston score improves both the AUC and the NRI for prediction of CHD and CVD events. This simple measure of multi-vessel CAC does not require re-measurement or a complicated calculation, and is available on all CAC scores that report CAC on a per-vessel basis11. Our results therefore point to a parsimonious method for improving CAC scoring, and have direct implications for clinical risk prediction and for future development of improved CAC scoring.
Traditional CAC Scoring
Arthur Agatston and Warren Janowitz developed CAC scoring in 19904. Their CAC score, reported as a single number, is elegant and has withstood over two decades of scientific scrutiny. However, this algorithm makes two implicit assumptions about the relationship of detectable calcium to incident CVD events8.
First, Agatston scoring assumes that an increased local density of calcium is associated with more coronary artery disease and greater CVD risk. This is inherent in the increased weight Agatston scoring places on denser, more highly attenuating plaque. However, it is now appreciated that less dense local calcium may signal greater risk, perhaps due to the inverse association between CAC density and a quantity of low attenuation lipid-rich core15.
Second, Agatston scoring implicitly assumes that identical CAC scores are equal with regard to their relationship to coronary artery disease and CVD events. For example, an Agatston CAC score of 100 situated entirely in the proximal LAD is implicitly considered equivalent to a CAC score of 100 spread across all four epicardial coronary arteries. The regional distribution of CAC, including both spatial distribution across arteries as well as along the length of individual arteries, is not accounted for.
It is important to note that these assumptions are in fact related8. For a given Agatston CAC score, presence of overall less dense calcium will translate into lower CAC scores for individual plaques, and therefore will by definition translate into more plaques and a diffusely distributed pattern of disease. These assumptions have distinct implications for the optimal way to express the CAC score.
Importance of Total Atherosclerosis Burden and Plaque Type
The close association between CAC and CVD events has traditionally been explained by the close relationship between CAC and total atherosclerosis burden16. Indeed, both pathology studies and imaging studies dating back several decades have suggested a direct relationship between the amount of CAC and the total volume of atherosclerosis2. Recent event-driven studies in several different patient populations have shown that it is the total atherosclerosis burden, rather than the presence of obstructive coronary artery disease or inducible ischemia, that is the most important predictor of CVD events17-20.
A recent study by Tota-Maharaj et al. suggests a mechanism for our primary finding21. In this cross-sectional analysis of 920 patients undergoing concomitant CAC scoring and coronary computed tomography angiography (CCTA), addition of number of vessels with CAC improved the relationship of the traditional Agatston CAC score to the segment involvement score (SIS), a validated CCTA measure of total coronary atherosclerosis. The greatest improvement in the association with total atherosclerosis occurred when traditional Agatston CAC scores were in the intermediate range (1-400). The results of the Tota-Maharaj et al. study reinforce older data showing that the number of vessels with CAC is strongly associated with the number of vessels with obstructive coronary disease on invasive angiography22.
In addition to improving the association with total atherosclerosis burden, addition of measures of regional CAC distribution may also indicate presence of higher risk plaque types. For a given Agatston CAC score, more diffuse CAC will correlate with lower attenuation plaque (on average), including a greater frequency of mixed plaque (higher risk) compared to fully calcified plaque. Studying similar participants from MESA, Criqui et al. found that a CAC “density score” was inversely related to CVD events, and adding the density score to the traditional Agatston CAC score improved global risk prediction23.
Prior Outcome Studies of CAC Distribution
In a retrospective clinical cohort of ~25,000 patients without known CHD referred for CAC scoring, Budoff et al found that the number of vessels with CAC was strongly related to all-cause mortality24. In another retrospective study of nearly 15,000 patients referred for clinical CAC scoring, Williams et al. found that the number of CAC lesions (another surrogate for diffuse CAC) was associated with greater all-cause mortality after adjusting for traditional risk factors25. Both the Budoff and Williams papers were limited by their retrospective design, potential for referral bias, and study of only all-cause mortality. In a prior study from MESA, Brown et al. derived a novel measure of CAC distribution called the “calcium coverage score”26. This score quantifies the percent length of the coronary arteries that is afflicted with CAC. This score differs from considering number of vessels with CAC by prioritizing CAC distribution along the length of individual arteries rather than spatially across the major epicardial arteries. At 41 month median follow-up, the calcium coverage score was strongly associated with hard CHD events. However, after this limited follow-up period, the p-value for the calcium coverage score vs. the Agatston score was 0.074 (AUC 0.68 vs. 0.66). No specific analysis was undertaken in participants with intermediate CAC scores. Likely due to its complexity, the calcium coverage score has not been widely adopted.
In a small proof of principle case-control study, Qian et al. calculated a “lesion-specific” CAC score including data on the number of vessels with CAC, the number of lesions with CAC, spatial distribution of lesions, and lesion-specific morphology27. In 60 patients with CAC, the lesion-specific CAC score outperformed traditional CAC scoring for prediction of cardiac events.
Future of CAC Scoring
First, our results must be validated in other cohort studies that have made CAC measurements on a per-vessel basis. This should include registry studies of clinical CAC scanning, as most clinical cardiac CT centers have routinely reported CAC on a per-vessel basis28.
These findings have implications for the future of clinical CAC scoring. The traditional Agatston CAC score has persisted for decades, but emerging evidence has suggested novel ways of improving the score28. An advantage of simple consideration of number of vessels with CAC is that it also easy to quantify on non-gated chest CTs ordered for non-cardiac indications, which is a rapidly expanding application of CAC scoring29.
Limitations
Our study has a few notable limitations. While we considered the number of coronary vessels with CAC (a measure of diffuse CAC across coronary arteries), data was not available to test indices of proximal vs. distal CAC (a measure of diffuse CAC within an individual coronary artery), the total number of CAC lesions, or a per segment CAC involvement score. These measures may be superior to the diffusivity index. While proximal coronary artery disease is considered to be a higher risk presentation on invasive coronary angiography, it is unknown if proximal CAC or an increased number of distinct CAC lesions confers a worse prognosis.
Conclusion
In conclusion, we have shown that readily available measures of diffuse CAC distribution add to the traditional Agatston CAC score for the prediction of CHD and CVD events. While we await development of a new comprehensive CAC scoring algorithm, clinicians may consider reporting and interpreting the number of vessels with CAC in addition to a total CAC burden score on routine ungated and gated non-contrast chest and cardiac CT scans, particularly when CAC burden is intermediate.
Supplementary Material
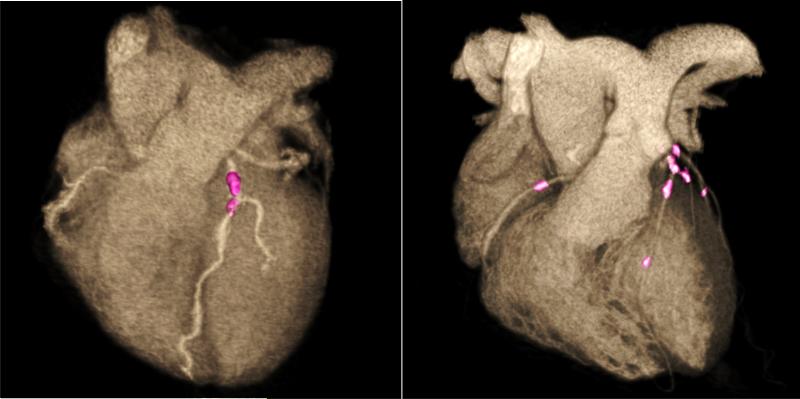
Figure 3. Illustration of More Diffuse Distribution of Coronary Artery Calcium.
Both cases have an Agatston CAC score of 200. The first case involves only 1 vessel, and the diffusivity index cannot be calculated as this metric requires multi-vessel CAC. The second case has 3-vessel involvement, with CAC=100 in the left anterior descending, CAC=50 in the left circumflex, and CAC=50 in the right coronary artery. The diffusivity index is (1- [100/200]) = 0.50 or 50%, consistent with a diffuse multi-vessel CAC pattern. Adapted in part from Alluri et al(8).
Perspectives.
Competency in Medical Knowledge: The traditional Agatston CAC score does not account for the regional distribution of calcified plaque in the coronary tree. In this study, we have shown that after adjustment for the total Agatston score, a more diffuse distribution of calcified plaque is associated with a worse cardiovascular prognosis compared to a more localized, concentrated CAC phenotype.
Translational Outlook: In the future, there will likely be improvements in the way we calculate the CAC score in clinical practice. Future research is needed to define how best to incorporate total CAC volume, CAC density, as well as the regional distribution of CAC into a single improved CAC score that best predicts cardiovascular events beyond standard risk scoring algorithms.
Acknowledgements
Example: This research was supported by contracts N01-HC-95159, N01-HC-95160, N01-HC-95161, N01-HC-95162, N01-HC-95163, N01-HC-95164, N01-HC-95165, N01-HC-95166, N01-HC-95167, N01-HC-95168 and N01-HC-95169 from the National Heart, Lung, and Blood Institute and by grants UL1-TR-000040 and UL1-TR-001079 from NCRR.
The authors thank the other investigators, the staff, and the participants of the MESA study for their valuable contributions. A full list of participating MESA investigators and institutions can be found at http://www.mesa-nhlbi.org.
Abbreviations
- CAC
coronary artery calcium
- CHD
coronary heart disease
- CVD
cardiovascular disease
- AUC
Area Under the Curve
- NRI
net reclassification improvement
Footnotes
Disclosures: The authors have no disclosures.
References
- 1.Nasir K, Clouse M. Role of nonenhanced multidetector CT coronary artery calcium testing in asymptomatic and symptomatic individuals. Radiology. 2012;264:637–49. doi: 10.1148/radiol.12110810. [DOI] [PubMed] [Google Scholar]
- 2.Rumberger JA, Simons DB, Fitzpatrick LA, Sheedy PF, Schwartz RS. Coronary artery calcium area by electron-beam computed tomography and coronary atherosclerotic plaque area. A histopathologic correlative study. Circulation. 1995;92:2157–62. doi: 10.1161/01.cir.92.8.2157. [DOI] [PubMed] [Google Scholar]
- 3.Sangiorgi G, Rumberger JA, Severson A, et al. Arterial calcification and not lumen stenosis is highly correlated with atherosclerotic plaque burden in humans: a histologic study of 723 coronary artery segments using nondecalcifying methodology. J Am Coll Cardiol. 1998;31:126–33. doi: 10.1016/s0735-1097(97)00443-9. [DOI] [PubMed] [Google Scholar]
- 4.Agatston AS, Janowitz WR, Hildner FJ, et al. Quantification of coronary artery calcium using ultrafast computed tomography. J Am Coll Cardiol. Mar. 1990;15:827–32. doi: 10.1016/0735-1097(90)90282-t. [DOI] [PubMed] [Google Scholar]
- 5.Callister TQ, Cooil B, Raya SP, Lippolis NJ, Russo DJ, Raggi P. Coronary artery disease: improved reproducibility of calcium scoring with an electron-beam CT volumetric method. Radiology. 1998;208:807–14. doi: 10.1148/radiology.208.3.9722864. [DOI] [PubMed] [Google Scholar]
- 6.Detrano R, Tang W, Kang X, et al. Accurate coronary calcium phosphate mass measurements from electron beam computed tomograms. Am J Card Imaging. 1995;9:167–73. [PubMed] [Google Scholar]
- 7.Rumberger JA, Kaufman L. A rosetta stone for coronary calcium risk stratification: agatston, volume, and mass scores in 11,490 individuals. AJR Am J Roentgenol. 2003;181:743–8. doi: 10.2214/ajr.181.3.1810743. [DOI] [PubMed] [Google Scholar]
- 8.Alluri K, Joshi PH, Henry TS, et al. Scoring of coronary artery calcium scans: History, assumptions, current limitations, and future directions. Atherosclerosis. 2015;239:109–117. doi: 10.1016/j.atherosclerosis.2014.12.040. [DOI] [PubMed] [Google Scholar]
- 9.Sianos G, Morel MA, Kappetein AP, et al. The SYNTAX Score: an angiographic tool grading the complexity of coronary artery disease. EuroIntervention. 2005;1:219–27. [PubMed] [Google Scholar]
- 10.Bild DE, Bluemke DA, Burke GL, et al. Multi-ethnic study of atherosclerosis: objectives and design. Am J Epidemiol. 2002;156:871–81. doi: 10.1093/aje/kwf113. [DOI] [PubMed] [Google Scholar]
- 11.Silverman MG, Harkness JR, Blankstein R, et al. Baseline subclinical atherosclerosis burden and distribution are associated with frequency and mode of future coronary revascularization: multi-ethnic study of atherosclerosis. JACC Cardiovasc Imaging. 2014;7:476–86. doi: 10.1016/j.jcmg.2014.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Detrano R, Guerci AD, Carr JJ, et al. Coronary calcium as a predictor of coronary events in four racial or ethnic groups. N Engl J Med. 2008;358:1336–45. doi: 10.1056/NEJMoa072100. [DOI] [PubMed] [Google Scholar]
- 13.Pencina MJ, D'Agostino RB, Sr, Steyerberg EW. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat Med. 2011;30:11–21. doi: 10.1002/sim.4085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Melander O, Newton-Cheh C, Almgren P, et al. Novel and conventional biomarkers for prediction of incident cardiovascular events in the community. JAMA. 2009;302:49–57. doi: 10.1001/jama.2009.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Motoyama S, Sarai M, Harigaya H, et al. Computed tomographic angiography characteristics of atherosclerotic plaques subsequently resulting in acute coronary syndrome. J Am Coll Cardiol. 2009;54:49–57. doi: 10.1016/j.jacc.2009.02.068. [DOI] [PubMed] [Google Scholar]
- 16.Erbel R, Budoff M. Improvement of cardiovascular risk prediction using coronary imaging: subclinical atherosclerosis: the memory of lifetime risk factor exposure. Eur Heart J. 2012;33:1201–13. doi: 10.1093/eurheartj/ehs076. [DOI] [PubMed] [Google Scholar]
- 17.Stone GW, Maehara A, Lansky AJ, et al. A prospective natural-history study of coronary atherosclerosis. N Engl J Med. 2011;364:226–35. doi: 10.1056/NEJMoa1002358. [DOI] [PubMed] [Google Scholar]
- 18.Arbab-Zadeh A, Nakano M, Virmani R, Fuster V. Acute coronary events. Circulation. 2012;125:1147–56. doi: 10.1161/CIRCULATIONAHA.111.047431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mancini GB, Hartigan PM, Shaw LJ, et al. Predicting outcome in the COURAGE trial (Clinical Outcomes Utilizing Revascularization and Aggressive Drug Evaluation): coronary anatomy versus ischemia. JACC Cardiovasc Interv. 2014;7:195–201. doi: 10.1016/j.jcin.2013.10.017. [DOI] [PubMed] [Google Scholar]
- 20.Bittencourt MS, Hulten E, Ghoshhajra B, et al. Prognostic value of nonobstructive and obstructive coronary artery disease detected by coronary computed tomography angiography to identify cardiovascular events. Circ Cardiovasc Imaging. 2014;7:282–91. doi: 10.1161/CIRCIMAGING.113.001047. [DOI] [PubMed] [Google Scholar]
- 21.Tota-Maharaj R, Al-Mallah MH, Nasir K, et al. Improving the Relationship between Coronary Artery Calcium Score and Coronary Plaque Burden: Addition of Regional Measures of Coronary Artery Calcium Distribution. Atherosclerosis. 2015;238:126–31. doi: 10.1016/j.atherosclerosis.2014.11.008. [DOI] [PubMed] [Google Scholar]
- 22.Budoff MJ, Georgiou D, Brody A, et al. Ultrafast computed tomography as a diagnostic modality in the detection of coronary artery disease: a multicenter study. Circulation. 1996;93:898–904. doi: 10.1161/01.cir.93.5.898. [DOI] [PubMed] [Google Scholar]
- 23.Criqui MH, Denenberg JO, Ix JH, et al. Calcium density of coronary artery plaque and risk of incident cardiovascular events. JAMA. 2014;311:271–8. doi: 10.1001/jama.2013.282535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Budoff MJ, Shaw LJ, Liu ST, et al. Long-term prognosis associated with coronary calcification: observations from a registry of 25,253 patients. J Am Coll Cardiol. 2007;49:1860–70. doi: 10.1016/j.jacc.2006.10.079. [DOI] [PubMed] [Google Scholar]
- 25.Williams M, Shaw LJ, Raggi P, et al. Prognostic value of number and site of calcified coronary lesions compared with the total score. JACC Cardiovasc Imaging. 2008;1:61–9. doi: 10.1016/j.jcmg.2007.09.001. [DOI] [PubMed] [Google Scholar]
- 26.Brown ER, Kronmal RA, Bluemke DA, et al. Coronary calcium coverage score: determination, correlates, and predictive accuracy in the Multi-Ethnic Study of Atherosclerosis. Radiology. 2008;247:669–75. doi: 10.1148/radiol.2473071469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Qian Z, Marvasty I, Rinehart S, Voros S. A lesion-specific coronary artery calcium quantification framework for the prediction of cardiac events. IEEE Trans Inf Technol Biomed. 2011;15:673–80. doi: 10.1109/TITB.2011.2162074. [DOI] [PubMed] [Google Scholar]
- 28.Tota-Maharaj R, Joshi PH, Budoff MJ, et al. Usefulness of Regional Distribution of Coronary Artery Calcium to Improve the Prediction of All-Cause Mortality. Am J Cardiol. 2015;115:1229–34. doi: 10.1016/j.amjcard.2015.01.555. [DOI] [PubMed] [Google Scholar]
- 29.Shemesh J, Henschke CI, Shaham D, et al. Ordinal scoring of coronary artery calcifications on low-dose CT scans of the chest is predictive of death from cardiovascular disease. Radiology. 2010;257:541–8. doi: 10.1148/radiol.10100383. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.