Assessment of a Simplified Spin and Gradient Echo (sSAGE) Approach for Human Brain Tumor Perfusion Imaging

Abstract

The goal of this study was to validate a simplified spin- and gradient-echo (sSAGE) approach to obtain T₁-corrected dynamic susceptibility contrast magnetic resonance imaging (DSC-MRI) data in a clinical brain tumor population. A five-echo SAGE sequence was used to acquire DSC-MRI data (n = 8 patients, 3 primary glioma, and 5 brain metastases). The ΔR₂^* and ΔR₂ time series obtained from a nonlinear fit of all echoes (SAGE) were compared to ΔR₂^* and ΔR₂ time series obtained analytically (sSAGE) using three echoes (two GE and one SE). Through the use of multiple echoes, both methods removed T₁ leakage effects from the ΔR₂^* and ΔR₂ time series, and the sSAGE ΔR₂^* and ΔR₂ time series were highly correlated with those from SAGE, with average correlations of 0.9. The resulting hemodynamic parameters included GE and SE cerebral blood volume (CBV), cerebral blood flow (CBF), mean vessel diameter (mVD), volume transfer constant (K^trans), and volume fraction of the extravascular extracellular space (v_e). For each metric, there was good correlation (>0.86) between sSAGE and SAGE, with no significant differences. The sSAGE method provides T₁-corrected GE and SE DSC-MRI parameters in an efficient and clinically feasible manner.

1. Introduction

Dynamic susceptibility-contrast magnetic resonance imaging (DSC-MRI) has the potential to report on vascular changes associated with tumor growth, as well as assess response to treatment. To maximize the contrast-to-noise ratio (CNR), clinical perfusion imaging often utilizes gradient echo (GE) sequences, which are sensitive to vessels of all sizes [1]. Spin echo (SE) sequences may provide complementary information due to their increased sensitivity to the microvasculature [2–5], at the cost of reduced CNR and signal-to-noise ratio (SNR) at longer echo times (TEs). Sequences that interrogate both GE and SE contrast simultaneously have been proposed, typically using a single GE and single SE sequence [6]. These combined sequences can provide a broad assessment of vascular parameters, including cerebral blood volume (CBV), cerebral blood flow (CBF), mean transit time (MTT), and mean vessel diameter (mVD) [1, 4, 6–9]. Unfortunately, these parameters cannot be reliably quantified with contrast agent (CA) extravasation [10–13], as is often the case in pathologies that involve a compromised blood-brain barrier (BBB), including brain tumors and stroke.

Under CA leakage, the most apparent sources of error are confounding T₁ leakage effects, although T₂ and T₂^* leakage effects are also known to adversely impact the perfusion parameters [13]. T₁ leakage effects typically manifest as higher post-bolus signal intensity and thus lower post-bolus ΔR₂^* (where R₂^* = 1/T₂^*). CBV, calculated from the integration of ΔR₂^*, is thus underestimated by T₁ leakage effects. Various methods have been utilized to minimize these T₁ leakage effects, including preload CA doses, pulse sequence optimizations, and post-processing correction methods [10–14]. A commonly used protocol involves a combination of a preload dose and post-processing correction using the Weisskoff method, which was previously shown to provide robust CBV estimates as validated by an intravascular iron oxide CA [11]. Alternatively, using a dual GE sequence [15], the signals from each echo can be combined to analytically remove the T₁ leakage effects, producing more robust perfusion parameters [13]. Although these methods have focused on GE perfusion parameters, SE and mVD metrics are similarly susceptible to T₁ leakage effects.

A combined spin- and gradient-echo (SAGE) method was proposed by Schmeideskamp et al. [4, 16] to provide T₁-insensitive perfusion measures using five echoes (two GE, two asymmetric SE, and a SE). We recently proposed a simplified SAGE (sSAGE) method that combines dual GE and a single SE (three total echoes) to similarly provide T₁-insensitive perfusion measures [17]. The original SAGE approach involves nonlinear fitting of the five echoes to a piecewise function to obtain T₁-insensitive R₂^* and R₂, which can be time-consuming. Alternatively, with the three-echo sSAGE method, T₁-insensitive ΔR₂^* and ΔR₂ time series can be computed analytically, thus precluding the need for nonlinear piecewise fitting. Instead, this method leverages the dual-gradient echo signal to correct the spin echo signal for T₁ leakage effects. This method was previously demonstrated in rat brain tumors on a preclinical system and compared with the full SAGE method [17]. For a rat brain with 1800 voxels and 200 repetitions, we found that the sSAGE method was over 450 times faster than the SAGE fitting. As the typical DSC acquisition in human brain has more than 25000 voxels, SAGE fitting could be prohibitive for routine clinical use. The sSAGE approach may be more practical in the clinical setting.

In the preclinical assessment of the simplified SAGE method, the sSAGE and SAGE methods showed similar DSC time series. Most importantly, no significant differences were found between the sSAGE- and SAGE-derived CBV measures, while single-echo CBV was significantly underestimated due to T₁ leakage effects. Based on the similar sSAGE and SAGE results observed in the preclinical assessment, the purpose of this study was to determine if sSAGE and SAGE provide similar results in a clinical study. Specifically, we aim to compare the sSAGE and SAGE sequences in human primary and metastatic brain tumors. As this approach only requires the acquisition and storage of three echoes and does not rely upon computationally demanding non-linear fitting algorithms, it could facilitate the more rapid clinical translation and adoption of SAGE-based DSC-MRI.

2. Methods

2.1 MRI Methods

MRI was performed at 3T (Achieva, Philips Healthcare, Best, Netherlands) using a 32-channel head coil (for high-grade glioma patients) or an 8-channel head coil (for brain metastases patients). The sSAGE- and SAGE-EPI sequences were used to obtain three and five echoes, respectively. Scan parameters were 1.8s repetition time (TR), field-of-view = 240 × 240 mm², voxel size = 3.16 × 3.16 × 5 mm³ (reconstructed to 2.5 × 2.5 × 5 mm³), number of echoes = 3 (sSAGE) or 5 (SAGE). Partial Fourier encoding and SENSE (acceleration factors 0.73 and 2.0, respectively) were used to obtain acceptable echo times. For the sSAGE acquisition, the 180° pulse follows immediately after the 2^nd gradient echo, as the first TE/2 period determines the where the SE (echo 3) occurs. In the original SAGE acquisition, the SE (echo 5) is determined by the second TE/2 period, due to the acquisition of two asymmetric SE. The TEs were TE₁ – TE₃ = 8.6 / 26 / 85 ms for sSAGE and TE₁ – TE₅ = 8.8 / 26 / 55 / 72 / 90 ms for SAGE.

Prior to contrast administration, a pre-contrast T₁ map was acquired using a multi-flip angle approach (TR = 7.6 ms, TE = 4.6 ms, flip angle = 2°–20° in 2° increments). For the dynamic studies, 250 dynamics were acquired over 7.5 minutes. After 60 s of baseline images, 0.1 mmol/kg gadolinium-diethylenetriaminepentacetate (Gd-DTPA) was injected intravenously (infusion rate 4 ml/s, followed by 20 ml saline flush). Dynamic perfusion data were acquired with the full SAGE sequence in both primary brain tumor patients (n = 3, 42–55 years old, 2 males) and in metastatic brain tumor patients (n = 5, 47–72 years old, 2 males) (Table 1). All patient studies were performed in accordance with Vanderbilt University’s Institutional Review Board (IRB) protocols.

Table 1.

Patient demographics and Pearson’s correlation coefficient (R) with SAGE

Patients: Primary Glioma	Age	Sex	Pathology	Pearson’s correlation (R) with SAGE (tumor ROI)
				sSAGE ΔR2*	sSAGE ΔR2	sSAGE T1-w
1	51	Male	Grade IV glioblastoma	0.97	0.95	0.98
2	55	Male	Grade III oligodendroglioma	0.92	0.88	0.94
3	42	Female	Grade IV glioblastoma	0.96	0.94	0.88
Patients: Metastatic Tumors	Age	Sex	Primary tumor site	Pearson’s correlation (R) with SAGE (tumor ROI)
				sSAGE ΔR2*	sSAGE ΔR2	sSAGE T1-w
1	62	Female	Lung - non-small cell	0.97	0.95	0.95
2	57	Male	Lung - non-small cell	0.81	0.87	0.80
3	72	Female	Melanoma	0.94	0.86	0.92
4	52	Female	Unknown	0.98	0.93	0.93
5	47	Male	Melanoma	0.78	0.78	0.75
Mean:				0.92	0.90	0.89

2.2 Post-processing

To avoid differences that may occur between multiple injections, all perfusion data were acquired with the full SAGE sequence. The 2^nd (GE) and 5^th echo (SE) signals were used to determine the single-echo-based ΔR₂^* and ΔR₂ time series. The first two echoes (GE) were used to compute the T₁-insensitive sSAGE ΔR₂^* time series and the T₁-weighted signal (extrapolated to TE=0, S_TE=0), using Equations 1–2:

$$\mathrm{\Delta }{R}_2^{*}(t)=\frac{1}{T{E}_2-T{E}_1}\left(\text{ln}\right(\frac{S_{T{E}_2,\mathit{\text{pre}}}}{S_{T{E}_2}(t)})-\text{ln}(\frac{S_{T{E}_1,\mathit{\text{pre}}}}{S_{T{E}_1}(t)}\left)\right)$$ (1)

$$S_{TE=0}=S_{T{E}_1}·{\left(\frac{S_{T{E}_1}}{S_{TE2}}\right)}^{\raisebox{1ex}{$T{E}_1$}\!\left/ \!\raisebox{-1ex}{$(T{E}_2-T{E}_1)$}\right.},$$ (2)

where S_TE1,pre and S_TE2,pre are the pre-bolus signals for TE₁ and TE₂, respectively, S_TE1(t) and S_TE2(t) are the dynamic signals from TE₁ and TE₂, respectively, and all other parameters are as defined above. As previously derived [17], the T₁-weighted signal was combined with the SE (Echo 5) to compute the T₁-insensitive sSAGE ΔR₂ time series from Equation 3:

$$\mathrm{\Delta }{R}_2(t)=\frac{1}{T{E}_{SE}}\left(\text{ln}\right(\frac{S_{T{E}_{SE},\mathit{\text{pre}}}}{S_{T{E}_{SE}}(t)})-\text{ln}(\frac{S_{TE=0,\mathit{\text{pre}}}}{S_{TE=0}(t)}\left)\right).$$ (3)

The SAGE-derived ΔR₂^* and ΔR₂ time-courses were obtained from all five echoes using nonlinear least squares fits to a piecewise function [16]. Briefly, the baseline signals were averaged to obtain the pre-bolus signal, and the voxel-wise R₂, R₂^*, signal intensity S^I₀, and γ were determined from Equation 4.

$$S(\tau )=\{\begin{array}{cc}\hfill S_0^I·e^{-\tau ·R_2^{*}}\hfill & \hfill 0<\tau <TE/2\hfill \\ \hfill \frac{S_0^I}{\delta }·e^{-TE·(R_2^{*}-R_2)}·e^{-\tau ·(2·R_2-R_2^{*})}\hfill & \hfill TE/2<\tau \le TE\hfill \end{array},$$ (4)

where γ is the slice profile mismatch between the excitation and refocusing pulses and was quantified using the mean pre-bolus signal [16]. Due to temporal inconsistencies previously observed with the full four-parameter fit, the slice profile mismatch γ was held constant for the dynamic time course [4, 17], yielding a reduced three-parameter fit. The dynamic perfusion data were fit with three parameters R₂, R₂^* and S^I₀ at each time point. S^I₀(t) was the SAGE T₁-weighted signal, while the SAGE fits for R₂^*(t) and R₂(t) were used to determine the T₁-insensitive ΔR₂^* and ΔR₂ time series.

The arterial input function (AIF) was selected from the T₁-insensitive sSAGE ΔR₂^* time courses using an automated method [18] specifically adapted for use with multi-echo acquisitions [19]. The AIF was converted to CA concentration using a quadratic relationship [20]. The ΔR₂^* and ΔR₂ time-courses in tissue were converted to CA concentration using the effective transverse relaxivities (i.e., r₂^* and r₂) of Gd-DTPA; at 3T, r₂^* and r₂ were assumed to be 87 mM⁻¹s⁻¹ [20] and 20.4 mM⁻¹s⁻¹ [21]. GE and SE CBV were determined from the ratio of the scaled integrals of the tissue CA concentration curve and the arterial input function (AIF) curve. To avoid artifactually low CBV values that are often observed in single-echo brain tumor data, negative CA concentrations were not included in the integration. CBF was taken as the maximum of the tissue impulse response function determined from the circular singular value decomposition of the AIF and tissue CA concentrations (23). Mean vessel diameter (mVD) maps were calculated from the ratio of the integrals of the single-echo, sSAGE and SAGE GE ΔR₂^* and SE ΔR₂ time series during bolus passage [1, 6, 7]. Each perfusion metric (rCBV, rCBF, and rmVD) is shown relative to the normal appearing white-matter ROI.

The pre-contrast T₁ map was combined with the T₁-weighted sSAGE and SAGE signals to produce ΔR₁ time series for each voxel [22, 23]. Using r₁ of 3.7 mM⁻¹s⁻¹ [24], the sSAGE and SAGE ΔR₁ were converted to CA concentration (C_t). As the AIF selection criteria for DSC and DCE often vary, a separate DCE-based AIF was obtained directly from the sSAGE C_t time series using previously published criteria [25]. DCE analysis was limited to tumor voxels exhibiting enhancement on the post-CA T₁-weighted image. Standard Tofts pharmacokinetic modeling of the sSAGE and SAGE C_t time series (250 dynamics) and the DCE-based AIF was performed to obtain maps of K^trans (CA transfer rate constant) and v_e (extracellular extravascular volume) [26, 27]. Voxels exhibiting non-physiological v_e values (>1) were excluded from analysis.

2.3 Statistical Analysis

To assess the similarity between the sSAGE and SAGE time series, Pearson’s correlation coefficient (R) was used. For comparisons of ΔR₂^* and ΔR₂, the correlations were calculated using 40 points from 10s before injection to 60s after injection. For T₁-weighted signal comparisons, correlations were calculated using 220 points from 10 s before injection to the end of the acquisition (6.5 min after injection).

Regions of interest (ROIs) for tumor and normal appearing white matter were drawn on the T₁-weighted post-CA images. Group means were compared using a paired t-test with a 5% significance level. Concordance correlation coefficient (CCC) and Pearson’s correlation coefficient (R) were used to assess agreement (accuracy and precision, respectively) between sSAGE and SAGE perfusion metrics across subjects.

3. Results

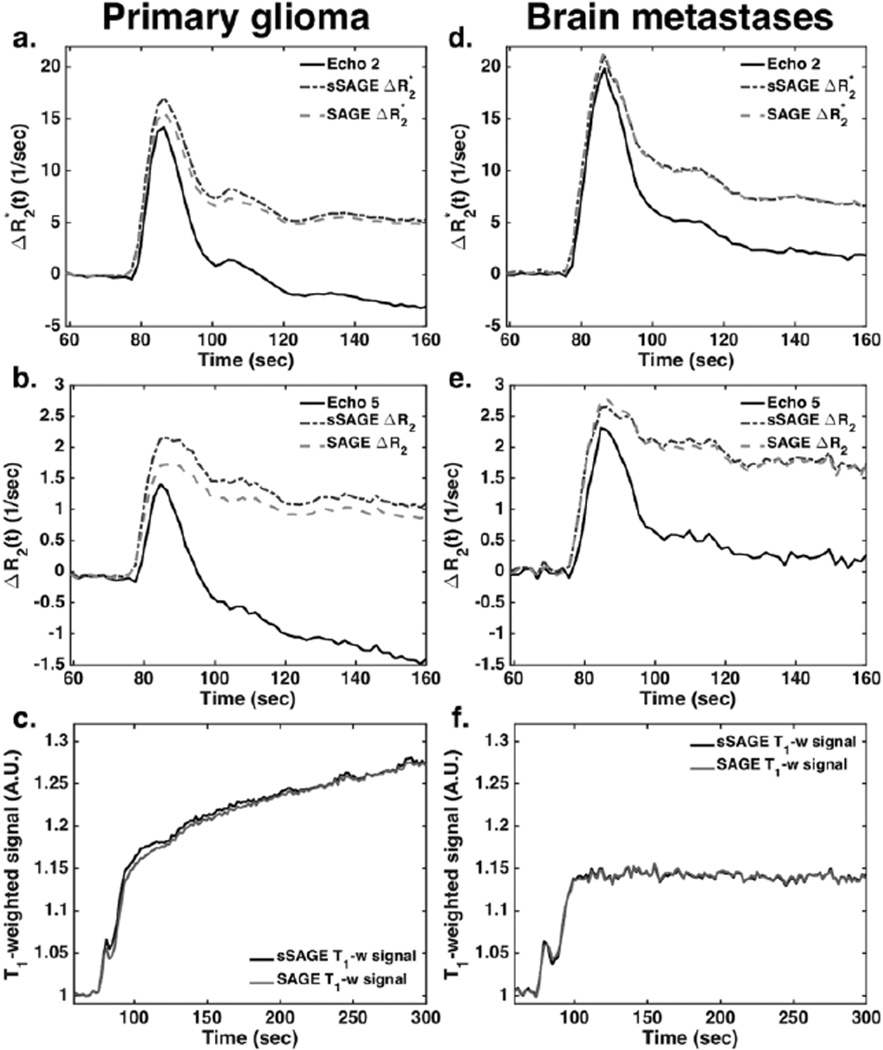
Figure 1 demonstrates representative dynamic DSC data in tumor ROIs from a primary glioma patient (left, a–c) and brain metastasis patient (right, d–f). In both cases, the single-echo ΔR₂^* and ΔR₂ (from echoes 2 and 5, respectively) are substantially reduced post-bolus (in some cases going below baseline) compared to sSAGE and SAGE due to T₁ leakage effects in the tumor tissue. The sSAGE and SAGE ΔR₂^* and ΔR₂ are inherently corrected for T₁ leakage effects and thus do not exhibit reduced post-bolus ΔR₂^* and ΔR₂. In addition, the sSAGE and SAGE time series for ΔR₂^*, ΔR₂, and T₁-weighted signal are in good agreement, with respect to shape and magnitude.

Figure 1.

Dynamic ΔR₂^* (a,b) and ΔR₂ (c,d) time series for a tumor ROI in a primary glioma patient (a–c) and brain metastases patient (d–f) following bolus injection of 0.1 mmol/kg Gd-DTPA. The sSAGE and SAGE-based T₁-weighted signals in a tumor ROI are also shown for each patient (c,f). In each case, the sSAGE and SAGE measures are similar, while the single-echo time-series are much lower, particularly at time points following the first pass of the contrast agent.

To quantify the similarity of the dynamic time series to the SAGE fits, Pearson’s correlation coefficient R was calculated between sSAGE and SAGE for each patient. These correlations are shown in Table 1, along with patient demographic information. Overall, sSAGE ΔR₂^* and ΔR₂ was consistently highly correlated with SAGE ΔR₂^* and ΔR₂. The average correlation was 0.92 (range 0.78–0.98) for ΔR₂^* and 0.90 (range 0.78–0.95) for ΔR₂. The sSAGE and SAGE T₁-weighted signals were also well correlated, with an average correlation of 0.89 (range 0.75–0.98).

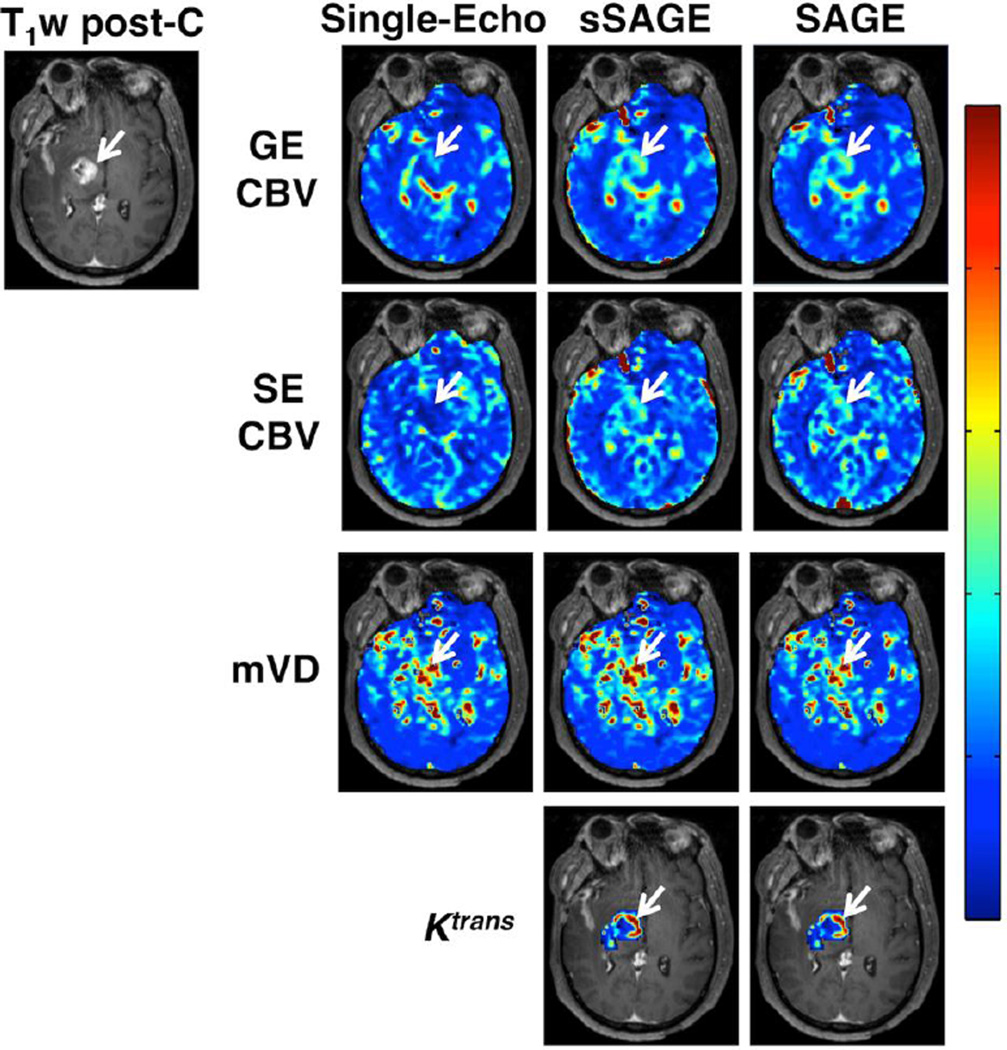
The GE and SE CBV maps are shown in Figure 2 for single-echo (echoes 2 and 5), sSAGE and SAGE. Both single-echo CBV maps (GE and SE) are substantially underestimated in the tumor region (indicated by the white arrow), with mean rCBVs of 1.3 and 0.6, respectively. The sSAGE- and SAGE-derived maps exhibited similar higher CBV (rCBV = 2.05 and 1.99 for GE sSAGE and SAGE, respectively, and 1.78 and 1.80 for SE sSAGE and SAGE, respectively). Combining the GE and SE information, the mVD maps shown in Figure 2 are also similar between single echo, sSAGE, and SAGE (mVD = 1.8, 1.33 and 1.24, respectively). Finally, the K^trans maps obtained using the extracted ΔR₁ time series from sSAGE and SAGE are nearly identical (K^trans = 0.42 and 0.39, respectively).

Figure 2.

DSC-MRI maps of GE CBV, SE CBV, mVD, and K^trans in a primary glioma patient (T₁-weighted post-contrast image shows tumor edge, indicated by arrow). The single-echo GE and SE CBV is lower than the sSAGE- and SAGE-based CBV, which showed similar results. There was little difference in mVD between single-echo, sSAGE, and SAGE in this patient. The sSAGE and SAGE derived K^trans maps showed good agreement.

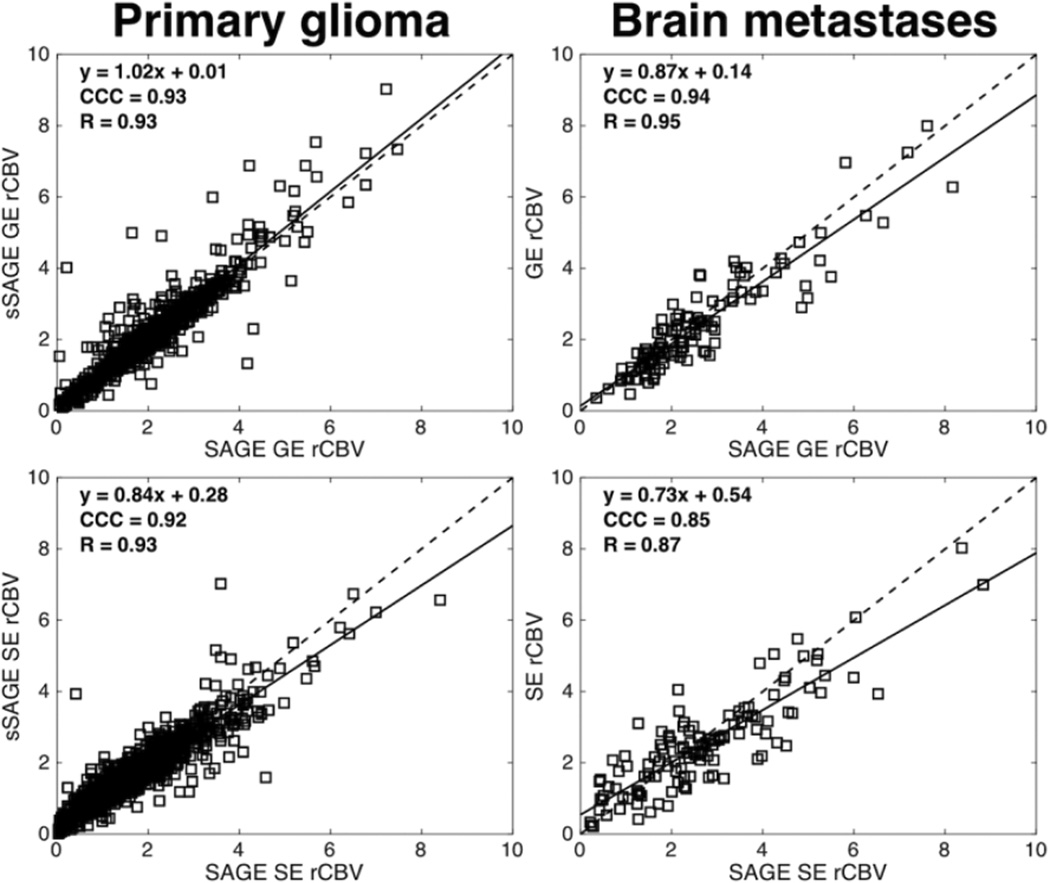
Figure 3 demonstrates example voxel-wise correlation between SAGE and sSAGE rCBV in whole tumor ROIs in a primary glioma patient (left) and brain metastases patient (right). Both the GE and SE sSAGE rCBV fall along to the line of unity, indicating agreement with GE and SE SAGE rCBV.

Figure 3.

Voxel-wise correlation plots between sSAGE and SAGE for GE rCBV (top) and SE rCBV (bottom) in a primary glioma patient (left) and brain metastases patient (right). Within a single patient, sSAGE and SAGE estimates of GE and SE CBV showed good agreement.

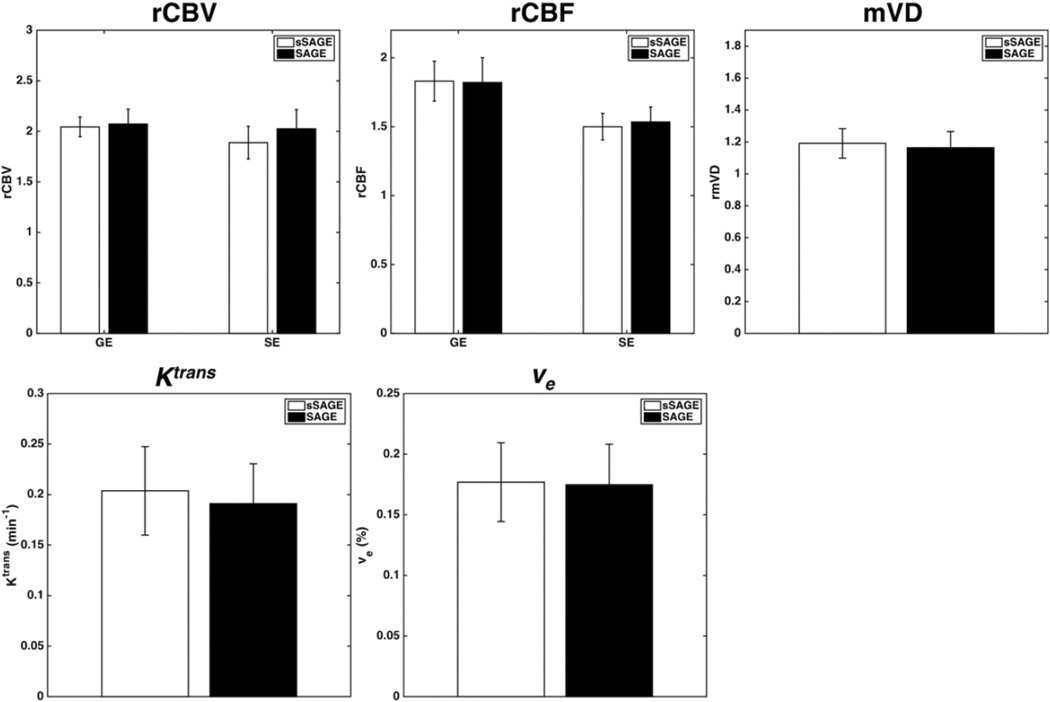
The bar plots in Figure 4 show mean pooled CBV, CBF, and mVD in tumor relative to normal tissue using sSAGE and SAGE ΔR₂^* and ΔR₂ (n = 8; 3 glioma and 5 brain metastases). There were no significant differences observed between sSAGE and SAGE for GE and SE CBV (p = 0.686 and 0.128, respectively), GE and SE CBF (p = 0.897 and 0.52, respectively), mVD (p = 0.566), K^trans (p = 0.116), and v_e (p = 0.779).

Figure 4.

Top: Bar plots showing mean GE and SE CBV, GE and SE CBF, and mVD relative to normal tissue for the sSAGE and SAGE methods. Bottom: Bar plots showing mean K^trans and v_e for the sSAGE, and SAGE methods. There were no significant differences between sSAGE and SAGE (p>0.05, n = 8).

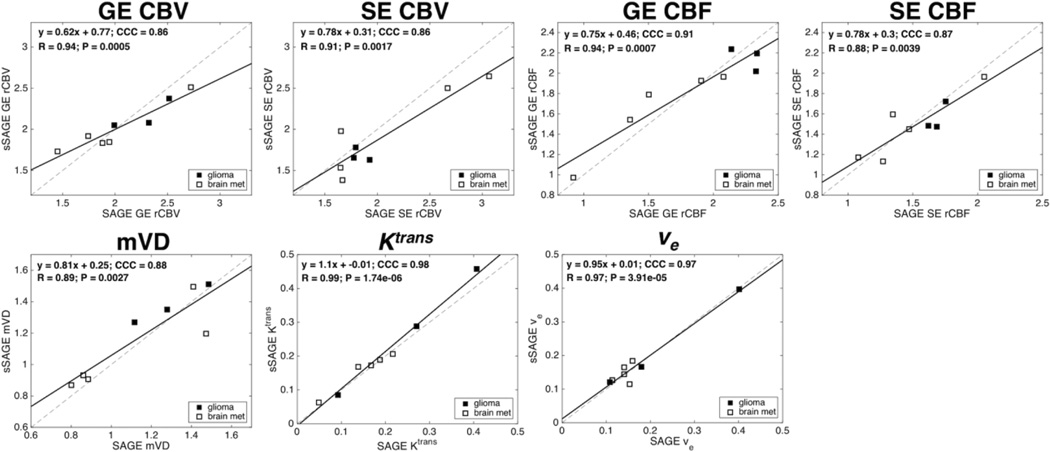
The correlation plots between sSAGE and SAGE are shown in Figure 5. Both patient groups are shown in each plot, with filled markers for glioma patients (n = 3) and open markers for brain metastases patients (n = 5). For every metric tested, the linear correlation was highly significant (p < 0.01), with high CCC and R. The CCC was greater than 0.86 for each metric, while R was greater than 0.88 for all metrics.

Figure 5.

Scatter plots showing mean GE and SE rCBV, GE and SE rCBF, mVD, K^trans and v_e from sSAGE and SAGE across all patients (n = 8; brain met patients are indicated by open markers). The linear regressions (slope and intercept, CCC, R and p-value) are shown for each plot, with significant correlations for each parameter.

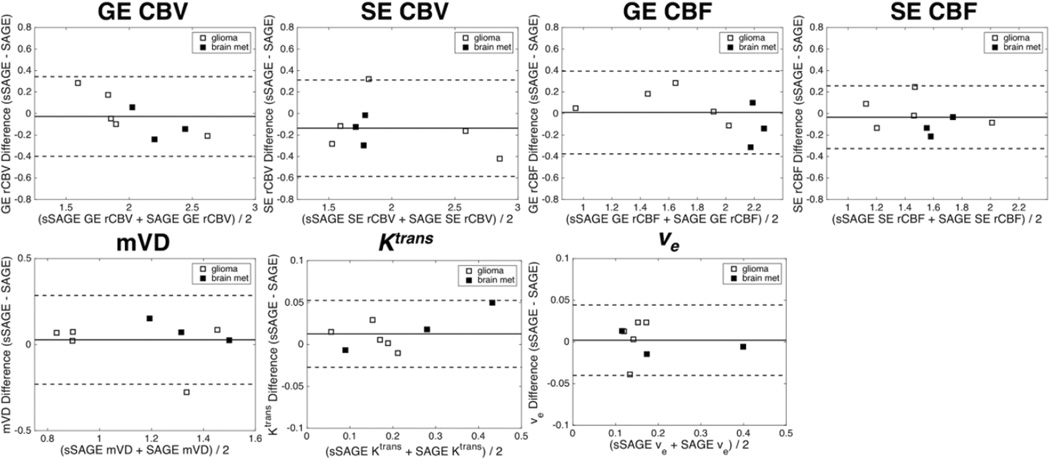
Figure 6 shows the Bland-Altman mean-difference plots for each metric between sSAGE and SAGE. Almost no bias was observed for GE CBV, GE and SE CBF, mVD, and v_e. A slight negative bias was observed for SE CBV, and a slight positive bias was observed for K^trans. There were no obvious effects of tumor type (glioma versus brain metastases) on the relative bias in each metric.

Figure 6.

Bland-Altman plots comparing sSAGE and SAGE GE and SE rCBV, GE and SE rCBF, mVD, K^trans and v_e in glioma (closed markers) and brain metastases (open markers) patients. There was minimal bias for each parameter (as determined by the average difference between the sSAGE and SAGE estimates).

4. Discussion

In this study, the three-echo sSAGE analytic approach was compared to a five-echo SAGE fitting approach in patients with primary glioma and brain metastases. A pooled analysis found no significant differences in any metric between sSAGE and SAGE. Each sSAGE and SAGE metric was well correlated, with high CCC and Pearson’s R values. In addition, the similarity between sSAGE- and SAGE-based metrics held for both tumor types. Our results indicate that sSAGE can be used to reliably obtain T₁-corrected SE and GE perfusion measures.

Leakage correction methods often focus on minimizing T₁ effects, as they typically dominate single-echo data. In addition to T₁ effects, contrast agent leakage can also manifest as T₂^* (or T₂) effects. T₂^* and T₂ effects result from altered susceptibility differences between the intravascular space, extravascular extracellular space, and intracellular space. Although correcting for both effects is important to obtain reliable CBV, this is complicated in single-echo data that simultaneously exhibits competing T₁ and T₂^* or T₂ leakage effects [13, 28]. The advantage of the dual-echo approach is that it completely removes T₁ leakage effects analytically, rather than simply minimizing them. The sSAGE approach further extends this analytic approach to remove T₁ leakage effects from SE data. Once these effects are separated, the data can be corrected for T₂ and T₂^* leakage effect using an appropriate pharmacokinetic or biophysical model [10, 11, 29, 30].

The original SAGE approach removes T₁ leakage effects from ΔR₂^* and ΔR₂ data by quantifying the absolute T₂^* and T₂ values [4]. One limitation of the sSAGE approach is that absolute T₂^* and T₂ values are not obtained; however, as DSC-MRI relies on ΔR₂^* and ΔR₂ to obtain perfusion metrics, absolute values are not needed. Furthermore, for clinical implementation, computationally efficient methods to remove T₁ leakage effects are needed. As the SAGE approach relies on nonlinear piece-wise fitting of the five echoes, the computation time grows quickly with repetitions and brain voxels. For example, on a computer with a 2.8 GHz quad-core processor and 16 GB of RAM, the computation time for deriving the ΔR₂^* and ΔR₂ SAGE time series for a single human brain slice (approximately 3000 voxels with 170 repetitions) was 3.5 hours. For sSAGE, total calculation times of approximately 1 second were obtained for an entire human brain volume (15 slices) and all repetitions.

There are several limitations of this study. In accordance with our protocol, only one injection was permitted per patient, precluding our ability to perform DSC with both the sSAGE and SAGE sequences. However, the benefit of this approach is that prevents differences that may occur with multiple injections. Multiple injections would also alter the extent of the T₁ leakage effects, where the first injection would act as a preload dose. A second limitation is that there were a limited number of patients in each cohort, though significant differences were still observed. For the purpose of this study, a relatively small patient population is sufficient. The final limitation is that we did not correct for T₂^* leakage effects, which will ultimately be necessary to obtain more accurate measures of rCBV. However, this is outside the scope of the present study and will be the subject of future investigations.

In conclusion, this study validates an analytic approach to obtain T₁-insensitive hemodynamic parameters, including GE and SE CBV and CBF, mVD, K^trans, and v_e, in a human patient population. The data can be acquired using a three-echo simplified SAGE sequence with comparable results to the five-echo SAGE sequence. The analysis of sSAGE data is substantially faster than nonlinear fitting of the five-echo SAGE data, making it a more clinically feasible method to obtain T₁-corrected data. SAGE-based approaches, including both the full and simplified versions, provide a wealth of information about tumor vascularity, vessel size, and permeability, within a single scan acquisition.