Temporal-spatial Mean-Shift Clustering Analysis to improve Functional MRI Activation Detection

Abstract

Cluster analysis (CA) is often used in functional magnetic resonance imaging (fMRI) analysis to improve detection of functional activations. Commonly used clustering techniques typically only consider spatial information of a statistical parametric image (SPI) in their calculations. This study examines incorporating the temporal characteristics of acquired fMRI data with mean-shift clustering (MSC) for fMRI analysis to enhance activation detections. Simulated data and real fMRI data was used to compare the commonly used cluster analysis with MSC using a feature space containing temporal characteristics. Receiver Operating Characteristic curves show that improvements in low contrast to noise scenarios using MSC over CA and our previous MSC technique at all tested simulated activation sizes. The proposed MSC technique with a feature space using both temporal and spatial data characteristics shows improved activation detection for both simulated and real Blood oxygen level dependent (BOLD) fMRI data (approximately 60% increase). The proposed techniques are useful in techniques that inherently have low contrast to noise ratios, such as non-proton imaging or high resolution BOLD fMRI.

1. Introduction

Different data analysis methods have been developed in functional magnetic resonance imaging (fMRI) to improve detection sensitivity and specificity. Techniques such as k-means and fuzzy clustering have been explored for improving activation isolation [1–6]. Cluster analysis (CA) based on random field theory is commonly used for the same end [7–9]. While these techniques are typically powerful for isolating activations in higher contrast to noise ratio (CNR) situations, low CNR performance may present issues when identifying areas of brain activity. This is especially true when studying fMRI techniques using non-BOLD contrasts mechanisms, magnetic source MRI and perfusion images for example [10–12], which often suffer from low CNR signals which can make reliable signal detection a challenge and can benefit from analysis methods that increase low CNR performance. Non-proton imaging methods, phosphorous or sodium imaging for example [13–17], also inherently tend to have low CNRs and can also similarly benefit from methods that address this issue. The proposed technique may even have benefits with BOLD fMRI in high resolution situations, or by allow fewer repetitions in BOLD fMRI imaging which can reduce confounding factors such as motion effects. Mean-shift clustering (MSC) [18–20] is a different clustering technique to consider for improving activation detection in fMRI analysis.

The MSC technique was introduced by Fukunaga et al. (1975) [18] for examining pattern recognition, and it has since been used in image segmentation on brain images [21] and some possible use in fMRI analysis [22]. The MSC technique was adapted for fMRI analysis for the first time by Ai et al. (2014) [22] using a feature space containing only spatial features (MSC-SS) which showed some promise in improving CNR when compared to a commonly used technique. The MSC technique is based on density estimation that is done on a predetermined feature space by calculating a mean shift vector based on different density estimations within a defined kernel, then shifting the kernel as dictated by the mean shift vector. This process is repeated as appropriate until convergence, at which time a cluster in the feature space can be identified. This process offers some advantages with regards to implementation. No probability distribution needs to be estimated or assumed as is done in many other methods. Since MSC is based on density estimation of a feature space, it does not make any assumption on the shape of the clusters either. Also, there is no limitation to what image characteristics can be chosen as features to use in the feature space in principle, allowing incorporation of image features that may normally not be used in other analysis techniques.

By selectively choosing the features used for the feature space, it would be possible to incorporate characteristics of the data that normally would not be part of the analysis when compared to some commonly used techniques. A simple and straightforward application of the MSC technique has been incorporated with fMRI analysis in our previous study using a feature space of z scores and mean neighboring z-scores [22]. The results showed improvements in detection power in low CNR scenarios over commonly used techniques. Using different feature spaces could potentially see further improvements in detection power. There could also be potential improvements in flexibility since there are in theory many different features that could be used for the feature space. Since the previous study only used spatial features, incorporating temporal features could potentially expand upon the possibilities of the MSC technique.

This study examines if improvements in fMRI activation detection can be achieved by using MSC in fMRI analysis with a feature space containing both spatial and temporal characteristics from data. The feature space used for this study is neighboring mean estimated z-scores and the power spectrum at the base frequency of the experimental design (MSC-ST). Depending on the technique used, SPIs could be generated using temporal information from the data. However, once generated, the SPI itself typically does not directly contain temporal information of the data. Most clustering techniques would operate on the generated SPI without using temporal information from the raw data directly, but it is possible to combine temporal information from the raw data and SPI usage with MSC, provided a proper feature space is used. This type of feature space was tested on both simulated and real fMRI data and evaluated against MSC-SS and CA to examine if further improvements to detection sensitivity and specificity can be made.

2. Methods

The proposed MSC technique was evaluated using both simulated and real fMRI data. MSC was applied to an SPI produced by Cross-Correlation Analysis (CCA). Comparisons were made with CCA+CA, MSC-SS, and MSC-ST

2.1. Simulated data

The simulated data was designed to emulate fMRI data using one hundred images, 128x128 matrix size, and with activations of various sizes (20x20, 10x10, 5x5 voxels) inserted. A block design (two and a half off/on cycles, 20 images per off or on cycle) and an event-related design (stimulation every 4 images) were used for comparison purposes. Gaussian white noise was generated at various CNRs (0.20, 0.40, 0.60, 0.80) and inserted into the simulated data for examination on how the proposed technique behaves at different CNRs. The procedure was repeated 2500 times at each CNR and the results averaged for evaluation purposes.

2.2. fMRI data

Ten subjects (5 females, 5 males, age 22–32) gave informed written consent with the approval of the University of Iowa’s (USA) Institutional Review Board. All subjects reported that they were right-handed, not using medications at the time of scanning, healthy, and had no history of any mental or psychiatric conditions. All ten subjects were scanned at the University of Iowa's Medical Education and Research Facility.

Blood Oxygen Level Dependent (BOLD) fMRI data was acquired on a Siemens 3T Trio scanner (Siemens Medical Solutions, Erlangen, Germany) using gradient echo EPI pulse sequence with the following parameters: TR = 2000ms, flip angle = 90 degrees, TE = 30ms, matrix = 64 x 64, FOV = 220mm, slice thickness = 5mm with 20% gap, voxel resolution = 3.44x3.44x5mm, 180 images. A T1 anatomical scan was also performed with the following parameters: TR = 1590ms, flip angle = 10 degrees, TE = 3.39ms, matrix = 128 x 128, FOV = 220mm, slice thickness = 2mm, voxel resolution = 1.72x1.72x2mm.

Unilateral electrical stimulation was delivered to the subject’s right median nerve using a Grass S48 stimulator (Grass Technologies, West Warwick, Rhode Island, USA). The stimulation voltage used was 15 volts above the motor threshold, which was individually defined as the minimum voltage required to obtain a thumb twitch. The stimulations were square wave pulses with 0.2ms duration delivered in a block design of four and a half off/on cycles (40 seconds off, 40 seconds on) with a randomized inter-stimulation interval (ISI) between 1.0–2.0 seconds was used. The randomized ISI was used to reduce any effect that expecting a stimulation occurring with a fixed stimulation interval might have on the resulting BOLD signal. The volunteers were asked to passively feel the stimulation, stay still, stay awake, and not actively perform anything for the duration of the scan.

2.3. MSC technique

The MSC technique is based on density estimation on a predetermined feature space of image characteristics, where a mean shift vector is calculated to identify local maximums in the aforementioned feature space to identify clusters. The density is calculated in a kernel of user defined size at point x inside of the feature space, which can be described as:

$$\widehat{f}(x)=\frac{c_k}{n{h}^d}\sum _{i=1}^{n}k\left({\Vert \frac{x-x_i}{h}\Vert }^2\right)$$ (1)

Where n is the number of data points, c_k is a constant, k is the kernel, h is kernel size, and d is the number of dimensions in the feature space. The local maximum density is identified at ∇f̂ (x) = 0 by moving the kernel based on the gradient ascent in the feature space. Equation 1 can be rewritten as (assuming g(x) = −k′(x)):

$$\nabla \widehat{f}=\frac{2c_k}{n{h}^{d+2}}\left[\sum _{i=1}^{n}g\left({\Vert \frac{x-x_i}{h}\Vert }^2\right)\right]\left[\frac{{\displaystyle \sum _{i=1}^n}{x}_{i}g\left({\Vert \frac{x-x_i}{h}\Vert }^2\right)}{{\displaystyle \sum _{i=1}^n}g\left({\Vert \frac{x-x_i}{h}\Vert }^2\right)}-x\right]$$ (2)

The second term of the equation 2:

$$m(x)=\frac{{\displaystyle \sum _{i=1}^n}{x}_{i}g\left({\Vert \frac{x-x_i}{h}\Vert }^2\right)}{{\displaystyle \sum _{i=1}^n}g\left({\Vert \frac{x-x_i}{h}\Vert }^2\right)}-x$$ (3)

is the mean shift vector where g is the kernel, h is the kernel size, x is the mean estimate inside the kernel, and x_i is the element inside the kernel. The mean shift vector, m(x), defines how the kernel will move along the density gradient towards the local maximum which corresponds with dense regions in the feature space. This calculation is performed at each data point, shifted by m(x) along the density gradient, and repeated until convergence is reached when local maximum is found where points associated with the same local maximum belong to the same cluster.

Since MSC is based on density estimates of a predetermined feature space containing image features, the feature space used for this study contains the mean estimated z-score of the eight neighboring voxels in the SPI using CCA (see section 2.4) and the power spectrum at the base frequency of the experimental design (from raw data). The mean z-score surrounding a voxel was used to take into consideration neighboring effects while the power spectrum at base frequency takes into consideration a temporal characteristic of the data. The values of the feature space were also normalized between 0–10 to standardize the sizes of the feature space.

2.4. Data Analysis

The general approach to the proposed MSC analysis method is applying MSC to a feature space constructed using selected characteristics of the data and an SPI generated using CCA. CCA was chosen to generate the SPI because the specific technique used to generate the SPI is less important for the purposes of this study, and the CCA technique allows easy control over the significance level while it is more difficult to do so with other techniques.

The BOLD fMRI data was pre-processed using Analysis of Functional NeuroImages (AFNI) (afni.nimh.nih.gov) [23]. Constant, linear, and quadratic trends were removed, three-dimensional motion correction was performed to minimize motion effects, all images were normalized to MNI coordinates (www.bic.mni.mcgill.ca), and a Gaussian filter with full width half maximum (FWHM) of 4mm was also applied. Custom Matlab (MathWorks Inc, Natick, MA, USA) software was used to perform CCA and the clustering portions of analysis (cluster size thresholding and MSC). CCA was performed using a reference function calculated from the stimulation paradigm convoluted with a hemodynamic response function modeled using a gamma variate function. Cluster size thresholds of 4 voxels were applied for both CCA and MSC-ST for evaluation purposes. SPIs were generated for individual subjects.

2.5. Evaluations

Evaluations between techniques were made via ROC curves while varying CNRs (0.20, 0.40, 0.60, 0.80), and varying simulated activation sizes (5x5, 10x10, 20x20). Kernel sizes between 0.01 and 5.00 were used for evaluations. Another comparison was also made via ROC curves when comparing the previous MSC-SS technique. Evaluations were focused upon false positive rates (FPRs) of 0.01 and/or 0.05 as these are two significance levels commonly used in fMRI analysis.

3. Results

Evaluations between CCA+CA and MSC-ST were made using ROC curves with the event-related simulated data at different CNRs (0.20, 0.40, 0.60, and 0.80). Improvements over CCA+CA can be seen (Figure 1, Table 1A/1B) at CNRs of 0.20 and 0.40. The improvements are present across almost all kernel sizes and activation sizes with the only exception being the 5x5 case with 0.50 kernel size. At CNR 0.60, improvements are seen in all 10x10 and 20x20 cases. CNR 0.80 shows that MSC-ST generally shows similar performance with CCA+CA in the 10x10 and 20x20 cases. Combining CA and MSC (MSC-ST+CA) manifests further improvements particularly in the CNR 0.2 cases and some in the 0.4 cases (Figure 2) when compared to plain MSC-ST (and by extension CCA+CA). MSC-ST+CA essentially shows the same trends seen with MSC-ST compared to CCA+CA. These improvements with MSC-ST+CA are visualized in a representative map generated with CNR 0.40, 20x20 activation sizes, 0.30 kernel size, and a z threshold of 1 (Figure 3). Many false positives are detected with CCA and CCA+CA, and many false negatives are also present with CCA and CCA+CA. In comparison, MSC-ST+CA has the least false positives and the least false negatives. Because of the generally superior performance of MSC-ST+CA, further evaluations will be focused on MSC-ST+CA (not plain MSC-ST) for the remainder of this study.

Figure 1.

Receiver operating characteristic curves of event-related simulation using MSC-ST (Kernel size = 0.30 cases shown) being evaluated against CCA and CCA+CA. CNRs of 0.20, 0.40, 0.60, and 0.80 were used. A: 5x5 simulated activation size. B: 10x10 simulated activation size. C: 20x20 simulated activation size.

Table 1A.

Comparing TPRs of CCA+CA, MSC-ST, and MSC-ST+CA at significance level of 0.01. Kernel sizes of 0.10, 0.20, 0.30, 0.40, and 0.50 used. CNRs of 0.20, 0.40, 0.60 and 0.80 used. Activation sizes of 5x5, 10x10 and 20x20 simulated.

5x5
Kernel size		0.1		0.2		0.3		0.4		0.5
CNR	CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA
0.2	0.19	0.26	0.36	0.26	0.36	0.26	0.36	0.26	0.35	0.25	0.31
0.4	0.60	0.63	0.67	0.63	0.67	0.63	0.67	0.63	0.67	0.63	0.68
0.6	0.89	0.77	0.78	0.77	0.78	0.77	0.78	0.79	0.79	0.80	0.81
0.8	0.98	0.84	0.84	0.84	0.84	0.85	0.85	0.86	0.86	0.88	0.89

10x10
Kernel size		0.1		0.2		0.3		0.4		0.5
CNR	CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA
0.2	0.23	0.38	0.53	0.38	0.53	0.38	0.53	0.38	0.52	0.37	0.47
0.4	0.67	0.83	0.87	0.84	0.87	0.83	0.87	0.83	0.88	0.84	0.85
0.6	0.91	0.93	0.94	0.93	0.94	0.93	0.94	0.94	0.94	0.94	0.95
0.8	0.99	0.96	0.96	0.96	0.96	0.96	0.96	0.97	0.97	0.97	0.97

20x20
Kernel size		0.1		0.2		0.3		0.4		0.5
CNR	CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA
0.2	0.25	0.46	0.63	0.46	0.63	0.45	0.63	0.45	0.62	0.44	0.56
0.4	0.69	0.93	0.96	0.93	0.96	0.93	0.96	0.93	0.95	0.92	0.92
0.6	0.92	0.98	0.99	0.98	0.99	0.98	0.99	0.99	0.99	0.98	0.98
0.8	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99

Table 1B.

Comparing TPRs of CCA+CA, MSC-ST, and MSC-ST+CA at significance level of 0.05. Kernel sizes of 0.10, 0.20, 0.30, 0.40, and 0.50 used. CNRs of 0.20, 0.40, 0.60 and 0.80 used. Activation sizes of 5x5, 10x10 and 20x20 simulated.

5x5
Kernel size		0.1		0.2		0.3		0.4		0.5
CNR	CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA
0.2	0.39	0.49	0.59	0.49	0.59	0.49	0.59	0.48	0.57	0.42	0.46
0.4	0.78	0.83	0.87	0.83	0.87	0.83	0.87	0.83	0.85	0.73	0.74
0.6	0.95	0.93	0.94	0.93	0.94	0.94	0.95	0.94	0.95	0.89	0.89
0.8	0.99	0.96	0.96	0.96	0.96	0.96	0.96	0.97	0.97	0.98	0.97

10x10
Kernel size		0.1		0.2		0.3		0.4		0.5
CNR	CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA
0.2	0.43	0.63	0.73	0.63	0.73	0.63	0.73	0.62	0.72	0.54	0.59
0.4	0.80	0.94	0.96	0.94	0.96	0.94	0.96	0.92	0.93	0.86	0.87
0.6	0.96	0.99	0.99	0.99	0.99	0.99	0.99	0.98	0.98	0.97	0.96
0.8	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.99	0.99

20x20
Kerne size		0.1		0.2		0.3		0.4		0.5
CNR	CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA	MSC-ST	MSC-ST+CA
0.2	0.44	0.71	0.81	0.71	0.80	0.71	0.80	0.69	0.78	0.61	0.66
0.4	0.81	0.98	0.99	0.98	0.99	0.98	0.99	0.95	0.96	0.92	0.93
0.6	0.96	1.00	1.00	1.00	1.00	1.00	1.00	0.99	0.99	0.98	0.98
0.8	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00

Figure 2.

Receiver operating characteristic curves of event-related simulation using MSC-ST+CA (Kernel size = 0.30 cases shown) being evaluated against MSC and CCA+CA. CNRs of 0.20, 0.40, 0.60, and 0.80 were used. A: 5x5 simulated activation size. B: 10x10 simulated activation size. C: 20x20 simulated activation size.

Figure 3.

Representative map generated with 20x20 activation sizes, CNR = 0.40, z-threshold = 2, event-related design. A: The simulated activation pattern B: Results with CCA C: Results with CCA+CA D: Results with MSC-ST+CA, kernel size = 0.30

A set of simulated data using a block-design was also used for the exact same comparisons with ROC curves. The block-design ROC curves generally ran higher when compared to the event-related design, but it still produced results with similar general trends seen with the event-related simulated data at the same FPRs of 0.01 and 0.05. Low CNRs (0.20, 040) with MSC-ST+CA still shows improvement over CCA+CA across the same kernel sizes and activation sizes. CNRs 0.60 and 0.80 generally sees improvements or similar performance in the 10x10 and 20x20 cases. There are differences in the results between using event-related and block-design simulated data in that block-design ROC curves ran higher generally (an example: Figure 4, kernel size = 0.30, 20x20 case), but similar trends are seen in both cases.

Figure 4.

Receiver operating characteristic curves of block-design compared to event-related using MSC-ST+CA. CNRs of 0.20, 0.40, 0.60, and 0.80 were used. Kernel size = 0.30, 20x20 activation size case shown.

With the effects of kernel size on MCS performances having been evaluated, the results and discussion are focused on the sizes of 0.10, 0.20, 0.30, 0.40, and 0.50 due to deteriorated performances outside of this range (Table 1A/1B). At kernel sizes of 0.10 to 0.40, the technique generally performed similarly with each other at FPR of 0.05. Some degradation in performance, if present, can usually be seen by kernel size 0.50 and 0.40 in some cases. At FPR 0.01, the technique tends to perform consistently across all tested kernel sizes.

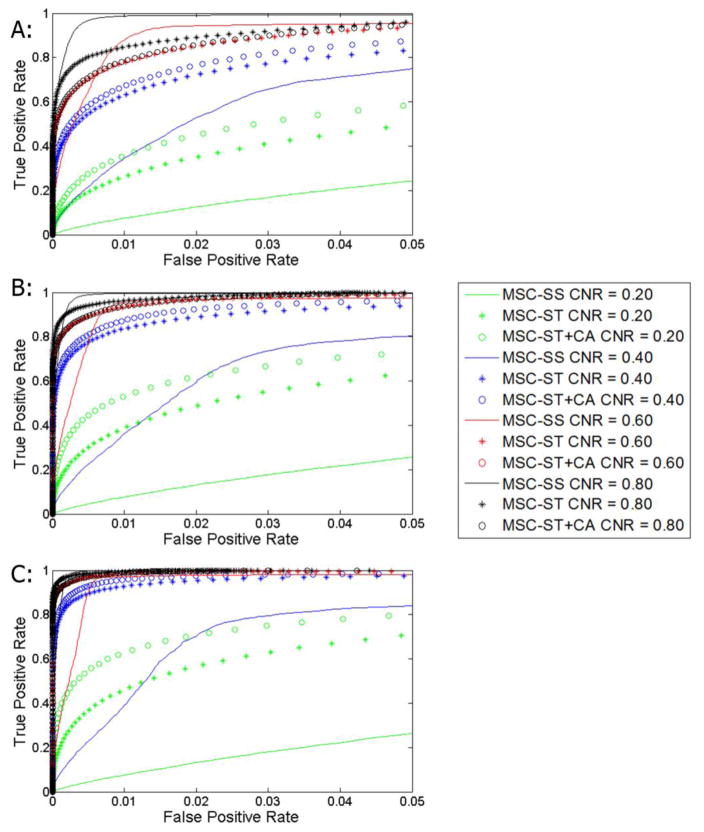
An evaluation was also made with the previously used MSC-SS against MSC-ST and MSC-ST+CA (Figure 5). Within the range of previously used kernel sizes of 0.10–0.50, kernel sizes of 0.30 for MSC-ST/ MSC- ST+CA and 0.50 for MSC-SS were chosen for use in this particular comparison while using 5x5, 10x10, and 20x20 simulated activation sizes with an event related design. The new MSC-ST and MSC-ST+CA outperformed the previously used MSC-SS in the lower CNR scenarios (0.20, 0.40) in all activation sizes. However, using a larger kernel size for MSC-SS such as 0.70 still shows MSC-ST+CA generally outperforming it at the CNRs of 0.20 and 0.40. The differences become smaller, and MSC-SS actually is superior in the 5x5 case.

Figure 5.

Receiver operating characteristic curves of simulated event related data with MSC-ST+CA (kernel size = 0.30) and MSC-SS (kernel size = 0.50). CNRs of 0.20, 0.40, 0.60, and 0.80 were used. A: 5x5 activation size B: 10x10 activation size C: 20x20 activation size

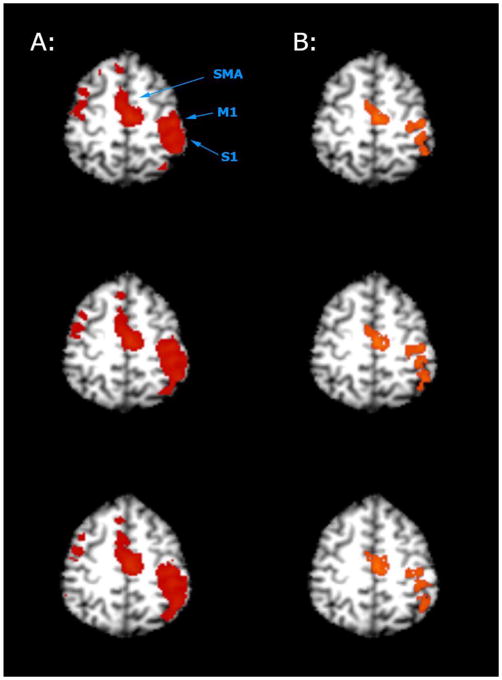
The proposed MSC-ST+CA technique was also tested with real BOLD fMRI data, with results showing that it is capable of detecting activations. From the averaged image (Figure 6), larger activations are present using MSC-ST+CA (kernel size = 0.10, z-threshold = 1) when compared to CCA+CA (z-threshold = 2.6, cluster threshold = 4 voxels). From the individual data (Table 2), an average activation size of 125.9 voxels were detected in the left M1/S1 area of the brain using CCA+CA with the same parameters used with the average image. The MSC-ST+CA average detected activation of 204.2 voxels was made, as before, with the same parameters. MSC-SS detected an average activation of 180.0 voxels using a kernel size of 0.20 and a z-threshold of 1. According to paired a t-test, MSC-ST+CA is significantly different when compared to CCA+CA (t = 3.26, p<0.05). However, MSC-ST+CA and MSC-SS at these tested parameters are not statistically different from each other (t = 1.56, p>0.05), likely due to a limited sample size of ten subjects.

Figure 6.

Multiple axial slices of averaged real fMRI data evaluated with MSC-ST and CCA+CA. A: MSC-ST (kernel size = 0.10, z-threshold = 1) B: CCA+CA (z-threshold = 2.6, cluster threshold = 4 voxels)

Table 2.

Evaluating CCA+CA (z-threshold = 2.6, cluster threshold = 4 voxels), MSC-ST+CA (kernel size = 0.10, z-threshold = 1), and MSC-SS (kernel size = 0.20, z-threshold = 1) using real individual fMRI data.

	CCA+CA		MSC_ST+CA		MSC_SS
Subject No.	Voxels	Avg Z	Voxels	Avg Z	Voxels	Avg Z
1	151	5.3	193	2.8	191	2.3
2	71	3.9	94	2.0	42	4.3
3	16	5.8	295	1.8	199	3.5
4	0	0.0	15	1.3	24	1.7
5	294	5.1	376	2.6	388	4.3
6	148	4.8	196	2.4	131	4.8
7	113	4.5	182	2.1	222	2.2
8	36	3.6	72	1.6	102	2.4
9	127	4.3	206	2.0	176	3.5
10	303	7.7	412	3.8	324	6.0
Mean	125.9	4.5	204.2	2.2	180.0	3.5
SD	105.5	2.0	127.8	0.7	114.6	1.4

4. Discussion

This study showed that incorporating temporal characteristics into MSC analysis for fMRI can yield improved results when compared to CCA, CCA+CA, and MSC-SS in all low CNR scenarios. The ROC curves indicate similar improvement trends between event-related and block-design simulated data. MSC techniques can be further optimized for detecting highly focused or low contrast activations. MSC+CA shows higher detection sensitivity when compared to MSC, but highly focused activations will be lost due to the application of a cluster size threshold. MSC has lower detection sensitivity when compared to MSC+CA, but it is more likely that highly focused activations will be retained without a cluster size threshold being used. The usage scenario for the individual MSC methods would depend on the analysis needs for a particular study.

MSC-ST+CA improves detections in low CNRs when compared to CCA and CCA+CA. Based on the ROC curves, MSC-ST+CA shows improved performance at CNRs of 0.20 and 0.40 at the tested kernel sizes (0.10, 0.20, 0.30, 0.40, and 0.50) and the tested simulated activation sizes (5x5, 10x10, 20x20). In this context, the proposed MSC based techniques offers an advantage when examining in low CNR situations over CCA+CA and especially CCA. MSC techniques can also be improved by selecting different feature spaces. By incorporating temporal information in its feature space, the performances of the proposed MSC-ST techniques are enhanced for detecting low CNR signals over the MSC-SS technique which uses only spatial information for its feature space. Further optimization of feature space selection has potential to further improve MSC techniques.

Performance of the proposed MSC techniques has dependence on the kernel size used. While we evaluated effects of kernel sizes over the range of 0.01–5.0, kernel sizes of 0.10 – 0.50 produced usable results with improvements over CCA and CCA+CA. This means that an optimal range of kernel sizes exists. If a smaller kernel size is used (0.01), the MSC technique performance does deteriorate. Conversely if a much larger kernel size is used (5.00), there will be cases where no activations would be detected. This is consistent with the previous study in that it suggests a range of optimal kernel sizes can be used for improved results. Our data suggest that such an optimal range of kernel sizes exists within the context of MSC-ST/MSC-ST+CA as well, though it is clearly different than that of the MSC-SS used in the previous study. This is likely due to the analysis process performed in this study includes a normalization process which was not part of the previous study.

In this study, the feature space had its values normalized between 0–10 in all dimensions with the intent of standardizing the relative kernel sizes between methods. The normalization process does change the range of usable kernel sizes, but this process is important as it standardizes the relative size of the used kernel without any particular dependence of the feature space used. For example, the previous spatial only feature space used essentially z-scores for both dimensions of the feature space, meaning that both dimensions would have values on approximately the same scale. In the case of this study, the values of the different dimensions of the spatial temporal feature space (a max of about 10) would have values on a very different scale compared to the values of the power spectrum (up to about 45), which skews the relative size of the kernel in each dimension. Even in the MSC-SS feature space, if there is a drastic CNR change, the range of values within the feature space would change as well. The same kernel size would have a different meaning relative to the range of values present. The normalization process addresses this issue. This also brings up the possibility of normalizing or weighting certain types of features/dimensions differently for purposes of optimization. This is also an area of optimization that can benefit from further study.

The MSC technique, if properly optimized, could be useful for isolating activations in lower CNR situations. Great benefits may be seen when studying non-BOLD contrasts mechanisms (magnetic source MRI and perfusion images for example) which often suffer from low CNR signals, making reliable signal detection difficult. Other imaging techniques that also inherently tend to have low CNRS, phosphorous or sodium imaging for example, can also similarly benefit from MSC based methods. Techniques that improves low CNR signal detection power also has uses with imaging techniques that have relatively high CNRS, BOLD fMRI for instance. It may allow for shorter scan times with which can reduce confounding effects such as motion effects. It may also allow for higher resolution scans, which inherently will lower CNR even if the technique being used is considered to have high CNR.

The proposed technique has a drawback in that it is difficult to come up with a method of calculating theoretical significance levels. The significance levels of this study are estimated based on a computer simulation using idealized situations, assuming Gaussian noise for example. Using idealized situations to estimate significant level is a common practice in scientific research in general. Consider that the commonly used t-test revolves around the theoretical assumption that the data follows a Gaussian distribution. Real fMRI data is not pure Gaussian noise and thus may induce challenges in estimating significant levels. These types of issue are common for all parametric tests used in fMRI and is not unique to this study. This does not mean improvements cannot be made on simulations for this study. It may be possible to incorporate undesirable artifacts and/or noise, movement or physiological noise for instance, in computer simulations for more accurate significance level estimations.

The ROC curves also indicate improvements in performance is not always seen in higher CNRs (0.60, 0.80), and there are cases where MSC-ST+CA does not outperform MSC-SS. These can be interpreted as a drawback of the technique since improvement is not seen in all tested cases. While MSC-ST+CA does not outperform MSC-SS in some cases, the areas where improvements can be seen are definitely in the lower CNR cases. However, there generally is not an issue when detecting signals/activations at high CNRs using current methods unlike at lower CNRs, especially considering that the techniques tested all essentially have or is close to 100% detection at a significance of 0.05. Also, MSC-ST+CA is still generally improved over MSC-SS in the low CNR cases. These drawbacks are not necessarily an issue considering the envisioned usage scenario of the presented technique.

5. Conclusion

By incorporating temporal characteristics in the feature space when applying MSC to fMRI analysis, improvements in activation detections can be seen over CCA, CCA+CA, and MSC-SS. The tested technique is able to produce lower false positive rates which would allow the use of low statistical thresholds when compared to CCA and CCA+CA in a simulated setting, while still being able to detect more activations using real fMRI data. Our ROC curves indicate that the MSC-ST technique is able to further improve activation detection in fMRI analysis in low CNR situations when combined with cluster analysis. With MSC-ST+CA, detection sensitivity can be further improved over MSC-ST without the application of a cluster threshold, but it is likely that highly focused activations will be lost. On the other hand, highly focused activations are more likely to be retained with MSC-ST without the application of a cluster threshold, but detection sensitivity is lower. MSC-ST offers a potentially powerful new tool for fMRI analysis, especially in low CNR situations. Future studies will exam effects of different feature space selection on activation detection in great detail.