Breast parenchymal patterns in processed versus raw digital mammograms: A large population study toward assessing differences in quantitative measures across image representations

Abstract

Purpose:

With raw digital mammograms (DMs), which retain the relationship with x-ray attenuation of the breast tissue, not being routinely available, processed DMs are often the only viable means to acquire imaging measures. The authors investigate differences in quantitative measures of breast density and parenchymal texture, shown to have value in breast cancer risk assessment, between the two DM representations.

Methods:

The authors report data from 8458 pairs of bilateral raw (“FOR PROCESSING”) and processed (“FOR PRESENTATION”) DMs acquired from 4278 women undergoing routine screening evaluation, collected with DM units from two different vendors. Breast dense tissue area and percent density (PD), as well as a range of quantitative descriptors of breast parenchymal texture (statistical, co-occurrence, run-length, and structural descriptors), were measured using previously validated, fully automated software. Feature measurements were compared using matched-pairs Wilcoxon signed-ranks test, correlation (r), and linear-mixed-effects (LME) models, where potential interactions with woman- and system-specific factors were also assessed. The authors also compared texture feature correlations with the established risk factors of the Gail lifetime risk score (r_G) and breast PD (r_PD), and evaluated the within woman intraclass feature correlation (ICC), a measure of bilateral breast-tissue symmetry, in raw versus processed images.

Results:

All density measures and most of the texture features were strongly (r ≥ 0.6) or moderately (0.4 ≤ r < 0.6) correlated between raw and processed images. However, measurements were significantly different between the two imaging formats (Wilcoxon signed-ranks test, p_w < 0.05). The association between measurements varied across features and vendors, and was substantially modified by woman- and system-specific image acquisition factors, such as age, BMI, and mAs/kVp, respectively. The strongest correlation, combined with minimal LME-model interactions, was observed for structural texture features. Overall, texture measures from either image representation were weakly associated with Gail lifetime risk (−0.2 ≤ r_G ≤ 0.2), weakly to moderately associated with breast PD (−0.6 ≤ r_PD ≤ 0.6), and had overall strong bilateral symmetry (ICC ≥ 0.6).

Conclusions:

Differences in measures from processed versus raw DM depend highly on the feature, the DM vendor, and image acquisition settings, where structural features appear to be more robust across the different DM settings. The reported findings may serve as a reference in the design of future large-scale studies on mammographic features and breast cancer risk assessment involving multiple DM representations.

1. INTRODUCTION

With 1.67 × 10⁶ breast cancer cases diagnosed annually worldwide and a sharp increase (20%) in incidence of the disease since 2008,¹ which is projected to rise further over the next two decades,² early breast cancer detection is a major clinical challenge. Mammography remains the cornerstone for early breast cancer detection,^3,4 and the transition from screen-film to digital mammograms (DMs) has enhanced the potential for imaging-based measures. In particular, image-derived indices of breast density^5,6 and parenchymal texture patterns⁷ have emerged as promising risk factors for breast cancer in epidemiologic studies, paving the way toward personalized recommendations regarding women’s cancer risk evaluation and screening.⁸

Breast density, which measures the amount of fibroglandular tissue within the breast, is a key biomarker not only because it is considered a well-established independent risk factor for breast cancer,⁵ but also because it influences the sensitivity of screening mammography.⁹ Its critical role has motivated multiple approaches toward its assessment in DMs, from visual categorical assessment¹⁰ and interactive quantitative techniques¹¹ to fully automated measurements.^12,13 Growing evidence also suggests that localized measures of the parenchymal tissue patterns may reflect changes in modifiable risk factors for breast cancer (i.e., factors, such as hormonal exposure, and BMI, which can be controlled or treated) and have a complementary role to breast density.^14,15

Digital mammography acquisition produces two types of images, both of which can be used for breast density and texture analysis.^16–25 The raw (i.e., “FOR PROCESSING”) images are proportional to the x-ray attenuation of the breast tissue, while the processed (i.e., “FOR PRESENTATION” or “FOR CLINICAL DISPLAY”) images are generated after vendor-specific postprocessing is applied to the raw images in an attempt to increase lesion conspicuity before clinical evaluation and interpretation.²⁶ Therefore, it would be reasonable to consider that raw images are more appropriate for quantitative analysis than processed images, as they retain the original x-ray attenuation information. However, routine collection of raw images is not widespread due to cost and storage considerations, usually leaving only the processed data available for retrospective examination. As a result, although several algorithms were originally designed to work on raw data,²⁷ many recent studies utilize processed DM images.^23–25

This raises the question of potential differences in image-derived measurements from raw and processed mammograms, and subsequent implications in related interpretation. Recent studies investigating associations of digital mammography quantitative descriptors with breast cancer risk^28–30 as well as intra- and inter-reader agreement^12,28,31 suggest that DM representation may have an effect. However, this topic remains largely unexplored, with breast density measurements in processed versus raw DM compared in few studies,^12,28,31 while the literature lacks reports for similar comparisons of parenchymal texture descriptors. To better understand the relationship between such measures from raw and processed DMs, we performed a systematic evaluation of a wide range of fully automated measures on large-population data collected with acquisition systems from two different vendors.

2. METHODS

2.A. Study population and digital mammograms acquisition

We report data from an entire one-year (September 1, 2010 to August 30, 2011) screening cohort at our institution (Hospital of the University of Pennsylvania), which included a total of 10739 consecutive women with no prior history of breast cancer who were screened routinely for breast cancer with digital mammography. The institutional review board waived the requirement to obtain written consent for this retrospective, Health Insurance Portability and Accountability Act (HIPAA)-compliant study. All women underwent bilateral, two-view full-field digital mammography under standard protocol, using either a Senographe Essential (General Electric Healthcare, Little Chalfont, Buckinghamshire, UK, here labeled as “Vendor 1”) or a Selenia Dimensions (Hologic, Inc., Bedford, MA, USA, labeled as “Vendor 2”) unit. The system of Vendor 1 was equipped with anode filter combinations of molybdenum and rhodium and had a pixel size of 0.10 mm/pixel; for the system of Vendor 2, there was a choice of using either a rhodium or a silver filter (determined either manually or automatically by the system) and the pixel size was equal to 0.07 mm/pixel.

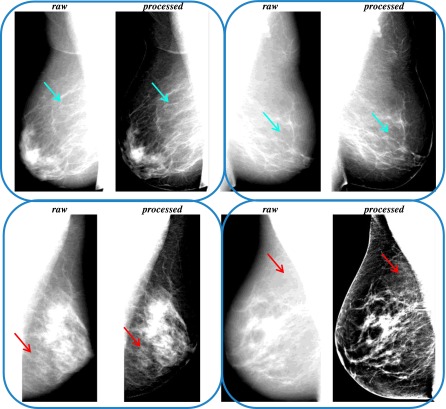
For the purposes of this study, we used the medio-lateral oblique (MLO) view as it offers the opportunity to visualize the maximum amount of breast tissue. Of the entire screening cohort, both raw and processed MLO images were available for 4389 women. From these, 295 pairs of raw and processed DM images were excluded due to woman- or DM-specific image artifacts (i.e., paddles, pacemakers, implants, etc.) in either one or both DM representations, leading to a final dataset of 8458 (Vendor 1: 2903, Vendor 2: 5555) pairs of raw and processed DM images, corresponding to unilateral or bilateral, when available, breast images from 4278 women. Example pairs of the collected raw and processed DMs are shown in Fig. 1.

FIG. 1.

Pairs of raw and processed medio-lateral oblique digital mammograms for different women, showing minor (upper row, blue arrows) or substantial (lower row, red arrows) effects of vendor-specific postprocessing algorithms on the breast parenchymal appearance (left: Vendor 1, right: Vendor 2). (See color online version.)

2.B. Automated estimation of image-derived quantitative descriptors

Raw images were first log-transformed, then inverted, and, finally, intensity-normalized by a z-score transformation specifically within the breast region which was automatically segmented in each image as described below; only z-score normalization was applied to processed images. These steps comprise common preprocessing which helps to alleviate differences between studies via intensity histogram alignment, while also maintaining the overall pattern, spatial relationship, and relative contrast of the pixels, toward appropriate texture analysis.³² Subsequently, 30 quantitative measures (Table I), characterizing breast density and parenchymal texture, were estimated from the two image representations. All measurements were performed using fully automated computational tools, which have been previously developed, extensively optimized, and validated.^{12,14,15,32,33}

TABLE I.

Breast density and parenchymal texture features measured in raw and processed digital mammograms.

Density features		T12	95th
DA	Dense tissue area	T13	95th mean
PD	Breast percent density	T14	Entropy
Structural texture features		T15	Kurtosis
T1	Box-counting fractal dimension	T16	Max
		T17	Mean
T2	Local binary pattern	T18	Min
Co-occurrence texture features		T19	Sigma
T3	Cluster shade	T20	Skewness
T4	Correlation	T21	Sum
T5	Energy	Run-length texture features
T6	Entropy	T22	Gray level non-uniformity
T7	Haralick correlation	T23	High gray level run emphasis
T8	Inertia	T24	Long run emphasis
T9	Inverse difference moment	T25	Low gray level run emphasis
Gray-level histogram texture features		T26	Run length non-uniformity
T10	5th	T27	Run percentage
T11	5th mean	T28	Short run emphasis

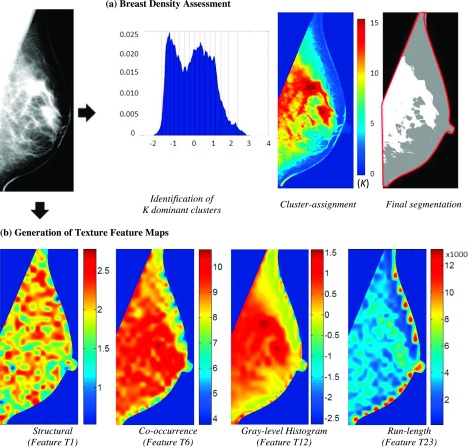
Specifically, the “Laboratory for Individualized Breast Radiodensity Assessment” (libra) software^12,33 was used to measure breast density in terms of both total dense tissue area (DA) and breast percent density (PD), defined as the ratio of the segmented DA to the total breast area. The libra algorithm is an adaptive multicluster fuzzy c-means segmentation approach, which has been shown to have good agreement to the widely used semiautomated Cumulus method for both raw and processed DM.¹² Briefly, the algorithm first applies an edge-detection algorithm to delineate the boundary of the breast and the pectoral muscle which together define the total breast tissue area. Then, the number of dominant clusters of similar gray-level intensity is determined as the number of local peaks in the gray-level histogram and a fuzzy c-means algorithm assigns each image pixel to the cluster for which that pixel’s intensity value has the highest membership score. In this manner, the breast tissue area is partitioned into clusters of similar gray-level intensity, which are finally aggregated by a trained support-vector machine classifier to the final DA segmentation [Fig. 2(a)]. In addition to the automated density measures, BIRADS density was also available from the clinical evaluation report on record.

FIG. 2.

Automated quantitative assessment of breast density and parenchymal texture. (a) Illustration of breast density assessment using the libra algorithm. The detected boundary of the total breast tissue is marked in red and the segmented dense tissue areas are marked in white in the final segmentation of the digital mammogram. (b) Examples of texture feature maps produced by the lattice-based texture analysis pipeline. The varying color patterns within the breast show that each texture feature reveals different aspects of the mammographic texture. (See color online version.)

An automated image analysis pipeline,^14,15 based on a novel lattice-based strategy, was used to extract a wide range of parenchymal texture features from the entire breast region. With this method, texture feature values are calculated within nonoverlapping 6.3 × 6.3 mm² local square regions surrounding each lattice point of a grid virtually overlaid on the entire segmented breast region, thereby generating a corresponding texture map for each texture descriptor. For breast regions close to the boundary of the breast, where the local square regions may not entirely fall within the breast, the pixels outside the breast were excluded from texture feature calculation. The particular approach of breast sampling has been shown to maximize the robustness of texture features across different systems, as well as their association with breast cancer risk.^15,32 In a second step, a feature vector, comprising of the mean of the corresponding texture values over all lattice points within the breast for all descriptors, characterizes the overall breast parenchymal texture. Following this two-step approach, we estimated a total of 28 texture descriptors, including structural,^34,35 co-occurrence,³⁶ gray-level histogram,³⁷ and run-length features,^38,39 which have all been previously established for mammographic pattern analysis and breast cancer risk assessment.^{7,14,15,23,35,40,41}

In Fig. 2(b), we show representative texture maps for each feature category, while detailed descriptions and mathematical notations of the features are available in Appendix A. Generally, these indices describe different aspects of the mammographic texture pattern. Gray-level histogram features are common first-order statistics which describe the distribution of gray-level intensity values within the breast tissue region. Co-occurrence and run-length features also consider the spatial relationships of pixel gray-level intensities and they reflect the coarseness, contrast, local variation, and spatial dependence of these image intensities in the breast parenchyma. Finally, structural features provide the architectural composition of the breast tissue by capturing the intrinsic complexity and the intensity variations between central and neighboring pixels.

2.C. Statistical analyses

Bland-Altman analysis was performed to ensure agreement in the segmented breast tissue area between processed and raw images toward appropriate subsequent comparisons of feature measurements.

To investigate the relationship between feature measurements in the two image representations, feature values were compared via Spearman’s rank correlation coefficient and the matched-pairs Wilcoxon signed-ranks test. A linear-mixed-effects (LME) model⁴² (unit of analysis: individual woman) was also applied to assess the linear relationship between feature values in processed versus raw images, in which we tested for potential interactions⁴³ with woman- [age, body mass index (BMI), and ethnicity] and system- (kVp and mAs) specific factors known to affect the mammographic parenchymal tissue patterns.³² These factors were handled as categorical variables using the following levels: age (≤49, [50 60), [60 70), [70 80), ≥80 y), BMI (<25, [25 30), ≥30 kg/m²), ethnicity (White, African-American, Other or missing), kVp (Vendor 1: ≤29, >29; Vendor 2: ≤30, >30), and mAs (Vendor 1: ≤52, (52 75], >75; Vendor 2: ≤121, (121 165], >165). The level definitions of kVp and mAs were based on the 25th and 75th percentiles of the corresponding distributions. Given that the processing algorithms and detector technology utilized by the two vendors are different, which, in turn, may impact the appearance of the breast parenchyma, comparisons were stratified by vendor.

Finally, we also assessed texture feature correlations with the established risk factors of the Gail lifetime risk score⁴⁴ (r_G) and breast PD (r_PD), using the Spearman’s rank correlation coefficient, and evaluated their bilateral symmetry, using the intraclass correlation (ICC) to assess within-woman texture feature similarity compared to the texture feature variability across all women.

All statistical experiments were performed using the stata (Release 13, StataCorp LP, College Station, TX, USA) and the sas (Release 9.4, SAS Institute, Inc., Cary, NC, USA) statistical software packages.

3. RESULTS

Our study population is summarized in Table II. Bland-Altman limits showed agreement in segmented breast tissue area in processed versus raw images for Vendor 1 (mean difference −0.48 cm², 95% limits of agreement [−17.62, 16.66] cm², range of averages [37.86, 516.04] cm²) and Vendor 2 (mean difference −7.75 cm², 95% limits of agreement [−45.06, 29.56] cm², range of averages [37.54, 554.79] cm²).

TABLE II.

Study population characteristics, stratified by the two different digital mammography vendor units.

	Vendor 1	Vendor 2
Number of women	1474	2804
Age (mean ± SD)	58.6 y ± 11.2	56.5 y ± 10.8
Age at first menstrual period (mean ± SD)	13.0 y ± 3.6	12.8 y ± 3.3
Age at first child birth (mean ± SD)	24.7 y ± 6.7	24.5 y ± 6.7
BMI (mean ± SD)	28.7 kg/mm2 ± 7.0	29.8 kg/mm2 ± 7.4
BI-RADS density
Type A	162 (11.0%)	330 (11.8%)
Type B	792 (53.7%)	1560 (55.7%)
Type C	482 (32.7%)	852 (30.4%)
Type D	31 (2.1%)	41 (1.5%)
Missing	7 (0.5%)	21 (0.8%)
Ethnicity
White	630 (42.7%)	1127 (40.2%)
African-American	740 (50.2%)	1425 (50.8%)
Other or missing	104 (7.1%)	252 (9.0%)
Gail lifetime risk score (mean ± SD)	8.2% ± 4.4	8.6% ± 4.3

Note: SD = standard deviation; BMI = body mass index; BIRADS = breast imaging reporting and data system.

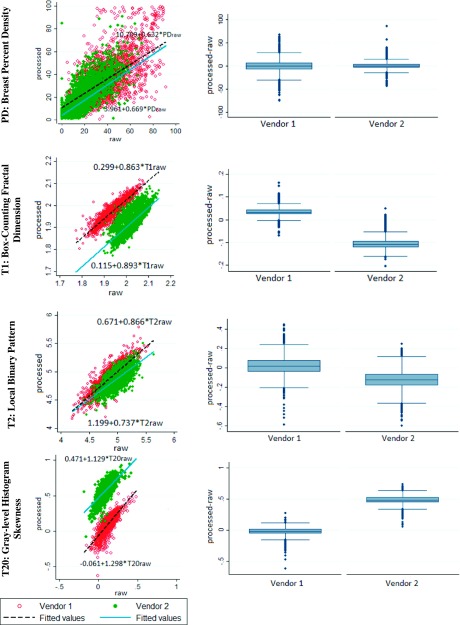
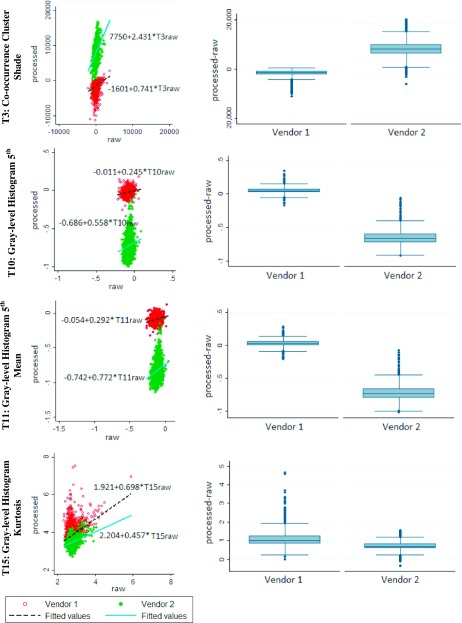
All feature measurements were statistically significantly different between raw and processed images (Wilcoxon signed-ranks test, p_w < 0.05), however, most features were strongly (r ≥ 0.6) or moderately (0.4 ≤ r < 0.6) correlated (Table III). For the correlated features, the LME slope was statistically different from zero and generally below unity. The magnitude of the slope varied substantially, not only across different features (e.g., features DA and T25 in Table III), but also between different vendors for the same feature (e.g., T23 in Table III). Strong agreement across the different DM representations, demonstrated as strong correlations and close-to-unity LME slopes in both vendors, was observed for breast PD and for three texture descriptors reflecting intrinsic parenchymal pattern complexity (features T1 and T2) and symmetry (feature T20) (Fig. 3). On the other hand, the lowest correlations in both vendors were seen in features T3, T10, T11, and T15, representing gray-level intensity co-occurrence and histogram statistics, respectively (Fig. 4).

TABLE III.

Statistical analysis of paired measurements in processed versus raw digital mammograms. For each of the 30 image-derived features, the linear-mixed-effects model, i.e., intercept, slope (b), 95% confidence interval for b and the coefficient of determination (R²), and the Spearman’s rank correlation coefficient (r) are provided.

		Vendor 1 (N = 2903 image pairs)			Vendor 2 (N = 5555 image pairs)
		LME model			LME model
Feature		(Intercept) b (CI)	R2	r	(Intercept) b (CI)	R2	r
Density	DA	(13.84) 0.70a [0.67 0.74]	0.68	0.81	(12.48) 0.41a [0.38 0.43]	0.50	0.53
	PD	(10.71) 0.63a [0.60 0.66]	0.83	0.68	(3.96) 0.67a [0.64 0.69]	0.68	0.73
Texture	T1	(0.30) 0.86a [0.85 0.88]	0.87	0.92	(0.12) 0.89a [0.87 0.91]	0.56	0.76
	T2	(0.67) 0.87a [0.85 0.88]	0.75	0.85	(1.20) 0.74a [0.72 0.75]	0.51	0.71
	T3	(−1 601.11) 0.74a [0.62 0.86]	0.08	0.25	(7 749.71) 2.43a [2.27 2.60]	0.17	0.43
	T4	(0.00) 0.60a [0.58 0.62]	0.65	0.79	(0.00) 0.05a [0.04 0.05]	0.30	0.42
	T5	(0.00) 0.59a [0.55 0.63]	0.34	0.59	(0.00) 0.09a [0.08 0.10]	0.07	0.27
	T6	(4.02) 0.53a [0.51 0.55]	0.56	0.72	(9.92) −0.01a [−0.02 0.00]	0.01	−0.24
	T7	(1 183 546) 0.35a [0.34 0.37]	0.64	0.78	(13 080 807) 1.64a [1.56 1.71]	0.42	0.65
	T8	(28.68) 0.68a [0.66 0.69]	0.79	0.86	(251.56) 1.27a [1.20 1.34]	0.29	0.54
	T9	(0.08) 0.57a [0.54 0.59]	0.56	0.72	(0.06) 0.14a [0.13 0.16]	0.22	0.34
	T10	(−0.01) 0.25a [0.20 0.29]	0.10	0.25	(−0.69) 0.56a [0.46 0.66]	0.06	0.28
	T11	(−0.05) 0.29a [0.25 0.34]	0.15	0.29	(−0.74) 0.77a [0.67 0.87]	0.10	0.34
	T12	(0.16) 0.51a [0.50 0.52]	0.82	0.88	(0.59) 0.83a [0.78 0.89]	0.25	0.46
	T13	(0.18) 0.50a [0.49 0.51]	0.83	0.89	(0.77) 0.85a [0.79 0.92]	0.20	0.42
	T14	(1.57) 0.72a [0.69 0.74]	0.56	0.62	(5.43) 0.14a [0.13 0.15]	0.20	0.47
	T15	(1.92) 0.70a [0.62 0.78]	0.08	0.15	(2.20) 0.46a [0.42 0.50]	0.09	0.21
	T16	(0.24) 0.49a [0.48 0.50]	0.85	0.90	(1.28) 0.82a [0.74 0.90]	0.11	0.29
	T17	(0.10) 0.52a [0.49 0.54]	0.60	0.72	(−0.03) −0.06a [−0.10–0.03]	0.05	−0.03
	T18	(−0.12) 0.49a [0.45 0.53]	0.35	0.47	(−0.90) 0.87 [0.78 0.96]	0.11	0.32
	T19	(0.05) 0.54a [0.52 0.56]	0.68	0.77	(0.31) 1.54a [1.46 1.62]	0.30	0.53
	T20	(−0.06) 1.30a [1.26 1.34]	0.75	0.81	(0.47) 1.13a [1.09 1.17]	0.52	0.62
	T21	(389.85) 0.52a [0.49 0.54]	0.60	0.72	(−113.81) −0.06a [−0.10 −0.03]	0.05	−0.03
	T22	(29.22) 0.68a [0.65 0.71]	0.48	0.59	(41.52) 0.24a [0.23 0.26]	0.36	0.57
	T23	(164.73) 1.07a [1.04 1.10]	0.73	0.79	(1 248.74) 0.48a [0.46 0.51]	0.31	0.40
	T24	(0.80) 0.20a [0.19 0.22]	0.37	0.71	(1.04) −0.04a [−0.08 0.00]	0.00	0.03
	T25	(0.00) 0.17a [0.15 0.18]	0.23	0.45	(0.00) 0.22a [0.18 0.25]	0.01	0.11
	T26	(2 459.26) 0.35a [0.34 0.36]	0.59	0.72	(2 897.15) 0.24a [0.23 0.25]	0.19	0.40
	T27	(0.62) 0.35a [0.34 0.36]	0.58	0.72	(0.73) 0.24a [0.23 0.25]	0.19	0.40
	T28	(0.81) 0.19a [0.17 0.20]	0.36	0.69	(1.01) −0.01a [−0.02 0.00]	0.00	0.02

^aIndicates statistical significance of the deviation of b from unity, assessed with a two-sided Wald test at the α = 0.05 level with the Bonferroni adjustment for 30 comparisons per vendor (i.e., α = 0.05/30 = 0.0017). All correlations were statistically significant at the α = 0.05 level. Boldface indicates strongly correlated features (r ≥ 0.6) in processed versus raw images. LME = linear-mixed-effects; CI = confidence interval.

FIG. 3.

Graphs for strongly correlated feature measurements. (Left column) Scatterplots and LME models for measurements in processed (y-axis) versus raw (x-axis) digital mammograms, and (right column) box plots of the differences between the corresponding measurements (processed minus raw).

FIG. 4.

Graphs for weakly correlated feature measurements. (Left column) Scatterplots and LME models for measurements in processed (y-axis) versus raw (x-axis) digital mammograms, and (right column) box plots of the differences between the corresponding measurements (processed minus raw).

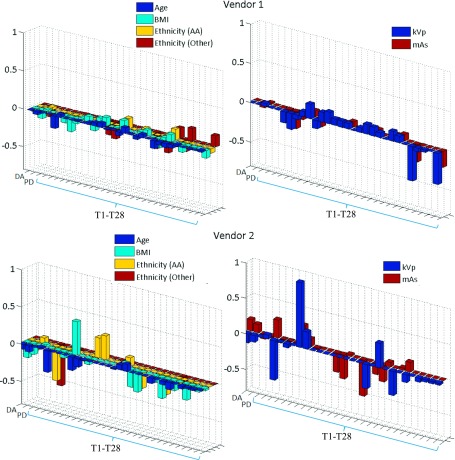
The linear relationship between measures in processed versus raw images varied considerably across different acquisition settings and woman-specific characteristics (Fig. 5). The LME slope was mostly modified by system-specific image acquisition factors, such as mAs and kVp, followed by age and BMI, while ethnicity had limited impact (Tables IV and V, Appendix B). Interestingly, the LME slopes for features T1 and T2 remained substantially stable for both vendors.

FIG. 5.

Modification of the LME-model slope by woman- and system-specific factors. Amount of change in the slope of the line fitted between feature values in processed versus raw digital mammograms, when the woman-specific factors of age, BMI, and ethnicity or the system-specific factors of kVp and mAs increase by one level. In case of the non-ordinal variable of ethnicity, this value represents the amount of change in the slope for the “African-American” (AA) and “Other or missing” (Other) subgroups with respect to the “White” subgroup.

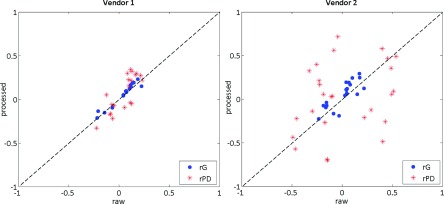
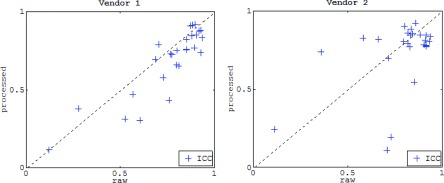
Overall, texture features from both image representations showed weak correlations with the Gail lifetime risk score and weak to moderate correlations with breast PD (Fig. 6). In terms of their association with breast PD, large differences between raw and processed DM texture measures were observed, especially when comparing different vendors, with several measures having inverted associations with breast PD depending on whether raw or processed DMs were used for texture analysis (e.g., for feature T6 in vendor 2, r_PD was equal to 0.41 and −0.49 in raw and processed images, Table VI, Appendix C). Most features demonstrated strong bilateral symmetry in both image representations, while intrawoman similarity was statistically significantly stronger in raw images especially within separate vendors (Fig. 7).

FIG. 6.

Feature correlations with the Gail lifetime risk score (blue circles) and breast percent density (red asterisks) for parenchymal texture feature measures in processed versus raw digital mammograms. Each mark denotes a texture descriptor. The dashed identity line is provided for reference. (See color online version.).

FIG. 7.

Per-woman bilateral texture feature similarity for feature measurements in processed versus raw digital mammograms. Each mark denotes a texture descriptor. The dashed identity line is provided for reference.

4. DISCUSSION

Our study represents an extensive evaluation of key quantitative descriptors obtained from processed versus raw DMs, and could have implications for designing large-scale studies where DM images from different vendors and presentation formats are utilized. Overall, our results suggest that the extent of differences in breast density and parenchymal texture measures from processed versus raw DMs depends highly on the specific feature as well as the machine vendor and physics settings of the image acquisition.

First, the consistently correlated breast PD confirmed the previously reported associations in density measurements across DM representations;^12,28,31,45 however, the linear relationship between breast PD measured in processed and raw images seems to interact highly with woman- and system-specific factors, such as age, BMI, and mAs/kVp, respectively. Our results are generally in line with previous similar analyses in smaller datasets,^28,31 with any significant differences likely occurring due to the larger size of our sample, spanning an entire one-year screening cohort.

Texture features, which provide more subtle characterization of the breast parenchyma, seem to be overall more affected by vendor-specific postprocessing than the breast density measures. Moreover, the slope values of the LME models showed that per-unit feature changes were generally lower in processed images, suggesting that raw images may be more sensitive to texture differences (Table III). However, texture features were also significantly correlated and associations between measurements from the two image representations could be sufficiently explained by linear relationships. It should be emphasized, though, that both the strength of the correlation and the linear model relating the feature measurements in processed versus raw DM depend highly on the specific feature and the DM unit.

Strongest agreement in measures between raw and processed DM for both vendors was demonstrated by three texture descriptors (T1, T2, and T20). Moreover, when tested for interactions with woman- and system-specific factors, the LME models of two of these features (T1 and T2) were minimally affected. Interestingly, these two features represent structural texture features, which were recently associated with enhanced robustness across different DM units.³² These findings suggest that features capturing intrinsic characteristics of the breast parenchyma, by considering the overall topology and structure of the pattern, may be more robust and invariant to image intensity transformations by postprocessing.

Regardless of the strength of correlation between the different image types, all texture features, when measured either in processed or raw mammograms, were weakly to moderately correlated with breast PD, and were also weakly correlated with Gail lifetime risk. Given that earlier studies have associated the same texture descriptors with potential value in breast cancer prediction,^{7,14,23,35,40,41} our results also support a potential independent role of mammographic texture analysis in breast cancer risk assessment. However, it is important to mention that we observed substantial differences between raw and processed DM texture measures in their associations with breast PD. Similar variations have also been reported previously by related studies,^23,24,38,46 which together suggest an important effect of DM representation on the associations of parenchymal texture descriptors with density. Furthermore, both image representations had strong bilateral feature similarity, suggesting an inherently strong agreement in bilateral parenchymal symmetry, regardless of the imaging format.

Finally, our findings revealed possible different effects of the vendor-specific postprocessing algorithms, given that feature correlations, their linear relationships, and their interactions with woman- and system-specific factors varied substantially across vendors. A more extensive comparison between DM units is warranted and generalized conclusions should, therefore, be limited. However, our findings also emphasize the need for standardization frameworks,³² which can alleviate differences and ensure comparable measurements across different digital mammography units, acquisition settings, and representations.

Overall, our analysis showed that the DM representation, specific imaging settings (DM unit and mAs/kVp), and the woman’s individual profile (age and BMI), can affect both the feature measurements in DM and potentially their associations with established risk factors for breast cancer. This could also imply potential effects on the robustness of the density and texture measures in assessing a woman’s breast cancer risk across varying screening conditions. A complementary case-control study on this open question would therefore be important future work toward evaluating DM quantitative measures from different imaging representations for inclusion in breast cancer risk assessment models.

The conclusions of this work may serve as a reference in the design of future studies aiming to develop more robust mammographic measures of breast density and parenchymal texture, as well as help guide statistical approaches for calibrating and/or standardizing parenchymal features in processed versus raw DMs. As such, our study could guide the design of future large-scale studies, involving multiple digital mammography representations, and the integration of computerized texture analysis for breast cancer risk assessment in clinical settings, where only processed mammograms are routinely available.

Certain limitations should also be acknowledged for our study. First, we included a set of breast density and texture features estimated using specific algorithms, while additional features have been used in previous studies.^{16–21,25,28–30} Moreover, our dataset consisted of images which were collected with digital mammography units from two different vendors, although there are generally more vendors with FDA-approved units for use in mammography facilities.⁴⁷ Furthermore, additional system-specific parameters (e.g., anode filter) might have an effect on the mammographic parenchymal tissue patterns. Our aim with this study was to perform comparisons between key mammographic features. Therefore, we chose to focus on (a) commonly used features that have been previously associated with breast cancer risk, (b) a single, yet systematically optimized and validated, implementation of breast density and texture assessment, (c) two leading DM vendors, and (d) image acquisition settings known to substantially affect mammographic images. Larger datasets, with broader feature implementations, and more complex interactions with system-specific factors could be explored in future studies, aiming at further elucidating the differences between measurements in raw versus processed DM and how these could be calibrated in different scenarios of image acquisition and subsequent image analysis.

5. CONCLUSIONS

In summary, breast density and parenchymal texture features are generally correlated in processed versus raw DMs. The extent of differences in these measures across different imaging representations depends highly on the specific feature and the image acquisition settings. Among the features examined, structural texture features demonstrated stronger agreement between raw and processed images and were minimally affected by woman- and system-specific factors. These results may serve as a reference in the design of future studies on mammographic measures of density and parenchymal texture. They may also contribute to the design of large-scale studies, involving multiple digital mammography representations, and to the integration of computerized texture analysis in breast cancer risk assessment for clinical settings, where only processed mammograms are routinely available.

APPENDIX A: TEXTURE FEATURE GENERATION

The structural features include (a) the local binary pattern (LBP), which captures intensity variations between central and neighboring pixels³⁴ and (b) the fractal dimension (FD), which reflects the degree of complexity and was estimated using the box-counting method.³⁵

The LBP at pixel (x_c, y_c) is estimated as

$${\displaystyle \text{LBP}\left(x_c,y_c\right)=\sum _{p=0}^{P-1}q\left(I_p-I_c\right)2^P,\left(x_p,y_p\right)=\left[x_c+Qcos\left(\frac{2\pi p}{P}\right),y_c-Qsin\left(\frac{2\pi p}{P}\right)\right]}$$ (A1)

where I_c and I_p are the gray level values for pixels $\left(x_c,y_c\right)$ and $\left(x_p,y_p\right)$, respectively, and q is a function which attributes values zero and one for negative and non-negative inputs, respectively. The neighborhood of each pixel is defined in terms of size and number of neighborhood pixels by the parameters Q and P, respectively, which were set equal to Q = 1 and P = 8 following previous optimization experiments.³²

The FD estimation relies on the concept of self-similarity. The fractal dimension of a bounded set S in Euclidean n-space is defined as

$${\displaystyle \text{FD}=\underset{r\to 0}{lim}\frac{log\left(N_r\right)}{log\left(\frac{1}{r}\right)},}$$ (A2)

where N_r is the least number of distinct copies of S in the scale r. In case of an image, where fractals are not deterministic, the FD is approximated by the box-counting dimension as follows. We consider a 3D spatial surface, with (x, y) denoting pixel position on the image plane and the third coordinate, z, denoting the pixel gray level. The image plane is partitioned into nonoverlapping blocks of size s × s, with s being an integer corresponding to the scale of the block. On each block, there is a column of boxes of size s × s × s′, where s′ is the height of each box and it is determined by s, the size of the image and the total number of gray levels. If we assign numbers to the boxes of a block and the minimum and maximum gray levels fall into the mth and lth boxes, respectively, then the boxes covering the block are counted in the number as n_B = l − m + 1. By considering the contributions of all blocks, N_r is counted as the sum of n_r over all blocks. Following this process for different values of r, FD can, then, be estimated from the least-squares linear fit of $log\left(N_r\right)$ versus$log\left(\frac{1}{r}\right)$.

The co-occurrence features reflect the spatial relationship between pixels and they are based on the assumption that this information is adequately encoded by the so-called gray-level co-occurrence matrix (GLCM).³⁶ GLCM is an M × M matrix, where each element, f(i, j), corresponds to the relative frequency with which two neighboring pixels, one with gray level i and the other with gray level j, occur in the image. Such matrices of gray-tone spatial dependence frequencies are a function of the distance (d) and the orientation $\left(\vartheta \right)$ between the neighboring pixels.

In this study, the GLCM matrices were estimated using M = 128 gray levels to balance computational precision withefficiency and d = 11 pixels, and the following features were computed by averaging over four orientations (0°, 45°, 90° and 135°), based on the premise that these features are orientation invariant and one single direction might not give sufficient information.^14,15,32

Feature	Mathematical notation	Qualitative description
Cluster shade	${\sum }_{ij}{\left(i-{\mu }_i+j-{\mu }_j\right)}^3*f(i,j)$	Asymmetry in gray-level values
Correlation	${\sum }_{ij}\left(\left(i-{\mu }_i\right)*\left(j-{\mu }_j\right)*f\left(i,j\right)\right)/\left({\sigma }_i*{\sigma }_j\right)$	Linear gray-level dependence
Haralick correlation	${\sum }_{ij}\left(ij*f\left(i,j\right)-{\mu }_i*{\mu }_j\right)/\left({\sigma }_i*{\sigma }_j\right)$
Energy	${\sum }_{ij}f{\left(i,j\right)}^2$	Certainty of gray-level co-occurrence
Entropy	$-{\sum }_{ij}f\left(i,j\right)*log\left(f\left(i,j\right)\right)$	Uncertainty of gray-level co-occurrence
Inertia	${\sum }_{ij}{\left(i-j\right)}^2*f(i,j)$	Local variation of gray-level intensity
Inverse difference moment	${\sum }_{ij}\left(f\left(i,j\right)\right)/\left(1+{\left(i-j\right)}^2\right)$	Local homogeneity in gray-level values

where μ_i = ∑_ji*f(i, j), μ_j = ∑_ij*f(i, j), ${\sigma }_i^2={\sum }_j{\left(i-{\mu }_i\right)}^2*f(i,j)$, and ${\sigma }_j^2={\sum }_i{\left(j-{\mu }_j\right)}^2*f(i,j)$.

The gray-level histogram features are 12 well-known first-order statistics,³⁷ which were calculated from the gray-level intensity histogram of the image using 128 histogram bins.^14,32

Feature	Mathematical notation	Qualitative description
Mean	∑k(k*g(k))/(K)	Mean gray-level value
Min	Min(k)	Minimum gray-level value
Max	max(k)	Maximum gray-level value
Fifth percentile	k : 5% of values ≤k	The histogram bin that 5% of gray-level values are less than or equal to
Fifth mean	$\left({\sum }_{k}k*g\left(k\right)\right)/\left({\sum }_{k}g\left(k\right)\right)$ for k ≤ fifth percentile	Mean value of the gray-level values which less than or equal to the 5th percentile
95th percentile	k : 95% of values ≥k	The histogram bin that 95% of gray-level values are less than or equal to
95th mean	$\left({\sum }_{k}k*g\left(k\right)\right)/\left({\sum }_{k}g\left(k\right)\right)$ for k ≥ 95th percentile	Mean value of the gray-level values which larger than or equal to the 95th percentile
Sum	∑kk*g(k)	Sum of gray-level values
Sigma	$\sqrt{{\sum }_k{(k-\text{Mean})}^2*g\left(k\right)}$	Variation of gray-level values around the mean
Entropy	−∑kg(k)*log(g(k))	Measure of histogram uniformity
Kurtosis	Sigma−4∑k(k − Mean)4*g(k) − 3	Measure of histogram flatness
Skewness	Sigma−3∑k(k − Mean)3*g(k)	Measure of histogram symmetry

where k is the histogram bin, g is the frequency of the histogram bin, and K = ∑_kg(k).

Run-length features capture the coarseness of a texture in specified directions.^38,39 A run is defined as a string of consecutive pixels which have the same gray-level intensity along a specific linear orientation. Fine textures tend to contain more short runs with similar gray-level intensities, while coarse textures have more long runs with significantly different gray-level intensities. Similarly to the GLCM, a run-length matrix R is defined, with each element, R(i, j), representing the number of runs with pixels of gray-level intensity equal to i and length of run equal to j along a specific orientation. The size of the matrix R is M × N, where N is equal to the possible maximum run length.

In correspondence with the co-occurrence features, the following run-length statistics were estimated for M = 128 gray levels, N = 11 pixels, and averaged values over four orientations (0°, 45°, 90° and 135°).^14,15,32

Feature	Mathematical notation	Qualitative description
Gray level nonuniformity	$1/n_r{\sum }_{i=1}^M{\left({\sum }_{j=1}^{N}R\left(i,j\right)\right)}^2$	Dissimilarity in runs across gray-level values
High gray level run emphasis	$1/n_r{\sum }_{i=1}^M{\sum }_{j=1}^{N}R(i,j)*i^2$	Runs of high-gray-level values
Long run emphasis	$1/n_r{\sum }_{i=1}^M{\sum }_{j=1}^{N}R\left(i,j\right)*j^2$	Emphasis on the long runs
Low gray level run emphasis	$1/n_r{\sum }_{i=1}^M{\sum }_{j=1}^N\left(R\left(i,j\right)\right)/\left(i^2\right)$	Runs of low-gray-level values
Run length nonuniformity	$1/n_r{\sum }_{j=1}^N{\left({\sum }_{i=1}^{M}R(i,j)\right)}^2$	Dissimilarity in runs across lengths
Run percentage	nr/#pixels	Homogeneity and distribution of runs
Short run emphasis	$1/n_r{\sum }_{i=1}^M{\sum }_{j=1}^N\left(R(i,j)\right)/\left(j^2\right)$	Emphasis on the short runs

where $n_r={\sum }_{i=1}^M{\sum }_{j=1}^{N}R(i,j)$ is the total number of runs.

APPENDIX B: TESTS FOR INTERACTIONS WITH WOMAN- AND SYSTEM-SPECIFIC FACTORS

TABLE IV.

Tests for interactions for Vendor 1. Slope of the line fitted between feature values in processed versus raw images for the first (b₁) and last (b_L) level^a of each interaction factor in case of Vendor 1. Features are classified into three groups, corresponding to G1: nonstatistically significant interaction (95% confidence intervals including zero value), G2: limited interaction (|b₁ − b_L| ≤ 0.15), and G3: high interaction (|b₁ − b_L| > 0.15) with the corresponding factor.

Age		G1		DA, T1, T2, T5, T6, T8, T13, T16, T19, T25, T26, T27
				T7	T9	T12	T24	T28
		G2	b1	0.33	0.53	0.53	0.17	0.16
			bL	0.39	0.65	0.48	0.27	0.25
				PD	T3	T4	T10	T11	T14	T15	T17	T18	T20	T21	T22	T23
		G3	b1	0.67	0.96	0.54	0.18	0.20	0.78	0.54	0.57	0.43	1.43	0.57	0.74	1.10
			bL	0.52	0.32	0.70	0.36	0.45	0.59	0.85	0.41	0.62	1.02	0.41	0.51	0.93
BMI		G1		T2, T3, T12, T15, T16, T19, T25, T27
				DA	T1	T6	T7	T8	T13	T17	T21	T23	T26
		G2	b1	0.74	0.84	0.67	0.35	0.66	0.44	0.37	0.37	1.04	0.39
			bL	0.64	0.88	0.53	0.40	0.80	0.48	0.44	0.44	0.95	0.36
				PD	T4	T5	T9	T10	T11	T14	T18	T20	T22	T24	T28
		G3	b1	0.75	0.71	0.95	0.75	0.20	0.20	0.55	0.37	1.33	0.59	0.34	0.32
			bL	0.52	0.52	0.57	0.55	0.37	0.42	0.81	0.52	1.09	0.78	0.14	0.12
Ethnicity	AA	G1		DA, T2, T3, T6, T7, T8, T10, T11, T12, T13, T15, T16, T18, T19, T23, T25, T26, T27
				PD	T1	T4	T5	T9	T14	T17	T20	T21	T22	T24	T28
		G2	b1	0.69	0.84	0.65	0.68	0.63	0.65	0.47	1.35	0.47	0.61	0.23	0.22
			bL	0.60	0.88	0.56	0.59	0.56	0.78	0.52	1.27	0.52	0.75	0.17	0.16
		G3	b1
			bL
	Other	G1		DA, T1, T2, T3, T4, T5, T6, T7, T8, T9, T12, T13, T14, T15, T16, T17, T19, T21, T25, T26, T27
				PD	T22	T28
		G2	b1	0.69	0.61	0.22
			bL	0.55	0.74	0.36
				T10	T11	T18	T20	T23	T24
		G3	b1	0.23	0.28	0.49	1.35	1.06	0.23
			bL	0.04	0.06	0.27	1.12	0.90	0.40
kVp		G1		DA, PD, T2, T3, T15, T20, T23, T27
				T1	T4	T6	T7	T9	T10	T11	T12	T13	T14	T16	T17	T18	T19	T21	T22	T25	T26
		G2	b1	0.85	0.67	0.62	0.36	0.67	0.23	0.25	0.49	0.48	0.68	0.48	0.44	0.42	0.57	0.44	0.65	0.19	0.38
			bL	0.89	0.53	0.56	0.43	0.56	0.36	0.40	0.57	0.56	0.75	0.54	0.57	0.53	0.63	0.57	0.74	0.14	0.35
				T5	T8	T24	T28
		G3	b1	0.78	0.68	0.57	0.51
			bL	0.57	0.87	0.13	0.12
mAs		G1		DA, T2, T3, T10, T11, T15, T19, T20, T23, T25, T26, T27
				PD	T1	T7	T8	T12	T13	T14	T16	T17	T18	T21
		G2	b1	0.69	0.84	0.38	0.70	0.49	0.49	0.64	0.49	0.42	0.43	0.42
			bL	0.56	0.89	0.42	0.85	0.56	0.55	0.77	0.54	0.53	0.54	0.53
				T4	T5	T6	T9	T22	T24	T28
		G3	b1	0.73	0.94	0.69	0.75	0.60	0.58	0.53
			bL	0.51	0.50	0.53	0.54	0.76	0.13	0.12

^aFor age, BMI, kVp, and mAs, b₁ and b_L correspond to the lowest and highest level, respectively. For ethnicity, b₁ represents the White subgroup and b_L corresponds to the African-American (AA) or to the Other or missing (Other) subgroups.

TABLE V.

Tests for interactions for Vendor 2. Slope of the line fitted between feature values in processed versus raw images for the first (b₁) and last (b_L) level^a of each interaction factor in case of Vendor 2. Features are classified into three groups, corresponding to G1: nonstatistically significant interaction (95% confidence intervals including zero value), G2: limited interaction (|b₁ − b_L| ≤ 0.15), and G3: high interaction (|b₁ − b_L| > 0.15) with the corresponding factor.

Age		G1		T1, T4, T5, T6, T10, T11, T12, T13, T17, T18, T19, T21, T24, T28
				T2	T9	T14	T26	T27
		G2	b1	0.71	0.15	0.16	0.25	0.25
			bL	0.81	0.11	0.09	0.17	0.17
				DA	PD	T3	T7	T8	T15	T16	T20	T22	T23	T25
		G3	b1	0.48	0.75	2.85	1.85	1.40	0.33	0.66	1.24	0.31	0.57	0.22
			bL	0.22	0.42	1.70	1.14	0.96	0.61	1.06	0.94	0.11	0.20	0.06
BMI		G1		T1, T3, T8, T10, T11, T12, T13, T14, T18, T19, T24
				T2	T4	T6	T15	T22	T26	T27	T28
		G2	b1	0.70	0.09	0.09	0.39	0.26	0.32	0.33	0.03
			bL	0.77	0.03	−0.04	0.52	0.20	0.19	0.19	−0.02
		G3		DA	PD	T5	T7	T9	T16	T17	T20	T21	T23	T25
			b1	0.64	0.68	0.20	1.23	0.27	1.16	0.13	1.22	0.13	0.60	0.54
			bL	0.23	0.40	0.04	2.13	0.10	0.69	−0.43	1.05	−0.43	0.33	0.11
Ethnicity	AA	G1		T2, T7, T8, T12, T13, T14, T16, T18, T19, T22, T24, T26, T27, T28
				PD	T1	T4	T5	T6	T9	T15	T20	T23	T25
		G2	b1	0.70	0.87	0.06	0.12	0.02	0.18	0.42	1.19	0.53	0.26
			bL	0.60	0.94	0.04	0.06	−0.03	0.12	0.53	1.10	0.42	0.18
				DA	T3	T10	T11	T17	T21
		G3	b1	0.50	2.69	0.45	0.64	0.03	0.03
			bL	0.33	2.23	0.71	0.96	−0.22	−0.22
	Other	G1		DA, PD, T1, T2, T4, T5, T7, T8, T9, T10, T11, T12, T13, T14, T15, T16, T17, T18, T19, T20, T21, T22, T24, T25, T26, T27, T28
				T6	T23
		G2	b1	0.02	0.53
			bL	−0.02	0.44
				T3
		G3	b1	2.69
			bL	2.14
kVp		G1		T1, T6, T9, T10, T11, T12, T13, T14, T15, T16, T18, T20, T22, T24
				DA	PD	T2	T4	T5	T23	T25	T26	T27	T28
		G2	b1	0.47	0.67	0.71	0.05	0.13	0.52	0.27	0.27	0.27	0.02
			bL	0.35	0.57	0.77	0.05	0.08	0.41	0.22	0.23	0.24	−0.01
				T3	T7	T8	T17	T19	T21
		G3	b1	2.61	1.43	1.21	0.08	1.43	0.08
			bL	2.06	2.34	1.45	−0.26	1.78	−0.26
mAs		G1		T10, T11, T15, T17, T21, T24, T25, T26, T27, T28
				T1	T2	T4	T5	T6	T9	T14	T20	T22
		G2	b1	0.96	0.76	0.05	0.29	0.00	0.15	0.15	1.08	0.25
			bL	0.83	0.71	0.03	0.28	−0.07	0.09	0.21	1.21	0.31
				DA	PD	T3	T7	T8	T12	T13	T16	T18	T19	T23
		G3	b1	0.24	0.55	2.23	1.48	1.16	1.03	1.07	1.07	0.82	1.66	0.38
			bL	0.56	0.78	2.73	2.02	1.38	0.49	0.40	0.05	0.51	1.19	0.65

^aFor age, BMI, kVp, and mAs, b₁ and b_L correspond to the lowest and highest level, respectively. For ethnicity, b₁ represents the White subgroup and b_L corresponds to the African-American (AA) or to the Other or missing (Other) subgroups.

APPENDIX C: CORRELATIONS WITH GAIL RISK, BREAST DENSITY, AND BILATERAL SYMMETRY

TABLE VI.

Parenchymal texture feature correlations with established risk factors and assessment of bilateral breast symmetry. Correlation coefficients with the Gail lifetime risk score (r_G), breast percent density PD (r_PD), and (c) per-woman (i.e., intraclass) correlation (ICC), for raw and processed digital mammograms.

	Vendor 1						Vendor 2
	Raw images			Processed images			Raw images			Processed images
Feature	rG	rPD	ICC	rG	rPD	ICC	rG	rPD	ICC	rG	rPD	ICC
T1	−0.08	−0.05	0.69	a	−0.07	0.69	−0.16	−0.47	0.82	−0.09	−0.57	0.86
T2	a	a	0.12	a	a	0.12	a	−0.17	0.11	a	−0.27	0.24
T3	a	−0.04	0.28	−0.05	a	0.38	0.03	−0.09	0.36	0.04	0.04	0.74
T4	0.04	a	0.85	0.05	−0.07	0.82	0.17	−0.08	0.83	0.29	0.56	0.84
T5	−0.05	a	0.89	a	−0.21	0.77	0.07	−0.33	0.85	0.19	0.33	0.55
T6	0.08	0.08	0.92	0.08	0.30	0.88	−0.03	0.41	0.91	−0.19	−0.49	0.81
T7	0.12	0.13	0.93	0.14	0.32	0.88	0.05	0.54	0.94	0.07	0.49	0.84
T8	a	0.10	0.93	a	0.15	0.83	−0.08	0.29	0.92	−0.17	−0.13	0.84
T9	a	a	0.90	a	−0.18	0.85	0.10	−0.25	0.88	0.24	0.40	0.85
T10	0.04	0.15	0.53	0.04	a	0.31	0.04	−0.11	0.58	0.11	0.03	0.82
T11	a	0.11	0.60	a	−0.04	0.31	0.05	−0.19	0.66	0.12	0.06	0.82
T12	0.13	0.17	0.87	0.18	0.30	0.91	0.03	0.51	0.91	a	0.09	0.77
T13	0.12	0.16	0.88	0.16	0.28	0.92	a	0.50	0.92	−0.04	a	0.77
T14	0.22	0.11	0.77	0.15	0.34	0.73	0.22	0.40	0.84	0.13	0.58	0.88
T15	−0.24	−0.07	0.57	a	−0.06	0.47	−0.21	−0.30	0.72	a	−0.14	0.70
T16	0.07	0.12	0.90	0.10	0.22	0.92	a	0.43	0.92	−0.12	−0.26	0.78
T17	0.15	0.23	0.71	0.19	0.22	0.79	0.04	0.49	0.82	0.19	0.36	0.79
T18	a	0.06	0.76	a	−0.09	0.43	0.08	−0.23	0.80	0.17	0.21	0.80
T19	0.10	0.09	0.93	0.12	0.23	0.74	a	0.50	0.93	−0.05	0.06	0.81
T20	−0.22	−0.22	0.80	−0.21	−0.33	0.75	−0.16	−0.45	0.83	−0.04	−0.22	0.77
T21	0.15	0.23	0.71	0.19	0.22	0.79	0.04	0.49	0.82	0.19	0.36	0.79
T22	−0.21	−0.07	0.77	−0.14	−0.22	0.73	−0.19	−0.49	0.84	−0.07	−0.44	0.85
T23	0.19	0.21	0.88	0.23	0.27	0.85	0.04	0.46	0.90	0.11	0.47	0.78
T24	0.07	0.13	0.80	0.09	−0.05	0.66	0.15	−0.22	0.71	0.06	0.17	0.11
T25	0.12	0.04	0.73	a	a	0.58	0.18	−0.04	0.80	0.25	0.72	0.90
T26	−0.14	−0.09	0.85	−0.15	−0.17	0.76	−0.23	−0.15	0.86	−0.23	−0.70	0.92
T27	−0.15	−0.09	0.85	−0.15	−0.17	0.76	−0.23	−0.15	0.86	−0.23	−0.70	0.92
T28	−0.07	−0.13	0.81	−0.10	0.05	0.65	−0.15	0.22	0.73	−0.07	−0.21	0.19

^aNonstatistically significant correlations at the α = 0.05 level.

CONFLICT OF INTEREST DISCLOSURE

Dr. Conant reports membership on the Hologic, Inc., Scientific Advisory Board. Since the original work was conducted, Dr. Keller has accepted a new position with Hologic, Inc. The other authors have no relevant conflicts of interest to disclose.