Performance of a clinical gridded electron gun in magnetic fields: Implications for MRI-linac therapy

Abstract

Purpose:

MRI-linac therapy is a rapidly growing field, and requires that conventional linear accelerators are operated with the fringe field of MRI magnets. One of the most sensitive accelerator components is the electron gun, which serves as the source of the beam. The purpose of this work was to develop a validated finite element model (FEM) model of a clinical triode (or gridded) electron gun, based on accurate geometric and electrical measurements, and to characterize the performance of this gun in magnetic fields.

Methods:

The geometry of a Varian electron gun was measured using 3D laser scanning and digital calipers. The electric potentials and emission current of these guns were measured directly from six dose matched true beam linacs for the 6X, 10X, and 15X modes of operation. Based on these measurements, a finite element model (FEM) of the gun was developed using the commercial software opera/scala. The performance of the FEM model in magnetic fields was characterized using parallel fields ranging from 0 to 200 G in the in-line direction, and 0–35 G in the perpendicular direction.

Results:

The FEM model matched the average measured emission current to within 5% across all three modes of operation. Different high voltage settings are used for the different modes; the 6X, 10X, and 15X modes have an average high voltage setting of 15, 10, and 11 kV. Due to these differences, different operating modes show different sensitivities in magnetic fields. For in line fields, the first current loss occurs at 40, 20, and 30 G for each mode. This is a much greater sensitivity than has previously been observed. For perpendicular fields, first beam loss occurred at 8, 5, and 5 G and total beam loss at 27, 22, and 20 G.

Conclusions:

A validated FEM model of a clinical triode electron gun has been developed based on accurate geometric and electrical measurements. Three different operating modes were simulated, with a maximum mean error of 5%. This gun shows greater sensitivity to in-line magnetic fields than previously presented models, and different operating modes show different sensitivity.

1. INTRODUCTION

MRI-linac guided radiotherapy is being actively developed and implemented by several groups as the logical next step in the evolution of radiation therapy. Since MRI-linac radiotherapy requires that an electromagnetically sensitive electron accelerator functions within the magnetic fringe field of an MRI scanner, the emergence of MRI-linac radiotherapy has driven increased efforts in linear accelerator simulation amongst the medical physics research community. Operation of the electron gun in external magnetic fields is one of the most sensitive and studied aspects of integrated MRI-linac systems,^1–5 and is the focus of this paper. An electron gun is used to inject a steady stream of electrons at kilovoltage (kV) energies into an accelerating waveguide, where they are accelerated to megavoltage (MV) energies. Assuming that the linear accelerator is of the straight ahead type (no bending magnet), the electron gun is the most sensitive part of the accelerator to external magnetic fields, as slow moving electrons are less magnetically stiff.

Two classes of electron gun are used in medical accelerators; diode and triode (or gridded).⁶ Diode electron guns have only two separate electric potentials; the cathode and focusing electrode, which are set to some negative voltage (typically on the order of tens of kilovolts) and the anode, which is held at ground. In a triode gun, a control grid is added just above the surface of the cathode. The grid is held at a third potential, typically within around one hundred volts of the cathode potential. However, because it is close to the cathode, this can create strong variations in the electric field at the cathode surface, and hence emitted current. The focusing electrode is held at the same electric potential as the grid in this configuration. A schematic of a triode electron gun is shown in Fig. 1.

FIG. 1.

(A) Photograph of the electron gun modeled in this work. On the left side is the cathode section, and on the right side is the anode section. (B) A rendering of the gun geometry developed based on a laser scan of the electron gun. (C) A photograph of the grid taken through a microscope lens.

Whilst diode electron guns are suitable for use in simple, low energy machines, the majority of linear accelerator manufacturers utilize a triode electron gun.^6,7 This is because a triode gun allows far more flexibility than a diode gun can achieve; for a given beam energy any beam current can be achieved, and for a given current any beam energy can be achieved (within physical limitations).⁸ This is not the case in diode guns, where the current and energy of the beam are intrinsically linked. It also allows a very simple and stable beam gating mechanism, as only a few hundred volts need to be switched to turn on or off the beam. On linear accelerators which use diode guns, beam gating must be carried out by radiofrequency (RF) pulse interruption methods, and this appears to result in quite long beam on/off latency.^9,10 Triode guns are also important for treatment machines which provide multiple treatment energies, and both photon and electron treatment modes. This is because both the target heating and the dose rate are correlated with the product of beam current and beam energy. In order to keep these parameters within an acceptable range, it is often desirable to decrease beam current when beam energy is increased. For electron therapy, the beam current must be further decreased, as the dose conversion efficiency is orders of magnitude higher.

Although the MRI-linac devices investigated in the published literature to date appear to utilize diode electron guns,^11–13 recent publications have focused on the potential of multimode MRI-linac devices to improve achievable dose distributions for deep seated tumors,^14,15 and beam gating using MRI-linacs.^16,17 As such, it is clear that triode electron guns are likely to find useful application in the next generation of MRI-linac systems. However, to date all published work in this area has focused on the performance of diode electron guns in magnetic fields. Further, no technical details on medical triode guns can be found in the literature. Therefore, the purpose of this work is two-fold; (1) to present an accurate model of a medical triode electron gun such that it may be utilized by future researchers and (2) to test the sensitivity of this gun in magnetic fields, in particular to assess whether different operating modes show different sensitivity to magnetic fields.

2. MATERIALS AND METHODS

2.A. Theory and background

The geometric structure of the electron guns typically used in medical linacs can be broadly classified as a Pierce gun.¹⁸ Electron guns in medical accelerators are operated in a steady state, and as such the physics of the system is essentially electrostatic and is described by Poisson’s law [Eq. (1)]

$${\displaystyle {\nabla }^{2}V=\frac{p}{{\epsilon }_0},}$$ (1)

where V is the electrostatic potential, p is the charge density (defined by the beam), and ε₀ is the electric vacuum permittivity. Although formulating the problem exclusively in terms of Poisson’s equation does neglect the self-magnetic fields of the beam, it has previously been shown that these effects are small for these guns.³

Accurate computational simulation of a DC electron gun comprises three important sub steps. The first is to calculate the electrostatic field arising from the applied electrode potentials and space charge of the beam, the second is to approximate thermionic electron emission in the presence of this electric field, and the third is to track the emitted electrons through this field. These steps are not independent of each other; therefore an iterative solving technique is required. Calculating the net electric field of the electrode and beam is a complicated problem, and for accurate results computational electrodynamics is required, in which complex geometry is discretized (meshed) into many subdomains. Examples of appropriate computational schemes include the finite element method and the finite difference technique.

Medical electron guns are typically operated in a space-charge limited mode of thermionic emission. This means that current is extracted from a hot (around 1200 K) cathode and is limited by the space charge associated with the cloud of electrons already extracted. The major advantage of operating in this regime is stability, as small fluctuations in temperature or cathode emissivity have minimal impact on emitted current. Space charge limited emission in one dimension is described by Child’s law [Eq. (2)]

$${\displaystyle J_{\mathrm{emitted}}=\frac{4{\epsilon }_0}{9}\sqrt{\frac{2q}{m_0}}\frac{V^{3/2}}{d^2},}$$ (2)

where J_emitted is the emission current, ε₀ is the permittivity of free space, q and m₀ are the electron charge and mass, and V is the potential difference at distance d from the cathode, and is a function of both the electrode potentials and the beam itself.⁶ Modelling thermionic emission is one of the most challenging aspects of electron gun simulation. In 2D or 3D, the above formulation is only strictly valid for an infinite planar diode, and so for realistic geometries the cathode face is discretized into a number of smaller faces over which the 1D formulation is applied. In order to ensure that this approach is valid, V must be sampled at a specified distance from the discretized faces, typically less than 1 mm. The presence of a grid adds further complexity to the simulation, as the sampling distance and meshing parameters become more sensitive. If the Maxwell-Boltzmann distribution of the emitted electrons is considered, the situation becomes still more complex. A detailed discussion of the various thermionic emission effects is beyond the scope of this paper, but is provided in Ref. 19.

The over-riding purpose of an electron gun in a therapeutic system is to inject a stream of electrons into the accelerating wave guide. An important figure of merit for the system performance is the capture efficiency—that is, the percentage of electrons injected into the linac which actually reach the target. It is obvious that for optimal capture efficiency, the injected electrons should have low transverse velocities and be confined to a small region of space around the axis of the accelerator. Both requirements can be quantified by examining the distribution of the electron beam in phase space. Phase space is a 6D position-momentum space: [x,y,z,px,py,pz]. However, for DC electron guns the longitudinal components are trivial, and the x and y components identical. Therefore, the beam can be sufficiently described in a 2D transverse phase space [x,px] along with information about the beam energy and current. It is often convenient to describe the phase space in terms of a divergence angle instead of transverse momentum: x′ = px/pz. This is referred to as trace space.

In order to characterize a distribution in phase space or trace space, one can fit an ellipse to the particle distribution. The most common approach to this is to calculate Twiss parameters, also known as the Courant-Snyder parameters. These parameters can be used to describe an ellipse which will encircle the central part of the beam. Mathematically, these are described as follows:

$${\displaystyle {\epsilon }_{x,\text{RMS}}=\sqrt{〈x^2〉〈x^{\prime 2}〉-{〈x{x}^{\prime }〉}^2},}$$ (3)

$${\displaystyle \alpha =〈x{x}^{\prime }〉/{\epsilon }_{x,\text{RMS}},}$$ (4)

$${\displaystyle \beta =〈x^2〉/{\epsilon }_{x,\text{RMS}}.}$$ (5)

The Twiss parameters allow one to quickly infer a lot of useful information about the beam. ε_x,RMS [Eq. (3)] quantifies the area of the beam in phase space; larger emittance corresponds to less ordered electron beams. α [Eq. (4)] determines the orientation of the ellipse, which describes whether a beam is diverging or converging. Another interpretation of α is that it reflects the distance from a beam waist. At a beam waist, α is zero, and the average transverse electron velocities are zero—an opportune time to capture the electron beam in an RF accelerator. The (RMS) beam width in space is described by $\sqrt{{\epsilon }_{x,\text{RMS}}.\beta }$. In the absence of space charge, accelerating fields, and non-linear transverse fields (conditions which are approximately met in a field free drift tube), emittance as defined in Eq. (3) is a constant, whilst the other parameters evolve as a function of the longitudinal component z. The RMS emittance only encapsulates the central 37% of the beam. Some authors add a factor of 4 or π to this definition in order to better describe the full beam. Unfortunately, it is often unclear exactly which definition is being used, which can make it difficult to compare different results. In this work, emittance is calculated according to Eq. (3) without any additional factors. Units of mm and mm rad are used.

2.B. Gun geometry

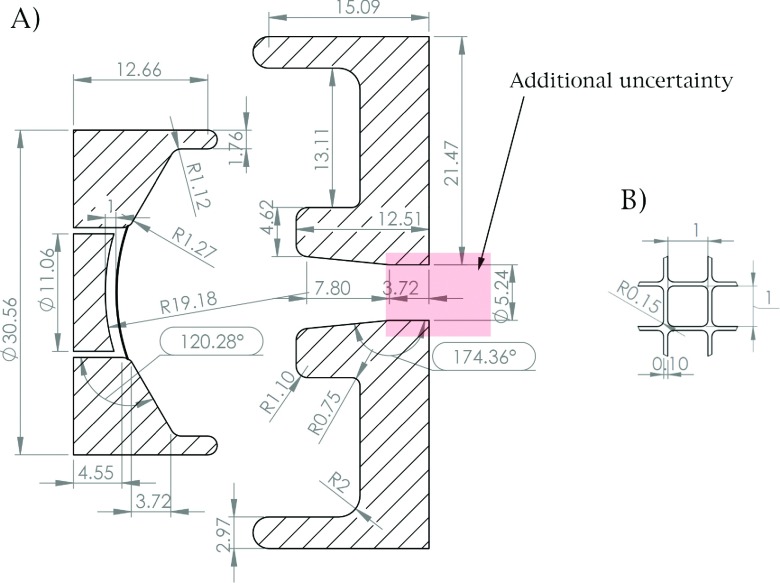
A commercial electron gun from a Varian high-energy linac was obtained through a spare parts supplier [Fig. 1(A)]. The geometry of the gun was measured using a 3D laser scanner operated by a third party engineering company.²⁹ The scan was rated as being accurate to within 0.1 mm. The control grid was too fine to be resolved by the 3D scan; in order to measure curvature of the grid, a thin film was placed over the grid and measured in a separate 3D scan. The wire thickness and spacing of the grid were measured using digital calipers (error rating of 0.01 mm). A microscope image of the grid is shown in Fig. 1(C). Based on these measurements, a geometrical model of the gun was developed. This geometry is detailed in the results Sec. 3.A and Fig. 2.

FIG. 2.

(A) Detailed sketch of the geometry used in this study measured by a 3D laser scanner. (B) A section of the measured grid geometry. Dimensions are in mm and degrees. The geometry of the anode drift tube is subject to additional geometric uncertainty as indicated by the shaded region.

2.C. Finite element model (FEM) of gun

A FEM of the gun geometry from Sec. 2.B was developed using the commercial software opera/scala, version 16 (Kidlington, UK). opera solves Poisson’s equation in the presence of thermionic electron emission. Child’s law was used to simulate thermionic space charge limited emission [Eq. (2)]. The type 1 emitter option (virtual cathode) was used, which is the most accurate model according to the opera user manual. The initial electron energy was set to the mean of the Maxwell-Boltzmann equation for a temperature of 1245 K (a typical dispenser cathode temperature). It is possible to sample additional energies from the Maxwell-Boltzmann distribution, but this significantly increases simulation time and does not strongly affect the solution. Opera requires that the user inputs a sample distance where the program calculates the electric field, which was set to 0.25 in this work. Importantly, this distance is less than 1/3 the cathode-grid spacing, as recommended in the opera user manual. The emitted electron current is strongly dependent on the electric field at the cathode, which in turn is altered by emitted current. Therefore, an iterative simulation procedure is required for accurate electron gun simulation. In this study, the convergence tolerance was 0.001; the model is considered solved when the relative RMS change in potential is less than this. A maximum limit of 21 iterations was set; in practice, the models normally resolved within ten iterations. Wherever possible, symmetry in the model was exploited and only a quarter of the geometry was solved, greatly reducing computational resources. The quarter model was discretized into around three million tetrahedral elements. In electron gun simulations, a high quality mesh near the cathode is crucial, as the emitted current is critically dependant on an accurate solution of the electric field here. We used quadratic elements of maximum size 0.15 mm near the cathode, and 1 mm elsewhere. To check for mesh independence, we also created a model with doubled mesh density and verified that the solution did not change. In opera, the number of macro particles representing the beam is a product of the mesh density, so this step also confirmed the number of macro particles was adequate to represent the beam. The emission current comprised of ∼15000 macro particles.

Next, parameter sweeps were carried out over the high voltage and grid voltage. The high voltage was varied from −5 to −30 kV in 5 kV steps, whilst the grid voltage was varied from 20 to 140 V in 7.5 V steps. The grid voltage is always quoted relative to the high voltage, and the focusing electrode is set to the same boundary condition as the grid. The electron beam phase space and current were extracted from the solved models for axial planes spaced every 2 mm, 21–39 mm from the cathode. This information was imported into matlab version 2014 (Nattick, MA) and an in house code was used to calculate the transverse emittance and current. The current emitted from the cathode was also recorded for each simulation.

2.D. Experimental measurement of gun operating modes

Although the above process allows one to derive approximate working regions of the gun for a given high voltage, it does not provide information about the conditions in which the gun is actually operated clinically. In order to acquire experimental data regarding the operating modes used clinically, the high voltage, grid voltage, and emission current were read directly from the console of six dose matched Varian TrueBeam linacs (Varian, Palo Alto) in service mode. Data were acquired for the 6X, 10X, and 15X photon modes, and 2D interpolation of the data from Sec. 2.C was used to compare simulated emission current as function of high voltage and grid voltage with the experimentally measured values. Based on these results, three gun models were built to represent the 6X, 10X, and 15X modes of operation.

2.E. Grid height determination

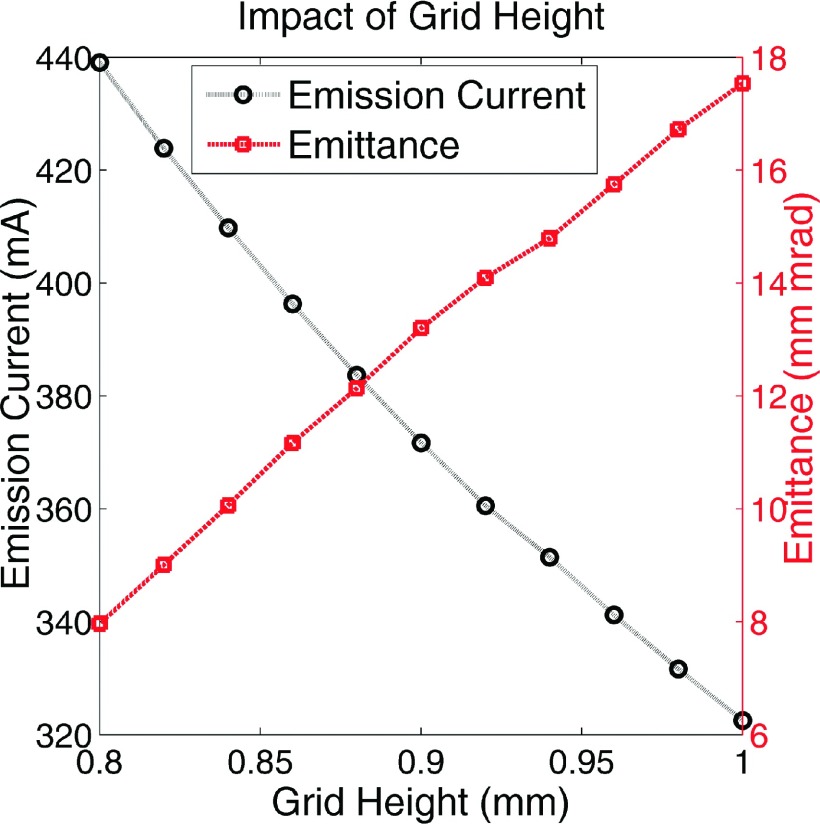
The most sensitive parameter in the model is the spacing between the grid and the cathode (grid height). Unfortunately, this is also the parameter with the largest uncertainty. This is because the grid had to be measured separately during the laser scan, and so in the worst case scenario the error could be 0.2 mm—that is, 0.1 mm from each scan. In order to obtain the best match to the experimental data (Sec. 2.D), we repeated the simulations characterizing beam parameters as a function of the electrode potentials (Sec. 2.C) for three different grid heights—0.84 (as measured by the 3D scan), 0.9, and 1.0 mm. The simulated emission current for each case was compared to the experimental data. The model with the grid height of 1.0 mm gave the best match to the experimental data, and is used throughout Sec. 3 (except for Sec. 3.D where data on the grid height determination are presented). As is also detailed in this section, the grid height does not have a major impact on the beam phase space other than beam current.

2.F. Gun sensitivity to magnetic fields

In order to test the sensitivity of the gun to magnetic fields, the opera FEM models of the 6X, 10X, and 15X photon beams based on Sec. 2.D were solved in constant parallel fields in-line and perpendicular to the beam direction. In-line field strengths of 0–200 G were tested in 10 G steps, and perpendicular field strengths from 0 to 35 G in 5 G steps. These values were chosen on the basis of being representative of the fringe field of MRI scanners in various proposed MRI-linac configurations, and being of adequate range to characterize the behaviour of the gun. As the gun is small (∼30 mm beam length), constant parallel fields provide a very close approximation to the averaged heterogeneous MRI fringe fields across the gun. For each simulation, the current and transverse phase space at the gun exit were recorded.

3. RESULTS

3.A. Gun geometry

Figure 2 shows a detailed sketch of the geometry used in all simulations.

The shaded part of the anode drift tube in Fig. 2 is subject to additional uncertainty beyond the 0.1 mm of the 3D laser scan. This is because the 3D scan has a limited ability to “see” down a narrow tube. The tapered section of the anode was measured with the 3D scan. After this, we extended the length of the anode drift tube with a straight cylinder, as this geometry best matches other available schematics of Varian triode guns⁶ and is consistent with previously published models.^2,3 However, it is also possible that the taper continues to some minimum. This part of the geometry can be very important for mitigating back bombardment,²⁰ and can have a strong effect on the gun sensitivity to in-line magnetic fields. This is discussed in Sec. 4.

3.B. Finite element model of gun

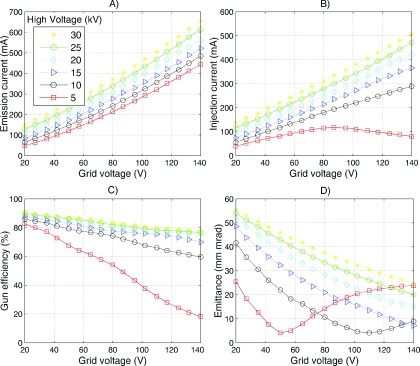
Figure 3 shows the particle trajectories of the solved model. Particles are color coded according to their kinetic energy. Figure 4 shows various gun metrics plotted as a function of both HV and grid voltage; (A) emission current, (B) injection current (current injected into the waveguide), (C) efficiency (injection current as percentage of emission current), and (D) emittance in trace space. The injection current is always less than the emission current as some part of the beam is blocked by the grid. This fraction increases as the grid voltage is turned up, which makes it more electrically attractive to electrons [Fig. 4(C)]. Also, if the current becomes too large, then the focusing electrode will no longer focus the beam, leading to further current loss from anode collisions. This effect can clearly be seen in the 5 and 10 kV series of Fig. 4(C). The emittance changes as total field (electrodes + space charge) changes. It can be seen that there is a certain amount of current which creates a minimum in emittance for a given HV setting. The data shown in Fig. 4(A) were used to compare the models to the experimental data in Sec. 3.C and optimize the model, as outlined in Sec. 3.D.

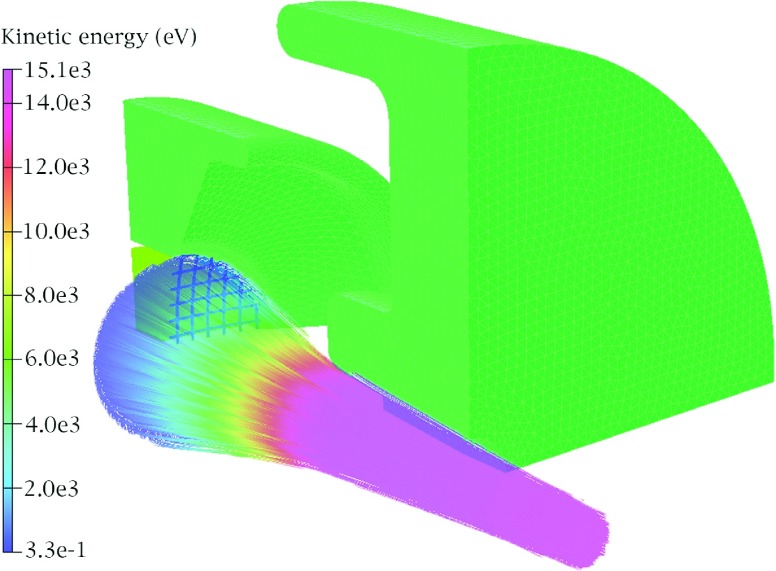
FIG. 3.

Gun solution at zero magnetic field. The 6X mode is shown and the particle trajectories are colored according to their energy. The solid structures represent one quarter of the gun geometry with the surface FEM mesh displayed.

FIG. 4.

(A) Emission current, (B) injection current (current injected into the waveguide), (C) gun efficiency (percentage of the emission current which exits the gun), and (D) emittance as a function of grid voltage (x axis) and high voltage (different series).

3.C. Experimental measurement of gun operating modes

The values for HV and grid voltages measured on the six TrueBeam linacs are shown in Table I, along with the interpolated emission current based on the data from Sec. 3.B. The mean absolute error in emission current between experimental and simulated data across the six Linacs is 3.2%, 5.1%, and 3.5% for the 6X, 10X, and 15X modes. Note that the fourth entry in the 10X measurements has been excluded from these averages, as the HV is clearly an outlier compared to the other linacs.

TABLE I.

Gun parameters (HV, grid voltage, and gun current) measured from six dose-matched TrueBeam linacs. The italicized entry for 10X was not included in this study, as the HV value is clearly an outlier compared to the other five data points. Note that error reported in the “mean” row for each mode is the absolute mean of all errors.

Mode	Measured high voltage (kV)	Measured grid voltage (V)	Measured emission current (mA)	Simulated emission current (mA)	% Error
6X (6 MV X rays)	14.998	105.6	373.4	372.8	−0.2
	14.971	87.7	323.9	308.2	−4.9
	14.965	95.3	341.6	331.4	−3.0
	15.023	87.0	320.9	306.1	−4.6
	14.989	92.8	306.3	323.8	5.7
	14.928	86.4	299.4	303.0	0.0
Mean	14.979 ± 0.03	92.5 ± 7.4	327.6 ± 26.8	322 ± 27	3.3 (absolute)
10X (10 MV X rays)	9.998	47.3	142.4	139.5	−2.0
	9.992	40.2	130.5	119.0	−8.8
	9.958	37.5	119.7	110.8	−7.4
	12.012	39.1	140.7	125.3	−11.1
	10.001	42.4	120.2	125.3	4.2
	9.946	40.6	123.5	119.9	−2.9
Mean	9.979 ± 0.025	41.6 ± 3.6	127.3 ± 9.5	122.9 ± 10.6	5.1 (absolute)
15X (15 MV X rays)	10.996	62.2	193.0	190.0	−1.6
	10.99	76.0	243.1	235.9	−2.9
	10.941	72.2	226.7	223.2	1.5
	11.02	62.8	197.8	191.6	−3.1
	10.993	72.6	207.6	224.9	8.3
	10.923	72.4	217.1	223.8	3.1
Mean	10.98 ± 0.03	69.7 ± 5.7	214.2 ± 18.8	214.0 ± 19.0	3.4 (absolute)

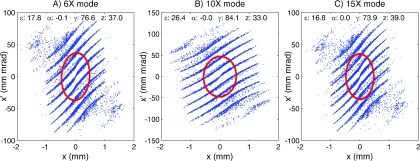
Based on the results in 3.1–3.3, three models were arrived at to represent the 6X, 10X, and 15X modes of operation. The beam current and energy for each mode are reported on in Table II. These data differ from the data shown in Table I in that they are solved explicitly rather than being interpolated from Sec. 3.B. The beam waist occurred at 38, 33, and 39 mm from the centre of the cathode for the 6X, 10X, and 15X mode, respectively. The phase space at the beam waist (or nearest sample plane) for each mode is shown in Fig. 5 (beam waist and phase space are defined in Sec. 2.A). The impact of the grid can clearly be seen in the segmented nature of the phase space distribution.

TABLE II.

The parameters used for each of the clinical mode simulations.

Mode	High voltage (kV)	Grid voltage (V)	Emission current (mA)	Injection current (mA)	Emittance (mm mrad)
6X	15	93	323	246	17.8
10X	10	42	124	100	26.4
15X	11	70	214	164	16.8

FIG. 5.

Phase space at the beam waist for the (A) 6X, (B) 10X, and (C) 15X modes. Printed on each plot are the Twiss parameters and resultant RMS phase ellipse, as described in Sec. 2.A. The z parameter is the distance from the cathode in mm.

3.D. Grid height determination

The results shown in all other sections of this paper are for a model with a cathode to grid height of 1 mm, as detailed in Fig. 2. However, the measured value was 0.84 mm. In this section we detail how this value was optimized. Table III shows the mean error for each mode for grid heights of 0.84, 0.9, and 1.0 mm (note that all these values are within the experimental uncertainty of the measured geometry). The model with grid height of 1.0 mm returned the lowest mean error values when compared to the experimental data in Table I. Figure 6 shows the impact of changing the grid height for the 6X mode. At first glance, it may appear that altering the grid height has a dramatic impact on the gun emittance—however, this is not quite correct. Altering the grid height has a strong impact on emission current, which does strongly impact emittance [also apparent in Fig. 4(D)]. However, for the range of grid heights investigated here, similar emittance is achieved when similar current is drawn from the cathode. As a representative example: for grid height 0.84 mm, HV = 15 kV, and grid = 93 V, 410 mA of current is extracted and the emittance is 10 mm mrad. For grid height 1.0 mm, the same current is drawn with the grid set to 115, resulting in an emittance 12 mm mrad. This gives a better indication of the impact altering the grid height on the phase space distribution.

TABLE III.

Mean error in simulated emission current for each mode for three different grid heights, compared to the experimental data in Table I.

	Mean error (%)
Mode	Grid height: 0.84 mm	Grid height: 0.9 mm	Grid height: 1.0 mm
6X	34	14	−2
10X	30	12	−3
15X	37	16	0

FIG. 6.

Impact of the grid height on the emission current and the emittance for the 6X mode. Note that the change in the emittance is primarily due to the changing current rather than the changing grid height.

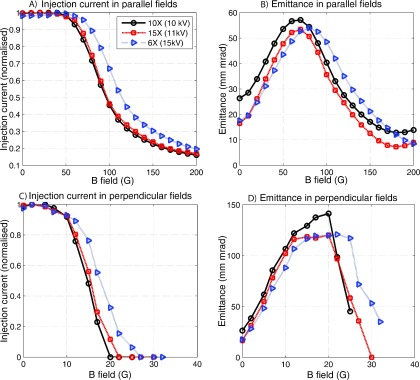
3.E. Gun sensitivity to magnetic fields

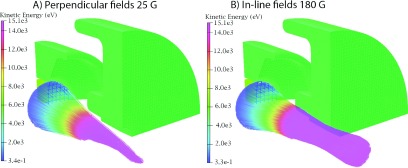
Figure 7 shows examples of the particle trajectories of the 6X mode in both (A) in-line and (B) perpendicular fields, whilst Fig. 8 shows the injection current and emittance results of operation in magnetic fields for the 6X, 10X, and 15X modes. The emittance results should be interpreted with caution; emittance only enables a particularly useful comparison between beams when the total current and energy are the same. For instance, for the in-line case, as the magnetic field increases the outer electrons are scraped off by the anode, the emittance begins to decrease—however, this comes at the cost of substantially reduced current.

FIG. 7.

Examples of particle trajectories in (A) perpendicular fields of strength 25 G and (B) in-line fields of strength 180 G. Note that only one quarter of the geometry is shown so that the particle trajectories can be seen. The 6X mode is shown and the particles are color coded according to their energy. The equivalent figure for zero field trajectories is shown in Fig. 3.

FIG. 8.

Injection current for in-line (A) and perpendicular (B) fields, and emittance for in-line (C) and perpendicular (D) fields.

Table IV shows a comparison of the three Pierce type electron guns which have previously been simulated in magnetic fields with this work. It can be seen that this model is around twice as sensitive in in-line magnetic fields as previously tested models. The sensitivity in in-line magnetic fields is primarily a function of the HV setting and the ratio of the cathode-to-anode radius. The sensitivity in perpendicular fields on the other hand is primarily a function of the HV setting; as such this model shows slightly less sensitivity to perpendicular fields than previously published models which used a lower HV setting.

TABLE IV.

A summary of previously published results of electron gun models in magnetic fields, and this work. The “sensitivity” metric in columns 3 and 4 is simply the field where the first beam loss occurs. Not all authors reported on this exactly, in which case it was graphically derived from plots and the “∼” symbol is used.

Model	Reference	In-line field sensitivity (G)	Perpendicular field sensitivity (G)	Gun type	Boundary conditions	Geometry
Litton	3	∼163	2	Non-gridded	From the literature	From the literature
Varian	3	∼141	5	Non-gridded	From the literature	From the literature
Alberta	1 and 5	100	NA	Non-gridded	Measured	Inferred
This work		40	7.5	Gridded	Measured	Measured

4. DISCUSSION

We have developed a finite element model of a clinical triode (i.e., gridded) electron gun based on accurate geometric and electrical measurements. The model matches emission current measured on six TrueBeam linacs to within 6% across the 6X, 10X, and 15X operating modes (Sec. 3.C). To the best of our knowledge, this is the first time in the literature that a model of a medical triode electron gun has been published. This work also contrasts with previous publications which examined electron gun sensitivity in external magnetic fields, in that measured (rather than inferred) geometry was used (Table IV). Previous studies have either tested models which are no longer used clinically³ or have inferred the gun geometry based on measurements of emission current and high voltage.² Regarding the latter approach, it is worth noting that this is a degenerate problem, meaning that multiple geometries can produce the same emission current at a given high voltage. This is important as gun geometry directly affects sensitivity to magnetic fields—particularly for the in-line case. The model simulated in this work is approximately twice as sensitive to operation in in-line magnetic fields as previous models.

Utilizing a gridded gun results in low beam on/off latency, which is an important aspect of a real time system architecture, and a current area of research for MRI-linac systems.^16,17 Gridded guns are also important in applications where continuously variable dose rate is desired, such as arc therapy.⁶ In addition, the grid enables much better control over beam parameters such that desirable phase space distributions can be injected into the waveguide over a wide range of HV and current settings. This control is important for multimode linacs, because the current which arrives at the target must be appropriate when considering both dose rate and target heating. Multimode electron accelerators are a current area of research for MRI-linacs.^14,15

Of the major manufactures, Tomotherapy, Cyber-Knife, and Siemens all utilize gridded guns. Varian uses gridded guns on multimode systems, and diode guns on low energy guides. On the other hand, Elekta utilizes diode guns even on its multimode guides.^21,22 Very long gating times (on the order of seconds) have been observed on these linacs, making them unsuitable for a real time system.^9,10 Interestingly, there is at least one system designed for real time treatments which does use a diode gun; the Brainlab Vero. This system only uses one beam mode, and is powered by a klystron.⁷ Although we could not find any data on the beam latency of the Vero system, a klystron based system would likely have much lower latency than a magnetron based system, since the RF drive power could be very quickly switched. MRI-linac systems utilizing only one beam mode could feasibly be constructed with good beam latency using a klystron based power source and diode gun—however, klystrons are more expensive and complex than magnetrons, and so it may still prove simpler to utilize a triode gun.

A number of comments can be made about the results in this paper. Most strikingly, this model was at least twice as sensitive to in-line magnetic fields as previously published models (Sec. 3.E). Including this work, four Pierce type electron gun models have now been tested in silico in magnetic fields (Table IV), and based on the amalgamated results some general comments on the most important parameters impacting gun sensitivity can be made. For perpendicular fields, the most important characteristic is the high voltage setting (HV). Larger HV means that the beam becomes more magnetically stiff, or difficult to bend. The model tested here is more robust in perpendicular fields than some previous studies,³ primarily due to the larger HV setting used. The HV is also an important factor for in-line fields, however here the geometry of the gun plays a larger role; specifically, the ratio of the cathode radius to the (minimum) anode radius. The larger this ratio, the more the electron beam must be focused to fit through anode, and this focusing is strongly affected by in-line magnetic fields. The two previous studies which tested electron guns in in-line magnetic fields both found that below 100 G, no beam loss occurred. The model investigated here shows substantially greater sensitivity, as the beam begins to drop off at 50 G. Also, due to the fact that different operating modes use different HV settings, different operating modes show different sensitivity.

The design of the anode drift tube is a particularly interesting aspect of gun performance in in-line magnetic fields. When one simulates an electron gun in silico (and without magnetic fields), this geometry has negligible impact on the results, as long as it is large enough for the beam to pass through unimpeded (it is essentially a field free region). In a real system which is coupled to a linac, however, the design of this geometry is crucial, as the anode drift tube plays a key role in mitigating cathode damage from back-accelerated electrons.²⁰ In order to minimize the amount of back-accelerated electrons reaching the cathode, the drift tube should have a minimum radius corresponding to the minimum beam radius. By choosing the injection point to be close to the beam waist, the minimum anode radius can be made as small as possible, minimizing the amount of back accelerated electrons which can return to hit the cathode. On the other hand, a drift tube design like this would substantially increase sensitivity to in-line magnetic fields. As indicated in Sec. 3.A, there was additional uncertainty in the dimensions of this geometry in this work due to limitations of the 3D scanning technology. As well as this, typically when these guns are replaced, the cathode section [Fig. 1(A), left] is simply bolted to the end of the accelerating waveguide, which also serves as the anode. The anode that ships with the gun is for the purpose of high voltage and cathode processing;³⁰ this strongly implies that the field forming (i.e., internal) parts of the anode are identical to the true anode. However, the internal dimensions of the drift tube may differ from this, as they will have negligible impact on high voltage and cathode processing. Given these sources of uncertainty, the sensitivity of this gun to in-line magnetic fields may be even greater than simulated in this work—which was already twice as sensitive as previous work.

We observed quite large uncertainty in simulated emission current, as this was extremely sensitive to the spacing between the grid and cathode (Sec. 3.D). We measured this as accurately as possible, but still observed variations in emission current of over 30% over the range of grid heights simulated. In the real world this uncertainty would not be a major issue; if the current were more or less than predicted, the grid voltage could be adjusted accordingly (Fig. 4). Indeed, when examining the variability in operating parameters of the six different guns measured in Table I, this appears to be exactly what is done practically.

This model operates at much higher emittance than previously published work.^2–4 Low emittance indicates a more ordered beam, and in general lower emittance results in decreased loss through a beam transport line. However, there is no published data on how important emittance actually is in medical accelerators, and there are no published data regarding the measured emittance of medical electron guns. Part of the reason for the increased emittance is the fact that the beam is simply larger than previous simulations (cathode radius of 5.53 mm compared to 2.31 mm). Given the accuracy with which we have measured the geometry, and the fact that we have closely matched the emission current across multiple modes, we believe that the phase space we have calculated is likely to be highly representative of reality.

A suprising aspect of this work was that the 15X mode used a substantially higher injection current than the 10X mode (Sec. 3.C). As beam energy increases, bremsstrahlung conversion efficiency increases, as does beam power (for the same current). As such, we expected to see injection current drop as the photon energy increased. A possible explanation for this result is the fact that different operating modes will have different capture efficiencies, and it may simply be that the 15X mode has lower capture efficiency than the 10X mode. Another factor is the different tungsten targets and flattening filters utilized for different operating modes.

The results in this paper along with the results presented in previous papers (Table IV) have some very clear implications for the design of electron guns which are to be used in MRI-linac systems. First, operating at a higher HV setting results in substantially increased robustness in magnetic fields (Sec. 3.E). However, whilst certainly achievable, redesigning an electron gun to operate at higher HV is not trivial. The HV setting directly affects the velocity of electrons injected into the waveguide, and for a given waveguide (and operating mode) there will be an injection velocity which is optimal. Additionally, higher HV increases the electrical hazard and risk of breakdown and arcing in the gun. Secondly, for in line fields the gun becomes more robust as the ratio of cathode radius to anode radius decreases - however, this ratio also effects the amount of current drawn from the gun and/or back bombardment power, and so it must be carefully optimized.

Although there have been proposals to redesign electron accelerators to function within magnetic fields,^4,20 at this stage all systems appear to be using conventional equipment in conjunction with magnetic shielding. It is therefore interesting to note that the external dimensions of this triode gun are much larger than the model which was previously investigated for shielding.²³ This means that as well as being more sensitive to magnetic fields, this gun would be more difficult to shield, as shielding could not be placed as close to the beam (unless internal shielding was incorporated during the manufacture stage). Whilst a triode gun design will require more complex housing to some extent, it is not clear how easily the gun could be made smaller, or whether other triode guns would also be this large.

The effects of electron beam collisions with the control grid were not modeled in this work. These include heating of the grid, electron scatter, and secondary electron emission. The former phenomenon leads to grid damage and heating. If the grid becomes hot enough, it can become a thermionic emitter and source of “dark current” (i.e., current which occurs even when the gun should be gated). Moreover, secondary electron emission will occur from the grid, which degrades the overall beam quality.²⁴ Although the electrons hitting the grid have energy of less than 100 eV (determined by the grid voltage) the grid is thermally light and in a vacuum, so it is plausible that substantial heating occurs. A back-of-the envelope calculation would suggest that intersection of the emitted electrons with the grid may not be a major issue in terms of heating; the forward beam power at the grid is of order 30 W, of which only ∼20% or 6 W will actually hit the grid [Sec. 3.B, Fig. 4(C)]. Meanwhile, the power from backward-accelerated electrons can be on the order of kilowatts.²⁰ The fact that the duty cycle of the gun is of the order 0.001 will further mitigate heating of the grid.⁶ Nevertheless, the impact of collisions between the emitted electrons and control grid is clearly significant enough in real world applications to have been the subject of a large body of work aimed at reducing them—mainly by utilizing some form of “shadow grid” which reduces the number of electrons intercepting the grid.^25–28 Both mechanical and chemical shadow grids have been proposed in the literature. The gun modeled in this work has no visible form of shadow grid; to check if some kind of chemical shadow grid may be present, we scanned the cathode surface using Raman spectroscopy. Raman spectroscopy provides information on chemical bonds via laser probing. We were not able to detect any presence of any shadow grid using this technique—however we cannot say with absolute certainty that one is not present.

In this work, we have developed and presented an FEM model of a clinical triode electron gun which matches available experimental data to within 5%, and characterized its performance in perpendicular and in-line magnetic fields. This is the first time we are aware of that a model of a clinical triode gun has been published in the literature. The modeled gun shows greater sensitivity to in-line magnetic fields than previously presented models, and different operating modes show different sensitivity.

CONFLICT OF INTEREST DISCLOSURE

Dragos Constantin is currently employed by Varian Medical Systems. Rebecca Fahrig is currently employed by Siemens Healthcare.