Longitudinal zonation pattern in Arabidopsis root tip defined by a multiple structural change algorithm

Abstract

Background and Aims The Arabidopsis thaliana root is a key experimental system in developmental biology. Despite its importance, we are still lacking an objective and broadly applicable approach for identification of number and position of developmental domains or zones along the longitudinal axis of the root apex or boundaries between them, which is essential for understanding the mechanisms underlying cell proliferation, elongation and differentiation dynamics during root development.

Methods We used a statistics approach, the multiple structural change algorithm (MSC), for estimating the number and position of developmental transitions in the growing portion of the root apex. Once the positions of the transitions between domains and zones were determined, linear models were used to estimate the critical size of dividing cells (L_critD) and other parameters.

Key Results The MSC approach enabled identification of three discrete regions in the growing parts of the root that correspond to the proliferation domain (PD), the transition domain (TD) and the elongation zone (EZ). Simultaneous application of the MSC approach and G2-to-M transition (CycB1;1DB:GFP) and endoreduplication (pCCS52A1:GUS) molecular markers confirmed the presence and position of the TD. We also found that the MADS-box gene XAANTAL1 (XAL1) is required for the wild-type (wt) PD increase in length during the first 2 weeks of growth. Contrary to wt, in the xal1 loss-of-function mutant the increase and acceleration of root growth were not detected. We also found alterations in L_critD in xal1 compared with wt, which was associated with longer cell cycle duration in the mutant.

Conclusions The MSC approach is a useful, objective and versatile tool for identification of the PD, TD and EZ and boundaries between them in the root apices and can be used for the phenotyping of different genetic backgrounds, experimental treatments or developmental changes within a genotype. The tool is publicly available at www.ibiologia.com.mx/MSC_analysis.

INTRODUCTION

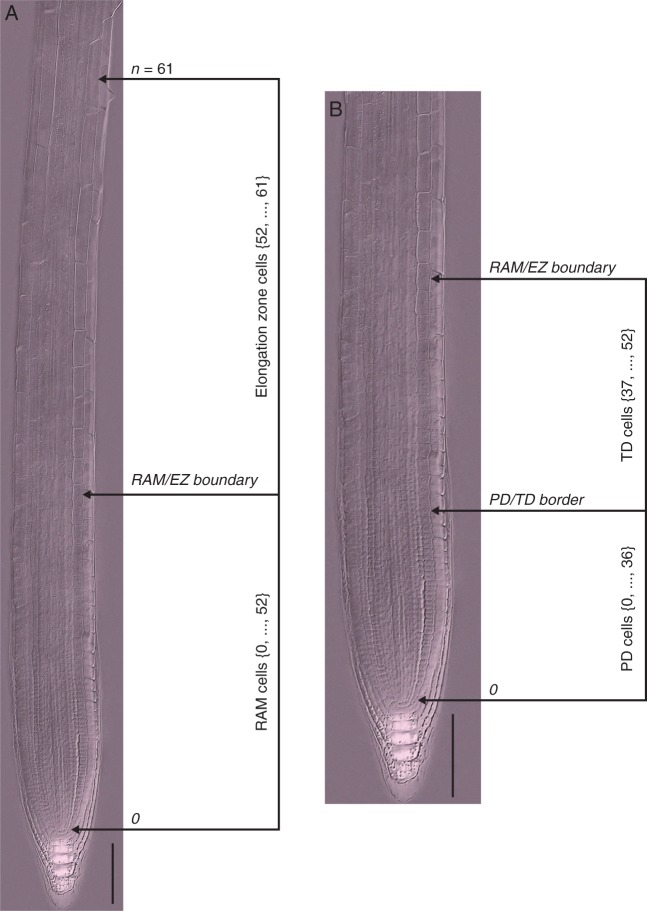
Plant growth and development are regulated by the combined activity of two processes that are closely linked: cell division and cell elongation. Fully elongated cells undergo terminal differentiation. Reliable and quantitative characterization of both processes in organs is thus essential for understanding their role during development. The Arabidopsis thaliana (arabidopsis) root is an important model system for molecular genetics and cellular studies of plant development, including understanding cell cycle regulation and the balance of proliferation and differentiation in complex organs. The root is an excellent model system because of, among other characteristics, its relatively simple longitudinal organization and the possibility of observing different developmental stages in the same root along its longitudinal axis. Another advantage of the root is that it has few cell types, organized concentrically around the vascular tissues, composed of xylem, phloem, vascular parenchyma and pericycle. Outside of the vascular tissues there are concentric rings of cells of endodermis, cortex and epidermis, covered at the very tip by the lateral root cap and columella cells. The growing part of the root consists of two zones: the root apical meristem (RAM) and the elongation zone (EZ) (Fig. 1A).

Fig. 1.

Anatomical topology of the arabidopsis root. (A) The root apical meristem (RAM) and elongation zone (EZ) of a wt arabidopsis Col-0 seedling root 7 d after sowing; composite image from a cleared root preparation. (B) RAM of the root shown in (A). The numbers represent cell positions with respect to QC (zero position). The n position corresponds to the first cortex cell adjacent to an epidermal cell that started to form a root hair bulge. Scale bars = 100 μm.

Microphotograph was published in Ivanov V.B., Dubrovsky J.G. 2013. Longitudinal zonation pattern in plant roots: conflicts and solutions. 2013. Trends in Plant Science, 18:237–243. Reproduced with permission of Elsevier.

The RAM includes the proliferation domain (PD), where cells have a high probability of dividing, and the transition domain (TD) (Baluška et al., 1996). The most distal portion of the PD contains the quiescent centre (QC), a stem cell niche, surrounded by the initial (stem) cells (Clowes, 1956; Dolan et al., 1993; Sabatini et al., 2003). In the TD domain cells can still divide but at a low probability and continue elongating at the same low rate as in the PD. Hence, cells in this domain are slightly longer than cells in the PD (Fig. 1B) (Ivanov and Dubrovsky, 2013). The EZ is the zone where cells of different tissues simultaneously start rapid elongation at rates much higher than those in the RAM. The EZ is followed by the differentiation zone (DZ), where elongated cells reach their final length and differentiation state. The rootward border of the DZ corresponds to the position at which cell elongation ceases (van der Weele et al., 2003; Ivanov and Dubrovsky, 2013). Therefore, identification of the boundary between the EZ and DZ is straightforward and is based on either cell length profile data or the appearance of the first root hair bulges, which is a hallmark of termination of elongation (Dolan et al., 1993; Ma et al., 2003; Dolan and Davies, 2004). Despite the importance of being able to fully characterize the apical–basal patterning of the root tip, no consensus on the domains and zones in the arabidopsis root apex has been attained (Ivanov and Dubrovsky, 2013). Here we applied a statistical algorithm for determining the number of zones and domains in the growing part of the root and the limits between neighbouring zones and domains. Our results support the existence of three discrete regions in the growing part of the arabidopsis root: the PD, the TD and the EZ.

A rigorous qualitative and quantitative description of these zones and domains and identification of their boundaries are essential for understanding the effects of different genetic, chemical and physical alterations of cell proliferation, growth, and differentiation during root growth and development. Comparisons between different experimental conditions require approaches that enable accurate evaluations of the size and number of cells within the RAM or its PD. This is generally done in the cortex cell layer (Casamitjana-Martínez et al., 2003; Dello Ioio et al., 2007; Tsukagoshi et al., 2010; Zhou et al., 2011; Garay-Arroyo et al., 2013). However, the lack of objective criteria and subjectivity in identifying the boundaries between root growth zones and domains indicates the need for development of new approaches.

Several previous papers have approached this problem. For example, Scheres and collaborators (Casamitjana-Martínez et al., 2003) determined the boundary between the RAM and the EZ as the point where cells begin to increase their lengths significantly. The onset of rapid cell elongation and absence of cell division in the EZ are taken as the only criterion to distinguish between these two regions. Although useful for rough qualitative evaluations, without measuring cell lengths the identification of the point where rapid elongation starts may vary among researchers. A relatively more objective way of determining this boundary implies finding the position at which cell length in a file is more than twice that of the previous cell (González-García et al., 2011). The latter method may yield biased results: before rapid elongation starts, a longer cell can be followed by a shorter cell in the TD, indicating that this criterion is not always sufficient for objective establishment of the RAM/EZ boundary. Recently, a geometric approach for identification of the point at which cell elongation starts was proposed that yields results similar to those obtained arbitrarily (French et al., 2012). This and other studies (Dello Ioio et al., 2007; Moubayidin et al., 2010; Tsukagoshi et al., 2010) do not specify how to identify the border between the PD and the TD of the RAM. Changes in cell proliferation precede the transition to rapid cell elongation: the mitotic index (percentage of dividing cells) decreases drastically (Ivanov and Dubrovsky, 2013) and endoreduplication starts (Hayashi et al., 2013). For this reason, the PD/TD boundary is associated with changes in cell proliferation, whereas the RAM/EZ boundary defines the point where a drastic shift to rapid elongation occurs.

The position of the PD/TD boundary is particularly difficult to establish because it fluctuates in time within a cell file and, additionally, is frequently different among different files of cells of the same type or different types (Baluška and Mancuso, 2013; Ivanov and Dubrovsky, 2013). Because of this, the PD/TD boundary can only be approximated with a certain error, which should be estimated (Ivanov and Dubrovsky, 2013). The position of this boundary can be determined as the point where average cell length along the RAM has slightly increased, or where the distances between nuclei in neighbouring cells along a cell file become greater than the diameter of the nuclei (Rost and Baum, 1988; Dubrovsky et al., 1998a, b; Garay-Arroyo et al., 2013). It is also possible to locate the beginning of the TD as the position where the mitotic index sharply decreases for the tissue under consideration (Ivanov and Dubrovsky, 2013). Nonetheless, the latter approach is difficult to implement and it is not valid for all species. All such criteria can lead to variable and subjectively defined boundaries and/or require considerable experience from the researcher in order to guarantee reproducible and reliable data. Because of the importance of each of the root developmental domains and/or zones in the cell proliferation/differentiation balance (Dello Ioio et al., 2007; Moubayidin et al., 2010; Tsukagoshi et al., 2010), establishing the PD/TD and RAM/EZ boundaries is essential for a complete phenotypical description of the root. This requires a quantitative approach, which enables the unambiguous identification of the different development stages along the root longitudinal axis.

Here, to identify the location of the PD/TD and RAM/EZ boundaries we applied a multiple structural change algorithm (MSC) to cell length profile data collected on fixed root preparations. Because the position of the EZ/DZ boundary corresponds to the location where root hair formation starts, this location can be used as a qualitative criterion to determine the shootward border of the EZ. For this reason the EZ/DZ boundary can be easily established, and is not considered in this study. We show here that by using the polygonal models obtained from a MSC algorithm it is possible to estimate: (1) the lengths of the PD, the TD and the EZ; (2) the distances from the QC at which the different developmental transitions start; (3) the critical sizes of dividing and transitioning to the EZ cells; and (4) the derivative of cell length as a function of position or gradient in cell length (Silk et al., 1986). We also show that the MSC yields similar results to those obtained with molecular markers that have been used to determine the PD/TD boundary, as well as those obtained by arbitrary estimations made by researchers experienced in root developmental biology.

XAANTAL1 (XAL1) or AGL12 is a member of the MADS box family of genes, which encode transcription factors important for regulating plant and animal development. This gene participates in the regulation of cell proliferation in the arabidopsis RAM (Tapia-López et al., 2008). Loss-of-function allelic mutants have shorter roots and lower root growth rates than wild type (wt), explained by a shorter RAM, lower rates of cell production and a longer cell cycle duration than wt roots (Tapia-López et al., 2008). We used the proposed MSC approach to analyse arabidopsis wt and loss-of-function xal1-2 (hereafter xal1) mutant roots. We found that XAL1 is necessary for the increase in length of the PD during the first days after seed germination and its loss of function altered the critical size of dividing cells. This example illustrates that the MSC approach is useful for root phenotyping at the cellular level and for comparing different experimental conditions or genotypes, and can be applied to better understand changes in cell growth rates, the distribution of cell divisions and, changes in the critical size of dividing cells and the longitudinal zonation pattern.

MATERIALS AND METHODS

Plant materials and growth conditions

Arabidopsis wt, xal1, CycB1;1_DB:GFP and pCCS52A1:GUS are in Col-0 ecotype. C24 and Col-0 were obtained from the Arabidopsis Biological Resource Center at the Ohio State University. Seeds carrying pCCS52A1:GUS were kindly donated by E. Kondorosi and CycB1;1_DB:GFP was constructed by P. Doerner (Ubeda-Tomás et al., 2009). All lines were homozygous; seeds were surface-sterilized and 2 d after vernalization sown on medium containing 0·2× MS (Murashige and Skoog) salts, 1 % sucrose and 1 % agar (except for CycB1;1:GFP seeds; see below). Petri dishes were maintained in vertical position. Plants were grown under long-day (16 h light/8 h dark) conditions in growth chambers at 22–24 °C. Seeds of the CycB1;1_DB:GFP line were plated on agar media N103 and N3003 that contained 0·3 % sucrose supplemented with 1 (N103) or 30 (N3003) mm of total nitrogen (N) (final concentrations of other components of the media were: CaCl₂ [3 mm], MgSO₄ [1·5 mm], KH₂PO₄ [1·5 mm], 1× MS microelements, MES [5 mm], sucrose, 3 g L⁻¹, pH 5·6). After 2–7 d of vernalization, Petri dishes were transferred to growth chambers with constant light and maintained in vertical position. Root growth increments were recorded daily by marking the root tip position over the surface of the dish and increments were measured using ImageJ (http://rsb.info.nih.gov/ij).

Microscopy

In seedlings 7–9 d after sowing (DAS), roots were cleared using Herr’s solution (Herr, 1971), which contains lactic acid (85 %), chloral hydrate, phenol, clove oil and xylene (2:2:2:2:1 by weight). Excised roots were transferred to Herr’s solution for at least 24 h at room temperature and subsequently mounted in the same solution and visualized using an Olympus BX60 microscope equipped with Nomarski optics and photographed.

pCCS52A1:GUS seedlings were subjected to the β-glucuronidase (GUS) reaction in the dark for 1 h at 37 °C and GUS staining solutions were prepared as described by Malamy and Benfey (1997). To restrict the diffusion of GUS blue precipitate, 2 mm K₃Fe(CN)₆ and K₄Fe(CN)₆ were added to the solution at the beginning. After GUS staining, seedlings were immersed in Herr’s clearing solution and stored in the dark at room temperature for 72 h and visualized as described above.

For simultaneous observation of the nuclei and green fluorescent protein (GFP) fluorescence (CycB1;1_DB:GFP), 7-DAS seedlings were fixed in 4 % formaldehyde in phosphate-buffered saline (PBS) solution supplemented with 0·05 µg mL^−l (final concentrations) of 4′,6-diamidino-2-phenylindole (DAPI) overnight at 4 °C. Preliminary experiments showed that this procedure did not quench the fluorescence activity of GFP. Then, material was washed in PBS four times (10 min each), mounted and analysed. Roots were mounted in a drop of PBS, covered with a coverslip and observed under an inverted laser scanning confocal Leica TCS NT microscope with a 63× HCX PL APO water immersion Leica objective. After the optical median section of the apical root portion was found, the intensity of the signal was set by using the look-up tables included in the Leica software. DAPI and GFP channels were set separately and colour intensity was always set to a standard for each individual root at a low scanning speed. These same settings for colour intensity and offset were used for more proximal root portions. Final scanning of each root portion was done sequentially, first for GFP and then for DAPI, and the average of four scans was saved as a TIF file. To improve contrast between the DAPI and GFP channels, images of GFP fluorescence were pseudo-coloured in magenta. Images of two channels of each root portion were merged and then the whole root tip image was assembled in Adobe Photoshop 5.5. from four to eight originally saved files.

Quantitative analysis

We implemented a semi-automated procedure to systematically and accurately measure cell lengths. The algorithm was constructed based on Java SRE and ImageJ 1·4 libraries. This works properly for multi-platform environments such as Windows, Linux and Mac OS. The software (executable file: Cell_Length_V2·0.jar) and its user manual (Cell_Length_V2.0.pdf) are available at http://www.ibt.unam.mx/labimage/proyectos/arabidopsis.

Using Nomarski micrographs, cell length profiles were obtained by measuring a straight line from one end to the other with ImageJ or Cell_Length_V2·0.jar software along a cortex file from the QC to the first cortex cell adjacent to an epidermal cell that had started to form a root hair bulge (Fig. 1A). For confocal images the data on meristem length, number of cells in the meristem, the fraction of GFP-expressing cells and root thickness were collected from assembled images. Root thickness was measured at the level corresponding to the PD/TD boundary for cortex determined by experienced biologists, which implies a subjective method, abbreviated here as the ExpBiol method. The PD/TD boundary determined by an ExpBiol method was defined for epidermis and cortex, arbitrarily based on relative changes in cell lengths or internuclear distances along the root, similar to other studies (Rost and Baum, 1988; Dubrovsky, 1997; Dubrovsky et al., 1998a, b; Tapia-López et al., 2008; Garay-Arroyo et al., 2013).

All statistical analyses were performed using R (R Foundation for Statistical Computing, version 2.15.1). MSC analyses, including estimation of the optimal number of breakpoints with the Bayesian information criterion (BIC) and estimation of breakpoint positions with their 95 % confidence intervals (CI) for all cell length profiles were performed using the breakpoints function of the R ‘strucchange’ package (Zeileis et al., 2002, 2003). The breakpoints function estimates multiple breakpoints simultaneously, implementing an algorithm that obtains global minimizers of the sum of squared residuals (Bai and Perron, 2003). Examples of MSC analyses using the breakpoints function are provided (Supplementary Data Text S1). The distribution function for the 95 % CI for the breakpoints is given in Bai (1997). For comparison of the results obtained with ExpBiol and MSC analyses, the intraclass correlation coefficient (ICC) was estimated (model, two-way; type, absolute agreement; unit of analysis, average measures) (McGraw and Wong, 1996; Hallgren, 2012). The ICC and its 95 % CI were calculated using the R ‘irr’ package (Matthias et al., 2012). We also developed a publicly available web site (www.ibiologia.com.mx/MSC_analysis), where the MSC algorithm can be performed.

RESULTS

Previously, van der Weele and collaborators (2003) concluded that the root has a velocity profile with linear phases (RAM, EZ and differentiation zone) separated by abrupt transitions. Based on this conclusion, we propose that cell length profiles, where cell length (L) is a function of cell position with respect to the QC (i), can be fitted by a polygonal model, also known as piecewise, segmented, broken-line regressions, multi-phase regressions or multiple structural change (MSC) models (Bai and Perron, 2003; Muggeo, 2003). In these models the points where the behaviour or response of the dependent variable, as a function of the independent one, change abruptly are commonly called breakpoints, change points, transition points or switch points (Muggeo, 2003). In the cell length profiles, the breakpoints correspond to the boundary between adjacent developmental zones (Fig. 1A, B).

There is no consensus about the existence of the TD in roots. Thus, the analysis of the longitudinal zonation pattern of the arabidopsis root apex consists of two main problems: establishing the number of domains and zones, and determination of the position of the breakpoints between them. Here, we show that an MSC approach can be productively used for solving these problems and objectively establishing the longitudinal patterning in the arabidopsis growing root portion.

The growing part of the root consists of three discrete regions

The problem of single and multiple structural changes in linear models has been studied mainly in statistics, econometrics and medicine (Auger and Lawrence, 1989; Bai and Perron, 1998, 2003; Kim et al., 2000; Muggeo, 2003). We know that the growing part of the arabidopsis root has at least one transition or breakpoint that corresponds to the RAM/EZ boundary. Some authors propose also the existence of a TD formed by a group of cells elongating at the same rate as the PD cells but with a very low probability of division. In contrast, other authors consider that such a domain does not exist. If the TD actually exists, then a polygonal model with two breakpoints can be obtained from cell length profiles of single cell files, and such breakpoints would correspond to PD/TD and RAM/EZ boundaries.

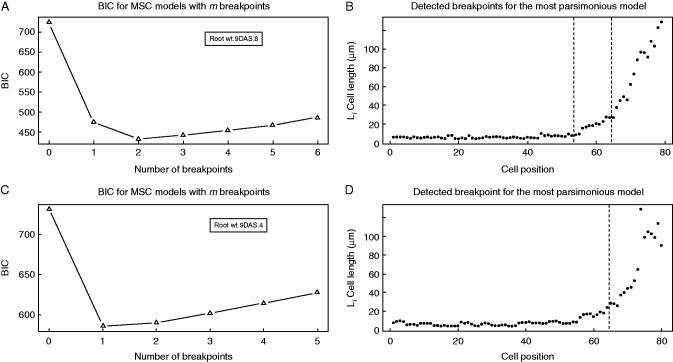
There are several procedures to estimate the number of breakpoints in MSC models (Yao, 1988; Liu et al., 1997; Bai and Perron, 1998, 2003; Kim et al., 2000, 2009). Comparing different methods for selecting the number of breakpoints, Bai and Perron (2003) concluded that the BIC (Yao, 1988) works well when there is at least one breakpoint, and Kim et al. (2009) also indicate that the BIC performs well in picking up small changes. This method adjusts the sum of squared residuals for models with different numbers of breakpoints, and the model with the lowest BIC value is accepted as the most parsimonious. To establish the number of regions in the growing part of the root, we analysed arabidopsis Col-0 wt and xal1 roots at two different ages, 7 and 9 DAS, without specifying the number of expected breakpoints. From cleared roots we obtained the cell length profile of a cortex cell file, from the QC to the first cortex cell adjacent to an epidermal cell that formed a root hair bulge (Fig. 1A). For each cell length profile we estimated MSC models with different numbers of breakpoints and their positions.

We found that for 58 % of Col-0 cell length profiles analysed (23 out of 40 cell files) the most parsimonious model was of two breakpoints (Fig. 2A, B). In these cell length profiles the most shootward breakpoint corresponded to the RAM/EZ boundary and the rootward breakpoint corresponded to the PD/TD boundary. In 42 % of cell length profiles analysed in Col-0 (17 out of 40 cell files), the most parsimonious model was of that of one breakpoint. This breakpoint corresponded to the RAM/EZ boundary (Fig. 2C, D). We found also that for these roots the second most parsimonious model was that with two breakpoints. When this model was applied, the same the RAM/EZ boundary was found, and additionally the PD/TD boundary was identified within the RAM.

Fig. 2.

Estimation of the number of breakpoints and their position by an MSC–BIC approach in Col-0 wt cortical cell length profiles. (A, C) MSC–BIC models with m breakpoints for representative cell length profiles shown in (B) and (D). The lowest value of BIC corresponds to the most parsimonious model for number of breakpoints within a cell file. (B, D) Representative cell length profiles of wt 9-DAS seedlings. Vertical dashed lines represent the breakpoint position estimated by an MSC approach.

Similar modelling was performed for the xal1 mutant. Out of 40 cell length profiles analysed, the most parsimonious model was of one, two and three breakpoints in 30, 62 and 8 % of the profiles (Supplementary Data Fig. S1). The small number of profiles with three breakpoints may represent an artefact as a consequence of greater variability in cell lengths. To verify the versatility of the approach, we compared Col-0 wt with a different wt accession, C24. We found that 17, 75 and 8 % of cases (n = 12 cortical cell length profiles) showed one, two and three breakpoints respectively (Supplementary Data Table S1).

Overall, our data support the existence of two developmental transitions in the growing part of the root. One of these transitions, the shootward, corresponds to the RAM/EZ boundary (Fig. 1A). In the next section, we will show that the second, rootward, transition corresponds to the PD/TD boundary (Fig. 1B).

The MSC modelling approach identifies the PD/TD boundary

Because the different domains and root growth zones are characterized by distinct and specific developmental processes, the distribution of unambiguous molecular markers for these processes could also be used to define the longitudinal zonation of the root (Ivanov and Dubrovsky, 2013). The distribution of molecular markers for the G2-to-M transition, CycB1;1_DB:GUS or CycB1;1_DB:GFP, has been used as a marker for the PD of the RAM (Colón-Carmona et al., 1999; Hauser and Bauer, 2000; Aida et al., 2004; Ticconi et al., 2004; Li et al., 2005; Cruz-Ramírez et al., 2012).

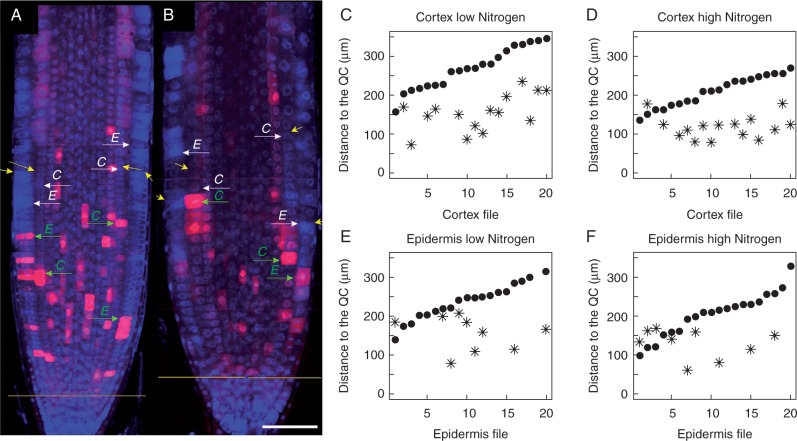
Cell length profiles were obtained from CycB1;1_DB:GFP roots grown on media with low (1 mm) and high (30 mm) concentration of total N. These cell length profiles were collected from assembled root images obtained under a confocal laser scanning microscope at a high magnification and for this reason did not include EZ cells. The CycB1;1_DB:GFP reporter detects cells in late G2 and early M phases of the cell cycle (Colón-Carmona et al., 1999). Therefore, the cell length profile was obtained for a root portion where GFP-positive cells were detected (presumptive PD) and shootward of this zone for a portion of at least half of the presumptive TD. Thus, if a breakpoint is detected, this should correspond to the PD/TD boundary. Roots grown on the media with high and low N content differed significantly in their growth rate and morphology and on medium with low N grew 2·5-fold faster than under high N (Table 1). This observation suggested that the PD would be of different lengths in seedlings grown under these contrasting conditions. Indeed, the PD length determined by the MSC approach was greater in low-N medium (Fig. 3).

Table 1.

Root growth and meristem characteristics in 7-DAS seedlings of CycB1;1_DB:GFP (BJ3) line grown in media with low and high concentrations of total N

	Low N			High N
	Mean (s.d.) (n)	95 % CI		Mean (s.d.) (n)	95 % CI
Root length (mm)	43·2 (6·9) (47)	41·2, 45·2		20·7 (5·3) (44)	19·1, 22·3
Rate of root growth during last 24 h (µm h−1)	400 (137) (47)	360, 440		160 (66) (44)	140, 180
Root thickness (μm)	146 (11) (29)	142, 150		123 (12) (36)	119, 127
Fraction of GFP-positive cells per cell file (%)
Epidermis	12·6 (7·5) (39)	10·2, 15·0		12·1 (9·8) (57)	9·5, 14·7
Cortex	11·7 (7·7) (35)	9·1, 14·3		13·9 (9·8) (43)	10·9, 16·9

Fig. 3.

Distribution pattern of CycB1;1_DB:GFP expression used as a molecular marker for PD determination and comparison of PD/TD border determinations by the ExpBiol method and MSC approach. (A, B) Root tip longitudinal median sections made by laser scanning confocal microscopy. GFP and DAPI channels were merged and images taken at different levels with respect to the root tip were assembled; the GFP signal is pseudo-coloured as magenta. (A) Roots grown on medium with 1 mm N. (B) Roots grown in medium with 30 mm N. Yellow arrows indicate the PD/TD boundary for cortex and epidermis files determined by ExpBiol based on changes in cell lengths or inter-nuclear distance; green arrows indicate the location within the PD where the cell expresses CycB1;1_DB:GFP and is closest to the PD/TD boundary in epidermis (E) or cortex (C) files; white arrows indicate the PD/TD boundary determined by the MSC approach. Scale bar = 50 μm. (C–F) X-axis numbers indicate different cell files analysed (n=10 roots, one file of cortex and one file of epidermis for each root). The position of the last PD cell determined by the MSC approach (black dots) and the position of the cells closest to the PD/TD boundary which expresses GFP (asterisks) in epidermis and cortex files for low- and high-N media are shown. Note that not each cell file had cells expressing CycB1;1_DB:GFP at the moment of fixation. For each condition, cell files are arranged in ascending order of the number of cells in the PD determined by the MSC approach.

The distribution of GFP-positive cells within the meristem was random (Fig. 3A, B). In most cases, those meristematic cells that were in mitosis were GFP-positive. The cells that were not in mitosis but were weakly GFP-labelled were cells in G2, as can be deduced from their size (these cells were approximately twice as long as recently divided cells). The breakpoint values estimated by the MSC approach corresponded to the last PD cells. Cells that expressed CycB1;1_DB:GFP at the moment of fixation were in most cases located rootward to the breakpoints estimated by the MSC approach (Fig. 3C–F), i.e. within the PD domain. Expression of CycB1;1_DB:GFP was found in a shootward position with respect to the breakpoint only in 6 % of cell files analysed (5 out of 80). These data indicate that the probability of cell division (GFP-positive cells) after the estimated breakpoint position was low, although rapid cell elongation had not yet started in the measured cell files. Our data indicate that the PD/TD breakpoint estimated by the MSC approach coincided well with the CycB1;1_DB:GFP expression pattern.

As mentioned above, changes in cell proliferation are associated with the PD/TD boundary before rapid elongation starts, and particularly, before the changes in elongation rates can be detected, cells enter the endoreduplicaction cycle (Hayashi et al., 2013). Thus, we proposed that the TD can also be defined as the region where cells start endoreduplication but have not yet started rapid elongation. Therefore, a molecular marker for endoreduplication could also be used to establish the PD/TD boundary. The CELL CYCLE SWITCH52A1 (CCS52A1) gene, an isoform of the substrate-specific activator of the anaphase-promoting complex/cyclosome (APC/C), promotes the onset of endoreduplication and its expression correlates with the transition from proliferation to endoreduplication (Vanstraelen et al., 2009). The pCCS52A1:GUS reporter gene (Vanstraelen et al., 2009) can be used as a molecular marker of the PD/TD boundary as it is expressed only in the TD and the EZ (Vanstraelen et al., 2009; Takahashi et al., 2013).

To test whether the breakpoint inside the RAM estimated by the MSC approach corresponds with the transition from proliferative state to endoreduplication, we obtained the cortex cell length profile of ten roots of the pCCS52A1:GUS reporter line. Using the MSC approach, we determined the breakpoint positions for these roots and estimated the 95 % CI of the position of the last PD cell of each cell file analysed. This position was close to the rootward (distal) border of the GUS-expressing region (seven out of ten cell files, or 70 %) (Fig. 4A–G). In 30 % of the analysed cell files, the last PD cell, estimated by the MSC approach was clearly in a more rootward position than the GUS-expressing region (Fig. 4H–J). Therefore, the PD/TD boundary estimated by MSC coincided with the onset of pCCS52A1:GUS expression in the majority of cases.

Fig. 4.

Determination of the PD/TD boundary in the CCS52A1:GUS line using the MSC approach; GUS expression marks the beginning of endoreduplication. (A–J) CCS52A1:GUS expression in wt roots (7 DAS) occurs in the TD and EZ. Yellow rectangles indicate the 95 % CI of the position of the last PD cell estimated by the MSC approach. Scale bar = 50 μm.

These data support the conclusion that the MSC approach enabled estimation of the position of the PD/TD boundary and this position coincided with the distribution of cells expressing the CycB1;1_DB:GFP marker and with the onset of pCCS52A1:GUS expression. This PD/TD transition occurred before rapid cell elongation started. Thus we conclude that there are two developmental transitions in the growing part of the root: PD/TD and RAM/EZ (Fig. 1A, B), the former related to changes in proliferation behaviour and the latter to the onset of rapid cell elongation.

Determination of the PD/TD boundary by the MSC approach coincides with subjective determination by an experienced root developmental biologist

In previous studies, the extension of the PD of the RAM was determined based on relative changes in cell length along a root meristem cell file. The PD/TD boundary has been determined at a point from the QC where, in the shootward direction, cell length or inter-nuclear distance increases significantly and where a cell becomes longer than the average cell length within the PD (Dubrovsky, 1997; Dubrovsky et al., 1998a, b; Tapia-López et al., 2008; Garay-Arroyo et al., 2013). Blind experiments to determine this boundary on the same roots by different biologists experienced in this technique (ExpBiol) gave similar results, but students or biologists that are inexperienced in this analysis obtained contrasting results (V.B.I., P.D. and J.G.D., unpubl. res.). Therefore, the ExpBiol is subject to biases depending on the researcher that conducts the analysis. Hence, we were interested in comparing the ExpBiol and MSC approaches to establishing the PD/TD boundary.

The PD/TD boundary was estimated on CycB1;1_DB:GFP roots grown on media with a low (1 mm) and high (30 mm) concentration of total N. Interestingly, PD length (estimated by ExpBiol) in arabidopsis varied depending not only on N availability but also among roots grown under the same nutrient conditions. The minimum–maximum numbers of cells in a cell file within the PD (estimated by ExpBiol) in individual roots were 13–41 (epidermis) and 24–48 (cortex) in low N and 9–30 (epidermis) and 10–29 (cortex) in high N. Considering this variation, we analysed the agreement between the PD/TD boundary estimated for each root when using the ExpBiol method and the MSC approach.

In statistics, inter-rater reliability (IRR) indicates ‘the degree of agreement between two or more coders who made independent ratings about the features of a set of subjects’ (Hallgren, 2012). To evaluate IRR for estimates of the number of PD cells obtained by the ExpBiol and MSC approaches, we calculated the intraclass correlation coefficient (ICC) (McGraw and Wong, 1996; Hallgren, 2012). Higher ICC values indicate higher agreement. An ICC estimate of 1 indicates perfect agreement and an estimate of 0 indicates only random agreement. The ICC estimated for all the CycB1;1_DB:GFP cell files was significantly greater than 0 [ICC =0·9, F(79,80) = 10·2, P = 2·44e−21, 95 % CI 0·85, 0·94], and was in the ‘excellent’ qualitative range proposed by Cicchetti (1994), confirming that the ExpBiol method (which has been traditionally used) and the MSC approach had a high degree of agreement as no statistical differences between the two approaches were detected (Table 2). Importantly, as determined by MSC analysis, in high-N medium the cortex PD length was ∼80 % shorter than that in roots grown in low-N medium. This indicates the versatility of the MSC approach. Given that different researchers may reach different results depending on their experience, the use of the MSC approach is recommended as it can eliminate subjective estimates and provide reproducibility within and across laboratories, irrespective of the experience of the observer.

Table 2.

Agreement between determinations of the PD/TD boundary by the ExpBiol method and the MSC approach in roots of CycB1;1_DB:GFP (BJ3) line (n=20)

	Distance from the PD/TD boundary to QC (μm)				Number of PD cells
	ExpBiol		MSC		ExpBiol		MSC
	Mean (s.d.)	95 % CI	Mean (s.d.)	95 % CI	Mean (s.d.)	95 % CI	Mean (s.d.)	95 % CI
Epidermis, low N	247 (37)	229, 264	241 (47)	218, 263	28 (10)	24, 33	27 (9)	23, 31
Epidermis, high N	199 (20)	190, 209	204 (57)	178, 231	18 (4)	16, 20	18 (5)	16, 21
Cortex, low N	245 (38)	227, 262	270 (54)	245, 295	33 (6)	30, 36	36 (6)	33, 39
Cortex, high N	195 (23)	185, 206	211 (40)	192, 229	22 (4)	20, 24	23 (5)	21, 26

The MSC approach can be used to estimate the critical size of dividing cells and the critical cell size for the initiation of rapid elongation

Organisms from bacteria to higher eukaryotes coordinate cell growth and cell division through size-sensing checkpoint mechanisms in order to maintain a constant cell size. Cells have to reach a certain critical size at which cell-cycle transitions are triggered, such as G1–S or G2–mitosis (Ivanov, 1971; Dobrochaev and Ivanov, 2001; Dolznig et al., 2004; Yang et al., 2006; Turner et al., 2012; Robert et al., 2014). Therefore, along the PD it is expected that cells are equal to or smaller than the critical size of dividing cells (L_critD). However, in the TD the probability of cell division is very low (Ivanov and Dubrovsky, 2013); therefore, cells that continue growing at the same relative growth rate as in the PD are longer than the L_critD (Hejnowicz, 1959; Hejnowicz and Brodzki, 1960; Ivanov and Maximov, 1999; van der Weele et al., 2003). In the EZ, rapid cell elongation is taking place among other processes due to water uptake into the central vacuole (reviewed by Dolan and Davies, 2004). We addressed in this study whether there is a critical cell length related to the onset of rapid elongation in the EZ, similar to the L_critD near the PD/TD boundary. We denote this cell length as the critical cell size for the initiation of rapid elongation (L_critE).

To estimate the maximum cell lengths that correspond to the PD and the TD, we used MSC analysis of sorted cell lengths. We called this analysis the sorted MSC (sMSC). For this procedure, we sorted cell lengths of a root cell file in ascending size order (Fig. 5A, B). Thus, cell length is a function of the cell length rank in the sorted cell length set (Fig. 5B). We assumed that there are three subsets of sorted cell lengths that correspond to the PD, TD and EZ. Then, after estimation of the breakpoints that correspond to the ranks of the longest PD and TD cells (Fig. 5B, C), we found the two linear equations that model the PD and TD cell length subsets after determining the breakpoints by MSC (Fig. 5D). Finally, we used these two linear equations for the PD and TD to estimate the maximum cell length in the PD and TD or the L_critD and L_critE, respectively (Fig. 5D). In this way the MSC approach can be used to estimate the critical size of dividing cells and the critical size for the initiation of rapid elongation. These parameters were subsequently used for comparison of different genotypes.

Fig. 5.

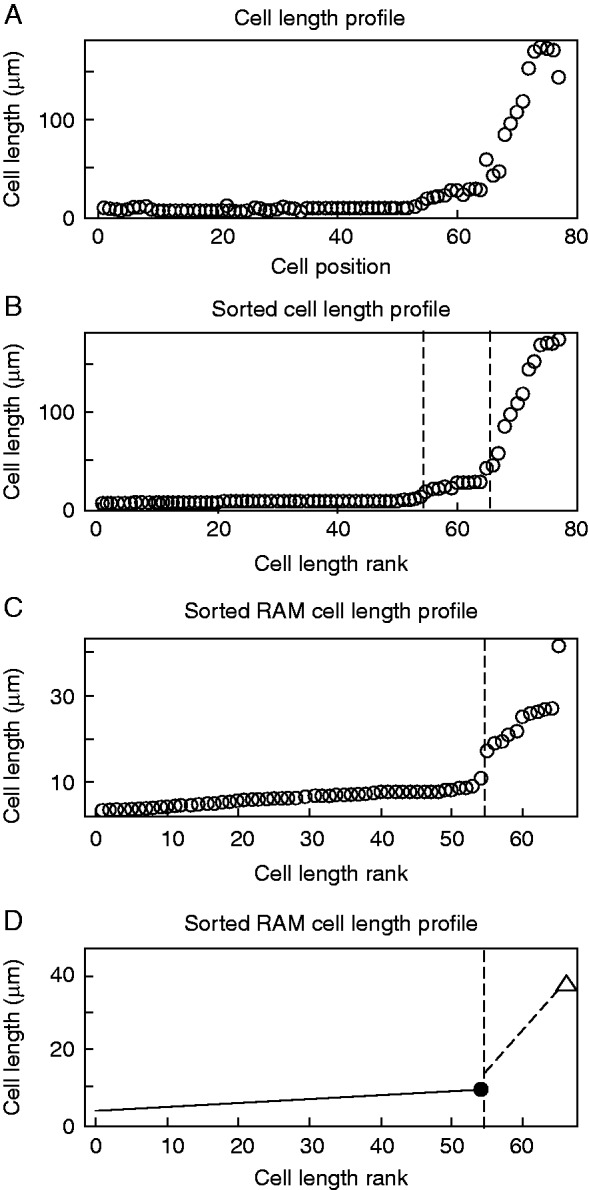
Estimation of the critical size of dividing and elongating cells by the sMSC approach. (A) Cortex cell length profile of the growing part of a representative root of wt Col-0, 9 DAS. (B) Sorted cell length profile in ascending order of the growing part of the root shown in (A). Vertical dashed lines represent positions of breakpoints, estimated by the MSC approach, that correspond to the PD/TD and the RAM/EZ boundaries of sorted cell lengths. (C) Sorted RAM cell length profile of the RAM of the root shown in (A) and (B). Vertical dashed line represents the breakpoint that delimitates the PD and TD cell length sets. (D) Linear models for PD and TD cell length sets. The black dot represents the estimated critical size of dividing cells (L_critD) and the white triangle represents the critical size for the initiation of rapid elongation (L_critE) for the file of the cortex shown in (A).

MSC analysis of arabidopsis wt and xal1 roots

We generated MSC models with two breakpoints for each cell length profile of wt and xal1 roots at 7 and 9 DAS. From these models we estimated: (1) the position of RAM/EZ and PD/TD boundaries by the MSC approach; (2) the linear equations for PD, TD and EZ; (3) the number of cells and length of each domain; (4) the derivative of cell length as a function of position (DLP), which corresponds to the slope of each linear equation; and (5) the L_critD and L_critE. Once the PD/TD and RAM/EZ boundaries were determined by the MSC approach, we compared the sizes of the RAM, PD and TD in wt and xal1 seedlings 7 and 9 DAS. We found that the number of cells and length of the wt PD and RAM increased from 7 to 9 DAS (Table 3). In contrast, no change was detected in the TD during this growth period in both genetic backgrounds (Table 3). Thus the RAM size increase in the wt was due to a larger population of proliferating cells in the PD at 9 DAS (Table 3).

Table 3.

Quantitative analysis of arabidopsis Col-0 wt and xal1 roots evaluated at 7 and 9 DAS by MSC analysis (n=20)

	wt				xal1
	7 DAS		9 DAS		7 DAS		9 DAS
	Mean (s.d.)	95 % CI	Mean (s.d.)	95 % CI	Mean (s.d.)	95 % CI	Mean (s.d.)	95 % CI
Number of PD cells	40 (7)	36, 43	49 (6)	46, 52	26 (6)	23, 28	28 (7)	24, 31
Number of RAM cells	55 (5)	52, 57	63 (5)	60, 65	36 (5)	34, 38	39 (5)	36, 41
PD length (µm)	245 (53)	220, 270	316 (53)	291, 340	189 (63)	160, 218	210 (63)	181, 240
TD length (µm)	215 (56)	188, 241	216 (56)	189, 242	216 (121)	160, 273	206 (78)	170, 243
RAM length (µm)	460 (61)	431, 488	531 (45)	510, 552	405 (145)	337, 473	417 (90)	375, 459
PD DLP (µm/cell position)	0·0 (0·1)	−0·04, 0·04	0·0 (0·1)	0·0, 0·1	0·1 (0·2)	0·0, 0·1	0·1 (0·2)	0·0, 0·1
TD DLP (µm/cell position)	1·5 (1)	0·8, 2·1	1·3 (1)	1·1, 1·6	2·7 (3·1)	1·2, 4·1	2·6 (2·2)	1·5, 3·6
EZ DLP (µm/cell position)	13 (4)	11, 15	11 (3)	10, 12	13 (11)	8, 18	15 (6)	12, 18
LcritD rank	43 (4)	41, 45	50 (5)	48, 53	29 (4)	27, 31	30 (5)	28, 32
LcritE rank	55 (5)	52, 57	63 (5)	60, 65	37 (4)	35, 39	38 (5)	36, 41

Interestingly, in the xal1 mutant we did not detect changes in PD and RAM lengths and corresponding numbers of cells from 7 to 9 DAS under our growth conditions (Table 3). Because accelerated root growth is related mainly to changes in the number of proliferating cells (Beemster and Baskin, 1998), the almost constant growth of xal1 roots from 3 to 11 DAS (Fig. 6A, B) suggested that xal1 PD hardly changes, at least during the first 10 d. Thus, XAL1 is necessary to maintain the steady increase in the number of cells within the PD, and as a consequence, accelerated root growth.

Fig. 6.

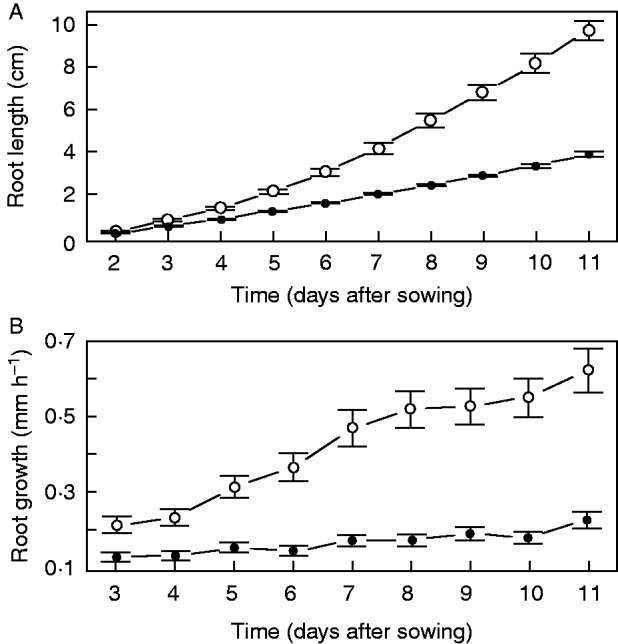
Growth of wt and xal1 roots. (A) Root growth dynamics in wt (white circles) and xal1 (black dots) roots. (B) Root growth rates over time in wt (white circles) and xal1 (black dots). Error bars represent 95 % CI, n = 20.

As xal1 root cells have a longer cell cycle than wt roots (Tapia-López et al., 2008), we asked whether this difference is associated with a change in the L_critD. We estimated the mean wt cortex L_critD as 8·9 μm (95 % CI 8·5, 9·3, n = 40), and the L_critD value for xal1 cortex cells as 11·4 μm (95 % CI 10·7, 12·0, n = 40). This suggests that the size-sensing mechanism that controls the critical cell size for division is altered by the loss of function of XAL1 and, as a consequence, the cell cycle duration of xal1 roots is longer, because it takes more time to reach the L_critD (assuming the same cell growth rate with respect to time). We also estimated the mean wt cortex cell critical size for the initiation of rapid elongation, L_critE, as 25 μm (95 % CI 23, 28, n = 40), and for xal1 cortex cells as 38 μm (95 % CI 32, 44, n = 40). This analysis showed that the loss of function of XAL1 altered both critical sizes. In summary, the MSC analysis suggested that XAL1 may be involved in the regulatory mechanisms that control critical cell size. Alternatively, XAL1 expression may depend on critical cell size.

DISCUSSION

We have applied the MSC model to establish the longitudinal zonation pattern of arabidopsis roots. This approach is useful to estimate different parameters, such as (1) the number of longitudinal domains and zones, (2) the number of cells and lengths of each domain and zone, (3) DLP and (4) the critical size of dividing cells (L_critD), and the critical size for the initiation of rapid elongation (L_critE). Using the BIC to estimate the most parsimonious models for number of breakpoints, we have detected two breakpoints or transitions in cell length profiles of the growing part of the root for the majority of roots. One of these breakpoints corresponds to the RAM/EZ boundary and the other one defines the PD/TD boundary. When one or three breakpoints were detected as the most parsimonious, this was mainly due to internal variability in cell length profiles in arabidopsis roots. Considering that (1) the two-breakpoint model was more common; (2) the one-breakpoint model was a particular case where the PD/TD boundary was not sharp enough; (3) CycB1;1_DB:GFP was expressed mainly in the PD and (4) pCCS52A1:GUS was expressed mainly in the TD, we can conclude that three distinct domains or zones (the PD, the TD and the EZ) should be recognized in the arabidopsis root.

Some authors consider that within individual cell files there is no TD before rapid elongation starts; it is thought that the transition zone is just one point along the root where cells leave the RAM and enter the EZ (Dello Ioio et al., 2007; Moubayidin et al., 2010). These authors also consider that the onset of elongation ‘is different for each cell type, giving a jagged shape to the boundary between dividing and expanding cells’ (Dello Ioio et al., 2007, p. 679). Root tissues stop dividing at different distances from the QC, but they all start rapid elongation at the same distance due to symplastic growth (reviewed in Ivanov and Dubrovsky, 2013). Hence, before rapid elongation, the symplastic nature of plant tissues yields a domain at which cells start endoreduplication but do not start rapid elongation; this region then corresponds to the TD (Baluška et al., 1996; Ivanov and Dubrovsky, 2013). Indeed, experimental evidence has shown that in arabidopsis endoreduplication precedes rapid cell elongation (Hayashi et al., 2013). Thus, for a particular cell file within the arabidopsis root, the TD can also be defined as the region where cells endoreduplicate and continue elongating at the same rate as in the PD. It has also been shown that phospholipase Dζ2, involved in vesicle trafficking, is strongly expressed in the transition zone (Li and Xue, 2007; Mancuso et al., 2007).

The MSC analysis used here clearly shows that before the onset of rapid elongation all cells within a file, irrespective of the tissue type, are distributed in two subsets separated by an identifiable transition: those in the PD and those in the TD. A clear difference between these two subsets and the difference between the RAM and EZ subsets provide additional evidence that the transition to elongation is not just one point along the root but comprises a domain of cells that have lost or are in the process of losing proliferation activity.

If we consider that the RAM does not include two domains (and the transition to the EZ is not considered to span several cells that constitute an identifiable domain of cells), the estimated RAM linear model should have a slope or DLP greater than zero. This would imply that, along the RAM, the relative cell elongation rate is greater than the relative cell division rate, but cell length profiles do not show a cell length distribution that corresponds to this scenario (Fig. 2). Within each domain, different relationships between relative elongation and cell division rates (Green, 1976) or DLPs cause a change in the mean cell length. We have found that on average the PD DLP is equal to zero and the TD DLP is greater than zero (Table 3). This implies that in the PD there is a balance between relative cell elongation and division rates (Baskin, 2000), while in the TD relative elongation rates are greater than relative division rates. So, our results support the existence of two domains within the RAM. Thus, cell length profiles that include the RAM and the EZ must be modelled by two-breakpoint MSC models.

The PD/TD boundary is difficult to recognize, partially because relative changes in cell lengths, which do not always steadily increase in the shootward direction, have to be evaluated. Using a molecular marker such as CycB1;1_DB:GFP, we found here that most GFP-expressing cells were within the PD defined by the MSC approach. However, the fact that in 6 % of cases GFP-expressing cells were found in the TD indicates two important aspects: (1) that some TD cells indeed are able to proliferate; and (2) that an estimation error must be considered. This same conclusion might also explain why in some cases pGUS:CCS52A1 expression is detected shootward of the MSC-determined position of the PD/TD boundary (Fig. 4H–J). Additionally, this discrepancy can be explained by the observation that in arabidopsis roots the endoreduplication cycle can also start in the EZ and that its duration is greater than that of the cell cycle in the RAM (Hayashi et al., 2013).

It is important to point out that the cells at the TD have unique physiological properties such as alterations in their cell-wall structure and the onset of vacuolization, which enables fast cell growth at the EZ (Verbelen et al., 2006; Baluška et al., 2010). It has also been described that cells in the TD are very sensitive to diverse external factors, such as gravity, light, oxidative stress and humidity (Verbelen et al., 2006). Thus, evaluating the extent to which such a domain is altered under different genetic and environmental conditions becomes very relevant. In this paper we propose an approach to the objective establishment of the boundaries between the PD and the TD and between the RAM and the EZ, as well as the sizes and numbers of cells constituting each domain.

Using the MSC, we have found that the PD in wt roots increases after 7 DAS, and such growth is related to an increase in the number of proliferating cells and accelerated root growth, after 7 DAS. This observation is in accordance with many studies where similar criteria to determine the RAM/EZ boundary have been used, and which report meristem length increase beyond 5 d after germination (DAG) and later (Galinha et al., 2007; Ubeda-Tomás et al., 2009; González-García et al., 2011; Makkena and Lamb, 2013). Moreover, a kinematic analysis of the arabidopsis root showed that accelerated root growth is mainly due to an increased cell production rate during the first 14 DAG and a steady increase in meristem length during the first 2 weeks of growth after germination (Beemster and Baskin, 1998). These results are similar to our observations of accelerated growth from 7 to 11 DAS (Fig. 6A, B), accompanied by an increase in the PD length. However, these results contrast with some previous studies that concluded that wt arabidopsis RAM reaches its maximum size 5 DAG (Dello Ioio et al., 2007; Achard et al., 2009; Moubayidin et al., 2010; Zhou et al., 2011), equivalent to our 7 DAS. This discrepancy about the age at which the RAM reaches its maximum size can be explained by the fact that this age is highly dependent on environmental conditions that vary among studies and by possible methodological differences in meristem length determination. In any case, these variations among laboratories highlight the need for a reliable approach to the identification of root growth zones along the longitudinal axis and their boundaries. In contrast, xal1 roots showed an almost constant root growth rate (Fig. 6A, B), possibly because the PD length hardly changes between, at least, 7 and 10 DAS. This result suggests that XAL1 is involved in the regulation of the transition from the PD to the TD.

Interestingly, the L_critD is altered by the loss of function of XAL1, suggesting that the longer cell cycle duration estimated in xal1 roots (Tapia-López et al., 2008) is possibly related to alterations in the size-sensing mechanisms that control the onset of cell division. Fully elongated cells of xal1 roots are shorter on average than wt ones (Tapia-López et al., 2008). Nonetheless, our results show that cells that enter the EZ are larger in xal1 than in wt roots. Cell elongation stops at shorter cell lengths in xal1 than in wt roots, although xal1 cells initiate rapid cell elongation at larger sizes. Our results suggest that the loss of function of XAL1 alters the two developmental transitions along the root (PD/TD and RAM/EZ), as well as critical cell sizes. Future studies will have to unravel how XAL1 is involved in the regulation of cell division rate, directly or indirectly, through the regulation of the mechanisms that control the L_critD.

In conclusion, the MSC approach for determination of the PD/TD boundary yields similar results to those based on specific molecular markers and those obtained by the ExpBiol subjective method. The MSC approach is an objective and versatile tool for determination of domains and zones and gives reliable results for roots with RAM of different lengths. The use of molecular markers implies genetic crosses and frequently a mixture of different genetic backgrounds. To avoid this problem, the MSC approach permits a direct characterization of the longitudinal zonation pattern. It can be used for different genetic backgrounds and treatments, and can be applied for analysis of developmental changes taking place with age. This approach potentially could also be applied to species other than arabidopsis to better characterize and understand the mechanisms underlying the homeostasis of the RAM in angiosperms.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Text S1: instructions to analyse the cell length profile of arabidopsis root using the ‘strucchange’ package of R (two examples). Figure S1: estimation of the number of breakpoints and their position by a MSC–BIC approach in xal1 9 DAS seedling. Table S1: quantitative analysis of arabidopsis C24 wt roots.