Biophysical rhizosphere processes affecting root water uptake

Abstract

Background Recent advances in imaging techniques now make it possible to visualize the biogeochemical and physical environment around the roots, the rhizosphere. Detailed images of pore space geometry and water content dynamics around roots have demonstrated the heterogeneity of the rhizosphere compared with the soil far from the roots. These findings have inspired new models of root water uptake which aim to describe such small-scale heterogeneity. However, the question remains of how far these image-based findings have really advanced our understanding of how roots extract water from soils.

Scope The rhizosphere processes affecting root water uptake are reviewed. Special attention is dedicated to the role of mucilage exuded by roots. Mucilage increases the soil moisture at negative water potentials and it keeps the rhizosphere wet when plants take up water, possibly maintaining the hydraulic connection between roots and soil. However, mucilage becomes viscous and hydrophobic upon severe drying and it limits the water fluxes across the rhizosphere during the rewetting phase. The role of mucilage in maintaining the hydraulic contact between the root surface and the surrounding soil, thereby softening the drops in water potential around the roots in dry soils, remains to be demonstrated.

Conclusion Despite detailed images of water content, water fluxes and soil structure in the rhizosphere, a general understanding of how the rhizosphere affects root water uptake is still lacking. The missing elements of the puzzle are the gradient in water potential around roots. Measurements of the xylem water potential at varying soil water potentials and transpiration rates supported by numerical models of root water uptake would allow the estimation of the water potential across the rhizosphere. Such measurements are crucial to comprehend how water enters the roots.

INTRODUCTION

Root water uptake

Around 65 years ago, Richards and Wadleigh (1952) wrote that the progress in understanding how water flows from the soil into the roots was limited by the difficulty in measuring moisture gradients in the immediate vicinity of the roots. Gardner (1960) calculated that these gradients are small until the ‘wilting point’ (matric potential of –1·5 MPa) is approached. Close to the wilting point, the gradients in soil moisture (and soil water potential) become larger and larger. In terms of root and soil conductivity, we can expect that significant gradients in water content develop around the roots when the soil conductivity approaches or becomes smaller than that of roots.

These gradients in soil moisture around the roots cover distances of some millimetres (Metselaar and De Jong van Lier, 2011) – a much smaller scale than that of the entire root system. At the entire root scale, high root length density and root activity in specific locations may create larger regions of water depletion along the soil profile. Indeed, heterogeneities in root water uptake and a depletion zone moving downwards along the soil profile are well known experimentally (e.g. Dardanelli et al., 2004) and have been well mimicked by root water uptake models (Doussan et al., 2006; Javaux et al., 2008). These models require many parameters, in particular regarding the distribution of radial and axial conductivities of the roots, which are not easily measurable for roots growing in soils. Measurements of moisture gradients around the roots would help to validate these models and to identify what parts of the root system are most active in taking up water.

Today, thanks to the advances in imaging techniques such as neutron radiography, magnetic resonance imaging (MRI), light transmission imaging and X-ray computed tomography (CT), measuring the profiles of water content as well as the soil structure around the roots has become possible. Garrigues et al. (2006) used a light transmission set-up to image the two-dimensional distribution of the water content in the root zone of 50- to 55-day-old lupines. They observed a region of water depletion moving downwards as the upper part of the soil dried. In a follow-up study, Doussan et al. (2006) successfully fitted the observed soil moistures to estimate the distribution of hydraulic conductivities of the root system.

Higher resolution three-dimensional images of water redistributions were obtained using MRI and neutron tomography. MRI experiments by MacFall et al. (1990) showed a large zone of water depletion around the root of a loblolly pine. Similar patterns of decreasing water contents towards the roots were observed using MRI by Segal et al. (2008), who compared barley species with and without root hairs. The authors found marked water depletion in the root hair region, possibly caused by water uptake by root hairs. Note that the calibration of the MRI images relied on the assumption that the rhizosphere had the same properties as the bulk soil, which might not be true.

Opposite gradients in water content were observed with neutron radiography and tomography. Neutron tomography measurements by Nakanishi et al. (2005) showed increasing water contents around a young root system. Similar puzzling observations were reported by Tumlinson et al. (2008) for corn seedlings. Moradi et al. (2011) performed high-resolution tomography of water distribution around the roots of lupine, maize and chickpea, and consistently found increasing water content towards the roots during the drying phase.

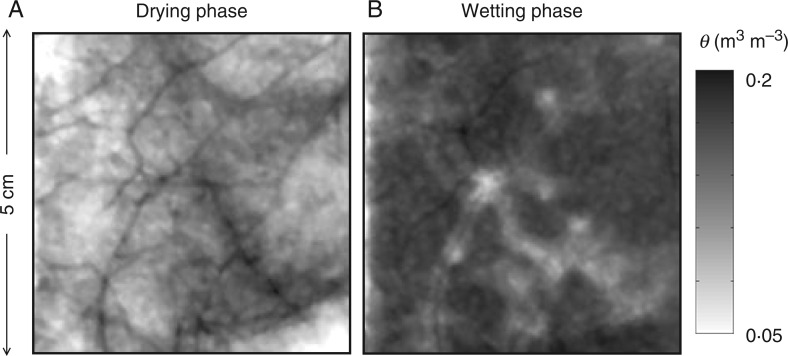
These apparently contradictory observations of water dynamics around the roots are probably the manifestation of the complex and time-dependent properties of the rhizosphere (Carminati et al., 2010; Carminati and Vetterlein, 2013). Two illustrative neutron radiographs of water content around the roots of a lupine growing in a sandy soil are shown in Fig. 1. The images are a close-up of the original radiographs of 15 × 15 cm and show the roots and the soil water content at two stages of a drying/wetting cycle. During the drying phase, the soil around the roots remained wetter than the adjacent bulk soil (left). After irrigation, the rhizosphere remained dry (right) and it slowly rewetted within 2–3 d. These observations demonstrated that the rhizosphere has time-dependent properties that differ from those of the bulk soil. More specifically, the rhizosphere must have a different water retention curve compared with the bulk soil.

Fig. 1.

Neutron radiography of the rhizosphere of a lupine during drying (A) and wetting (B). The picture shows the water content distribution (dark = wet). Note the high water content in the rhizosphere during the drying period, and the almost opposite pattern (dry rhizosphere) after irrigation. The images are adapted from Carminati et al. (2010).

Carminati (2012) proposed that the water retention curve of the rhizosphere is primarily controlled by the adsorption of water by mucilage exuded by roots. Mucilage is a gel that is capable of adsorbing large volumes of water (McCully and Boyer, 1997), but it becomes hydrophobic after drying (Ahmed et al., 2015a). These two properties can explain both profiles of water content shown in Fig. 1. The effect of mucilage on the soil physical properties is discussed in detail in the next sections.

The main conclusions arising from the highly resolved two- and three-dimensional images of the rhizosphere are that: (1) the physiochemical environment around the roots differs from that of the bulk soil; and (2) the imaged gradients in soil moisture cannot be straightforwardly interpreted as the effect of root water uptake These conclusions require a rethink of the role of radial flow equations applied to soil with uniform properties in depicting water uptake by roots.

In this opinion paper, we review the rhizosphere physical processes actually or supposedly affecting root water uptake. Special attention is dedicated to our own work on the role of mucilage exuded by roots. Then, we present a conceptual model of how mucilage improves the continuity of the water flow across the root–soil interface and how this affects root water uptake in dry soil. Finally, we identify the aspects of rhizosphere processes that remain unclear and the variables and parameters that should be measured with high priority.

Theory of water flow in soil and roots: setting the framework

Water flows from the soil towards the root surface and then into the roots following a gradient in water potential (Passioura, 1988). The gradients in water potential across the root tissue depend on the flow rate and the hydraulic conductivity of the root according to the following equation:

$$q\left(r_{\text{root}}\right)=–k_{\text{root}}({\psi }_{\text{root}}–{\psi }_{\text{x}})$$ (1)

where q is the radial flux of water (water flow per cross-section) (m s^–1), r_root is the root radius (m), k_root is the radial hydraulic conductivity of the root (m s^–1 MPa^–1), and ψ_root and ψ_x are the water potential (Pa) at the root surface and in the xylem, respectively.

The equation of the water flow in soils in radial co-ordinates is given by the Buckingham–Darcy equation:

$$q\left(r\right)=-k_{soil}\frac{d{\Psi }_m}{dr}$$ [2]

where r > r_root, k_soil is the soil hydraulic conductivity (m² s^–1 MPa^–1), which is function of the soil water content [and of the soil matric potential ψ_m (Pa)], and $\frac{d{\Psi }_m}{dr}$ is the gradient in soil matric potential. When the soil matric potential is expressed as matric head $h=\frac{{\psi }_m}{\rho g}$ (m), where ρ is the water density and g is gravity, the hydraulic conductivity k_soil has the units of m s^–1. Note that here we assumed that the gradients in gravitational potential are much smaller compared with $\frac{d{\Psi }_m}{dr}$.

Typically, when the soil is wet k_soil >> |q(r_root)| and ψ_m is negligible [see Eqn (2)]. In this stage, the soil has little or no influence on root water uptake. As the soil dries, its hydraulic conductivity decreases by several orders of magnitude and the gradients in matric potential $\left(\frac{d{\Psi }_m}{dr}\right)$ must increase to sustain the flux.

The gradients in water potential around a root can be calculated solving the Richards’ equation in radial co-ordinate:

$$\frac{\partial \theta }{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left[r{k}_{soil}\left({\Psi }_m\right)\frac{d{\Psi }_m}{dr}\right]$$ [3]

The Richards’ equation predicts that in wet soils the profile of matric potential around the roots is pretty flat, i.e. there are no significant dissipations of water potential in the soil. However, as the soil dries and k_soil drops, large gradients in ψ_m occur in the first millimetres around the roots (Metselaar and De Jong van Lier, 2011). The gradients become steeper towards the root surface for two reasons: (1) the flow velocity increases like 1/r due to the radial geometry of the process; and (2) the fact that ψ_m decreases toward the root (which is necessary to drive water towards the root) and the common assumption of uniform properties around the roots (i.e. the rhizosphere and the adjacent bulk soil have identical hydraulic properties) result in a hydraulic conductivity k_soil that decreases toward the roots. From the facts that both the fluxes q and k_soil decrease towards the root, it follows that the absolute value of $\frac{d{\Psi }_m}{dr}$ increases close to the root surface.

Equation (3) predicts that there is a critical matric potential below which a given root water uptake cannot be sustained. The critical matric potential depends on the soil hydraulic conductivity and the water retention curve. Close to this critical point, the largest drop in water potential occurs in the first 1–2 mm around the roots (Metselaar and De Jong van Lierm, 2011). At this stage, the hydraulic conductivity of the rhizosphere plays a crucial role in determining how plants extract water from the soil.

In the next section, we discuss what processes affect the hydraulic conductivity of the rhizosphere.

BIOPHYSICAL PROCESSES IN THE RHIZOSPHERE

Roots modify the soil properties in several ways. First of all, roots alter the soil pore size distribution. As roots grow, soil particles are displaced and rearranged in the rhizosphere (Dexter, 1987). It was found that root expansion causes compaction around the root (Bruand et al., 1996). Daly et al. (2015) combined X-ray CT with measurements of the soil water retention curve and pore-scale simulations of the unsaturated conductivity of planted and unplanted soils. The authors found significant differences between the pore size distributions of planted and unplanted samples. In particular, they found that roots decrease the soil macroporosity. Whalley et al. (2005) analysed the pore structure of aggregates from the rhizosphere of wheat and barley and they compared it with that of aggregates from the bulk soil. They found a similar aggregate porosity but a greater number of larger pores in the aggregates collected in the rhizosphere. High-resolution X-ray CT by Aravena et al. (2014) showed the compaction of soil aggregates around the roots of sweet pea. By employing a numerical model of water flow, the authors calculated that the increase in the aggregate–aggregate contact area enhances the intra-aggregate flow and facilitates root water uptake. However, soil densification around the roots may not be the general rule. For instance, Feeney et al. (2006) showed that plant roots and associated micro-organisms increase soil porosity.

As transpiration increases during the day, roots shrink and can lose part of the contact with the soil (Huck et al., 1970). North and Nobel (1997) studied the root–soil contact in the cactus Opuntia ficus-indica, whose young distal root segments are covered with stable rhizosheaths while the older root segments are bare. Root shrinkage and the contact with the soil were estimated from a resin-impregnated cross-section. Roots shrank by 30 % and the contact of the bare roots with the soil decreased from 80 % to 30 %. Nobel and Cui (1992) calculated the effect of a gap between soil and root on the total hydraulic conductance of the root–soil continuum. They estimated that at negative water potentials, the gap can become the limiting factor for root water uptake. These calculations were made by separately estimating the conductivity of the different components (root, soil and gaps) and then piecing them together as a flow in-series. Carminati et al. (2013) used X-ray CT to image the formation of air-filled gaps around the roots of lupines during a drying cycle. Gaps of up to 0·1–0·35 mm formed around the tap root only after transpiration had already decreased. Lateral roots shrank less and their eventual gaps were below the resolution limit. The authors concluded that gaps are not the cause but rather a consequence of reduced water availability to roots. However, it is likely that once gaps are initiated, they may further limit the water exchanges between soil and roots.

One mechanism that limits the loss of contact between roots and soil is the formation of a stable layer of soil particles that strongly adhere to the roots (North and Nobel, 1997; McCully, 1999). Rhizosheaths are believed to be formed by the combination of root hairs and root exudates (Watt et al., 1994). An analogue of mucilage exuded by roots (polygalacturonic acid; PGA) was shown to increase aggregate stability (Czarnes et al., 2000). As roots shrink, it is expected that the rhizosheaths maintain the contact with the soil. Root hairs possibly help to bridge the root to the soil and increase the effective radius of the root (Segal et al., 2008).

Besides stabilizing the soil around the roots, root exudates also change the ability of the rhizosphere to hold water. The mucilaginous component of root exudates, in particular, has a remarkable capability to absorb water: at saturation, mucilage can contain an amount of water 300 times its dry weight. Impressed by this property, McCully and Boyer (1997) hypothesized that mucilage may act as a reservoir of water that can be taken up by roots when the soil dries. The authors measured the water content of mucilage at varying water potentials and found that most of the water absorbed by mucilage was drained at relatively high water potentials. They concluded that mucilage per se should not play a large role on soil–plant water relations. Mucilage would anyway be useful for stabilizing the rhizosheath and keeping the roots in contact with the soil.

Interestingly, Read and Gregory (1997) found that the mucilaginous fraction of root exudates has a lower surface tension than water. Mucilage is mainly composed of polysaccharides, but it also contains lipids which may be responsible for the reduced surface tension (Read et al., 2003). Taking lecithin as an analogue of mucilage lipids and mixing it with a soil, Read et al. (2003) found a reduction in the amount of water held by the soil at negative water potentials. The authors speculated that such a lowering of the water retention curve could help roots to extract water more easily from the small pores, but this would be associated with a decrease in hydraulic conductivity. The latter point was demonstrated by the simulations of Dunbabin et al. (2006), which showed a decrease in root water uptake due to the surfactants released by the roots. The lipids present in mucilage are probably the explanation for the reduced wettability of the rhizosphere measured by Hallett et al. (2003).

After being exuded from the root tip, mucilage undergoes several changes: it shrinks and swells as the soil dries out and is rewetted, and it is partly degraded by micro-organisms, some of which themselves produce a gel (extracellular polymeric substances; EPS) whose properties are similar to those of mucilage (Chenu, 1993; McCully, 1999; Walker, 2003; Or et al., 2007). The resulting substance around the roots is referred to as mucigel, and its properties vary along the root (Watt et al., 2006).

This introduction was meant to describe the state of the art of the research on the biophysics of the rhizosphere and its effects on root water uptake. The cited studies clearly show that roots influence the hydraulic behaviour of the rhizosphere in a complex, sometimes contradictory and generally unclear way. Mucilage, in particular, has the ability to alter dynamically the water retention curve of the rhizosphere. In the next section we will present recent results and current understanding on the effects of root exudates, particularly mucilage, on the soil hydraulic properties and root water uptake.

EFFECT OF MUCILAGE ON WATER FLOW IN SOIL

Effect of mucilage on the soil hydraulic properties

When it is fully saturated, mucilage can absorb an amount of water that is several hundred times its dry weight. Although most of this water is drained at relatively high (less negative) matric potentials (McCully and Boyer, 1997), the remaining water may be sufficient to increase the rhizosphere water content at low (more negative) water potentials. However, it is also possible that the low surface tension of mucilage reduces the water retention in the rhizosphere, as shown by Read et al. (2003) using lecithin as an analogue of mucilage.

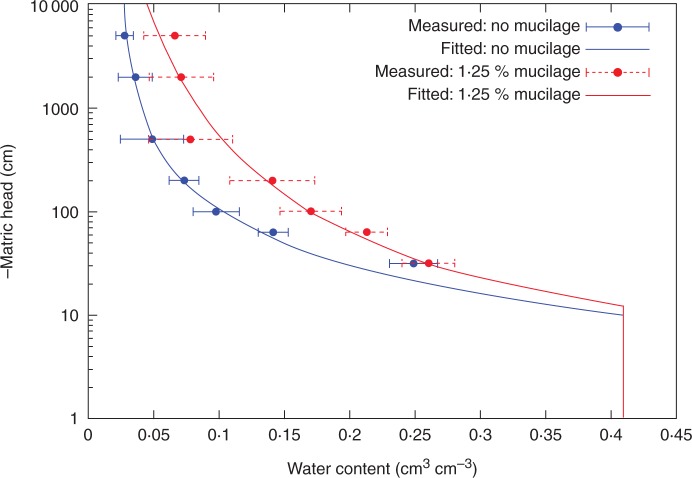
To test the effect of mucilage on the soil water retention curve, Ahmed et al. (2014) mixed mucilage from chia seeds with a fine sandy soil. Mucilage from chia seeds was chosen for three reasons: it has physical properties that are similar to those of mucilage from corn plants, i.e. it forms a gel upon immersion in water and it turns hydrophobic upon drying (Benard et al., 2015); it has a chemical composition similar to that of mucilage from corn mucilage, i.e. it contains a significant content of uronic acids and a small fraction of lipids; and it is easy to collect in quantities large enough to study bulk soil properties. Ahmed et al. (2014) found that a sandy soil containing a mucilage concentration of 1·25 % (g of dry mucilage per g of dry soil) held more water than the same sandy soil without mucilage at any negative matric potentials. The results are shown in Fig. 2. In Fig. 2 the matric potential ψ_m (Pa) is expressed in matric head h (m) (1 hPa ≈ 1 cm).

Fig. 2.

Water retention curve of fine sand with and without mucilage from chia seeds at a concentration of 1·25 % (g of dry mucilage per g of dry soil). The figure is modified from Ahmed et al. (2014).

Figure 2 shows that mucilage increases the water retention at any matric potentials. The air-entry value was only slightly increased by mucilage, and the larger differences were found at matric potentials of approximately h = –100 cm. These results show the opposite trend compared with the studies of Read et al. (2003), who used lecithin as an analogue of mucilage. Figure 2 shows that for the tested mucilage concentration of 1·25 % (g g^–1) in a sandy soil, the effect of mucilage in retaining water is higher than the effect of the reduced surface tension.

The results of Ahmed et al. (2014) are in line with the observations of Ghezzehei and Albalasmeh (2015), who conducted experiments using a synthetic analogue of rhizodeposits (PGA) mixed with glass-bead and sand media. They used environmental scanning electron microscopy to show enhanced water retention by PGA in the particle–particle contact. They also showed macroscopic enhancement of water retention in soils mixed with PGA – measured with a dew-point potentiometer

Kroener et al. (2014) developed a quantitative model of the influence of mucilage on the soil water retention curve. The basic idea was that by absorbing water, mucilage decreases the matric potential at any given water content. The decrease in water potential is a function of the concentration of mucilage in the liquid phase (g of dry mucilage per g of water). The model was calibrated based on experiments of mucilage from chia seeds mixed with a sandy soil. The model should be further validated using varying mucilage concentrations and soil textures.

It is interesting to calculate whether the enhanced water retention by mucilage can explain the higher water contents observed in the rhizosphere (Fig. 1A). According to Carminati et al. (2010), the water content in the rhizosphere of lupines in a sandy soil was approx. 0·05 higher than in the bulk soil. A similar increase in water content was shown in Fig. 2 for a mucilage concentration of 1·25 %. The question is whether a mucilage concentration of 1·25 % in the rhizosphere is realistic. Measurements of the root mucilage exudation rate vary from approximately M = 20 μg d^–1 in maize seedlings (Chaboud, 1983) up to M = 700 μg d^–1 in mature maize (Ahmed et al., 2015a) – the data refer to the exudation rate per root tip. Assuming a soil bulk density of ρ_bulk = 1·4 g cm^–3, a root radius of r_root = 0·05 cm, rhizosphere radius of r_rhizo = 0·15 cm and root elongation rate of dL = 1 cm d^–1, and using the relationship:

$$C=\frac{M}{{\rho }_{bulk}\pi \left(r_{rhizo}^2-r_{root}^2\right)dL}$$ [4]

we obtain a mucilage concentration C varying between 0·02 and 0·8 % (g g^–1), which is slightly lower than the mucilage concentration of 1·25 % (g g^–1) of Fig. 2. However, as it is likely that C is not uniform in the rhizosphere, but that it rather increases towards the root surface, we can expect that 1·25 % (g g^–1) is a realistic value for the mucilage concentration in the first 0·1–0·5 mm near the root surface.

Besides affecting the relationship between water content and matric potential, mucilage also affects the soil hydraulic conductivity. Kroener et al. (2014) measured the saturated conductivity of a sandy soil mixed with varying mucilage concentrations. The saturated conductivity decreased with increasing mucilage concentration. At a concentration of approx. 1 % (g g^–1), mucilage decreased the saturated conductivity by two orders of magnitude. Such a reduction is primarily caused by the higher viscosity of mucilage compared with water.

It is likely that mucilage viscosity also affects the hydraulic conductivity under unsaturated conditions. Two processes are expected to determine the shape of the unsaturated conductivity: the viscosity of mucilage (which increases as mucilage dries) and the high water retention of mucilage, which keeps the rhizosphere wet (and possibly conductive) while the bulk soil dries out. Depending on the relative importance of the two processes, it is possible that mucilage either increases or decreases the hydraulic conductivity of soils at a given negative matric potential. If the increase in viscosity is not compensated by an enhancement of water retention, mucilage probably decreases the hydraulic conductivity at negative matric potentials. In contrast, if the water retention is sufficiently increased, mucilage can increase the soil conductivity in dry soils.

Effect of mucilage on soil water repellency

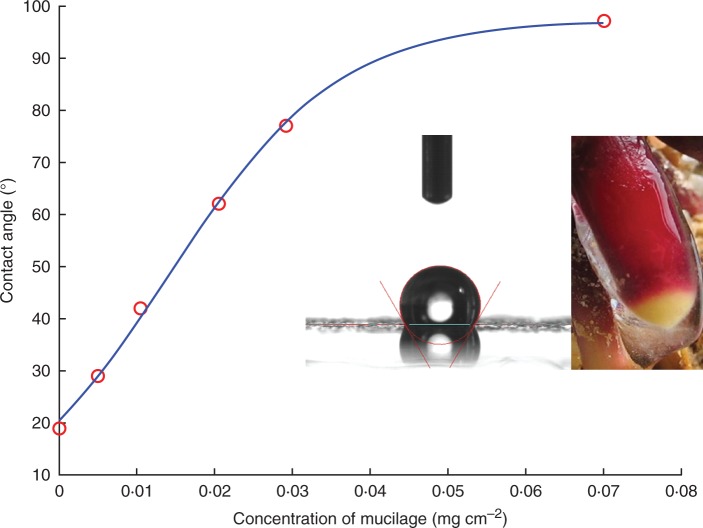
Despite its large capacity to absorb water, mucilage turns hydrophobic upon drying. Figure 3 shows the contact angle between a drop of distilled water placed on a glass slide covered with a varying amount of dry mucilage from maize plants (Ahmed et al., 2015b). The figure shows that at concentrations >0·06–0·07 mg cm^–2 (mg of dry mucilage per cm² of solid surface), mucilage turned hydrophobic (contact angle >90°). The contact angle increased as a function of the mucilage concentration. Interestingly, the contact angle did not quickly relax, but the part of the mucilage that was covered by water did rewet and to the touch it felt like a wet gel.

Fig. 3.

Contact angle of water as a function of grams of mucilage per surface as measured with the sessile drop method. Mucilage was collected from brace roots of maize and was allowed to dry on a glass side. The inset shows a picture of a water droplet on a surface covered with a high concentration of mucilage and a picture of a brace root of maize covered with mucilage. The figure is modified from Ahmed et al. (2015b).

The water repellency of dry mucilage is a good candidate to explain why the rhizosphere shown in Fig. 1B remained dry upon irrigation. To test this explanation, Kroener et al. (2015) performed capillary rise experiments using soils of different soil texture mixed with varying amount of mucilage from chia seeds. The capillary rise experiments showed that there was a critical mucilage concentration at which the soil switched from being wettable to not wettable. The critical mucilage concentration increased with decreasing soil particle diameter. Close to the critical concentration, the wetting front became irregular and water flowed through small-scale preferential pathways (these pathways are probably the connected wettable pores not covered with a sufficient amount of mucilage). The experiments support the hypothesis that mucilage caused the slow rewetting of the rhizosphere shown in Fig. 1B.

The capillary rise experiments of Kroener et al. (2015) were well described using a pore-scale percolation approach. The percolation theory deals with the problem of relating the macroscopic connectivity of a system based on the microscopic distribution of connected/disconnected elements (Berkowitz and Balberg, 1993). The central idea is that mucilage is heterogeneously distributed through the pore space and this microscopic distribution affects the connectivity of the pathway of water through the porous medium. The contact angle of each pore is a function of the mucilage concentration per pore surface, which depends on the pore radius and grams of dry mucilage. Note that the specific pore surface is inversely related to the particle diameter. If the wettable pores form a connected network spanning from one side to the other of the flow domain, water can flow through the soil. Otherwise water cannot penetrate through the pore space and the soil is hydrophobic. The percolation model was used to predict the critical mucilage concentration at which soils of varying particle size turn hydrophobic. The theoretical results were in good agreement with the experimental results. Benard et al. (2015) successfully extended the model of Kroener et al. (2015) to unsaturated conditions.

The percolation model describes the initial phase of the rhizosphere rewetting. Over time, the part of mucilage in contact with water rehydrates, its contact angle decreases and the wetting front advances. Carminati et al. (2010) observed that the rewetting of the rhizosphere of the mature roots of lupine took around 2 d. Interestingly, the rewetting of the rhizosphere of the most distal root segments (approx. 3 cm from the root tip) was as fast at the rewetting of the bulk soil (Carminati, 2013). This observation suggests an alteration of mucilage due to microbial degradation (which increase the fraction of lipids in the mucilage) or changes in mucilage structure during drying. In fact, when the molecule chains comprising mucilage get together, they may form new physical and chemical bonds that impede mucilage swelling.

To include the rewetting dynamics of the rhizosphere in the equations of water flow in soils (the Richards’ equation), Carminati (2012) and Kroener et al. (2014) proposed to decouple the changes in water potential and water content in the rhizosphere. The core idea of the model was that the changes in water content respond with some delay to the changes in soil matric potential. This concept results in a non-equilibrium relationship between water content and matric potential in the rhizosphere. A similar non-equilibrium relationship also appears in the relationship between hydraulic conductivity and soil matric potential.

Although the mechanisms of water repellency in the rhizosphere have been explained, the consequences on root water uptake are less clear. Zarebanadkouki and Carminati (2014) used neutron radiography to trace the transport of D₂O into roots of lupines growing in soil samples that were divided in several compartments by capillary barriers – the technique is described in detail in Zarebanadkouki et al. (2012, 2014). D₂O was simultaneously injected into two soil regions, one that was kept wet and one that was allowed to dry, and the transport of D₂O into roots was imaged using neutron radiography. The time-series radiography showed that the roots in the soil compartment that was allowed to dry and subsequently rewetted took up 4–8 times less water than the roots that were kept in a moist soil. The reduction in water uptake persisted for 2–3 h and it was larger in long roots (10–15 cm) compared with short roots (5–10 cm), which is in line with the findings of Carminati (2013) who reported a faster rhizosphere rewetting in the young root segments.

The experiments of Zarebanadkouki and Carminati (2014) showed that there was a temporary reduction in water uptake after the soil was allowed to dry and subsequently rewetted. However, it is not clear if such a reduction was caused by the rhizosphere or by the roots themselves, whose conductivity could have decreased upon drying. In a successive study, Zarebanadkouki et al. (2015) used neutron radiography to image the rewetting of the rhizosphere and the rehydration of the roots in real time after irrigation. By image processing, it was possible to calculate the radial profile of the water content around the roots. Before irrigation, the water content increased towards the roots. After irrigation, the region closer to the root remained drier and it rewetted in 3–4 h. From the image analysis, it was possible to estimate the rehydration and swelling of the roots after irrigation. The rehydration of the roots was used to calculate the water fluxes into the roots. Using complementary measurements of xylem water pressure, the authors calculate the hydraulic conductivity of the root–rhizosphere. The hydraulic conductivity of the root–soil continuum was initially very low and it recovered by two to three orders of magnitude within 3 h after irrigation. It is unlikely that such a large change in conductivity occurred in the root tissue and it is more plausible that it occurred in the rhizosphere as it slowly rewetted. The estimated low conductivity of the rhizosphere after a severe drying/wetting cycle supports the hypothesis that the rhizosphere water repellency temporarily limits the local root water uptake upon a drying/wetting cycle.

CONCEPTUAL MODEL

In the previous sections we reviewed how the rhizosphere affects root water uptake. In particular we showed that mucilage alters the soil hydraulic properties, it enhances the soil water retention, it increases the viscosity of the soil solution and it causes water repellency. Although some of these physical aspects of mucilage–soil relations have been clarified, further research is needed to understand the implications of such rhizosphere processes on root water uptake.

Here, we propose a conceptual model of how mucilage and root hairs enhance the ability of roots to extract water from soils at unsaturated conditions. We focus on the drying phase and we do not discuss the rewetting kinetics of the rhizosphere upon irrigation, which have been treated in detail elsewhere (Kroener et al., 2014; Ahmed et al., 2015b; Benard et al., 2015)

The conceptual model is illustrated in Fig. 4. Mucilage is exuded by the root tips, it binds to the soil particle, and it forms a network that is capable of holding a certain amount of water against suction. As roots take up water, the bulk soil starts to dry. Similarly, mucilage loses part of its water and it shrinks. As long as the soil is relatively wet, the gradients in water potential needed to drive water towards the root surface are expected to be small – see, for instance, the arguments by Passioura (1980) and Draye et al. (2010). Under these conditions, the profiles of water content towards the roots simply reflect the shape of the soil water retention curve and how it changes towards the roots.

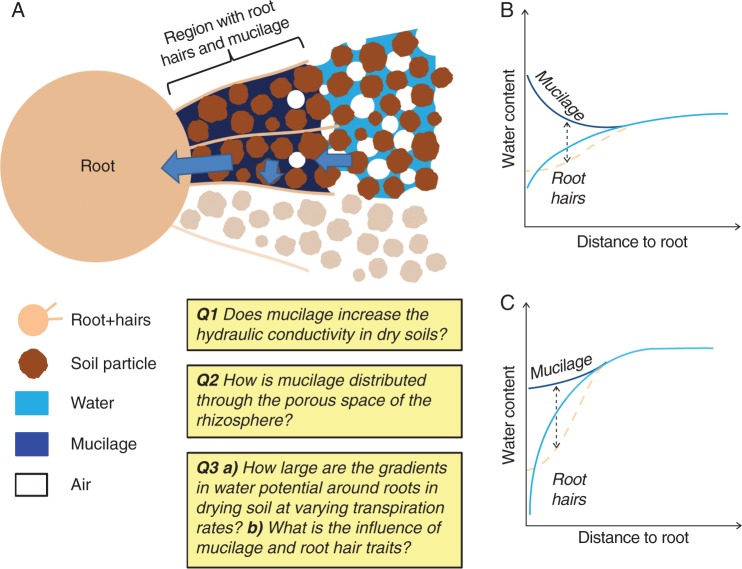
Fig. 4.

Conceptual model of root water uptake including the effect of mucilage and root hairs. (A) Illustration of the spatial distribution of mucilage in the rhizosphere and the related increase in water content. The hypothesis is that mucilage increases the soil water content around the roots and keeps the space between root hairs wet and possibly conductive. (B) Putative profiles of water content as a function of distance from the root surface, including the effect of mucilage and root hairs. (C) Putative profile of matric potential as a function of distance from the root surface, including the effect of mucilage and root hairs. Three key questions to be addressed with high priority are highlighted.

As the soil becomes dry, significant gradients in water potential develop across the rhizosphere to drive water towards the root surface. If the soil around the roots had uniform soil properties, this would result in decreasing water content toward the roots. Over time, this water depletion would become more pronounced until a critical point when the conductivity of the soil close to the roots becomes so low that it can no longer sustain the root water uptake. This process is attenuated by mucilage. In fact, the retention of water by mucilage ensures that the rhizosphere remains wet and that the conductivity of the soil close to the root does not drop as quickly. The expected profiles of water content towards the root surface with and without mucilage are shown in Fig. 4B. Neutron tomograms (Moradi et al., 2011) of water distribution around roots show a profile of water content similar to the dark blue line in Fig. 4B, supporting our concept.

The function of mucilage in maintaining the rhizosphere wet becomes even more evident when we include the putative role of root hairs in water uptake. There is relatively little work on the uptake of water by root hairs. Recently, Dodd and Diatloff (2016) compared transpiration rates and the leaf elongation rate of barley mutants with and without root hairs during a drying experiment. There were no significant differences between genotypes, but the authors suggested that additional physiological adjustment may have compensated the lack of root hairs (for instance an enhanced root growth). The authors also admitted that the transpiration rates could have not been high enough to see an effect. Segal et al. (2008) used nuclear magnetic resonance (NMR) to image the distribution of water around the same barley mutants. They found that barleys with root hairs had a marked dry region around the roots and interpreted it as the effect of water depletion between root hairs. Following this idea, the authors simulated the water uptake by root hairs. The simulations showed that the space between root hairs was quickly depleted of water, suggesting that the function of root hairs in water uptake was not to increase the root surface, but it was rather to extend the root radius. The profile of water content resulting from these considerations on the role of root hairs is shown in Fig. 4B.

In this case, mucilage would also play a key role. It would maintain the rhizosphere and the space between the root hairs wet and would facilitate the water flow into the root hairs for a large, more negative range of water potentials. In this sense, mucilage would be functional for the effective capture of water by root hairs. Such a hypothesis needs be tested experimentally.

Although there is sufficient evidence that mucilage increases the soil water content in the rhizosphere as shown in Fig. 4B, much less is known on the role of mucilage in modulating the profiles in water potential. Mucilage increases the water retention at the expense of an increased viscosity. Depending on the relative importance of the two processes (higher water retention and higher viscosity), mucilage can either increase or decrease the unsaturated conductivity. The profiles in Fig. 4C correspond to the case when mucilage increases the unsaturated conductivity of the rhizosphere, thereby attenuating the gradients in water potential around the roots and facilitating the uptake of water from dry soils. In this case, the presence of mucilage would increase the water potential felt by the plant (the water potential at the root surface would become less negative). It is important to mention that this effect would be particularly important for high transpiration rates, when the drops in water potential around the roots are expected to be large.

Mucilage also has the function of maintaining the mechanical contact between the root surface and the soil particles. Albalasmeh and Ghezzehei (2014) showed that PGA (used as a mucilage analogue) glued soil particles together upon drying. The effect of such soil aggregation is well demonstrated by the formation of a stable rhizosheath around the roots (Watt et al., 1994). The rhizosheath is defined as the soil that adheres to the roots after they have been pulled out of the soil. The formation of a stable rhizosheath is believed to be caused by mucilage, that binds the particle, and root hairs, that connect the glued particles to the main roots. The combination of mucilage and root hairs helps the roots to stay in intimate contact with the soil, which is of particular importance in dry soils and at high transpiration rates, when roots are prone to shrink and lose contact with the soil (Huck et al., 1970; Carminati et al., 2013). The enhanced contact is likely to increase the ease with which the water flows across the root–soil interface, avoiding the formation of a large drop in water potential around the root.

In a review of root phenes important for water uptake in dry soils, Lynch et al. (2014) reported that rhizosheath layers are mainly present on young regions of the root, while they are lost from the more mature portions of the root. A similar feature may apply to mucilage, which is exuded at the root tip and is partly degraded as the rhizosphere ages. The fact the young roots are characterized by immature, non-conducting xylem vessels casts doubts on the role of mucilage and rhizosheath for plant water relations (Lynch et al., 2014). However, there is limited experimental evidence that the distal root segments do not take up water and, even in this case, such a conclusion may not apply to all root types and soil moisture conditions. Future measurements of water uptake by roots in soils with heterogeneous soil moisture distributions will answer this open question.

Our conceptual model, in which mucilage and root hairs contribute to favour the hydraulic connection between soil and root, is still largely speculative. To prove it, there are a series of variables and parameters that have to be measured. Such key areas of research are discussed in the next section.

CHALLENGES

Despite the fact that it is well accepted that the physiochemical properties of the rhizosphere are different from those of the bulk soil and that such differences impact the water dynamics in the rhizosphere during drying/wetting cycles, it is not yet clear what the consequences of such rhizosphere processes on root water uptake are.

Experiments with natural and artificial mucilage showed the capacity of mucilage to enhance the water retention of soil. However, the enhanced water retention is associated with an increase in viscosity and, depending on the relative importance of the two processes, mucilage may either increase or decrease the ability of plants to extract water from soils.

At present, there is limited experimental information on water flow across soils mixed with mucilage, in particular at low water potentials, when the gradients in water potential around roots are expected to become significant. Measuring the unsaturated conductivity of soils with mucilage is a first step to understand the role of mucilage in soil–plant water relations.

Key question 1. Does mucilage increase the soil hydraulic conductivity at negative water potentials?

Corollary questions concern the relationship between mucilage concentration, soil particle size distribution and unsaturated conductivity.

A challenge in measuring the unsaturated conductivity of soils mixed with mucilage at negative water potentials is that such measurements may require some weeks, during which mucilage may be degraded and lose its properties to retain water. Also, it is not clear how to mix mucilage and soil particles in a way that properly reflects the mucilage distribution in the rhizosphere. Whether mucilage is deposited in the large or the small pores would make a big difference: a preferential deposition of mucilage in the large pores would increase the water content and the hydraulic conductivity of the rhizosphere at moderately negative water potentials; a higher deposition in the small pores would have a stronger effect on the water content at more negative water potentials. A satisfying pore-scale model of where mucilage is deposited is missing. This gap in the knowledge identifies a second research priority.

Key question 2. How is mucilage distributed through the pore space of the rhizosphere?

Corollary questions regard the extent to which mucilage diffuses far from the roots and how soil moisture and soil texture affect such diffusion.

However, once these questions are answered, one last question remains: how does mucilage affect water uptake by roots growing in soils? The existing measurements of water content around the roots do not contain all the information necessary to answer this question. The missing information is the gradient in water potential around the roots.

Key question 3. What are the gradients in water potential around roots growing in drying soil at varying transpiration demands?

Accurate measurements of water potential around the roots, coupled with measurements of water fluxes into the roots, obtained for instance using the method of Zarebanadkouki et al. (2014), would allow estimation of the hydraulic conductivity of the rhizosphere, which could then be compared with the conductivity of the bulk soil. Optimally, experiments with plant varieties producing different amounts of mucilage would be of great advantage. Screening different plant varieties for mucilage production is definitely a key research area.

However, it has to be admitted that precise estimation of the gradients in water potential across the rhizosphere is challenging. An alternative solution is to measure the water potential at the two outmost sides of the rhizosphere: the bulk soil and the root xylem.

This is not a new idea. It was introduced by Passioura (1980). The idea consisted of cutting a leaf and keeping the water in the leaf xylem at atmospheric pressure by pressurizing the soil–root system. The applied pressure (called the balancing pressure) is equal to the work to move water from the soil, across the root–soil interface, into the roots and along the xylem at the rate controlled by transpiration. Passioura (1980) performed drying experiments during which the transpiration rate was increased and decreased at daily intervals. The results showed that when the soil was wet, the relationship between the transpiration rate and balancing pressure was linear. The slope of the relationship was interpreted as the plant conductance. As the soil dried, the relationship became non-linear, and the apparent conductance of the plant–soil system started to decrease. The deviation of the curve from the linear slope was interpreted as the drop in water potential across the rhizosphere; which would answer key question 3!

Passioura (1980) also reported a puzzling hysteresis in the relationship between transpiration rate and balancing pressure in the increasing/decreasing transpiration cycles in dry soils. He suggested that the hysteresis could have originated by the loss of contact of the roots with the soil or by the accumulation of solutes at the root surface, but a final proof of this process is still missing.

Coupling these measurements with imaging techniques that allow visualization of the root architecture and the structure and moisture of the rhizosphere could be the ultimate experiment to measure the rhizosphere properties and finally learn how plants modify the soil to extract water, in particular when water is scarce.

Note that in this article we focused on the physical aspects of the soil–root interactions and we did not discuss interactions with biological and chemical processes. However, a better understanding of the feedbacks between physical, biological and chemical processes in the rhizosphere is a high priority research area. For instance, it would be interesting to see how the mucilage exudation rate and its chemical composition vary with soil conditions (e.g. soil moisture and nutrient concentration) and among plant species. Also, it would be of great importance to identify the genetic mechanisms regulating mucilage exudation.

CONCLUSION

Despite the detailed images of water content dynamics in the rhizosphere, we do not yet fully understand how mucilage exudation affects root water uptake in varying soil environments. A similar conclusion holds for other physical processes occurring in the rhizosphere: formation of gaps at the root–soil interface; soil compaction around roots; formation of stable rhizosheaths; water uptake by root hairs; and physical interactions with micro-organisms.

The reason is that in addition to imaging moisture gradients, we need to measure the gradients in water potential around the roots. Although accurate measurements of soil water potential at a resolution high enough to resolve the gradients in the rhizosphere are challenging, measuring the difference in water potential between the xylem and the soil is possible. Combining such measurements with high-resolution imaging of soil moisture, soil structure and water fluxes across the rhizosphere is a promising way finally to learn what mechanisms plants use to improve water extraction from soils.