Estimation of the hydraulic conductivities of lupine roots by inverse modelling of high-resolution measurements of root water uptake

Abstract

Background and Aims Radial and axial hydraulic conductivities are key parameters for proper understanding and modelling of root water uptake. Despite their importance, there is limited experimental information on how the radial and axial hydraulic conductivities vary along roots growing in soil. Here, a new approach was introduced to estimate inversely the profile of hydraulic conductivities along the roots of transpiring plants growing in soil.

Methods A three-dimensional model of root water uptake was used to reproduce the measured profile of root water uptake along roots of lupine plant grown in soil. The profile of fluxes was measured using a neutron radiography technique combined with injection of deuterated water as tracer. The aim was to estimate inversely the profiles of the radial and axial hydraulic conductivities along the roots.

Key Results The profile of hydraulic conductivities along the taproot and the lateral roots of lupines was calculated using three flexible scenarios. For all scenarios, it was found that the radial hydraulic conductivity increases towards the root tips, while the axial conductivity decreases. Additionally, it was found that in soil with uniform water content: (1) lateral roots were the main location of root water uptake; (2) water uptake by laterals decreased towards the root tips due to the dissipation of water potential along the root; and (3) water uptake by the taproot was higher in the distal segments and was negligible in the proximal parts, which had a low radial conductivity.

Conclusions The proposed approach allows the estimation of the root hydraulic properties of plants growing in soil. This information can be used in an advanced model of water uptake to predict the water uptake of different root types or different root architectures under varying soil conditions.

Introduction

The uptake of water from the soil and its transport to the shoots is an essential function of the root system (Lobet et al., 2014). Root water uptake has to fulfil the transpiration demand to prevent plants from dehydration. Transpiration is driven by the difference in vapour pressure between the atmosphere and the leaves, and depends on the stomatal conductance (Tardieu et al., 2015). The water loss from leaves generates a suction that is transmitted along the xylem down to the roots (Wheeler and Stroock, 2008). The resulting gradient in water potential between leaves and soil drives root water uptake (Passioura, 1988; Steudle, 2000). The radial flow of water from the root surface into the xylem vessels is controlled by the radial conductivity, which depends on several anatomical features of the root tissue (Steudle, 2000). The axial flow of water in the xylem vessels up to the shoot is controlled by the axial conductivity, which depends on the maturation, size and abundance of the xylem vessels (Martre et al., 2001). The distribution of radial and axial conductivities and along the root system influences the rate and location of root water uptake (Frensch and Steudle, 1989; Zwieniecki et al., 2002; Javaux et al., 2008; Bramley et al., 2009).

Although the distribution of hydraulic conductivities along the root system is a key parameter to understand how plant roots function in acquiring water from the soil (Leitner et al., 2014), quantitative measurement of these parameters for plants growing in soil remains challenging (Vadez, 2014). Currently, most of the experimental data reporting the spatial distributions of hydraulic conductivities along roots are based on measurements of water flow into excised roots grown in soil-less cultures. Frensch and Steudle (1989) employed the root pressure probe technique to measure the hydraulic properties of excised primary roots of maize. They determined the hydraulic conductivity of root segments by applying gradients of hydrostatic and osmotic pressure across them (to induce water flow across root). Their results indicated that: (a) except for the apical zone (the first 2 cm of the root tip), the radial hydraulic conductivity was much more important in limiting water uptake than the axial hydraulic conductivity; (b) the radial conductivity was rather constant along the rest of the root segment in hydrostatic, but not in osmotic experiments where it decreased with distance from the root tip; and (c) the change in axial conductivity along the root was much bigger than the change in the radial conductivity. Zwieniecki et al. (2002) employed a pressure chamber technique to measure water flow into excised nodal roots of maize that were successively cut into smaller segments. These results were numerically simulated to reconstruct the profile of radial and axial resistance along the root. Their results showed that: (a) the radial resistance of maize root used in their study was 40 times higher than the axial resistance; (b) the location of root water uptake depends on the ratio of axial to radial resistance; and (c) a low ratio of axial to radial resistance results in the hydraulic isolation of the distal root segments. Tyree et al. (1994) and Tsuda and Tyree (2000) used the high pressure flow meter technique to measure root hydraulic conductivity.

To separate the contribution of axial and radial conductivity, all these techniques rely on measuring water flow into excised roots that are successively cut into smaller segments. Alternatively, the axial conductivity can be estimated based on anatomical features such as abundance and size of xylem vessels (Frensch and Steudle, 1989; Biondini, 2008; Bramley et al., 2009). Frensch and Steudle (1989) showed that the measured values of axial conductivities were smaller by a factor of 2 and 5 than those calculated according to Poiseuille’s equation.

The hydraulic properties of roots grown in soil may differ from those of roots grown in soil-less culture; for instance, root hydraulic properties change in response to soil drying (Nobel and Cui, 1992; North and Nobel, 1997). Under drought stress, early development and modifications of the endodermis and exodermis, the main resistances to water flow, have been reported (Enstone et al., 2002; Meyer et al., 2008). Additionally under drought stress, the expression and activity of aquaporins, which are proteins in the cell membrane that regulate the flow of water, may also vary, affecting the root radial conductivity (Knipfer et al., 2011; McLean et al., 2011; Caldeira et al., 2014; Li et al., 2015).

Root water uptake models can be divided into empirical, macroscopic models, such as those of Feddes et al. (1978) and Dardanelli et al. (2004), and more detailed models that explicitly couple the water flow into and along the root architecture with the water flow in soils (Roose and Fowler, 2004; Doussan et al., 2006; Javaux et al., 2008). The latter type of models can be used to simulate the response of different root systems to varying external conditions, such as drought (Doussan et al., 2006; Bechmann et al., 2014; Lobet et al., 2014). However, these models require detailed information about the spatial distribution of the root hydraulic conductivity, whose measurement is still challenging. A method that allows estimation of the spatial distribution of hydraulic conductivity along roots growing in soil is thus needed to model and predict root water uptake properly.

Doussan et al. (1998) modelled the hydraulic architecture of a maize root system to estimate inversely the spatial distribution of hydraulic conductivities along the roots based on the fluxes of water measured by Varney and Canny (1993). Doussan et al. (1998) were aware that without a priori knowledge of the distribution of hydraulic conductivities along the roots the same set of experimental data could be fitted by different profiles of hydraulic conductivities – in other words, the solution of the inverse problem was not unique. To solve this problem, the authors imposed simple constraints to the root conductivity distribution as a function of the distance to the tip.

We combined the root architecture model of Doussan et al. (1998) with recent high resolution images of root water uptake by Zarebanadkouki et al. (2012, 2013, 2014), who measured the profile of water uptake of 3-week-old lupines at a spatial resolution of approx. 5 cm. The objective of this study is to estimate inversely the profile of conductivities fitting the water fluxes measured by Zarebanadkouki et al. (2013) and additional information of (1) the root architecture; (2) the xylem water potential at the collar of the plant; (3) the soil water potential distribution; and (4) the actual transpiration.

The challenge in solving the inverse problem is that the number of parameters of the Hydraulic Tree Model (which are the radial and axial conductivities of the root segments) was higher than the number of experimental observations. To ensure the uniqueness of the solution, we reduced the number of parameters using three different and flexible scenarios. In the first two scenarios, we imposed that the radial and axial conductivities are linear or exponential functions of the distance to the root tip. In both cases, the conductivities can either increase or decrease towards the root tips. In the third scenario, we assumed step-wise distribution of the radial and axial conductivities along the root. To reduce the number of parameters, we allowed a maximum of three steps along lateral roots with a maximum length of approx. 18 cm. In contrast to the first two scenarios, the third one does not impose that the conductivities are monotonic functions of the distance to the root tip

Materials and Methods

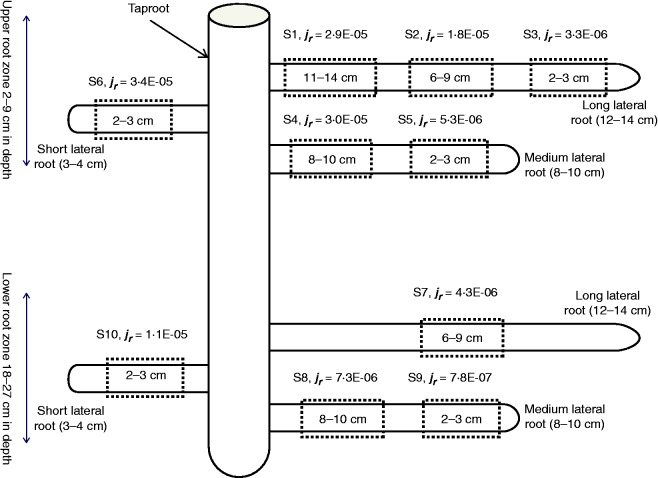
We used the Hydraulic Tree Model of Doussan et al. (1998) to fit the local flow of water reported by Zarebanadkouki et al. (2013). Zarebanadkouki et al. (2013) measured the local fluxes of water into different root segments of 3-week-old lupines grown in soil. The root system was made up of one taproot and 66 individual lateral roots. The root system was split into an upper and a lower zone. In each of these two zones, the roots were sub-grouped according to their length into three types: long roots (>12 cm), medium roots (8–10 cm) and short roots (<4 cm). The radial fluxes of water were estimated for ten different segments along the root system as illustrated in Fig. 1.

Fig. 1.

Schematic diagram of a lupine root system and the locations along the root system where radial fluxes of water were measured in Zarebanadkouki et al. (2013). The radial fluxes (j_r) are given in m s^–1. The value given in the rectangles shows the distance from the root tip where the radial fluxes are averaged. The root system was divided into upper and lower root zones. In each zone, three roots with different lengths were selected and the water fluxes were measured at different locations along each root (ten root segments).

In addition to these data sets, we used the two-dimensional root system architecture, the measured xylem potential at the collar of plant, the soil water potential distribution and the actual transpiration. Root architecture and soil water potential were extracted from the neutron radiographs according to the protocol described in Zarebanadkouki et al. (2012). Transpiration rates were taken from Zarebanadkouki et al. (2013). For the soil water potential, we assumed a uniform water potential in the soil based on the measured soil water contents and the retention curve reported in Zarebanadkouki et al. (2016). In their samples, soil water content varied from 0·1 to 0·2 cm³ cm^–3, which corresponded to a soil water potential range of –150 to –50 hPa. Since these variations are small compared with their difference from the xylem water potential (–2500 hPa), we assumed that the soil water potential was constant. The xylem water potential at the collar of the plant was measured by pressuring the above-ground part of the plant with a Scholander bomb (Scholander et al., 1965). The pressure at which the first drop of water came out from the cut end of the xylem tissue gave the absolute value of the water potential in the xylem. This measured xylem water potential of –2500 hPa was used as the top boundary condition for the root collar of the modelled plant.

Hydraulic Tree Model of Doussan

Doussan et al. (1998) developed an algorithm to solve the steady-state water flow within the root system by taking into account the spatial distribution of soil water potential. They simplified the root architecture as a system of interconnected nodes in which water flows radially from the soil into the roots and longitudinally inside the xylem vessels. The root system is split into small segments with typical length of 0·25 cm and the root hydraulic properties are assumed to be homogeneous within each single segment (as well as the xylem potential). The radial water flow Q_r(L³ T^–1) between the soil–root interface and the root xylem nodes is written as

$${\mathit{Q}}_{\mathit{r}}={\mathit{k}}_{\mathit{r}} {\mathit{s}}_{\mathit{r}}\left[{\mathit{H}}_{\mathit{s}}-{\mathit{H}}_{\mathit{x}}\right]={\mathit{K}}_{\mathit{r}}\left[{\mathit{H}}_{\mathit{s}}-{\mathit{H}}_{\mathit{x}}\right]$$ (1)

where H_s and H_x are the total water potential at the root surface in the soil and in the xylem [P], k_r is the intrinsic radial conductivity of the root (L P^–1 T^–1), s_r is the surface area of the root segment (L²), and K_r =k_rs_ris defined as the radial conductance of the segment with surface s_r (L³ P^–1 T^–1). In the present notation, matrices and vectors are bold. The total water potential is the sum of the hydrostatic potential (in the plant) or matric potential (in the soil) and the gravitational potential, while the osmotic potential is neglected.

The axial water flow in the root Q_x(L³ T^–1) is given by:

$${\mathit{Q}}_{\mathit{x}}=-\frac{{\mathit{k}}_{\mathit{x}}}{\mathit{l}}\text{d}{\mathit{H}}_{\mathit{x}}{=-\mathit{K}}_{\mathit{x}}\left[\text{d}{\mathit{h}}_{\mathit{x}}+ d\mathit{z}\right]$$ (2)

where H_x is the water potential in the xylem, h_x is the hydrostatic potential in the xylem,l is the length of the root segment (L), ${\mathit{K}}_{\mathit{x}}=\frac{{\mathit{k}}_{\mathit{x}}}{\mathit{l}}$ is the axial conductance of the root segment of length l (L³ P^–1 T^–1) and k_x is here called axial conductivity (L⁴ P^–1 T^–1) – note that in other studies (e.g. Doussan et al. 1998) k_x is called conductance, as it includes the information of the cross-section of the xylem vessel; we call k_x axial conductivity to distinguish it from the axial conductance K_x and also because k_x is an intrinsic propertiy that does not depend on the length of the root segment l, while K_x decreases with increasing l.

In the forward finite differences notation, eqns (1) and (2) are written as:

$$K_{x,i}\left(H_{x,i}-\mathrm{ }{H}_{x,i+1}\right)=\mathrm{ }{K}_{x,i-1}\mathrm{ }\left(H_{x,i-1}-\mathrm{ }{H}_{x,i}\right)+\mathrm{ }{K}_{r,i}\mathrm{ }\left(H_{s,i}-H_{x,i}\right)$$ (3)

where the right-hand side term refers to the water flowing into node i (both from the ‘child’ node i–1 with an axial conductance K_x,i–1and from the soil surrounding segment i:i–1). This equation is valid for nodes without branching. In the case of branching, the right-hand side includes a sum over axial flow rates of all children segments.

When generalized to all the nodes of the root system, the water potential distribution in the xylem is obtained by solving a system of linear equations like eqn (3). Under water potential boundary conditions, H_col (P), the equations can be written in matrix notation as:

$$H_x={\mathit{c}}^{-1}\left(\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}\left(-{\mathit{K}}_{\mathit{r}}\right) {\mathit{H}}_{\mathit{s}}- \left[\begin{array}{c}{K}_{x,1 }{H}_{\mathrm{col}}\\ \begin{array}{c}0\\ ⋮\end{array}\\ 0\end{array}\right]\right)$$ (4)

where c (dimensions n_p × n_pwith n_p being the number of root nodes) is derived from the so-called ‘conductance matrix’ C described in Couvreur (2013) (c is obtained retrieving the first column and the first line of C), H_col is the collar water potential (P), diag (K_r) (dimensions n_p× n_p) is a diagonal matrix containing the radial conductances on its diagonal, H_s (dimensions n_p× 1) contains the total soil water potentials, and H_x (dimensions n_p× 1) is the unknown xylem water potential vector. K_x,1 is the axial conductance of the first segment. The conductance matrix (C) is a combination of both hydraulic conductances and architecture as shown in eqn (5)

$$\mathbf{C}=\mathbf{I}\mathbf{M}.\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}\left(\left[\begin{array}{c}-{\mathit{K}}_{\mathit{x}}\\ {-\mathit{K}}_{\mathit{r}}\end{array}\right]\right).{\mathbf{I}\mathbf{M}}^T$$ (5)

IM (dimensions (n_p + 1) × 2n_p) is the connectivity matrix whose ‘(i, j)’ entry is 1 if root node ‘i’ is connected to root or soil node ‘j’, and 0 elsewhere (see Doussan et al., 1998), $\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}\left(\left[\begin{array}{c}-{\mathit{K}}_{\mathit{x}}\\ {-\mathit{K}}_{\mathit{r}}\end{array}\right]\right)$ (dimensions 2n_p × 2n_p) stands for the diagonal matrix whose diagonal elements are the axial and radial conductances, and IMT^T is the transpose of the matrix IM. In the present notation, dot (.) indicates a matrix product. Combination of eqns (1) and (4) gives the fluxes from the root–soil interface to the xylem vessels as well as the collar water potential (Couvreur, 2013):

$${\mathit{Q}}_{\mathit{r}}=\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}\left({\mathit{K}}_{\mathit{r}}\right).\left({\mathit{H}}_{\mathit{s}}+ {\mathit{c}}^{-1}.\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}\left({\mathit{K}}_{\mathit{r}}\right).{\mathit{H}}_{\mathit{s}}+ H_{\mathrm{col}}.{{\mathit{c}}_1^{-1}K}_{x,1 }\right)$$ (6a)

$$T_{\mathrm{act}}= \sum _{i=1}^{n_p}{Q}_{r,i}$$ (6b)

where $c_1^{-1}$ is the first column of the c^–1 matrix and T_act is transpiration rate at the collar of plant (L³ T^–1) (Couvreur, 2013). Equation (6a) was built and solved in Matlab under known water potential boundary conditions at the root collar and constant and homogeneous water potential boundary conditions at the soil–root interfaces.

Modelling approach

We applied the Hydraulic Tree Model of Doussan et al. (1998) to the lupine root system studied in Zarebanadkouki et al. (2013). The root architecture was implemented in Matlab. The entire root architecture of the lupine was split into 1977 nodes by dividing the root system into small segments with typical length of 0·25 cm and using their centres as simulation nodes. Each node was connected to the neighbouring nodes from the same root or from the taproot by an oriented link accounting for the axial conductance between two successive compartments. Each node was connected to the soil–root interface node by an oriented link having a given radial conductance. Nodes were numbered serially in the upstream direction, starting from taproot first, and then branched roots (Doussan et al., 1998). The soil nodes were numbered in the same way as the root nodes. Finally, we built matrixes C c, and H_s for the whole set of nodes based on the protocol given above and in Doussan et al. (1998).

We inversely estimated the radial and axial hydraulic conductivities (k_r and k_x) of the root system to reproduce the profile of root water uptake measured at ten different locations along the root system in Zarebanadkouki et al. (2013) (Fig. 1). The inverse problem was solved by minimizing a pre-defined objective function using the ‘global optimization toolbox’ in Matlab (‘pattern search’ algorithm). The ‘pattern search’ algorithm finds the global minimum of a pre-defined objective function. This solver has the advantage of accepting lower and upper pre-defined boundaries for the solution. It also allows imposing linear and non-linear constrains to the solution. The objective function (OF) to be minimized was defined as the root mean square of relative differences between measured and simulated radial fluxes of water at ten different locations presented as s1 to s10 in Fig. 1 and the measured and simulated actual transpiration [eqn (6b)]. Note that consequently during optimization we had 11 known parameters.

$$\mathrm{OF}= \sum \left(\left|\frac{{\left(\left[\begin{array}{c}{T}_{\mathrm{act}}\\ {\mathit{J}}_{\mathit{r}},\end{array}\right]- \left[\begin{array}{c}{T}_{\mathrm{act},\mathrm{obs}}\\ {\mathit{J}}_{\mathit{r},\mathbf{obs}}\end{array}\right]\right)}^2}{{\left[\begin{array}{c}{T}_{\mathrm{act}}\\ {\mathit{J}}_{\mathit{r}}\end{array}\right]}^2}\right|\right)$$ (7)

with T_act,obs and J_r,obs and the observed actual transpiration (L.T^–1) and the radial fluxes (L.T^–1), respectively. Note that the radial fluxes inserted in this equation for each location were first averaged along the root segments with given length, as reported in Zarebanadkouki et al (2013).

Finding a unique solution for the profile of hydraulic conductivities at the resolution of 0·25 cm was challenging, i.e. in the inverse problem there will be far more unknowns than the 11 measurements (ten radial fluxes plus the total transpiration). To reduce the number of unknowns in the inverse problem, we made the following assumptions: (1) the root system was made of one tap root and several lateral roots, and we neglected secondary laterals and cluster roots; and (2) the radial and axial conductivities of the tap root and the laterals were functions of the distance from the root tip.

Then we investigated different shapes of the profiles of hydraulic conductivities along the root. In scenario 1 and 2, we assumed that the conductivities were linear and exponential functions of the distance to the root tip. Scenario 1 and 2 allowed either increasing or decreasing conductivities towards the root tips; however, the functions had to be monotonic. In scenario 3, we described the conductivities as step-wise functions. To reduce the number of parameters, we assumed that the roots had a maximum of three zones with different radial and axial conductivities. The location and extent of the zones were let vary. The advantage of scenario 3 is that it allows a flexible and non-monotonic shape of the conductivities. The three scenarios are described in detail in the following sections.

Scenario 1

The profiles of the radial and axial hydraulic conductivity of the laterals were described with linear functions:

$$\begin{array}{l}{\mathit{k}}_{\mathit{r}}=a.\mathit{z}+b\\ {\mathit{k}}_{\mathit{x}}=c.\mathit{z}+d\end{array}$$ (8)

where a and c can be positive or negative numbers and b and d are positive numbers. If a is negative, the radial conductivity (k_r) linearly decreases with distance from the root tip [z, (L)] and if it is positive it increases. The same applies to the profile of axial conductivity (k_x): if c is negative, the axial conductivity decreases with distance from the root tip and, if it is positive, it increases. Note that for each individual root type (lateral and taproot) these four parameters are optimized. This scenario contains eight parameters to optimize.

Scenario 2

The profiles of radial and axial conductivity as a function of distance from the root tip were described by exponential functions:

$$\begin{array}{l}{\mathit{k}}_{\mathit{r}}=a.e^{b.\mathit{z}}\\ {\mathit{k}}_{\mathit{x}}=c.e^{d.\mathit{z}}\end{array}$$ (9)

where b and d can be positive or negative numbers, while a and c are positive numbers. If b is negative, the radial conductivity (k_r) decreases with increasing distance from the root tip [z, (L)], while if b is positive k_r increases. The same applies to the axial conductivity (k_x); if d is negative k_x decreases with distance from the root tip, while if d is positive k_x increases. Note that for each individual root type (lateral and taproot) these four parameters are optimized. This scenario contains eight parameters to optimize.

Scenario 3

The profiles of hydraulic conductivity along the lateral roots were described using a step-wise function with two transition points separating three zones. We chose three zones because the radial fluxes were also measured at three locations along an individual lateral root (Zarebanadkouki et al., 2013) and a similar scenario was also tested in Doussan et al. (1998). The position of the three zones was let vary during the optimization. The parameters to be optimized in this scenario are three radial conductivities of laterals (kr₁, kr₂, kr₃), three axial conductivity of laterals (kx₁, kx₂, kx₃) and two locations separating the three zones, n₁ and n₂. The radial and axial conductivities were defined as:

$$\left\{\begin{array}{ccc}{\mathit{k}}_{\mathit{r}}\left(z\right)={kr}_1& \mathrm{and}& {\mathit{k}}_{\mathit{x}}\left(z\right)={kx}_{1}for\hspace{1em}z>n_2\\ {\mathit{k}}_{\mathit{r}}\left(z\right)={kr}_2& \mathrm{and}& {\mathit{k}}_{\mathit{x}}\left(z\right)={kx}_2\begin{array}{cc}for& n_2\ge z\ge n_1\end{array}\\ {\mathit{k}}_{\mathit{r}}\left(z\right)={kr}_3& \mathrm{and}& {\mathit{k}}_{\mathit{x}}\left(z\right)={kx}_3\begin{array}{cc}for& z<n_1\end{array}\end{array}\right.$$ (10)

where z is the distance from the root tip. Estimation of the hydraulic conductivities along the taproot is problematic since there was no information about water fluxes into the taproot. To reduce the number of unknowns, we impose constant radial and axial conductivity along the taproot. Our sensitivity analysis also showed that our model is not sensitive to the radial conductivity of the taproot (discussed in detail in the Results). This scenario requires ten parameters.

Sensitivity analysis and parameter uncertainty

Before any effort to solve an inverse problem, it is very important to find out whether the pre-defined objective function is sensitive to the parameters to be optimized. A sensitivity analysis was performed for scenario 2 around the optimal solution. It is a local sensitivity analysis where two selected parameters of eqn (9) were let vary simultaneously. We considered each single pair of variables of scenario 2. The range of variation for each parameter was ±20 %. We arbitrarily chose 20 % for two reasons. First, we considered only small variations of the parameters to evaluate the local sensitivity. Secondly, the exponential shape of the functions in scenario 2 led to significant changes of the simulated conductivities even with small parameter changes.

The uncertainty of the resulting parameters was quantified by estimation of confidence intervals of parameters. The uncertainty is related to the curvature of the objective function at the optimum solution, i.e. a sharper curvature gives a narrower confidence interval (more certainty). We estimated 95 % confidence intervals for the estimated profiles of radial and axial conductivity using linear regression analysis for our non-linear problem following the approach of Lambot et al. (2002). This approach is based on the calculation of Hessian matrix at the optimal solution (minimum of the objective function).

Results

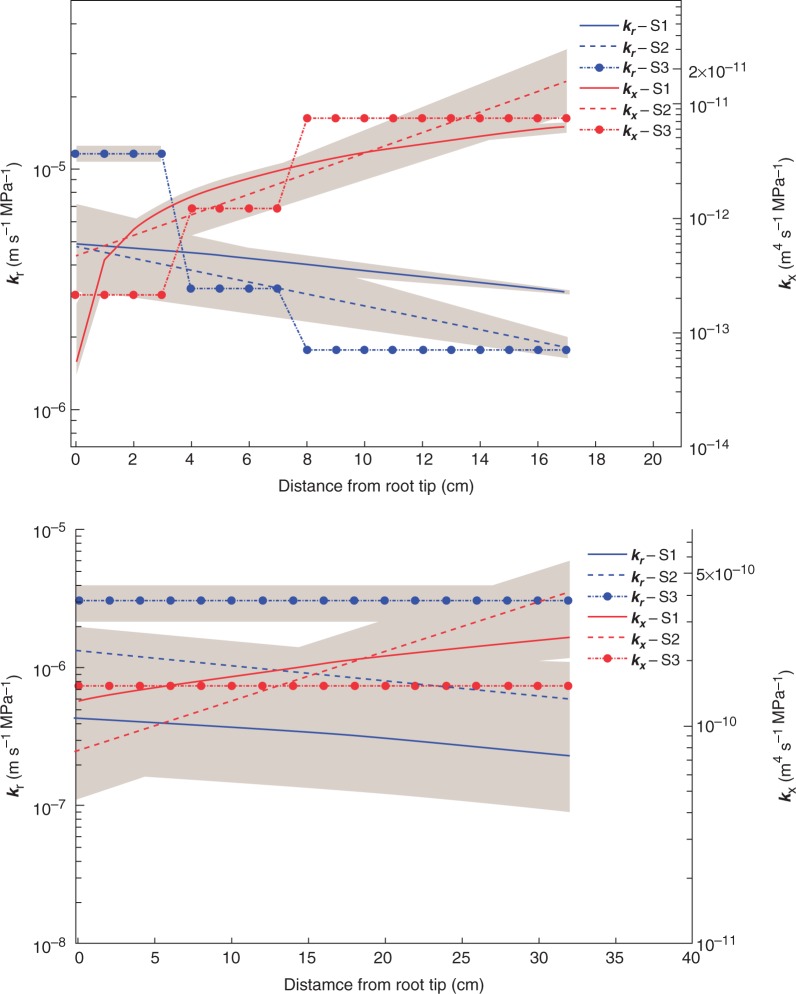
Figure 2 shows the profiles of radial conductivity (k_r) and axial conductivity (k_x) along the roots that best fitted the measured water fluxes. The results of all scenarios showed that the radial hydraulic conductivity was higher at the distal parts of the root and decreased towards the proximal parts. The axial conductivity showed the opposite trend. In scenarios 2 and 3, k_r of lateral roots decreased by three and seven times from the distal to the proximal segments, respectively. k_x of lateral roots increased by approx. 300 times in both scenarios 2 and 3. k_r predicted by scenarios 1 and 2 was rather similar. Scenario 2 predicted a larger variation in k_x of lateral roots from the distal to proximal parts. The differences between k_r and k_x predicted by the different scenarios were always smaller than one order of magnitude. We also estimated the 95 % confidence intervals for both k_r and k_x of the lateral root. In general, the ranges of estimated confidence intervals were small in all scenarios, particularly in scenario 3. The ranges of estimated confidence intervals were larger for distal root segment than the proximal segment. The small confidence interval indicates that the best solutions were reached and had a sharp global minimum.

Fig. 2.

Profile of hydraulic conductivities as a function of distance from root tip. (A) Profile of radial conductivity (k_r) and axial conductivity (k_x) along lateral roots. (B) Profile of radial and axial conductivity along the taproot. We used three different scenarios to estimate the profile of the conductivities. In scenario 1 and 2, we imposed a linear and exponential function to estimate the profile of conductivities, respectively. In scenario 3, k_r and k_x of the lateral root were estimated using a step-wise function with three transition zones and those of the taproot were fitted to be homogenous along the taproot. The grey strips around the lines show the 95 % confidence interval of estimated conductivities. The data of k_r and k_x obtained from scenario 2 are given in Supplementary Data Tables S1 and S2.

Estimatedk_randk_x of the tap root showed a larger variation among different scenarios. These larger variations are in fact due to the lack of having measured fluxes along the taproot. The 95 % confidence intervals showed large uncertainties in the estimation of k_randk_x of the taproot. It is worth noting here that the optimized radial conductivities in the three scenarios were always smaller than those of the laterals. Combined with a much lower total surface area of this root type, we observe that this root does not significantly affect the actual plant transpiration. This explains the uncertainty on the radial conductivity of the laterals. For this plant, the taproot is mainly a conducting rather than an extracting organ. Therefore, its k_x needs to be large enough to conduct water and k_r small enough not to extract water. Higher k_x and lower k_r will not affect the root water uptake distribution much, which leads to a wide 95 % confidence interval.

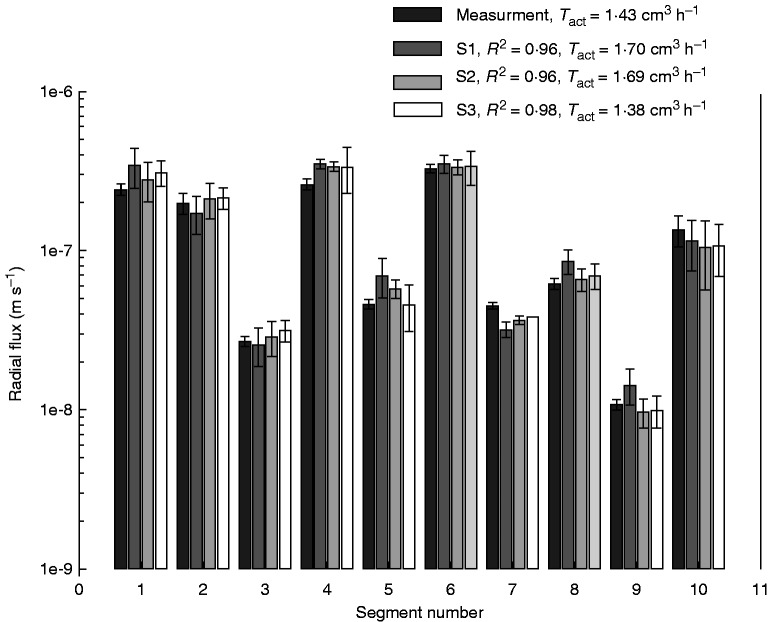
Figure 3 shows the measured and the simulated radial fluxes of water into different locations along the root segment. The radial fluxes were modelled using scenarios 1, 2 and 3. The model was able to fit the profiles of root water uptake in all scenarios, in particular with scenario 2 and 3.

Fig. 3.

Measured and simulated radial fluxes into different locations along the root system illustrated in Fig. 1. Error bars show the standard deviations of average fluxes into different segment types (S1–S10). R² refers to the correlation coefficient between measured and simulated fluxes, and T_act is the transpiration rate.

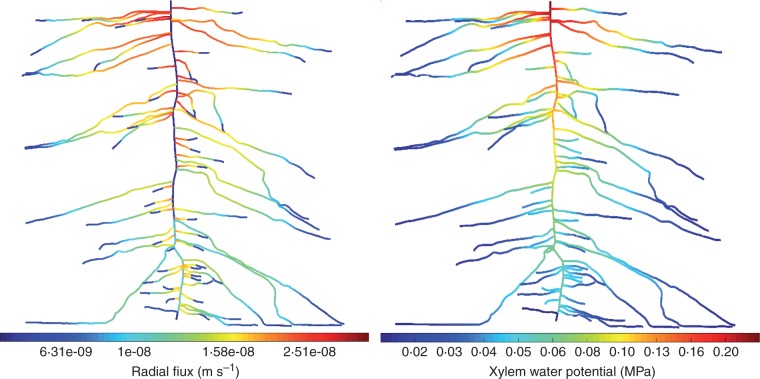
Taking advantage of the 3-D architectural model of Doussan et al. (1998), we visualized the spatial distribution of water flux and the xylem water potential along the entire root system of lupine (Fig. 4). The results are based on scenario 2 but do not change dramatically if the other scenarios are used. The simulations show that: (1) root water uptake was not uniform along the root system; (2) lateral roots were the main location of root water uptake in homogeneous soil conditions; (3) the lateral roots in the upper soil were more involved in water uptake than the laterals located in the lower zone; (4) root water uptake in the proximal parts of the lateral roots was higher than in the distal parts; (5) water uptake by the taproot was high in the distal part, but it was negligible in the proximal part; and (6) root water uptake was not only a function of the distance from the root tip and it depended mainly on the architecture of the root system (this means that the axial conductivity of the taproot is limiting). A similar pattern of root water uptake was reported by Dara et al. (2015) who estimated root water uptake of lupines based on soil water depletion.

Fig. 4.

Radial fluxes (m s^–1) (left) and (minus) absolute xylem water potential (MPa) (right) along a 3-week-old root system of lupine simulated in scenario 2. The root system is extracted from the neutron radiographs of Zarebanadkouki et al. (2013).

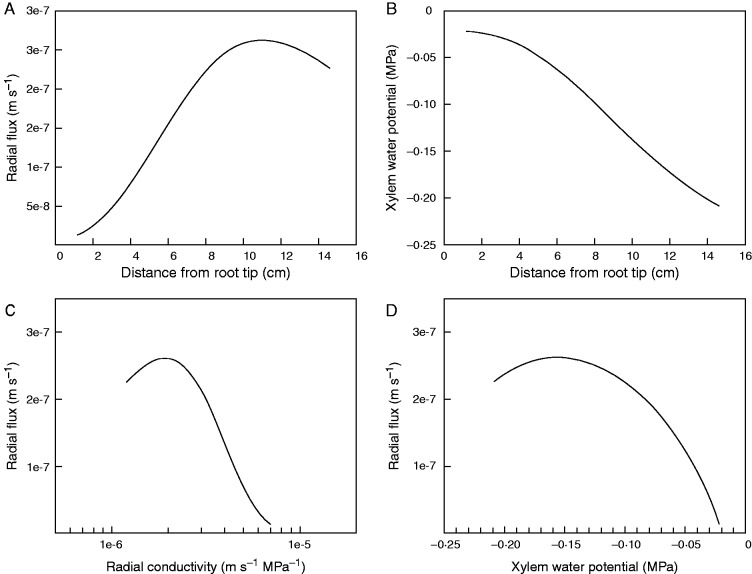
The profiles of root water uptake and xylem water potential along an individual lateral root are shown in Fig. 5. The selected root was 14·5 cm long and located at a depth of 5 cm from the soil surface. We found that the highest radial flux occurred at a distance of 11 cm from the root tip. Excluding the first 1·5 cm of the root tip, where the xylem conductivity was low (probably because the xylem vessels were not yet developed (Frensch and Steudle, 1989), root water uptake increased by 20 times from a distance of 1·5 to 11 cm from the root tip. Water uptake decreased by 1·5 times from a distance of 11 to 14·5 cm from the root tip. As expected, the lowest xylem water potential was found in the proximal parts of the root and increased towards the distal parts where it approached the soil water potential (Fig. 5B). Figure 5 also shows the profile of root water uptake along a root as a function of the radial conductivity and xylem water potential. We did not find a simple correlation between root water uptake and radial conductivity (Fig. 5C), and the same conclusion holds for the xylem water potential (Fig. 5D).

Fig. 5.

(A) Profile of root water uptake and (B) xylem water potential as a function of distance from the root tip. (C) Relationship between root water uptake and radial hydraulic conductivity. (D) Relationship between root water uptake and xylem water potential. The simulated root had a length of 14·5 cm and it was located at a depth of 5 cm from the soil surface. The results are based on scenario 2.

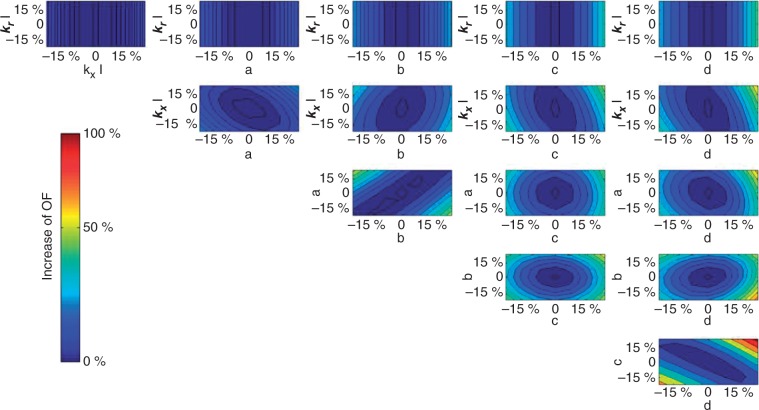
Finally, we tested the sensitivity of the model to the parameters of the radial and axial conductivities. The question was to find out with our set of available data whether the model of Doussan et al. (1998) is sensitive to the profile of conductivities. Since the profiles of simulated root water uptake and hydraulic conductivities in scenario 3 and 2 were rather close, we decided to test the sensitivity of the model only for the parameters used in scenario 2. In scenario 2, we needed only eight parameters to describe the profile of hydraulic conductivities/conductances along roots, which makes the sensitivity analysis easier and more straightforward. Figure 6 shows the results of the sensitivity analysis. Labels k_rI and k_xI stand for the radial conductivity and axial conductivity of the taproot, respectively. Indeed, in scenario 2, radial conductivity of the taproot can be considered as constant without affecting the results dramatically. The model was insensitive to the radial conductivity of the principal in the here-considered range of variation. Indeed, the radial conductivity of the taproot was very low as compared with that of laterals, and increasing its value by 20 % did not affect the water uptake. From the other sub-plots, we can draw the following conclusions: the parameters a and b as well as c and d were correlated [the parameters are defined in eqn (9)]. This is due to the shapes of the functions, i.e. increasing the exponent can be compensated by decreasing the factor by which this function is multiplied. The parameters (except k_rI) were well defined: a clear valley in the objective function was found corresponding to the global minimum. The solution was unique with the considered scenario and d is the most critical parameter: small variations of its value led to large changes in the objective function and in the water uptake. This parameter is critical: it explains how fast the xylem vessels mature and allows the transport of the water absorbed at the root tip.

Fig. 6.

Sensitivity analysis of the model parameters. The colour intensity shows the increase of the objective function defined in eqn (7). The results are based on the radial and axial conductivities calculated in scenario 2 [see eqn (9) and main text for the explanation of the parameter names].

Discussion

We estimated the profile of radial and axial conductivities along the roots of a transpiring plant grown in soil. To this end, we used the Hydraulic Tree Model of Doussan et al. (1998) to reproduce the profile of root water uptake along the root system of lupines reported in Zarebanadkouki et al. (2013). To reduce the number of unknown of the inverse problem and ensure uniqueness of the inverse solution, we used three flexible and different functions of the profiles of conductivities along the roots The results of all scenarios showed that the radial conductivity increases towards the root tips, while the intrinsic axial conductivity decreases. This result confirms the current opinion of how root anatomy and root maturation affect the root conductivities: over time, the radial conductivity decreases due to the formation and maturation of casparian strips and suberin lamellae. In contrast, the axial conductivity increases due to the development and maturation of conductive xylem vessels (Steudle and Peterson, 1998; Enstone et al., 2002).

Besides revealing the spatial distribution of hydraulic conductivities along roots, another important significance of this work is to predict the distribution of root water uptake along the root system with a high spatial resolution. The results showed that root water uptake was not uniformly distributed along the root system even in homogeneous soil conditions. Similar findings were also reported by Dara et al. (2015) for lupines growing is soil. We found that the profile of root water uptake along the roots cannot be simply described by the developmental stage of the root (distance from the root tip), but it depends on the architecture of the root system. The distal parts of the roots (young segments) showed different contributions in root water uptake depending on the distance from the taproot. By increasing the distance from the taproot, the contribution of the young root segment to root water uptake decreased due to the increasing axial resistance that water has to overcome.

In Zarebanadkouki et al. (2013), the profile of root water uptake was estimated with a spatial resolution of 4 cm and it was concluded that root water uptake increased towards the most proximal parts. Instead, simulations of root water uptake at a finer resolution showed that along an individual lateral root, the maximum water uptake occurs at a distance of 11 cm from the root tip and it decreases towards both proximal and distal parts. These results differ from the simulations of Landsberg and Fowkes (1978), who found an increasing uptake towards the proximal part in soil with a homogenous soil water potential. The reason is that they assumed uniform root conductivities. In our case, the increase of axial conductance and the decrease of radial conductivity in the proximal parts favour the uptake in the more distal parts, resulting in a maximum at 11 cm. The results also show that water uptake by the taproot was negligible due its low radial conductivity. The combination of low radial conductivity and high axial conductance confers to the taproot an excellent ability to collect water from lateral roots and transport it to the shoots.

It is interesting to estimate how the ability of the root to extract water from soil changes as the root elongates. Does water uptake increase linearly with root length or is there a trade-off between root length and water uptake capacity? The answer to this question is not straightforward and cannot be simply estimated from the profile of conductivities. We used our model to simulate the total water uptake by a single growing root (from 1 to 17 cm), using the profile of conductivities obtained from scenario 2. The results showed that root water uptake increases with root growth (Fig. 7). For roots shorter than approx. 7 cm, the increase in water uptake is rather linear. As roots grow further, root water uptake starts to increase less rapidly. With further root growth, the uptake reaches a constant value. These results show that there is a trade-off between root growth and maximum root water uptake. The explanation is that as the root grows the total root surface increases but the radial conductivity of the proximal segments decreases as the root ages. Additionally, as the roots elongate, the axial path becomes longer and the dissipation of pressure along the root becomes more significant. However, the maturation of the xylem vessels and their increasing axial conductivity facilitate the longitudinal transport of water along the old, proximal segments. This combination of increasing axial conductivity and decreasing radial conductivity with age explains the profile of water uptake shown in Fig. 5 and the total uptake for varying root lengths shown in Fig. 7.

Fig. 7.

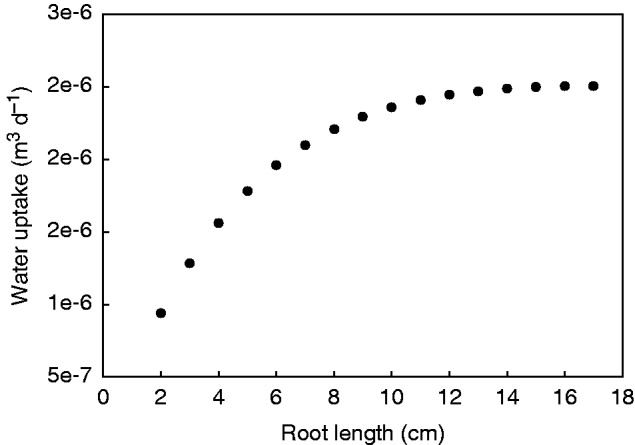
Root water uptake as a function of root growth. Root water uptake (total water taken up by root at the basal end of the root) was simulated using the radial and axial conductivities obtained in scenario 2.

The fluxes reported here refer to plants growing in uniformly wet soils, when the soil conductivity is not a limit for root water uptake. However, as the soil dries, its hydraulic conductivity decreases and becomes relevant for water uptake (Passioura, 1988; Draye et al., 2010). Measurements and models of root water uptake showed that in wet soils root water uptake mainly occurs in the upper part of the root system; but, as the top soil layers dry, root water uptake moves downwards to the lower part of the root system (Roose and Fowler, 2004; Doussan et al., 2006; Garrigues et al., 2006; Couvreur et al., 2012; Dara et al., 2015). Roose and Flower (2004) simulated root water uptake in soil with heterogeneous water content and showed that the regions near the base of the root system (i.e. close to the ground surface) and near the root tips will take up more water than the middle region of the root system, due to the highly non-linear nature of water flow in the soil. Yet, Schwartz et al. (2016) showed that the specific non-equilibrium rhizosphere properties may generate more uniform uptake profiles. Furthermore, in dry conditions, the interface between roots and soil undergoes complex dynamics. It has been shown that under dry conditions, roots shrink and lose their contact with the soil (Nobel and Cui, 1992; Carminati et al., 2013). It has also been shown that in dry conditions the rhizosphere turns hydrophobic (Carminati et al., 2010; Moradi et al., 2012; Zarebanadkouki and Carminati, 2014; Zarebanadkouki et al., 2016). The rhizosphere hydrophobicity is more pronounced in the proximal, older root segments, while the rhizosphere of the distal root segments is rapidly rewetted (Carminati, 2013). Therefore, after repeated drying/wetting cycles, we can expect a shift of water uptake towards the distal, younger root segments.

Here, for simplicity, we assumed that root segments with equal distance from the root tip had identical hydraulic properties. This assumption implies that the rates of root growth and root maturation were constant. However, the root growth rate depends on the supply of water, oxygen and nutrients, as well as on the developmental stage of the plants (Bengough et al., 2006; Watt et al., 2006). Detailed measurements of root growth would help to remove this assumption and to obtain detailed information on the profiles of root conductivities.

The significance of this study is to propose a method to estimate the hydraulic properties of a root system. Using the model of Doussan et al. (1998) and measurements of local fluxes into the roots (Zarebanadkouki et al., 2012), we reconstructed the potential profiles of radial and axial conductivities along the roots. The estimated root properties can be used to simulate root water uptake under different scenarios, for example as the soil dries, assuming no time variation of root hydraulic properties. These data can be also used to understand ‘which type of roots and root architecture better extract water from drying soil’ (Lynch, 2013). The answer to this question relies on modelling approaches which require a good knowledge of root hydraulic properties (Leitner et al., 2014). Finally, this experiment could be repeated for several genotypes to compare their hydraulic properties and try to understand their different water uptake behaviours.

Supplementary Data

Supplementary data are available online at www.aob.oxfordjopurnals.org and consist of the following. Table S1: profile of hydraulic conductivities along lateral roots as a function of the distance from the root tip obtained from scenario 2. Table S2: profile of hydraulic conductivities along the taproot as a function of the distance from the root tip obtained from scenario 2.