CN-Wheat, a functional–structural model of carbon and nitrogen metabolism in wheat culms after anthesis. I. Model description

Abstract

Background and Aims Improving crops requires better linking of traits and metabolic processes to whole plant performance. In this paper, we present CN-Wheat, a comprehensive and mechanistic model of carbon (C) and nitrogen (N) metabolism within wheat culms after anthesis.

Methods The culm is described by modules that represent the roots, photosynthetic organs and grains. Each of them includes structural, storage and mobile materials. Fluxes of C and N among modules occur through a common pool and through transpiration flow. Metabolite variations are represented by differential equations that depend on the physiological processes occurring in each module. A challenging aspect of CN-Wheat lies in the regulation of these processes by metabolite concentrations and the environment perceived by organs.

Key Results CN-Wheat simulates the distribution of C and N into wheat culms in relation to photosynthesis, N uptake, metabolite turnover, root exudation and tissue death. Regulation of physiological activities by local concentrations of metabolites appears to be a valuable feature for understanding how the behaviour of the whole plant can emerge from local rules.

Conclusions The originality of CN-Wheat is that it proposes an integrated view of plant functioning based on a mechanistic approach. The formalization of each process can be further refined in the future as knowledge progresses. This approach is expected to strengthen our capacity to understand plant responses to their environment and investigate plant traits adapted to changes in agronomical practices or environmental conditions. A companion paper will evaluate the model.

INTRODUCTION

Improving crop production and adapting it to environmental changes constitute major challenges. A better understanding of plant–environment interactions would help to address these challenges. Modelling offers a suitable framework for studying plant functioning and integrating the knowledge of different research areas. An extensive literature is dedicated to the modelling of carbon (C) and nitrogen (N) metabolism and allocation within plants. A majority of these models are based on empirical rules (e.g. Jones et al., 1986; Brisson et al., 2009) or teleonomic principles, such as the optimization and coordination theories (Hirose and Werger, 1987; Chen et al., 1993). These approaches provide straightforward estimations of the global functioning of plants as observed in given conditions and could also capture plant responses to a large range of C and N availabilities (e.g. Louarn et al., 2015). Nevertheless, plants are not fundamentally driven by central regulatory mechanisms and empirical rules may be impaired by environmental variations. In contrast, mechanistic models explicitly account for biological processes of plants and deal with concepts and variables that can be assessed and measured experimentally (Tabourel-Tayot and Gastal, 1998; Luquet et al., 2006; Bertheloot et al., 2011; Grafahrend-Belau et al., 2013).

In mechanistic models, the behaviour of the system is not driven by global rules, but rather is an emergent property of responses at local scale (Minchin and Thorpe, 1996; Minchin, 2007). One of the key interests of the mechanistic approach is to allow investigation of how each of the processes that takes place at local scale impacts the behaviour of the whole system. When addressing larger scales, this approach therefore makes it possible to benefit from knowledge from disciplines at smaller scales. A central difficulty in this exercise lies in the knowledge gaps, which make it difficult to ‘close’ the system; these gaps have to be dealt with by integrating hypotheses. Another important difficulty is that the system must be divided into sub-systems with defined boundaries and interactions, and any choice made here will have associated drawbacks. The variety of existing models reflects the variety of strategies used to overcome these limitations.

Functional–structural plant models (FSPMs) represent one approach in the description of plants in sub-systems; here the plant is described as a collection of interconnected organs (Prusinkiewicz and Lindenmayer, 1990; Godin and Sinoquet, 2005). FSPMs consist in an explicit description of plant architecture, making it possible to specify the environment perceived by phytoelements. FSPMs constitute a promising means for the development of mechanistic models whereby physiological processes can be formalized at organ scale while accounting for the local environment, such as light or temperature [i.e. the phylloclimate (Chelle, 2005)]. Most present FSPMs have mainly addressed the representation of realistic plant architecture to assess interactions with the (a)biotic environment (Saint-Jean et al., 2004; Cici et al., 2008; Robert et al., 2008; Barillot et al., 2014). Based on calculations of local light interception, various FSPMs account for the assimilation of carbon, but assimilate partitioning is generally solved using a supply–demand approach whereby the supply synthesized by sources is shared among sinks according to their ‘demand’ (Luquet et al., 2006; Evers et al., 2010; Sarlikioti et al., 2011; Bertheloot et al., 2011). By contrast, an example of mechanistic treatment of sink–source relations for C has been proposed by Allen et al. (2005). Recently, Bertheloot et al. (2011) proposed the model NEMA for N economy, whereby physiological processes are dependent on N concentrations and on a pool of mobile N shared by all organs. NEMA represents a step towards the mechanistic modelling of N metabolism, but it includes a demand-driven approach for dry mass allocation, which prevents a mechanistic treatment for C–N relations.

In this paper we present CN-Wheat, a comprehensive process-based model that accounts for C–N distribution within wheat plants after anthesis. Whenever possible, we have specified the domain of validity of the physiological processes implemented, but the originality of CN-Wheat lies in the fact that it provides a holistic view of plant functioning by using a fully mechanistic approach for integration of C–N metabolism at plant level. A detailed description of the model structure, hypotheses and formalisms is given here. In a companion paper we will describe parameter estimation and also evaluate the model.

MODEL DESCRIPTION

After anthesis, wheat culms develop their own root system (e.g. Klepper et al., 1984); furthermore, Williams (1964) reported for a perennial grass that translocation of carbon assimilates between large culms did not occur. Consequently, CN-Wheat is defined at culm scale, the crop being represented as a population of individual culms (Fig. 1). Culms are considered as a set of botanical modules representing the root system, each photosynthetic organ and the whole grains. These organs include structural, storage and mobile materials, variations in which are represented by differential equations driven by the main metabolic activities. Fluxes of metabolites among organs occur through a common pool, hereafter called phloem.

Fig. 1.

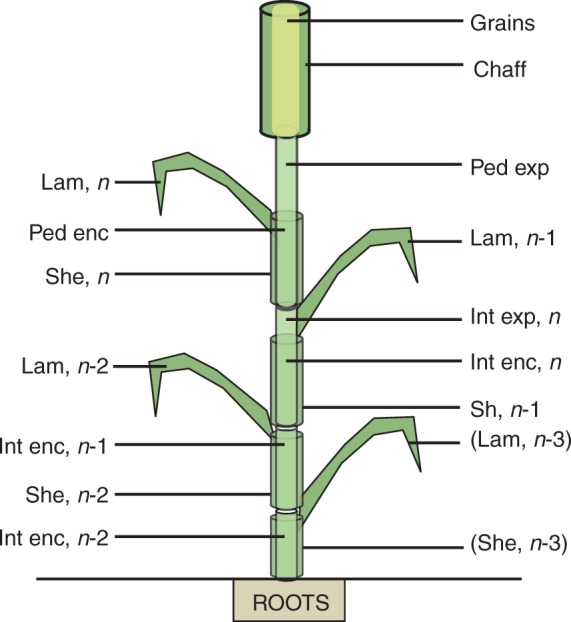
Botanical description of the culm structure of wheat as implemented in the model. Culm structure is defined as a single root compartment and photosynthetic organs are organized in phytomers, chaff and grains. Phytomers are numbered acropetally according to their rank (n being the uppermost phytomer) and are composed of a lamina (Lam), a sheath (She) and an internode (Int) or a peduncle (Ped). Parts of the internode n and peduncle are either exposed (exp) or enclosed (enc), i.e. surrounded by the previous sheath.

As the present work focuses on post-anthesis stages, we assume that the only growing organs are grains and roots, meaning that photosynthetic organs have reached their final structural mass at anthesis. Besides, a sub-model of tissue death is used to drive the (1) loss of structural N and dry mass, (2) green area time course for photosynthetic organs, and (3) the remobilization of C and N.

Model inputs are: (1) the soil nitrate concentration at anthesis; (2) the meteorological data, including incident photosynthetically active radiation (PAR), air temperature, humidity, CO₂ and wind speed; and (3) the relative distribution of incident PAR among photosynthetic organs. Model initialization requires a complete description of the culm at anthesis, i.e. photosynthetic and total areas and structural N and dry masses, as well as initial metabolite concentrations in aerial organs and roots.

Model overview

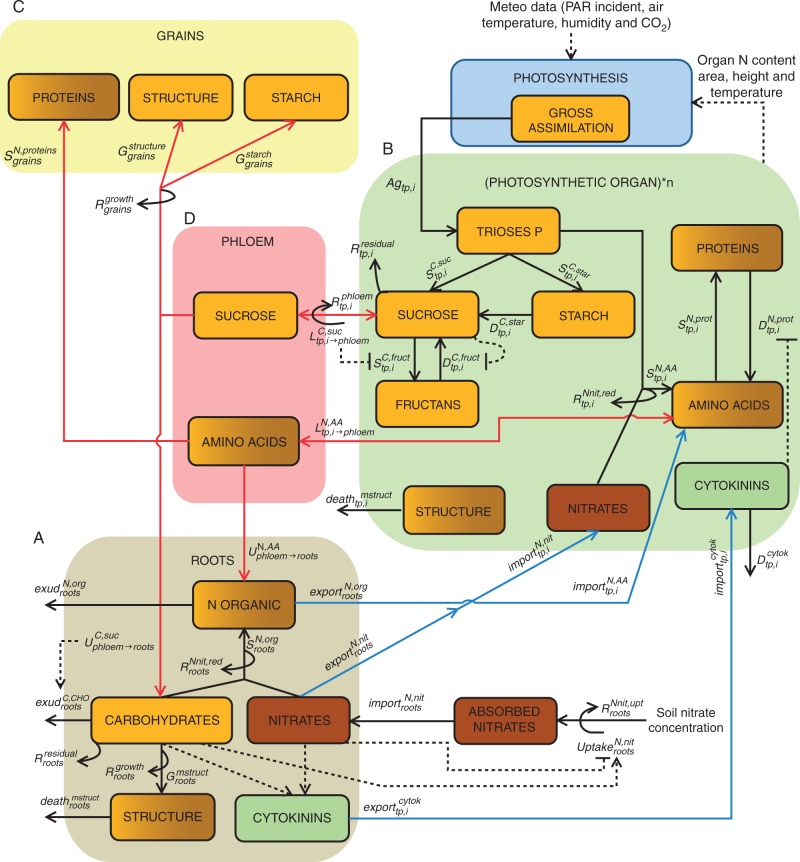
For the sake of simplicity, i.e. computation time and number of parameters, we only accounted for the main C–N metabolites commonly encountered in plants. Some of these forms have been considered as essential precursors and/or regulators (e.g. triose phosphates, nitrates) for modelling the acquisition and distribution of the most important metabolites in terms of mass (e.g. sucrose, fructans, amino acids, proteins). The main physiological processes modelled are related to resource acquisition (photosynthesis, N uptake), respiration, the synthesis of storage and mobile metabolites, exudation of C–N by roots and tissue death. The following section is dedicated to a general description of the structure of CN–Wheat model, and the main functions represented for each type of organ. The C–N metabolites involved in these functions and the underlying assumptions are also briefly presented as well as the underlying assumptions made for the different physiological processes (Fig. 2).

Fig. 2.

Overview of the model of C and N distribution within wheat architecture for post-anthesis stages. The model consists in a culm described as a root compartment (A), a set of photosynthetic organs (B) and the whole grains (C); each organ includes different metabolites. Inter-organ fluxes occur through transpiration flow [export of nitrates, amino acids and cytokinins from roots to photosynthetic organs (blue arrows)] and through a common pool called phloem (D, red arrows) containing sucrose and amino acids. Definitions and equations of fluxes are detailed in the main text. Regulation is denoted by dotted lines.

Plant structure and organ functioning.

All organs (roots, photosynthetic organs and grains) consist of structural, storage and mobile materials. Fluxes among organs occur through a so-called phloem, representing a common pool of mobile metabolites, i.e. sucrose and amino acids (AAs) (Hayashi and Chino, 1986; Winter et al., 1992; Caputo and Barneix, 1999; Lalonde et al., 2003).

The root system is represented by a single compartment defined by its structural N and dry masses (Fig. 2A). The main functions occurring in roots are (1) nitrate uptake and distribution among photosynthetic organs, (2) organic N synthesis, (3) respiration, (4) C–N exudation, (5) structural mass death and (6) cytokinin synthesis. Both nitrate uptake and organic N synthesis are regulated by nitrate and carbohydrate concentrations in roots. Root supply in carbohydrates results from the unloading of phloemic sucrose. Losses of C–N through exudation and tissue death have been introduced in order to have a realistic C–N balance in roots. Lastly, roots produce cytokinins, which regulate protein degradation in shoot.

Above-ground architecture is described explicitly, i.e. the culm is represented as a collection of subunits called phytomers, each consisting of an internode and a leaf composed of a sheath and a lamina (Fig. 1). The culm ear is supported by the peduncle and is composed of the chaff and whole grains. All aerial organs except grains are considered to be photosynthetic. Photosynthetic organs are defined by their type, denoted tp (tp being lamina, sheath, internode, peduncle or chaff) and numbered acropetally according to the phytomer i they belong to. The essential functions performed by photosynthetic organs (Fig. 2B) are (1) fixation of C by photosynthesis and water transpiration, (2) C respiration, (3) synthesis of different carbohydrates, (4) synthesis of AAs and protein turnover, (5) tissue death and its consequences for resource capture and turnover, and (6) loading of sucrose and AAs into the phloem. Assimilation of C is calculated by using a biochemical model (Farquhar et al., 1980), regulated by the incident PAR and N content of each organ. Carbohydrate synthesis is modelled for triose phosphates, sucrose (the main form of C in cereals), starch and fructans. Amino acid synthesis is calculated from the concentrations of triose phosphates and nitrates. These AAs are partly used for the synthesis of proteins, which represent the main pool of N in photosynthetic organs. Protein degradation occurs simultaneously with their synthesis and is downregulated by the cytokinins exported from roots. A sub-model triggers the death of a part of the tissue when proteins drop below a given threshold. The loading of sucrose and AAs into the phloem allows the supply of C–N to sink organs (mainly roots and grains).

The model accounts for a whole-grain compartment whose initial mass at flowering is an input of the model (and can be varied to reflect the number of grains). The growth of grains is divided into two stages: the formation of grain structure and grain filling (Fig. 2C). The supply of C to grains is regulated by sucrose concentration in the phloem. In addition, C unloading is coupled to the import of AAs used for the synthesis of grain proteins.

Definition of parameters and variables.

Definitions and units of parameters and variables are detailed in Tables 1 and 2. Except for structural N and dry mass (expressed in grams), all compartments are expressed in micromoles of C or N under the form of the considered metabolite. As a signal, cytokinins are expressed in arbitrary units (AUs) and are not taken into account in the mass balance. In CN-Wheat, metabolite concentrations are expressed relative to organ structural dry mass, as proposed by several authors (Tabourel-Tayot and Gastal, 1998; Thornley, 1998; Luquet et al., 2006).

Table 1.

Description and units of model parameters

Parameter	Description	Unit
Root uptake of nitrates and N mineralization
$K_{roots}^{N,nitHATS}$	Affinity coefficient of nitrate uptake for HATS	µmol N g−1
${Vmax}_{roots}^{N,nitHATS}$	Maximum rate of nitrate uptake for HATS	µmol N g−1 s−1
$K_{roots}^{N,nitLATS}$	Rate of nitrate uptake for LATS	m3 g−1 s−1
$K_{roots}^{C,CHO}$	Regulation of nitrate uptake by carbohydrate concentration in roots	µmol C g−1
$r_{influx:netuptake}$	Ratio of nitrate influx on net uptake	Dimensionless
${Miner}_{soil}^{N,nit}$	Rate of N mineralization in soil	µmol N m−3 s−1
Syntheses
$K_{roots}^{{SN,org}_{CHO}}$	Affinity coefficient for organic N synthesis according to root carbohydrates	µmol C g−1
$K_{roots}^{S{N,org}_{nit}}$	Affinity coefficient for organic N synthesis according to Root nitrates	µmol N g−1
${Smax}_{roots}^{N,org}$	Maximum rate of organic N synthesis in roots	µmol N g−1 s−1
$K_{roots}^{CHO,cytok}$	Affinity coefficient for cytokinin synthesis according to root carbohydrates	µmol C g−1
$n_{CHO}$	Parameter for the regulation of cytokinin synthesis by carbohydrates in roots	Dimensionless
$K_{roots}^{nit,cytok}$	Affinity coefficient for cytokinin synthesis according to root nitrates	µmol N g−1
$n_{nit}$	Parameter for the regulation of cytokinin synthesis by nitrates in roots	Dimensionless
${Smax}_{roots}^{cytok}$	Maximum rate of cytokinin synthesis in roots	AU g−1 s−1
$K_{tp,\hspace{0.5em}i}^{C,star}$	Affinity coefficient for starch synthesis in (tp,i)	µmol C g−1
${Smax}_{tp,i}^{C,star}$	Maximum rate of starch synthesis in (tp,i)	µmol C g−1  s−1
${Ks}_{tp,i}^{C,fruc}$	Affinity coefficient for fructan synthesis in (tp,i)	µmol C g−1
${Smaxpot}_{tp,i}^{C,fruc}$	Potential maximum rate of fructan synthesis in (tp,i)	µmol C g−1 s−1
${Kl}_{tp,i}^{C,fruc}$	Affinity coefficient for fructan synthesis inhibition by sucrose loading in (tp,i)	µmol C g−1
$n_{fruc}$	Parameter for inhibition of fructan synthesis by sucrose loading	Dimensionless
$K_{tp,i}^{C,suc}$	Affinity coefficient for sucrose synthesis in (tp,i)	µmol C g−1
${Smax}_{tp,i}^{C,suc}$	Maximum rate of sucrose synthesis in (tp,i)	µmol C g−1 s−1
$K_{tp,i}^{{S\hspace{0.5em}N,AA}_{triosesP\hspace{0.5em}}}$	Affinity coefficient for amino acid synthesis according to triose phosphates in (tp,i)	µmol C g−1
$K_{tp,i}^{S\hspace{0.5em}{N,AA}_{nit}}$	Affinity coefficient for amino acid synthesis according to nitrates in (tp,i)	µmol N g−1
${Smax}_{tp,i}^{N,AA}$	Maximum rate of amino acid synthesis in (tp,i)	µmol N g−1 s−1
$K_{\hspace{0.5em}tp,i}^{N,prot}$	Affinity coefficient for protein synthesis in (tp,i )	µmol N g−1
${Smax}_{tp,i}^{N,prot}$	Maximum rate of protein synthesis in (tp,i)	µmol N g−1 s−1
Degradations
${\delta }_{tp,i}^{C,star}$	Relative rate of starch degradation in (tp,i)	s−1
${Kd}_{tp,i}^{C,fruc}$	Affinity coefficient for fructan degradation in (tp,i)	µmol C g−1
${Dmax}_{tp,i}^{C,fruc}$	Maximum rate of fructan degradation in (tp,i)	µmol C g−1 s−1
${\delta max}_{tp,i}^{N,prot}$	Maximum rate of protein degradation in (tp,i)	s−1
${Kd}_{tp,i}^{N,prot}$	Affinity coefficient for inhibition of protein degradation by cytokinins in (tp,i)	AU cytokinin g−1
$n_{cytok}$	Parameter for inhibition of protein degradation by cytokinins	Dimensionless
${\delta }_{tp,i}^{cytok}$	Rate of cytokinin degradation in (tp,i)	s−1
Inter-organ fluxes
$K_{roots}^{U\hspace{0.5em}C,suc}$	Affinity coefficient for sucrose unloading to roots	µmol C g−1
${Umax}_{phloem\to roots}^{C,suc}$	Maximum rate of sucrose unloading to roots	µmol C g−1 s−1
$K_{roots}^{N,nitexport}$	Relative rate of nitrate export from roots	s−1
$K_{roots}^{N,AAexport}$	Relative rate of amino acid export from roots	s−1
$K_{roots}^{cytokexport}$	Relative rate of cytokinin export from roots	s−1
$K_{roots}^{Tr}$	Parameter for the regulation of root exports by culm transpiration	mmol water m−2 s−1
$r_{roots}^{C,exud}$	Proportion of C sucrose unloaded exuded by roots	Dimensionless
${\mathrm{\sigma }}^{C,suc}$	Conductivity for sucrose in (tp,i)	g2 µmol−1 m−2 s−1
${\mathrm{\sigma }}^{N,AA}$	Conductivity for amino acids in (tp,i )	g2 µmol-1 m-2 s−1
${\beta }_{tp,i}$	Scale factor to estimate the section of (tp,i) with the phloem	${\left(g\hspace{0.5em}{m}^{-3}\right)}^{\raisebox{1ex}{$-2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$
Growth of roots and grains
$K_{roots}^{C,mstruct}$	Affinity coefficient for root structural growth	µmol C g−1
${Gmax}_{roots}^{C,mstruct}$	Maximum rate of root structural growth	µmol C g−1 s−1
$K_{grains}^{C,mstruct}$	Affinity coefficient for grain structural growth	µmol C
${Smax}_{grains}^{C,mstruct}$	Maximum rate of grain structural growth	s−1
$K_{grains}^{C,star}$	Affinity coefficient for starch synthesis in grains	µmol C g−1
${Smax}_{grains}^{C,star}$	Maximum rate of starch synthesis in grains	µmol C g−1 s−1
$t_{grains}^{initfilling}$	Beginning of the period of grain filling	Hours from anthesis
$t_{grains}^{stopfilling}$	End of the period of grain filling	Hours from anthesis
Tissue death
${\delta }_{roots}^{mstruct}$	Death rate of root structural mass	s−1
$d_{tp,i}$	Fraction of maximum protein concentration below which photosynthetic tissues die	Dimensionless
${ratedeath}_{tp,i}^{area}$	Rate of tissue death in (tp,i)	m2 s−1
Conversion factors
${MM}_C$	Molar mass of C	g mol−1
${MM}_N$	Molar mass of N	g mol−1
${conv}_{units}^{Nstruct}$	Conversion factor from µmol of N to g of structural N	g mol−1$\hspace{0.5em}{10}^{-6}$
${conv}_{units}^{mstruct}$	Conversion factor from µmol of C to g of structural dry mass	g mol−1$\hspace{0.5em}{10}^{-6}$
$r_{C:mstruct}$	Mean contribution of C to structural dry mass	g C g−1
$r_{N:mstruct}$	Mean contribution of N to structural dry mass	g N g−1

Table 2.

Description and units of model variables

Variable	Description	Unit
$\Delta t$	Time step of the model	s
Roots and soil
$M_{roots}^{struct}$, $N_{roots}^{struct}$	Root structural dry mass and N mass, respectively	g
$\left[{\text{C}}_{\text{roots}}^{CHO}\right]$	Carbohydrate concentration in roots	µmol C g−1
$\left[N_{roots}^{nit}\right]$	Nitrate concentration in roots	µmol N g−1
$\left[N_{roots}^{org}\right]$	Organic N concentration in roots	µmol N g−1
$\left[{cytok}_{roots}^{}\right]$	Cytokinin concentration in roots	AU g−1
$\left[N_{soil}^{nit}\right]$	Nitrate concentration in soil	µmol m−3
Photosynthetic organs
$M_{tp,i}^{struct}$, $N_{tp,i}^{struct}$	Structural dry mass and N mass of photosynthetic organ (tp,i)	g
$A_{tp,i}^{Green}$	Green area of photosynthetic organ (tp,i)	m2
${Ag}_{tp,i}$	Gross photosynthesis of photosynthetic organ (tp,i)	µmol C m−2 s−1
${Tr}_{tp,i}$	Transpiration rate of photosynthetic organ (tp,i). See (Supplementary Data 2)	mmol water m−2 s−1
$\left[C_{tp,i}^{triosesP}\right]$	Triose phosphates concentration in photosynthetic organ (tp,i)	µmol C g−1
$\left[C_{tp,i}^{star}\right]$	Starch concentration in photosynthetic organ (tp,i)	µmol C g−1
$\left[C_{tp,i}^{fruct}\right]$	Fructan concentration in photosynthetic organ (tp,i)	µmol C g−1
$\left[C_{tp,i}^{suc}\right]$	Sucrose concentration in photosynthetic organ (tp,i)	µmol C g−1
$\left[N_{tp,i}^{nit}\right]$	Nitrate concentration in photosynthetic organ (tp,i)	µmol N g−1
$\left[N_{tp,i}^{AA}\right]$	Amino acid concentration in photosynthetic organ (tp,i)	µmol N g−1
$\left[N_{tp,i}^{prot}\right]$	Protein concentration in photosynthetic organ (tp,i)	µmol N g−1
$\left[{cytok}_{tp,i}^{}\right]$	Cytokinin concentration in photosynthetic organ (tp,i)	AU g−1
Grains
$C_{grains}^{mstruct}$	Structural C in grains	µmol C
$M_{grains}^{struct}$	Structural mass of grains	g
$C_{grains}^{star}$	C starch in grains	µmol C
$N_{grains}^{prot}$	N proteins in grains	µmol N
Phloem and culm
$\left[{\text{C}}_{\text{phloem}}^{suc}\right]$	Sucrose concentration in phloem	µmol C g−1
$\left[N_{phloem}^{AA}\right]$	Amino acid concentration in phloem	µmol N g−1
$M_{\hspace{0.5em}culm}^{struct}$	Total structural dry mass of culm	g
${Tr}_{culm}\hspace{1em}$	Total transpiration of the culm. See Supplementary Data 2	mmol water m−2 s−1

In a general manner, the concentration of a metabolite X in an organ is denoted $\left[{\text{C}}_{\text{organ}}^{X\hspace{0.5em}}\right]$ (µmol C g⁻¹) or $\left[{\text{N}}_{\text{organ}}^{X\hspace{0.5em}}\right]$ (µmol N g⁻¹), the derivative of a metabolite is denoted $\frac{d{C}_{organ}^X}{dt}$ (µmol C s⁻¹) or $\frac{d{N}_{organ}^X}{dt}$ (µmol N s⁻¹ ) and the rates of activities (synthesis, degradation, loading, etc.) are expressed in µmol C or N g⁻¹ s⁻¹ .

Photosynthesis and transpiration

Organ photosynthesis is computed by using the biochemical FCB model (Farquhar et al., 1980) coupled to the semi-empirical BWB model of stomatal conductance (Ball, 1987). Parameters of the FCB model were taken from previous work (Müller et al., 2005; Braune et al., 2009; Evers et al., 2010). Details of calculations and parameters are given in (Supplementary Data 1). Photosynthesis calculation is performed for each organ and is regulated by (1) the absorption of PAR, (2) organ temperature and (3) surface N density. All photosynthetic organs intercept light; those having an enclosed and exposed part are considered as two distinct modules. In addition, a sub-model of stomatal conductance is used to introduce limitations of CO₂ supply. Temperature dependence of photosynthetic parameters is accounted for by using Arrhenius functions. Calculation of organ temperature (Supplementary Data 2) was adapted from Evers et al. (2010). Briefly, this method is based on the Penman–Monteith equations, whereby organ temperature is calculated from the net absorption of radiation, transpiration and resistance to heat estimated from wind, organ width and height. Nitrogen dependence of the photosynthetic parameters is introduced following Braune et al. (2009). In the present model, the surface N density of an organ is calculated as the sum of nitrates, AAs, proteins and structural N and divided by organ green area. This sub-model also provides two major variables used in CN-Wheat: organ gross photosynthesis (${Ag}_{tp,i}$) and transpiration (${Tr}_{tp,i}$). The total culm transpiration (${Tr}_{culm}$) is thus calculated as: ${Tr}_{culm}=\hspace{0.5em}\sum {Tr}_{tp,i}$. In the present version of the model, the transpiration of aerial organs is not regulated by soil water status, meaning that soil water is assumed not to be limiting.

Respiration

In most studies, a growth and a maintenance component are estimated for modelling plant respiration (McCree, 1970; Amthor, 2000). Nevertheless, Thornley and Cannell (2000) pointed out the limits of this paradigm and proposed a new approach based on quantification of the respiratory costs related to the main physiological processes. Organ respiration was implemented following this approach, which was straightforward thanks to the nature of the variables used in the present model. The total respiration rate of a given organ$\hspace{0.5em}{R}_{tp,i}^{total}$ (µmol C s⁻¹) is given by:

$$R_{organ}^{total}\left(t\right)=R_{organ}^{growth}\left(t\right)+R_{organ}^{phloem}\left(t\right)+R_{organ}^{Nnit,upt}\left(t\right)+R_{organ}^{Nnit,red}\left(t\right)+R_{organ}^{residual}\left(t\right)$$ (1)

Respiration rates are related to local growth ($R_{organ}^{growth}$), phloem loading ($R_{organ}^{phloem}$), nitrate uptake from soil ($R_{organ}^{Nnit,\hspace{0.5em}upt}$, only estimated for roots) and nitrate reduction ($R_{organ}^{Nnit,red}$). CN-Wheat does not explicitly estimate nitrate reduction but rather the synthesis of organic N. We therefore replaced the rate of nitrate reduction initially used in Thornley and Cannell (2000) with the rate of organic N synthesis, assuming that the two processes are closely related. $R_{organ}^{residual}$ is an important category that mainly includes maintenance processes (protein turnover, futile cycles, ion gradients, etc.). This sub-model is fully described in (Supplementary Data 3).

Nitrate uptake by roots and concentration in soil

The rate of nitrate influx (eqn 2) is modelled as the resultant of the two active transport systems identified in plants (Doddema and Telkamp, 1979; Pace and McClure, 1986): (1) a high-affinity system (HATS) modelled by using a Michaelis–Menten function of nitrate concentration in soil (eqn 3); and (2) a low-affinity system (LATS) represented by a linear function of nitrate concentration in soil (eqn 4). Based on Siddiqi et al. (1989, 1990), we also introduced a negative feedback of root nitrate concentration on the parameters related to HATS and LATS functions (eqn 5).

The rate of nitrate net uptake (eqn 6) is calculated from the nitrate influx weighted by a parameter accounting for nitrate efflux [$r_{influx:net\hspace{0.5em}uptake}$, estimated from Devienne et al. (1994)] and root carbohydrate concentration (eqn 7). In the end, eight parameters are needed to calculate nitrate net uptake.

The rate of nitrate influx (µmol N s⁻¹) is given by:

$${Influx}_{roots}^{N,nit}\left(t\right)=\left(HATS\left(t\right)+LATS\left(t\right)\right)\mathrm{*}{M}_{roots}^{struct}\left(t\right)$$ (2)

The two transport systems HATS and LATS (µmol N g⁻¹  s⁻¹ ) are calculated as follows:

$$HATS\left(t\right)=\frac{\left[N_{soil}^{nit}\right]\left(\mathrm{t}\right)\mathrm{*}{Vmax}_{roots}^{N,nit\hspace{0.5em}HATS}}{\left[N_{soil}^{nit}\right]\left(\mathrm{t}\right)+K_{roots}^{N,nit\hspace{0.5em}HATS}}$$ (3)

$$LATS\left(t\right)=K_{roots}^{N,nit\hspace{0.5em}LATS}\mathrm{*}\left[N_{soil}^{nit}\right]\left(t\right)$$ (4)

where ${Vmax}_{roots}^{N,nitHATS}$ and $K_{roots}^{N,nitHATS}$ are the maximum rate of nitrate influx at saturating soil concentrations and the corresponding affinity coefficient, respectively. Nitrate concentrations in soil and roots are denoted $\left[N_{soil}^{nit}\right]$ and $\left[N_{roots}^{nit}\right]$, respectively. $K_{roots}^{N,nit\hspace{0.5em}LATS}$ is the rate of nitrate influx at low soil concentrations. Parameter dependence on nitrate concentration in roots is given by:

$$p=A\mathrm{*}exp\left(-\lambda \mathrm{*}\left[N_{roots}^{nit}\right]\right)$$ (5)

where p is ${Vmax}_{roots}^{N,nit\hspace{0.5em}HATS}$, $K_{roots}^{N,nit\hspace{0.5em}HATS}$ or $K_{roots}^{N,nit\hspace{0.5em}LATS}$, A is a dimensionless parameter and λ is expressed in s⁻¹, g m⁻³ or m³ µmol⁻¹ s⁻¹, respectively.

Net nitrate uptake rate (µmol N s⁻¹ ) is written as:

$${Uptake}_{roots}^{N,nit}\left(t\right)={Influx}_{roots}^{N,nit}\left(t\right)\mathrm{*}{r}_{influx:netuptake}\mathrm{*}{f}_{CHO}\left(t\right)$$ (6)

The regulation of nitrate uptake by root carbohydrate concentration ($\left[{\text{C}}_{roots}^{CHO\hspace{0.5em}}\right]$) is dimensionless and may vary from 0 to 1 (eqn 7).

$$f_{CHO\left(t\right)}=\frac{\left[{\text{C}}_{roots}^{CHO}\right]\left(t\right)}{\left[{\text{C}}_{roots}^{CHO}\right]\left(\mathrm{t}\right)+K_{roots}^{C,CHO}}$$ (7)

with $K_{roots}^{C,CHO}$expressed in µmol C g⁻¹.

The derivative of soil nitrate concentration (µmol N m⁻³) is calculated as the balance between the rate of N mineralization (${Miner}_{soil}^{N,nit}$) and the rate of N uptake by a culm multiplied by culm density (eqn 8):

$$\frac{d{N}_{soil}^{nit}}{dt}={Miner}_{soil}^{N,nit}\left(t\right)-{Uptake}_{roots}^{N,nit}\left(t\right)\times culmdensity$$ (8)

In the present implementation, the rate of nitrate mineralization is approximated as a first-order kinetic depending on soil nitrate concentration. Incorporating instead a comprehensive model of soil processes, such as PASTIS (Garnier et al., 2003), would make it possible to take into account the factors that regulate N mineralization, such as soil composition, humidity and temperature.

Organ death and C–N remobilization

This section deals with tissue death and the resulting loss of green area and structural N and dry mass. Early signals and mechanisms implied in senescence are not in the scope of the model but CN-Wheat accounts for the final impact of senescence, i.e. tissue death and green area reduction.

Roots.

We assumed that the mortality rate of root structural dry mass (${death}_{roots}^{mstruct}$, g s⁻¹ ) follows a first-order kinetic (Johnson and Thornley, 1985; Asseng et al., 1997) (eqn 9):

$${death}_{roots}^{mstruct}\left(t\right)={\delta }_{roots}^{mstruct}\mathrm{*}{M}_{roots}^{struct}\left(t\right)$$ (9)

where ${\delta }_{roots}^{mstruct}$ (s⁻¹) is the constant rate of tissue death. Similarly for structural N:

$${death}_{roots}^{Nstruct}\left(t\right)={\delta }_{roots}^{mstruct}\mathrm{*}{N}_{roots}^{struct}\left(t\right)$$ (10)

Photosynthetic organs.

In CN-Wheat, a section of a photosynthetic organ dies when its protein concentration drops below a threshold (Bertheloot et al., 2011). This threshold ($d_{tp,i}$) is defined as a fraction of the maximum value of protein concentration reached during the organ’s lifespan. When this condition is met, the loss of green area takes place at a constant rate (${rate\_death}_{tp,i}^{area}$, m² s⁻¹ ). Following the death of photosynthetic tissues, organ structural N and dry masses are reduced proportionally to the decrease in green area. Sucrose and AAs of the dead tissue are moved to the corresponding compartments of the green tissue. Starch and fructans are remobilized towards the sucrose compartment of the green tissue (${remob}_{tp,i}^{C,starch}$ and ${remob}_{tp,i}^{C,fructans}$, µmol C s⁻¹ ; respectively). Similarly, proteins of a dead tissue are remobilized as AAs in the remaining green tissue (${remob}_{tp,i}^{N,proteins}$, µmol N s⁻¹).

This sub-model is run at the beginning of each time step, meaning that tissue death may be interrupted if protein concentration rises in the living tissue.

Cytokinins

An extensive literature on senescence has pointed out the preponderant role of cytokinins as inhibitors of tissue death (Mok and Mok, 1994; Badenoch-Jones et al., 1996; Wingler et al., 1998; Yang et al., 2002; Criado et al., 2009; Koeslin-Findeklee et al., 2015). These studies reported that cytokinins are synthesized in roots and exported to photosynthetic organs through the transpiration flow, where they inhibit the degradation of photosynthetic proteins. We introduced these regulations in CN-Wheat in order to simulate realistic kinetics of protein concentration and tissue death. The main functions are described below and detailed equations are given in Table 3.

Table 4.

Main equations of the model. Description and units of parameters and variables are detailed in Table 1 and Table 2, respectively

Equation	Description	Unit	Equation number
Roots
$G_{roots}^{mstruct}\left(t\right)=\frac{\left[{\text{C}}_{\text{roots}}^{CHO}\right]\left(t\right)*\hspace{0.5em}{\hspace{0.5em}Gmax}_{roots}^{C,mstruct}}{\left[{\text{C}}_{\text{roots}}^{CHO\hspace{0.5em}}\right]\left(t\right)+K_{roots}^{C,mstruct}}*M_{roots}^{struct}\left(t\right){*conv}_{units}^{mstruct}$	Rate of structural dry mass growth in roots	g s−1	T4·1
$G_{roots}^{Nstruct}\left(t\right)=G_{roots}^{mstruct}\left(t\right)*{conv}_{units}^{Nstruct}$	Rate of structural N mass growth in roots	g s−1	T4·2
${\hspace{0.5em}U}_{phloem\to roots}^{C,suc}\left(\mathrm{t}\right)=\frac{\left[{\text{C}}_{\text{phloem}}^{suc}\right]\left(t\right)*\hspace{0.5em}{\hspace{0.5em}Umax}_{phloem\to roots}^{C,suc}}{\left[{\text{C}}_{\text{phloem}}^{suc}\right]\left(t\right)+K_{roots}^{U\hspace{0.5em}C,suc}}$	Rate of sucrose unloading from phloem to roots	µmol C g−1 s−1	T4·3
$S_{roots}^{N,org}\left(t\right)=\hspace{0.5em}\frac{{Smax}_{roots}^{N,org}}{\frac{1+\hspace{0.5em}{K}_{roots}^{S\hspace{0.5em}{N,org}_{nit}}}{\left[N_{roots}^{nit}\right]\left(t\right)}*\frac{1+\hspace{0.5em}{K}_{roots}^{{S\hspace{0.5em}N,org}_{CHO\hspace{0.5em}}}}{\left[{\text{C}}_{\text{roots}}^{CHO\hspace{0.5em}}\right]\left(t\right)}}$	Rate of organic N synthesis in roots	µmol N g−1 s−1	T4·4
${exud}_{roots}^{C,CHO}\left(t\right)={\hspace{0.5em}U}_{phloem\to roots}^{C,suc}\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}{r}_{roots}^{C,exud}$	Rate of C exudation by roots	µmol C g−1 s−1	T4·5
${export}_{roots}^{N,nit}\left(t\right)=\left[N_{roots}^{nit}\right]\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}{K}_{roots}^{N,nit\hspace{0.5em}export}*f_{Tr}\left(t\right)$	Rate of nitrate export from roots to photosynthetic organs. $f_{Tr}$ is detailed in eqn (12)	µmol N s−1	T4·6
$U_{phloem\to roots}^{N,AA}\left(t\right)=U_{phloem\to roots}^{C,suc}\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}\frac{\left[N_{phloem}^{AA}\right]\left(t\right)}{\left[{\text{C}}_{\text{phloem}}^{suc}\right]\left(t\right)}$	Rate of amino acid unloading from phloem to roots	µmol N g−1 s−1	T4·7
${exud}_{roots}^{N,org}\left(t\right)={exud}_{roots}^{C,CHO}\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}\frac{\left[N_{roots}^{AA}\right]\left(t\right)}{\left[{\text{C}}_{\text{roots}}^{suc}\right]\left(t\right)}$	Rate of N exudation by roots	µmol N g− s−1	T4·8
${export}_{roots}^{N,AA}\left(t\right)=\left[N_{roots}^{AA}\right]\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}{K}_{roots}^{N,AA\hspace{0.5em}export}*f_{Tr}\left(t\right)$	Rate of organic N export from roots to photosynthetic organs. $f_{Tr}$ is detailed in eqn (12)	µmol N s−1	T4·9
Photosynthetic organs
$S_{tp,i}^{C,X}\left(t\right)=\hspace{0.5em}\frac{\left[C_{tp,i}^{triosesP}\right]\left(t\right)*{Smax}_{tp,i}^{C,X}\hspace{0.5em}}{\left[C_{tp,i}^{triosesP}\right]\left(t\right)+K_{tp,i}^{C,X}}$	Rate of X synthesis. Superscript X refers to either sucrose or starch	µmol C g−1 s−1	T4·10
$S_{tp,i}^{N,AA}\left(t\right)=\hspace{0.5em}\frac{{Smax}_{tp,i}^{N,AA}}{\frac{1+\hspace{0.5em}{K}_{tp,i}^{S\hspace{0.5em}{N,AA}_{nit}}}{\left[N_{tp,i}^{nit}\right]\left(t\right)}*\frac{1+\hspace{0.5em}{K}_{tp,i}^{{S\hspace{0.5em}N,AA}_{triosesP\hspace{0.5em}}}}{\left[{\text{C}}_{tp,i}^{triosesP\hspace{0.5em}}\right]\left(t\right)}}$	Rate of amino acid synthesis in photosynthetic organs	µmol N g−1 s−1	T4·11
$D_{tp,i}^{C,starch}\left(t\right)=\hspace{0.5em}\left[C_{tp,i}^{starch}\right]\left(t\right)*{\delta }_{tp,i}^{C,star}$	Rate of starch degradation	µmol C g−1 s−1	T4·12
$S_{tp,i}^{C,fruc}\left(t\right)=\hspace{0.5em}\frac{\left[C_{tp,i}^{suc}\right]\left(t\right)*\hspace{0.5em}{Smax}_{tp,i}^{C,fruc}}{\left[C_{tp,i}^{suc}\right]\left(t\right)+{Ks}_{tp,i}^{C,fruc}}$	Rate of fructan synthesis	µmol C g−1 s−1	T4·13
${Smax}_{tp,i}^{C,fruc}=\hspace{0.5em}\frac{{Smaxpot}_{tp,i}^{C,fruc}*{\left({Kl}_{tp,i}^{C,fruc}\right)}^{n_{fruc}}}{{\left({Kl}_{tp,i}^{C,fruc}\right)}^{n_{fruc}}+{\left(L_{tp,i\hspace{0.5em}\to phloem}^{C,suc}\left(t\right)\right)}^{n_{fruc}}}$	Function of fructan synthesis inhibition by sucrose loading	µmol C g−1 s−1	T4·14
$D_{tp,i}^{C,fruc}\left(t\right)=\hspace{0.5em}\frac{{Dmax}_{tp,i}^{C,fruc}*\hspace{0.5em}{Kd}_{tp,i}^{C,fruc}}{\left[C_{tp,i}^{suc}\right]\left(t\right)+{Kd}_{tp,i}^{C,fruc}}$	Rate of fructan degradation	µmol C g−1 s−1	T4·15
$L_{tp,i\hspace{0.5em}\to phloem}^{C,suc}\left(t\right)=\max \left(\left[C_{tp,i}^{suc}\right],\left[C_{phloem}^{suc}\right]\right)\left(t\right)*\left(\left[C_{tp,i}^{suc}\right]\left(t\right)-\left[C_{phloem}^{suc}\right]\left(t\right)\right)*G\left(t\right)$	Rate of sucrose loading to phloem	µmol C s−1	T4·16
${\mathrm{G}}^{C,suc}\left(t\right)=\hspace{0.5em}{\mathrm{\sigma }}^{C,suc}*S_{tp,i}\left(t\right)$	Conductance between an organ and the phloem for sucrose	g2 µmol−1 s−1	T4·17
$S_{tp,i}\left(t\right)=\hspace{0.5em}{\beta }_{tp,i}*{\left(M_{tp,i}^{struct}\left(t\right)\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	Section between organ and phloem	m2	T4·18
${import}_{tp,i}^{N,nit}\left(t\right)=\hspace{0.5em}{export}_{roots}^{N,nit}\left(t\right)*\frac{{Tr}_{tp,i}\left(t\right)*A_{tp,i}^{Green}\left(t\right)}{{Tr}_{culm}\left(t\right)*A_{culm}^{Green}\left(t\right)}$	Rate of nitrate import from roots	µmol N s−1	T4·19
$S_{tp,i}^{N,prot}\left(t\right)=\hspace{0.5em}\frac{\left[N_{tp,i}^{AA}\right]\left(t\right)*\hspace{0.5em}{Smax}_{tp,i}^{N,prot}}{\left[N_{tp,i}^{AA}\right]\left(t\right)+K_{\hspace{0.5em}tp,i}^{N,prot}}$	Rate of protein synthesis	µmol N g−1 s−1	T4·20
$D_{tp,i}^{N,prot}\left(t\right)=\hspace{0.5em}\left[N_{tp,i}^{prot}\right]\left(t\right)*{\delta }_{tp,i}^{N,prot}\left(t\right)$	Rate of protein degradation	µmol N g−1 s−1	T4·21
${\delta }_{tp,i}^{N,prot}\left(t\right)=\frac{{\delta max}_{tp,i}^{N,prot}*{\left({Kd}_{tp,i}^{N,prot}\right)}^{n_{cytok}}}{{\left({Kd}_{tp,i}^{N,prot}\right)}^{n_{cytok}}+{\left[{cytok}_{tp,i}^{}\right]}^{n_{cytok}}}\hspace{0.5em}$	Downregulation of relative rate of protein degradation by cytokinins	s−1	T4·22
${import}_{tp,i}^{N,\mathrm{\hspace{0.5em}}\mathrm{A}\mathrm{A}}\left(t\right)=\hspace{0.5em}{export}_{roots}^{N,\mathrm{\hspace{0.5em}}AA}\left(t\right)*\frac{{Tr}_{tp,i}\left(t\right)}{{Tr}_{culm}\left(t\right)}$	Rate of amino acid import from roots	µmol N s−1	T4·23
$L_{tp,i\hspace{0.5em}\to phloem}^{N,AA}\left(t\right)=\max \left(\left[N_{tp,i}^{AA}\right],\left[N_{phloem}^{AA}\right]\right)\left(t\right)*\left(\left[N_{tp,i}^{AA}\right]\left(t\right)-\left[N_{phloem}^{AA}\right]\left(t\right)\right)*G\left(t\right)$	Rate of amino acid loading to phloem	µmol N s−1	T4·24
${\mathrm{G}}^{N,AA}\left(t\right)=\hspace{0.5em}{\mathrm{\sigma }}^{N,AA}*S_{tp,i}\left(t\right)$	Conductance between an organ and the phloem for sucrose	g2 µmol−1 s−1	T4·25
Grains
$G_{grains}^{struct}\left(t\right)=\left\{\begin{array}{l}{C}_{grains}^{mstruct}\left(t-1\right)*\hspace{0.5em}\frac{\left[C_{phloem}^{suc}\right]\left(t\right)*\hspace{0.5em}{Smax}_{grains}^{C,mstruct}}{\left[C_{phloem}^{suc}\right]\left(t\right)+K_{grains}^{C,mstruct}},for\hspace{0.5em}\mathrm{t}\mathrm{\hspace{0.5em}}\le \mathrm{\hspace{0.5em}}{t}_{grains}^{init\hspace{0.5em}filling}\\ \hspace{0.5em}0,for\hspace{0.5em}\mathrm{t}\mathrm{\hspace{0.5em}}>\mathrm{\hspace{0.5em}}{t}_{grains}^{init\hspace{0.5em}filling}\hspace{0.5em}\end{array}\right.$	Rate of structural growth in grains	µmol C s−1	T4·26
$G_{grains}^{star}\left(t\right)=\left\{\begin{array}{l}\frac{\left[C_{phloem}^{suc}\right]\left(t\right)*\hspace{0.5em}{Smax}_{grains}^{C,star}}{\left[C_{phloem}^{suc}\right]\left(t\right)+K_{grains}^{C,star}},for\hspace{0.5em}\mathrm{t}>\hspace{0.5em}{t}_{grains}^{init\hspace{0.5em}filling}\\ \hspace{0.5em}0,for\hspace{0.5em}\mathrm{t}\mathrm{\hspace{0.5em}}\le \mathrm{\hspace{0.5em}}{t}_{grains}^{init\hspace{0.5em}filling}\hspace{0.5em}or\hspace{0.5em}\mathrm{t}\mathrm{\hspace{0.5em}}>\hspace{0.5em}{t}_{grains}^{stop\hspace{0.5em}filling}\hspace{0.5em}\end{array}\right.$	Rate of starch synthesis in grains	µmol C g−1 s−1	T4·27
$S_{grains}^{N,prot}\left(t\right)=\hspace{0.5em}\left({G_{grains}^{struct}\left(t\right)+G}_{grains}^{star}\left(t\right)*M_{grains}^{struct}\left(t\right)\right)*\frac{\left[N_{phloem}^{AA}\right]\left(t\right)}{\left[C_{phloem}^{suc}\right]\left(t\right)}$	Rate of protein synthesis in grains	µmol N s−1	T4·28

Table 3.

Equations related to cytokinins

Equation	Description	Unit	Equation number
$S_{roots}^{cytok}\left(t\right)=\hspace{0.5em}{Smax}_{roots}^{cytok}*\frac{{\left[C_{roots}^{CHO}\right]}^{n_{CHO}}\left(t\right)}{{\left[C_{roots}^{CHO}\right]}^{n_{CHO}}\left(t\right)+{\left(K_{roots}^{CHO,cytok}\right)}^{n_{CHO}}}*\frac{{\left[N_{roots}^{nit}\right]}^{n_{nit}}\left(t\right)\hspace{0.5em}}{{\left[N_{roots}^{nit}\right]}^{n_{nit}}\left(t\right)+{\left(K_{roots}^{nit,cytok}\right)}^{n_{nit}}}$	Rate of cytokinin synthesis in roots	AU g−1  s−1	T3·1
${export}_{roots}^{cytok}\left(t\right)=\left[{cytok}_{roots}^{}\right]\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}{K}_{roots}^{cytok\hspace{0.5em}export}*f_{Tr}\left(t\right)$	Rate of cytokinin export to shoot	AU s−1	T3·2
${import}_{tp,i}^{cytok}\left(t\right)={export}_{roots}^{cytok}\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}\frac{{Tr}_{tp,i}\left(t\right)}{{Tr}_{culm}\left(t\right)}$	Rate of cytokinin import into a photosynthetic organ	AU s−1	T3·3
$D_{tp,i}^{cytok}\left(t\right)=\left[{cytok}_{tp,i}^{}\right]\left(t\right)\mathrm{*}\mathrm{\hspace{0.5em}}{\delta }_{tp,i}^{cytok}*M_{tp,i}^{struct}$	Rate of cytokinin degradation in photosynthetic organs	AU g−1  s−1	T3·4

Production in roots and export.

The derivative of cytokinins in roots (eqn 11) is calculated as the balance between synthesis and the rate of export to shoot.

$$\frac{d{cytok}_{roots}^{}}{dt}=S_{roots}^{cytok}\left(t\right){\mathrm{*}M}_{roots}^{struct}-{export}_{roots}^{cytok}$$ (11)

The rate of cytokinin synthesis ($S_{roots}^{cytok}$, eqn T3·1) is regulated from root concentrations in carbohydrates (which provide the carbon skeleton) and nitrates, as reviewed by Sakakibara et al. (2006). The rate of cytokinin export to shoot (${export}_{roots}^{cytok}$, eqn T3·2) is proportional to concentration and is weighted by a function of culm transpiration ($f_{Tr\left(t\right)}$). The function $f_{Tr\left(t\right)}$ is calculated from the surface rate of culm transpiration (${Tr}_{culm}$, mmol water m⁻² s⁻¹):

$$f_{Tr\left(t\right)}=\frac{{Tr}_{culm}\left(t\right)}{{Tr}_{culm}\left(\mathrm{t}\right)+K_{roots}^{Tr}}$$ (12)

where $K_{roots}^{Tr}$ is expressed in mmol water m⁻² s⁻¹.

Cytokinins in photosynthetic organs.

The derivative of cytokinins in photosynthetic organs (eqn 13) is the difference between their import from roots and degradation:

$$\frac{d{cytok}_{tp,i}^{}}{dt}=\left({import}_{tp,i}^{cytok}\left(t\right)-D_{tp,i}^{cytok}\left(t\right)\right)\mathrm{*}{M}_{tp,i}^{struct}$$ (13)

The rate of cytokinin import (${import}_{tp,i}^{cytok}$) is regulated by root export and organ contribution to overall culm transpiration (eqn T3·3). The cytokinin degradation rate ($D_{tp,i}^{cytok}$) is described by a first-order kinetic (eqn T3·4).

Carbon and nitrogen distribution among culm organs

Roots.

This section describes the mass balances of the root compartments and the related flux equations (Fig. 2A). The import of carbohydrates into roots arises from phloem unloading of sucrose. Some of the organic N is also supplied to roots through phloem unloading of AAs, which are co-transported with sucrose. Nitrate import into roots is calculated from net uptake. Export of nitrates and organic N from roots to photosynthetic organs occurs through the transpiration flux. Carbohydrate exudation is approximated as a fraction of the sucrose unloaded from the phloem. This fraction was estimated from previous work on Poaceae species (Barber and Martin, 1976; Whipps, 1984; Keith et al., 1986; Asseng et al., 1997). Exudation of N is then calculated from C exudation (Vančura and Hanzlíková, 1972; Klein et al., 1988; Janzen, 1990; Owen and Jones, 2001). Root carbohydrates and nitrates are used for organic N synthesis, although this process mainly occurs in photosynthetic organs in wheat (Minotti and Jackson, 1970).

The model of C–N economy for roots involves 12 parameters related to root growth, unloading of C from phloem, synthesis of organic N and exudation and export of N to shoot. Details of the derivatives related to each compartment are given below and illustrated in Fig. 2A.

Structural N and dry mass

The derivative of root structural dry mass (eqn 14) results from the balance between the rates of growth ($G_{roots}^{mstruct}$) and death (${death}_{roots}^{mstruct}$):

$$\frac{d{M}_{roots}^{struct}}{dt}=G_{roots}^{mstruct}\left(t\right)-{death}_{roots}^{mstruct}\left(t\right)$$ (14)

Root growth ($G_{roots}^{mstruct}$) is modelled as a function of carbohydrate concentration according to a Michaelis–Menten function (eqn T4·1). Similarly, the derivative of structural N mass is given by:

$$\frac{d{N}_{roots}^{struct}}{dt}=G_{roots}^{Nstruct}\left(t\right)-{death}_{roots}^{Nstruct}\left(t\right)$$ (15)

The rate of structural N loss through root death (${death}_{roots}^{Nstruct}$) is described in eqn (10), while the increase in structural N ($G_{roots}^{Nstruct}$) is calculated from the growth in total structural mass based on an N content of 2 % (eqn T4·2).

Carbohydrates

The derivative of carbohydrates in roots (eqn 16) is the balance between phloem unloading ($U_{phloem\to roots}^{C,suc}$) and their consumption through (1) organic N synthesis ($S_{roots}^{N,org}$), (2) exudation (${exud}_{roots}^{C,CHO}$), respiration ($R_{roots}^{total}$) and structural growth ($G_{roots}^{mstruct}$):

$$\frac{d{C}_{roots}^{CHO}}{dt}=\left(U_{phloem\to roots}^{C,suc}\left(t\right)-\frac{S_{roots}^{N,org}\left(t\right)}{r_{N:AA}}\mathrm{*}{r}_{C:AA}-{exud}_{roots}^{C,CHO}\left(t\right)\right)\mathrm{*}{M}_{roots}^{struct}\left(t\right)-R_{roots}^{total}\left(\mathrm{t}\right)-G_{roots}^{mstruct}\left(t\right)$$ (16)

The rate of sucrose unloading ($U_{phloem\to roots}^{C,suc}$) is calculated from sucrose concentration in the phloem by using a Michaelis–Menten equation (eqn T4·3). Organic N synthesis rate ($S_{roots}^{N,org}$) is modelled as a bi-substrate Michaelis–Menten kinetic (Thornley and France, 2007a) depending on the root concentrations of both carbohydrates and nitrates (eqn T4·4). Constants $r_{N:AA}$ and $r_{C:AA}$, are used to estimate the consumption of carbohydrate by organic N synthesis and represent the number of N and C atoms per mole of AA, respectively. Exudation of C is calculated from C unloading (eqn T4·5). Total respiration rate of roots ($R_{roots}^{total}$) is the sum of [$R_{roots}^{growth}\left(t\right)+R_{roots}^{Nnit,upt}\left(t\right)+R_{roots}^{Nnit,red}\left(t\right)+R_{roots}^{residual}\left(t\right)$].

Nitrates

The derivative of nitrates within roots (eqn 17) is calculated as a difference between the rate of net nitrate uptake (${Uptake}_{roots}^{N,nit})$, the rate of export towards photosynthetic organs (${export}_{roots}^{N,nit}$) and the consumption related to organic N synthesis ($S_{roots}^{N,org}$):

$$\frac{d{N}_{roots}^{nit}}{dt}={Uptake}_{roots}^{N,nit}\left(t\right)-{export}_{roots}^{N,nit}\left(t\right)-\left(S_{roots}^{N,org}\left(t\right)\mathrm{*}{M}_{roots}^{struct}\left(t\right)\right)$$ (17)

The export is calculated from nitrate concentration and follows a linear function of their concentration weighted by culm transpiration (eqn T4·6).

Organic N

The derivative of organic N (eqn 18) results from the balance between (i) AA unloading from phloem ${(U}_{phloem\to roots}^{N,AA}$), (ii) organic N synthesis ($S_{roots}^{N,org}$), (iii) exudation (${exud}_{roots}^{N,org}$), (iv) exportation to photosynthetic organs (${export}_{roots}^{N,org}$) and (v) consumption related to N structural growth (${growth}_{roots}^{Nstruct}$).

$$\frac{d{N}_{roots}^{org}}{dt}={(U}_{phloem\to roots}^{N,AA}\left(t\right)+S_{roots}^{N,org}\left(t\right)-{exud}_{roots}^{N,org}\left(t\right)\left)\mathrm{*}{M}_{roots}^{struct}\right(t)-{export}_{roots}^{N,org}(t)-G_{roots}^{Nstruct}(t)$$ (18)

The rate of AA unloading from phloem ${(U}_{phloem\to roots}^{N,AA}$) is calculated from sucrose unloading (eqn T4·7). N exudation rate (${exud}_{roots}^{N,organic}$) is estimated from C exudation and the N:C ratio of roots (eqn T4·8). The export of organic N to shoot (${export}_{roots}^{N,org}$, µmol N) is calculated as for nitrate export (eqn T4·9).

Photosynthetic organs.

This section describes the processes modelled in each photosynthetic organ. Main assumptions are presented below and then the formalisms are detailed for each metabolite (Fig. 2B).

Triose phosphates, which are the net product of the Calvin cycle, are considered as the most relevant common precursor for the synthesis of sucrose, starch and AAs (Lawlor et al., 1987; Atkin et al., 2000; Foyer et al., 2000). Sucrose is the main form of C in CN-Wheat and most of the intra-organ fluxes of C and respiratory costs occur through this compartment. Sucrose is also loaded to the phloem following a transport-resistance formalism. Starch is a minor pool of C (Schnyder, 1993; Trevanion, 2000; Scofield et al., 2009), although it constitutes a short-term storage providing some C (along with sucrose) during dark periods. Fructans constitute a major long-term storage of C in wheat and their degradation is a crucial source of C for grain filling (Blacklow et al., 1984; Winzeler et al., 1990; Schnyder, 1993; Cairns et al., 2000). Both synthesis and degradation of fructans occur concurrently in CN-Wheat, the balance between the two processes being driven by substrate concentrations. Fructan synthesis into an organ depends on the availability of sucrose. This formalism alone would lead to a larger accumulation of fructans in organs having a strong concentration of sucrose, i.e. in lighted organs like laminae. Nevertheless, several studies have shown that fructans are not usually accumulated in laminae but rather in shaded/enclosed parts of plants, such as internodes or the enclosed peduncle (Blacklow et al., 1984; Cairns and Pollock, 1988; Gebbing, 2003). To be consistent with these studies, we assumed downregulation of fructan synthesis by sucrose loading into the phloem, resulting in a lower accumulation of fructans in light-exposed organs compared with shaded ones. Besides, fructan degradation is considered to be downregulated through retro-inhibition by the end product (Bancal et al., 2012), i.e. sucrose in this model.

Regarding N metabolism, import and distribution of nitrates and AAs from roots are regulated by the transpiration stream. Synthesis of AAs is calculated from concentrations of nitrates and triose phosphates. Amino acids play a central role in the metabolism of N in CN-Wheat: (1) they are considered as a mobile form of N exchanged among organs through the phloem, and (2) AAs are directly related to protein turnover, expressed as concomitant activities of synthesis and degradation.

To sum up, 24 parameters are used for the modelling of C–N economy in photosynthetic organs. Parameters are identical for photosynthetic organs, whatever their type or position on the culm. Differential equations of the compartments are detailed below and illustrated in Fig. 2B.

Structural N and dry mass

It is assumed that photosynthetic organs have completed their growth at anthesis. Consequently, the model only accounts for variations of structural N and dry masses that result from tissue death (see Organ death and C–N remobilization section).

Triose phosphates

The derivative of triose phosphates (eqn 19) depends on gross photosynthesis (${Ag}_{tp,i}$) and their consumption for sucrose ($S_{tp,i}^{C,suc}$), starch ($S_{tp,i}^{C,star}$) and AA ($S_{tp,i}^{N,AA}$) synthesis:

$$\frac{d{C}_{tp,i}^{triosesP}}{dt}={Ag}_{tp,i}\left(t\right)\mathrm{*}{A}_{tp,i}^{Green}\left(t\right)-\left(S_{tp,i}^{C,suc}\left(t\right)+S_{tp,i}^{C,star}\left(t\right)+\frac{S_{tp,i}^{N,AA}\left(t\right)}{r_{N:AA}}\mathrm{*}{r}_{C:AA}\right)\mathrm{*}{M}_{tp,i}^{struct}\left(t\right)$$ (19)

where $A_{tp,i}^{Green}$ is the green area. Synthesis rates of sucrose and starch ($S_{tp,i}^{C,suc}$, $S_{tp,i}^{C,star}$, respectively) are modelled by Michaelis–Menten functions (eqn T4·10), while the synthesis of AAs ($S_{tp,i}^{N,AA}$) is calculated by using the same formalism as for roots (eqn T4·11).

Starch

The derivative of starch (eqn 20) depends on its synthesis ($S_{tp,i}^{C,starch}$), degradation ($D_{tp,i}^{C,starch}$) and remobilization (${remob}_{tp,i}^{C,starch}$) rates in case of tissue death:

$$\frac{d{C}_{tp,i}^{star}}{dt}=\left(S_{tp,i}^{C,star}\left(t\right)-D_{tp,i}^{C,star}\left(t\right)\right)\mathrm{*}{M}_{tp,i}^{struct}\left(t\right)-{remob}_{tp,i}^{C,star}\left(t\right)$$ (20)

The rate of starch degradation $D_{tp,i}^{C,starch}$ (eqn T4·12) is proportional to starch concentration (Daudet et al., 2002). The C released by starch degradation and remobilization is targeted to the sucrose compartment.

Fructans

The derivative of fructans (eqn 21) is expressed as for starch. Fluxes of C towards and from fructans only occur with the sucrose compartment.

$$\frac{d{C}_{tp,i}^{fruc}}{dt}=\left(S_{tp,i}^{C,fruct}\left(t\right)-D_{tp,i}^{C,fruct}\left(t\right)\right)\mathrm{*}{M}_{tp,i}^{struct}\left(t\right)-{remob}_{tp,i}^{C,fruc}\left(t\right)$$ (21)

The rate of fructan synthesis ($S_{tp,i}^{C,fruct}$) depends on sucrose concentration, following a Michaelis–Menten kinetic (eqn T4·13). The downregulation of fructan synthesis by the rate of sucrose loading is detailed in eqn (T4·14). The rate of fructan degradation ($D_{tp,i}^{C,fruct}$) is downregulated through retro-inhibition by sucrose concentration (eqn T4·15).

Sucrose

The derivative of sucrose (eqn 22) is calculated as:

$$\frac{d{C}_{tp,i}^{suc}}{dt}=\left(S_{tp,i}^{C,suc}\left(t\right)+D_{tp,i}^{C,star}\left(t\right)+D_{tp,i}^{C,fruc}\left(t\right)-S_{tp,i}^{C,fruc}\left(t\right)\right)\mathrm{*}{M}_{tp,i}^{struct}\left(t\right)+{remob}_{tp,i}^{C,star}\left(t\right)+{remob}_{tp,i}^{C,fruc}\left(t\right)-L_{tp,i\to phloem}^{C,suc}\left(t\right)-R_{tp,i}^{total}\left(t\right)$$ (22)

where $L_{tp,i\to phloem}^{C,suc}$ is the loading of sucrose into the phloem. $L_{tp,i\to phloem}^{C,suc}$ is estimated using a transport-resistance formalism (Minchin et al., 1993; Thornley and France, 2007b; Feller et al., 2015) driven by the gradient of sucrose concentration between an organ (tp,i ) and the phloem (eqn T4·16). This formalism accounts for mass flows actuated by osmotic pressure (Münch, 1930; Thornley, 1976). The equation requires calculation of a conductance (eqn T4·17), which is estimated from the organ conductivity and section through which sucrose flux occurs (eqn T4·18). The total respiration rate of photosynthetic organs ($R_{tp,i}^{total}$) is the sum of ($R_{tp,i}^{phloem},R_{tp,i}^{Nnit,red},R_{tp,i}^{residual})$.

Nitrates

The derivative of nitrates (eqn 23) is calculated as the difference between the rate of import from roots (${import}_{tp,i}^{N,nit}$) and consumption for AA synthesis ($S_{tp,i}^{N,AA}$):

$$\frac{d{N}_{tp,i}^{nit}}{dt}={import}_{tp,i}^{N,nit}\left(t\right)-\left(S_{tp,i}^{N,AA}\left(t\right)\mathrm{*}{M}_{tp,i}^{struct}\left(t\right)\right)$$ (23)

The import rate of nitrates (${import}_{tp,i}^{N,nitrates}$) is calculated from root export and the contribution of the organ (tp,i) to total culm transpiration (eqn T4·19)

Proteins

The derivative of proteins (eqn 24) depends on their synthesis ($S_{tp,i}^{N,proteins}$), degradation ($D_{tp,i}^{N,proteins}$) and remobilization (${remob}_{tp,i}^{N,proteins}$) rates in case of tissue death.

$$\frac{d{N}_{tp,i}^{prot}}{dt}=\left(S_{tp,i}^{N,prot}\left(t\right)-D_{tp,i}^{N,prot}\left(t\right)\right){\mathrm{*}M}_{tp,i}^{struct}\left(t\right)-{remob}_{tp,i}^{N,prot}\left(t\right)$$ (24)

The rate of protein synthesis ($S_{tp,i}^{N,prot}$) is calculated as a Michaelis–Menten function of AA concentration (eqn T4·20). The rate of protein degradation ($D_{tp,i}^{N,proteins}$, eqn T4·21) is calculated as a first-order kinetic (Bertheloot et al., 2011) downregulated by cytokinin concentration (eqn T4·22).

Amino acids

The derivative of AAs (eqn 25) depends on their synthesis, protein turnover (synthesis, degradation, and remobilization), import from roots (${import}_{tp,i}^{N,AA}$) and loading to the phloem ($L_{tp,i\to phloem}^{N,AA}$):

$$\frac{d{N}_{tp,i}^{AA}}{dt}=\left(S_{tp,i}^{N,AA}\left(t\right)+D_{tp,i}^{N,prot}\left(t\right)-S_{tp,i}^{N,prot}\left(t\right)\right)\mathrm{*}{M}_{tp,i}^{struct}\left(t\right)+{import}_{tp,i}^{N,AA}\left(t\right)+{remob}_{tp,i}^{N,prot}\left(t\right)-L_{tp,i\to phloem}^{N,AA}\left(t\right)$$ (25)

The rate of AA import (${import}_{tp,i}^{N,AA}$) is estimated from root export (${export}_{roots}^{N,organic}$) and distributed among organs according to organ transpiration (eqn T4·23). Loading of AA into the phloem $L_{tp,i\to phloem}^{N,AA}$ (eqns T4·24 and T4·25) is written as for sucrose with an appropriate value for conductivity (${\mathrm{\sigma }}^{N,AA}$).

Grains.

The development of cereal grains can be divided into two distinct phases: grain enlargement and grain filling (Wardlaw, 1970; Briarty et al., 1979; Jenner et al., 1991; Emes et al., 2003). The first stage corresponds to the structural growth resulting from the division of endosperm cells. During grain filling, the endosperm is used as a store where carbohydrates are accumulated (especially starch). Times of grain filling initiation and cessation are parameters of CN-Wheat ($t_{grains}^{initfilling}$, $t_{grains}^{stopfilling}$, respectively). Grain proteins are synthesised during both growing phases (Fig. 2C). The phloem is assumed to supply the sucrose and AAs required for the synthesis of grain structure, starch and proteins (Jenner et al., 1991).

The derivative of grain structural mass (eqn 26) is given by the balance between the rates of growth ${(G}_{grains}^{struct}$) and respiration ($R_{grains}^{growth,struct}$).

$$\frac{d{C}_{grains}^{mstruct}}{dt}=G_{grains}^{struct}\left(t\right)-R_{grains}^{growth,struct}\left(t\right)$$ (26)

The structural mass growth ($G_{grains}^{struct}$) follows an exponential-like function whose coefficient is calculated at each time step by using a Michaelis–Menten equation depending on sucrose concentration of the phloem (eqn T4·26).

The rapid accumulation of starch that characterizes the filling period is given by eqn (27):

$$\frac{d{C}_{grains}^{star}}{dt}=\left(G_{grains}^{star}\left(t\right)\mathrm{*}{M}_{grains}^{struct}\left(t\right)\right)-R_{grains}^{growth,star}\left(t\right)$$ (27)

The structural mass of grains expressed in g ($M_{grains}^{struct}$) is obtained from the conversion of $C_{grains}^{mstruct}$ (µmol C) by using a mean contribution of C mass to total dry mass of 38·4 %. The rate of starch synthesis ($G_{grains}^{star}$) is calculated as a Michaelis–Menten function depending on sucrose concentration of the phloem (eqn T4·27).

Simultaneously with the two stages described above, N is accumulated in grains leading to the synthesis of proteins. In CN-Wheat, structural and storage proteins have been pooled in an single compartment (Shewry and Halford, 2002). Although these two categories of proteins are thought to be regulated by different mechanisms (Martre et al., 2003), we assumed that protein synthesis depends on AA unloading from phloem ($S_{grains}^{N,proteins}$, eqn T4·28). As N and dry mass accumulation seem to be related (Dreccer et al., 1997), AA unloading in grains is calculated from sucrose unloading (co-transport).

Phloem.

The derivatives of phloemic sucrose (eqn 28) and AAs (eqn 29) are written as the sum of the different loading and unloading fluxes that occur with culm organs (Fig. 2D):

$$\frac{d{C}_{phloem}^{suc}}{dt}=\sum _{i=1}^{nborgtp}\left(L_{tp,i\to phloem}^{C,suc}\left(t\right)\right)-\left(U_{phloem\to roots}^{C,suc}\left(\mathrm{t}\right)\mathrm{*}{M}_{roots}^{struct}\left(t\right)\right)-G_{grains}^{struct}\left(t\right)-\left(G_{grains}^{star}\left(t\right)\mathrm{*}{M}_{grains}^{struct}\right)$$ (28)

$$\frac{d{N}_{phloem}^{AA}}{dt}=\sum _{i=1}^{nborgtp}\left(L_{tp,i\to phloem}^{N,AA}\left(t\right)\right)-\left(U_{phloem\to roots}^{N,AA}\left(t\right)*M_{roots}^{struct}\left(t\right)\right)-S_{grains}^{N,prot}\left(t\right)$$ (29)

Model implementation and conditions of simulation

CN-Wheat describes the culm as a set of modules representing the roots, photosynthetic organs and grains. Each module consists of different metabolites and is connected to a common pool to allow C–N fluxes. In order to represent this system, CN-Wheat is implemented in Python by using the odeint package from the SciPy library (Oliphant, 2007), which enables the solution of the set of differential equations defined for each module.

DISCUSSION

CN-Wheat represents a step in the progress towards a mechanistic FSPM by establishing a scheme for a comprehensive mechanistic modelling of C–N metabolism. By accounting for the main physiological processes involved in both shoot and root metabolism (resource acquisition, respiration, exudation and tissue death), CN-Wheat is expected to have complete and realistic C–N balances. The different hypotheses implemented in CN-Wheat represent a trade-off between simplicity and accounting for the spatial and metabolic scales required for a mechanistic representation of C–N allocation in plant architecture. The central hypothesis of the model is that the physiological processes that drive C–N fluxes are regulated by local metabolite concentrations. As a consequence, this model does not involve any demand:supply ratio, priority rules, sink strength parameters or plant plan (except for the scheduling of grain filling). Under this assumption, the adaptive responses of plants to their environment (e.g. light–N relations, shoot:root ratio) are expected to be emergent properties of the model arising from the integration of local responses. As a consequence of this strategy, choices have been made for the (1) metabolites, (2) scale levels and (3) processes to be accounted for.

Metabolites were selected because of their role(s) as transport, storage, precursors or regulating forms of metabolism. Sucrose was considered as the main form of C, although hexoses are the actual substrate for synthesis, degradation and respiration processes (Grafahrend-Belau et al., 2013), but their introduction in CN-Wheat would have increased the model complexity. Hexoses may therefore be accounted for within the sucrose compartment of the present model. For similar reasons, CN-Wheat accounts for an overall compartment of AAs that does not distinguish the different forms, although glutamine and glutamate play central roles in N metabolism.

In order to represent the whole plant structure, CN-Wheat is based on an explicit description of the above-ground organs while the root system is described by a single compartment. Future developments of the model should allow better representation of root architecture (length, diameter, surface, density, etc.). To allow fluxes across the culm architecture, we assumed that all organs are connected to a common pool of C and N, which can be seen as an abstraction of the phloem. Properly speaking, the phloem is linked to each organ and displays gradients of sucrose and AA concentrations along the vasculature (Lacointe and Minchin, 2008). In order to reduce model complexity, we made the approximation that this complex network could be idealized as a pool defined by single concentrations of sucrose and AAs. Sink organs (roots and grains) unload C and N from the phloem following Michaelis–Menten equations, while sources (photosynthetic organs) passively load C and N to the phloem using a transport-resistant formalism (Thornley and France, 2007b).

As a consequence of the central hypothesis according to which physiological processes are driven by metabolite concentration, CN-Wheat has to maintain a correct balance of these concentrations. A central issue is the requirement of model closure, meaning that the model has to put forward a comprehensive view in which no process having a significant impact on metabolites is ignored. On several occasions we could not find the information required to formalize with reasonable confidence in the bibliography. In such cases, we made assumptions on the underlying mechanisms in order to put forward a mathematical formalism that has good overall behaviour, but remains to be properly validated.

This was the case for roots, when we had to build a consistent proposition to integrate their overall metabolism. The implemented scheme allows CN-Wheat to estimate incoming and outgoing fluxes of C–N (phloem unloading, uptake and exudation), although the individual formalisms remain to be assessed in a wider range of conditions. Calculation of nitrate uptake was implemented in CN-Wheat following Drouet and Pagès (2007), but explicit regulations by root nitrates (Siddiqi et al., 1989; Taulemesse et al., 2015) and carbohydrates had to be integrated into this sub-model in order to obtain realistic concentrations of nitrates in both shoot and roots. It is known in wheat that large concentrations of nitrate can be found in the culm base. As a consequence, simulated concentrations of nitrates in roots may also include nitrates in the culm base and those contained in the xylem, a part of the plant that is not explicitly identified in the present model. Besides, root exudation represents significant losses of carbohydrates and AAs (Keith et al., 1986; Janzen, 1990) that must be accounted for in order to obtain realistic C–N balances. In the present version of CN-Wheat we have introduced simple equations that provide rough estimates of root exudation and this important aspect deserves further development. Carbohydrate and AA exudation are relatively independent processes (Jones et al., 2009), so relating them through the C:N ratio in the roots does not reflect a mechanistic link. Besides, both C and N exudation involves balances between ex-fluxes and reuptake. It has, however, been shown that reuptake is low in usual conditions, due to competition with soil microbes and stabilization through biochemical reactions (Owen and Jones, 2001; Farrar et al., 2003; Jones et al., 2009). Thus, integrating CN-Wheat with a mechanistic soil model will be the subject of future work.

Some assumptions were also made for photosynthetic organs. The mechanisms involved in the differential synthesis of fructans between lighted and shaded organs (Gebbing, 2003) have not been elucidated. Consequently, the regulation of fructan synthesis by sucrose loading, as proposed here, has not been shown experimentally. However, this speculation is consistent with an experiment in which fructan synthesis was observed in Lolium temulentum leaves excised from the stem and which had therefore altered unloading activities (Cairns and Pollock, 1988). Regarding senescence, an abundant literature (Gan and Amasino, 1997; Wingler et al., 1998; Masclaux et al., 2000; Yang et al., 2002) reports multiple regulation pathways involving environmental factors (light, temperature, drought, ozone), gene networks (SAG genes), trophic status (C–N content) and hormones (cytokinins). Nevertheless, we did not find any mechanistic bases for predicting tissue death. Besides, running simulations without allowing for tissue death did not result in any unlikely metabolite concentration or inability to support respiratory costs. Another speculation in our model is the way we formalized the production and action of cytokinins. Cytokinins are synthesized in roots and exported by the transpiration flow to photosynthetic tissues in which they downregulate protein degradation (Mok and Mok, 1994; Badenoch-Jones et al., 1996; Wingler et al., 1998; Yang et al., 2002; Koeslin-Findeklee et al., 2015). Although this role is well recognized, its formalization in CN-Wheat is, at present, purely conceptual. As a consequence of this modelling choice, the distribution of cytokinins (according to organ transpiration) is therefore involved in the establishment of the vertical gradient of protein content observed along the culm. In contrast with CN-Wheat, the model NEMA published by Bertheloot et al. (2011) assumes that the vertical gradient of N among photosynthetic organs results from regulation of N synthesis by (1) the availability of substrate in a common pool and (2) a speculative relation with light. In CN-Wheat, protein synthesis depends only on AA concentration. We did not assume direct regulation of protein synthesis by light as there is no direct support for such regulation in the bibliography; instead, light has an indirect effect on the amount of AAs (due to nitrate distribution and triose phosphate amounts). However, our simulations showed very moderate gradients of AAs among photosynthetic organs, thus leading to moderate gradients in protein synthesis. This is consistent with the bibliography. For instance, Hirel et al. (2005) reported that AAs did not vary between maize leaves at different positions along the plant. Therefore, the dependence of protein synthesis on AAs is not sufficient to create the observed vertical gradient of N. On the other hand, it is known that cytokinins reduce protein degradation and significant vertical gradients of cytokinins have been reported (Saha et al., 1986; Benková et al., 1999). For this reason, we introduced into CN-Wheat a regulation of protein degradation by cytokinins. The formalization of the cytokinin sub-model is quite speculative and has yet to be assessed, but the role given to cytokinins is based on several pieces of experimental evidence (Mok and Mok, 1994; Badenoch-Jones et al., 1996; Wingler et al., 1998; Yang et al., 2002; Koeslin-Findeklee et al., 2015).

In conclusion, we have proposed a mechanistic model of C–N distribution in wheat culm by accounting for a realistic description of both plant structure and functioning. While simplified assumptions have been made, the originality of CN-Wheat lies in the proposition of an integrated view of plant functioning based on a coherent and mechanistic approach. The assumptions made on metabolites, activities and regulations are in agreement with a recent review on the integrated networks driving plant functioning (White et al., 2016). The challenging aspect of the model is the regulation of physiological processes by metabolite concentrations at organ scale, which is required to represent the main processes involved in the balance of C and N masses. The model can provide some guidelines for exploring the role of local processes in the development of the whole plant, to help in the understanding of experimental results or the nature of genotypic differences. Then, these guidelines could be assessed and validated against experimental results, which may in turn be used to improve the model formalisms. We also believe that the model can be useful in several domains of plant science, including physiology for studying particular processes, while having a comprehensive model of plant functioning, soil biology for investigating the interactions between root exudates and soil biosphere and also eco-physiology and agronomy for identifying plant traits and defining ideotypes adapted to low-N agricultural practices. Besides, this work is a first step towards a model encompassing the full growth cycle, i.e. accounting for the interactions between the C–N status of the plant and its morphogenesis (leaf growth and tillering).

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. SI 1: supplementary information about the photosynthesis model. SI 2: supplementary information for organ temperature calculation. SI 3: supplementary information about the respiration model.