Significance
The best examples of color terms across languages are often held to reflect universal focal colors in the opponent pairs red vs. green and yellow vs. blue. An opposing view holds that best examples reflect categories that are determined by local linguistic convention. We argue for a synthesis of these two proposals. We show that best examples of color terms across languages can be predicted from color term extensions using a statistical model that indicates which samples are most representative of a distribution. This model accounts for universal tendencies in best example choices across languages, and also accounts for cross-language variation. Our findings suggest that general statistical principles may illuminate fundamental aspects of color naming across languages.
Keywords: semantic universals, semantic variation, color categories
Abstract
Focal colors, or best examples of color terms, have traditionally been viewed as either the underlying source of cross-language color-naming universals or derived from category boundaries that vary widely across languages. Existing data partially support and partially challenge each of these views. Here, we advance a position that synthesizes aspects of these two traditionally opposed positions and accounts for existing data. We do so by linking this debate to more general principles. We show that best examples of named color categories across 112 languages are well-predicted from category extensions by a statistical model of how representative a sample is of a distribution, independently shown to account for patterns of human inference. This model accounts for both universal tendencies and variation in focal colors across languages. We conclude that categorization in the contested semantic domain of color may be governed by principles that apply more broadly in cognition and that these principles clarify the interplay of universal and language-specific forces in color naming.
Focal colors, or best examples of color terms, are at the center of the debate over language and color cognition. An influential view (1) holds that focal colors are the source of cross-language color-naming universals. In this view, color naming across languages is constrained by the Hering primaries (2) in the opponent pairs red vs. green and yellow vs. blue as well as black and white. The best examples of these six color terms are often understood to be universal privileged points or foci in color space, such that languages differ in their color-naming systems primarily by grouping these universal foci into categories in different ways. There is some empirical support for this view: the best examples of color terms across languages tend to cluster near these six points (3, 4), and an early study (5)—but not a recent follow-up (6)—also found these colors to be cognitively privileged.
However, Roberson et al. (6) claimed that this influential view has matters exactly backward. They argued that color categories are not constrained by universal foci but are instead defined at their boundaries by local linguistic convention, which varies across languages (6). They proposed that “Once a category has been delineated at the boundaries, exposure to exemplars may lead to the abstraction of a central tendency so that observers behave as if their categories have prototypes” (ref. 6, p. 395). In this view, best examples do not reflect a universal cognitive or perceptual substrate but are merely an after effect of category construction by language.
A proposal by Jameson and D’Andrade (7) has the potential to reconcile these two opposed stances. They suggested that there are genuine universals of color naming but that these do not stem from a small set of focal colors (7). Instead, in their view, universals of color naming stem from irregularities in the overall shape of perceptual color space, which is partitioned into categories by language in a near-optimally informative way (7). This proposal (also see refs. 8–11) has been shown to explain universal tendencies and cross-language variation in the extensions of color categories (12, 13). (Other approaches to the same question are discussed in refs. 14–20.) However, it is the best examples of color categories and not their extensions that are at the heart of the debate.
Here, we address this open issue, completing the reconciliation of the two standard opposed views. Following the work by Roberson et al. (6), we argue that best examples of color categories across languages are not reflections of underlying universal focal colors. However, we argue that best examples do not vary arbitrarily either. Instead, we note that color categories across languages reflect the functional need for informative communication about color (7, 12, 13) and argue that best examples are derived from the resulting informative categories. In this view, all languages are driven by the same functional forces; thus, unrelated languages will often independently settle on similar informative color-naming systems—and when they do, the best examples of those color categories should also be similar. However, color categories may also vary across languages, representing different informative partitions of color space—and when categories do vary, the best examples of those categories should vary with them. Here, we test this account by asking whether best examples of categories across languages can be predicted from category extensions and whether such predictions account for both universal tendencies and cross-language variation in focal colors.
Pursuing these ideas requires an account of how the best example of a category is determined. To this end, we use a rational model that formally characterizes the best example of a category in terms of the support that it provides to a Bayesian inference. This model was originally proposed (21) to account for patterns of human inference that have been taken to suggest a cognitive heuristic of “representativeness” (22), as described below. To preview our results, we find that this model accounts for both universal tendencies and variation in focal color choices across languages.
The remainder of the paper proceeds as follows. We first describe the data that we consider and a set of competing models, including the representativeness model, that predicts best examples of color categories from the extensions of those categories. We test these models against universal tendencies in the data and find that the representativeness model outperforms competing models, consistent with preliminary results using a different measure of model performance (23). In a separate test, we then consider cross-language variation in the same data and again find that the representativeness model outperforms its competitors. We close by discussing the implications of our findings.
Predicting Best Examples of Color Categories
Evaluating formal models of color foci requires a good source of color-naming data. The primary data that we considered were those of the World Color Survey (WCS), which collected color-naming data from native speakers of 110 unwritten languages worldwide (24). Participants in the WCS were shown each of 330 color chips of the stimulus array in Fig. 1A and asked to name each chip with a color term in their native language; we refer to the resulting data as “naming data.” Afterward, participants were asked to pick out those cells in the stimulus array that were the best examples (foci) of each color term that they used; we refer to these as “focus data.”
Fig. 1.
Color stimuli from the WCS. (A) The color-naming stimulus array. The rows correspond to 10 levels of Munsell value (lightness), and the columns correspond to 40 equally spaced Munsell hues. The color in each cell corresponds approximately to the maximum available Munsell chroma for that hue–value combination. (B) The chips of the stimulus array as plotted in CIELAB color space. The irregularity of the outer surface of the color solid can be seen, most notably in the yellow region. Reprinted from ref. 13.
We compared several models that predict best examples of color categories from the extensions of those categories. We represented each color in the stimulus array as a point in a standard 3D perceptual color space, CIELAB (Fig. 1B). (We also explore representations based on the CIELUV color space in SI Appendix.) For short distances at least, Euclidean distance between two colors in CIELAB is roughly proportional to the perceptual dissimilarity of those colors (25) (but also see ref. 26). We generate focal color predictions at the individual speaker level: for each named color category used by each speaker in each language of the WCS, we used each model to predict that speaker’s focus data from that speaker’s naming data. We provide overviews of our models and analyses here; additional details are in Materials and Methods and SI Appendix.
Representativeness Model.
Why do people believe that the sequence of coin flips HHTHT (where H is heads and T is tails) is more likely to be produced by a fair coin than the sequence HHHHH? Using simple probability theory, it is easy to show that the two sequences are, in fact, equally likely. Cognitive psychologists have proposed that people use a heuristic of representativeness instead of performing probabilistic computations in such scenarios (22). We might then explain why people believe that HHTHT is more likely to be produced by a fair coin than HHHHH by arguing that the former is more representative of the output produced by a fair coin than the latter. However, how do we define the notion of representativeness to which the heuristic appeals? Numerous proposals have been made, connecting representativeness to existing quantities, such as similarity (22) and likelihood (27). Tenenbaum and Griffiths (21) provided a rational analysis (28) of representativeness by trying to identify the problem that such a quantity solves. They noted that one sense of representativeness is being a good example of a concept, and they showed how this could be quantified in the context of Bayesian inference (21).
Formally, given some observed data d and a set of hypothetical sources , we assume that a learner uses Bayesian inference to infer which generated d. In that context, Tenenbaum and Griffiths (21) defined the representativeness of data d for hypothesis h to be the evidence that d provides in favor of a specific h relative to its alternatives:
| [1] |
where is the likelihood—the probability of d if h is true—and is the prior distribution on hypotheses, renormalized over . In the case of flipping a coin, the numerator corresponds to the probability of a sequence of flips under a fair coin, whereas the denominator integrates over all ways in which a coin could be unfair. The numerator is, thus, equal for HHHHH and HHTHT, but the denominator is greater for HHHHH, because it is probable under a coin biased toward heads. Being representative thus requires being probable under h and improbable under alternatives to h. This measure was shown to outperform competing accounts based on similarity and likelihood in predicting human representativeness judgments for a number of simple stimuli. We propose that this measure can also be used to predict focal colors or best examples of named color categories from the extensions of those categories.
Given a Gaussian distribution that characterizes the category named by color term t, we can adopt the representativeness measure given in Eq. 1 to determine how good an example each color chip x is of color term t. Substituting x in for the observed data d and t for hypothesis h, we obtain the expression
| [2] |
where is given by the density function of a Gaussian fit to the category named by color term t, and the priors are proportional to the number of chips in named color category . This model can be seen as formalizing the claim by Rosch and Mervis (29) that category prototypes or best examples reflect not just high similarity to other members of the category (captured here in the numerator) but also, low similarity to members of other categories (captured in the denominator).
We test this measure against the alternative proposals mentioned above (22, 27): a likelihood model and two similarity models (a prototype model and an exemplar model). In addition, we explore a model that selects as the focus for category t that chip in the extension of t that has the highest chroma. Chroma or saturation corresponds to how colorful or “ungray” a given color is, and in exploring this model, we follow the suggestion (7, 12) that focal colors tend to be those with high chroma (but also see ref. 30). These models represent different ways in which the best example of a category may be predicted from the extension of that category. As with the representativeness model, for a given color x and color term t, each model assigns a score indicating how good x is as an example of t.
Likelihood Model.
In this model, the goodness score of color x as an example of color category t is given by the log of the density function of the Gaussian distribution that was fit to the naming data for t. Thus,
| [3] |
This model is similar to the representativeness model but lacks the denominator that captures competition among categories in that model.
Prototype Model.
In this model, we define the focus or prototype of color category t to be the centroid over the color chips in the extension of category t (31). The score for this measure is then the similarity of x to that prototype :
| [4] |
where characterizes the similarity between two colors as a function of CIELAB distance,
| [5] |
and following previous work (12).
Exemplar Model.
The exemplar model uses a scoring metric similar to that of the prototype model, except that, rather than computing the similarity of color x to a single prototype, we compute its similarity to each color chip that falls in the extension of category t and sum the results:
| [6] |
where is the set of color chips that falls in the extension of category t.
Chroma Model.
The score for this model is given by the similarity of color x to that color chip that has the highest chroma (saturation) value within the extension of category t. Thus, we compute
| [7] |
where is the chip within the extension of t that has the highest chroma value. In the case of ties for —that is, several chips with the same maximum value for chroma—we randomly select a chip from the set of ties.
Results
We assessed these models as follows. For each speaker of each language in the WCS, we first considered that speaker’s naming data and modeled the categories in those data as either a set of Gaussian probability distributions (for the representativeness and likelihood models) or a set of 3D points in CIELAB (for the prototype, exemplar, and chroma models). Then, for each such category, we determined how good an example of that category each of the 330 chips in the stimulus array is according to each model. This procedure yielded, for each model, a ranking of chips in the array by predicted goodness, and we compared this model prediction with empirical WCS focus data that specify which chip(s) were, in fact, selected by that speaker as the best example(s) of that category. Thus, we compare model predictions with empirical data on a per speaker basis. Below, we present both qualitative and quantitative evaluations of the models.
Distribution of Foci.
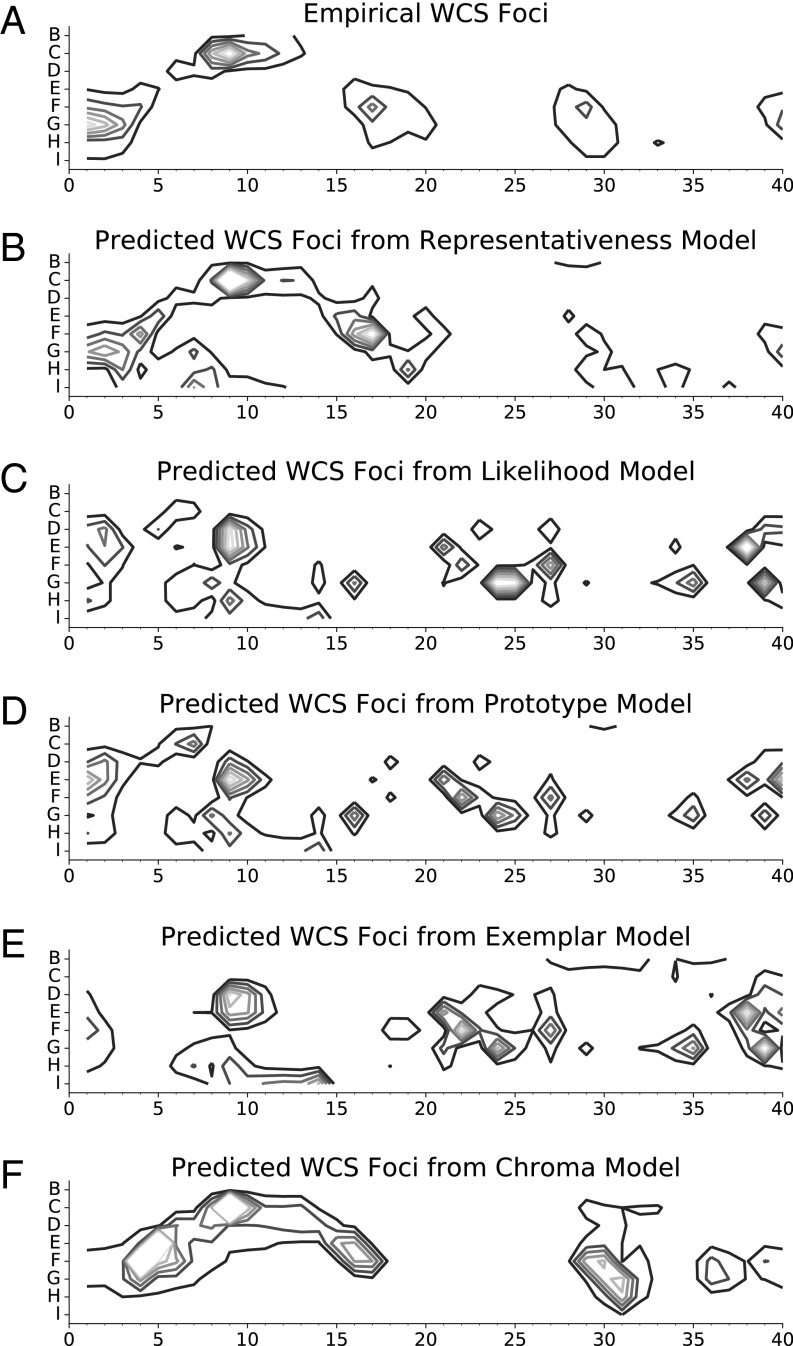
A simple means of assessing the models is to generate predicted focal choices from each model’s ranking of chips and then, compare the distribution of those predicted focal choices with the distribution of actual focus data from the WCS. Some speakers in the WCS provided more than one focus (best example) for some categories; if a speaker provided n foci for a given category, we selected the n top-ranked chips as a given model’s predicted focal choices for that category and speaker. In this manner, we obtained, for each model, one predicted focal choice for each empirical focal choice in the data. We then counted the number of times that each of the 330 color chips in the stimulus array was selected as a focal choice, yielding a distribution of focal choices over the stimulus array. Interestingly, every chip in the stimulus array was selected at least once as a focus for some color term by some speaker of some language. We compared this empirical distribution of foci across the array with the distribution predicted by each of the models. Following an earlier analysis of WCS focus data (4), we plotted these distributions over the chromatic portion of the array, where the 2D layout makes contours easily interpretable. The resulting contour plots of the empirical WCS focus distribution and the five models’ predicted focus distributions are shown in Fig. 2.
Fig. 2.
Contour plots of the focus distributions (A) in the WCS and as predicted by (B) the representativeness model, (C) the likelihood model, (D) the prototype model, (E) the exemplar model, and (F) the chroma model. Each contour line corresponds to 100 focal choices.
The empirical distribution is shown in Fig. 2A, and it replicates earlier findings (4). The distribution predicted by the representativeness model (Fig. 2B) matches this empirical distribution qualitatively fairly well. Moreover, at least on informal inspection, the representativeness model appears to approximate the empirical distribution more closely than do the competing models. The chroma model (Fig. 2F) at first appears to also approximate the empirical distribution fairly well, but closer inspection reveals that several of the peaks of the model distribution do not align correctly with those of the empirical distribution (also see ref. 30).
This qualitative assessment is reinforced by a quantitative one that considered all chips of the array and not just the chromatic portion. The quadratic form (QF) distance (32) is a measure of the difference between two histograms defined over the same similarity space, and this measure is sensitive to the similarity structure of that space (Materials and Methods). We computed the QF distance between the WCS empirical focus distribution shown in Fig. 2A and each of the model distributions shown in Fig. 2 B–F, with similarity determined by the function defined above. The results are shown in Table 1, with the best model score indicated. The representativeness model outperforms the other models, diverging less from the empirical distribution than its competitors.
Table 1.
Quantitative assessment of each model against WCS focus distribution
| Model | QF distance | Rank position |
| Representativeness | 1.17* (76) | 27.67* (104) |
| Likelihood | 1.74 (6) | 42.65 (1) |
| Prototype | 1.96 (3) | 48.30 (0) |
| Exemplar | 1.64 (24) | 38.98 (5) |
| Chroma | 2.13 (1) | 78.51 (1) |
Numbers in parentheses indicate the number of languages for which the model performs best.
Best model score.
Each model produces as output a ranking of the stimulus chips, where rank is assigned in descending order. Thus, another natural way to assess the models is to note the position of the true empirical focal choice in this ranked list. The average rank position for each model is presented in Table 1. As before, we find that the representativeness model outperforms the other models, ranking the true foci higher on average.
Language-Level Analysis.
The analyses above considered all focus choices in the WCS as a single distribution, pooling together choices made by different speakers of different languages. Color naming varies across languages, and therefore a natural question is whether the representativeness model also outperforms its competitors when each language is considered separately. Such a language-level analysis would be appropriate if we are to take seriously the hypothesis that category boundaries are determined in part by local linguistic convention (6). We considered separately each of 110 languages of the WCS and conducted analyses like those described above but at the language level, pooling together focus choices that were made by speakers of a single language. For each language, we noted which model best predicted focus choices by speakers of that language by each of our two metrics. Table 1 (language counts in parentheses) shows that, by both metrics, the representativeness model again outperforms its competitors and exhibits the best performance for a majority of the WCS languages. [Four paired t tests compared average QF distance per language predicted by the representativeness model with that predicted by each other model, in each case averaging across speakers and color terms for each language. The representativeness model outperformed each other model (P < 0.001), Bonferroni-corrected for multiple comparisons. Analogous results were also obtained when measuring rank position rather than QF distance.] We also conducted similar analyses for two languages outside the WCS [Berinmo (6) and Dani (33)], and the results were similar. Full details of this cross-language analysis, including results for individual languages, are presented in SI Appendix. These analyses highlight both cross- and within-language (i.e., interindividual) variation in focus choices.
Color Categories with Unusual Extensions
So far, we have shown that a model of focal colors as representative members of categories accounts well for the distribution of WCS best example choices across the stimulus array, as well as the distribution of best example choices within many languages. These results are consistent with the proposal that color foci are representative members of categories and that their location in color space reflects category extensions, which are, in turn, shaped by the functional need for color-naming systems to be informative (12, 13). However, the analyses that we have seen so far do not discriminate between this hypothesis and a natural alternative: the traditional view of color foci as reflections of unalterably universal privileged points in color space. For languages with common color-naming systems, the two hypotheses make the same prediction: foci should tend to fall in the canonical positions shown in Fig. 2A. This prediction is made by the traditional universal foci account, because these positions are the proposed locations of the universal foci. Roughly the same outcome is predicted by our account as seen in Fig. 2B.
In a final investigation, then, we attempt to discriminate between these two hypotheses. The hypotheses diverge in their predictions for color categories that have unusual extensions. If foci are a universal groundwork for color naming, then in such unusual cases, foci will fall in the universal (canonical) positions, despite the noncanonicality of the category extensions. In contrast, our account predicts that, in such cases, foci should follow the category extensions and fall in noncanonical positions. What is not yet known is (i) whether the representativeness model accounts for noncanonical empirical distributions better than universal foci do and (ii) whether the representativeness model also outperforms the other competing models considered above on noncanonical or unusual categories generally. To test these open questions, we began by defining a formal model of the universalist account and a measure of category unusualness.
Universalist Model.
Like the other models that we consider, the universalist model assigns a score indicating how good a given color chip x is as an example of color term t. The score for the universalist model is determined by the empirical WCS focus distribution shown in Fig. 2A gated by the extension of category t:
| [8] |
where is the number of times that color chip x was chosen as a best example of any term by any speaker in any language in the WCS, and is one if and zero otherwise.
Category Unusualness.
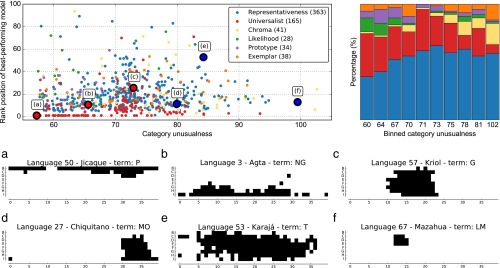
For each major color term in the WCS, we computed the unusualness of the category named by this term based on its average Hausdorff distance (34) to all other major color categories (Materials and Methods). [We considered a color term to be a major color term in a language if it was used by a plurality of speakers of the language for at least 10 of the 330 chips of the stimulus array (13); otherwise, we considered it a minor term and excluded it from this analysis.] We also pooled together the focus choices for this term across speakers of the language in question as well as the analogous focus predictions by each of the models. Finally, we noted which model performed best for this category (had the lowest rank position of the empirical focus distribution; we also consider QF distance in SI Appendix).
Fig. 3 shows the results of this analysis. The scatterplot in Fig. 3 shows each category as a dot. The dot’s position represents the category’s unusualness (horizontal axis) and the score (rank position) of the best performing model for that category (vertical axis: lower is better). The dot’s color represents the best performing model for that category. It can be seen that the universalist model (red) is best for many categories of low unusualness (Fig. 3 a–c)—this outcome is unsurprising, because the universalist model is based on universal tendencies in focus choices. However, for higher values of unusualness, the representativeness model (blue) begins to outperform the universalist model and others as predicted. This progression of increasing dominance for the representativeness model with increasing category unusualness is shown more schematically in the stacked barplot in Fig. 3. These findings suggest that, when boundaries fall in noncanonical positions, foci do as well. Moreover, foci for unusual categories are better predicted by representativeness than they are by expectations based on strictly universal foci or the other models.
Fig. 3.
Effect of category unusualness. In the scatterplot (Top Left), each dot represents a color category in the WCS, and the dot’s color represents the best performing model for that category. The horizontal axis represents category unusualness, and the vertical axis represents the model performance (rank position) of the best performing model for that category. In the bar chart (Top Right), the horizontal axis again represents category unusualness, this time partitioned into 10 bins with the same number of categories per bin. The stacked bars show, for each level of unusualness, the proportion of categories at that level of unusualness that were best predicted by each model. The bottom panels show example categories labeled in the scatterplot at varying unusualness scores, highlighting the types of categories that (a–c) the universalist and (d–f) the representativeness models best predict. Additional details of these categories are in SI Appendix.
Discussion
Focal colors, or best examples of color terms, are at the center of the debate over color naming. Focal colors have traditionally been viewed as either the underlying source of color-naming universals or derived from category boundaries that vary widely with local linguistic convention. In contrast, we have argued for an account of this disputed construct that synthesizes aspects of these traditionally opposed views and accounts for data that challenge each one. We have proposed that focal colors are representative members of color categories. This simple idea accounts for universal tendencies in focal colors, but also correctly predicts some deviation from those universal tendencies, particularly for color categories with unusual extensions. Our proposal coheres naturally with a recent explanation of color naming in terms of the functional need for informative communication over irregularly shaped perceptual color space (7, 12). That view explains cross-language universals and variation in color naming without reference to a small set of focal colors, and it leaves the nature of focal colors unexplained. Our proposal fills that gap. Taken together, the two proposals suggest a single overall account of color naming: color categories across languages assume the forms that they do because of functional pressure for informative communication given the structure of color space, and foci are representative members of those categories.
Materials and Methods
Treatment of the Data.
The WCS color-naming data that we analyze are available at www.icsi.berkeley.edu/wcs/data.html. Because our analyses concern the relation between category extension (naming data) and best examples (focus data) on a per speaker basis, we considered only those categories for which both naming and focus data were available for the same speaker.
QF Distance.
QF distance is a measure of the difference between two histograms, and , over the same set of points in space, and it takes into account the similarities between those points (32). QF distance is defined as
| [9] |
where is an interpoint similarity matrix. In our analyses, we defined over the color chips of the stimulus array with , where characterizes the similarity between two colors as a function of CIELAB distance,
| [10] |
and following previous work (12).
Computing Category Unusualness.
We took the extension of a major color term to be that set of chips in the stimulus array that was named by that color term by a plurality of speakers and represented that set of chips as a set of points in CIELAB space. We took the dissimilarity between any two categories and to be the Hausdorff distance between the two corresponding sets of points. The Hausdorff distance (34) is determined by finding, for each point in each set, the nearest point in the other set and selecting the largest of the resulting distances:
| [11] |
where
| [12] |
and is the Euclidean distance between points x and y in CIELAB space. The unusualness of category c, , is the average dissimilarity of c to all major color categories in the WCS:
| [13] |
where i indexes over all N major color categories in the entire WCS.
Supplementary Material
Acknowledgments
We thank Paul Kay and Alexandra Carstensen for helpful comments on an early version of this paper and the anonymous reviewers for valuable feedback. This work was supported by Grants IIS-0845410, IIS-1018733, and SMA-1228541 from the National Science Foundation (to T.L.G.); and Grant SBE-1041707 from the National Science Foundation (to T.R.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1513298113/-/DCSupplemental.
References
- 1.Kay P, McDaniel CK. The linguistic significance of the meanings of basic color terms. Language (Baltim) 1978;54(3):610–646. [Google Scholar]
- 2. Hering E (1964) Outlines of a Theory of the Light Sense, trans Hurvich LM, Jameson D (1964) (Harvard Univ Press, Cambridge, MA)
- 3.Berlin B, Kay P. Basic Color Terms: Their Universality and Evolution. Univ of California Press; Berkeley, CA: 1999. [Google Scholar]
- 4.Regier T, Kay P, Cook RS. Focal colors are universal after all. Proc Natl Acad Sci USA. 2005;102(23):8386–8391. doi: 10.1073/pnas.0503281102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Heider ER. Universals in color naming and memory. J Exp Psychol. 1972;93(1):10–20. doi: 10.1037/h0032606. [DOI] [PubMed] [Google Scholar]
- 6.Roberson D, Davies I, Davidoff J. Color categories are not universal: Replications and new evidence from a stone-age culture. J Exp Psychol Gen. 2000;129(3):369–398. doi: 10.1037//0096-3445.129.3.369. [DOI] [PubMed] [Google Scholar]
- 7.Jameson KA, D’Andrade RG. It’s not really red, green, yellow, blue: An inquiry into perceptual color space. In: Hardin CL, Maffi L, editors. Color Categories in Thought and Language. Cambridge Univ Press; Cambridge, UK: 1997. pp. 295–319. [Google Scholar]
- 8.Jameson K. Why GRUE? An interpoint-distance model analysis of composite color categories. Cross Cult Res. 2005;39(2):159–204. [Google Scholar]
- 9.Jameson K. Culture and cognition: What is universal about the representation of color experience? J Cogn Cult. 2005;5(3):293–348. [Google Scholar]
- 10.Komarova N, Jameson K, Narens L. Evolutionary models of color categorization based on discrimination. J Math Psychol. 2007;51(6):359–382. [Google Scholar]
- 11.Jameson K. Where in the World Color Survey is the support for the Hering primaries as the basis for color categorization? In: Cohen J, Matthen M, editors. Color Ontology and Color Science. MIT Press; Cambridge, MA: 2010. pp. 179–202. [Google Scholar]
- 12.Regier T, Kay P, Khetarpal N. Color naming reflects optimal partitions of color space. Proc Natl Acad Sci USA. 2007;104(4):1436–1441. doi: 10.1073/pnas.0610341104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Regier T, Kemp C, Kay P. Word meanings across languages support efficient communication. In: MacWhinney B, O’Grady W, editors. The Handbook of Language Emergence. Wiley-Blackwell; Chichester, UK: 2015. pp. 237–263. [Google Scholar]
- 14.Yendrikhovskij S. Computing color categories from statistics of natural images. J Imaging Sci Technol. 2001;45(5):409–417. [Google Scholar]
- 15.Steels L, Belpaeme T. Coordinating perceptually grounded categories through language: A case study for colour. Behav Brain Sci. 2005;28(4):469–489. doi: 10.1017/S0140525X05000087. [DOI] [PubMed] [Google Scholar]
- 16.Dowman M. Explaining color term typology with an evolutionary model. Cogn Sci. 2007;31(1):99–132. doi: 10.1080/03640210709336986. [DOI] [PubMed] [Google Scholar]
- 17.Puglisi A, Baronchelli A, Loreto V. Cultural route to the emergence of linguistic categories. Proc Natl Acad Sci USA. 2008;105(23):7936–7940. doi: 10.1073/pnas.0802485105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lindsey DT, Brown AM. World Color Survey color naming reveals universal motifs and their within-language diversity. Proc Natl Acad Sci USA. 2009;106(47):19785–19790. doi: 10.1073/pnas.0910981106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Baronchelli A, Gong T, Puglisi A, Loreto V. Modeling the emergence of universality in color naming patterns. Proc Natl Acad Sci USA. 2010;107(6):2403–2407. doi: 10.1073/pnas.0908533107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baronchelli A, Loreto V, Puglisi A. Individual biases, cultural evolution, and the statistical nature of language universals: The case of colour naming systems. PLoS One. 2015;10(5):e0125019. doi: 10.1371/journal.pone.0125019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tenenbaum JB, Griffiths TL. The rational basis of representativeness. In: Moore J, Stenning K, editors. Proceedings of the 23th Annual Conference of the Cognitive Science Society. Cognitive Science Society; Edinburgh: 2001. pp. 1036–1041. [Google Scholar]
- 22.Kahneman D, Tversky A. Subjective probability: A judgment of representativeness. Cogn Psychol. 1972;3(3):430–454. [Google Scholar]
- 23.Abbott JT, Regier T, Griffiths TL. Predicting focal colors with a rational model of representativeness. In: Miyake N, Peebles D, Cooper R, editors. Proceedings of the 34th Annual Conference of the Cognitive Science Society. Cognitive Science Society; Austin, TX: 2012. pp. 60–65. [Google Scholar]
- 24.Cook RS, Kay P, Regier T. The World Color Survey database: History and use. In: Cohen H, Lefebvre C, editors. Handbook of Categorization in Cognitive Science. Elsevier; Amsterdam: 2005. pp. 223–242. [Google Scholar]
- 25.Brainard DH. Color appearance and color difference specification. In: Shevell SK, editor. The Science of Color. 2nd Ed. Elsevier; Amsterdam: 2003. pp. 191–216. [Google Scholar]
- 26.Komarova NL, Jameson KA. A quantitative theory of human color choices. PLoS One. 2013;8(2):e55986. doi: 10.1371/journal.pone.0055986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gigerenzer G, Hoffrage U. How to improve Bayesian reasoning without instruction: Frequency formats. Psychol Rev. 1995;102(4):684–704. [Google Scholar]
- 28.Anderson JR. 1990. The Adaptive Character of Thought, Studies in Cognition (Lawrence Erlbaum Associates, Inc., Hillsdale, NJ)
- 29.Rosch E, Mervis C. Family resemblances: Studies in the internal structure of categories. Cogn Psychol. 1975;7(4):573–605. [Google Scholar]
- 30.Witzel C, Franklin A. Do focal colors look particularly “colorful”? J Opt Soc Am A Opt Image Sci Vis. 2014;31(4):A365–A374. doi: 10.1364/JOSAA.31.00A365. [DOI] [PubMed] [Google Scholar]
- 31.Reed SK. Pattern recognition and categorization. Cogn Psychol. 1972;3(3):382–407. [Google Scholar]
- 32.Hafner J, Sawhney HS, Equitz W, Flickner M, Niblack W. Efficient color histogram indexing for quadratic form distance functions. IEEE Trans Pattern Anal Mach Intell. 1995;17(7):729–736. [Google Scholar]
- 33.Heider ER. Probabilities, sampling, and ethnographic method: The case of Dani colour names. MAN (N.S.) 1972;7(3):448–466. [Google Scholar]
- 34.Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing images using the Hausdorff distance. IEEE Trans Pattern Anal Mach Intell. 1993;15(9):850–863. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.