Negative cooperativity in the nitrogenase Fe protein electron delivery cycle

Significance

Nitrogenase catalyzes N₂ reduction to ammonia, the largest N input into the biogeochemical nitrogen cycle. This difficult reaction involves delivery of electrons from the Fe protein component to the catalytic MoFe protein component in a process that involves hydrolysis of two ATP per electron delivered. MoFe contains two catalytic halves, each of which binds an Fe protein. The prevailing picture has been that the two halves function independently. Here, it is demonstrated that electron transfer (ET) in the two halves exhibits negative cooperativity: Fe→MoFe ET in one-half partially suppresses ET in the other. These findings thus show that conformational coupling in nitrogenase not only gates ET within each half, as shown previously, but introduces negative cooperativity between the two halves.

Abstract

Nitrogenase catalyzes the ATP-dependent reduction of dinitrogen (N₂) to two ammonia (NH₃) molecules through the participation of its two protein components, the MoFe and Fe proteins. Electron transfer (ET) from the Fe protein to the catalytic MoFe protein involves a series of synchronized events requiring the transient association of one Fe protein with each αβ half of the α₂β₂ MoFe protein. This process is referred to as the Fe protein cycle and includes binding of two ATP to an Fe protein, association of an Fe protein with the MoFe protein, ET from the Fe protein to the MoFe protein, hydrolysis of the two ATP to two ADP and two P_i for each ET, P_i release, and dissociation of oxidized Fe protein-(ADP)₂ from the MoFe protein. Because the MoFe protein tetramer has two separate αβ active units, it participates in two distinct Fe protein cycles. Quantitative kinetic measurements of ET, ATP hydrolysis, and P_i release during the presteady-state phase of electron delivery demonstrate that the two halves of the ternary complex between the MoFe protein and two reduced Fe protein-(ATP)₂ do not undergo the Fe protein cycle independently. Instead, the data are globally fit with a two-branch negative-cooperativity kinetic model in which ET in one-half of the complex partially suppresses this process in the other. A possible mechanism for communication between the two halves of the nitrogenase complex is suggested by normal-mode calculations showing correlated and anticorrelated motions between the two halves.

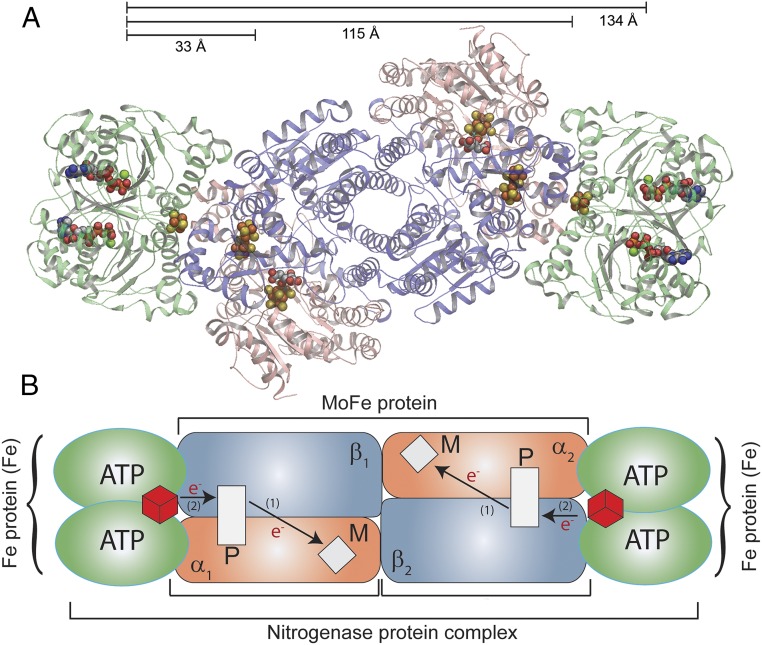
The Mo-dependent nitrogenase, which catalyzes biological reduction of dinitrogen (N₂) to two ammonia (NH₃) molecules, comprises two component proteins called the MoFe protein and the Fe protein (1–4). The MoFe protein is a symmetric dimer of αβ units, each of which contains one active site FeMo cofactor (FeMo-co; [7Fe-9S-Mo-C-R-homocitrate]) and an electron carrier P cluster ([8Fe-7S]) (Fig. 1) (5, 6). The Fe protein is an α₂ dimer with one redox-active [4Fe-4S] cluster and two ATP binding sites, one in each subunit (7). To initiate catalysis, a reduced Fe protein containing two bound ATP [Fe^red(ATP)₂] transiently associates with each αβ half of the MoFe protein, creating a ternary [MoFe(Fe^red(ATP)₂)₂] complex with the two Fe proteins situated on opposite ends of the MoFe protein ∼100 Å apart (Fig. 1) (8–10). While an Fe protein is associated with the MoFe protein it undergoes a sequence of events referred to as the “Fe protein cycle.” The end result of this cycle is the transfer of an electron from the Fe protein to the FeMo-co and hydrolysis of the two ATP molecules. The order of the key steps during this cycle has only been established recently (11). The first step is electron transfer (ET) with an observed rate constant of k_ET ∼140 s⁻¹ (12, 13). This process has been shown to occur in two steps: a conformationally gated ET from the P cluster to FeMo-co followed by rapid reduction of the oxidized P cluster by the Fe^red protein, with the two steps collectively referred to as “deficit spending” ET (14). ATP hydrolysis then follows with an observed rate constant of k_ATP ∼70 s⁻¹, followed by events associated with P_i release, which occur with an overall rate constant k_Pi ∼16–25 s⁻¹ (11, 15, 16). This is followed by dissociation of the oxidized Fe^ox(ADP)₂ protein from the MoFe protein, which is seen to occur with a rate constant k_diss >700 s⁻¹ when flavodoxin is the reductant, to complete the Fe protein cycle (16). This cycle must be repeated a minimum of eight times on each αβ half of the MoFe protein to provide the eight electrons/protons necessary to reduce N₂ to 2NH₃ and 2H⁺ to H₂ according to the minimal stoichiometry for each catalytic unit (1, 3, 4):

$${\text{N}}_2+8{\text{e}}^{-}+8{\mathrm{H}}^{+}+16\text{ATP}\to 2{\text{NH}}_3+{\text{H}}_2+16\hspace{0.17em}\text{ADP}+16\hspace{0.17em}\text{Pi}.$$ [1]

The prevailing picture of these events is that the two halves of the [MoFe(Fe^red(ATP)₂)₂] complex function independently (1, 17, 18). However, a previous kinetic study that examined electron delivery by Fe^red(ATP)₂ isolated from one organism to MoFe from another organism (a heterologous complex) was inconsistent with this picture and indicated a strong negative cooperativity between reactions at the two halves (19), a phenomenon in which reaction at one-half of an enzyme to some extent suppresses reaction at the other. In the present work, quantitative kinetic measurements of ET, ATP hydrolysis, and P_i release in the presteady state, as well as calculations of protein motion, establish whether the two halves of the physiologically relevant homologous [MoFe(Fe^red(ATP)₂)₂] complex between nitrogenase components derived from Azotobacter vinelandii indeed function independently or not.

Fig. 1.

Nitrogenase complex. (A) Ribbon diagram of the symmetrical ternary [MoFe(Fe^red (ATP)₂)₂] complex (PDB ID code 1G21) with the MoFe protein subunits in salmon (α subunits) and blue (β subunits) at the center with two Fe proteins (green) bound on each end. Distances between the ATP binding sites on one Fe protein and the P cluster, the interface on the opposite face, and to the ATP binding sites on the other Fe protein are noted. (B) A cartoon schematic of nitrogenase is shown with the [4Fe-4S] cluster of the Fe protein as red cubes in both Fe proteins, the P clusters as white rectangles, and FeMo-co as white diamonds. The path of electron movement is denoted by arrows and the numbers (1) and (2) and indicate the order of ET.

Results and Discussion

ATP Hydrolysis.

The presteady-state time course for ATP hydrolysis that occurs after mixing of a large excess of ATP with a solution of Fe^red and MoFe protein (4:1 ratio) is presented in Fig. 2 (see also SI Appendix, Figs. S1 and S2 as controls). Based on the previously measured association rate constant and the protein concentrations used, the binding of Fe^red and MoFe protein is rapid and not rate-limiting (13). Experiments with a range of ATP concentrations (SI Appendix, Fig. S3) confirmed that ATP binding, which is ∼90% saturating at the concentrations used (20), is not rate-limiting. Hence, the time course in Fig. 2 represents the kinetics of ATP hydrolysis by the complex [MoFe(Fe^red(ATP)₂)₂], as measured by ADP formation.

Fig. 2.

Presteady-state ATP hydrolysis. Presteady-state, quench-flow measurements of the time course of ATP hydrolysis by nitrogenase (micromoles of ADP formed per micromole of MoFe protein). The reaction was initiated by mixing MoFe protein (10 μM) against Fe protein (40 μM) with [α-³²P]ATP (2 mM) with quenching at the noted times by addition of acetic acid. ADP formed (●) was quantified as noted in Materials and Methods. A shows the time course up to 500 ms, and B shows the time course up to 100 ms. The solid lines are a fit to a burst phase followed by a linear steady state (Eq. 3), where k_ATP = 38 s⁻¹, A = 1.96 μM ADP/μM MoFe protein, and V = 11.8 μM ADP (μM MoFe)⁻¹⋅s⁻¹.

The ATP hydrolysis time course appears as two phases: rapid initial hydrolysis (exponential burst, t: 0 → ∼40 ms) followed by a linear steady-state phase beyond 80 ms. Fitting the ATP hydrolysis data to a presteady-state exponential “burst” followed by a steady-state rate (Eq. 3) gives a rate constant for the exponential phase of k = 38 s⁻¹ with a steady-state rate of 12 s⁻¹ (Fig. 2). The presteady-state rate constant is roughly half the value we reported earlier (11), with the difference arising from a more efficient quenching of the reaction by formic acid, rather than the EDTA quench used previously. The new value nonetheless remains consistent with the key finding of the earlier study: ATP hydrolysis follows ET (11). The rate constant for the linear phase (12 s⁻¹) is consistent with the turnover number of nitrogenase for substrate reduction with dithionite as the reductant (21).

Although the value for the rate constant for ATP hydrolysis was as expected, the quantity of ATP hydrolyzed per MoFe protein in the initial phase was well below the expected four ADP formed for independent reaction of the two halves of the [MoFe(Fe^red(ATP)₂)₂] complex. The fit of the ATP hydrolysis data to the two-phase model yields an amplitude of A = 1.96 ± 0.31 ADP/MoFe protein for the number of ATP hydrolyzed in the presteady-state phase (Fig. 2; Eq. 3), approximately half the value of four ATP/MoFe protein that would be expected if the two Fe proteins within the [MoFe(Fe^red(ATP)₂)₂] complex functioned independently.

Substoichiometric ATP hydrolysis might have been explained by the presence of ∼50% inactive Fe protein, as suggested in earlier studies (15, 22). However, this interpretation was later withdrawn by Clarke et al. (22), who instead attributed substoichiometric ET to “complex behavior” with completely active proteins. In keeping with this revised interpretation, our analytical procedures demonstrate that the nitrogenase used here is fully active (>95%) based on its purity, metal content, ATP binding stoichiometry, and substrate reduction specific activity. Thus, substoichiometric ADP formation is a genuine aspect of catalysis: ATP hydrolysis is about half of what is expected if both bound Fe proteins proceeded through the cycle simultaneously.

Stopped-Flow ET.

Given the observation that only approximately two ATP are hydrolyzed within the [MoFe(Fe^red(ATP)₂)₂] ternary complex in presteady state when hydrolysis of four ATP would be expected if both Fe proteins bound to the MoFe protein proceeded independently (Fig. 2), we sought to quantify the corresponding number of electrons transferred during the presteady-state phase. If the two bound Fe proteins acted independently, and each transferred one electron in the initial event, then transfer of two electrons should be observed.

The time course of the ET reaction was monitored by observing the increase in the absorption at 430 nm associated with oxidation of the [4Fe-4S] clusters of the Fe proteins bound in the [MoFe(Fe^red(ATP)₂)₂] complex, as formed in the mixing dead time (Fig. 3). An exponential rise to maximum is observed, with a rate constant of k_ET ∼140 s⁻¹, in agreement with earlier reports (12, 13), and our finding that ET precedes ATP hydrolysis (discussed above) and P_i release in the “Fe-protein” cycle (11). At later times, in steady state, this absorbance difference actually decreases as released Fe^ox is rereduced and the system passes into a steady-state ratio of Fe^ox/Fe^red.

Fig. 3.

ET kinetics. Presteady-state, SF measurements of the absorbance change at 430 nm (left ordinate) for ET from Fe^red to MoFe protein within the [MoFe(Fe^red(ATP)₂)₂] complex. Red line, result of global fit to negative cooperativity in Fig. 4, Scheme C, using the derived rate constants listed; right ordinate, stoichiometry of reduction derived from Scheme C. Conditions: MoFe protein (10 µM) is mixed with Fe protein (37.5 µM) in a ratio of ∼1:4 with 10 mM MgATP in an SF spectrophotometer.

Unfortunately, the ET stopped-flow (SF) experiment cannot be used to count the number of electrons transferred, because the change in extinction coefficient upon oxidation of Fe^red(ATP)₂ is not known with adequate accuracy, with values between 3,800 and 8,400 mM⁻¹⋅cm⁻¹ having been reported (23–27). As a result, we adopted an alternative counting strategy.

Rapid-Freeze Quench ET.

Electron paramagnetic resonance (EPR) was used to quantify the number of electrons transferred by monitoring the resulting loss in intensity of the S = 3/2 signal of the resting-state FeMo-co (denoted M^N) upon reduction to the EPR silent, singly reduced FeMo-co state. To capture the presteady-state event, a rapid-freeze quench (RFQ) approach was used (22, 28, 29). Previous RFQ studies reported a rapid decrease in the M^N EPR signal to about 40% of the resting value after 10 ms, followed by a plateau that lasted until ∼100 ms, and then a decrease in the intensity to about 10% remaining signal by 1 s (22, 28, 29). Initially, the puzzling observation of only partial reduction of FeMo-co in the initial phase was explained by assuming that the Fe protein was only half-active. The later studies, which determined that the Fe protein used was fully active (22), thus left the observation of partial reduction of the two FeMo-co in the presteady state unexplained.

We reexamined the ET quantitation using RFQ. SI Appendix, Fig. S4 presents the results for RFQ-EPR measurements in which a solution of Fe protein and MoFe protein at a ratio of 4:1 was rapidly mixed with ATP to initiate the reaction then rapidly frozen after a variable time delay (30). If the presteady-state ET measured spectroscopically after rapid mixing represented a “simple” ET process characterized by the rate constant measured by SF and involving both of the FeMo-co in the complex, the M^N EPR signal should essentially vanish after ∼30–40 ms (Fig. 3). Instead, in the RFQ experiments, at 35 ms after initiation of reaction the amplitude of the FeMo-cofactor EPR signal has only decreased to ∼40% of its initial intensity, and the intensity remains between 40–50% out to 100 ms (SI Appendix, Fig. S4A). By 35 ms, the S = 3/2 signal from FeMo-co that has been doubly reduced [denoted the E₂(2H) state] starts to appear. These two signals [M^N and E₂(2H)] were decomposed as described previously into their sums (SI Appendix, Fig. S4B) (28, 31). Interestingly, the E₂(2H) signal that has appeared by 35 ms accounts for ∼20% of the total through 100 ms, roughly in accordance with the predictions of the traditional kinetic model of Thorneley and Lowe (21). We thus conclude that the “half-reactivity” seen here and first seen by Clarke et al. (22) is intrinsic to the function of fully active nitrogenase. The observation that only one of the two FeMo-co is reduced in the presteady state parallels the observation that half of the expected ATP molecules are hydrolyzed in the presteady state. Both suggest that electron delivery involves only one of the two bound Fe proteins.

P_i Release.

P_i release was reported to occur with a rate constant of ∼17 s⁻¹, consistent with this release following ET and ATP hydrolysis (11). This process has now been reexamined quantitatively. A plot of P_i released per [MoFe(Fe^red(ATP)₂)₂] complex versus time (SI Appendix, Fig. S5) gives a rate constant similar to the earlier reported value (15). However, the quantitation (SI Appendix, Fig. S5) now shows that only ∼1.6 P_i are released per complex after ∼140 ms, consistent with the hydrolysis of only approximately two ATP during the presteady-state.

In aggregate, the stoichiometry for ATP hydrolysis, number of electrons transferred, and the stoichiometry of P_i release are consistent with only one of the two bound Fe proteins in the complex proceeding through the Fe protein cycle in the presteady state, whereas the other Fe protein in the ternary complex does not independently initiate an Fe protein cycle.

Kinetic Analysis.

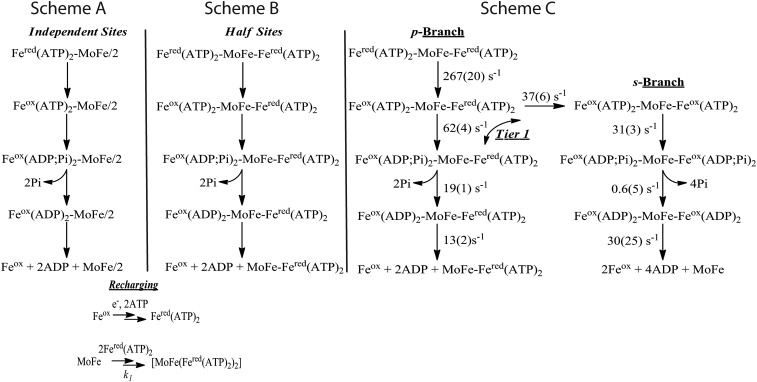
To explain the above stoichiometric measurements revealing that the presteady-state amounts of ATP hydrolysis, ET, and P_i release all are about one-half of the values expected if the two halves of the nitrogenase complex were working independently, we attempted to globally fit the ATP hydrolysis, ET, and P_i release data to alternative models. A model in which the two halves of the complex operate independently with the observed rate constants for the individual steps is shown in Fig. 4, Scheme A. As can be seen in Fig. 5, such a model fits the presteady-state ATP hydrolysis data poorly, exhibiting an unsatisfactory overestimate of the number of ATP hydrolyzed at every time. This finding, together with the observation of roughly half the expected ET, ATP hydrolysis, and P_i release stoichiometry suggests, instead, a model where the two halves of nitrogenase exhibit negative cooperativity (32).

Fig. 4.

Kinetic schemes. (Scheme A) Independent-sites model: Each half of the [MoFe(Fe^red(ATP)₂)₂] complex functions independently. (Scheme B) Half-sites reactivity model: One-half of the complex undergoes electron delivery, and in so doing completely suppresses electron delivery in the other half. (Scheme C) Negative cooperativity model: rate constants listed on the scheme were obtained by freely floating these parameters in the global fit to the differential equations of the scheme (SI Appendix) as described in the text; parentheses contain the statistical 95% confidence limits (±). Also as described, redox state of the s and p halves of MoFe protein are not indicated because electron delivery is independent of MoFe protein reduction level. Recharging (bottom): Simplified scheme in which Fe^red(ATP)₂ is regenerated by rapid reduction of Fe^ox and ATP binding and MoFe protein binding Fe^red(ATP)₂ in a single second-order step for binding of Fe^red(ATP)₂ to MoFe at the reported second-order rate constant, k₁ = 5 × 10⁷ M⁻¹⋅s⁻¹ (19), because the overall process is almost instantaneous relative to the other reactions in the scheme.

Fig. 5.

ATP hydrolysis data fits. Presteady-state, quench-flow measurements of the time course of ATP hydrolysis by rapidly mixing MoFe protein (10 μM) and Fe protein (40 μM) with [α-³²P]ATP (2 mM) (●). Dashed black line: half-sites model, Scheme B, using rate constants, k_ET = 140 s⁻¹, k_ATP = 36 s⁻¹, k_Pi = 16 s⁻¹, and k_off = 11.9 s⁻¹, as derived from the phenomenological fits to the experimental data, along with the recharging model. Solid black line: independent-sites model, Scheme A, calculated analogously. Red line: calculated from the rate parameters obtained by the global fit to negative cooperativity Scheme C, as given in the scheme. (Inset) Data and simulations to longer times.

The extreme of negative cooperativity is incorporated in a model with “half-sites” reactivity (32–34), wherein the second site is completely prevented from reacting until the events on the first side are complete (Fig. 4, Scheme B). The fit of ATP hydrolysis data to such a half-sites model (Fig. 6) is distinctly different, but no better, than the independent-sites model, in that the half-sites model significantly underestimates the number of ATP hydrolyzed at all times up to 100 ms.

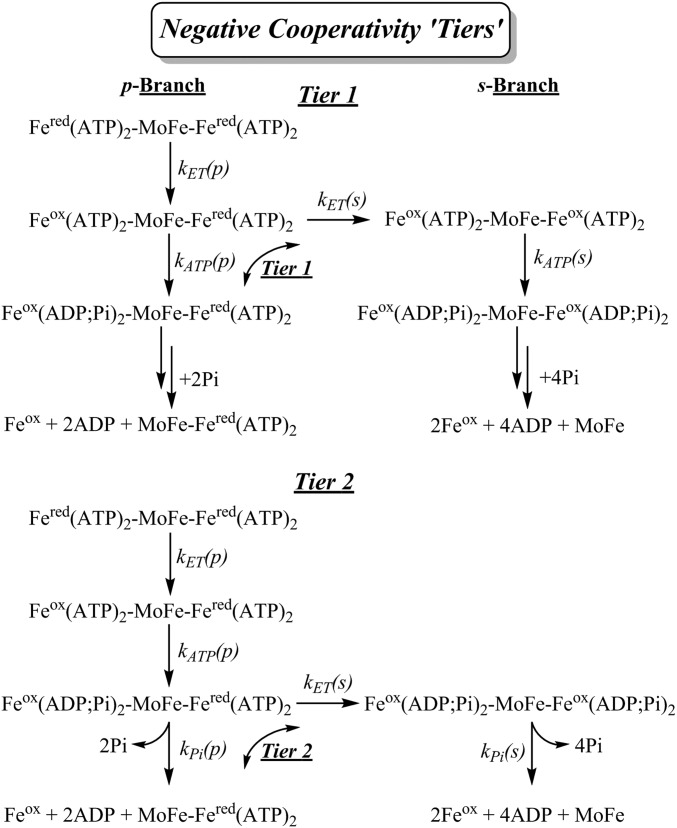
Fig. 6.

Kinetic schemes with negative cooperativity manifest at tiers 1 and 2. Simplified negative cooperativity schemes with branching between primary (p) and seconday (s) branches at tiers 1 and 2. As a notable simplification discussed in the text, along the p branch the complex exhibits half-sites reactivity. When ET occurs in the second half this generates the s branch where the two halves of the complex react. When this branching ET occurs at tier 1 in competition with ATP hydrolysis, the two halves of the resulting symmetrical s branch complex react synchronously in subsequent steps along the reaction pathway. When ET in the second half occurs at tier 2, in competition with P_i release, the second half undergoes prompt ATP hydrolysis to again create a symmetrical s-branch complex, and the two halves subsequently react synchronously. Tier 3 follows straightforwardly.

The failure of either limiting scheme, independent sites or half-sites, to describe the presteady-state ATP hydrolysis data led us to explore “negative cooperativity” (34) kinetic schemes in which electron delivery in one-half of the complex partially suppresses, but does not necessarily completely abolish, the Fe protein cycle (ET, ATP hydrolysis, and P_i release) in the second half. It is not possible to establish a complete global kinetic scheme that simultaneously describes the progress curves for each step in the entire electron delivery process: ET, ATP hydrolysis, P_i release, and, finally, release of Fe^ox(ADP)₂. A complete scheme that incorporates all of these steps would also need to include every combination of redox state for the two FeMo-co of MoFe protein and every combination of redox and nucleotide states for the two Fe proteins. That would require far more rate constants than can be determined from the three progress curves. As a further complication, recent structural observations (35) suggest that the two ATP molecules within a single Fe protein are probably hydrolyzed in a sequential manner as well.

We therefore examined simplified negative-cooperativity models with the goal of capturing the essential phenomena underlying the observations reported here. We considered kinetic schemes in which a randomly selected primary Fe^red(ATP)₂ undergoes ET, which suppresses ET from the other, secondary, Fe^red(ATP)₂. This secondary ET becomes partially allowed (lesser ET rate constant; negative cooperativity) after one of the three steps (three tiers) of the electron delivery process for the initiating Fe^red(ATP)₂: tier 1 immediately after the primary ET, tier 2 after the follow-up primary ATP hydrolysis, and tier 3 after the primary P_i release; Fig. 6 illustrates the approach for tiers 1 and 2. At each tier, the partially allowed ET event in the secondary half of the complex occurs in competition with the corresponding reaction that follows ET in the primary half (e.g., ATP hydrolysis in tier 1). Such competition divides the kinetic scheme into two branches, the primary (p) branch, where only the primary half of the complex carries outs the electron delivery process (half-sites reactivity), and the secondary (s) branch, where both halves undergo electron delivery.

Of these three models, only the tier 1 model (presented in full in Fig. 4, Scheme C) produced excellent global fits to the progress curves for ET, ATP hydrolysis, and P_i release. In this model, the initiating electron delivery to one FeMo-co within the [MoFe(Fe^red(ATP)₂)₂] ternary complex induces conformational changes that partially suppress ET on the second half, with the secondary ET in competition with hydrolysis of ATP in the initiating half of the complex. This competition causes the scheme to partition into the two branches. The complexes where the “primary” half of the complex proceeds through ATP hydrolysis and P_i release without ET in the “secondary” half follow the p branch, which exhibits half-sites reactivity. The complexes where the second ET occurs before ATP hydrolysis in the primary half follow the s branch of the scheme, in which both halves undergo electron delivery. On this branch of the model, the two halves of the complex are taken to undergo synchronous ATP hydrolysis, P_i release, and dissociation of Fe^ox (ADP)₂.

Figs. 3 and 5 and SI Appendix, Fig. S5 show that the unconstrained global fit of the progress curves for ET, ATP hydrolysis, and P_i release to the tier 1 negative cooperativity model (Fig. 4, Scheme C; corresponding differential equations are given in SI Appendix) provides an excellent description of all three measurements, and this fit furthermore captures the half-sites-like behavior in the RFQ measurements of FeMo-co reduction (SI Appendix, Fig. S4). The “microscopic” rate constants obtained in the global fit to Fig. 4, Scheme C are listed in the scheme. Necessarily, none of these correspond directly to the rate constants reported above for the individual phenomenological fits. However, as one of the tests of Scheme C, we explored a constrained version in which the rate constant for the initiating ET step was fixed at the phenomenological rate constant that describes the ET progress curve of Fig. 3, k_ET(p) = 140 s⁻¹. This constrained version failed.

Given that the X-ray structure of the ternary structure of MoFe protein plus two Fe proteins with nonhydrolyzable ATP analogs is symmetric (10), we assume ET first occurs randomly within one-half of the symmetric [MoFe(Fe^red(ATP)₂)₂] complex. This process is conformationally gated (14), and one plausible source of negative cooperativity would be that the “gate opening” on one-half induces conformational changes that make it the primary (p) half, while generating conformational constraints that act to inhibit gate opening on the other half, now the secondary (s) half. The inhibition of events in the second half could take other forms, for example by preventing the second Fe protein from achieving the catalytic binding state. However, each variation would manifest in identical kinetic described by Fig. 4, Scheme C.

The global fit to Fig. 4, Scheme C describes the initiating ET process by a “microscopic” rate constant, k_ET(p) = 267 s⁻¹, nearly double the overall phenomenological ET rate constant. If the initiating ET in the p half of the complex is followed by ATP hydrolysis in that half, this step occurs with rate constant, k_ATP(p) = 62 s⁻¹, and it creates a “p branch” of the scheme, in which p hydrolysis is followed by release of this primary P_i, without electron delivery by the secondary Fe^red(ATP)₂. In short, along the p branch of Scheme C, the “gate” on the secondary half remains closed during the entire sequence of steps in electron delivery on the primary half of the complex.

However, ATP hydrolysis along the p branch of Scheme C competes with ET “leakage” in the secondary (s) half of the complex. Within the illustrative picture developed in the preceding paragraph, we imagine that the gating conformational changes that initiate ET in the primary half also inhibit (negative cooperativity) but do not preclude gate-opening and ET in the secondary half. The global fit to Scheme C yields as the rate constant for s-half ET in competition with p-half ATP hydrolysis, k_ET(s) = 37 s⁻¹, roughly one-fourth the phenomenological rate constant and one-seventh the initiating ET rate constant that defines the p half of the complex.

This leakage ET reaction in the s half of the complex generates a symmetrical complex in which ET has occurred in both halves, with both halves ready to undergo ATP hydrolysis and the following steps. At this point, the model has captured the phenomenon—and consequences—of negative cooperativity. To complete the kinetic scheme for the ET process in the most general way would require more rate constants than can be characterized by the present measurements. Therefore, as a simplification that does not compromise the essence of the negative cooperativity, Scheme C assumes that this state proceeds along the s branch of the scheme with synchronous ATP hydrolysis and P_i release in the two halves of the complex. The branching ratio for following p/s branches is k_ATP(p)/k_ET(s) = 62/37 ∼ 1.7/1 in favor of p-branch ATP hydrolysis and P_i release, over secondary ET and traversal of the s branch. The partitioning between branches with one and two electrons transferred, p and s branches, respectively, corresponds to (1.7/(1.7+1)) ∼ 63% of the complexes following the p branch, ∼37% following the s. To quantify the energetics of negative cooperativity associated with suppression of the second ET event, we may define a free energy of negative cooperativity, ΔG_neg, induced by the initial ET step in terms of the ratio of the secondary to primary ET rate constants,

$$\mathrm{\Delta }{\text{G}}_{\text{neg}}=-\mathrm{RT}\hspace{0.17em}\ln \left(k_{ET}\left(\mathit{s}\right)/k_{ET}\left(p\right)\right)=-\mathrm{RT}\hspace{0.17em}\ln \left(\mathrm{37}/\mathrm{267}\right)\mathrm{\sim }+1.2\hspace{0.17em}\text{kcal}/\text{mol}.$$ [2]

Although Scheme C clearly captures the key negative cooperativity displayed by the electron-delivery process, it is perhaps worth emphasizing that each branch of the kinetic Scheme C contains a major simplification. On the p branch of the scheme, it is the assumption that once hydrolysis has occurred in the p half of the complex, electron delivery within the s half of the complex is completely suppressed and the p half of the complex proceeds to release 2P_i followed by dissociation of the Fe^ox(ADP)₂, with subsequent reassociation of a Fe^red(ATP)₂ to reinitiate the process. The p branch thus exhibits the limiting behavior: half-sites reactivity.

However, if tier 1 ET does occur in the second half of the complex, generating a symmetrical MoFe protein in which both FeMo-co have been reduced, this follows the s branch of the scheme, whose major simplification is the assumption that the two halves of the complex progress together synchronously through their Fe protein cycles. ATP is synchronously hydrolyzed in both halves of the complex, again with a lower rate constant for this step than in the p branch. Likewise, on this branch the release of P_i and dissociation of Fe^ox(ADP)₂ occur synchronously in the two halves, and do so with rate constants that both differ from those in the p branch and from the observed rate constant.

Unlike both the independent-sites and limiting half-sites models, the global fit to the negative cooperativity model, with rate parameters listed on Scheme C, reproduces the measurements of ATP hydrolysis extremely well (Fig. 5). The number of ATP hydrolyzed before steady state is a weighted average of that number in the two branches: two ATP/MoFe protein for the p branch and four for p + s. The weights are determined by the branching ratio derived within this model. This ratio, in fact, is governed by the extent of ATP hydrolysis before steady state. With the fit value of 63% of the complexes following the p branch, 37% the s branch, as calculated above, then according to the model ∼2.7 ATP/MoFe protein are hydrolyzed during the presteady-state phase. This analysis highlights the excellent consistency of the global fit with experiment, as follows. Not only does the progress curve for ADP formation calculated with Scheme C correspond well with that observed (Fig. 5), but also the hydrolysis of ∼2.7 ATP/MoFe protein would result from ET by 1.35 Fe^red(ATP)₂, which in fact corresponds to the number calculated for the presteady-state SF measurement of ET (Fig. 3).

Although the release of Fe^ox(ADP)₂ is incorporated in Scheme C of Fig. 4, experimental observations of this process could not be included in our global fit because dissociation cannot be measured during turnover; Fe^ox(ADP)₂ undergoes “recharging” to Fe^red(ATP)₂ during the turnover experiment, and thus does not accumulate during turnover. However, the slope of the linear, steady-state ATP hydrolysis is controlled by and defines the Fe^ox(ADP)₂ release rate. The Scheme C fitting process yielded a rate constant of 13 s⁻¹ for the release of one Fe^ox(ADP)₂ in the p branch. Statistically, the rate constant for release of two Fe^ox(ADP)₂ in the s branch is poorly defined, but the slope in the heuristic fit corresponds to the weighted average of these constants for Fe^ox(ADP)₂ and the slope in that fit, ∼11 s⁻¹, indicates that release in the s branch is indeed the slowest process in the Fe protein cycle.

From the excellent ability of the Scheme C model to reproduce experimental results, it is clear that, despite its simplifications, the model in fact captures the essence of the negative cooperativity manifested in the ATP hydrolysis progress curves, whereas any model with a “finer-grained” treatment would introduce an untreatable number of highly correlated parameters as noted above. The three rate constants derived from the phenomenological fits to the kinetic progress curves for ET, ATP hydrolysis, and P_i release are revealed to be weighted composites of the differing rate constants associated with the two branches.

One incidental outcome of the application of Scheme C is a correlation between the observed absorbance changes at 430 nm upon ET from Fe^red to FeMo-co and the extent of ET, which yields a value for the change in extinction coefficient associated with oxidation of Fe^red. In Fig. 3, the left ordinate is the observed absorbance change at 430 nm as measured during ET in the SF experiment, and the right ordinate is the stoichiometric value for the number of Fe proteins oxidized as calculated from the rate constants obtained in the global fit to Scheme C. Correlation of the two scales yields an estimate for the total change in extinction coefficient for that Fe protein at 430 nm of Δε = 3,700 M⁻¹⋅cm⁻¹.

Mechanism to Impose Negative Cooperativity.

For ET in one-half of the [MoFe(Fe^red(ATP)₂)₂] complex to suppress ET in the other half, which is manifested as negative cooperativity, demands conformational changes whose influences are felt across the protein complex, over 135 Å (Fig. 1). A mechanism for how the two halves of nitrogenase might communicate is suggested from a coarse-grained modeling of large-amplitude vibrational motions of the protein complex. A covariance analysis of the displacement of amino acid residues reveals a cross-correlation between the motion of the two Fe proteins (Fig. 7), suggesting that the motion of one of the two Fe proteins causes a response at the other spatially distant Fe protein, and vice versa. The observed correlation holds for the complexes with Fe(ATP)₂, Fe(ADP)₂, and the mixed ATP/ADP complex. The vibrational normal mode contributing most to such correlation (SI Appendix, Fig. S6) shows highest overlap with the conformational change from the ATP-bound Fe protein to the ADP-bound structures of nitrogenase (SI Appendix, Fig. S7). This normal mode corresponds to an out-of-phase rocking motion of the Fe proteins on the surface of the MoFe protein. When the Fe protein in one site (Fe₁, Fig. 7B) moves toward the location of the ADP-bound Fe protein, the other Fe protein moves in the opposite direction, toward the location (Fe₂, Fig. 7B) of ATP-bound Fe protein, on the opposing end of the MoFe protein. Such a model is consistent with a rolling of an Fe protein across the MoFe protein surface, as suggested from X-ray structures of nitrogenase complexes trapped in different nucleotide states (10). Relevant to this study is the earlier report that the maturation of the P clusters within the MoFe protein seems to occur in a stepwise fashion, with one side maturing before the other (36). This could be another manifestation of properties of one-half of the MoFe protein being modulated by events on the other half.

Fig. 7.

Correlated movement of the two Fe proteins. (A) Covariance matrix (in square angstroms) showing the correlation between the displacement of amino acid residues in ATP-bound Fe protein nitrogenase complex. For sake of clarity, the matrix is divided into quadrants corresponding to the various possible subunit pairs (see Fig. 1). Regions of correlated (in-phase) and anticorrelated (out-of-phase) motions are shown in red and blue, respectively. The regions of cross-correlation between the two Fe proteins (upper right corner) are highlighted with dotted boxes. (B) Collective motion corresponding to the rocking motion of the Fe protein on the MoFe protein surface is depicted. The position of the Fe proteins (green) in the ADP-bound structure (PDB ID code 2AFI) is shown using a faded cartoon representation. The length of the arrows is proportional to the displacement of the amino acid residues obtained through coarse-grained normal mode analysis.

Conclusions

The present work establishes that the Fe protein cycle within the physiologically relevant, homologous [MoFe(Fe(ATP)₂)₂] ternary complex is indeed “complex,” as recently concluded by Clarke et al. for a heterologous complex (22). The two-branch, negative-cooperativity kinetic scheme (Fig. 4, Scheme C) assumes that the ET event within one functional half of the symmetrical dimer induces conformational changes that allow ATP hydrolysis and subsequent steps in this primary, p, half of the complex, while allosterically suppressing, but not eliminating, ET to FeMo-co in the other (secondary, s) half. The global fit of this kinetic model to the presteady-state progress curves for ET, ATP hydrolysis, and P_i release provides an excellent description of all three measurements while capturing the “half-sites” behavior in the RFQ measurements of FeMo-co reduction (22, 28, 29) reproduced in the present experiments.

The analysis presented above emphasizes that this two-branch scheme is highly simplified, and it is unlikely to be unique, although other simplified variants we explored gave distinctly poorer descriptions. Nonetheless, its ability to globally and quantitatively describe the multistep kinetics of electron delivery within the ternary complex suggests that the Fig. 4, Scheme C model indeed captures the essential elements of negative cooperativity in ET, ATP hydrolysis, and P_i release observed in the presteady state for nitrogenase.

As a measure of the energetics of negative cooperativity, we have defined a free energy of negative cooperativity induced by the tier 1 primary ET step through the ratio of the secondary to primary ET rate constants: ΔG_neg = −RT ln(k_ET(s)/k_ET(p)) ∼ +1.2 kcal/mol. Considering that MoFe is a protein of ∼245,000 Da, the small magnitude of ΔG_neg implies a remarkably subtle allosteric coupling between the two halves of the enzyme. A possible mechanism for this negative allosteric control is suggested by a normal mode analysis of MoFe protein showing correlated motions between the two MoFe protein αβ halves.

The utility of negative cooperativity in the nitrogenase mechanism is not obvious, just as, to our knowledge, there are no cases of substantiated advantages of this phenomenon in other enzymes (32–34, 37). That said, it can be imagined that when the events on one side are communicated to the other side, this may facilitate conformational changes that contribute to unidirectional electron flow from the Fe protein to the FeMo-co, or that favor the dissociation of the discharged Fe protein.

Materials and Methods

Materials, Buffers, Protein Purification, and Activity Assays.

All reagents, unless stated otherwise, were purchased from Sigma-Aldrich. [α-³²P]ATP radionucleotide was purchased from PerkinElmer. Nitrogenase proteins were expressed and purified from A. vinelandii strains DJ995 (wild-type MoFe protein with His tag) and DJ884 (wild-type Fe protein) as described previously (38). Septum-sealed vials, degassed and under an argon atmosphere, were used for all manipulation of proteins. Gas-tight syringes were used to transfer all gases and liquids. The purity, metal content, and specific activity of the two nitrogenase proteins were consistent with fully active proteins. Proton, acetylene, and N₂ reduction specific activities were determined at 30 °C as reported.

Quench-Flow Studies for ATP Hydrolysis.

Presteady-state ATP hydrolysis (ATPase) assays were conducted at 25 °C on a rapid chemical quench-flow instrument (KinTek Corp.) housed in a nitrogen-filled glove box (<5 ppm O₂) as described previously (11). ATPase experiments were carried out in buffer containing 50 mM Mops buffer, pH 7.4, with 10 mM sodium dithionite. An 18-μL volume of 20 μM MoFe protein and 80 μM Fe protein in syringe A was mixed with an 18-μL volume of ATP (0.5, 1, 2, 4, or 6 mM), 8 mM MgCl₂ containing 1.5 μCi [α-³²P]ATP in syringe B, followed by varying aging times from 0 to 0.5 s. Reactions were rapidly quenched by addition of 45 μL of 0.7 N formic acid added from syringe C. Aliquots (0.9 μL) of the quenched reactions were spotted onto a TLC plate (EMD Chemicals) and developed in 0.6 M potassium phosphate buffer, pH 3.4, for 70 min, air-dried, and exposed overnight to a phosphorimaging screen. The [α-³²P]ATP and the [α-³²P]ADP were quantified with a Storm PhosphorImager (Molecular Dynamics) with ImageQuant software (Molecular Dynamics) (11).

SF ET Measurements.

Primary ET from the Fe protein to the MoFe protein was measured at 25 °C using SF spectrophotometry. All mixtures were prepared in 100 mM Mops, pH 7.4, and were kept under an argon atmosphere. One syringe contained 80 µM Fe protein, 20 µM MoFe protein, and 10 mM DT. The other syringe was loaded with 10 mM DT and 20 mM MgATP. As turnover occurred in the [Fe^red(MgATP)₂-MoFe] complex, the oxidation of the [4Fe-4S] cluster of the Fe protein was monitored by an increase in absorbance at 430 nm. Data were fit to a single exponential curve.

RFQ EPR ET Measurements.

Anaerobic enzyme and substrate solutions were loaded into sample loops of an Update RFQ Instrument in a Coy glove box containing an atmosphere of N₂ with 5% H₂. The RFQ samples were prepared by rapidly mixing a 210-µL volume of a solution of 200 µM MoFe protein and 800 µM Fe protein with a 210-µL solution containing 50 mM ATP, 58 mM MgCl₂, 78 mM phosphocreatine, 0.2 mg/mL creatine phosphokinase, 1.3 mg/mL BSA, and 50 mM sodium dithionite. Both solutions were prepared in 200 mM Mops buffer at pH 7.4. After rapid mixing and passage through a calibrated delay line at 22 °C, samples were collected by rapid freezing on counter rotating copper wheels at liquid N₂ temperature. Teflon scrapers were positioned to remove the frozen solution from the wheels, and the resulting powder was collected in liquid nitrogen and packed into X-band EPR tubes. Control samples were collected by rapidly mixing the MoFe- and Fe-protein solution with 200 mM Mops buffer containing 50 mM sodium dithionite, at pH 7.4.

The MoFe and Fe proteins are isolated in buffers containing ∼350 mM NaCl and 500 mM NaCl, respectively. This results in significant concentrations of NaCl being carried over into the EPR samples with a final concentration of ∼200 mM NaCl in the RFQ-EPR samples. Because nitrogenase has been shown to be inhibited by high concentrations of NaCl (30), we buffer-exchanged the MoFe protein into 50 mM Mops buffer at pH 7.4 containing 150 mM NaCl and exchanged the Fe protein into 50 mM Mops buffer at pH 7.4 containing 50 mM NaCl. This resulted in a final concentration of ∼27 mM NaCl in the RFQ samples.

The X-band EPR spectra of each sample were collected at 4 K and 0.5-mW microwave power on an ESP 300 Bruker spectrometer equipped with an Oxford ESR 900 cryostat. The reduction of the S = 3/2 FeMo-co resting state was quantified by comparing the amplitude of 1a EPR signal at g₂ = 3.66 to the amplitude of the RFQ control samples prepared in the absence of MgATP.

P_i Release Kinetics.

The time course of phosphate release was determined in an SF instrument (Auto SF-120; Kintek Corp.) using the coumarin (N-[2-(1-maleimidyl)ethyl]-7-(diethylamino) coumarin-3-carboxamide) (MDCC) labeled phosphate binding protein assay, as described. Before each experiment, the SF syringes and flow lines were treated with a P_i -MOP [SF buffer with 300 µM 7-methylguanine and 0.2 units/mL purine nucleoside phosphorylase] for 15 min to remove contaminating P_i and then were rinsed with SF buffer (11). Two-micromolar MoFe protein and 8 µM Fe protein were rapidly mixed with a solution of 10 µM MDCC-PBP, 20 mM MgCl₂, and 3 mM ATP and the change in fluorescence was monitored over time. A control time course, conducted without nitrogenase, was used to correct for the presence of contaminating phosphate. MDCC-PBP fluorescence enhancement was converted to [P_i] after calibration in the SF using [NaH₂PO₄] standards as described (11). Data were fit as described below.

Phenomenological Fitting of Data.

The quenched-flow ATP hydrolysis data were fit using a phenomenological description that incorporated an exponential rise phase plus a linear steady-state phase:

$$\left[\text{ADP}\right]=A\left(1-{\mathrm{e}}^{-\mathit{kt}}\right)+Vt,$$ [3]

where A and k are the presteady-state amplitude and rate constant, respectively, V is the velocity of the linear phase, and t is reaction time.

Global Fitting of Data.

Global fits of ATP hydrolysis, P_i release, and ET kinetic traces to half sites or negative cooperativity models were conducted using numerical integration in MATLAB with the built-in function lsqcurvefit (SI Appendix, Methods). The numerical integrations used the MATLAB ode45 solver, which uses the explicit Runge−Kutta (4, 5) formula, Dormand−Prince pair (39). The 95% confidence intervals for the kinetic parameters were calculated with the built-in nlparci function in MATLAB and are presented along with the parameters.

Normal Mode Analysis.

To characterize the mechanical aspects of the long time-scale dynamics of the nitrogenase complex, a normal mode vibrational analysis based on the anisotropic Gaussian network model was performed (40, 41), where the nitrogenase complex was represented by beads centered at the position of the alpha carbons. The details of these calculations are provided elsewhere (42). The presence of the various cofactors (iron/sulfur clusters, nucleosides, and homocitrate) was considered by adding extra beads as follows. (i) For the cubane of the Fe protein and the P-cluster, a bead was placed at the geometric center of each cluster. (ii) For the FeMo-co two beads were added: one at the center of the Fe1, Fe2, Fe3, and Fe4 tetrahedron and the other at the center of the Fe5, Fe6, Fe7, and Mo tetrahedron. (iii) The homocitrate was described by a bead at its geometric center. (iv) ATP and ADP were modeled with three beads located at the center of the adenine ring, the ribose ring and the phosphate groups. The dynamical properties of the nitrogenase complex with and without these cofactors (i.e., with and without these extra beads) as quantified by the covariance analysis are very similar. Different choices of the location of the beads also gave consistent results. The calculations were performed on the crystal structure of the complex between the Fe protein and the MoFe protein from A. vinelandii with an ATP analog and ADP bound to the Fe protein [Protein Data Bank (PDB) ID codes 2AFK and 2AFI, respectively] (8, 10). As previously discussed (42), the model is able to reproduce faithfully the relative magnitude of the experimental X-ray beta factors, creating confidence that the approach is able to describe the overall large amplitude motions of the nitrogenase complex.