Significance
Our measurements have shown that the face-centered cubic (δ)-phase of plutonium exhibits little or no volume change but softens drastically as temperature rises over a very broad range. This behavior constrains any microscopic theory of plutonium to require that more than one thermodynamically accessible configuration exists, that the higher energy one has a smaller volume, and contrary to most models, the higher energy, smaller volume configuration must be more compressible. Until the recent neutron-scattering discovery of dynamic magnetism in plutonium, no evidence for such configurations existed. With that discovery, we are able to justify our microscopic theory that captures the observed neutron-scattering and temperature behavior of δ-plutonium.
Keywords: δ plutonium, elastic moduli, thermal expansion, DFT
Abstract
The electronic and thermodynamic complexity of plutonium has resisted a fundamental understanding for this important elemental metal. A critical test of any theory is the unusual softening of the bulk modulus with increasing temperature, a result that is counterintuitive because no or very little change in the atomic volume is observed upon heating. This unexpected behavior has in the past been attributed to competing but never-observed electronic states with different bonding properties similar to the scenario with magnetic states in Invar alloys. Using the recent observation of plutonium dynamic magnetism, we construct a theory for plutonium that agrees with relevant measurements by using density-functional-theory (DFT) calculations with no free parameters to compute the effect of longitudinal spin fluctuations on the temperature dependence of the bulk moduli in δ-Pu. We show that the softening with temperature can be understood in terms of a continuous distribution of thermally activated spin fluctuations.
The plutonium δ-phase (face-centered cubic, fcc), depending on gallium concentration, can on heating expand (above ∼2 at % Ga), contract (less than ∼2 at % Ga), or maintain volume independent of temperature from approximately 500 to 800 K (∼2 at % Ga) (1). Reminiscent of the Invar effect (2, 3), Lawson et al. (1) made the critically important observation that this could be modeled by assuming that two configurations were thermodynamically accessible in δ-Pu. This assumption introduces a strong constraint on a microscopic theory. Separated by 1,400 K, the higher energy configuration is assumed to have smaller volume than the lower energy one. Thus, as temperature rises, the Boltzmann factor increases the occupied fraction of the higher energy state, compensating for ordinary thermal expansion effects. This model could be made to fit δ-Pu’s volume versus temperature dependence as measured by elastic neutron scattering for the range of Ga concentrations typically used to stabilize the δ-phase (4). However, measurements of the elastic moduli of polycrystalline Pu–Ga alloys by Suzuki et al. (5) showed that the bulk modulus softened substantially on warming in temperature regions where the atomic volume remained fixed. In an attempt to include elastic softening as temperature increased and volume decreased, Lawson et al. (1) made the unusual conjecture that the higher energy state with smaller volume, required to get the thermal expansion correct, must make no contribution to the bulk modulus. The usual situation is that a higher energy state with lower volume is stiffer, not softer as required here. Although the multiple-configuration assumption is now strongly supported by recent measurements (6), the yet-unexplained anomalous behavior (softening on warming with no volume change) remains a critical missing component of a fundamental understanding of δ-Pu.
The detailed issue then is that the bulk and shear moduli of δ-Pu soften with temperature at a rate an order of magnitude greater than other metals with similar melting points and exhibit the extremely unusual property that the rate is insensitive to whether δ-Pu–Ga expands or contracts when heated. This makes the 12-parameter fit of Lawson et al. (1), and their analysis revealing a possible electronics-based free-energy driver for softening on heating, difficult to justify on fundamental grounds. Nevertheless, density and elasticity measurements point toward δ-Pu, pure or alloyed with Ga, being a mixture of at least two electronic configurations that are both thermally accessible below the melting point. A consequence of this realization is that no single-configuration electronic-structure model has succeeded or even can succeed in accounting for either large changes in the bulk modulus with temperature or the negative thermal expansion. In the superconductor PuCoGa5, measurements have shown that multiple plutonium valence configurations lead to unusual elastic softening (7). Earlier inelastic neutron-scattering measurements by Trouw et al. (8), confirmed by the statistically improved recent neutron-scattering measurements by Janoschek et al. (6), reveal that multiple electronic configurations are present in δ-Pu that are also thermally accessible with the higher energy state approximately 1,400 K above the ground state.
The primary neutron-scattering experimental result is the clear presence of dynamic magnetism (magnetic spin fluctuations) centered around one or perhaps two energies. The measurements were performed on a heavily Ga-stabilized δ-242Pu sample, thus its thermal expansion coefficient was the normal positive one and hence the qualitative behavior of the volume and moduli with temperature is expected to be ordinary. However, the microscopic properties of the components of the admixture proposed by the dynamical mean-field theory (DMFT) results are not presented (6), only the fact that an admixture exists. Our motivation is to provide a microscopic theory that yields multiple configurations where higher energy ones are both smaller in volume and softer elastically, and that agrees with the small-Q magnetic form factor.
Experimental Method
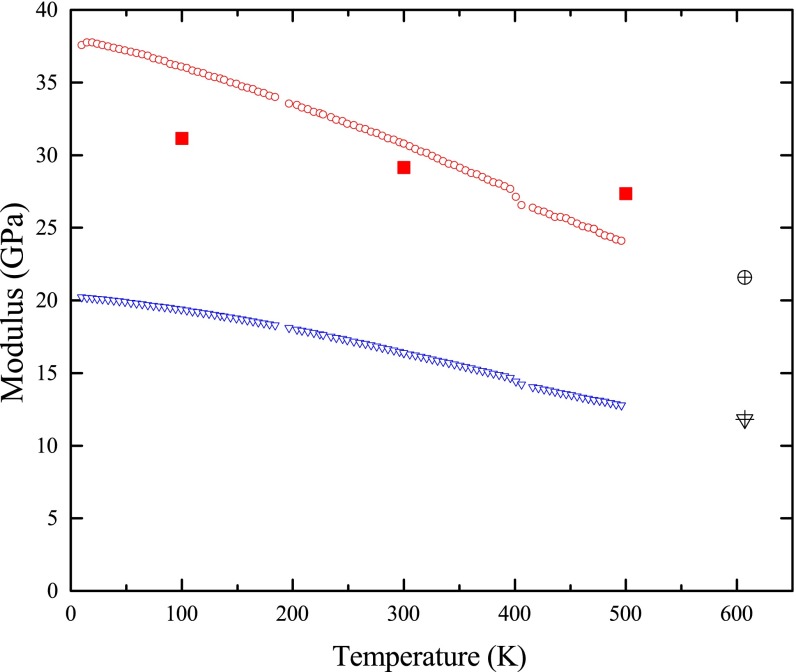
Most of the elastic moduli measurements shown in Fig. 1 were made on Pu-2.36 at % Ga electrorefined alloy carefully homogenized, and one measurement on a Pu-0.2 at % Ga alloy that exhibited all of the phase transformations of pure Pu. The linear coefficient of thermal expansion for the Pu-2.36 at % Ga (1) is less than −1.6 × 10−6⋅K−1, approximately one order of magnitude lower than, say, copper. Resonant ultrasound spectroscopy was used to extract the elastic moduli. This technique (9) measures the mechanical resonance frequencies to determine the complete elastic tensor. The rectangular parallelepiped specimens used for the temperature dependence were 0.1311 g, 0.1995 × 0.2045 × 0.2078 cm3 with geometrically determined density of 15.466 g/cm3 at 295 K, and 1.3396 g, 0.4746 × 0.3768 × 0.4843 cm3 with geometric density of 15.467 g/cm3 at 295 K. The absolute error in the determination of bulk modulus B and shear modulus G was ∼0.3%. The errors were primarily caused by errors in the geometry, thus the precision of the measured temperature dependence is substantially greater than the accuracy. The specimen was not annealed after cutting and polishing, leaving traces of strain-induced surface α−plutonium that are the cause of the slight jump at the α−β transition. Also shown is a single measurement made at 607 K on the Pu 0.2 at % Ga, the Ga to stabilize against cracks on cooling from the melt. We found to within 5% that B = 20.6 GPa, and within 1% G = 11.8 GPa. This is to be compared with the value (extrapolated linearly from 550 K) of the specimen used for the solid curves of B = 22 GPa and G = 12 GPa. We conclude that the bulk and shear modulus of pure and Ga-stabilized δ-plutonium are the same at temperatures where they coexist. This is important because the theoretical results presented here are for pure plutonium.
Fig. 1.
Measured bulk modulus plotted as open circles, shear as open triangles for Pu 2.36 at % Ga δ-phase alloy measured in ref. 3. Solid squares, DFT theory computation of B from the results of the calculation plotted in Fig. 4. Crossed triangles and circles, Pu 0.2 at % Ga (essentially pure plutonium), clearly located at the extrapolation to above 550 K of the corresponding Ga stabilized specimen results of ref. 5.
Theoretical Model
In a previous δ-Pu model (1), two energy states are assumed to exist that have significantly different atomic volumes. For Invar this assumption is valid because there do exist two states, namely low and high magnetic spin states. For Pu, however, the two states used in the accompanying DMFT calculation were invoked without magnetism (1) and with very different atomic volumes (21 Å3 and 25 Å3). Experimentally, however, δ-Pu has never been seen to exist at volumes even close to 21 Å3. In fact, it was shown (10) that compression of gallium-stabilized δ-Pu has a strongly destabilizing effect that helps decompose the δ-Pu–Ga into α-Pu and Pu3Ga. At 21 Å3 one would therefore not expect δ-Pu–Ga to prevail at all. Another problem with the previous model (1) is that as the lower volume state is excited with rising temperature, the bulk modulus stiffens, opposite to the experimental finding.
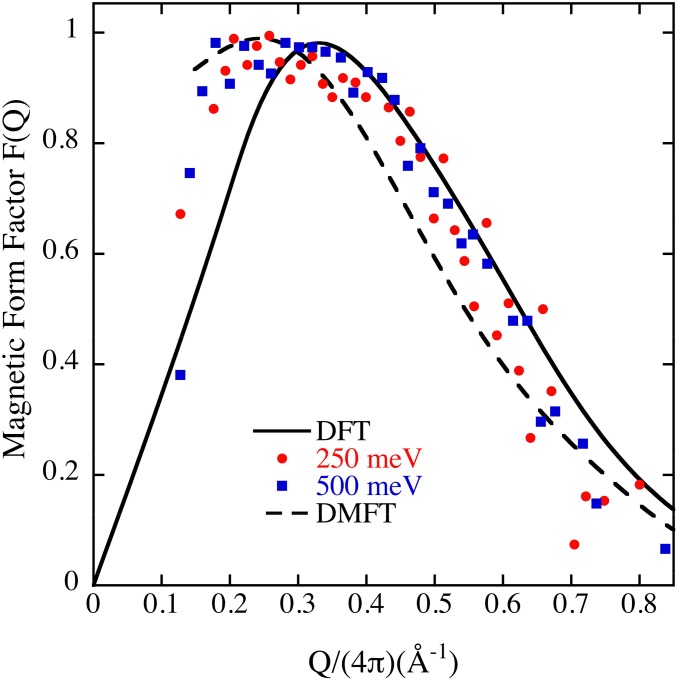
Now we return to the original idea to connect the δ-plutonium Invar effect and the anomalous temperature behavior of the elastic moduli to magnetism. Previous measurements, for example Lashley et al. (11), claim with certainty that there is no magnetism in δ-plutonium. This has been disproved by Janoschek et al. (6). The situation is more complex than in Invar but it appears that the magnetic moments, which are very well described by theory in terms of the magnetic form factor (12) (and Fig. 2), are fluctuating. If this is the case, excitation of magnetic moments through spin fluctuations is a plausible mechanism for the aforementioned anomalies in δ-plutonium. To explore this hypothesis, we follow the recipe described recently for longitudinal spin fluctuations (13).
Fig. 2.
DFT (full line), neutron spectroscopy (solid symbols) (6), and DMFT (dashed line) (6) magnetic form factor for δ-plutonium. Reprinted from ref. 12.
It has been argued that in the static limit, the magnetic moments are disordered in δ-Pu with no long-range order (14). At finite temperatures, however, the magnetic moments may fluctuate around a mean value that can be estimated from DFT calculations. These magnetic moments populate a continuous probability distribution that is statistically weighted by the Boltzmann factor and is, in this regard, a generalization of the two-state model (1), and is suggested by the width of the neutron-scattering results (6). In practice we perform calculations within the so-called disordered-local moment (DLM) model that has been used and described for δ-Pu before (15). This model describes a situation where the magnetic moments are randomly distributed spatially and thus represent a snapshot of a spin-fluctuation system, and we invoke the ergodic hypothesis. That is, there is equivalence between spatial averages at a single instant (snapshot) and time averages as long as each configuration is thermodynamically accessible and equally probable. Thus, no net static magnetic moment exists.
For computational details of this method and the calculations, see Landa et al. (14). The new aspect in regard to the present spin-fluctuation theory is to compute the energy dependence of the magnitude of the fluctuating spin moments. This corresponds to longitudinal spin fluctuations in the material. Because spin–orbit and orbital–orbital interactions are important within the band-theoretical approach for plutonium (16) and they are not yet implemented in the DLM model, we have opted to compute the energies from a ferromagnetic (FM) configuration. The computational aspects of the FM calculations were detailed earlier by Söderlind (16) and therefore not repeated here.
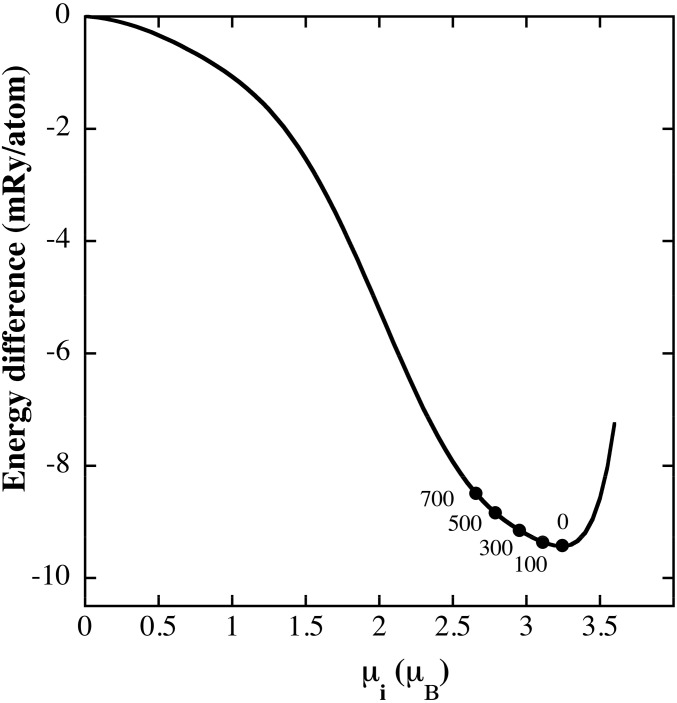
In a complete model for spin fluctuations one considers the spin’s ability to rotate relative to each other as well as changing their magnitude. This model can in principle be constructed but cannot be efficiently solved when coupled to first-principles theory for plutonium. In a case where there is no long-range magnetic order, transverse (rotating) spin fluctuations are expected to be much less important than longitudinal fluctuations because there is no cumulative effect of the former. Indeed, this is the likely scenario for plutonium and we therefore focus on the latter longitudinal type here. The longitudinal thermal spin-fluctuation model for the DLM state (13) begins with calculating the total energy as a function of spin magnitude at the theoretical DLM equilibrium atomic volume (25.15 Å3) (14). Using the fixed-spin-moment method (17) we obtain the total energy as a function of magnetic spin-moment magnitude (μi) ranging from 0 μB to 3.6 μB in steps of 0.2 μB (i = 19). The energy minimum is located around 3.2 μB (Fig. 3), but through thermal excitation other moments are statistically populated (pi) according to their Boltzmann factor:
Here Z is the normalizing factor
Ei, kB, and T are the excitation energy (taken from Fig. 3), the Boltzmann constant, and temperature, respectively. From the probabilities, pi, we define the magnitude of a quadratic mean magnetic moment that depends on the temperature
This definition of a quadratic mean moment was shown to give better results than ref. 13, an arithmetic mean value (m is a sum of all μipi). In our case, the difference between the two definitions is small and always less than 4% for any temperature.
Fig. 3.
Calculated energy [milli-Rydbergs per atom (mRy/atom)] as a function of fixed spin moment (μi). Mean magnetic moments, m, are shown as solid circles with the associated temperature in K.
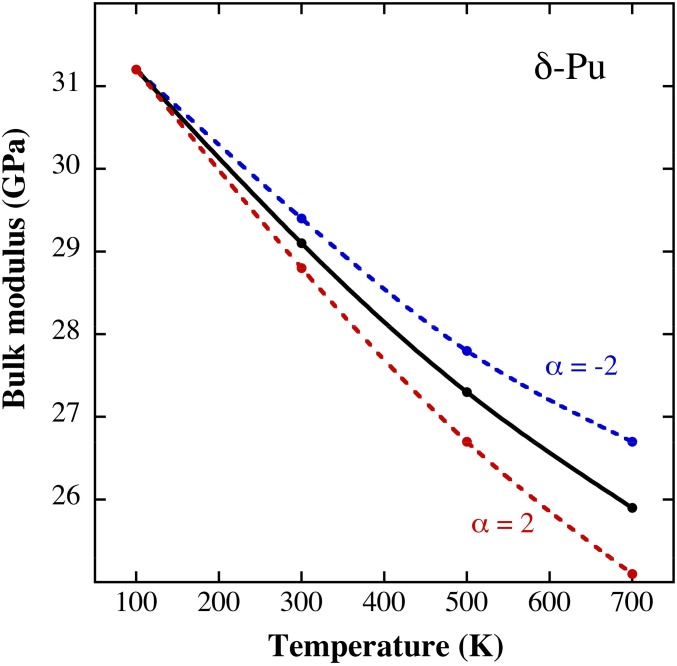
Next, we calculate the bulk modulus B(T) at 25.15 Å3 within the DLM method and with the spin moment constrained to the quadratic mean magnetic moment, m(T). Evaluation of B at a fixed 25.15 Å3 is supported by measurements, which show that there is almost no thermal expansion. This is a constraint that is unusual, validated by measurements, and essential to the final result. The results from these calculations are shown in Fig. 4 and at selected temperatures in Fig. 1. Here we also analyze the influence of a small positive and negative thermal expansion (linear coefficient α = ±2 × 10−6⋅K−1). Notice first that B softens with temperature quite significantly and reproduces the anomalous behavior seen experimentally in Fig. 1. Second, small changes in the thermal expansion do not change this conclusion, again in quantitative agreement with measurements (18).
Fig. 4.
Calculated (solid black) temperature dependence of the bulk modulus (gigapascal) for δ-Pu. The curves denoted “α = ±2” represent calculations assuming a constant linear coefficient of thermal expansion of ±2 × 10−6⋅K−1.
The understanding of the softening of the bulk modulus in the model is found in the energy function shown in Fig. 3. Because the shape of this function is asymmetric around the energy minimum, with a tilt toward smaller magnetic moments, the magnitude of the mean fluctuating spin moment will decrease with temperature as shown in Fig. 3. A gradual loss of magnetism tends to increase the chemical bonding that in a normal metal leads to densification. In contrast, for δ-Pu no (or little) densification actually occurs on warming as determined by measurements. Hence, the inability of a fluctuating moment to change the volume dynamically and locally in fact leads to a negative random strain that, in the usual way, reduces the bulk modulus.
Because both the energy as a function of magnetic moment as well as the temperature dependence of the moment are available from our model, it is possible to straightforwardly calculate the temperature dependence of the magnetic susceptibility. One has to remember that δ-Pu is rather unusual in that the orbital contribution to magnetism is important and that the orbital moment is antiparallel to the spin moment and thus significantly reduces the magnetic susceptibility. Accounting for both spin and orbital components, but excluding difficult-to-model possible effects of radiation damage and alloying, and using the model presented here we find a weakly temperature-dependent susceptibility (increasing ∼15% on decreasing temperature from 600 to 200 K) in qualitative agreement with experiment where the susceptibility increases monotonically a few percent from 600 to 300 K (19) and approximately an additional monotonic increase of 10% from 300 to approximately 50 K (20). However, the two measurements are ∼12% different in absolute value at 300 K, but if scaled by that amount, produce a smooth featureless curve from 50 to 600 K.
Summary
The elastic behavior of plutonium is unexpected because there is a very significant softening of both shear and bulk moduli with increasing temperature in the δ-phase whereas there is little or no volume change. A previous model made the important assumption of two configurations that captured this nonintuitive behavior with an approach used successfully for the Invar alloys but where the two configurations are not of magnetic nature but rather identified by DMFT calculations. Another approach suggested by Eriksson et al. (21) for δ-Pu also provides for multiple states with no magnetic involvement.
We argue that the recent observation of dynamic magnetism in (fcc) δ-plutonium leads to a theory closer to the original magnetic models for the Invar alloys and that agrees with relevant measurements. Here, the theory considers longitudinal spin fluctuations where the spin’s magnitude varies statistically and continuously as determined by a continuum of Boltzmann factors. The approach is founded on DFT electronic-structure calculations and is entirely free of adjustable parameters. Because the magnitude of the spin fluctuations is predicted to decrease with increasing temperature, and despite the measured atomic volume remaining fixed (no thermal expansion), the bulk modulus softens significantly with increasing temperature. This result is in good agreement with measurements.
Acknowledgments
We thank B. Sadigh for helpful discussions, and the Los Alamos Science Campaigns and Laboratory Directed Research and Development. This work was supported as part of the Materials Science of Actinides, an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences under Award DE-SC0001089. The detailed calculations were performed under the auspices of the US DOE by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Lawson AC, et al. Invar model for δ-phase Pu: Thermal expansion, elastic and magnetic properties. Philos Mag. 2006;86(17-18):2713–2733. [Google Scholar]
- 2.Weiss R. The origin of the Invar effect. Proc Phys Soc. 1963;82(2):281–287. [Google Scholar]
- 3.Lawson AC, Roberts JA, Martinez B, Richardson JW. Invar effect in Pu-Ga alloys. Philos Mag. 2002;82(18):1837–1845. [Google Scholar]
- 4.Lawson A, et al. Electron Correlations and Materials Properties. Springer; New York: 1999. Lattice effects in the light actinides; pp. 75–96. [Google Scholar]
- 5.Suzuki Y, et al. Temperature dependence of elastic moduli of polycrystalline β plutonium. Phys Rev B. 2011;84(6):0641051. [Google Scholar]
- 6.Janoschek M, et al. The valence-fluctuating ground state of plutonium. Sci Adv. 2015;1(6):e1500188. doi: 10.1126/sciadv.1500188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ramshaw BJ, et al. Avoided valence transition in a plutonium superconductor. Proc Natl Acad Sci USA. 2015;112(11):3285–3289. doi: 10.1073/pnas.1421174112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Trouw F, Rhyne JJ, Mitchell JN. Pu neutron scattering studies - Magnetism and structure. J Nucl Mater. 2009;385(1):35–37. [Google Scholar]
- 9.Migliori A, et al. Resonant ultrasound spectroscopic techniques for measurement of the elastic-moduli of solids. Physica B. 1993;183(1-2):1–24. [Google Scholar]
- 10.Hecker SS, Timofeeva LF. A tale of two diagrams. Los Alamos Sci. 2000;26(2):244–251. [Google Scholar]
- 11.Lashley J, Lawson A, McQueeney R, Lander G. Absence of magnetic moments in plutonium. Phys Rev B. 2005;72(5):054416. [Google Scholar]
- 12.Söderlind P, Zhou F, Landa A, Klepeis JE. Phonon and magnetic structure in δ-plutonium from density-functional theory. Sci Rep. 2015;5:15958. doi: 10.1038/srep15958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dong ZH, et al. Thermal spin fluctuation effect on the elastic constants of paramagnetic Fe from first principles. Phys Rev B. 2015;92(22):224420. [Google Scholar]
- 14.Landa A, Söderlind P, Ruban A. Monte Carlo simulations of the stability of δ-Pu. J Phys Condens Matter. 2003;15(24):L371–L376. [Google Scholar]
- 15.Niklasson AM, et al. Modeling the actinides with disordered local moments. Phys Rev B. 2003;67(23):235105. [Google Scholar]
- 16.Söderlind P. Quantifying the importance of orbital over spin correlations in δ−Pu within density-functional theory. Phys Rev B. 2008;77(8):085101. [Google Scholar]
- 17.Schwarz K, Mohn P. Itinerant metamagnetism in Yco2. J Phys F Met Phys. 1984;14(7):L129–L134. [Google Scholar]
- 18.Migliori A, et al. Thermodynamics and the elastic moduli of Pu. J Supercond. 2002;15(5):499–503. [Google Scholar]
- 19.Méot-Reymond S, Fournier J. Localization of 5f electrons in δ-plutonium: Evidence for the Kondo effect. J Alloys Compd. 1996;232(1):119–125. [Google Scholar]
- 20.Wirth BD, et al. Fundamental studies of plutonium aging. MRS Bull. 2001;26(09):679–683. [Google Scholar]
- 21.Eriksson O, Becker J, Balatsky A, Wills J. 1999. Novel electronic configuration in δ−Pu. J Alloys Compd., 287:1–5.