Visualization of the spontaneous emergence of a complex, dynamic, and autocatalytic system

Significance

Chemical reproduction is central to biology, and understanding how chemical systems may give rise to complex systems that form self-reproducing cell-like structures is a leading goal for scientists. Here we use an ultrasensitive optical microscopy technique to directly monitor the formation and dynamics of self-replicating supramolecular structures at the single-particle level. As a result, we are able to quantify the kinetics of these systems and changes in nanoparticle distribution over time. Our ability to observe a variety of complex phenomena may contribute to understanding how cell-like systems can emerge from much simpler chemical components and provides a general route to studying assembly and disassembly on the nanoscale.

Abstract

Autocatalytic chemical reactions are widely studied as models of biological processes and to better understand the origins of life on Earth. Minimal self-reproducing amphiphiles have been developed in this context and as an approach to de novo “bottom–up” synthetic protocells. How chemicals come together to produce living systems, however, remains poorly understood, despite much experimentation and speculation. Here, we use ultrasensitive label-free optical microscopy to visualize the spontaneous emergence of an autocatalytic system from an aqueous mixture of two chemicals. Quantitative, in situ nanoscale imaging reveals heterogeneous self-reproducing aggregates and enables the real-time visualization of the synthesis of new aggregates at the reactive interface. The aggregates and reactivity patterns observed vary together with differences in the respective environment. This work demonstrates how imaging of chemistry at the nanoscale can provide direct insight into the dynamic evolution of nonequilibrium systems across molecular to microscopic length scales.

Autocatalysis is a fundamental class of chemical reactions that drives many biological processes and underpins research into the origins of life on Earth (1). Surfactant molecules can self-reproduce through physical autocatalysis, a process in which aggregates of these monomers, in the form of micelles or vesicles, catalyze the formation of additional monomers. Several chemical models of physical autocatalysis have been developed that involve biphasic reaction conditions (2). In these systems, reactants are partitioned between aqueous and organic phases and react to give amphiphilic products, which aggregate into micelles or vesicles. Autocatalysis occurs in these reactions because the product aggregates take organic precursor molecules into the aqueous phase, allowing more efficient mixing of the reaction components and thereby increasing the rate of reaction. Understanding the dynamics of individual lipid aggregates during growth and division is a long-standing problem in the field of prebiotic chemistry (3–7) because vesicles are widely thought to have compartmentalized and catalyzed reactions in the prebiotic world (8–10). A full understanding of these dynamics has not yet been achieved in large part owing to analytical limitations.

Although physical autocatalysts have been widely studied for 25 years, their behavior remains poorly understood (2). Furthermore,direct observation of individual lipid aggregates remains elusive. At the single-particle level, division of giant vesicles (>1 µm) has been visualized in real time, using optical microscopy (11). However, smaller aggregates such as micelles and submicron vesicles can only be imaged directly with electron microscopy, which strongly perturbs the system and precludes real-time analysis (4, 12). Ensemble methods such as dynamic light scattering (12) and fluorescence resonance energy transfer (7) enable the analysis of aggregate populations, and ensemble spectroscopic methods are frequently used to record the concentration of individual molecular species in reaction mixtures. The critical nanometer scale on which physicochemical self-replication occurs, however, has not been imaged dynamically. As a result, we struggle to understand the dynamics of even the simplest supramolecular aggregates such as micelles and vesicles. As a corollary we do not fully comprehend how protocells may evolve out of chemical mixtures and ultimately to what degree they are relevant to primitive life. Here, we show that interferometric scattering microscopy (iSCAT) (13–15) can be used to monitor physical autocatalysis in situ because it enables the direct observation of the generation of new lipid aggregates at the reactive interface, without the use of labels or any other perturbations to the system, down to single micelles.

Results

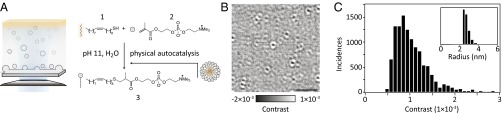
Our system consists of a biphasic reaction between aqueous and organic components placed above a microscope cover glass (Fig. 1A). The reaction of thiol 1 with enone 2 at high pH yields a single amphiphilic product, 3. The product 3 aggregates into micelles at millimolar concentrations and enables the reagents to mix more efficiently, thus behaving as a physical autocatalyst.

Fig. 1.

Visualizing physical autocatalysis by iSCAT. (A) Schematic of the biphasic reaction of aqueous 2 with neat water-insoluble 1 carried out on a microscope coverslip. iSCAT relies on illuminating the sample with a coherent light source and imaging the reflected and backscattered light from the sample. (B) Representative differential iSCAT image of single micelles of 3 bound to microscope cover glass after subtraction of the static scattering background. (Scale bar: 2 µm.) (C) iSCAT contrast histogram of a sample of 3 in water. Inset shows dynamic light scattering number distribution of 3 (1 mM).

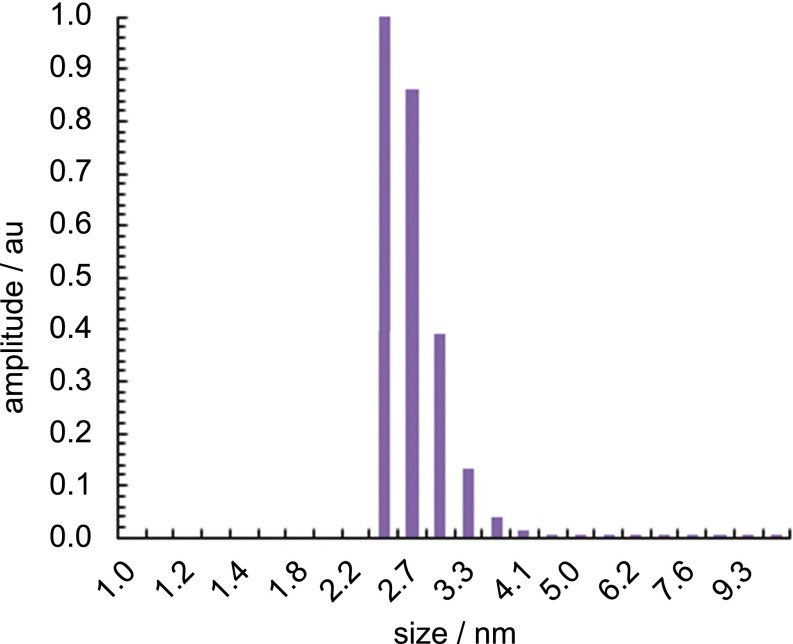
Compound 3 is an analog of a physical autocatalyst that we previously characterized (16). At present we are unable to reliably detect the smaller micelles of the earlier system using iSCAT, and so compound 3, bearing a longer hydrophobic tail, was selected as it forms larger micelles (R_H ∼ 3 nm, Figs. S1–S3), which can reliably be detected by iSCAT. Unsaturation in the alkyl chain was introduced to keep the corresponding thiol 1 a liquid at room temperature for experimental simplicity, allowing the thiol to be used neat rather than as a solution in an organic solvent. The corresponding saturated compound, 1-octadecanethiol, is a solid at room temperature.

Fig. S1.

DLS mass distribution of 3 (1 mM in H₂O).

Fig. S3.

DLS intensity distribution of 3 (1 mM in H₂O).

Fig. S2.

DLS number distribution of 3 (1 mM in H₂O).

To determine the sensitivity limits of iSCAT in visualizing the reaction products directly, we monitored binding of individual micelles to a microscope cover glass from a solution of pure 3. Binding of micelles to the cover glass changes the local refractive index and thus the scattering properties of the surface, which is detected by the iSCAT microscope. The resulting differential images consist of diffraction-limited spots, with a contrast on the order of 0.1% (Fig. 1B). Given an average micelle hydrodynamic radius of 3 nm determined by dynamic light scattering (DLS) (Fig. 1C, Inset), an iSCAT contrast of 0.18% for a single 500-kDa unlabeled protein (13) and the unimodal distribution in the detected signal for the aggregates in iSCAT and dynamic light scattering (Fig. 1C) demonstrates that these signatures arise from individual micelles. At this point a quantitative conversion from iSCAT contrast to hydrodynamic radius is not achievable; the contrast depends not only on the particle polarizability and hence volume, but also on the effective refractive index, which may vary with particle size. In addition, the detected signal depends in part on the focal position and optical path length, requiring a constant focus position across measurements. Nonetheless, the comparison between iSCAT contrast and the DLS size distribution demonstrates that we can detect the smallest micelles present in samples of 3.

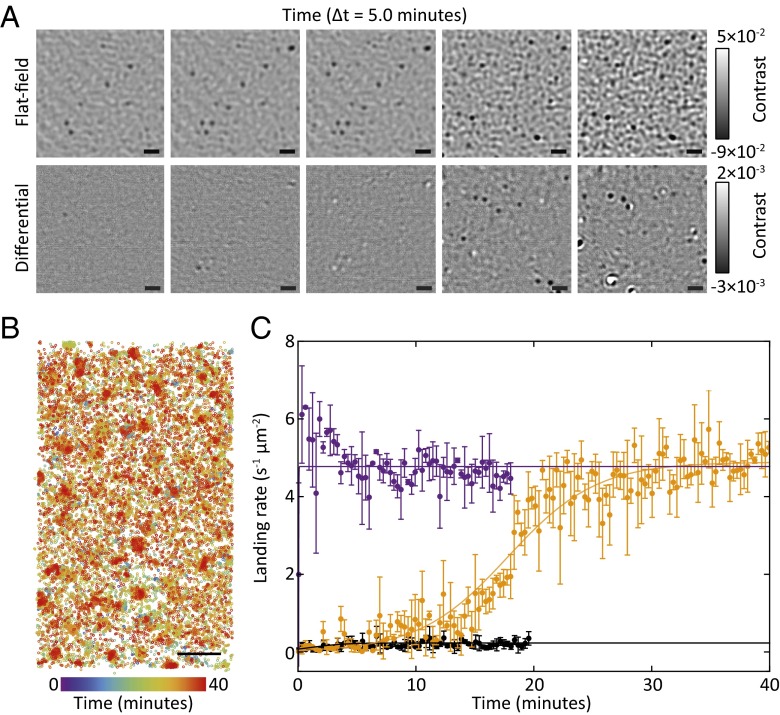
To monitor the synthesis of 3 in situ we take advantage of the stochastic binding of micelles to the cover glass surface, analogous to localization-based superresolution fluorescence microscopy (17). In contrast to fluorescence imaging, light scattering does not saturate or bleach. Thus, a surface partially covered by micelles acts as a new scattering background that can be subtracted. Subtraction of consecutive images reveals only changes in surface scattering (18), even though the respective raw scattering images are essentially indistinguishable (Fig. 2A). This is because the rough cover glass surface and any micelles or vesicles already present dominate the signal (15). In our assay micelle binding results in dark spots, whereas departing/rupturing particles generate a bright, positive contrast.

Fig. 2.

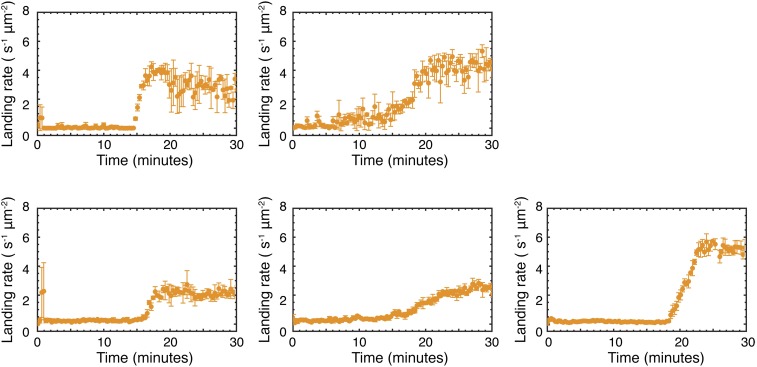
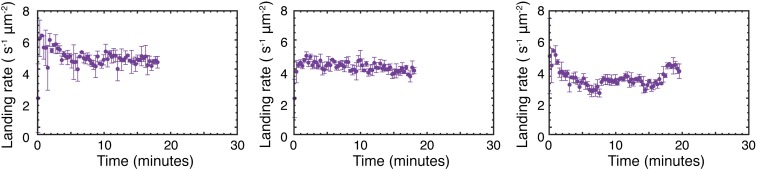
Quantification of reaction kinetics by label-free superresolution imaging. The binding of aggregates of 3 to a glass surface is monitored by iSCAT. The binding and unbinding of particles is detected as a change in the local refractive index and counted, allowing quantification of the binding/unbinding rates per unit area. (A, Top) Flat-field images of aggregates of 3 binding to a microscope cover glass over 25 min. (A, Bottom) Corresponding background-subtracted images, highlighting binding (dark colors) and unbinding (white) events of single aggregates to the surface. Images are taken from the same dataset as the orange line in C. Each image is the average of 150 frames. (B) Superresolution map identifying the center of mass for each binding event over time. Counting each binding event in this map per unit time gives the data shown in C. Data are the same as the orange line in C albeit cropped to a 8.1 × 4.8 μm window. (Scale bars: 1 μm.) Kinetic curves for these reactions and additional replicates are included in Figs. S8–S10. (C) Characterization of reaction kinetics by counting the number of binding events per unit time and area. Background-subtracted images (illustrated in A, Bottom) are analyzed and each binding/unbinding event is counted to give the kinetic curves shown. Data points with error bars represent the average and SD of three consecutive 1-s measurements sampled once every 6 s. Solid lines are fits to sigmoidal kinetics for the reaction between 1 and 2 (orange) and the reaction between 1 and 2 seeded with 3 (purple). The seeded reaction features a high rate of reaction immediately upon addition of 1, without the lag period required to build up product/catalyst as observed in unseeded reactions. The black line and corresponding data points refer to the negative control, consisting of thiol 1 and an aqueous solution of Cs₂CO₃. Note that solid lines do not represent a detailed kinetic model and are intended only to highlight major trends.

Fig. S8.

Reactions between 1 and 2. Each panel shows the result of an identical repeat reaction between 1 and 2 as described under Materials and Methods, Experiment.

Fig. S9.

Seeded reactions between 1 and 2 in the presence of 3 (0.5 mM). Each panel shows the result of an identical repeat reaction between 1 and 2 in the presence of preformed 3 as described under Materials and Methods, Experiment.

Fig. S10.

Negative controls in which Cs₂CO₃ (200 mM) and thiol 1 are mixed in the absence of MPC 2. Each panel shows the result of an identical repeat reaction between Cs₂CO₃ and 2 in the absence of 1 or 3 as described under Materials and Methods, Experiment.

Before the onset of the autocatalytic reaction, consecutive image subtraction (Materials and Methods, Data Processing) reveals no binding to the surface as expected in the absence of micelles in solution (Fig. 2A). Approximately 15 min after establishing the interface, we observe binding of micelles to the surface, the rate of which then rapidly accelerates and also involves unbinding events as the surface saturates. We can generate a superresolution map of binding events (Fig. 2B), because we can detect and localize each particle arriving at or departing from the surface.

A corresponding time course of binding events allows us to determine the landing rate per unit area as a function of time (Fig. 2C). We observe an exponential increase in the landing rate after an initiation period, which tails off, resembling a Langmuir adsorption isotherm as the available binding sites on the cover glass surface become occupied (Fig. 2C, orange). The exact shape of the time course and final binding is somewhat variable (Fig. S4) but the overall trend is consistent and reproducible.

Fig. S4.

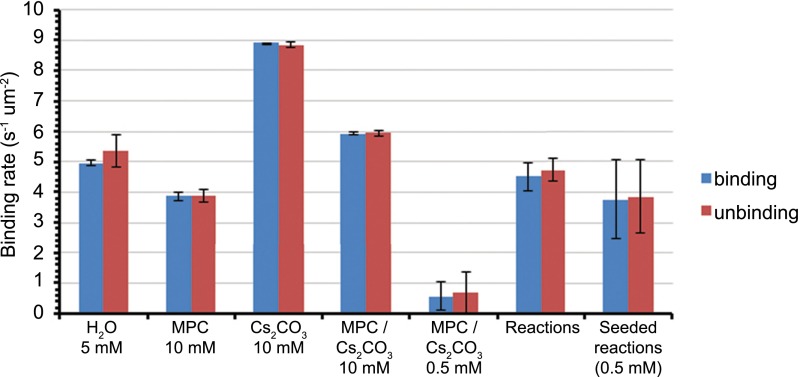
Comparison of saturation binding rate between controls and reactions. Each bar corresponds to the average and SD of three measurements of the equilibrium or saturation binding/unbinding rate per unit area. From left to right: pure 3 (5 mM) in H₂O, pure 3 (10 mM) in aqueous MPC 2 (600 mM), pure 3 (10 mM) in aqueous Cs₂CO₃ (200 mM), pure 3 (10 mM) in aqueous MPC 2 (600 mM)/Cs₂CO₃ (200 mM), pure 3 (0.5 mM) in aqueous MPC 2 (600 mM)/Cs₂CO₃ (200 mM), saturation binding rate observed in reactions (average of 5 experiments), and saturation binding rate observed in reactions seeded with 0.5 mM 3.

The observed variation of the saturation point between and within experiments is likely a consequence of multiple factors. The maximum landing rate is given by the availability of binding sites on the substrate. The availability of binding sites itself depends on several competing dynamic processes such as unbinding events, formation of a supported lipid bilayer, deformation of individual aggregate structures, and the size of the aggregate products. Some of these processes have been reported to be dependent on the local density of particles on the substrate (19). Hence variation in the maximum landing rate is not unexpected.

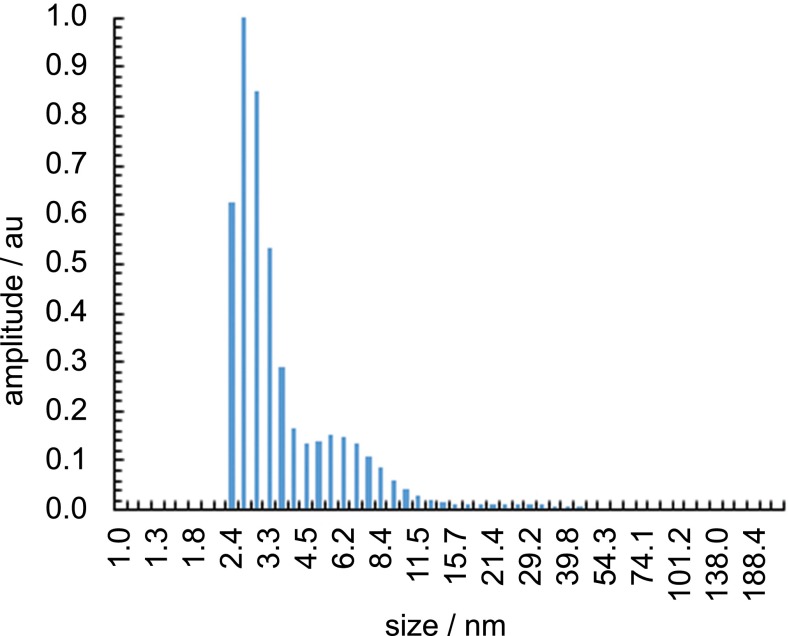
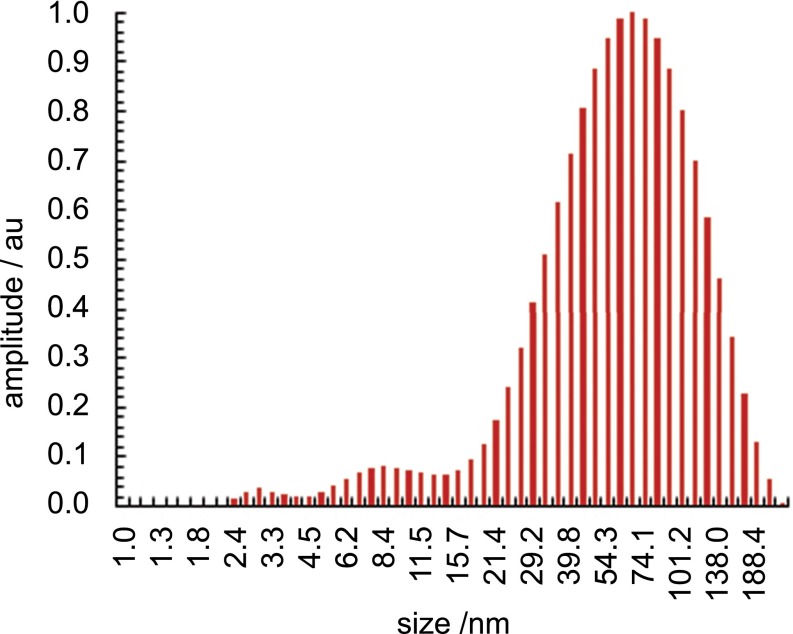
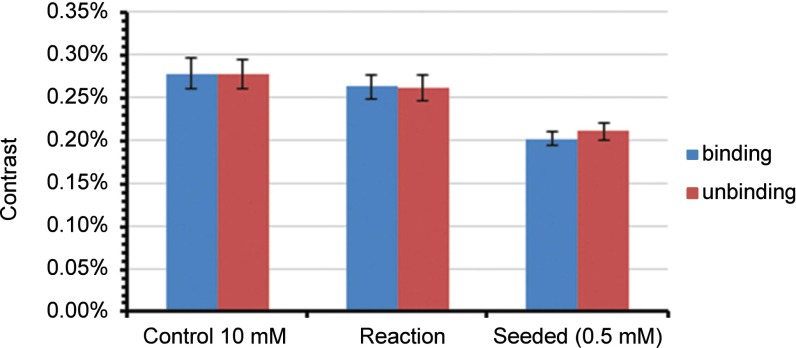
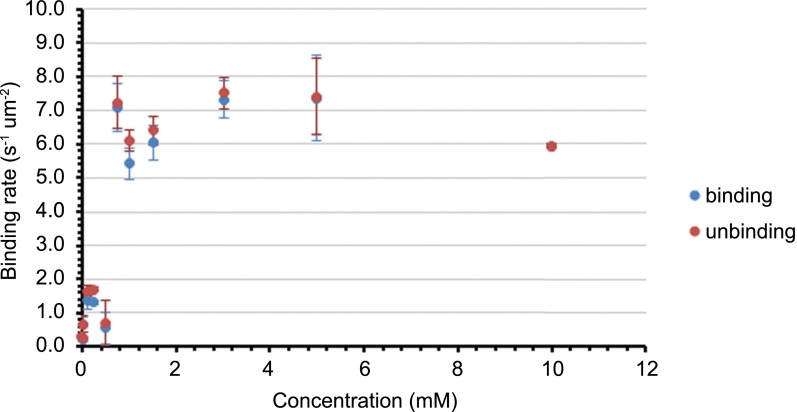
Beyond characterization of the landing rate, we can monitor the particle size distribution as it evolves in time. Under these conditions, the average particle contrast converges around 0.26 ± 0.02% (Fig. S5). This result is consistent with positive controls carried out in the reaction medium, giving an average particle contrast of 0.28 ± 0.02% (Fig. S6). The absolute contrast is sensitive to the refractive index of the solution and the focal position, and consequently is somewhat higher in the reaction mixture than in pure water. Positive controls carried out in the presence of starting material 2 and Cs₂CO₃ reveal a sharp critical micelle concentration between 0.5 mM and 0.75 mM (Fig. S7), with an equilibrium binding rate, above this concentration, in agreement with the saturation binding rate observed in reactions.

Fig. S5.

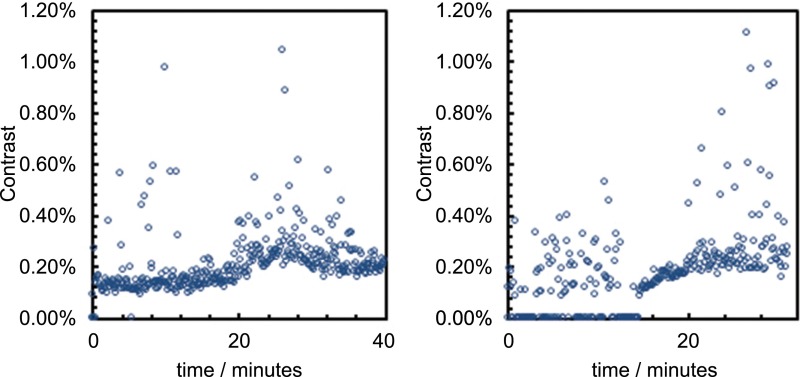
Change in size distribution of binding particles over time. (Left) The reaction shown in Fig. 2C (orange line) and Fig. S9. (Right) The reaction shown in Fig. S10.

Fig. S6.

Comparison of average particle contrast with positive control. Each bar corresponds to the average and SD of three measurements of the average particle contrast at the saturation binding point under the following conditions (left to right): positive control of 10 mM 3 in aqueous MPC 2 (600 mM)/Cs₂CO₃ (200 mM), unseeded reactions between 1 and 2 as shown in Fig. 2, and reactions between 1 and 2 in the presence of preformed 3 (0.5 mM) as shown in Fig. 2.

Fig. S7.

Saturation binding rate of 3 vs. concentration of 3. Each point corresponds to the mean and SD of the saturation binding rate (average over 5 min) of pure 3 in aqueous MPC 2 (600 mM)/Cs₂CO₃ (200 mM). Figs. S5–S7 plot the kinetics of multiple replicates of the reaction between 1 and 2, seeded reactions carried out in the presence of 0.5 mM 3, and negative controls in which MPC 2 is omitted. These data were used to generate Fig. 2 and Figs. S4–S7. All reactions were carried out under standard conditions as described in Materials and Methods. Each data point shows the mean and SD of three consecutive data points, where each data point consists of 1 s of data (1,000 frames) recorded every 6 s.

In negative control experiments where 2 is omitted, no micelles are formed (Fig. 2C, black). By contrast, inclusion of 0.5 mM of 3 in the aqueous solution to initiate the catalyzed reaction eliminates the lag period, and rapidly forms the product upon addition of 2 (Fig. 2C, purple). The final binding rate in this case is close to the average binding rate observed in the unseeded reactions (Fig. S4) and quantitatively distinct from the much lower binding rate observed in a positive control of 0.5 mM 3 in the absence of any thiol 1 (Fig. S4).

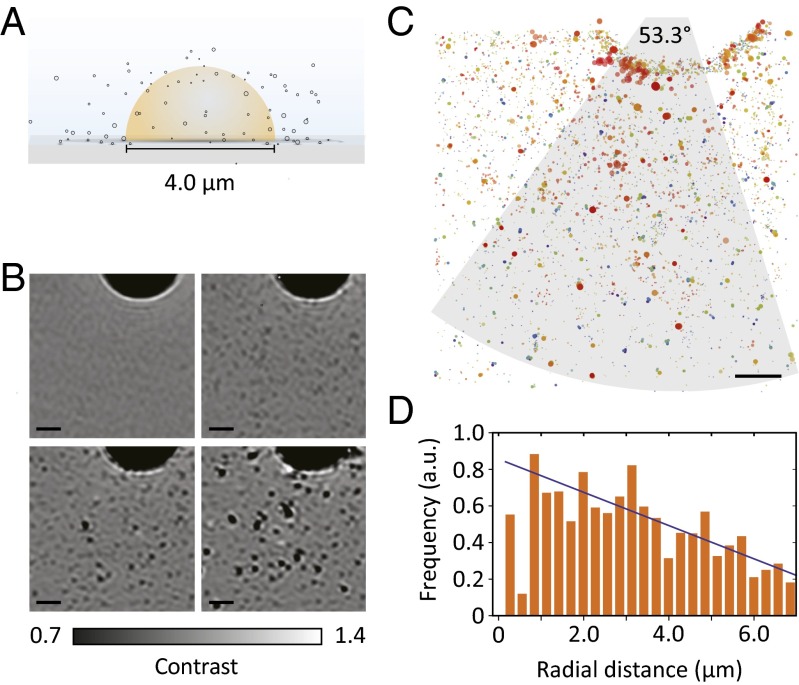
Given that iSCAT can be used to detect and quantify the autocatalytic synthesis of 3 at the single-particle level, we attempted to directly image the reactive interface. To do so we generated micrometer-sized thiol droplets on the glass coverslip and surrounded them with an aqueous solution of 2 (Fig. 3A). This allowed the direct visualization of the thiol–water interface and the production of new aggregates (Fig. 3B).

Fig. 3.

Direct observation of the reactive interface. (A) Illustration of the reaction geometry. (B) Flat-field images demonstrating the reaction about the thiol–water interface. Progress of the reaction is from Left to Right and Top to Bottom. (C) Superresolution map of the binding sites within the first 7 min of the reaction shown in B. The color and size of the plot markers encode the arrival time and signal intensity of binding events, respectively. (D) Negative correlation between the frequency of binding events per unit area and the distance from the reactive interface. Shown is the dependence of the bound product density, found within the arc sector depicted by the gray region in C, on the radial distance away from the droplet interface, where a radial distance of zero corresponds to the interface. Solid line shows the fit to a linear function. (Scale bars: 1 μm.)

Here, small lipid aggregates diffuse out of the thiol–water interface (Fig. 3C). Remarkably, there is a clear spatial association of reactivity with the thiol–water interface: Near the interface there are high levels of activity and many lipid aggregates form, whereas far from the interface the rate of binding is lower (Movie S1). These observations can be quantified, demonstrating that the binding rate is negatively correlated to the distance away from the interface (Fig. 3D). This observation agrees with the proposed biphasic reaction mechanism: If the reaction is indeed occurring at the thiol–water interface, the binding rate should decrease with distance from the interface. Conversely, if the binding arises from reactivity at a distant interface, or from a homogeneous reaction in the aqueous phase, the rate of binding should be independent of the distance from the observed interface. As such, the quantification of this correlation supports the proposed mode of reactivity, providing spatial information that would be difficult to obtain by other methods (16).

One hour after the addition of 2, the interface around these droplets breaks down almost entirely, and complex extended lipid structures emerge (Movies S2–S4). These lipid structures proliferate rapidly and lead to events consistent with the growth and division of individual nanometer-scale vesicles: New material is seen to rapidly grow and separate from existing vesicles, although it is difficult to isolate individual events owing to the large number of vesicles.

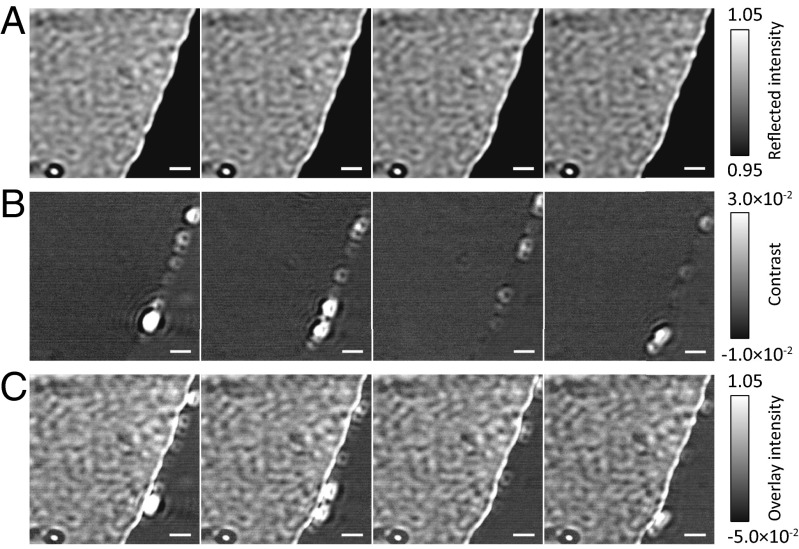
We are also able to generate macroscopic water–thiol interfaces where the interfacial curvature is negligible on the nanometer scale (Fig. 4). Here, the reactive behavior is rather different. Whereas we previously found proliferation of aggregates around the interface, here we observe the steady retreat of the organic phase and corresponding movement of the aqueous phase across the coverslip. Interestingly, the retreat of the thiol phase was not a continuous process as might be expected. Instead, we could discern the formation of individual aggregates at the interface and merging with an intermediate phase, which pushes the thiol phase back in a series of discrete events. Consecutive image subtractions of these data clearly reveal discrete events (Fig. 4B). Overlaying the differential series on the flat-field images reveals colocalization of these events with the retreating interface (Fig. 4C and Movie S5). It is likely that these discrete events correspond to the formation of individual vesicles at the interface.

Fig. 4.

Discrete movement of thiol–water interface. The interface between the aqueous (light shading) and thiol (dark shading) phases moves toward the right in discrete bursts rather than as a continuous process. (A) Flat-field images. (B) Consecutive subtraction images highlighting individual bursts of activity. (C) Composite image of A and B highlighting colocalization of activity and the motion of the interface. Δt = 400 ms. (Scale bars: 1 µm.) An animated version of Fig. 4 is shown in Movie S5.

Discussion

We have demonstrated the spontaneous formation of complex aggregates from simple precursors by directly visualizing an autocatalytic reaction on the nanometer scale. Through label-free, superresolution imaging of individual micelles and thus direct probing of the supramolecular product/catalysts, we can obtain quantitative kinetic data that allow the study of a physical autocatalytic reaction. Further, we are able to directly image the reactive interface and distinguish between processes occurring at different regions of the multiphasic system, thereby revealing the complexity and diversity of the dynamics of physical autocatalysts on the nanometer scale.

The capability to observe the products of a chemical reaction, label-free and in real time, provides us with the opportunity to study complex nonequilibrium systems at the single-particle level, so that we may better understand the collective behavior of autocatalytic aggregates. Understanding how complex supramolecular dynamics give rise to the formation of extended membranes, and the production, growth, and division of vesicles, is a fundamental problem relevant to the origins of life (1, 2, 20). Here we examine a model bond-forming autocatalytic system, which rapidly generates molecular and supramolecular complexity to demonstrate a general method by which we can directly image and study nanoscopic dynamics with high spatiotemporal resolution.

Materials and Methods

iSCAT Setup.

The iSCAT experimental setup is not described in complete detail here, but is similar to that discussed by Ortega-Arroyo et al. (13) A 445-nm diode laser was used as the incident light source with an approximate incident power of 10 kW/cm² on the sample. Frames were recorded at 1 kHz with an exposure time of 0.56 ms, using a CMOS camera (Photonfocus MV-D1024-160-CL-8). Unless noted otherwise, images were recorded at 333× magnification (31.8 nm per pixel), corresponding to an 8.1 × 8.1-µm² window.

Focus in the z axis is maintained using an autofocus system relying on the total internal reflection (TIRF) of a 638-nm beam (21). Movement in the z axis results in a corresponding movement in the xy plane of a totally internally reflected beam, which is detected and used as the basis for automated correction of the z position. This system can maintain the z position to within 5 nm.

Sample Preparation and Coverslips.

All samples were purified before use, prepared using ultrapure Milli-Q water, and filtered through 0.2-µm polytetrafluoroethylene (PTFE) filters before analysis by iSCAT.

Borosilicate glass coverslips (no. 1.5, 24 × 50 mm; VWR) were cleaned by sequential rinsing with distilled water, ethanol, and distilled water and then sonicated for 10 min while standing in fresh HCl (approx. 0.4 M). The cover slips were washed with Milli-Q water and dried under a stream of dry nitrogen.

Silicone wells (4.5-mm diameter, 1.7-mm depth; Grace BioLabs) were prepared by washing sequentially with Milli-Q water and EtOH and then drying under a stream of dry nitrogen.

All coverslips and wells were prepared on the same day as analysis using fresh reaction components.

Experiment.

A typical reaction was performed as follows. Milli-Q water (15 μL) was deposited into a silicone well and the glass surface inspected to ensure satisfactory cleanliness. Thiol 1 (2 μL, 0.3 eq relative to 2) was gently deposited atop the aqueous layer and the system was allowed to equilibrate for several minutes. A solution (15 μL) of MPC 2 (1.2 M) and Cs₂CO₃ (400 mM) was injected into the aqueous layer and mixed gently using a micropipette. One second of data, equivalent to 1,000 frames, was then recorded every 6 s.

Negative controls were performed by omitting MPC 2 from the second aqueous solution. Seeded experiments were performed by supplementing the initial aqueous solution with a 0.5 mM solution of 3. Positive controls were performed by measuring the binding rate of preequilibrated solutions of 3 in MPC 2 (600 mM) and Cs₂CO₃ (200 mM) in the absence of thiol 1.

Direct examination of the thiol–water interface was achieved by first depositing thiol 1 (2 μL) on the glass surface and then displacing it by injection of Milli-Q water (4 μL). The reaction site of interest was located and then a solution of MPC 2 (1.2 M) and Cs₂CO₃ (400 mM) was injected into the aqueous layer. Data were recorded manually, typically capturing 5,000–10,000 frames (5–10 s) at a time.

Data Processing.

Data were processed and analyzed using National Instruments LabVIEW 2011 and the FIJI distribution of ImageJ. To correct for illumination inhomogeneity and fixed pattern noise, a flat-field image was taken by running a temporal median filter over a sequence of images acquired when the sample was displaced (22). Differential imaging was achieved by subtracting sets of images temporally offset by a time Δt. The signal-to-noise ratio was then improved by spatially (2 × 2 binning) and temporally averaging the differential images (100 images).

For the generation of superresolution images and quantification of reaction kinetics, a running temporal average was applied to the differential images. By subtracting a running temporal average from the differential images we reduced the rate of false positives and increased the recovery rate of true positives, given that single (un)binding events would be counted multiple times, in contrast to a signal attributed to spurious noise. To avoid repeated counts, single (un)binding events were identified only on the basis of having a trajectory length with at least four localizations and at most twice the size of the temporal average.

Particle detection was performed as described by Spillane et al. (23) Briefly, diffraction-limited spots were identified by a combination of the nonmaximum suppression algorithm and selecting pixels that exceeded at least two times the SD of the image, estimated by the median absolute deviation. Candidate particles were then segmented into regions of interest corresponding to ∼1 μm² and fitted to a 2D Gaussian function. Particle tracks, used for the quantification of the kinetics, were generated by a modified cost matrix method described by Jaqaman et al. (24). Here assignments within the cost matrix were determined by a greedy approach, namely by minimizing the distance between features in consecutive frames found within a search radius of 40 nm, rather than solving the linear assignment problem. Features with the minimum distance exceeding the search radius were classified as having no connectivity.

The possibility of each diffraction-limited spot being attributed to more than one micelle is excluded by consideration of the binding rate. Namely, if the landing rate of the micelles is high, corresponding to a high particle density, so too is the likelihood of having more than one particle land within a diffraction-limited area simultaneously (i.e., within a single exposure time or effective exposure time given by averaging multiple frames together to enhance the signal-to-noise ratio). To estimate how likely this would be, we refer to the observed maximal rates of particle landing (i.e., the saturation points) in the assay, which are ∼4 particles⋅s⁻¹⋅µm⁻² (Fig. 2). Assuming a diffraction limit area = π(0.125 µm)² ∼ 0.05 µm², we have a landing rate of less than 1 particle⋅s⁻¹ per diffraction limited spot. Now, considering an effective temporal window (t) of 0.1 s (equivalent to averaging 100 frames taken at 1,000 fps), we now have a landing rate per diffraction-limited spot of 0.025 particle⋅t⁻¹. Assuming a Poisson-distributed process, the probability that more than one particle lands under such a scenario can be estimated to be <0.1%. Under these circumstances this effect can be neglected; for higher densities, however, one can minimize this issue by increasing the temporal resolution of the detection.

General Experimental

Reactions using oxygen- or moisture-sensitive materials were performed using anhydrous solvents under an atmosphere of anhydrous argon in flame-dried flasks, using standard Schlenk techniques. Analytical TLC was performed using precoated glass plates (silica gel 60 F254; Merck) and visualized using aqueous ceric ammonium molybdate (CAM) or aqueous basic potassium permanganate stains. Flash column chromatography was performed using Apollo Scientific silica gel 60 (0.040–0.063 nm), Merck 60 Å silica gel, VWR (40–63 µm) silica gel, and Sigma-Aldrich silica gel. Pressure was applied at the column head via a flow of nitrogen with the solvent system used to purify each compound in parentheses in the corresponding synthetic protocol. Concentrations are given in vol/vol%.

Reactions at 0 °C were performed using an ice-water bath. Other temperatures were obtained using the heating plate of the stirrer.

Solution NMR spectra were recorded at room temperature. ¹H and ¹³C NMR experiments were carried out using Bruker AVN-400 (400/100 MHz), DQX-400 (400/100 MHz), or AVC-500 (500/125 MHz) spectrometers. ³¹P NMR spectra were recorded using a Bruker DRX-500 (500/200 MH) spectrometer. Chemical shifts (δ) are reported in parts per million from the residual solvent peak and coupling constants (J) are quoted in hertz. Resonances are described as s (singlet), d (doublet), t (triplet), q (quartet), and m (multiplet). Assignments were made with the assistance of gCOSY, DEPT-135, gHSQC, and gHMBC or gHMQC NMR spectra.

Low-resolution mass spectra were recorded using a Walters LCT premier XE. High-resolution mass spectra (EI and ESI) were recorded using a Bruker MicroTOF spectrometer by the internal service at the University of Oxford.

DLS measurements were recorded using a Viscotek 802 instrument and the data were processed using OmniSize 2.0 software. Data are the average of 10 × 10-s measurements. Samples were prepared using ultrapure Milli-Q water and filtered through 0.2-µm PTFE filters before analysis.

Chemicals

Dry CH₂Cl₂ was collected fresh from an mBraun SPS-800 solvent purification system, having been passed through an anhydrous alumina column. Ethanol was used as purchased from Sigma-Aldrich.

Commercially available reagents were purchased from Sigma-Aldrich, Fisher Scientific, Apollo Scientific, Acros Organics, Alfra Aesar, or TCI UK and were used without purification. Petroleum ether refers to petroleum boiling in the range 40–60 °C. Deuterated solvents were purchased from Sigma-Aldrich (CDCl₃, CD₃OD).

Chemical Synthesis

Oleyl Thiol 1.

To a stirred solution of oleyl alcohol (85%, 1 mL, 2.7 mmol) and Et₃N (0.56 mL, 4.0 mmol, 1.5 eq) in CH₂Cl₂ (15 mL) was added mesyl chloride (0.23 mL, 3.0 mmol, 1.1 eq) dropwise at 0 °C. The reaction was stirred until the alcohol was fully consumed (TLC control, eluting in 20% ether in hexane) and then diluted with H₂O (10 mL). The layers were separated and the organic layer was washed sequentially with aqueous HCl (1 M, 10 mL), NaHCO₃ (saturated, 10 mL) and brine (10 mL). The organic layer was dried (MgSO₄) and concentrated in vacuo to give the crude mesylate (1.1 g), which was used without further purification.

The crude mesylate (1.1 g) and thiourea (250 mg, 3.3 mmol, 1.05 eq) were refluxed in EtOH (2 mL) for 5 h. Aqueous NaOH (2.5 M, 2 mL) was added and the solution refluxed for a further 2 h. The solution was allowed to cool to room temperature and acidified with HCl (2 M) and then extracted twice with Et₂O (15 mL). The combined organic layers were washed with brine (30 mL), dried (MgSO₄), and concentrated in vacuo. The crude product was purified by column chromatography (eluting with hexane) to give pure oleyl thiol 1 (200 mg, 0.70 mmol, 26% yield).

¹H NMR (400 MHz, CDCl₃) δ 5.38 (m, 2H), 2.51 (q, J = 7.4 Hz, 2H), 1.98 (m, 4H), 1.59 (q, J = 7.4 Hz, 2H), 1.44–1.16 (m, 22H), 0.88 (t, J = 6.7 Hz, 3H).

¹³C NMR (101 MHz, CDCl₃) δ 130.12, 129.94, 34.21, 32.76, 32.06, 29.93, 29.88, 29.68, 29.56, 29.48, 29.37, 29.20, 28.53, 27.37, 27.33, 24.81, 22.84, 14.28.

HRMS (EI/FI) m/z calcd for C₁₈H₃₆S [M]⁺: 284.2538, found 284.2531.

Lipid 3.

A solution of MPC 2 (100 mg, 0.34 mmol) and oleyl thiol 1 (106 mg, 0.37 mmol, 1.1 eq) in EtOH (1 mL) was degassed by bubbling Ar gas through it for 15 min. Catalytic diisopropylamine was added and the reaction was stirred for 18 h. The solvent was removed in vacuo and the residue washed with hexane and then purified by flash column chromatography (65/35/5 CHCl₃/MeOH/H₂O). The sample was freeze-dried to give pure 3 (125 mg, 0.22 mmol, 64%).

¹H NMR (500 MHz, CD₃OD) δ 5.49–5.40 (m, 2H), 4.41–4.32 (m, 4H), 4.15 (dt, J = 7.0, 4.9 Hz, 2H), 3.75–3.70 (m, 2H), 3.31 (s, 9), 2.89 (dd, J = 12.9, 7.4 Hz, 1H), 2.79 (h, J = 6.9 Hz, 1H), 2.68 (dd, J = 12.9, 6.4 Hz, 1H), 2.60 (t, J = 7.3 Hz, 2H), 2.16–2.02 (m, 4H), 1.64 (p, J = 7.3 Hz, 2H), 1.51–1.35 (m, 22H), 1.32 (d, J = 6.9 Hz, 3H), 0.98 (t, J = 6.8 Hz, 3H).

¹³C NMR (126 MHz, CD₃OD) δ 176.74, 131.53, 131.48, 67.44 (dt, J = 6.7, 3.0 Hz), 65.20 (d, J = 7.8 Hz), 64.67 (d, J = 5.4 Hz), 60.41 (d, J = 5.0 Hz), 54.96–54.37 (m), 41.58, 36.28, 33.62, 33.41, 33.08, 33.06, 30.77, 30.75, 30.59, 30.55, 30.52, 30.48, 30.35, 30.20, 30.13, 29.87, 29.85, 28.13, 23.75, 17.22, 14.50.

³¹P NMR (202 MHz, CD₃OD) δ 0.83.

HRMS (ESI) m/z calcd for C₂₉H₅₉NO₆PS [M+H]⁺: 580.37952, found 580.37900.

DLS histograms (1 mM) are shown in Figs. S1–S3.