Significance
Mechanosensation is central to life. Bacteria, like the majority of walled cells, live and grow under significant osmotic pressure. By relying on mechanosensitive regulation, bacteria can adapt to dramatic changes in osmotic pressure. Studying such mechanical sensing and control is critical for understanding bacterial survival in a complex host and natural environment. Here, we investigate the fundamental design principles of Escherichia coli’s passive mechanosensitive response to osmotic downshocks by implementing single-cell high-resolution imaging. We explain the observed cell volume changes by modeling flux of water and solutes across the cell membrane. A better characterization of bacterial mechanosensitive response can help us map their reaction to environmental threats.
Keywords: osmotic downshock, bacterial mechanosensing, single-cell imaging
Abstract
For most cells, a sudden decrease in external osmolarity results in fast water influx that can burst the cell. To survive, cells rely on the passive response of mechanosensitive channels, which open under increased membrane tension and allow the release of cytoplasmic solutes and water. Although the gating and the molecular structure of mechanosensitive channels found in Escherichia coli have been extensively studied, the overall dynamics of the whole cellular response remain poorly understood. Here, we characterize E. coli’s passive response to a sudden hypoosmotic shock (downshock) on a single-cell level. We show that initial fast volume expansion is followed by a slow volume recovery that can end below the initial value. Similar response patterns were observed at downshocks of a wide range of magnitudes. Although wild-type cells adapted to osmotic downshocks and resumed growing, cells of a double-mutant () strain expanded, but failed to fully recover, often lysing or not resuming growth at high osmotic downshocks. We propose a theoretical model to explain our observations by simulating mechanosensitive channels opening, and subsequent solute efflux and water flux. The model illustrates how solute efflux, driven by mechanical pressure and solute chemical potential, competes with water influx to reduce cellular osmotic pressure and allow volume recovery. Our work highlights the vital role of mechanosensation in bacterial survival.
Biology offers an array of intriguing mechanical solutions, both active and passive, often exceeding what is currently possible with man-made methods. Understanding how biological systems achieve different functionalities under mechanical stimuli can inform new, thus-far-unexplored design principles. One such passive control system is the bacterial response to sudden decreases in external osmolarities.
A Gram-negative cell’s fluid cytoplasm is separated from the external environment by the inner membrane, the periplasmic space, and the outer membrane. Ordinarily, the total solute concentration within the cytoplasm is higher than that of the environment, resulting in a positive osmotic pressure on the cell wall (termed turgor pressure) (1). Escherichia coli is able to respond to both increases and decreases in external concentrations. An increase in external osmolarity (hyperosmotic shock or upshock) results in water efflux from the cell interior, causing cellular volume to shrink and osmotic pressure to drop to zero (2). E. coli responds by actively accumulating specific solutes (osmolytes), such as potassium, proline, and glycine-betaine (2). Accumulation of osmolytes in the cell’s cytoplasm causes reentry of water, cell volume increase, and recovery of osmotic pressure (3, 4). A downward shift in external osmolarity (termed hypoosmotic shock or downshock) causes fast water influx into the cell’s cytoplasm. As a result, the osmotic pressure increases and the cell expands in a nonlinear fashion (5, 6). Turgor pressure in E. coli has been estimated to lie between 0.3 and 3 atm (5, 7), rising up to 20 atm upon a large downshock (6). An increase in the inner membrane tension, caused by the expansion, is thought to activate the nonspecific export of solutes through mechanosensitive channels (MSCs), such as MscS and MscL (Fig. 1A) (8). As the solutes leave the cell, so does the cytoplasmic water, enabling the cell to recover original volume and pressure (Fig. 1A).
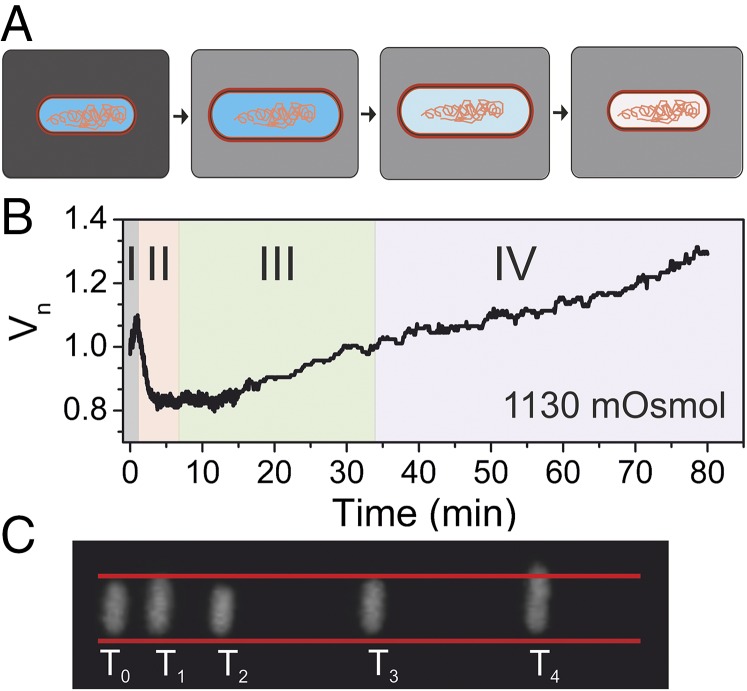
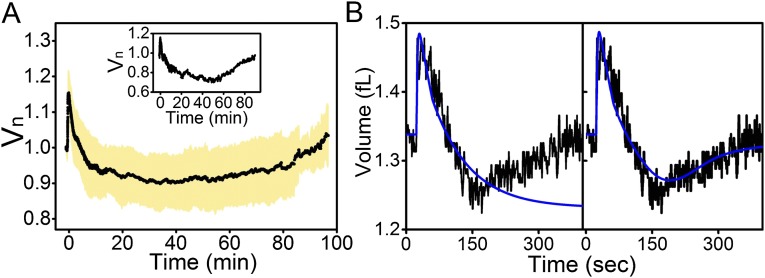
Fig. 1.
Characteristic cell volume response to a sudden downshock. (A) Upon a sudden decrease in external concentration, cell volume expands, which leads to opening of mechanosensitive channels. Consequently, solutes exit the cell, allowing recovery of cell volume through loss of cytoplasmic water. (B) A characteristic single-cell volume response for a 1,130-mOsmol downshock. The trace was normalized by the initial volume, that is, the volume before the downshock. Different phases of the recovery response are indicated with different colors. In gray is the expansion phase (phase I), followed by two volume recovery phases. Phase II (in orange) is characterized by volume decrease, and phase III (in green), by volume increase upon reaching the minimum volume. Phase IV (in purple) indicates recommenced growth. Initial 15 min are sampled at 5 Hz and an additional 1 h at a frame every 5 s. (C) Still images from different phases in B. is the very beginning of the recording, before the downshock. = 45 s, = 4 min, = 35 min, and = 70 min. Red lines are drawn to indicate the size of the cell before the downshock. In comparison, the cell size at is slightly larger (phase I), at smaller (phase II), at it reaches the initial size (phase III), and at it is significantly larger (phase IV).
Mechanosensitive channels are found in a wide range of cells (9–11), displaying great diversity. The precise gating mechanism of these pressure-controlled channels has attracted a lot of attention from scientific community. Despite the efforts, it remains a challenge (12). To our current knowledge, E. coli possesses seven different mechanosensitive channels (13). Of those seven, four play the dominant role: the mechanosensitive channel of small conductance (MscS), the large mechanosensitive channel (MscL) (9, 14, 15), the mechanosensitive channel of miniconductance (MscM) (16), and the potassium-dependent mechanosensitive channel (MscK) (17). Since their discovery in giant spheroplasts of E. coli (13, 18), crystal structures of some of the channels have been obtained (19–21), and channel function has been extensively studied in vitro (13, 18, 19, 22–25). The most widely used in vitro technique, electrophysiology, enabled measurements of channels’ pressure sensitivity, open dwell time, conductance, as well as ion selectivity (18, 26). For example, in vitro-measured opening time of MscS or MscL is on the order of 20–30 ms (27, 28), and the channels close immediately upon the decrease in tension (13).
In contrast to in vitro studies, in vivo studies are rare and mostly focused on estimating bacterial population survival with or without MSCs present (13, 28, 29). For example, we know that, if either MscS or MscL alone is present in the cell membrane, populations of cells can easily survive the abrupt osmotic downshock (28). When both channels are lacking, the survival rate decreases (29, 30). On a single-cell level, a recent study looked at the nature of cells dying upon downshocks and found that it depends on the flow rate with which the shock is administered (29).
However, in vitro studies of mechanosensitive channel gating and population survival studies cannot be easily translated into insights on the passive control of the whole-cell volume and pressure. Here, by looking at the response to hypoosmotic shocks on a single-cell level, we show that the volume recovery after initial fast expansion proceeds on a much slower timescale, on the order of minutes. In addition, cellular volume can decrease below the initial value. We present a theoretical model that explains our experimental observations. A competition between water efflux and influx and solute efflux through mechanosensitive channels gives rise to the observed characteristic slower volume recovery. The chemical potential of water and solutes serve as effective “control” variables in this passive dynamic system.
Results
Characterizing Whole-Cell Downshock Response.
E. coli’s response to downshocks has previously been characterized using light scattering in a stop flow device and within the first second postshock (28). We applied a single-cell microscopy assay previously developed (3), to extend the length of observation and investigate the response to downshocks in a range of shocks of different magnitudes.
Fig. 1B shows a characteristic volume recovery trace of a single wild-type cell subjected to a large osmotic downshock (c = 1,130 mOsmol), delivered with a local flow rate of 0.68 μL/min. At this rate, full transition to the lower osmolarity media is completed within 0.8 s (Materials and Methods). Cytoplasmic volume was monitored via cytoplasmically expressed eGFP, sampled at a frame every 0.2 s for initial 15 min, and at a frame every 5 s for the rest of the 75-min recording. Characteristic phases were identified and indicated with different background colors as follows: (I) expansion phase, observed immediately after downshock; (II) decrease phase of volume recovery, observed postexpansion, lasting several minutes; as the volume decreases in this phase, a characteristic “overshoot” below the initial volume is often observed; (III) increase phase of volume recovery, observed after minimum volume () has been reached and lasting until initial volume is reestablished, that is, ∼30 min; (IV) cell growth phase, observed post-volume recovery. Fig. 1C gives raw images corresponding to different phases shown in Fig. 1B.
We analyzed volume changes in 609 wild-type cells before, during, and after downshock for the following shock magnitudes: 103, 190, 460, 790, 960, 1,130, and 1,337 mOsmol. Fig. 2, Left, shows average traces with SDs of 103- to 1,130-mOsmol shocks. All cells quickly expand in phase I and show characteristic slow volume recovery in phase II. As the shock increases, the length of phase II and the overshoot increase. SI Appendix, Fig. S1, Left, shows average traces with SDs over longer time periods; phase IV, that is, growth, is visible for all shock magnitudes. SI Appendix, Fig. S3, Left, shows average trace with SDs of our largest shock, 1,337 mOsmol. We observe expansion in phase I; however, only small recovery in phase II is visible, with no characteristic overshoot and no phase IV. In fact, a large number of cells in 1,337-mOsmol condition lyse during our recording (SI Appendix, Fig. S10).
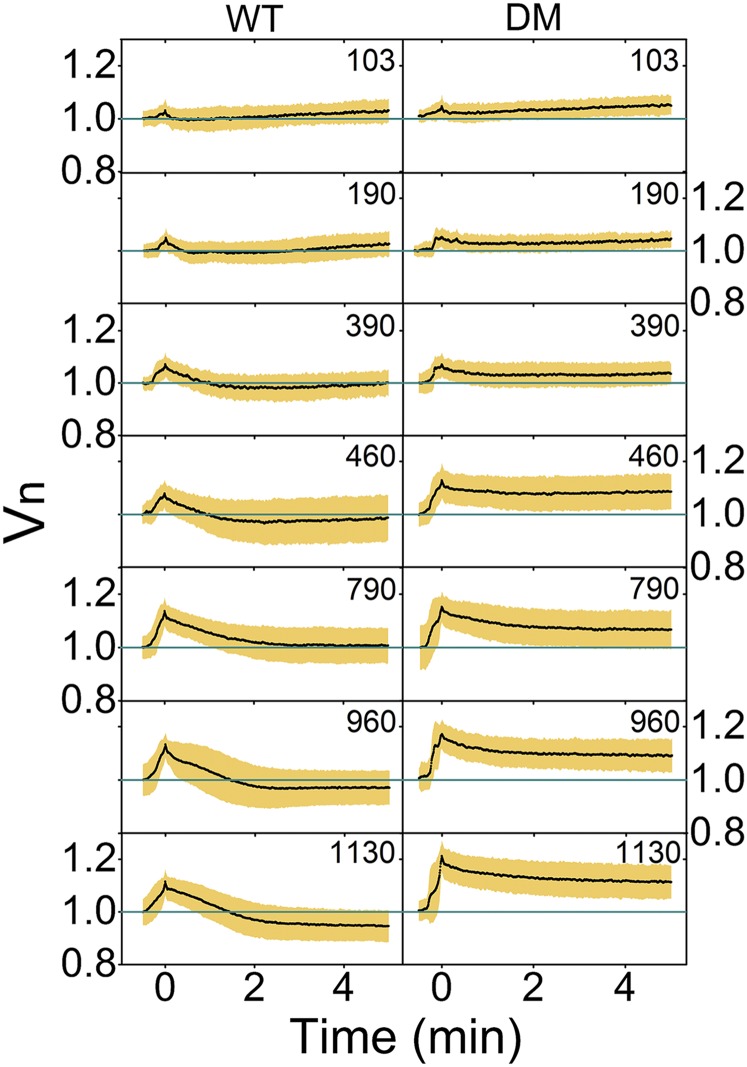
Fig. 2.
Cell volume response of the wild-type cells at different downshock magnitudes shows slow volume recovery and an “overshoot.” We use descriptive statistics to present our datasets and plot average volume traces with SDs constructed from 609 (WT) and 480 [double mutant (DM)] traces as a function of time. A zoom-in to first 5 min of downshock response sampled every 0.375 s is given. In total, 64 (WT) and 66 (DM) cells were used for 103 mOsmol, 94 (WT) and 52 (DM) cells were used for 190 mOsmol, 66 (WT) and 54 (DM) for 390 mOsmol, 56 (WT) and 80 (DM) for 460 mOsmol, 90 (WT) and 68 (DM) for 790 mOsmol, 116 (WT) and 50 (DM) for 960 mOsmol, and 106 (WT) and 77 (DM) cells for the 1,130-mOsmol downshock. Volume expands in all conditions and increases with the shock magnitude. Slow recovery follows volume expansion. For the wild-type cells, volume drops below the initial value, increasingly so with the larger shocks.
To confirm that the characteristic slow volume recovery after expansion is due to mechanosensitive channels, we characterized the response of a mutant strain lacking the channels contributing the most to downshock response (30), MscS and MscL (double mutant). Fig. 2, Right, shows average traces with SDs of the double-mutant cells exposed to downshocks of same magnitudes as in Fig. 2, Left. In total, 480 cells were analyzed. The double-mutant strain quickly expands for all shock magnitudes, similarly to the wild type. The response of the double-mutant strain in phase II and phase III is similar to that of the wild type for shocks of <390 mOsmol. For shocks of ≥390 mOsmol, the double mutant shows a smaller decrease in volume postexpansion and no overshoot. In addition, phase IV was not observed within 35 min postdownshock for any of our shocks (SI Appendix, Fig. S2). SI Appendix, Fig. S3, Right, shows average traces with SDs of the double mutant exposed to the largest shock. The response is similar to that of the wild type, where the number of lysing cells during our recording in 1,337-mOsmol condition increased for the double mutant (see also SI Appendix, Fig. S10 and analysis of observed lysis in Growth Rate upon Downshock Does Not Depend on the Shock Magnitude).
During sample preparation, we attached individual cells to the coverslip surface. To investigate whether the observed characteristic response to a sudden downshock is specific to surface-attached cells only, we repeated the experiment on freely floating cells (Materials and Methods and SI Appendix, Fig. S4). We were particularly interested in phases II and III, that is, slow volume recovery and overshoot. In the case of free cells, the shock was completed in microfuge tubes. Imaging began 3–4 min postshock and continued at specific time points, giving a population averaged volume (SI Appendix, Fig. S4, and Materials and Methods). SI Appendix, Fig. S4 shows that characteristic phases II–IV are similar to those observed for the individual cell given in Fig. 1B. Phase I, that is, expansion, could not be captured with this method as it was completed before the imaging began.
In Figs. 1 and 2, the shock was induced by removing a given osmolarity of NaCl. To examine whether the characteristic response observed is specific to the solute that causes the downshock, we have induced the shock by removing sucrose in SI Appendix, Fig. S5. The magnitude of the downshock in SI Appendix, Fig. S5 was 590 mOsmol and the response observed is very similar to that of the 790-mOsmol NaCl-induced shock shown in Fig. 2.
Maximum Volume Expansion Occurs Fast, on the Order of Seconds.
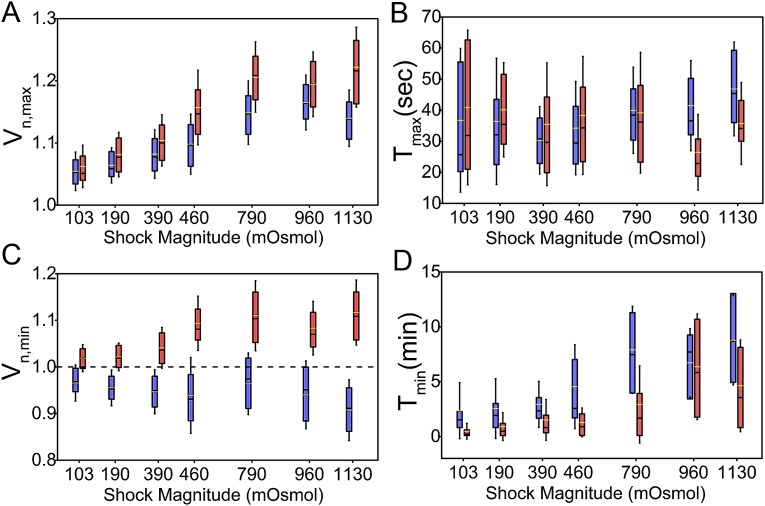
To quantify the extent of postdownshock volume expansion in the wild-type strain, in Fig. 3A (blue) we plot maximum volumes, , against the magnitude of the downshock. increases with the shock magnitude up to 790 mOsmol, at which point it reaches 15% and expansion saturates. The time it takes to reach is 30 s (Fig. 3B, blue) for all shock magnitudes.
Fig. 3.
Analysis of maximum and minimum volume and time. (A) Box plot of maximum volume, , and (B) the time at which maximum volume is reached, , as a function of shock magnitude. The wild type is shown in blue, and the double mutant, in red. The upper/lower whiskers indicate 1.5× the SD value. The upper/lower edges of the boxes indicate the third/first quartile. The black line indicates the median, and the yellow line, the average value. increases with the shock magnitudes and saturates at and above 790 mOsmol. is independent from the shock magnitude for the wild type (blue) and slightly smaller for the double mutant (red) for the two largest shock magnitudes. (C) and (D) plotted against the shock magnitude for wild type (blue) and double mutant (red). in C is slightly below 1 for the wild type and decreases with the shock magnitude. for the double mutant stays above 1 in all conditions. increases with the shock magnitude for both wild-type and double-mutant cells.
We compare the of the wild type to that of the double mutant. and for the double mutant are given in Fig. 3 A and B in red. Similarly to the wild type, the double mutant expands more with increasing shock magnitude. However, for shocks mOsmol, of the double mutant saturates at a slightly higher value, 20%. The time it takes to reach for the double-mutant strain lasts 30 s, similar to the wild type, with the only difference that at higher shock magnitudes full expansion is slightly faster, lasting 20 s.
Upon Expansion, Volume Recovery Is Slow, on the Order of Minutes, and Volume Can Decrease Below the Initial Value.
To determine the length of the time volume decreases from to (minimal, postshock value) in phase II, we identified the time point, , at which is reached. Fig. 3C shows a box plot of and Fig. 3D of against the downshock magnitude. Wild-type cells (in blue) show increasing overshoot with increasing shock magnitude, reaching for the highest shock. In contrast, the double mutant (in red) does not overshoot in any of the conditions. The time it takes to reach increases with the shock magnitude both for the wild type and the double mutant, reaching 8 min for the wild type, and 5 min for the double mutant. is consistently lower at different shock magnitudes for the double mutant compared with the wild type.
Growth at High Osmolarities, Together with Downshock, Do Not Change Membrane Permeability to Water.
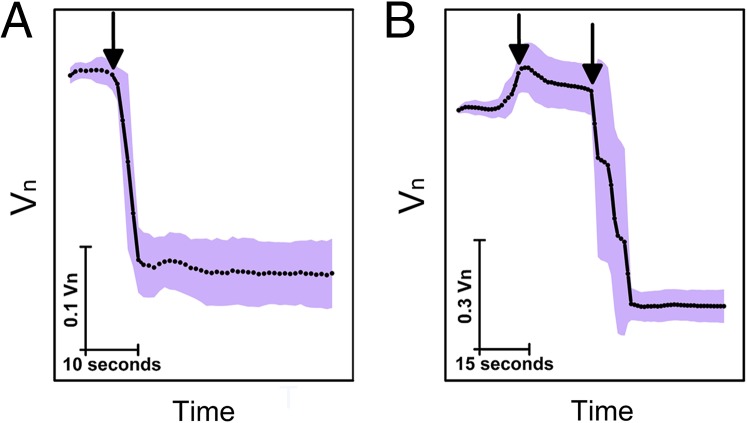
To gain more information on the physical mechanism behind the slow volume decrease in phase II, we considered the possibility that, despite fast gating of mechanosensitive channels [within tens of milliseconds (27, 28)], water exits the cell slowly. This could be the case if the cell envelope changes during growth at high osmolarities in such a way that water can no longer pass as fast. The change in envelope permeability properties with respect to water could be caused by changes in lipid composition of the bilayers, number of porins present in the outer membrane, aquaporin numbers in the inner membrane (AqpZ), as well as changes in the number of any other channels that might be facilitating water transport across the cell envelope. Alternatively, a change in water flux for any (or a combination of) the above-named reasons could occur after initial expansion immediately postdownshock. Fig. 4A shows average volume of 13 cells grown in media of 1,370 mOsmol subjected to a sudden upshock of 1,272 mOsmol. Fig. 4B shows the average volume of 30 cells grown at 1,370 mOsmol, subjected to a 1,130-mOsmol downshock followed by an immediate 2,160-mOsmol upshock. In both cases, upon the upshock, the cytoplasmic volume shrinks within seconds. Fast reduction of volume shows that water can exit the cell fast in a postdownshock expanded cell. SI Appendix, Fig. S6 shows cells grown in media of a different osmolarity, 1,200 mOsmol, subjected to the same sequence of upshocks as in Fig. 4A. Cell volume shrinks fast for these cells as well. Thus, the membrane permeability with respect to water does not change with the osmolarity of the growth media or the downshock magnitude.
Fig. 4.
Cells, either grown at high osmolarities or subjected to a downshock, were exposed to a subsequent upshock. Normalized, average volume of (A) 13 and (B) 30 cells plotted against time in seconds. SD is given as a shaded area in light purple. (A) Cells grown in media of high osmolarity, 1,370 mOsmol, were subjected to a further increase of external osmolarity (upshock of 1,272 mOsmol). Arrow indicates the time at which shock was administered. Cell volume decreased within seconds posthyperosmotic shock. (B) Cells grown in the same media were subjected to a 1,130-mOsmol downshock indicated with the first arrow. Upon the downshock, volume expanded. At 1 min after the downshock, cells were exposed to a strong upshock of 2,160 mOsmol, indicated by the second arrow. Upon the upshock, cell volume decreased within seconds.
Model of E. coli Response to Downshock Explains Experimentally Observed Volume Changes.
To understand the cellular response to a sudden downshock we observed experimentally, we developed the following model. An E. coli cell is separated from its environment by the semipermeable membrane. Normally, the solute concentration in a cell is higher than that of the environment, giving rise to osmotic pressure:
| [1] |
Here, , , R, and T denote solute concentration inside the cell, solute concentration in the environment, ideal gas constant, and thermodynamic temperature. The constant ϕ is the molar osmotic coefficient (31) (we use osmotically active solute concentrations and set ϕ to 1).
Osmotic pressure in Eq. 1 strains the cell wall, giving rise to mechanical pressure. To quantify it, we consider the elasticity of the cell wall, defined as follows:
| [2] |
where σ is the cell wall tension. We note that, in our model, we take into account only the elasticity of the cell wall, under the assumption that it is significantly larger compared with bilayer(s) elasticity.
For a bacterial cell represented as a cylinder with a thin wall of thickness l, cell wall tension σ is given as the following:
| [3] |
where r denotes the cell radius and P is the pressure applied to the cylindrical cell wall. At a given point in time and for a pressurized cell, the volume is set by the balance between osmotic pressure () and mechanical pressure (P) derived from the cell wall strain.
Water moves across the semipermeable cell membrane in accordance with the chemical potential gradient; therefore, water flux is given as the following:
| [4] |
We assume that the periplasmic space is in equilibrium with the external environment throughout our considerations [the outer membrane contains large number of porins (32)].
Given that osmotic pressure is proportional to the solute concentration difference, we can write the following:
| [5] |
Here, t denotes time, is the molar volume of water, and is the superficial area of the cell. K (moles per pascal⋅second) is an effective “conductivity” coefficient that characterizes the relationship between pressure difference and flow speed in moles. It depends on the nature of the flow process, which we expect to have both diffusive and quasilaminar components (33). Here, we assume that water flows mainly through porins (AqpZ) and that the total number of AqpZ does not change. Under these assumptions, changes in the surface area of the cell will not increase the water conductance and we keep constant.
To derive the expression for mechanical pressure, P, we take into account recent experiments depicting cell wall stress stiffening (5). Deng et al. (5) found that the elasticity of the cell wall in E. coli behaves as , where γ = 1.22. Here, we assume γ = 1, in rough agreement with experimental data and to simplify our model. We note that the assumption does not change the model behavior:
| [6] |
where and denote elasticity of the cell wall and pressure when cell is at its original volume before the downshock (). From Eqs. 2–6 follows:
| [7] |
Combining Eqs. 1–7, we get the following (SI Appendix):
| [8] |
V denotes the cell volume and is the initial, osmotically active solute concentration difference across the cell membrane, that is, before the downshock.
The expression for osmotic pressure (Eq. 1) and mechanical pressure (Eq. 8), as well as Eq. 5 enable us to fully characterize cell volume changes caused by the water flux in and of the cell.
Upon a sudden downshock and before the activation of MSCs, the environmental solute concentration is greatly smaller than the cellular solute concentration. Here, we assume the membrane thickness and the cell surface area do not change considerably; thus, the cell will expand at a fast rate and cell volume conforms to the following:
| [9] |
Upon reaching a critical value, , mechanosensitive channels open and cell volume can be described as follows:
| [10] |
where is the given in Eq. 9 and we use A to characterize the relative conductivity of the membrane with opened channels. For example, gives 3 times higher conductivity compared with the cell membrane with closed mechanosensitive channels.
At the point of channel opening, the water chemical potential difference is still large, with the inside lower than the outside. Thus, more water rushes into the cell through newly opened holes (Fig. 5B, Left). We note that water can flow both in and out of the cell through the channels, whose individual size reaches 3 nm upon opening (34, 35). During this period, the osmotic pressure inside the cell further increases, as the inward flow of water exceeds the outward flow of cytoplasmic solutes (Fig. 5B, Left). At the critical point at which Eq. 10 equals zero, inward pressure starts pushing both the water and the solutes out of the cell.
Fig. 5.
Model of cellular response to a sudden downshock. (A) A sudden decrease in external osmolarity leads to cell volume expansion and opening of mechanosensitive channels (panels 1 and 2). Upon channel opening, the water flux into the cell increases, as the water now flows inward through the channels as well (panel 3, blue arrow). Consequently, solutes exit the cell down the solute chemical potential and due to increased pressure inside the cell (panel 3, blue and red arrows). Solute efflux through the channels tips the competition between water influx and efflux toward efflux, which allows the recovery of cell volume to proceed (panel 4, blue arrow). (B) Cell volume (black), water influx (blue), water efflux (orange), and solute efflux (red) are given against time for the wild type (Left) and the double mutant (Right). All are solutions to the mathematical model equations using four free parameters obtained from the best fit to the representative cell volume trace in 960-mOsmol downshock condition. Eq. 10 was used to plot the cell volume. The first part of Eq. 10 was used for the water influx and the second part of Eq. 10 for the water efflux. Eq. 14 was used for solute efflux. Vertical gray lines indicate following events in sequential order: osmotic shock, opening of the mechanosensitive channels, the point in time when is reached, and closing of the channels. (C) Cell volume as predicted by the mathematical model given as a function of time. Parameters used in the best fit to the average cell volume in 960-mOsmol downshock condition were varied by ±100% for all parameters. Only one parameter is varied at a time, and the others are kept fixed. Green color indicates the lowest value used, and red, the highest (color scale is given on the Right). Increasing increases , but lowers . Increasing α and A decreases but increases , whereas increasing K and increases and decreases , with a stronger effect on the reduction. increase has little effect on , but it decreases . (D) Representative trace of the wild type (Top) and the double mutant (Bottom) for the 960-mOsmol condition is given in black. Blue line shows the result of best fit to the average trace. Shaded orange regions show fit confidence intervals; from lighter to darker orange, these are as follows: 50%, 90%, 95%, and 99%. There is a good agreement between the model and the experimental data.
Simultaneously, the opening of mechanosensitive channels rendered the cell membrane permeable to solutes, which causes solute flux down the solute chemical potential:
| [11] |
where is the diffusion coefficient of solutes and is solute concentration. Taking into account the number of mechanosensitive channels () and the cross-sectional area of a representative mechanosensitive channel (), we get the inner solutes outward flow (Fig. 5B and SI Appendix):
| [12] |
where denotes the total amount of internal solutes in moles and is the thickness of the cell membrane. We substitute the unknown parameters of the solute diffusion () and channel number () with a combined chemical flow parameter α normalized to the initial volume :
| [13] |
We thus have the following:
| [14] |
As the solutes exit, the outward flow becomes larger than the inward flow of water and the cell begins to shrink. At the same time, the overall concentration difference decreases further (Fig. 5B).
, the volume at which MSCs open and close, is expected to be the same (13). Thus, our model predicts that, to reach the cell volume that is smaller than initial, as experimentally observed in Figs. 2 and 3, needs to be small.
The qualitative predictions of our model are given in Fig. 5B and results of the fit to the Eqs. 10 and 14 in Fig. 5D, Top, and SI Appendix, Table S2. We chose a representative trace of 960-mOsmol downshock and used four parameters during the fitting routine (Materials and Methods): A, , α, and K. Some of the parameters in our equations are physical quantities that have been experimentally estimated, and we used these estimates to fix them (SI Appendix, Table S2). For example, we experimentally measured μm3. The initial difference between internal and external concentration we used, Osmol/L, is based on the experimental estimates of turgor pressure and the thickness of the cell wall, l. Measured values for turgor pressure are 300 kPa (7) and 29 kPa (5), so we use the in-between value, 100 kPa, to fix . Thickness of the cell wall was measured to be 5 nm (36). For the normalized volume at which the mechanosensitive channels open, best fit yields . Fig. 5C gives predictions of our model in a scenario where one of the model parameters changes, whereas others are kept fixed. For example, the double-mutant strain is expected to have smaller A and α, as these parameters describe the water and solute conductivity of the membrane with mechanosensitive channels opened. Our model predicts that with smaller A and α, the cell volume expansion increases and overshoot decreases (Fig. 5C), as is seen in the double mutant’s response to the downshocks (Fig. 2, Right). To test our model predictions further, we performed the fit to a representative trace of the double-mutant strain, considering the same shock magnitude as for the wild type (960 mOsmol). Fig. 5D, Bottom, and SI Appendix, Table S3 show the results of the fit. In line with our expectations, A and α obtained from the best fit are smaller in comparison with the wild type. The best fit yields for the double mutant is . Increase in in Fig. 5C results in higher cell volume expansion, but smaller overshoot, consistent with double-mutant response in Fig. 2, Right. SI Appendix, Fig. S7 shows the fit to all of the average traces obtained for the wild type and the double mutant at different shock magnitudes (Fig. 2). Good agreement between the experimental results and the fits are visible across all of the conditions. Fit parameters are plotted against the shock magnitude at the Bottom of SI Appendix, Fig. S7. A and α are higher for the wild type than the double mutant across all shock magnitudes. The inverse is true for the , which is higher for the double mutant compared with the wild type. obtained for the wild type at higher shock magnitudes saturates, in agreement with expectations.
Fig. 6B, Left, shows a prediction from the fit against the experimental data of the representative, wild-type cell volume trace shown in Fig. 5D at later time points, that is, minutes after the downshock. At later time points, experimental data show disagreement with the fit predictions.
Fig. 6.
Active response and postshock growth rates. (A) Black line shows average volume against time of 36 wild-type strains exposed to a 1,310-mOsmol downshock. Cells were grown in MM9 supplemented with NaCl and transferred into sodium phosphate buffer supplemented with 5 mM KCl. Shaded orange region indicates SD. Cell volume expanded and recovered, dropping below the initial volume. Within the last 30 min, volume increase is visible. Inset shows an example of an individual trace, where volume increase occurs after is reached at 60 min postdownshock. (B, Left) Wild-type representative trace (black) and the result of the global fit (blue) taken from Fig. 5D and shown on a longer timescale. (Right) The fit (blue) is performed with the addition of the active pumping component (see SI Appendix for details on the extended model) and plotted against the same wild-type representative trace shown on the Left and in Fig. 5D (black).
To examine the possibility that the observed disagreement is due to the contribution of active transport processes, we exposed E. coli grown in media of 1,130 mOsmol to a sudden downshock by transferring them into sodium phosphate buffer supplemented with 5 mM potassium chloride (Fig. 6A). As E. coli cannot grow in 5 mM KCl only, the increase of volume observed in phase III in Fig. 6A is likely due to active potassium import, presumably by some of the components of the osmoregulatory network responsible for the recovery from a hyperosmotic shock, such as Trk, Kup, and Kdp pumps (2). We also hypothesize that, if the disagreement between our model predictions and the experimental observation is due to active transport processes, cells subjected to a downshock in buffer media will not show an increase in cell volume upon reaching . Traces in SI Appendix, Fig. S8 show the downshock response of cells in rich modified M9 (MM9) media (taken from Fig. 2) against the cells subjected to the same shock magnitude in the buffer only. Four different shock magnitudes were selected, and in each, phase III of the recovery response is absent in the buffer, in agreement with our hypothesis. We further examined whether the addition of active transport component into our model (SI Appendix) recovers phase III observed in the experimental trace in Fig. 5D. Fig. 6B, Right, shows the result of the fit to the extended model. The fit is in very good agreement with the representative experimental trace.
Growth Rate upon Downshock Does Not Depend on the Shock Magnitude.
SI Appendix, Fig. S9 shows growth rates of individual cells after experiencing and recovering from the downshock of a given magnitude (phase IV, SI Appendix, Fig. S2), as well as population growth curves and growth rates of cells grown at high osmolarities (up to OD of 0.25–0.4) and subjected to a sudden downshock (Materials and Methods). In both cases, growth rate does not depend on the magnitude of the downshock. Doubling time of individual cells observed in the microscope tunnel slide and the population growth rate measured in the plate reader are similar, 0.6 . SI Appendix, Fig. S9C shows lag time of population growth curves upon a downshock of a given magnitude. Both the wild type and the double mutant exhibit longer lag times with higher shock magnitudes, where the double-mutant lag time sharply increases for the two largest shocks.
We examined the survival rate of the wild-type and the double-mutant strain to compare them with previous reports (29, 30). We consider a cell to be lysed if during the experimental time its total fluorescent intensity drops to background levels (Materials and Methods). SI Appendix, Fig. S10A shows probability density of a cell lysing during 75-min experimental recording time, for each shock magnitude. In SI Appendix, Fig. S10B, we classify the wild type, and in SI Appendix, Fig. S10C, double-mutant cells, into bursters, faders, rupturers, and blebers following previously described definitions (29). The percentage and type of cell lysis at our local flow rate of 0.68 μL/min is consistent with previously published studies (29). The number of lysed cells is larger for the double mutant, and for the double mutant, lysis starts at lower downshock magnitudes in agreement with previous reports (29, 30).
Discussion
By monitoring changes in volume of individual cells, we were able to explain E. coli’s response to sudden decreases in external osmolarity. We found that, upon a sudden downshock, cell volume expands within s irrespective of the shock magnitude. The volume expansion increased with shock magnitude and saturated at 15%. Previous estimates of the material properties of the cell wall used atomic force microscopy to show peptidoglycan expansion of 12% per 1 atm (37). This estimate is in agreement with our observation. Our results indicate that E. coli’s membrane can expand beyond what is expected for a lipid vesicle. The result is in line with a recent study that showed E. coli’s spheroplasts can increase their volume by more than three times, presumably by maintaining membrane reservoirs (38).
Despite the fact that mechanosensitive channels open on millisecond timescales, as observed in in vitro experiments (27, 28), the total cell volume recovery is significantly slower, taking minutes to complete. We reasoned that this could be caused by either hindered water transport across E. coli’s membrane, as a result of growth at high osmolarity or as a consequence of the downshock, or by slow solute efflux. We found evidence for the latter. Our mathematical model considers postdownshock water and solute transport according to chemical potential difference, and takes into account cell wall stress stiffening properties. The model is in agreement with experimental data and suggests that, postdownshock, water rushes into the cell cytoplasm down the chemical potential gradient. Cell volume expands and increases tension in the cell wall, which results in opening of MSCs. At the point of channel opening, even more water flows into the cell, further increasing wall tension. This effectively pushes the solutes, as well as the water, out of the cell. Furthermore, opening of the channels renders the membrane permeable to the solutes, which now move down the solute chemical potential as well. At a critical point, water no longer enters the cell but starts to exit.
Our experimental traces show clear overshoot during volume recovery that increases with shock magnitude. The observation suggests relatively low threshold for channel opening and closing. The fit of the representative trace in Fig. 5D to the equations in our mathematical model predicts that MSC channels open/close at 4% volume expansion in the wild-type strain. This is a relatively small value given the extent of maximum volume expansion we observe (15%). In the model we have assumed, guided by the in vitro studies, that MSCs open and close at the same lipid bilayer tension (13). The value predicted by the model is thus a result of balancing the observed with . However, it is possible that, in a live cell, the at which the channels open and close is not the same; in particular, because the response is the combined effect of seven different MSCs, where the number of individual channels of a given type can vary, and cooperative channel gating effects are possible (39–41).
When comparing the volume expansion of the mutant strain lacking MscL and MscS to that of the wild type, we found no difference for shocks up to 790 mOsmol, at which point the double-mutant strain expanded slightly more ( 20%) and slightly faster. Larger and faster expansion is consistent with our model. In the wild-type strain, the peak volume expansion is reached several seconds later compared with the double mutant, as upon opening of MSCs water influx competes with solute efflux and water efflux. In the double mutant, there is far less of such competition. Consequently, the water influx upon the downshock is larger and the cell volume expands more.
Overall, we found the most obvious differences between the double-mutant and the wild-type response at large shocks. The result is in agreement with previous population studies (30). However, small differences between the response of the wild-type and the double-mutant strain are visible even for smaller shocks. For example, some overshoot is observed even for smaller shocks in the wild-type strain, but none is visible in the double-mutant response. For shocks of ≥790 mOsmol, double mutant showed no growth within the 35-min observation period. At this point, we do not understand the nature of the damage caused by the absence of MscS and MscL, nor whether it is reversible. However, our results show that lack of MscS and MscL does not result solely in instant rupture or bursting. In fact, most of the nongrowing double-mutant cells that were subjected to 960- and 1,130-mOsmol downshock do not show any obvious damage as observed by fluorescent microscopy. It is possible that these cells continue growth, but at a later time.
Based on our fit parameters in the case of the wild-type trace given in Fig. 5D, MSCs will open at 4% volume increase, which corresponds to an increase in cell wall and membrane tension of 7 mN/m, which is in rough agreement with the in vitro measurements of channel opening membrane tensions, usually 5–15 mN/m (42, 43). At our measured , and based on our fit parameters, the cell wall and the inner, outer membrane tension increases by 30 mN/m.
Our study reveals the main characteristics of E. coli’s passive response to downshock, namely, fast volume expansion followed by a slow volume recovery that can overshoot below the preshock volume. Additionally, we observed a degree of cell-to-cell variability, not only for cells exposed to a given downshock but also when comparing the trends between different shock magnitudes. The observed heterogeneity may be expected, as recent studies show significant variation in MscL numbers within the population, as well as between different growth conditions (including growth on glucose in different external osmolarities) (39). Apart from MscL, the case could be similar for the six other MSCs in E. coli. Additionally, for the large number of MscL channels measured (up to 1,000) (39), cooperative gating is possible (40) and could further increase cell-to-cell variability in the overall downshock responses.
Materials and Methods
Construction of E. coli Strains.
Strains BW25113 with pWR20 and MscLMscS (double mutant) with pWR21 plasmid were used in the study for single-cell fluorescent microscopy experiments. BW25113 is the Keio collection parent strain (44). The plasmids pWR20 and pWR21 carry genes for constitutive expression of enhanced green fluorescent protein (eGFP) and kanamycin (kan) or ampicilin (amp) resistance, respectively (3). MscLMscS strain was constructed from BW25113 single-knockout strains with the mscL or mscS genes replaced with kan cassette (available from Keio collection) (44). After PCR verification of both single mutants, kan resistant mscL mutant was transformed with pCP20 plasmid to eliminate the antibiotic resistance (45). The deletion of the kan cassette and the plasmid curing was verified by kanamycin, chloramphenicol, and ampicillin sensitivity tests. Subsequently, P1 vir lysate was prepared from MscS strain carrying kan cassette, here used as the donor, for the transfection of the recipient strain, MscL. P1 transductants were plated onto selective media (LB containing 50 μg⋅mL−1 kanamycin). MscLMscS strain was verified by PCR and transformed with pWR21 plasmid.
E. coli Growth and Culturing.
E. coli strains were grown from frozen stocks (made from single colonies) in MM9 medium with 0.3% glucose, MEM essential amino acids (Sigma Aldrich), and supplemented with 0, 50, 125, 225, 300, 450, 550, 650, or 750 mM NaCl at 37 °C to an OD of 0.2–0.4, aerobically with shaking (see also SI Appendix for media osmolarities). MM9 is of the same composition as M9 (46) except sodium phosphate buffer only was used, and the media were supplemented with 1 mM KCl. MM9 was chosen over M9 to allow adjustment of potassium concentration from zero to the desired value. Media was supplemented with 50 μg/mL kanamycin. Upon reaching OD of 0.2–0.4, cells were kept at room temperature and used for sample preparation for up to 4 h (up to maximum OD of 0.65). For SI Appendix, Fig. S5, cells were grown as above except in MM9 supplemented with 450 mM sucrose. Growth curves in SI Appendix, Fig. S9 were obtained as follows: 300 μL of MM9 medium supplemented with 50, 125, 225, 300, 450, 550, 650, or 750 mM NaCl was inoculated with 2 μL of wild-type and double-mutant cells from frozen stock. OD was measured in a plate reader (BMG) every 7.5 min at 37 °C, until stationary phase. To obtain growth curves after the downshock, cells were initially inoculated as above. At an early exponential phase (OD, 0.2–0.35), 2 μL of cells from each growth media were transferred into a well with MM9 medium with no additional salt. OD was measured every 7.5 min until stationary phase.
Microscopy.
Cells were observed in epifluorescence using a Nikon Eclipse Ti microscope with perfect focus (4) at 21 °C. At the beginning of each experiment, a field of view with 10 or more “flat” cells was chosen as described in ref. 3 (SI Appendix). Images of cells expressing eGFP were acquired at an exposure time of 0.1 s using a 512 × 512 pixel back-thinned electron-multiplying charge-coupled device camera (Andor Technologies). Epi-illumination light was shuttered in-between image recordings to reduce photobleaching (SI Appendix, Fig. S11). Images were captured at every 0.2 or 0.375 s during the first 15 min and every 5 s for the rest of the recordings. Total recording time was up to 75 min.
Sample Preparation and Osmotic Shock.
Microscope tunnel slide was prepared as in ref. 47; cells were attached to the coverslip surface as in ref. 48; and to administer a sudden osmotic shock (either downshock or upshock), the tunnel is flushed with 25 μL of the low- or high-osmolarity medium, with an average rate of 2.5 μ/L as in refs. 3 and 47. To characterize the characteristic noise in the downshock experiment, we performed a control flush. The 3D histogram in SI Appendix, Fig. S11, obtained from cells grown in MM9 and flushed with MM9, shows that the noise magnitude is small for the scale of volume changes we are observing. Osmotic shocks in microfuge tubes were performed in two different ways as follows. (i) Cells from grown cell culture were imaged in a tunnel slide before the downshock; no attachment was used. A volume of 1.3 mL of cell culture was then spun down, and growth medium was removed. Tunnel slide was prepared as above and placed in the microscope. Cells were downshocked by adding 0.1 mL of MM9. A volume of 10 μL of downshocked cells was flushed into the tunnel slide. Thirty different fields of view were chosen, and cells were imaged at a frame every 1 min for 1.5 h. (ii) Several different tunnel slides were prepared before start of the experiment. Cells from the growth culture were imaged before the downshock with no attachment. A volume of 1 mL of cell culture was spun down, and growth medium was removed. Cells were shocked into 1 mL of MM9 and kept in the microfuge tube. At 2.5, 10, 20, and 30 min postdownshock, samples were added to the prepared tunnel slides for imaging.
Speed of Local Flow for Downshock Delivery.
A green fluorescent dye [10 μM Sodium Green (Molecular Probes) prepared in 10 mM Tris buffer] was used to determine the local speed of downshock delivery. Microscope tunnel slide was prepared as described above. A sudden shock was administered by flushing 25 μL of Sodium Green dye through the channel at an average flow rate of 2.5 μL/s while recording at a frame every 0.2 s. The dye was both flushed in and subsequently flushed out several times. To obtain the local flow rate close to the coverslip surface, we started with transforming fluorescent intensity in arbitrary units to microliters by taking into account the size of the field of view, the number of pixels in the image frame, and the size of the channel. Next, the difference in intensity between two adjacent frames was calculated to get the flux across a unit surface. We obtained the local flow rate of 0.68 μL/min as an average of the linear fits of the intensity profiles given in SI Appendix, Fig. S12.
Image Analysis.
Data analysis was performed on cells uniformly attached to the coverslip surface (“flat” cells) by a process of background subtraction and thresholding as described in ref. 3 and SI Appendix. Cells stuck to the surface were assumed to be a spherocylinder (2 μm long and 1 μm in diameter) and cell area obtained from image analysis was converted to volume according to the following formula: (SI Appendix, Fig. S11). When analyzing cells that were downshocked in the microfuge tube and imaged with no surface attachment, cells that were close to the coverslip surface and did not move significantly were chosen for time-lapse analysis.
Singe-Cell Data Analysis.
Traces recorded at a frame every 0.2 s were resampled to 0.375 s and further analyzed with the traces recorded at 0.375 s. Volume traces obtained upon image analysis were normalized. We used average volume of first five data points, corresponding to the first 1.8 s of recording. Next, normalized traces were passed through a median filter with the width of 5 points per window frame. Normalized and filtered traces were aligned by in phase I. Total of 609 cells was analyzed for the wild type, and 480 for the double mutant. To obtain the growth rate from single-cell measurements in SI Appendix, Fig. S9B, we analyzed the phase IV part of the average traces given in SI Appendix, Fig. S1. The part of the trace starting at the beginning of phase IV, that is, when cell volume reaches 1, was fitted to an exponential. To obtain the cumulative bar diagrams in SI Appendix, Fig. S10, we used definitions of cell lysis types described before (29). We assumed a cell to be lysed if the cell’s fluorescent intensity dropped to background level during our observation. The cells that lysed during our recording were included in the analysis only, but excluded from the rest of our analysis. is the average value around the absolute maximum value identified in each trace (we averaged 5 points either side of the maximum value). is the difference between the start of the shock and the point in time is reached. To identify and in the wild-type traces, we apply a running window (10 points wide) starting from and identify the minimum position within the trace. The double-mutant traces often leveled off rather than continuously decreased. Thus, we modified our algorithm and identified if the average value of the current running window decreases below the average value plus 3 SDs of the neighboring window. Once the condition is no longer satisfied, (and ) in the trace has been reached.
Growth Curve Analysis.
OD measurements were converted to cell density as follows. Thirty wells of 200 μL of bacterial culture were grown to OD of 0.15 in MM9 medium. The wells were pooled, and 125 μg/mL chloramphenicol was added to inhibit further cell division or growth. Cells were then concentrated to ∼20× initial concentration, diluted down to 0.0625, 0.125, 0.25, 0.5, 1, 2, 3, 5, 7, 10, and 11 times initial concentration. OD was measured in the plate reader using the same conditions as the growth curves. Cells at 1× concentration were counted using bright-field illumination and in a tunnel slide of known height (100 μm) to give the true cell density. Obtained calibration curve is given in SI Appendix, Fig. S13. A second-degree polynomial was used to convert the growth curve ODs to cell number () (49). Calibrated growth curves were fitted using a Gaussian fitting algorithm (50) to give both the maximum growth rate and lag time as defined by the tangent to the inflection point in each condition shown in SI Appendix, Fig. S9.
Model Fitting Procedures.
To simulate the model, Eqs. 10 and 14 were used to calculate the volume and moles of internal solute during the downshock. To provide the initial volume for the model, we used the measured , and the initial value for was based on previously published results (7). The opening of mechanosensitive channels was simulated by a conditional statement such that when A is positive, and zero otherwise. An adaptive Markov chain Monte Carlo sampling procedure (51) was used to fit the model to the averaged wild-type and double-mutant traces for the 960-mOsmol downshock. During fitting, simulation of the model was performed by the ode function in Matlab (52). Fig. 5D shows the posterior confidence intervals of 50,000 simulations that comprised the Markov chain for the final parameters listed in SI Appendix, Tables S2 and S3. Upon obtaining the best fit, we used the fit parameters to generate Fig. 5B. Water influx was obtained from the first part of the Eq. 9 before channels open and Eq. 10 after. Similarly, water efflux was obtained from the second part of Eq. 9 and Eq. 10. Solute efflux was obtained from Eq. 14. To obtain Fig. 5C, we have varied the parameters obtained from the best fit to the wild-type data by ±100% for all parameters, with a step size of 10%. Total cellular volume was plotted by solving Eq. 10.
Supplementary Material
Acknowledgments
We thank all of the members of T.P. and F.B. laboratories for their comments and support, and Meriem El Karoui for granting access to her microscope during the course of the project. R.B. was supported through a Biotechnology and Biological Sciences Research Council (BBSRC) Crossing Biological Membranes Network (CBMNet) Scholarship; Y.L., J.Y., and F.B. by National Natural Science Foundation of China Grant 31370847, Recruitment Program of Global Youth Experts, and Human Frontier Science Program Grant RGP0041/2015; T.P. by BBSRC CBMNet and Human Frontier Science Program Grant RGP0041/2015; S.H. by the Darwin Trust and Industrial Biotechnology Innovation Centre grant (to T.P.); and K.S. by the BBSRC Industrial Collaborative Awards in Science and Engineering grant (to T.P.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.M.W. is a Guest Editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1522185113/-/DCSupplemental.
References
- 1.Koch AL. How bacteria grow and divide in spite of internal hydrostatic pressure. Can J Microbiol. 1985;31(12):1071–1084. doi: 10.1139/m85-204. [DOI] [PubMed] [Google Scholar]
- 2.Wood JM. Bacterial responses to osmotic challenges. J Gen Physiol. 2015;145(5):381–388. doi: 10.1085/jgp.201411296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pilizota T, Shaevitz JW. Fast, multiphase volume adaptation to hyperosmotic shock by Escherichia coli. PLoS One. 2012;7(4):e35205. doi: 10.1371/journal.pone.0035205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pilizota T, Shaevitz JW. Origins of Escherichia coli growth rate and cell shape changes at high external osmolality. Biophys J. 2014;107(8):1962–1969. doi: 10.1016/j.bpj.2014.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Deng Y, Sun M, Shaevitz JW. Direct measurement of cell wall stress stiffening and turgor pressure in live bacterial cells. Phys Rev Lett. 2011;107(15):158101. doi: 10.1103/PhysRevLett.107.158101. [DOI] [PubMed] [Google Scholar]
- 6.Booth IR, Blount P. The MscS and MscL families of mechanosensitive channels act as microbial emergency release valves. J Bacteriol. 2012;194(18):4802–4809. doi: 10.1128/JB.00576-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cayley DS, Guttman HJ, Record MT., Jr Biophysical characterization of changes in amounts and activity of Escherichia coli cell and compartment water and turgor pressure in response to osmotic stress. Biophys J. 2000;78(4):1748–1764. doi: 10.1016/s0006-3495(00)76726-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Corry B, Martinac B. Bacterial mechanosensitive channels: Experiment and theory. Biochim Biophys Acta. 2008;1778(9):1859–1870. doi: 10.1016/j.bbamem.2007.06.022. [DOI] [PubMed] [Google Scholar]
- 9.Kung C, Martinac B, Sukharev S. Mechanosensitive channels in microbes. Annu Rev Microbiol. 2010;64:313–329. doi: 10.1146/annurev.micro.112408.134106. [DOI] [PubMed] [Google Scholar]
- 10.Martinac B, Kloda A. Mechanosensory transduction. In: Egelman EH, editor. Comprehensive Biophysics. Elsevier; Amsterdam: 2012. pp. 108–141. [Google Scholar]
- 11.Sackin H. Mechanosensitive channels. Annu Rev Physiol. 1995;57:333–353. doi: 10.1146/annurev.ph.57.030195.002001. [DOI] [PubMed] [Google Scholar]
- 12.Pak OS, Young YN, Marple GR, Veerapaneni S, Stone HA. Gating of a mechanosensitive channel due to cellular flows. Proc Natl Acad Sci USA. 2015;112(32):9822–9827. doi: 10.1073/pnas.1512152112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Edwards MD, et al. Characterization of three novel mechanosensitive channel activities in Escherichia coli. Channels (Austin) 2012;6(4):272–281. doi: 10.4161/chan.20998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berrier C, Besnard M, Ajouz B, Coulombe A, Ghazi A. Multiple mechanosensitive ion channels from Escherichia coli, activated at different thresholds of applied pressure. J Membr Biol. 1996;151(2):175–187. doi: 10.1007/s002329900068. [DOI] [PubMed] [Google Scholar]
- 15.Booth IR, Edwards MD, Miller S. Bacterial ion channels. Biochemistry. 2003;42(34):10045–10053. doi: 10.1021/bi034953w. [DOI] [PubMed] [Google Scholar]
- 16.Schumann U, et al. YbdG in Escherichia coli is a threshold-setting mechanosensitive channel with MscM activity. Proc Natl Acad Sci USA. 2010;107(28):12664–12669. doi: 10.1073/pnas.1001405107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li Y, Moe PC, Chandrasekaran S, Booth IR, Blount P. Ionic regulation of MscK, a mechanosensitive channel from Escherichia coli. EMBO J. 2002;21(20):5323–5330. doi: 10.1093/emboj/cdf537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Martinac B, Buechner M, Delcour AH, Adler J, Kung C. Pressure-sensitive ion channel in Escherichia coli. Proc Natl Acad Sci USA. 1987;84(8):2297–2301. doi: 10.1073/pnas.84.8.2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chang G, Spencer RH, Lee AT, Barclay MT, Rees DC. Structure of the MscL homolog from Mycobacterium tuberculosis: A gated mechanosensitive ion channel. Science. 1998;282(5397):2220–2226. doi: 10.1126/science.282.5397.2220. [DOI] [PubMed] [Google Scholar]
- 20.Bass RB, Strop P, Barclay M, Rees DC. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science. 2002;298(5598):1582–1587. doi: 10.1126/science.1077945. [DOI] [PubMed] [Google Scholar]
- 21.Perozo E, Cortes DM, Sompornpisut P, Kloda A, Martinac B. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature. 2002;418(6901):942–948. doi: 10.1038/nature00992. [DOI] [PubMed] [Google Scholar]
- 22.Sukharev SI, Sigurdson WJ, Kung C, Sachs F. Energetic and spatial parameters for gating of the bacterial large conductance mechanosensitive channel, MscL. J Gen Physiol. 1999;113(4):525–540. doi: 10.1085/jgp.113.4.525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sukharev S, Betanzos M, Chiang CS, Guy HR. The gating mechanism of the large mechanosensitive channel MscL. Nature. 2001;409(6821):720–724. doi: 10.1038/35055559. [DOI] [PubMed] [Google Scholar]
- 24.Blount P, et al. Membrane topology and multimeric structure of a mechanosensitive channel protein of Escherichia coli. EMBO J. 1996;15(18):4798–4805. [PMC free article] [PubMed] [Google Scholar]
- 25.Ou X, Blount P, Hoffman RJ, Kung C. One face of a transmembrane helix is crucial in mechanosensitive channel gating. Proc Natl Acad Sci USA. 1998;95(19):11471–11475. doi: 10.1073/pnas.95.19.11471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 1981;391(2):85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 27.Chiang CS, Anishkin A, Sukharev S. Gating of the large mechanosensitive channel in situ: Estimation of the spatial scale of the transition from channel population responses. Biophys J. 2004;86(5):2846–2861. doi: 10.1016/S0006-3495(04)74337-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Boer M, Anishkin A, Sukharev S. Adaptive MscS gating in the osmotic permeability response in E. coli: The question of time. Biochemistry. 2011;50(19):4087–4096. doi: 10.1021/bi1019435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bialecka-Fornal M, Lee HJ, Phillips R. The rate of osmotic downshock determines the survival probability of bacterial mechanosensitive channel mutants. J Bacteriol. 2015;197(1):231–237. doi: 10.1128/JB.02175-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Levina N, et al. Protection of Escherichia coli cells against extreme turgor by activation of MscS and MscL mechanosensitive channels: Identification of genes required for MscS activity. EMBO J. 1999;18(7):1730–1737. doi: 10.1093/emboj/18.7.1730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dick DAT. Cell Water. Butterworths; London: 1966. pp. 16–25. [Google Scholar]
- 32.Hancock RE. Role of porins in outer membrane permeability. J Bacteriol. 1987;169(3):929–933. doi: 10.1128/jb.169.3.929-933.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mauro A. Nature of solvent transfer in osmosis. Science. 1957;126(3267):252–253. doi: 10.1126/science.126.3267.252. [DOI] [PubMed] [Google Scholar]
- 34.Wang Y, et al. Single molecule FRET reveals pore size and opening mechanism of a mechano-sensitive ion channel. eLife. 2014;3:e01834. doi: 10.7554/eLife.01834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Louhivuori M, Risselada HJ, van der Giessen E, Marrink SJ. Release of content through mechano-sensitive gates in pressurized liposomes. Proc Natl Acad Sci USA. 2010;107(46):19856–19860. doi: 10.1073/pnas.1001316107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yao X, et al. Atomic force microscopy and theoretical considerations of surface properties and turgor pressures of bacteria. Colloids Surf B Biointerfaces. 2002;23(2):213–230. [Google Scholar]
- 37.Yao X, Jericho M, Pink D, Beveridge T. Thickness and elasticity of Gram-negative murein sacculi measured by atomic force microscopy. J Bacteriol. 1999;181(22):6865–6875. doi: 10.1128/jb.181.22.6865-6875.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sun Y, Sun TL, Huang HW. Physical properties of Escherichia coli spheroplast membranes. Biophys J. 2014;107(9):2082–2090. doi: 10.1016/j.bpj.2014.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bialecka-Fornal M, Lee HJ, DeBerg HA, Gandhi CS, Phillips R. Single-cell census of mechanosensitive channels in living bacteria. PLoS One. 2012;7(3):e33077. doi: 10.1371/journal.pone.0033077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ursell T, Huang KC, Peterson E, Phillips R. Cooperative gating and spatial organization of membrane proteins through elastic interactions. PLoS Comput Biol. 2007;3(5):e81. doi: 10.1371/journal.pcbi.0030081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Grage SL, et al. Bilayer-mediated clustering and functional interaction of MscL channels. Biophys J. 2011;100(5):1252–1260. doi: 10.1016/j.bpj.2011.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Belyy V, Kamaraju K, Akitake B, Anishkin A, Sukharev S. Adaptive behavior of bacterial mechanosensitive channels is coupled to membrane mechanics. J Gen Physiol. 2010;135(6):641–652. doi: 10.1085/jgp.200910371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sukharev S. Purification of the small mechanosensitive channel of Escherichia coli (MscS): The subunit structure, conduction, and gating characteristics in liposomes. Biophys J. 2002;83(1):290–298. doi: 10.1016/S0006-3495(02)75169-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Baba T, et al. Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: The Keio collection. Mol Syst Biol. 2006;2:2006.0008. doi: 10.1038/msb4100050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Datsenko KA, Wanner BL. One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products. Proc Natl Acad Sci USA. 2000;97(12):6640–6645. doi: 10.1073/pnas.120163297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cold Spring Harbor Laboratory M9 minimal medium (standard) Cold Spring Harb Protoc. 2010 doi: 10.1101/pdb.rec12295. [DOI] [Google Scholar]
- 47.Pilizota T, Shaevitz JW. Plasmolysis and cell shape depend on solute outer-membrane permeability during hyperosmotic shock in E. coli. Biophys J. 2013;104(12):2733–2742. doi: 10.1016/j.bpj.2013.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Pilizota T, et al. A molecular brake, not a clutch, stops the Rhodobacter sphaeroides flagellar motor. Proc Natl Acad Sci USA. 2009;106(28):11582–11587. doi: 10.1073/pnas.0813164106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Koch AL. Turbidity measurements of bacterial cultures in some available commercial instruments. Anal Biochem. 1970;38(1):252–259. doi: 10.1016/0003-2697(70)90174-0. [DOI] [PubMed] [Google Scholar]
- 50.Swain PS, et al. Inferring time-derivatives, including cell growth rates, using Gaussian processes. BioRxiv. 2016 doi: 10.1101/055483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Haario H, Laine M, Mira A, Saksman E. DRAM: Efficient adaptive MCMC. Stat Comput. 2006;16(4):339–354. [Google Scholar]
- 52.The MathWorks, Inc. MATLAB and Statistics Toolbox Release. The MathWorks, Inc.; Natick, MA: 2015. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.