Significance
Lipid membranes exhibit a variety of morphologies tailored to perform specific functions of cells and their organelles. A unique lipid structure is the nuclear envelope which houses the genome and plays a vital role in genome organization and signaling pathways. The nuclear envelope is composed of two fused membranes with thousands of toroid-shaped pores with extremely high curvatures, the origin of which remains an open question in biology. Here, we show that the architecture of this “ultradonut” may be generated by nanoscale buckling instabilities triggered by membrane stresses during nuclei growth. Our findings may help understand the impact of membrane mechanics on the geometry and the functionality of the nucleus and more generally, other double-membrane organelles in cells.
Keywords: nuclear envelope, lipid membranes, topology, buckling instability
Abstract
The nuclear envelope is a unique topological structure formed by lipid membranes in eukaryotic cells. Unlike other membrane structures, the nuclear envelope comprises two concentric membrane shells fused at numerous sites with toroid-shaped pores that impart a “geometric” genus on the order of thousands. Despite the intriguing architecture and vital biological functions of the nuclear membranes, how they achieve and maintain such a unique arrangement remains unknown. Here, we used the theory of elasticity and differential geometry to analyze the equilibrium shape and stability of this structure. Our results show that modest in- and out-of-plane stresses present in the membranes not only can define the pore geometry, but also provide a mechanism for destabilizing membranes beyond a critical size and set the stage for the formation of new pores. Our results suggest a mechanism wherein nanoscale buckling instabilities can define the global topology of a nuclear envelope-like structure.
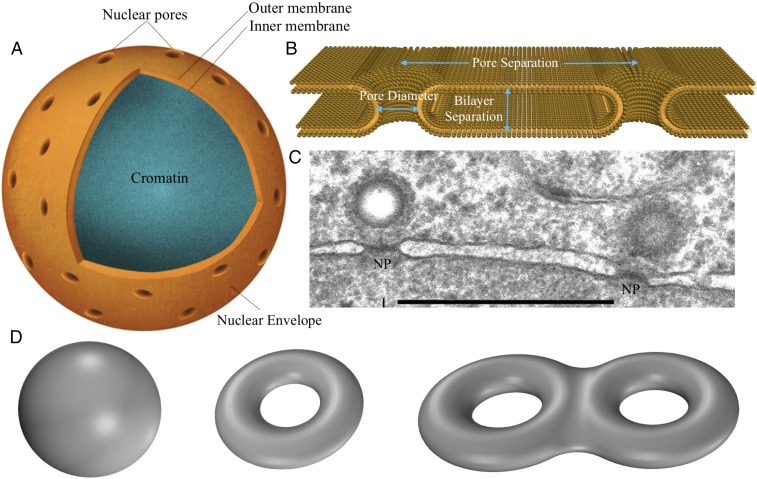
The cell nucleus is bounded by two lipid bilayers arranged in a unique geometry called the nuclear envelope. These two bilayers are shaped into concentric spheres that are maintained at a remarkably uniform spacing of nm (1), and yet are fused together at thousands of pores (holes) at an average spacing of nm from each other [based on areal density measurements (2–4)]. At these pores, the membranes locally take on a toroid shape with a radius of curvature on the order of nm (Fig. 1). Lipid structures such as vesicles, spherocylinders (bacterial membranes), and biconcave discoids (red blood cell membranes) are all closed structures with no holes, and hence possess a zero genus (5) (Fig. 1). A donut, on the other hand, is also a closed structure but has one hole, and as a result has a genus of 1 (Fig. 1). If we fuse two donuts, we get a shape with a genus of 2, and if we fuse thousands of donuts and bend them to form a sphere, we obtain a nucleus-membrane–like structure (Fig. 1). This structure, therefore, can be thought of as an “ultradonut” with a genus on the order of thousands. How the two membranes assemble in a unique arrangement with such a large number of local fusions is a fundamental question in both physics and biology that is still unresolved (6–10). To seek an answer to this puzzle, we ask three natural questions based on the common notions in the field of membrane physics.
Fig. 1.
Nuclear envelope and the topology. (A) Nuclear envelope with two concentric membrane spheres fused at thousands of sites with toroid-shaped pores. (B) Key geometric parameters that define the nuclear envelope architecture. These include the pore diameter, bilayer separation, and the pore separation. The forces and mechanisms that regulate this unique geometry are not yet understood. (C) Experimental image showing a section of the nuclear envelope with nuclear pores labeled as NP lying in the same observed plane. Other NPs might be out of the plane of observation. [Scale bar, 500 nm (14).] The image shows the uniform bilayer separation and the typical pore separation. Beyond 100 nm, the bilayers essentially become flat and lose the curvature memory associated with the pore region. (D) Shapes exhibiting different genus: sphere has a genus of 0, donut has a genus of 1, and two fused donuts have a genus of 2.
First, can membrane curvature-mediated interactions determine optimal pore number and interpore separation? This principle has been successfully used to predict the interactions of membrane-embedded proteins and nanoparticles (11–13). However, in the case of nuclear envelope, Fig. 1C (14) shows that the curved shapes of the membranes at the pores do not persist over interpore length scales; The “curvature memory” of the membranes is lost beyond nm and they remain essentially flat in between the pores. As a result, a pore does not sense the presence of other pores in its vicinity via the membrane, suggesting that the curvature-mediated interactions by themselves cannot determine the interpore separation, the critical length scale required to define the genus.
Second, can the system energy provide an optimal pore number and interpore separation? For a membrane, the system energy comprises three contributions (15): (i) the elastic bending energy of the surface given by the well-known Helfrich–Canham energy (16, 17), which penalizes geometric deviation from a flat state; (ii) the energy due to the in-plane stress that resists areal change; and (iii) the energy due to the out-of-plane stress that resists changes in volume (details are presented in Methods). We can now consider two concentric bilayer spheres with an in-plane stress λ and out-of-plane stress p connected with n pores at equilibrium. Let us assume that the addition of each new pore changes the bending energy by , area by , and volume by . For noninteracting n pores (as discussed above), the system energy is , minus the energy of the spheres with no pores (a constant). Without invoking any specific values of the parameters, we can draw three possible outcomes: (i) > 0, which implies that the addition of each new pore increases the system energy and it is, therefore, optimal to have zero pores. (ii) < 0, which means that the addition of each new pore decreases the system energy and it is, therefore, optimal to have the maximum number of pores allowed by the surface area of the spheres; and (iii) = 0, which suggests that system energy is insensitive to the number of pores and the system, therefore, can have an arbitrary number of pores. Therefore, all three outcomes do not furnish a critical length scale that determines the genus of nucleus membranes.
Third, can the nuclear pore complex (NPC), the massive protein structure housed at the pore sites, determine the pore spacing? The chronological sequence of pore formation and NPC assembly has been experimentally observed in a study by Kiseleva et al. (18). The study reveals that first an isolated pore is formed from the fusion of membranes and next, NPC proteins assemble at the pore site. Thus, pore nucleation precedes NPC assembly, and NPC–membrane interaction is unlikely to be the determinant of pore spacing.
In this paper, we investigate the local geometry and the stability of membranes in the presence of membrane stresses. Using nonlinear computational modeling, we show that modest in- and out-of-plane stresses can define a pore-like geometry and trigger buckling instabilities that can lead to sites for fusion between two bilayers. Whereas tensile in-plane stress confers remarkable robustness and is able to predict observed local pore geometries, small values of compressive stress, along with modest out-of-plane stress, destabilize the bilayer and trigger buckling instabilities. We propose a mechanism by which local nanoscale instabilities define a critical length scale and determine the observed global topology.
Methods
We model a bilayer as a 2D surface ω. The strain-energy density W for isotropic membranes is dependent on the mean curvature and the Gaussian curvature (16, 17, 48–52). Equilibrium configurations render stationary the augmented energy functional
| [S1] |
where λ and p are the Lagrange-multiplier fields associated with the area and volume constraints (53–55).
For the well-known Helfrich–Canham energy (16, 17), the equilibrium equation reduces to
| [S2] |
We simulate axisymmetric geometries parametrized by meridional arclength s and azimuthal angle Thus,
| [S3] |
where is the radius from the axis of symmetry and is the elevation above a base plane. Because there is an angle such that
| [S4] |
The mean and Gaussian curvatures in the axisymmetric setup are given by (54, 55)
| [S5] |
| [S6] |
The equilibrium equation (Eq. S2) simplifies to
| [S7] |
where
| [S8] |
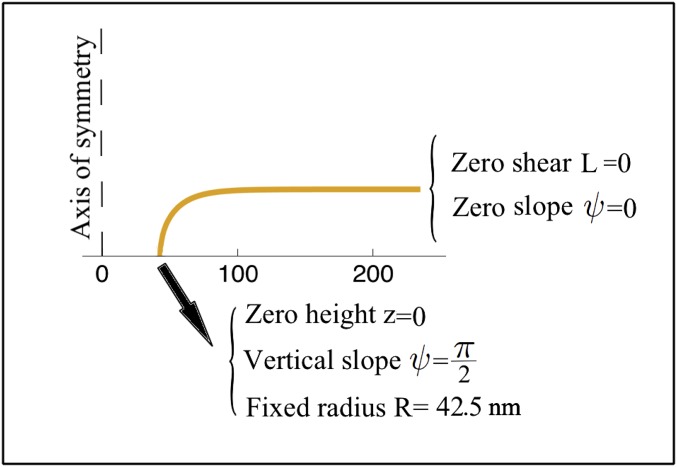
To compute the equilibrium geometry we solve the system of equations comprising S4 (both parts), S5, S7, and S8 for the unknowns , and L. To solve these equations, we prescribe the following five boundary conditions at the two ends of the simulation domain as shown in Fig. 1:
-
i)For the near end at :
[S9] -
ii)For the far end:
[S10]
The last condition arises from the equilibrium and the periodicity requirements and is equivalent to a clamped roller support.
We solve the set of ordinary differential equations along with the boundary conditions in MATLAB using “bvp4c solver.” We simulated the effects of the mechanical state of the membrane, defined by the in-plane stress (λ, also called tension) and the out-of-plane stress (p, also called pressure) on the bilayer geometry. We perform these simulations for different bilayer sizes.
Results
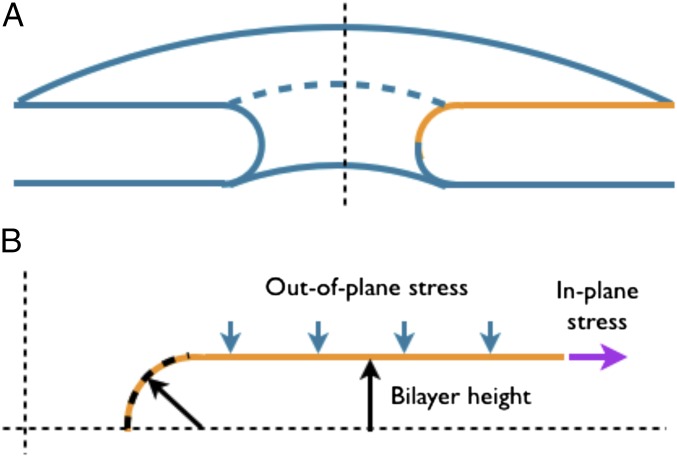
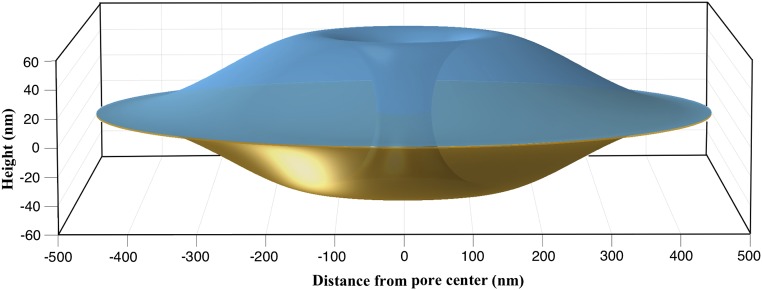
We investigated the equilibrium shapes of a circular bilayer with a preexisting pore of radius nm [observed pore radius in mammalian cells (19)]. We modeled the bilayer as an elastic and axisymmetric 2D surface. The symmetry enables simulation of just one curve (shown in yellow in Fig. 2; also shown is the resulting 3D surface of revolution) to compute the bilayer morphology. We primarily focused our attention on the outer (upper) membrane as the inner (lower) membrane is kinematically constrained due to its connection with an underlying filamentous sheet (nuclear lamina). We simulated the effects of the mechanical state of the membrane, defined by the in-plane stress (λ, also called tension) and the out-of-plane stress (p, also called pressure) on the bilayer geometry (Fig. 2). Because the pore radius was prescribed, bilayer geometry near and away from the pore is determined by a single parameter: the bilayer height (Fig. 2). The orthogonal curvatures in the circumferential and the meridional directions at the pore are given by the inverse of the prescribed pore radius and the computed bilayer height. In addition to the stresses, we also examined the effect of the bilayer size on the equilibrium shape. Fig. 3 shows a strong influence of on the bilayer geometry and stability and reveals two key findings.
Fig. 2.
Simulated membrane geometry. (A) Because of axisymmetry, only the curve in yellow was simulated. The solid of revolution was obtained by revolving the curve around the vertical axis. (B) The simulated curve subjected to the in-plane and out-of-plane stresses. The arrows indicate the positive directions of the in-plane and out-of-plane stresses. The boundary conditions employed in the simulations are shown in Fig. S1.
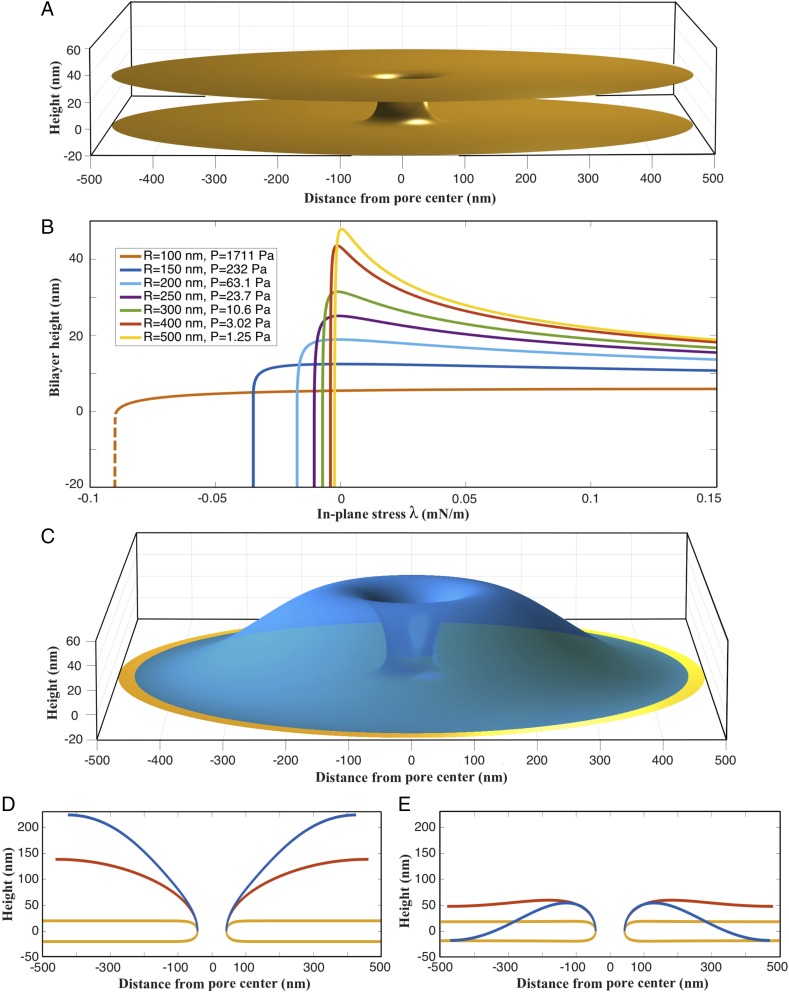
Fig. 3.
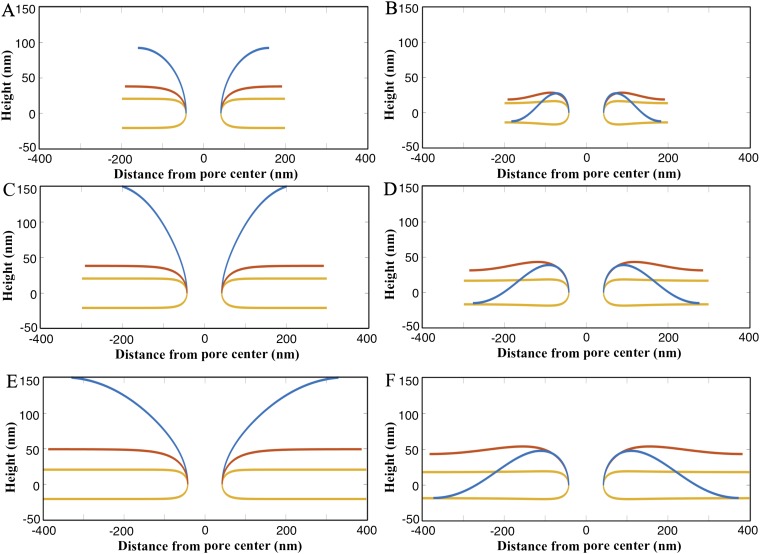
Impact of in- and out-of plane stresses on membrane geometry. (A) Three-dimensional geometry of a bilayer with , mN/m, and . (B) The deflection response of bilayers with different radii R as a function of in-plane stress when subjected to critical out-of-plane stress . The bilayers show initial expansion upon λ-reduction. However, they undergo snap-through buckling instability at critical . (C) Three-dimensional geometry of a buckled bilayer with , mN/m, and . (D) Two-dimensional geometry of an expanding bilayer for P = 0. The red curve is for λ = −0.04 mN/m and the blue curve is for λ = −0.06 mN/m. (E) Two-dimensional geometry of the buckled bilayer for P = 1.25 Pa. The red curve is for λ = 0.0005 mN/m and the blue curve is for λ = −0.0024 mN/m.
Fig. S1.
Prescribed boundary conditions for the simulation of an axisymmetric bilayer.
First, in the tension regime (positive λ-values), the bilayer exhibits a remarkable uniform height away from the pore. Fig. 3A shows the 3D geometry of one such simulated bilayer ( nm, mN/m, and Pa) (see Fig. S2 for more bilayer geometries). The bilayer height initially decreases with the in-plane stress but becomes insensitive at higher in-plane stress values (Fig. 3B). Moreover, for higher normal stresses (parameter p), the bilayer height becomes highly insensitive to the in-plane stress. Collectively, these results show that the experimentally observed half-separation between bilayers of nm can be achieved for a wide range of values. In addition, these simulations also show that bilayers can maintain a uniform height over long distances in the tensile regime (Fig. S3).
Fig. S2.
Deflection response due to a reduction in the in-plane stress for (A) a 200-nm-radius bilayer at ; (B) a 200-nm-radius bilayer at ; (C) a 300-nm-radius bilayer at ; (D) a 300-nm-radius bilayer at ; (E) a 400-nm-radius bilayer at ; and (F) a 400-nm-radius bilayer at .
Fig. S3.
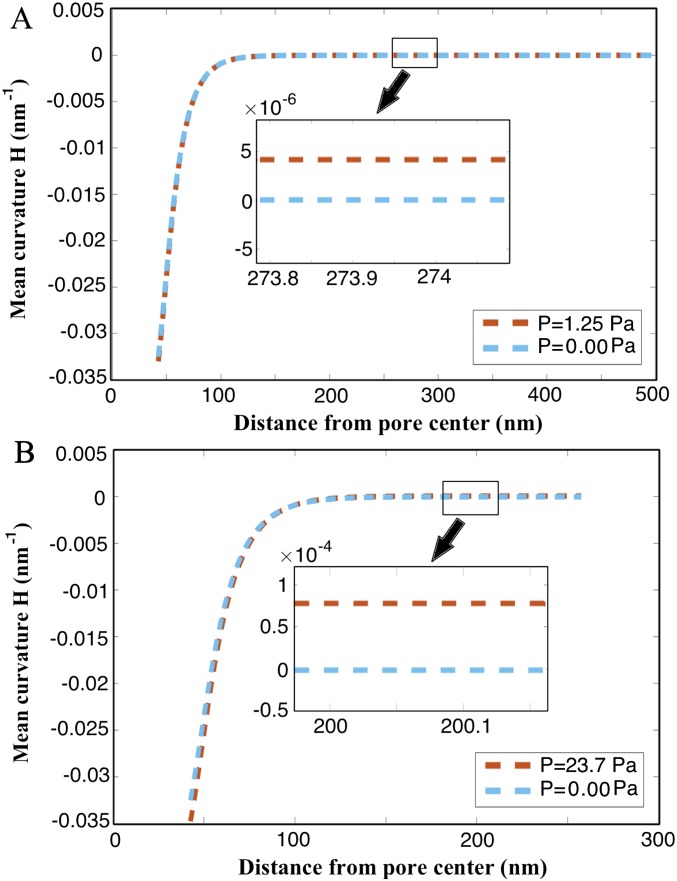
Mean curvature variation along the bilayer for (A) a 500-nm-radius patch size and 0.15-mN/m in-plane stress and (B) a 250-nm-radius patch size and 0.15-mN/m in-plane stress.
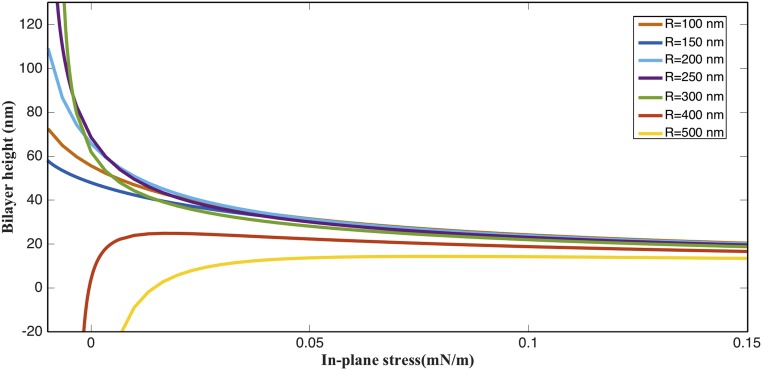
Second, in the compression regime (negative λ-values), the bilayer height drops precipitously below a threshold in-plane stress at each of the chosen values of p and R (Fig. 3B). This drop shows the presence of a buckling instability where the outer bilayer moves toward the inner bilayer above a critical pressure () and below a critical negative in-plane stress (); the pressures in Fig. 3B are the critical pressures. For example, Fig. 3C shows the 3D geometry of a buckled bilayer with , mN/m, and . This buckling instability is similar to a snap-through buckling instability observed in columns, plates, and shells (20). If only the in-plane stress is present, the simulated curved bilayer always buckles outward owing to the convex curvature at the pore. If , the bilayer continues to expand out and buckle outward for negative (compressive) in-plane stress. Thus, owing to the curvature at the pore, a buckling instability that moves the membrane inward uniquely requires the presence of a compressive normal stress. The buckling response is, therefore, greatly influenced by the pore geometry, as has been previously observed in the context of short toroidal segments (21, 22). Fig. 3 D and E shows the contrasting outward and inward buckling of a 500-nm-radius bilayer for and , respectively. Interestingly, for , even tensile in-plane stress in the membrane inward can trigger inward buckling (Figs. S4 and S5). These results show that two separate bilayers can be brought together for fusion in a preexisting bilayer–pore geometry by triggering buckling instability in one or both of the bilayers (Fig. S6 and Movies S1–S3).
Fig. S4.
Deflection response of the bilayers with different radii for a nominal . Bilayers with radii equal and smaller to 300 nm continue to expand out and do not undergo instability. In contrast, bilayers with 400- and 500-nm radii undergo buckling instability. Also note that the bilayer with R = 500 nm undergoes instability at tensile in-plane stress. This shows the high vulnerability of larger bilayers (500-nm radius) to in-plane stress reduction.
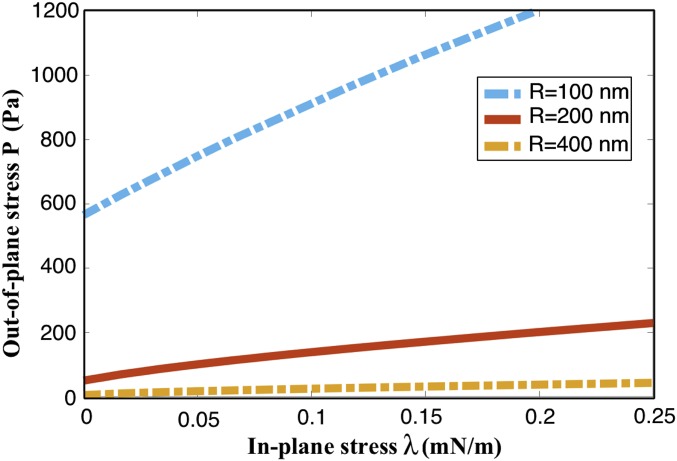
Fig. S5.
Magnitude of out-of-plane stress (p) required to bend the membrane to fusion point for a range of positive in-plane stress values. For every size, a bilayer can undergo inward deformation even in the presence of tensile in-plane stresses due to the applied out-of-plane stress.
Fig. S6.
Three-dimensional geometry of the buckled bilayer. In this scenario we assume both bilayers are buckling toward each other. This does not influence the stresses required to buckle because of the sharp decrease in the bilayer height near the critical point.
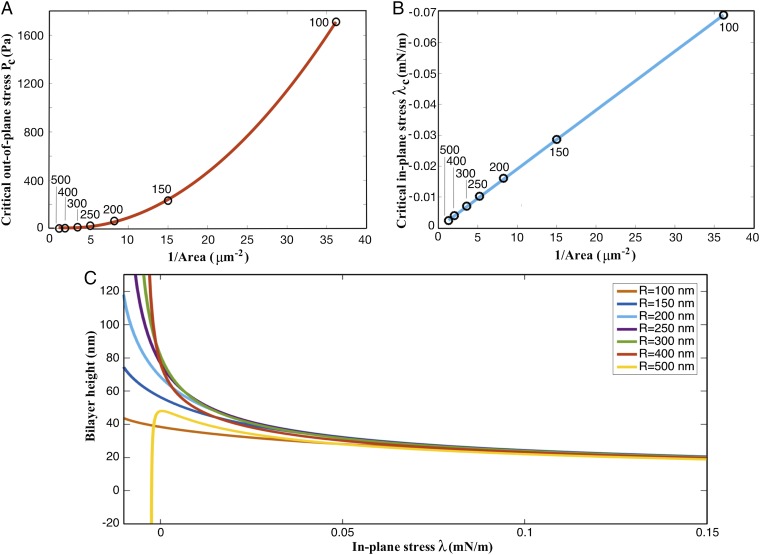
The buckling response is extremely sensitive to the area of the membrane in between the pores (bilayer size). Both and decrease with an increase in the bilayer size (Fig. 4 A and B). The critical out-of-plane stress () rapidly increases as the radius is decreased below R = 250 nm. The critical in-plane stress (, corresponding to ), on the other hand, shows a linear variation with the inverse of the area. The linear fit reveals that (κ is the bending modulus and A is the area of the simulated bilayer). These results indicate that the propensity for buckling depends significantly on the bilayer area in between adjacent pores. Fig. 4C shows the contrasting stability of the bilayers at a modest . For small interpore areas, the bilayer buckles outward at negative in-plane stresses, whereas for larger area, it bends inward. These results suggest that interpore spacings significantly larger than 500 nm should not exist because the bilayer is highly vulnerable to even nearly vanishing values of in-plane and normal compressive stresses. Consistent with these numerical findings, the interpore spacing in mammalian nuclei is observed to be in the range of nm. The proposed mechanism therefore provides a critical length scale and suggests that nanoscale buckling instabilities can potentially define the global topology of the double-membrane structure. Three important remarks are in order here.
Fig. 4.
Ease of buckling depends on the bilayer size. (A) Critical out-of-plane stress () needed to buckle a bilayer inward as a function of the inverse of the bilayer area (text adjacent to the data points shows the corresponding bilayer radius). The critical pressure undergoes a significant increase for nm. (B) Critical in-plane stress () needed to buckle a bilayer inward as a function of the inverse of the bilayer area (text adjacent to the data points shows the corresponding bilayer radius). The critical stress varies linearly with the inverse of the area. The slope of the curve is (κ is the bending modulus and A is the area of the simulated bilayer). (C) The deflection response of bilayers with different radii R as a function of in-plane stress when subjected to . Bilayers with deform outward, whereas bilayer with buckle inward. The plot reveals the propensity of larger bilayers to undergo instability at minimal in- and out-of-plane stresses.
First, it is conceivable that transient reductions in the in-plane stress in nuclear membranes due to fusion of cytoplasmic vesicles (18) can trigger buckling instabilities and set the stage for membrane fusion. Pioneering experimental and theoretical studies have indeed established that lipid uptake can generate compressive in-plane stress and trigger instabilities in planar membranes and spherical vesicles (23–25). The experimental study by Bassereau and coworkers (23) reveals that lipid recruitment can generate a compressive in-plane stress on the order of mN/m in spherical vesicles. This finding further supports our prediction that bilayers with radius smaller than 250 nm should be less vulnerable to buckling instabilities (Fig. 4B).
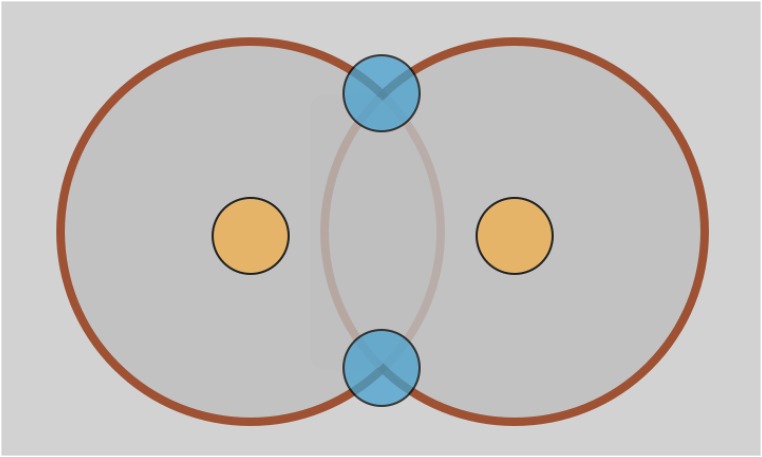
Second, because of the assumption of axisymmetry, our simulations predict a circular ring over which the two membranes meet (Fig. 3C and Fig. S7). This suggests that a new pore can form anywhere along this ring around a preexisting pore. Although the exact location cannot be predicted, the radial separation between the old and the new pores will be equal to the predicted critical length scale. Furthermore, the presence of other preexisting pores in the neighborhood will lead to similar circular rings around each pore. As a result, the intersection of these fusion rings will likely become “hot spots” for the creation of new pores (Fig. S7). In addition, the propensity of these hot spots to undergo membrane fusion could be further enhanced by aggregation of fusion proteins facilitated by curvature gradients at these junction sites.
Fig. S7.
Figure showing the interaction of fusion domains around two neighboring pores (shown in yellow). The blue regions indicate the hot spots at the interaction of two fusion domains. The inner radius of the red annulus indicates the predicted critical length scale that determines the pore separation. The width of the red annulus is controlled by the density of the existing pores. If the density is high, the width is small, and if the density is low, the width is large, leading to a bigger fusion domain where the two membranes meet.
Third, the role of the critical pressure is to counter the tendency to deform outward and make the membrane nearly flat (with a gentle bias toward inward deformation) (see the red curves in Fig. 3 D and E). Once this geometry is achieved, the membrane essentially responds as a planar membrane subjected to the applied in-plane stress. This is evident in Fig. 3E. The curved membrane in the pore region undergoes minimal deformation. The rest of the membrane undergoes deformation about the highest point which maintains its horizontal angle during the deformation. For these reasons, the highest point essentially serves as a fixed (clamped) support for the rest of the membrane. The interesting consequence is that the predicted critical in-plane stress is the same as would be calculated for a flat circular membrane with no curvature at the boundaries. The curved membrane system analyzed here, therefore, uniquely captures the combined role of the in- and out-of plane stresses on membrane buckling. We note that the tendency to buckle outward could in principle come from the curvature of the nucleus itself. But, because the curvature of the nucleus is 1/500 nm, and is orders of magnitude smaller than the pore curvature of 1/20 nm, symmetry-breaking is likely dominated by the local pore geometry.
Discussion
The nuclear envelope is a unique lipid bilayer structure with an intricate nanoscale architecture and vital biological functions (26). Using simple arguments we showed that in- and out-of-plane stresses can give rise to the pore geometry and the geometric topology observed in cell nuclei. A minimal in-plane stress of mN/m and an out-of plane stress of Pa is sufficient to explain the geometry and the topology of the double-bilayer structure. As these stresses are much smaller than the maximum stresses membranes can endure (27–29), our findings may be of value to understanding the nanoarchitecture of the nuclear envelope. Because our model predicts a stable structure over a wide range of tensile stresses, nuclei may be able to easily adjust to the changes in nuclear stresses in a biological setting and yet acquire and maintain their geometry (30).
Our study reveals that minimal compressive out-of-plane stress in a bilayer can trigger inward buckling instabilities as long as the in-plane stress is vanishingly small. For modest stresses, our study predicts a critical interpore separation of 250–500 nm. Bilayers smaller than 250-nm radius are very stable, whereas bilayers greater than 500-nm radius are highly unstable. As water can freely pass through the NPCs, we expect the transmembrane pressure across the two bilayers to be very small (nearly vanishing) (31). As shown in ref. 23, vesicle fusion leads to an in-plane stress of −0.01 mN/m. If we invoke these physiological stresses, the length scale proposed in this study emerges as a natural outcome. A similar scale is observed in vivo for the interpore distance in nuclei in mammalian cells, suggesting perhaps that lipid membrane mechanics may be an important contributor to these geometries. This is a major finding of our analysis that provides a critical length scale and shows that the critical length scale is a function of the mechanical state of the nuclear membranes. As argued earlier, other common notions such as membrane-mediated interactions and optimal system energy cannot explain the optimal genus of a fused double-bilayer structure.
Historically, buckling instabilities have been a subject of much interest. Leonhard Euler derived the celebrated Euler buckling formula for slender columns in the mid-18th century and the buckling of plates and shells was analyzed in the early 20th century (20). In the last few decades, buckling instabilities have been used to model and understand the force-deformation response of a wide variety of biological structures including DNA (32), cytoskeletal filaments (33–36), membranes (37–41), white blood cells (42), viruses (43), and tissues (44–47). Here we present an example in which the buckling of curved membranes can explain the ultradonut topology of the nuclear envelope. Because intracellular mechanical stresses impact most membrane-bound organelles, it would not be surprising if buckling instabilities contribute to the geometry and the morphological remodeling of other intracellular structures.
Supplementary Material
Acknowledgments
This work was supported by National Science Foundation Grants CMMI 1437330 (to A.A.) and CMMI 1437395 (to T.P.L.); and NIH Grants R01 EB014869 and R01 GM102486 (to T.P.L.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1604777113/-/DCSupplemental.
References
- 1.Franke WW, Scheer U, Krohne G, Jarasch ED. The nuclear envelope and the architecture of the nuclear periphery. J Cell Biol. 1981;91(3 Pt 2):39s–50s. doi: 10.1083/jcb.91.3.39s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Belgareh N, Doye V. Dynamics of nuclear pore distribution in nucleoporin mutant yeast cells. J Cell Biol. 1997;136(4):747–759. doi: 10.1083/jcb.136.4.747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.D’Angelo MA, Anderson DJ, Richard E, Hetzer MW. Nuclear pores form de novo from both sides of the nuclear envelope. Science. 2006;312(5772):440–443. doi: 10.1126/science.1124196. [DOI] [PubMed] [Google Scholar]
- 4.Dultz E, Ellenberg J. Live imaging of single nuclear pores reveals unique assembly kinetics and mechanism in interphase. J Cell Biol. 2010;191(1):15–22. doi: 10.1083/jcb.201007076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kreyszig E. Differential Geometry. Dover Publications, Inc.; Mineola, NY: 1991. pp. 172–174. [Google Scholar]
- 6.Rothballer A, Kutay U. Poring over pores: Nuclear pore complex insertion into the nuclear envelope. Trends Biochem Sci. 2013;38(6):292–301. doi: 10.1016/j.tibs.2013.04.001. [DOI] [PubMed] [Google Scholar]
- 7.Talamas JA, Hetzer MW. POM121 and Sun1 play a role in early steps of interphase NPC assembly. J Cell Biol. 2011;194(1):27–37. doi: 10.1083/jcb.201012154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fichtman B, Ramos C, Rasala B, Harel A, Forbes DJ. Inner/outer nuclear membrane fusion in nuclear pore assembly: Biochemical demonstration and molecular analysis. Mol Biol Cell. 2010;21(23):4197–4211. doi: 10.1091/mbc.E10-04-0309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Doucet CM, Hetzer MW. Nuclear pore biogenesis into an intact nuclear envelope. Chromosoma. 2010;119(5):469–477. doi: 10.1007/s00412-010-0289-2. [DOI] [PubMed] [Google Scholar]
- 10.Torbati M, Lele TP, Agrawal A. An unresolved LINC in the nuclear envelope. Cell Mol Bioeng. 2016;9(2):252–257. doi: 10.1007/s12195-016-0431-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kim KS, Neu J, Oster G. Curvature-mediated interactions between membrane proteins. Biophys J. 1998;75(5):2274–2291. doi: 10.1016/S0006-3495(98)77672-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Reynwar BJ, et al. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature. 2007;447(7143):461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- 13.Reynwar BJ, Deserno M. Membrane-mediated interactions between circular particles in the strongly curved regime. Soft Matter. 2011;7(18):8567–8575. [Google Scholar]
- 14.Ogawa-Goto K, et al. Microtubule network facilitates nuclear targeting of human cytomegalovirus capsid. J Virol. 2003;77(15):8541–8547. doi: 10.1128/JVI.77.15.8541-8547.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Phillips R, Kondev J, Theriot J, Garcia H. Physical Biology of the Cell. Garland Science; New York: 2012. pp. 427–480. [Google Scholar]
- 16.Canham PB. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J Theor Biol. 1970;26(1):61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 17.Helfrich W. Elastic properties of lipid bilayers: Theory and possible experiments. Z Naturforsch C. 1973;28(11):693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 18.Kiseleva E, Rutherford S, Cotter LM, Allen TD, Goldberg MW. Steps of nuclear pore complex disassembly and reassembly during mitosis in early Drosophila embryos. J Cell Sci. 2001;114(Pt 20):3607–3618. doi: 10.1242/jcs.114.20.3607. [DOI] [PubMed] [Google Scholar]
- 19.Yang Q, Rout MP, Akey CW. Three-dimensional architecture of the isolated yeast nuclear pore complex: functional and evolutionary implications. Mol Cell. 1998;1(2):223–234. doi: 10.1016/s1097-2765(00)80023-4. [DOI] [PubMed] [Google Scholar]
- 20.Timoshenko SP, Gere JM. Theory of Elastic Stability. Dover Publications, Inc.; Mineola, NY: 2009. pp. 46–162. 348–439, 457–520. [Google Scholar]
- 21.Stein M, McElman JA. Buckling of segments of toroidal shells. AIAA J. 1965;3(9):1704–1709. [Google Scholar]
- 22.Hutchinson JW. Initial post-buckling behavior of toroidal shell segments. Int J Solids Struct. 1967;3(1):97–115. [Google Scholar]
- 23.Solon J, et al. Negative tension induced by lipid uptake. Phys Rev Lett. 2006;97(9):098103. doi: 10.1103/PhysRevLett.97.098103. [DOI] [PubMed] [Google Scholar]
- 24.Rao M, Sarasij RC. Active fusion and fission processes on a fluid membrane. Phys Rev Lett. 2001;87(12):128101. doi: 10.1103/PhysRevLett.87.128101. [DOI] [PubMed] [Google Scholar]
- 25.Girard P, Jülicher F, Prost J. Fluid membranes exchanging material with external reservoirs. Eur Phys J E Soft Matter. 2004;14(4):387–394. doi: 10.1140/epje/i2004-10020-6. [DOI] [PubMed] [Google Scholar]
- 26.Stewart CL, Roux KJ, Burke B. Blurring the boundary: The nuclear envelope extends its reach. Science. 2007;318(5855):1408–1412. doi: 10.1126/science.1142034. [DOI] [PubMed] [Google Scholar]
- 27.Olbrich K, Rawicz W, Needham D, Evans E. Water permeability and mechanical strength of polyunsaturated lipid bilayers. Biophys J. 2000;79(1):321–327. doi: 10.1016/S0006-3495(00)76294-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mazumder A, Roopa T, Basu A, Mahadevan L, Shivashankar GV. Dynamics of chromatin decondensation reveals the structural integrity of a mechanically prestressed nucleus. Biophys J. 2008;95(6):3028–3035. doi: 10.1529/biophysj.108.132274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Neelam S, et al. Direct force probe reveals the mechanics of nuclear homeostasis in the mammalian cell. Proc Natl Acad Sci USA. 2015;112(18):5720–5725. doi: 10.1073/pnas.1502111112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Starr DA, Fridolfsson HN. Interactions between nuclei and the cytoskeleton are mediated by SUN-KASH nuclear-envelope bridges. Annu Rev Cell Dev Biol. 2010;26:421–444. doi: 10.1146/annurev-cellbio-100109-104037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li Y, et al. Moving cell boundaries drive nuclear shaping during cell spreading. Biophys J. 2015;109(4):670–686. doi: 10.1016/j.bpj.2015.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Forth S, et al. Abrupt buckling transition observed during the plectoneme formation of individual DNA molecules. Phys Rev Lett. 2008;100(14):148301. doi: 10.1103/PhysRevLett.100.148301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chaudhuri O, Parekh SH, Fletcher DA. Reversible stress softening of actin networks. Nature. 2007;445(7125):295–298. doi: 10.1038/nature05459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Brangwynne CP, et al. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J Cell Biol. 2006;173(5):733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schaap IA, Carrasco C, de Pablo PJ, MacKintosh FC, Schmidt CF. Elastic response, buckling, and instability of microtubules under radial indentation. Biophys J. 2006;91(4):1521–1531. doi: 10.1529/biophysj.105.077826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Murrell MP, Gardel ML. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc Natl Acad Sci USA. 2012;109(51):20820–20825. doi: 10.1073/pnas.1214753109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nelson P, Powers T, Seifert U. Dynamical theory of the pearling instability in cylindrical vesicles. Phys Rev Lett. 1995;74(17):3384–3387. doi: 10.1103/PhysRevLett.74.3384. [DOI] [PubMed] [Google Scholar]
- 38.Powers TR, Goldstein RE. Pearling and pinching: Propagation of Rayleigh instabilities. Phys Rev Lett. 1997;78(13):2555. [Google Scholar]
- 39.Hu M, Diggins P, Deserno M. Determining the bending modulus of a lipid membrane by simulating buckling. J Chem Phys. 2013;138(21):214110. doi: 10.1063/1.4808077. [DOI] [PubMed] [Google Scholar]
- 40.Shenoy VB, Freund LB. Growth and shape stability of a biological membrane adhesion complex in the diffusion-mediated regime. Proc Natl Acad Sci USA. 2005;102(9):3213–3218. doi: 10.1073/pnas.0500368102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Walani N, Torres J, Agrawal A. Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc Natl Acad Sci USA. 2015;112(12):E1423–E1432. doi: 10.1073/pnas.1418491112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang L, Castro CE, Boyce MC. Growth strain-induced wrinkled membrane morphology of white blood cells. Soft Matter. 2011;7(24):11319–11324. [Google Scholar]
- 43.Lidmar J, Mirny L, Nelson DR. Virus shapes and buckling transitions in spherical shells. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;68(5 Pt 1):051910. doi: 10.1103/PhysRevE.68.051910. [DOI] [PubMed] [Google Scholar]
- 44.Li B, Cao YP, Feng XQ, Gao H. Mechanics of morphological instabilities and surface wrinkling in soft materials: A review. Soft Matter. 2012;8(21):5728–5745. [Google Scholar]
- 45.Richman DP, Stewart RM, Hutchinson JW, Caviness VS., Jr Mechanical model of brain convolutional development. Science. 1975;189(4196):18–21. doi: 10.1126/science.1135626. [DOI] [PubMed] [Google Scholar]
- 46.Budday S, Steinmann P, Kuhl E. Physical biology of human brain development. Front Cell Neurosci. 2015;9:257. doi: 10.3389/fncel.2015.00257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Budday S, Kuhl E, Hutchinson JW. Period-doubling and period-tripling in growing bilayered systems. Philos Mag (Abingdon) 2015;95(28-30):3208–3224. doi: 10.1080/14786435.2015.1014443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jenkins JT. The equations of mechanical equilibrium of a model membrane. SIAM J Appl Math. 1977;32(4):755–764. [Google Scholar]
- 49.Lipowsky R. The conformation of membranes. Nature. 1991;349(6309):475–481. doi: 10.1038/349475a0. [DOI] [PubMed] [Google Scholar]
- 50.Seifert U. Configurations of fluid membranes and vesicles. Adv Phys. 1997;46(1):13–137. [Google Scholar]
- 51.Steigmann DJ. Fluid films with curvature elasticity. Arch Ration Mech Anal. 1999;150:127–152. [Google Scholar]
- 52.Deserno M. Fluid lipid membranes: From differential geometry to curvature stresses. Chem Phys Lipids. 2015;185:11–45. doi: 10.1016/j.chemphyslip.2014.05.001. [DOI] [PubMed] [Google Scholar]
- 53.Steigmann DJ, Baesu E, Rudd RE, Belak J, McElfresh M. On the variational theory of cell-membrane equilibria. Interfaces Free Bound. 2003;5(4):357–366. [Google Scholar]
- 54.Agrawal A, Steigmann DJ. Modeling protein-mediated morphology in biomembranes. Biomech Model Mechanobiol. 2009;8(5):371–379. doi: 10.1007/s10237-008-0143-0. [DOI] [PubMed] [Google Scholar]
- 55.Agrawal A, Steigmann DJ. Boundary-value problems in the theory of fluid films with curvature elasticity. Contin Mech Thermodyn. 2009;21(1):57–82. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.