Two-loads Method for Distinguishing among the Muscle Force, Velocity, and Power Producing Capacities

Abstract

It has been generally accepted that muscles could have different mechanical capacities, such as those for producing high force (F), velocity (V), and power (P) outputs. Nevertheless, the standard procedures of the evaluation of muscle function both in research and routine testing are typically conducted under a single mechanical condition, such as under a single external load. Therefore, the observed outcomes do not allow for distinguishing among the different muscle capacities. As a result, the outcomes of most of the routine testing procedures have been of limited informational value, while a number of debated issues in research have originated from arbitrarily interpreted experimental findings regarding specific muscle capacities. A solution for the discussed problem could be based on the approximately linear and exceptionally strong F-V relationship typically observed from various functional tasks performed under different external loads. These findings allow for the 'two-loads method' proposed in this Current Opinion: the functional movement tasks (e.g., maximum jumping, cycling, running, pushing, lifting, or throwing) should be tested against just 2 distinctive external loads. Namely, the F-V relationship determined by 2 pairs of the F and V data could provide the parameters depicting the maximum F (i.e., the F-intercept), V (V-intercept), and P (calculated from the product of F and V) output of the tested muscles. Therefore, the proposed two-loads method applied in both research and routine testing could provide a deeper insight into the mechanical properties and function of the tested muscles and resolve a number of debated issues in the literature.

1. Introduction

Various assessments of muscle function have been widely employed not only in research, but also in routine testing in physical medicine, rehabilitation, sports, ergonomics, and other human movement related areas. Since the time of seminal studies of Fleishman [1], the implicit presumption of a number of the applied research and testing procedures has been that muscle function is a multi-factorial phenomenon based on partly independent capacities of the involved muscles to produce certain components of the movement performance. However, most of the contemporary research and routine testing procedures are based on muscle function tests performed under a single pre-defined movement condition. Typically single outcomes of such tests (e.g., the jump height, cycling frequency, or exerted force) 'a priori' cannot distinguish among different muscle capacities. From that perspective, the present article focuses on the possibility to distinguish among the muscular force (F), velocity (V), and power (P) producing capacities from maximum performance functional movements (e.g., cycling, running, lifting, or throwing) conducted against 2 different external loads.

2. Shortcomings of standard tests of muscle capacities

An important set of partly independent muscle mechanical capacities can be derived from their classical force-velocity (F-V) and, consequently, power-velocity (P-V) relationships [2]. Specifically, the relationships distinguish among the muscle capacities for producing high F, V, and P outputs typically observed when acting against a high, low, and intermediate resistance, respectively. The same capacities could be partly independent when comprehensively assessed from various tests and conditions [1, 3, 4]. They could also be selectively altered due to the applied training or rehabilitation interventions [5, 6]. Finally, it has been generally accepted that the differences in the discussed muscle capacities could originate from various morphological [7] and neural factors [8].

The discussed multi-factorial structure of mechanical capacities of muscles inevitably leads to a major methodological shortcoming of the contemporary routine procedures for testing muscle function. Namely, the tests are usually conducted under a single mechanical condition. As a result, the muscle capacities, such as those for producing high F, V and P outputs cannot be distinguished from single outcomes of such tests. This inevitably leads to a fundamental problem in the contemporary literature both regarding the design of various research and testing procedures, as well as interpretation of their results. For example, there are hundreds, if not thousands, of manuscripts published on testing various maximum performance functional movements. However, the authors have arbitrarily interpreted the observed outcomes either regarding the observed capacities of tested muscles or the outcomes of the applied rehabilitation and training interventions. A notorious example could be the height of maximum vertical jumps that has been indiscriminately interpreted as either an index of muscle F [9], or V [10], or P [6], or as a relationship among them [11].

3. Force-velocity relationship of muscles performing functional tasks

Of essential importance for this study is the F-V relationship of muscles performing various maximum performance functional movements. Namely, while being approximately hyperbolic when observed from isolated muscles and single joint movements [2, 5, 12], the F-V relationship obtained from multi-joint functional movement tasks proved to be exceptionally strong and close to linearity [see Jaric [3] for review]. Specifically, manipulation of external loads typically provides a range of F and V data that allow for applying a linear regression model:

$$\mathrm{F}(\mathrm{V})={\mathrm{F}}_0-a\mathrm{V},$$ (eq. 1)

where a is the slope, while F₀ (i.e., F-intercept observed under zero V) corresponds to the maximum F (see Figure 1a). The V-intercept:

$${\mathrm{V}}_0={\mathrm{F}}_0/a,$$ (eq. 2)

reveals the maximum V of the tested muscles at zero F. Finally, due to the linearity of the relationship the maximum P (i.e., the maximum product of F and V) is observed at F₀/2 and V₀/2:

$${\mathrm{P}}_0={\mathrm{F}}_0\ast {\mathrm{V}}_0/4.$$ (eq. 3)

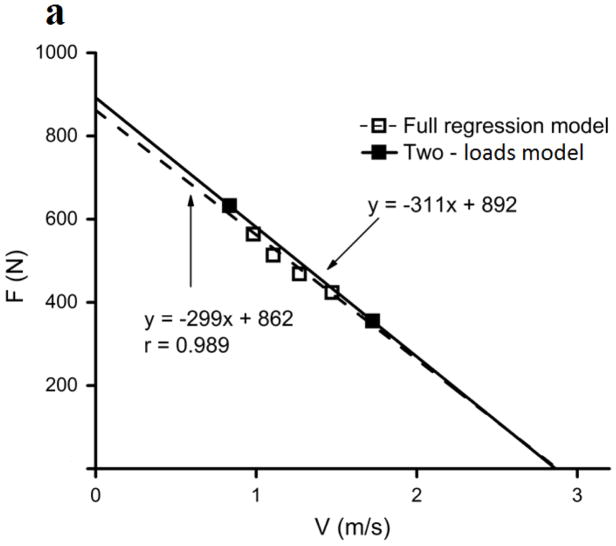
Figure 1.

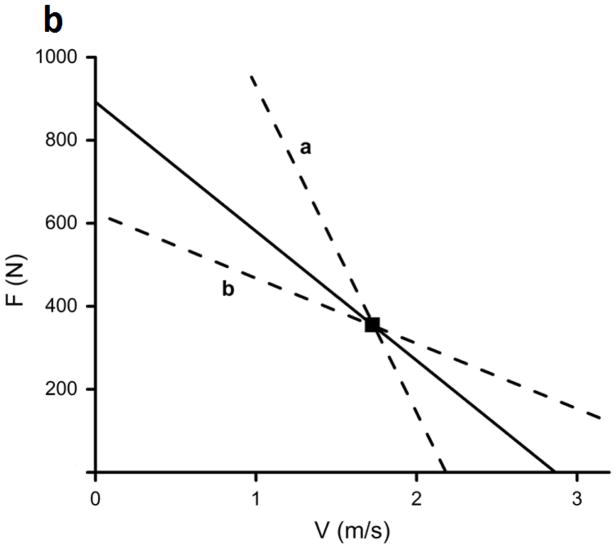
(a) Force-velocity (F-V) relationship obtained from a linear regression model applied on 6 experimental points observed from bench press exercise performed against 6 different loads ranging from 20 to 57.5 kg (mass of the involved arm segments is included; data presented by solid line, and both open and filled squares). The same relationship is also shown through a two-loads model as a line determined by the first and last experimental point (dashed line and filled squares). (b) Just one of the experimental points is shown together with the same F-V relationship as in Figure 1a (solid line). Dashed lines illustrate 2 out of an infinite number of possible F-V relationships corresponding to the same point illustrating a trade-off between F₀ and V₀.

Such results have been consistently observed from cycling [13–16], jumping [17–19], running [20, 21], leg push offs [4, 22–24], lifting [13, 25, 26] etc. Of utmost importance is that most of the cited studies revealed the correlation coefficients of the linear model applied to individual sets of data well above 0.9. In addition, no significant differences in the strength of the relationships were found between the linear and polynomial regression models applied on the same sets of F and V data [18, 19, 25] suggesting that the assessed F-V relationships could be considered linear for further computation. Of importance could also be that the parameters depicting the maximum F, V and P of the tested muscles (i.e., the regression parameters F₀, V₀, and P₀, respectively) proved to be highly reliable [17, 18, 24–26] and at least moderately valid [15, 17–19]. Finally, several studies have already showed that the same parameters could also be sensitive enough to detect the differences among various populations regarding the discussed muscle capacities [13, 16, 23, 27].

The linear model of the F-V relationship, as well as the resulting parabolic P-V relationship obtained from loaded functional movements have both been frequently used in recent research. The relationships were able to reveal the imbalance of F and V capacities of the tested muscles [4, 28], detect the bilateral deficit [22, 23], explore the optimum load magnitude for maximizing muscle power output [29], investigate the role of muscle mechanics in running performance [20, 21], and discern among the mechanical and neural mechanisms that could contribute to observed mechanical outputs [30, 31]. Finally, the discussed linear F-V relationship and, consequently, the parabolic P-V relationship could considerably simplify both the testing and modelling procedures in various areas of human movement studies [3]. The following section will present the possibility of using a simplified procedure for the assessment of the F-V relationship that could distinguish among the muscle F, V, and P capacities in routine tests of muscle function.

4. 'Two-loads method' for testing muscle force, velocity, and power capacities

Several authors have already argued that the procedure of obtaining the linear F-V relationship from loaded functional movements procedure could be developed into a routine method for testing muscle mechanical capacities [3, 13, 24–27, 32]. However, one could also argue that the same procedure could be somewhat cumbersome and time consuming when applied in routine testing due to both a need for a number of loading conditions and regression modelling.

The solution for the problems discussed above could come from two key findings presented in the previous text. First, since the F-V relationship obtained from a series of loaded functional movements proved to be exceptionally strong, the number of experimental points (i.e., of the different loads applied) should only have a minor effect upon the observed F-V relationship. Second, since the F-V relationship is also a linear one, the magnitude of the applied loads should also play a minor role. As a result, one could propose a simple 'two-loads method': the capacities of tested muscles to provide a high F, V, and P output could be distinguished through functional movements tested against just two external loads.

An example of such an approach is illustrated in Figure 1a through a typical individual F-V relationship obtained from our recent study [25]. Thanks to both the linearity and the strength of the F-V relationship observed from all 6 of the applied loads (i.e., 6 experimental points), the shape of the same relationship observed from just 2 of the most distinctive loads is almost identical. Since the analytical solution of obtaining a line drawn through 2 points and the is trivial, it does not need calculation of its intercepts needed for the assessment of F₀, V₀, and P₀ to be presented here. However, of utmost importance here is that the line parameters directly depict the muscular F, V, and P producing capacities in the same way as the parameters obtained from the regression models do (see eq. 1–3). Note that the data obtained in our recent studies suggest an exceptionally high concurrent validity of the parameters obtained from the two-loads method with respect to the same parameters obtained from the standard approach based on a number of loads applied. For example, the correlation coefficients between the same parameters were 0.994, 0.995, and 0.984 (when obtained from loaded jumps; [18]) and 0.958, 0.961, and 0.981(loaded bench press; [25]) for F₀, V₀, and P_max, respectively.

An important methodological problem of employing the proposed method should be the selection of 2 particular testing loads. There are no data in the literature yet that address this problem, but a plausible solution could be the selection of two more, rather than less distinctive loads (as shown in Figure 1a). Namely, if each individual load provides F and V magnitudes with a similar error score, the error of the obtained F-V relationship (and, therefore, of F₀, V₀, and P_max) would be smaller if calculated from more distant experimental points.

Finally, to juxtapose the depicted F-V relationships obtained from the two-loads method (Figure 1a) with results of routine testing methods, Figure 1b shows an outcome of a test hypothetically conducted under just one loading condition. The obtained single experimental point apparently does not allow for the assessment of the linear F-V relationship since its slope cannot be defined. As shown with 2 dashed lines representing just 2 out of an infinite number of possible F-V relationships, there is a nonlinear trade-off between the possible F and V capacities of the tested muscles. For example, the muscles could be either relatively strong but slow (i.e., high F₀ and low V₀; line a), or weak but fast (low F₀ and high V₀; line b). Moreover, the muscle capacities observed from the same point cannot be interpreted since its position relative to the maximum F (i.e., zero V), V (zero F), and P (the middle section of the line) of the tested muscles cannot be assessed. Therefore, the same functional movements tested under just 2 different loads (see Figure 1a) should provide the outcomes of markedly higher informational value regarding the specific muscular capacities than the single loading condition typically applied both in contemporary research and routine testing.

5. Limitations and further research

Several limitations and possible directions of further research of the proposed two-loads method need to be recognized. First, note that the F-V relationship observed from in vitro muscles and single-joint movements is generally considered to be curvilinear, while the linear shape has been observed only from functional multi-joint tasks. Nevertheless, it should be noted that the functional movement tasks are extensively used in routine testing. Moreover, such movements are also not only generally considered to be more ecologically valid, but also more familiar for subjects than single joint movement tests typically performed using isometric and obtained from the isokinetic devices [3]. Second, regarding the parameters F₀, V₀, and P₀ discussed linear F-V relationships, note that 2 of them allow for the calculation of the third one (see eq. 3). Therefore, despite both the apparent and distinctive physiological meaning of the obtained F, V, and P producing capacity of the tested muscles, they are not fully independent. Third, the future routine testing procedures should require load standardization. As previously discussed, it is likely that more distinctive external load could provide more reliable and valid outcomes, but, nevertheless, further research is needed. Fourth, the effect of the functional movement pattern on the obtained F-V relationship also needs further exploration. For example, vertical jumps allow for a marked adaptation of the movement pattern to the altered external load that markedly confounds the F and P output, but not the jump height [33]. Fifth, the type of the external load should also be considered since different combinations of the inertial (i.e., acceleration dependent) and gravitational loads (i.e., a constant one) could have distinctive effects upon the F, V, and P outputs [34]. As a consequence, both the F-V relationships patterns and its parameters could be load type specific. Sixth, note that the segment of the discussed F-V relationship that corresponds to eccentric muscle contractions has not been explored yet. Finally, parameters obtained from the two-loads method, such as the basic properties of the F₀, V₀, and P₀their reliability, validity, and sensitivity, certainly need further evaluation.

6. Conclusions

As compared to the typically applied single loading condition, the functional movements tested against different external loads could provide an elaborate and ecologically valid assessment of distinctive muscle capacities. Specifically, the functional tasks (e.g., maximum jumping, running, cycling, rowing, lifting, throwing) tested against only 2 distinctive external loads could reveal parameters that distinguish among the F, V, and P producing capacities of the tested muscles. For example, a high F₀ relative to V₀ would reveal a 'strong' individual, an opposite outcome would reveal a 'fast' individual, while relatively high values of both F₀ and V₀ would be required for an individual to be 'powerful'. Therefore, the standard methods of routine testing of muscle capacities need to be revisited at least regarding functional tasks that allow for manipulation of external loads. As compared with the routine testing procedures conducted under a single mechanical condition, the two-loads method could provide a deeper insight into the properties and function of tested muscles, as well as resolve a number of debated issues in the literature.

Key Points.

1. This paper examines limitations of standard methods for testing muscle capacities through trials typically conducted under a single mechanical condition.

2. Approximately linear and typically strong force-velocity relationships observed from functional movements tested under varying loading conditions have revealed reliable and valid parameters depicting the force, velocity, and power producing capacities of the tested muscles.

3. We should re-consider the methodology of testing for functional tasks that allow for manipulation of external load (e.g., various cycling, jumping, running, lifting, or throwing tests).

4. Just 2 maximum performance trials performed against two distinctive loads (i.e., the two-loads method) could reveal the force-velocity relationship and, therefore, directly distinguish among the force, velocity, and power producing capacities of the muscles performing the tested functional task.