Muscle Contributions to Frontal Plane Angular Momentum during Walking

Abstract

The regulation of whole-body angular momentum is important for maintaining dynamic balance during human walking, which is particularly challenging in the frontal plane. Whole-body angular momentum is actively regulated by individual muscle forces. Thus, understanding which muscles contribute to frontal plane angular momentum will further our understanding of mediolateral balance control and has the potential to help diagnose and treat balance disorders. The purpose of this study was to identify how individual muscles and gravity contribute to whole-body angular momentum in the frontal plane using a muscle-actuated forward dynamics simulation analysis. A three-dimensional simulation was developed that emulated the average walking mechanics of a group of young healthy adults (n=10). The results showed that a finite set of muscles are the primary contributors to frontal plane balance and that these contributions vary throughout the gait cycle. In early stance, the vasti, adductor magnus and gravity acted to rotate the body towards the contralateral leg while the gluteus medius acted to rotate the body towards the ipsilateral leg. In late stance, the gluteus medius continued to rotate the body towards the ipsilateral leg while the soleus and gastrocnemius acted to rotate the body towards the contralateral leg. These results highlight those muscles that are critical to maintaining dynamic balance in the frontal plane during walking and may provide targets for locomotor therapies aimed at treating balance disorders.

INTRODUCTION

The generation of whole-body angular momentum is important for maintaining dynamic balance during normal and pathological movement (e.g., Bruijn et al., 2011; Herr and Popovic, 2008) and has been used to detect falls (Martelli et al., 2011) and control bipedal robots with stable well-coordinated movements (e.g., Goswami and Kallem, 2004; Hofmann et al., 2009). Whole-body angular momentum is a useful measure to assess balance control as it accounts for the mass, inertia, and linear and rotational velocities of all the body segments about the body’s center of mass. Previous studies have shown that the range of angular momentum during walking is kept low through the cancellation of angular momenta between body segments (e.g., Bennett et al., 2010; Herr and Popovic, 2008). However, the range of whole-body angular momentum has been found to increase when dynamic balance is compromised in the presence of perturbations (Martelli et al., 2013; Sheehan et al., 2015). Angular momentum has been investigated over a range of walking tasks such as steady-state walking (Herr and Popovic, 2008), walking at increasing speeds (Bennett et al., 2010), incline/decline walking (Silverman et al., 2012) and stair ascent/descent (Silverman et al., 2014). Angular momentum has also been analyzed during other movement tasks such as sit-to-stand (Reisman et al., 2002; Riley et al., 1997) and recovering from a trip (Pijnappels et al., 2004; Potocanac et al., 2014), and in different patient populations including elderly (Kaya et al., 1998; Pijnappels et al., 2005; Simoneau and Krebs, 2000), amputee (D’Andrea et al., 2014; Pickle et al., 2014; Sheehan et al., 2015; Silverman and Neptune, 2011) and post-stroke (Nott et al., 2014) subjects, and children with cerebral palsy (Bruijn et al., 2011). Collectively, these studies suggest that whole-body angular momentum is an important measure to quantify dynamic balance during human movement.

The primary mechanism to actively regulate angular momentum is muscle force generation, which accelerates the body segments and generates ground reaction forces that alter angular momentum about the body’s center-of-mass to restore and maintain dynamic balance. We previously used a two-dimensional musculoskeletal model to analyze the contributions of gravity and individual muscles to sagittal plane whole-body angular momentum and found in early stance, the uniarticular hip and knee extensors, biarticular hamstrings and ankle dorsiflexors generate backward angular momentum while the ankle plantarflexors generate forward momentum (Neptune and McGowan, 2011). In late stance, the plantarflexors are the primary contributors, but the uniarticular and biarticular muscles generate angular momentum in opposite directions. The uniarticular soleus generates primarily forward angular momentum while the biarticular gastrocnemii generate backward momentum. Gravity contributes to the body’s angular momentum in early stance and to a lesser extent in late stance, which is counteracted by the plantarflexors. However, it is not clear which muscles are the primary contributors to frontal plane angular momentum.

Walking is most unstable in the mediolateral direction (Bauby and Kuo, 2000; Dean et al., 2007; McAndrew et al., 2011), and therefore poor regulation of frontal plane angular momentum may compromise balance control and lead to an increased risk of falling. For example, previous work has shown that the range of frontal plane angular momentum is greater, and therefore less tightly regulated, in lower-limb amputees compared to non-amputees (D’Andrea et al., 2014; Pickle et al., 2014; Sheehan et al., 2015; Silverman and Neptune, 2011), which may explain why they are more susceptible to falling (Miller et al., 2001). Thus, understanding how individual muscles contribute to the regulation of frontal plane whole-body angular momentum has the potential to provide additional insight into the diagnosis and treatment of balance disorders.

The purpose of this study was to build upon our previous work and use a three-dimensional musculoskeletal model and forward dynamics simulation of healthy walking to analyze how gravity and individual muscles contribute to frontal plane whole-body angular momentum. This analysis will provide further insight into how muscles work in synergy to regulate whole-body angular momentum and maintain dynamic balance during human walking.

METHODS

A previously described three-dimensional bipedal musculoskeletal model (Peterson et al., 2010) was developed using SIMM/Dynamics Pipeline (MusculoGraphics, Inc.) and consisted of ten rigid-body segments representing the thorax, pelvis, and right and left legs, with each leg consisting of a thigh, shank, foot and toes. The thorax also included the mass and inertial properties of the head and arms. The model had 23 degrees-of-freedom that fully characterized the kinematic motions of the sagittal, frontal and transverse planes during human walking. A six degree-of-freedom joint was defined between the ground and pelvis. The thorax and each thigh had three rotational degrees-of-freedom with respect to the pelvis. There was one rotational degree-of-freedom defined at the knee, ankle, subtalar and metatarsalphalangeal (MTP) joints. Foot-ground contact was modeled using 31 viscoelastic elements with coulomb friction distributed along the bottom of each foot (Neptune et al., 2000). The model’s dynamical equations-of-motion were derived using SD/FAST (PTC).

The model was driven by 38 Hill-type musculotendon actuators for each leg that were combined into 15 muscle groups for analysis (i.e., those muscles with similar anatomical and biomechanical function were combined together, Table 1). Musculoskeletal geometry was based on Delp et al. (1990) and the muscle force-producing properties were governed by passive force-length-velocity, active force-length-velocity and tendon force-length relationships (Zajac, 1989). The pelvis-thorax joint was controlled passively by three viscoelastic torsional springs that represented the abdominal and lower back muscles. Muscle activation/deactivation dynamics were modeled with a nonlinear first-order differential equation (Raasch et al., 1997), with activation and deactivation time constants based on Winters and Stark (Winters and Stark, 1988). Passive torques were applied at each joint to represent ligament and passive tissue forces (Anderson and Pandy, 1999; Davy and Audu, 1987).

Table 1.

Muscles included in the musculoskeletal model and their corresponding analysis group.

Muscles	Analysis Groups
Iliacus	IL
Psoas
Adductor Longus	AL
Adductor Brevis
Pectineus
Quadratus Femoris
Superior Adductor Magnus	AM
Middle Adductor Magnus
Inferior Adductor Magnus
Sartorius	SAR
Rectus Femoris	RF
Vastus Medialis	VAS
Vastus Lateralis
Vastus Intermedius
Anterior Gluteus Medius	GMEDA
Middle Gluteus Medius
Anterior Gluteus Minimus
Middle Gluteus Minimus
Posterior Gluteus Medius	GMEDP
Posterior Gluteus Minimus
Piriformis
Gemellus
Tensor Fasciae Latae	TFL
Superior Gluteus Maximus	GMAX
Middle Gluteus Maximus
Inferior Gluteus Maximus
Semitendinosus	HAM
Semimembranosus
Gracilis
Biceps Femoris Long Head
Biceps Femoris Short Head	BFSH
Medial Gastrocnemius	GAS
Lateral Gastrocnemius
Soleus
Tibialis Posterior	SOL
Flexor Digitorum Longus
Tibialis Anterior	TA
Extensor Digitorum Longus

A walking simulation of a complete gait cycle was generated using dynamic optimization that fine-tuned the muscle excitation patterns using a simulated annealing optimization algorithm (Goffe et al., 1994) with the objective function defined to minimize the difference between the simulated and experimentally measured walking data. Bimodal patterns were used to define the muscle excitations that were described by the onset, offset and amplitude of each mode (Peterson et al., 2010). The muscle excitation timing was loosely constrained to match published EMG patterns (Neptune et al., 2008). The objective function used (Eq. 1) quantified the differences between the simulated (Y_ij) and experimentally (${\widehat{Y}}_{\mathit{ij}}$) measured kinematic (hip, knee and ankle joint angles and pelvis translations) and 3D ground reaction force (GRF) data normalized by the standard deviation (SD) of the experimental walking data at each time step i and variable j while minimizing muscle stress (second term) as follows:

$$\text{Objective function}={\Sigma }_{i=1}^{n_{\text{step}}}\left({\Sigma }_{j=1}^{n_{\text{vars}}}{wt}_j\frac{{(Y_{\mathit{ij}}-{\widehat{Y}}_{\mathit{ij}})}^2}{{\mathit{SD}}_{\mathit{ij}}^2}+ws{\Sigma }_{k=1}^{n_{\mathit{musc}}}{\left(\frac{F_{\mathit{ik}}}{A_k}\right)}^2\right)$$ (1)

where n_step is the number of time steps, n_vars is the number of quantities evaluated, n_musc is the number of muscles, F_ik is the muscle force at time step i for muscle k, A_k is the physiological cross-sectional area of muscle k, wt_j is the weighting factor for quantity j and ws is the weighting factor for muscle stress. The weighting factors were determined in an iterative manner such that the overall objective function (Eq. 1) was minimized. The muscle stress term was included to help minimize unnecessary co-contraction. To assess the overall quality of the simulation, the root-mean-square (RMS) difference between each simulated and experimental kinematic and GRF variable j was computed as follows:

$${RMS\text{Difference}}_j=\sqrt{\frac{{\Sigma }_{i=1}^{n_{\text{step}}}{(Y_{ij}-{\widehat{Y}}_{ij})}^2}{n_{\text{step}}}}$$ (2)

Experimental Data

Body segment kinematic and ground reaction force data were collected from 10 healthy subjects (five females; age = 28.7±5.8 yrs, mass = 69.6±13 kg, height = 1.73±0.12 m) as they walked for 30 seconds at 1.2 m/s on a split-belt instrumented treadmill (Tecmachine, France). All subjects provided informed consent to an Institutional Review Board approved protocol. The GRF and kinematic data were collected at 2000 Hz and 100 Hz, respectively, using Vicon Workstation v4.5 software and post-processed using Visual3D (C-motion, Inc.). The GRF and kinematic data were low-pass filtered at 20 and 6 Hz, respectively. The GRF data were normalized to body weight, and then the kinematic and GRF data were normalized to the gait cycle and averaged across subjects to obtain a group average dataset that was used in Eq. 1.

Muscle Contributions to Angular Momentum

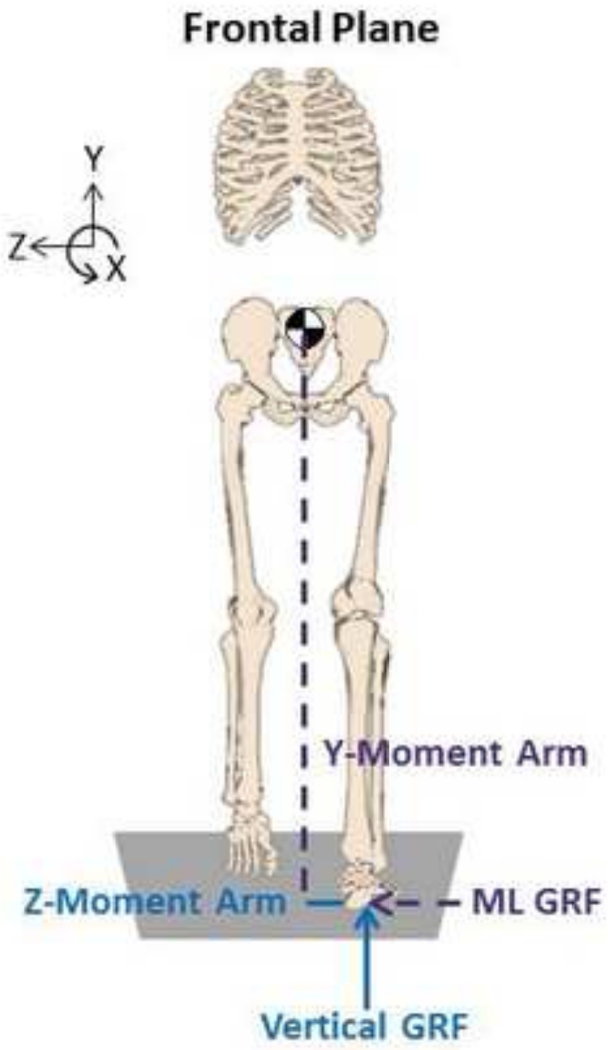
To identify how individual muscles and gravity contribute to frontal plane whole-body angular momentum, we quantified their contributions to the external moment (i.e., time rate of change of angular momentum) over the gait cycle using the following relation (Fig. 1):

$$\underset{H}{\overset{.}{-}}=\stackrel{‒}{r}\times {\stackrel{‒}{F}}_{GRF}={\stackrel{‒}{M}}_{\mathit{ext}}$$ (3)

where $\stackrel{\cdot }{\stackrel{‒}{H}}$ is the time rate of change of whole-body angular momentum, $\stackrel{‒}{r}$ is the moment arm vector from the body’s center-of-mass to each foot’s center-of-pressure, and ${\stackrel{‒}{F}}_{GRF}$ is each muscle’s and gravity’s contribution to the ground reaction forces determined using a ground reaction force decomposition technique (Neptune et al., 2004). The $\stackrel{‒}{r}\times {\stackrel{‒}{F}}_{GRF}$ term represents the external moment (${\stackrel{‒}{M}}_{\mathit{ext}}$) generated about the body’s center-of-mass by the individual muscles and gravity that act to change the time rate of change of whole-body angular momentum.

Figure 1.

Frontal plane angular momentum was defined about the x-axis. The ground reaction forces (GRFs) and foot placement contribute to the external moment about the body center-of-mass (COM), which equals the time rate of change of angular momentum (Eq. 3). Only the contributions to the right-leg external moment are shown for clarity.

RESULTS

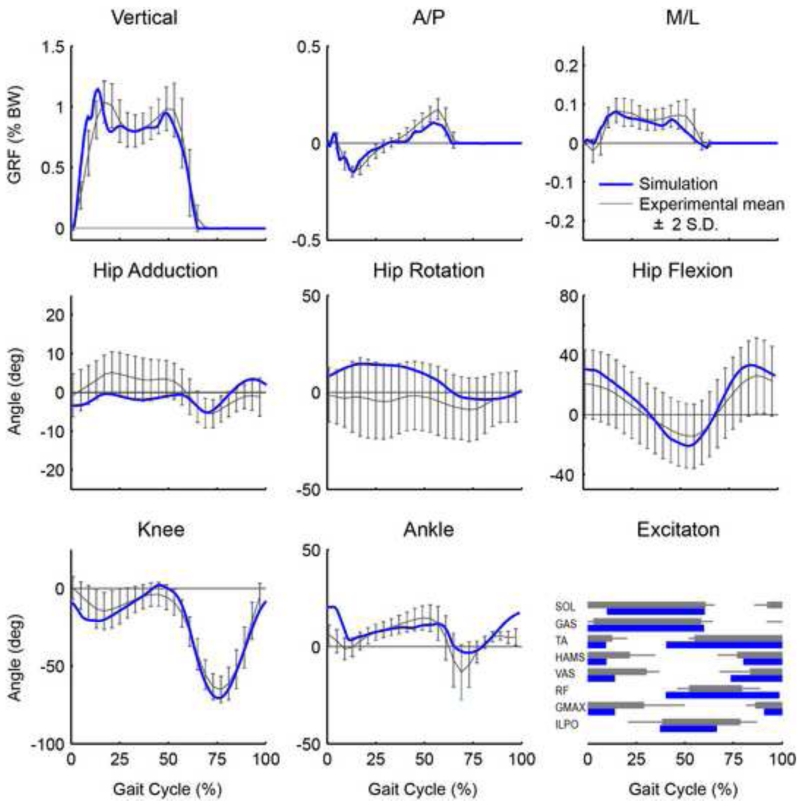
The 3D walking simulation tracked the group-averaged kinematic and GRF data within +/− 2 S.D. of the experimental data (Fig. 2) with an average root mean square kinematic (joint angles) and kinetic (3D GRFs) difference of 3.58 degrees and 0.024 % BW, respectively. Thus, overall the simulation fell within a normal distribution of the experimental data, and therefore was considered consistent with normal walking mechanics.

Figure 2.

Simulation tracking results. The simulated joint angles and ground reaction forces (black) agreed well with the experimental data (grey). The grey regions represent experimental means ± 2 SD. Also shown is a comparison between the model excitations with available experimentally measured EMG timing (mean onset and offset values ± 2 SD).

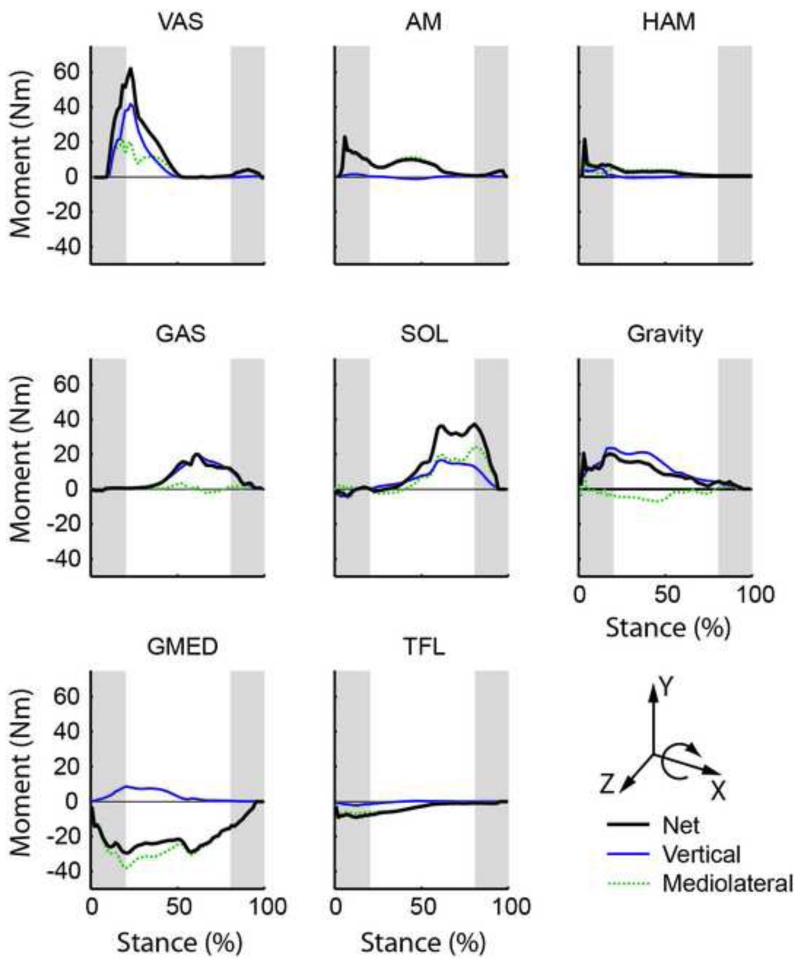
In early stance, VAS, adductor magnus (AM) and gravity were the primary contributors to positive frontal plane angular momentum (i.e., they acted to rotate the body towards the contralateral leg) while the gluteus medius (GMED), and to a lesser extent the tensor fasciae latae (TFL), were the primary contributors to negative frontal plane momentum (i.e., they acted to rotate the body towards the ipsilateral leg) (Fig. 3, compare Net values). In late stance, GMED continued to generate negative angular momentum while SOL and GAS were the primary contributors to positive angular momentum. All other muscles had negligible contributions.

Figure 3.

Individual muscle contributions to the time rate of change of frontal plane angular momentum ($\underset{H}{\overset{\cdot }{}}$ about the x-axis). M/L is the contribution from the mediolateral ground reaction force, Vertical is the contribution from the vertical ground reaction force. Net is the summed contribution from the mediolateral and vertical components. All other muscle contributions were small and not shown. Positive (negative) values indicate the muscle acts to rotate the body towards the contralateral (ipsilateral) leg. Shaded regions indicate timing of the double support phase.

DISCUSSION

Walking is a dynamic task that requires the successful execution of several biomechanical functions including the generation of body support, forward propulsion, leg swing and balance control. Whole-body angular momentum provides a quantitative measure of balance control that needs to be regulated throughout the gait cycle to maintain dynamic balance. Inadequate regulation of angular momentum has been shown to be indicative of poor dynamic balance and greater fall risk (Pijnappels et al., 2004; Sheehan et al., 2015), which is consistent with research showing that post-stroke hemiparetic subjects with lower clinical balance scores associated with fall risk have difficulty regulating their frontal plane angular momentum (Nott et al., 2014).

Angular momentum is regulated through the generation of ground reaction forces that produce an external moment about the body’s center-of-mass (Eq. 3). The importance of generating appropriately directed ground reaction forces to stabilize sagittal-plane mechanics was recently shown in human standing (Gruben and Boehm, 2012b) and walking (Gruben and Boehm, 2012a; Maus et al., 2010). We previously showed during walking that in late stance the uniarticular (SOL) and biarticular (GAS) plantarflexors generate sagittal-plane angular momentum in opposite directions, despite sharing a common tendon (Neptune and McGowan, 2011). The difference between these muscles was due to their relative contributions to the horizontal and vertical ground reaction forces (Neptune and McGowan, 2011). Similarly, in amputees who are more susceptible to falling than non-amputees (Miller et al., 2001), we found that an increased range of frontal plane angular momentum that was correlated with differences in ground reaction force patterns in both the intact and residual legs compared to non-amputees (Silverman and Neptune, 2011).

In the frontal plane, angular momentum is controlled by the generation of both the vertical and mediolateral GRFs (Fig. 1). In the present study, we found muscle net contributions to frontal plane angular momentum were consistent with their contributions to the mediolateral ground reaction force (Fig. 3). The two exceptions were GAS and gravity, whose contributions to frontal plane angular momentum were dominated by their contributions to the vertical GRF (Fig. 3). We found that gravity, like GMED, contributes to the medial GRF which is consistent with others (John et al., 2012). The medially directed GRF creates a negative external moment that acts to rotate the body towards the ipsilateral leg. Pandy et al. (2010) found that gravity’s contribution to the mediolateral GRF switched from lateral to medial over the stance phase and that this contribution is sensitive to the leg angle. They predicted that with wider step widths, gravity and GMED would act in synergy to accelerate the center-of-mass medially (i.e., contribute to a medially-directed GRF as found in the present study). This led them to conclude that the idea of mediolateral balance during normal walking being maintained through the dynamic equilibrium between gravity and the hip abductor muscles (MacKinnon and Winter, 1993) was too simplistic. However, gravity’s contribution to the net external moment is dominated by its contribution to the vertical GRF, which creates a destabilizing moment that acts to rotate the body towards the contralateral leg (MacKinnon and Winter, 1993). Thus, the net external moment created by gravity (and other muscles, Fig. 3) is counteracted primarily by GMED (Fig. 3). Therefore, the interaction between gravity and the hip abductor muscles is indeed an important mechanism to maintain dynamic equilibrium in the frontal plane. This is consistent with previous studies showing there exists a correlation between a higher range of frontal plane angular momentum and a lower peak hip abduction moment during incline and decline walking (Silverman et al., 2012) and that there is a critical balance between gravity and hip abductor activity to ensure frontal plane balance control (Jansen et al., 2014; John et al., 2012).

Not only is the generation of appropriate GRFs essential to regulating the body’s angular momentum, but foot placement, by determining the relative moment arm from the body’s center-of-mass to the foot center-of-pressure, also plays an important role (Eq. 2; Fig. 1). In the frontal plane, modulating step width has been shown to be an effective balance-control mechanism (Bauby and Kuo, 2000; Townsend, 1985). Older adults who are more susceptible to falls walk with increased step widths (Dean et al., 2007; Schrager et al., 2008), which act to increase the distance from the body center-of-mass to the center-of-pressure. This increased distance would increase the rate of change in angular momentum (Eq. 2) and presumably make them more unstable, which is consistent with the conclusion that greater angular momentum is related to greater fall risk (Sheehan et al., 2015). However, decreases in hip abductor strength have also been shown to be an important fall predictor in older adults (Hilliard et al., 2008). Thus, the inability to generate appropriate abductor muscle force and corresponding medial GRFs may be compensated for by increasing their step width to generate appropriate frontal plane angular momentum and maintain dynamic balance. However, others have associated wider steps with increased step width variability and decreased balance control (McAndrew Young and Dingwell, 2012) and some have observed higher rate of falls in subjects who walk with wider steps (Gehlsen and Whaley, 1990; Maki, 1997; Moe-Nilssen and Helbostad, 2005; Nelson et al., 1999). Thus, future work is needed to directly compare the angular momentum patterns between populations with different preferred step widths and identify the biomechanical mechanisms that contribute to any observed differences.

An important finding of our study is the critical role of the ankle plantarflexors in maintaining dynamic balance during walking, as they have significant contributions to whole-body angular momentum in both the frontal (Fig. 3) and sagittal (Neptune and McGowan, 2011) planes. Previous studies have shown that the plantarflexors are important in balance recovery during walking (Pijnappels et al., 2005) and standing (Runge et al., 1999) perturbations and that individuals with a history of falls have reduced ankle plantarflexor output (LaRoche et al., 2010). We have previously analyzed whole-body angular momentum as a measure of dynamic balance in healthy (Neptune and McGowan, 2011; Silverman et al., 2012), amputee (Silverman and Neptune, 2011) and post-stroke (Nott et al., 2014) subjects and found that the ankle plantarflexors are essential in maintaining appropriate angular momentum in both the frontal and sagittal planes. For example, pitching the body forward, as happens during a trip, represents a large increase in the sagittal plane angular momentum that is counteracted primarily by the plantarflexors (Neptune and McGowan, 2011). Similarly, a perturbation in the mediolateral direction in late stance would also be primarily compensated for by the ankle plantarflexors (Fig. 3). The finding that the plantarflexors, which are primarily sagittal plane muscles, are important for maintaining frontal plane balance is somewhat counterintuitive. However, the plantarflexors contribute to both the vertical and mediolateral ground reaction forces which create an external moment about the body’s center-of-mass that acts to rotate the body in the frontal plane (Fig. 1). Thus, the plantarflexors play a critical role in controlling angular momentum in both the frontal and sagittal planes, which is essential to maintaining dynamic balance.

Not only does the critical role of the plantarflexors have important implications for the diagnosis and treatment of balance and movement disorders, but also in the design and prescription of ankle-foot prosthetic and orthotic (AFO) devices. For example, below-knee amputees have difficulty regulating their angular momentum because of the functional loss of the ankle muscles (D’Andrea et al., 2014; Pickle et al., 2014; Sheehan et al., 2015; Silverman and Neptune, 2011), which may explain why they have an increased risk and fear of falling relative to non-amputees (Miller et al., 2001). Previous work has shown that the range of frontal plane angular momentum is significantly greater for those with below-knee amputations than for non-amputees in response to mediolateral perturbations (Sheehan et al., 2015). Similarly, AFOs are widely prescribed to improve walking ability for those with various neurological deficits by assisting with foot clearance during swing while stabilizing the ankle during stance and keeping it in a near neutral position. As a result, ankle motion and plantarflexor function during stance is limited and may hinder the ability of those with volitional plantarflexor output to regulate angular momentum in response to external perturbations, and therefore compromise their dynamic balance. Indeed, a recent study analyzed the influence of a clinically prescribed AFO on dynamic balance in healthy young adults and found that walking with an AFO resulted in a greater range of angular momentum in both the frontal and sagittal planes, which were correlated with the reduced peak hip abduction and reduced ankle plantarflexor moments, respectively (Vistamehr et al., 2014).

The results from our simulation analysis were able to determine which muscles have the capacity to effectively control angular momentum in the frontal plane during walking. While these results are from a single simulation, it is unlikely that the natural variation in anatomy or walking mechanics that exists between individuals would substantially change our interpretation. For example, varying the strength or moment arm of the vastus lateralis within normal ranges likely observed across individuals would affect how much moment this muscle can produce at the knee, but the resulting vastus lateralis output would still produce a positive external moment about the center of mass during early stance, and therefore its contributions to controlling angular momentum would be similar. However, we recognize that the model assumes generic parameters for an average healthy adult and therefore cannot necessarily predict compensatory strategies that may be used by individuals with advanced muscle weakness or neuromuscular disease. Understanding compensatory strategies in specific populations or those populations and tasks that produce a highly variable response would require using a modified musculoskeletal model and population or subject specific simulations. However, by identifying which muscles are mechanically capable of controlling angular momentum during normal walking, our results provide a starting point for developing treatment strategies that target the functional roles these muscle play.

Another limitation of this study is that we only analyzed steady-state walking at a fixed speed to gain insight into how individual muscles and gravity regulate whole-body angular momentum to maintain frontal plane balance. To fully understand how angular momentum is regulated during human movement, future experimental and simulation analyses are needed of additional movement tasks in which whole-body angular momentum is perturbed and individual muscles respond to restore dynamic balance.

In summary, maintaining mediolateral balance is an essential element in locomotor tasks such as walking, which is actively controlled by individual muscle forces. Previous simulation studies have investigated mediolateral body control by analyzing muscle contributions to the linear accelerations of the whole-body center-of-mass (Jansen et al., 2014; John et al., 2012; Pandy et al., 2010) or frontal plane trunk angular accelerations (Klemetti et al., 2014). The present study builds upon this previous work by analyzing muscle contributions to the time rate of change of whole-body angular momentum, which is an important biomechanical measure that provides insight into how the sum of all the body segment linear and angular momenta about the body center-of-mass is controlled through foot placement and the generation of appropriate GRFs (both vertical and mediolateral) to maintain dynamic balance. Collectively, these studies highlight how a number of muscle groups work together in synergy to maintain frontal plane balance during human walking. Of particular importance are the contributions of the hip abductor (GMED) and ankle plantarflexors (SOL, GAS), as they are the primary muscle groups that counteract the contributions from gravity and other muscle groups in order to maintain dynamic balance. Thus, locomotor therapies that target these muscle groups may be helpful in improving dynamic balance during walking.