Abstract
The physics of the crossover between weak-coupling Bardeen–Cooper–Schrieffer (BCS) and strong-coupling Bose–Einstein condensate (BEC) limits gives a unified framework of quantum-bound (superfluid) states of interacting fermions. This crossover has been studied in the ultracold atomic systems, but is extremely difficult to be realized for electrons in solids. Recently, the superconducting semimetal FeSe with a transition temperature Tc=8.5 K has been found to be deep inside the BCS–BEC crossover regime. Here we report experimental signatures of preformed Cooper pairing in FeSe, whose energy scale is comparable to the Fermi energies. In stark contrast to usual superconductors, large non-linear diamagnetism by far exceeding the standard Gaussian superconducting fluctuations is observed below T*∼20 K, providing thermodynamic evidence for prevailing phase fluctuations of superconductivity. Nuclear magnetic resonance and transport data give evidence of pseudogap formation at ∼T*. The multiband superconductivity along with electron–hole compensation in FeSe may highlight a novel aspect of the BCS–BEC crossover physics.
 The crossover between the weak-coupling limit and strong-coupling limit provides important information for quantum bound states of interacting fermions. Here, Kasahara et al. report thermodynamic evidence for prevailing phase fluctuations of superconductivity, highlighting unusual normal state in the BCS-BEC crossover regime.
The crossover between the weak-coupling limit and strong-coupling limit provides important information for quantum bound states of interacting fermions. Here, Kasahara et al. report thermodynamic evidence for prevailing phase fluctuations of superconductivity, highlighting unusual normal state in the BCS-BEC crossover regime.
In the Bardeen–Cooper–Schrieffer (BCS) regime, weakly coupled pairs of fermions form the condensate wave function, while in the Bose–Einstein condensate (BEC) regime, the attraction is so strong that the fermions form local molecular pairs with bosonic character. The physics of the crossover is described by two length scales, the average pair size or coherence length ξpair and the average interparticle distance 1/kF, where kF is the Fermi wave number. In the BCS regime, the pair size is very large and kFξpair≫1, while local molecular pairs in the BEC regime lead to kFξpair≪1. The crossover regime is characterized by kFξpair∼1, or equivalently the ratio of superconducting gap to Fermi energy Δ/ɛF of the order of unity. In this crossover regime, the pairs interact most strongly and new states of interacting fermions may appear; preformed Cooper pairing at much higher temperature than Tc is theoretically proposed1,2. Experimentally, however, such preformed pairing associated with the BCS–BEC crossover has been controversially debated in ultracold atoms3,4 and cuprate superconductors5,6,7,8. Of particular interest is the pseudogap formation associated with the preformed pairs that lead to a suppression of low-energy single-particle excitations. Also important is the breakdown of Landau's Fermi liquid theory due to the strong interaction between fermions and fluctuating bosons. In ultracold atomic systems, this crossover has been realized by tuning the strength of the interparticle interaction via the Feshbach resonance. In these artificial systems, Fermi liquid-like behaviour has been reported in thermodynamics even in the middle of crossover3, but more recent photoemission experiments have suggested a sizeable pseudogap opening and a breakdown of the Fermi liquid description4.
On the other hand, for electron systems in bulk condensed matter, it has been extremely difficult to access the crossover regime. Perhaps, the most frequently studied systems have been underdoped high-Tc cuprate superconductors5,6,7,8 with substantially shorter coherence length than conventional superconductors. In underdoped cuprates, pseudogap formation and non-Fermi liquid behaviour are well established, and unusual superconducting fluctuations have also been found above Tc (refs 6, 7). However, the pseudogap appears at a much higher temperature than the onset temperature of superconducting fluctuations8. It is still unclear whether the system is deep inside the crossover regime and to what extent the crossover physics is relevant to the phase diagram in underdoped cuprates. It has been also suggested that in iron-pnictide BaFe2(As1−xPx)2, the system may approach the crossover regime in the very vicinity of a quantum critical point9,10, but the fine-tuning of the material to a quantum critical point by chemical substitution is hard to accomplish. Therefore, this situation calls for a search of new systems in the crossover regime.
Among different families of iron-based superconductors, iron chalcogenides FeSexTe1−x exhibit the strongest band renormalization due to electron correlations, and recent angle-resolved photoemission spectroscopy studies for x=0.35−0.4 have shown that some of the bands near the Brillouin zone centre have very small Fermi energy, implying that the superconducting electrons in these bands are in the crossover regime11,12. Among the members of the iron chalcogenide series, FeSe (x=0) with the simple crystal structure formed of tetrahedrally bonded layers of iron and selenium is particularly intriguing. FeSe undergoes a tetragonal–orthorhombic structural transition at Ts≈90 K, but in contrast to other Fe-based superconductors, no long-range magnetic ordering occurs at any temperature. Recently, the availability of high-quality bulk single crystals grown by chemical vapour transport13 has reopened investigations into the electronic properties of FeSe. Several experiments performed on these crystals have shown that all Fermi surface bands are very shallow14,15,16; one or two electron pockets centred at the Brillouin zone corner with Fermi energy 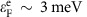 , and a compensating cylindrical hole pocket near the zone centre with
, and a compensating cylindrical hole pocket near the zone centre with 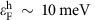 . FeSe is a multigap superconductor with two distinct superconducting gaps Δ1≈3.5 and Δ2≈2.5 meV (ref. 14). Remarkably, the Fermi energies are comparable to the superconducting gaps; Δ/ɛF is ∼0.3 and ∼1 for hole and electron bands, respectively14. These large Δ/ɛF(≈1/(kFξpair)) values indicate that FeSe is in the BCS–BEC crossover regime. In fact, values of 2Δ1/kBTc≈9 and 2Δ2/kBTc≈6.5, which are significantly enhanced with respect to the weak-coupling BCS value of 3.5, imply that the attractive interaction holding together the superconducting electron pairs takes on an extremely strong-coupling nature, as expected in the crossover regime. Moreover, the appearance of a new high-field superconducting phase when the Zeeman energy is comparable to the gap and Fermi energies, μ0H∼Δ∼ɛF, suggests a peculiar superconducting state of FeSe (ref. 14). Therefore, FeSe provides a new platform to study the electronic properties in the crossover regime.
. FeSe is a multigap superconductor with two distinct superconducting gaps Δ1≈3.5 and Δ2≈2.5 meV (ref. 14). Remarkably, the Fermi energies are comparable to the superconducting gaps; Δ/ɛF is ∼0.3 and ∼1 for hole and electron bands, respectively14. These large Δ/ɛF(≈1/(kFξpair)) values indicate that FeSe is in the BCS–BEC crossover regime. In fact, values of 2Δ1/kBTc≈9 and 2Δ2/kBTc≈6.5, which are significantly enhanced with respect to the weak-coupling BCS value of 3.5, imply that the attractive interaction holding together the superconducting electron pairs takes on an extremely strong-coupling nature, as expected in the crossover regime. Moreover, the appearance of a new high-field superconducting phase when the Zeeman energy is comparable to the gap and Fermi energies, μ0H∼Δ∼ɛF, suggests a peculiar superconducting state of FeSe (ref. 14). Therefore, FeSe provides a new platform to study the electronic properties in the crossover regime.
Here we report experimental signatures of preformed Cooper pairing in FeSe below T*∼20 K. Our highly sensitive magnetometry, thermoelectric and nuclear magnetic resonance (NMR) measurements reveal an almost unprecedented giant diamagnetic response as a precursor to superconductivity and pseudogap formation below T*. This yields profound implications on exotic bound states of strongly interacting fermions. Furthermore, the peculiar electronic structure with the electron–hole compensation in FeSe provides a new playground to study unexplored physics of quantum-bound states of interacting fermions.
Results
Giant superconducting fluctuations
It is well known that thermally fluctuating droplets of Cooper pairs can survive above Tc. These fluctuations arise from amplitude fluctuations of the superconducting order parameter and have been investigated for many decades. Their effect on thermodynamic, transport and thermoelectric quantities in most superconductors is well understood in terms of standard Gaussian fluctuation theories17. However, in the presence of preformed pairs associated with the BCS–BEC crossover, superconducting fluctuations are expected to be strikingly enhanced compared with Gaussian theories due to additional phase fluctuations. Moreover, it has been suggested that such enhanced fluctuations can lead to a reduction of the density of states (DOS), dubbed the pseudogap1,2.
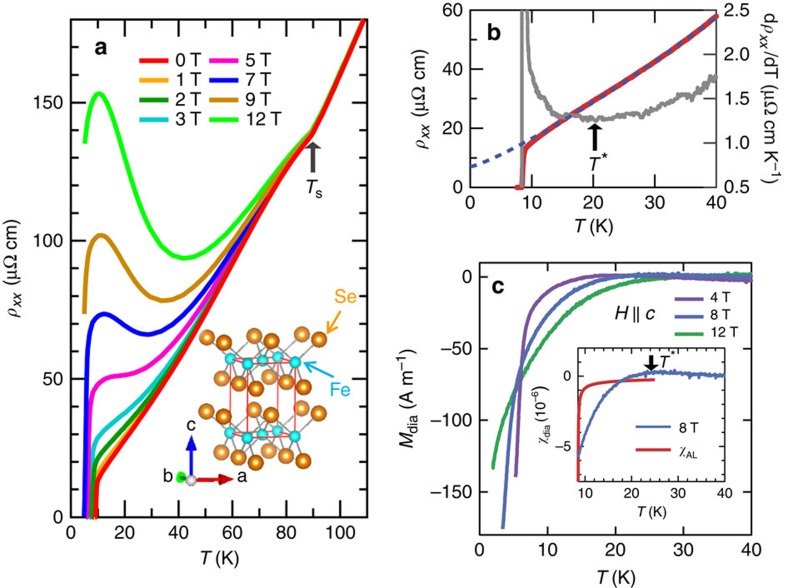
Quite generally, superconducting fluctuations give rise to an enhancement of the normal-state conductivity, which manifests itself as a downturn towards lower T of the resistivity versus temperature curve above Tc. The high-field magnetoresistance of compensated semimetals is essentially determined by the product of the scattering times of electron and hole bands14. The large, insulating-like upturn in ρxx(T) at high fields is thus an indication of the high quality of our crystals (Fig. 1a). At low temperatures, however, the expected downturn behaviour is observed, implying large superconducting fluctuations. Even at zero field, dρxx(T)/dT shows a minimum around T*∼20 K (Fig. 1b), indicating the appearance of excess conductivity below ∼T*. However, a quantitative analysis of this excess conductivity is difficult to achieve because it strongly depends on the extrapolation of the normal-state resistivity above T* to lower T. In addition, the resistivity may be affected by a change of the scattering time when a pseudogap opens at T* as observed in underdoped cuprates18.
Figure 1. Excess conductivity and diamagnetic response of a high-quality single crystal of FeSe.
(a) T dependence of ρxx in magnetic fields (H||c). The structural transition occurs at Ts=90 K, which is accompanied by a kink in ρxx(T). Inset shows the crystal structure of FeSe. (b) T dependence of ρxx (red) and dρxx/dT (grey). Below T* shown by arrow, ρxx shows a downward curvature. The blue dashed line represents ρxx(T)=ρ0+ATα with ρ0=7 μΩ cm A=0.6 μΩ cm K−2 and α=1.2. (c) Diamagnetic response in magnetization Mdia for H||c. The inset shows the diamagnetic susceptibility χdia at 8 T (blue) compared with the estimated χAL in the standard Gaussian fluctuations theory (red).
We therefore examine the superconducting fluctuations in FeSe through the diamagnetic response in the magnetization. The magnetization M(T) for magnetic field H parallel to the c axis (Supplementary Fig. 1) exhibits a downward curvature below ∼T*. This pronounced decrease of M(T) can be attributed to the diamagnetic response due to superconducting fluctuations. Figure 1c shows the diamagnetic response in the magnetization Mdia between 0 and 40 K for μ0H=4, 8 and 12 T, obtained by subtracting a constant M as determined at 30 K. Although there is some ambiguity due to weakly temperature-dependent normal-state susceptibility, we find a rough crossing point in Mdia(T, H) near Tc. Such a crossing behaviour is considered as a typical signature of large fluctuations and has been found in cuprates19. The thermodynamic quantities do not include the Maki—Thompson-type fluctuations. Hence, the fluctuation-induced diamagnetic susceptibility of most superconductors including multiband systems can be well described by the standard Gaussian-type (Aslamasov–Larkin, AL) fluctuation susceptibility χAL (refs 20, 21, 22), which is given by
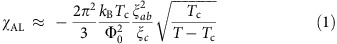 |
in the zero-field limit23. Here Φ0 is the flux quantum and ξab (ξc) is the effective coherence lengths parallel (perpendicular) to the ab plane at zero temperature. In the multiband case, the behaviour of χAL is determined by the shortest coherence length of the main band, which governs the orbital upper critical field. The diamagnetic contribution χAL is expected to become smaller in magnitude at higher fields, and thus |χAL| yields an upper bound for the standard Gaussian-type amplitude fluctuations. In the inset of Fig. 1c, we compare χdia at 8 T with χAL, where we use ξab (=5.5 nm) and ξc (=1.5 nm)14,15. Obviously the amplitude of χdia of FeSe is much larger than that expected in the standard theory, implying that the superconducting fluctuations in FeSe are distinctly different from those in conventional superconductors.
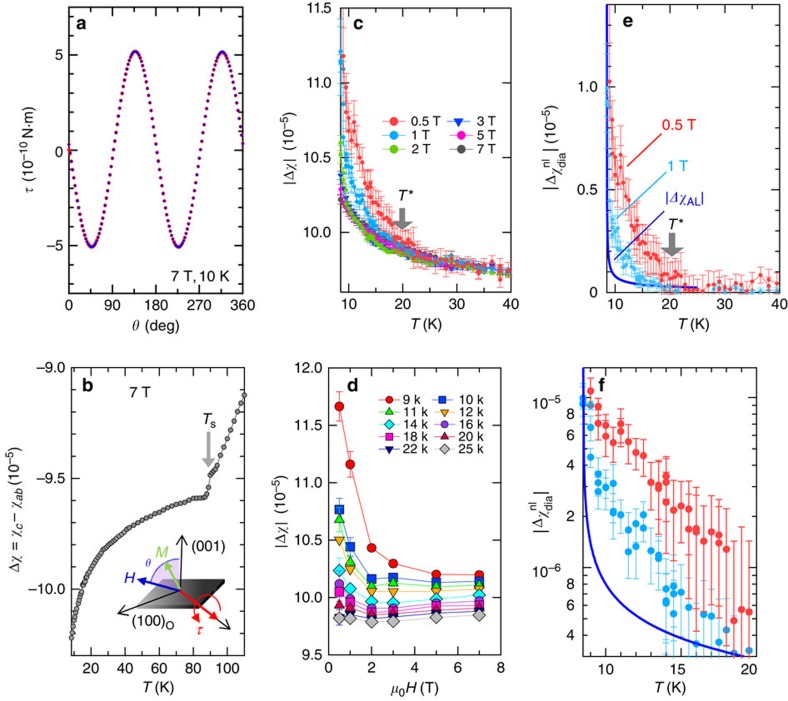
The highly unusual nature of superconducting fluctuations in FeSe can also be seen in the low-field diamagnetic response. Since the low-field magnetization below 2 T is not reliably obtained from conventional magnetization measurements, we resort to sensitive torque magnetometry. The magnetic torque τ=μ0VM × H is a thermodynamic quantity that has a high sensitivity for detecting magnetic anisotropy. Here V is the sample volume, M is the induced magnetization and H is the external magnetic field. For our purposes, the most important advantage of this method is that an isotropic Curie contribution from impurity spins is cancelled out24.
At each temperature and field, the angle-dependent torque curve τ(θ) is measured in H rotating within the ac (bc) plane, where θ is the polar angle from the c axis. In this geometry, the difference between the c axis and ab plane susceptibilities, Δχ=χc−χab, yields a π-periodic oscillation term with respect to θ rotation, 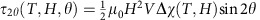 (Fig. 2a; Supplementary Fig. 2; Supplementary Note 1)25,26. In the whole measurement range, Δχ is negative, that is, χab>χc, which is consistent with magnetic susceptibility27 and NMR Knight-shift measurements28,29. Figure 2b shows the T dependence of Δχ at 7 T, which is determined by the amplitude of the sinusoidal curve. At Ts, Δχ(T) exhibits a clear anomaly associated with the tetragonal–orthorhombic structural transition. On approaching Tc, Δχ shows a diverging behaviour. Figure 2c,d depicts the T and H dependence of |Δχ|(T,H), respectively. Above T*∼20 K, |Δχ|(T, H) is nearly field independent. Below T*, however, |Δχ|(T,H) increases with decreasing H, indicating non-linear H dependence of M. This non-linearity increases steeply with decreasing temperature. Since |Δχ| points to a diverging behaviour in the zero-field limit on approaching Tc (Fig. 2d), this strongly non-linear behaviour is clearly caused by superconducting fluctuations.
(Fig. 2a; Supplementary Fig. 2; Supplementary Note 1)25,26. In the whole measurement range, Δχ is negative, that is, χab>χc, which is consistent with magnetic susceptibility27 and NMR Knight-shift measurements28,29. Figure 2b shows the T dependence of Δχ at 7 T, which is determined by the amplitude of the sinusoidal curve. At Ts, Δχ(T) exhibits a clear anomaly associated with the tetragonal–orthorhombic structural transition. On approaching Tc, Δχ shows a diverging behaviour. Figure 2c,d depicts the T and H dependence of |Δχ|(T,H), respectively. Above T*∼20 K, |Δχ|(T, H) is nearly field independent. Below T*, however, |Δχ|(T,H) increases with decreasing H, indicating non-linear H dependence of M. This non-linearity increases steeply with decreasing temperature. Since |Δχ| points to a diverging behaviour in the zero-field limit on approaching Tc (Fig. 2d), this strongly non-linear behaviour is clearly caused by superconducting fluctuations.
Figure 2. Diamagnetic response detected by magnetic torque measurements above Tc.
(a) The magnetic torque τ as a function of θ. Torque curves measured by rotating H in clockwise (red) and anticlockwise (blue) directions coincide (the hysteresis component is <0.01% of the total torque). (b) Anisotropy of the susceptibility between the c axis and ab plane, Δχ, at 7 T. The inset is schematics of the θ-scan measurements. (c) The T dependence of |Δχ| at various magnetic fields. (d) The H dependence of |Δχ| at fixed temperatures. (e) Temperature dependence of the non-linear diamagnetic response at μ0H=0.5 T (red) and 1 T (blue) obtained by 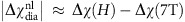 . Blue line represents the estimated |ΔχAL| in the standard Gaussian fluctuations theory. (f)
. Blue line represents the estimated |ΔχAL| in the standard Gaussian fluctuations theory. (f) 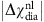 plotted in a semi-log scale at low temperatures. Error bars represent s.d. of the sinusoidal fit to the τ(θ) curves.
plotted in a semi-log scale at low temperatures. Error bars represent s.d. of the sinusoidal fit to the τ(θ) curves.
Thus, the diamagnetic response of FeSe contains H-linear and non-linear contributions to the magnetization; Δχ(T) can be written as 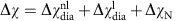 , where
, where 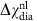 and
and 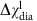 represent the diamagnetic contributions from non-linear and linear field dependence of magnetization, respectively, and ΔχN is the anisotropic part of the normal-state susceptibility, which is independent of H. Since Δχ(T) is almost H independent at high fields (Fig. 2d),
represent the diamagnetic contributions from non-linear and linear field dependence of magnetization, respectively, and ΔχN is the anisotropic part of the normal-state susceptibility, which is independent of H. Since Δχ(T) is almost H independent at high fields (Fig. 2d), 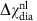 is estimated by subtracting H-independent terms from Δχ. In Fig. 2e, we plot
is estimated by subtracting H-independent terms from Δχ. In Fig. 2e, we plot 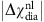 estimated from
estimated from 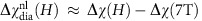 , which we compare with the expectation from the Gaussian fluctuation theory at zero field given by
, which we compare with the expectation from the Gaussian fluctuation theory at zero field given by 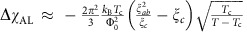 . Near Tc,
. Near Tc, 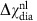 at 0.5 T is nearly 10 times larger than ΔχAL. It should be noted that since
at 0.5 T is nearly 10 times larger than ΔχAL. It should be noted that since 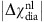 increases with decreasing H,
increases with decreasing H, 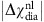 in the zero-field limit should be much larger than
in the zero-field limit should be much larger than 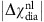 at 0.5 T. Thus, the non-linear diamagnetic response dominates the superconducting fluctuations when approaching Tc in the zero-field limit. We note that, although the AL diamagnetic contribution contains a non-linear term visible at low fields, this term is always smaller than the AL fluctuation contribution at zero field20,21,22.
at 0.5 T. Thus, the non-linear diamagnetic response dominates the superconducting fluctuations when approaching Tc in the zero-field limit. We note that, although the AL diamagnetic contribution contains a non-linear term visible at low fields, this term is always smaller than the AL fluctuation contribution at zero field20,21,22.
Our magnetization and torque results provide thermodynamic evidence of giant superconducting fluctuations in the normal state of FeSe by far exceeding the Gaussian fluctuations. We stress that, since the energy scale of kBT*∼2 meV is comparable to 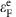 , it is natural to attribute the observed fluctuations to preformed pairs associated with the BCS–BEC crossover. In the presence of those pairs, superconducting phase fluctuations5 arising from the mode coupling of fluctuations are expected to be significantly enhanced and to produce a highly non-linear diamagnetic response, as observed in the experiments. This non-linear response with large amplitude is profoundly different from the Gaussian behaviour in conventional superconductors.
, it is natural to attribute the observed fluctuations to preformed pairs associated with the BCS–BEC crossover. In the presence of those pairs, superconducting phase fluctuations5 arising from the mode coupling of fluctuations are expected to be significantly enhanced and to produce a highly non-linear diamagnetic response, as observed in the experiments. This non-linear response with large amplitude is profoundly different from the Gaussian behaviour in conventional superconductors.
Pseudogap formation
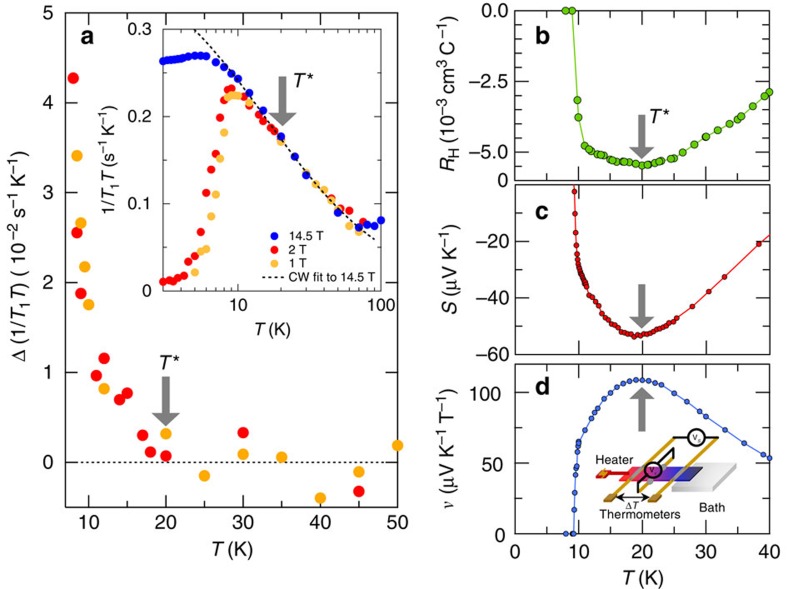
Next, we discuss the possible pseudogap formation associated with the preformed pairs, which suppresses the DOS and hence leads to a change in quasiparticle scattering. We have measured the relaxation time T1 of 77Se NMR spectroscopy in FeSe single crystals (Supplementary Fig. 3) at different fields applied along the c axis. At 14.5 T close to the upper critical field, the temperature dependence of 1/T1T, which is dominated by the dynamical spin susceptibility χ(q) at the antiferromagnetic wave vector q=(π, π), can be fitted well by a Curie–Weiss law in a wide temperature range below Ts (Fig. 3a, inset). At low fields of 1 and 2 T, however, 1/T1T(T) shows a noticeable deviation from this fit (dashed line in Fig. 3a, inset), and the difference between the fit and the low-field data Δ(1/T1T) starts to grow at ∼T* (Fig. 3a, main panel). As the superconducting diamagnetism is an orbital effect that is dominated at q=0, the spin susceptibility χ(π, π) is not influenced by the orbital diamagnetism. Therefore, the observed deviation of 1/T1T(T) is a strong indication of a depletion of the DOS, providing spectroscopic evidence for the psedugap formation below ∼T *. The onset temperature and the field dependence of the non-linear contribution of 1/T1T(T) bear a certain similarity to the features of the diamagnetic susceptibility, pointing to the intimate relation between the pseudogap and preformed pairs in this system.
Figure 3. Possible pseudogap formation below T* evidenced by NMR and transport measurements.
(a) Temperature dependence of the NMR relaxation rate divided by temperature 1/T1T. Inset: at 14.5 T, the temperature dependence of 1/T1T between ∼10 and 70 K is fitted to a Curie–Weiss law ∝(T+16 K)−1 (dashed line). Main panel: the difference between the Curie–Weiss fit and the low-field data Δ(1/T1T) is plotted as a function of temperature. (b) Hall coefficient, RH. (c) Seebeck coefficient, S. (d) Nernst coefficient, ν, in the zero-field limit as functions of temperature. Inset in d is a schematic of the measurement set-up of the thermoelectric coefficients.
The pseudogap formation is further corroborated by the measurements of Hall (RH), Seebeck (S) and Nernst (ν) coefficients (Fig. 3b–d). The negative sign of the Hall and Seebeck data indicates that the transport properties are governed mainly by the electron band, which is consistent with the previous analysis of the electronic structure in the orthorhombic phase below Ts (ref. 16). Obviously, at T *∼20 K, all the coefficients show a minimum or maximum. Since the Hall effect is insensitive to superconducting fluctuations, the minimum of RH(∝(σh−σe)/(σh+σe)), where σe(h) is the conductivity of electrons (holes), suggests a change of the carrier mobility at ∼T *. The thermomagnetic Nernst coefficient consists of two contributions generated by different mechanisms: ν=νN+νS. The first term represents the contribution of normal quasiparticles. The second term, which is always positive, represents the contribution of fluctuations of either amplitude or phase of the superconducting order parameter. On approaching Tc, νS is expected to diverge30. As shown in Fig. 3d, however, such a divergent behaviour is absent. This is because in the present very clean system, νN is much larger than νS (Supplementary Fig. 4a; Supplementary Note 2). Since νN and S are proportional to the energy derivatives of the Hall angle and conductivity at the Fermi level, respectively, 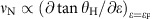 and
and 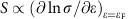 both sensitively detect the change of the energy dependence and/or anisotropy of the scattering time at the Fermi surface (see also Supplementary Fig. 4b,c for ν/T(T) and S/T(T)). Therefore, the temperature dependence of the three transport coefficients most likely implies a change in the quasiparticle excitations at T *, which is consistent with the pseudogap formation. We also note that anomalies at similar temperatures have been reported for the temperature dependence of the thermal expansion13 as well as of Young's modulus29. Recent scanning tunnelling spectroscopy data also suggest some suppression of the DOS at low energies in a similar temperature range31.
both sensitively detect the change of the energy dependence and/or anisotropy of the scattering time at the Fermi surface (see also Supplementary Fig. 4b,c for ν/T(T) and S/T(T)). Therefore, the temperature dependence of the three transport coefficients most likely implies a change in the quasiparticle excitations at T *, which is consistent with the pseudogap formation. We also note that anomalies at similar temperatures have been reported for the temperature dependence of the thermal expansion13 as well as of Young's modulus29. Recent scanning tunnelling spectroscopy data also suggest some suppression of the DOS at low energies in a similar temperature range31.
Discussion
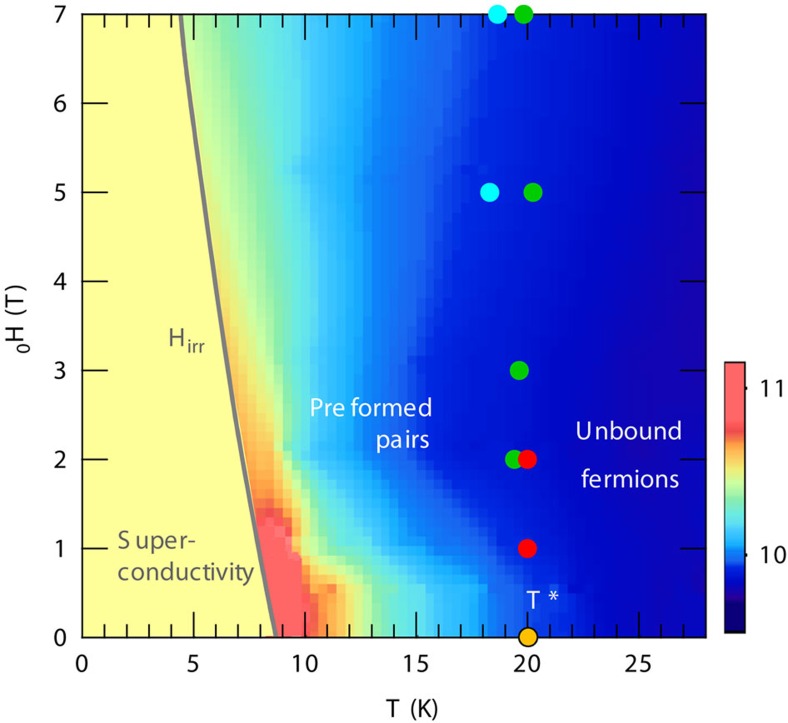
Figure 4 displays the schematic H–T phase diagram of FeSe for H||c. The fluctuation regime associated with preformed pairing is determined by the temperatures at which dρxx(H)/dT shows a minimum and ν(H) shows a peak (Supplementary Fig. 5a,b; Supplementary Note 3) in magnetic fields, as well as by the onset of Δ(1/T1T) (Fig. 3a). The diamagnetic signal, NMR relaxation rate and transport data consistently indicate that the preformed pair regime extends over a wide range of the phase diagram. The phase fluctuations dominate at low fields where the non-linear diamagnetic response is observed (Fig. 2d). This phase-fluctuation region continuously connects to the vortex liquid regime above the irreversibility field Hirr, where a finite resistivity is observed with a broad superconducting transition (Fig. 1a).
Figure 4. H–T phase diagram of FeSe for H||c.
Solid line is the irreversibility line Hirr(T) (ref. 14). The colour represents the magnitude of Δχ (in 10−5, scale shown in the colour bar) from magnetic torque measurements (Fig. 2c). Preformed pair regime is determined by the minimum of dρxx(H)/dT (blue circles), the peak of Nernst coefficient νpeak (green circles) and the onset of Δ(1/T1T) in the NMR measurements (red circles).
Let us comment on the electronic specific heat, which is another thermodynamic quantity related to the DOS of quasiparticles. The specific heat C at comparatively high temperatures, however, is dominated by the phonon contribution ∝T3 (refs 29, 32), which makes it difficult to resolve the pseudogap anomaly. Also, the reduction of C/T may partly be cancelled with the increase by the strong superconducting fluctuations found in the present study. It should be also stressed that FeSe exhibits a semimetallic electronic structure with the compensation condition, that is, the electron and hole carrier densities should be the identical. Such a compensated situation of the electronic structure may alter significantly the chemical potential shift expected in the BEC theories for a single-band electronic structure. How the entropy in crossover semimetals behaves below T * is a fundamentally new problem, which deserves further theoretical studies.
Finally, we remark that the preformed Cooper pairs and pseudogap develop in the non-Fermi liquid state characterized by a linear-in-temperature resistivity, highlighting the highly unusual normal state of FeSe in the BCS–BEC crossover regime. The resistivity above T * can be fitted up to ∼50 K as ρxx(T)=ρxx(0)+ATα with α=1.1−1.2, where the uncertainty arises from the fact that ρxx(0) is unknown (Fig. 1b). Thus, the exponent α close to unity indicates a striking deviation from the Fermi liquid behaviour of α=2. This non-Fermi liquid behaviour in FeSe is reminiscent of the anomalous normal-state properties of high-Tc cuprate superconductors. The main difference between these systems and FeSe is the multiband nature of the latter34,35; the Fermi surface consists of compensating electron and hole pockets. The present observation of preformed pairs together with the breakdown of Fermi liquid theory in FeSe implies an inherent mechanism that brings about singular inelastic scattering properties of strongly interacting fermions in the BCS–BEC crossover.
Methods
Sample preparation and characterization
High-quality single crystals of tetragonal β-FeSe were grown by low-temperature vapour transport method at Karlsruhe Institute of Technology and Kyoto University13. As shown in Fig. 1b, taking ρxx(Tc+)≈10 μΩ cm as an upper limit of the residual resistivity leads to the residual resistivity ratio (RRR)>40. The large RRR value, large magnetoresistance below Ts, quantum oscillations at high fields15,16, a very sharp 77Se NMR line width29, and extremely low level of impurities and defects observed by scanning tunnelling microscope topographic images14,33, all demonstrate that the crystals used in the present study are very clean. The tetragonal structure is confirmed by single-crystal X-ray diffraction at room temperature. The tetragonal [100]T/[010]T is along the square edges of the crystals, and below the structural transition, the orthorhombic [100]O/[010]O along the diagonal direction.
Magnetization and magnetic torque measurements
The magnetization was measured using a vibrating sample option (VSM) of the Physical Properties Measurement System by Quantum Design. Supplementary Figure 1 shows temperature dependence of the magnetization in a single crystal of FeSe for several different fields. We obtained the diamagnetic response in the magnetization, Mdia, by shifting the curves to zero at 30 K, that is, by subtracting a constant representative of the normal-state magnetization ignoring the small paramagnetic Curie–Weiss contribution.
Magnetic torque is measured by using a micro-cantilever method25,26. As illustrated in the inset of Fig. 2b, a carefully selected tiny crystal of ideal tetragonal shape with 200 × 200 × 5 μm3 is mounted on to a piezo-resistive cantilever. The crystals contain orthorhombic domains with typical size of ∼5 μm below Ts. Supplementary Figure 2a–f shows the magnetic torque τ measured in various fields, where the field orientation is varied within a plane including the c axis (θ=0,180°) and the field strength H=|H| is kept during the rotation. The torque curves at 0.5 and 1T (Supplementary Fig. 2a and b) are distorted at 8.5 K, which is expected in the superconducting state of anisotropic materials36 whereas those above 9 K are perfectly sinusoidal.
NMR measurements
77Se NMR measurements were performed on a collection of several oriented single crystals, and external fields (1, 2 and 14.5 T) are applied parallel to the c axis. Since 77Se has a nuclear spin I=1/2, and thus no electric quadrupole interactions, the resonance linewidth of the NMR spectra are very narrow with full width at half maximum of a couple of kHz (Supplementary Fig. 3). The nuclear spin-lattice relaxation rate 1/T1 is evaluated from the recovery curve R(t)=1−m(t)/m(∞) of the nuclear magnetization m(t), which is the nuclear magnetization at a time t after a saturation pulse. R(t) can be described by R(t)∝exp(−t/T1) with a unique T1 in the whole measured region, indicative of a homogeneous electronic state. In general, 1/T1 for H||c is related to the imaginary part of the dynamical magnetic susceptibility χ(q, ω) by the relation
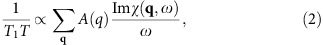 |
where A(q) is the transferred hyperfine coupling tensor along the c axis at the Se site and ω=γn/H with γn/(2π)=8.118 MHzT−1 is the NMR frequency. 1/T1T at the Se site is mainly governed by the magnetic fluctuations at the Fe sites, that is, particularly in FeSe, the short-lived stripe-antiferromagnetic correlations at q=(π, π) in the tetragonal notation. It should be noted that the superconducting diamagnetism is an orbital effect that is dominated at q=0 and thus it does not affect the dynamical spin susceptibility at q=(π, π).
Thermoelectric measurements
The thermoelectric coefficients were measured by the standard d.c. method with one resistive heater, two Cernox thermometers and two lateral contacts (Fig. 3d, inset). The Seebeck signal S is the transverse electric field response Ex (||x), while the Nernst signal N is a longitudinal response Ex (||x) to a transeverse temperature gradient ∇xT(||x) in the presence of a magnetic field Hz (||z), that is, S≡Ex/(−∇xT) and N≡Ey/(−∇xT), respectively. The Nernst coefficient is defined as ν≡N/μ0H.
Data availability
The data that support the findings of this study are available on request from the corresponding authors (T.S. or Y.M.).
Additional information
How to cite this article: Kasahara, S. et al. Giant superconducting fluctuations in the compensated semimetal FeSe at the BCS–BEC crossover. Nat. Commun. 7:12843 doi: 10.1038/ncomms12843 (2016).
Supplementary Material
Supplementary Figures 1-5 and Supplementary Notes 1-3
Acknowledgments
We thank K. Behnia, I. Danshita, H. Kontani, A. Perali, M. Randeria and Y. Yanase for fruitful discussions. This work was supported by Grants-in-Aid for Scientific Research (KAKENHI) (nos 25220710, 15H05745, 15H02106 and 15H03688) and on Innovative Areas ‘Topological Material Science' (no. 15H05852), and ‘J-Physics' (nos. 15H05882, 15H05884 and 15K21732). The work of A.L. was supported by NSF grants no. DMR-1606517 and no. ECCS-1560732, and in part by Wisconsin Alumni Research Foundation.
Footnotes
Author contributions S.K. and T.Wo. prepared the samples. S.K., T.Y., A.S., R.K, Y.S., T.Wa., K.I., T.T., F.H. and C.M. carried out the measurements. S.K., K.I., H.v.L., A.L., T.S. and Y.M. interpreted and analysed the data. T.S., Y.M., H.v.L., S.K. and A.L. wrote the manuscript with inputs from all authors.
References
- Sá de Melo C. A. R. When fermions become bosons: pairing in ultracold gases. Phys. Today 61, 45–51 (2008). [Google Scholar]
- Randeria M. & Taylor E. Crossover from Bardeen-Cooper-Schrieffer to Bose-Einstein condensation and the unitary Fermi gas. Annu. Rev. Condens. Matter Phys. 5, 209–232 (2014). [Google Scholar]
- Nascimbène S., Navon N., Jiang K. J., Chevy F. & Salomon C. Exploring the thermodynamics of a universal Fermi gas. Nature 463, 1057–1060 (2010). [DOI] [PubMed] [Google Scholar]
- Sagi Y., Drake T. E., Paudel R., Chapurin R. & Jin D. S. Breakdown of Fermi liquid description for strongly interacting fermions. Phys. Rev. Lett. 114, 075301 (2015). [DOI] [PubMed] [Google Scholar]
- Emery V. J. & Kivelson S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1994). [Google Scholar]
- Corson J., Mallozzi R., Orenstein J., Eckstein J. N. & Bozovic I. Vanishing of phase coherence in underdoped Bi2Sr2CaCu2O8+δ. Nature 398, 221–223 (1999). [Google Scholar]
- Li L. et al. Diamagnetism and Cooper pairing above Tc in cuprates. Phys. Rev. B 81, 054510 (2010). [Google Scholar]
- Keimer B., Kivelson S. A., Norman M. R., Uchida S. & Zaanen J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015). [DOI] [PubMed] [Google Scholar]
- Hashimoto K. et al. A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe2(As1−xPx)2. Science 336, 1554–1557 (2012). [DOI] [PubMed] [Google Scholar]
- Shibauchi T., Carrington A. & Matsuda Y. A quantum critical point lying beneath the superconducting dome in iron-pnictides. Annu. Rev. Condens. Matter Phys. 5, 113–135 (2014). [Google Scholar]
- Lubashevsky Y., Lahoud E., Chashka K., Podolsky D. & Kanigel A. Shallow pockets and very strong coupling superconductivity in FeSexTe1−x. Nat. Phys. 8, 309–312 (2012). [Google Scholar]
- Okazaki K. et al. Superconductivity in an electron band just above the Fermi level: possible route to BCS-BEC superconductivity. Sci. Rep. 4, 4109 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böhmer A. E. et al. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys. Rev. B 87, 180505(R) (2013). [Google Scholar]
- Kasahara S. et al. Field-induced superconducting phase of FeSe in the BCS-BEC cross-over. Proc. Natl Acad. Sci. USA 111, 16309–16313 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terashima T. et al. Anomalous Fermi surface in FeSe seen by Shubnikov-de Haas oscillation measurements. Phys. Rev. B 90, 144517 (2014). [Google Scholar]
- Watson M. D. et al. Dichotomy between the hole and electron behavior in the multiband FeSe probed by ultra high magnetic fields. Phys. Rev. Lett. 115, 027006 (2015). [DOI] [PubMed] [Google Scholar]
- Larkin A. I. & Varlamov A. Theory of Fluctuations in Superconductors Clarendon Press (2005). [Google Scholar]
- Kontani H. Anomalous transport phenomena in Fermi liquids with strong magnetic fluctuations. Rep. Prog. Phys. 71, 026501 (2008). [Google Scholar]
- Welp U. et al. High-field scaling behavior of thermodynamic and transport quantities of YBa2Cu3O7−δ near the superconducting transition. Phys. Rev. Lett. 67, 3180–3183 (1991). [DOI] [PubMed] [Google Scholar]
- Ullah S. & Dorsey A. T. Effect of fluctuations on the transport properties of type-II superconductors in a magnetic field. Phys. Rev. B 44, 262–273 (1991). [DOI] [PubMed] [Google Scholar]
- Ussishkin I., Sondhi S. L. & Huse D. A. Gaussian Superconducting fluctuations, thermal transport, and the Nernst effect. Phys. Rev. Lett. 89, 287001 (2002). [DOI] [PubMed] [Google Scholar]
- Soto F. et al. In-plane and transverse superconducting fluctuation diamagnetism in the presence of charge-denisty waves in 2H-NbSe2 single crystals. Phys. Rev. B 75, 094509 (2007). [Google Scholar]
- Aslamazov L. G. & Larkin A. I. Fluctuation-induced magnetic susceptibility of superconductors and normal metals. J. Exp. Theor. Phys. 40, 321 (1975). [Google Scholar]
- Watanabe D. et al. Novel Pauli-paramagnetic quantum phase in a Mott insulator. Nat. Commun. 3, 1090 (2012). [DOI] [PubMed] [Google Scholar]
- Okazaki R. et al. Rotational symmetry breaking in the hidden-order phase of URu2Si2. Science 331, 439–442 (2011). [DOI] [PubMed] [Google Scholar]
- Kasahara S. et al. Electronic nematicity above the structural and superconducting transition in BaFe2(As1−xPx)2. Nature 486, 382–385 (2012). [DOI] [PubMed] [Google Scholar]
- Grechnev G. E. et al. Magnetic properties of superconducting FeSe in the normal state. J. Phys.: Condens. Matter 25, 046004 (2013). [DOI] [PubMed] [Google Scholar]
- Baek S.-H. et al. Orbital-driven nematicity in FeSe. Nat. Mater. 14, 210–214 (2015). [DOI] [PubMed] [Google Scholar]
- Böhmer A. E. et al. Origin of the tetragonal-to-orthorhombic phase transition in FeSe: a combined thermodynamic and NMR study of nematicity. Phys. Rev. Lett. 114, 027001 (2015). [DOI] [PubMed] [Google Scholar]
- Yamashita T. et al. Colossal thermomagnetic response in the exotic superconductor URu2Si2. Nat. Phys. 11, 17–20 (2015). [Google Scholar]
- Rössler S. et al. Emergence of an incipient ordering mode in FeSe. Phys. Rev. B 92, 060505(R) (2015). [Google Scholar]
- Lin J.-Y. et al. Coexistence of isotropic and extended s-wave order parameters in FeSe as revealed by low-temperature specific heat. Phys. Rev. B 84, 220507(R) (2011). [Google Scholar]
- Watashige T. et al. Evidence for time-reversal symmetry breaking of the superconducting state near twin-boundary interfaces in fese revealed by scanning tunneling spectroscopy. Phys. Rev. X 5, 031022 (2015). [Google Scholar]
- Chubukov A. V., Eremin I. & Efremov D. V. Superconductivity versus bound-state formation in a two-band superconductor with small Fermi energy: Applications to Fe pnictides/chalcogenides and doped SrTiO3. Phys. Rev. B 93, 174516 (2016). [Google Scholar]
- Loh Y. L., Randeria M., Trivedi N., Chang C.-C. & Scalettar R. Superconductor-Insulator Transition and Fermi-Bose Crossovers. Phys. Rev. X. 6, 021029 (2016). [Google Scholar]
- Kogan V. G. Uniaxial superconducting particle in intermediate magnetic fields. Phys. Rev. B 38, 7049–7050 (1988). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures 1-5 and Supplementary Notes 1-3
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding authors (T.S. or Y.M.).