Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Oct 11;6:35156. doi: 10.1038/srep35156

Magnetocaloric Properties of Fe-Ni-Cr Nanoparticles for Active Cooling

V Chaudhary 1,2,3, RV Ramanujan 3,a
PMCID: PMC5057077  PMID: 27725754

Abstract

Low cost, earth abundant, rare earth free magnetocaloric nanoparticles have attracted an enormous amount of attention for green, energy efficient, active near room temperature thermal management. Hence, we investigated the magnetocaloric properties of transition metal based (Fe70Ni30)100−xCrx (x = 1, 3, 5, 6 and 7) nanoparticles. The influence of Cr additions on the Curie temperature (TC) was studied. Only 5% of Cr can reduce the TC from ~438 K to 258 K. These alloys exhibit broad entropy v/s temperature curves, which is useful to enhance relative cooling power (RCP). For a field change of 5 T, the RCP for (Fe70Ni30)99Cr1 nanoparticles was found to be 548 J-kg−1. Tunable TCin broad range, good RCP, low cost, high corrosion resistance and earth abundance make these nanoparticles suitable for low-grade waste heat recovery as well as near room temperature active cooling applications.

Energy efficient magnetocaloric materials for magnetic cooling have attracted intense research interest due to unsustainable energy consumption and limitations of current cooling technology1,2,3,4,5,6,7,8,9. A well-known milestone in magnetic cooling is the development of a compressor free wine cooler based on magnetic cooling, developed by Haier, BASF and Astronautics corporation10,11. Magnetic cooling has already been shown to use 35% less power than conventional cooling11. Magnetic cooling is an energy efficient, low noise and low vibration technology which does not use ozone layer depleting hydrofluorocarbons and is, therefore, environmentally friendly12. The magnetocaloric effect (MCE) is the change in temperature of a material due to the adiabatic application or removal of an external magnetic field13. This temperature change is related to the magnetic entropy change (∆SM). Generally, MCE is large in the vicinity of the Curie temperature (TC), where the magnetic spins undergo an order - disorder phase transition.

Gd5(SixGe1−x)4 and other R5T4 (R = Rare earth, T = Transition metal) materials can exhibit promising magnetocaloric performance and are known as “Giant magnetocaloric materials”14,15. However, issues surrounding rare-earths are very complex due to strategic reasons and economics. China is the main supplier of rare earths since several decades, accounting for ~97% and ~90% of world production in 2009 and 2013, respectively16. This control may result in supply instabilities. In addition, rare earth based materials are corrosion prone and not earth abundant. These undesirable factors motivate us to develop non rare earth based magnetocaloric materials17,18,19,20,21,22,23.

First order transition materials (FOTM) which exhibit simultaneous magnetic and structural transition result in high isothermal entropy change24,25,26. However, the narrow working temperature span and large magnetic and thermal hysteresis in FOTM limit real-world applications5,13,27,28. The magneto-structural transition is often associated with field and temperature hysteresis, which reduce maximum operating frequency. In addition, the repetitive structural transition in FOTM can cause result in mechanical instability, which cause failure of the system2,29,30. On the other hand, second order transition materials (SOTM) exhibit a magnetic transition. These materials generally have lower isothermal entropy change compared to those of FOTM. However, SOTM are superior in terms of negligible magnetic and temperature hysteresis and also exhibit large working temperature span, and therefore, high relative cooling power (RCP)5,13,28,31,32. Hence, there is a considerable interest in rare earth free, cost effective and readily available Fe based materials exhibiting a second order magnetic phase transition5,13,28,31,33,34,35.

Typically, bulk magnetocaloric materials have been developed for cooling systems. The magnetocaloric effect in nanostructured materials has received considerable interest recently since they possess additional advantages5,13,28,31,32,36,37,38. These nanomaterials can be useful for active magnetic cooling devices, microfluidic reactors and other systems. Slow heat transfer in bulk solids is one of the most difficult issues which diminish the efficiency of thermal management systems. The dispersion of magnetic particles in a suitable fluid can solve this challenge, the large surface area of nanoparticles and dispersion in fluid results in better thermal contact and therefore faster heat exchange compared to bulk systems. Furthermore, such ferrofluids can be used for self-pumping, automatic, magnetic cooling28,39,40.

γ-Fe80−xNixCr20 (14 ≤ x ≤ 30) alloys have competing exchange interactions, hence the local spin orientation depends on its environment41. The effective exchange interaction can be positive, negative, or nearly zero. This exchange interaction is governed by the concentration, distribution, and strength of the six different exchange interactions (Jij) between the different magnetic atoms. By using neutron scattering technique, Men’shikov et al.42 reported the values of the exchange integrals: Jij (Ni–Ni) = 52 meV, Jij (Fe–Ni) = 36 meV, Jij (Ni–Cr) = 122 meV, Jij (Fe–Cr) = 39 meV, Jij (Fe–Fe) = −7 meV, Jij (Cr–Cr) = −227 meV.

Our earlier studies show that γ-FeNiB nanoparticles are suitable candidates for low grade waste heat recovery while γ-FeNiMn can be used for slightly above room temperature applications5,13. On the other hand, alloying of iron based material with Cr will improve corrosion resistance43, e.g., increasing Cr content in the magnetic Fe73.5−xSi13.5B9Nb3Cu1Crx alloy results in a corrosion resistant material for marine or SiO2 contaminated environments44,45. Therefore, Fe-Ni-Cr alloys possess both good corrosion resistance and good magnetocaloric properties.

We report the effect of alloying of Fe70Ni30 with Cr on magnetic phase transition temperature (TC) and magnetocaloric properties of alloy nanoparticles. Six compositions: Fe70Ni30, (Fe70Ni30)99Cr1, (Fe70Ni30)97Cr3, (Fe70Ni30)95Cr5, (Fe70Ni30)94Cr6, and (Fe70Ni30)93Cr7 were synthesized, the nomenclature is Cr0, Cr1, Cr3, Cr5, Cr6 and Cr7, respectively. The theoretical values of TC were compared with experimental results. In addition, these nanoparticles were coated with oleic acid (80%) and ammonium hydroxide (20%) and dispersed in oleic acid to make the ferrofluid. The ferrofluid was used as a heat transfer medium in a self-pumping magnetic cooling prototype.

Results

X-ray Diffraction and Transmission Electron Microscopy Analysis

Figure 1 shows the XRD patterns of Cr0, Cr1, Cr3, Cr5, Cr6 and Cr7 nanoparticles after heating at 700 °C for 2 h followed by quenching. All the samples exhibit three main diffraction peaks (111, 200 and 220) of the γ-FeNi phase with lattice parameter (a) in the range of 3.5919(4)–3.5983(3) Å and space group Fm-3m. Adding Cr to Fe70Ni30 does not shift in the diffraction peak positions much as the atomic radius of Cr does not differ much from the corresponding value for Fe and Ni. The average crystal sizes, calculated by the Scherrer formula after subtracting the instrumental line broadening, were ~9 nm, ~12 nm, ~10 nm, ~13 nm, ~12 nm and ~11 nm for Cr0, Cr1, Cr3, Cr5, Cr6 and Cr7 nanoparticles, respectively. All the samples exhibit asymmetric broadening in the 111 diffraction peak.

Figure 1. XRD patterns of Cr0, Cr1, Cr3, Cr5, Cr6 and Cr7 nanoparticles after annealing at 700 °C for 2 h and then quenching in water.

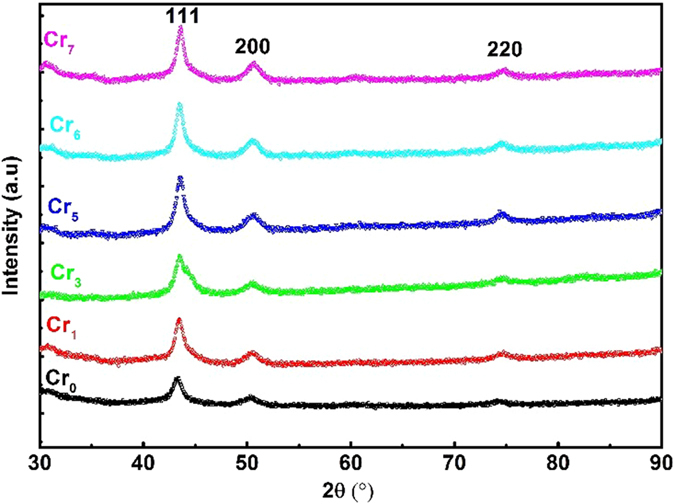
Figure 1

Open in a new tab

Figure 2 shows the bright field transmission electron micrograph of Cr3 and Cr5 nanoparticles. The particle size for Cr3 is in the range of 3 nm to 21 nm, with an average size of 9 nm, while the particle size for Cr5 is in the range of 4 nm to 25 nm range, with an average size of 12 nm. These values are close to the value obtained from XRD data. The lattice fringes of 2.1 Å and 2.11 Å for Cr3 and Cr5, respectively, correspond to the 111 planes of the fcc phase (inset of Fig. 2).

Figure 2.

Figure 2

Open in a new tab

Bright field TEM micrographs of (a) Cr3 and (b) Cr5 nanoparticles, insets show lattice fringe images corresponding to 111 planes.

Curie temperature

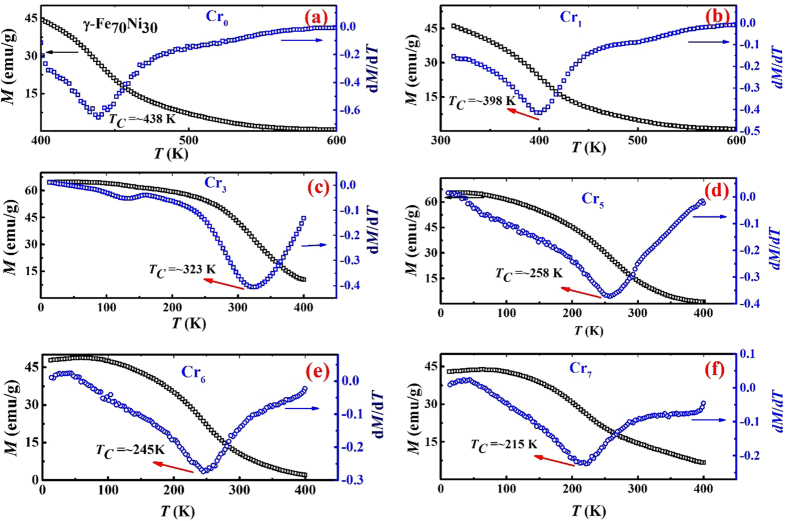
The Curie temperature is the temperature at which the ferromagnetic phase changes to the paramagnetic phase. For MCE applications, we need to determine the TC of that material. It should be noted that the MCE is maximum at its TC and relatively small or almost zero (depending on the TC distribution and the order of the phase transition) at temperatures away from TC. Fig. 3(a,b,c) shows the temperature dependence of magnetization, M(T) (left) and dM/dT (right) for (Fe70Ni30)100−xCrx (x = 0, 1, 3, 5, 6 and 7) nanoparticles, measured upon cooling under a field of 0.1 T. The Curie temperatures (TC) of Cr0, Cr1, Cr3, Cr5, Cr6 and Cr7 were found to be 438 K, 398 K, 323 K, 258 K, 245 K and 215 K, respectively.

Figure 3.

Figure 3

Open in a new tab

Left axis shows the temperature dependence of magnetization M(T) for (a) Cr0, (b) Cr1, (c) Cr3, Cr5, Cr6 and Cr7 while the right axis shows the corresponding derivative with respect to temperature (dM/dT). The Curie temperature for Cr0, Cr1, Cr3, Cr5, Cr6 and Cr7 is 438 K, 398 K, 323 K, 258 K, 245 K and 215 K, respectively.

TC was determined from the minima of the plot of dM/dT versus T. The reduction of TCcan be understand from the mean field model TC = J(r)eff ZT S (S + 1)/3kB, where J(r)eff is the effective exchange interaction, ZT is coordination number, S is the atomic spin quantum number and kB is the Boltzmann constant5.

The Bethe-Slater curve qualitatively describes the variation in strength of direct exchange as a function of the ratio of the interatomic distance to diameter of the 3d electrons (ra/r3d)46. A pair interaction of two atoms sharing two electrons can be used to explain the trend of this curve. A value of 1.5 for ferromagnetic spin coupling was assumed empirically in this curve to separate positive from negative exchange interactions (Jex)46 (Fig. 4(a)). For a ratio ra/r3d less than 1.5, when the electrons from two neighbouring atoms are close to each other, the Pauli Exclusion Principle requires the spins of these electrons to be antiparallel, which results in antiferromagnetic interaction between these atoms. If the ratio ra/r3d is greater than 1.5, 3d electrons can be further away from each other, filling two different orbital states, resulting in ferromagnetic interactions. After reaching a maximum value, the exchange coupling starts to decrease because of decreasing spatial overlap of the wave functions of the electrons. For the same value of x, TC for (Fe70Ni30)100−xCrxis lower than that of (Fe70Ni30)100−xMnx alloys5,31. This is because the value of JCrCris more negative than that of JMnMn. Hence, the effective exchange interaction (J(r)eff) is less in the case of (Fe70Ni30)100−xCrx. The coordination number (ZT) is the same in both cases (due to the same crystal structure), which results in a reduction in TC.

Figure 4.

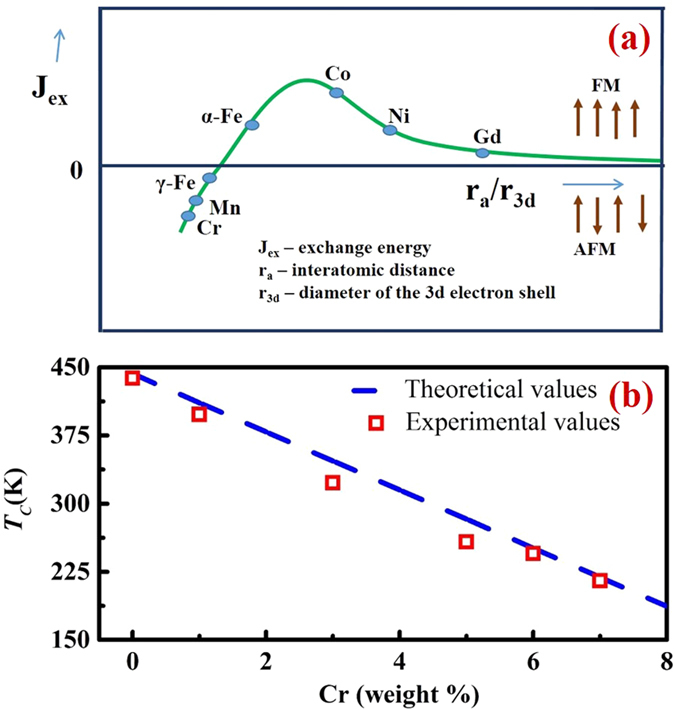
Figure 4

Open in a new tab

(a) The Bethe-Slater curve (schematic) showing the dependence of the exchange interaction on the ratio of interatomic distance to the diameter of the 3d electron shell46 (b) Phase diagram for the ternary system (Fe70Ni30)100−xCrx for x = 0 to 8. Dashed blue line represents the values predicted from the equation TC = TC1 + (TC/dc) (c) while points (red square) are experimental results.

The experimental values of TC were compared with values calculated from the expression TC = TC1 + (dTC/dc) c, TC1 is the Curie temperature of the parent alloy Fe70Ni30, dTC/dc is the rate of change of Curie temperature with concentration (c)46. The dTC/dc value for Cr is −3.2 × 103 K/at %46. A value of TC for Fe70Ni30 was obtained from the binary Fe-Ni phase diagram. This is close to the experimental value of 438 K. Fig. 4(b) shows the change in Curie temperature with Cr% in the ternary system (Fe70Ni30)100−xCrx.

The dashed blue line and red square represent the expression TC = TC1 + (dTC/dc) c and experimental data, respectively. The experimental TC values for Cr0, Cr1, Cr3, Cr6 and Cr7 are reasonably close to those calculated from the expression. This facile tuning of TC makes these alloys useful for near room temperature cooling.

Magnetocaloric Effect

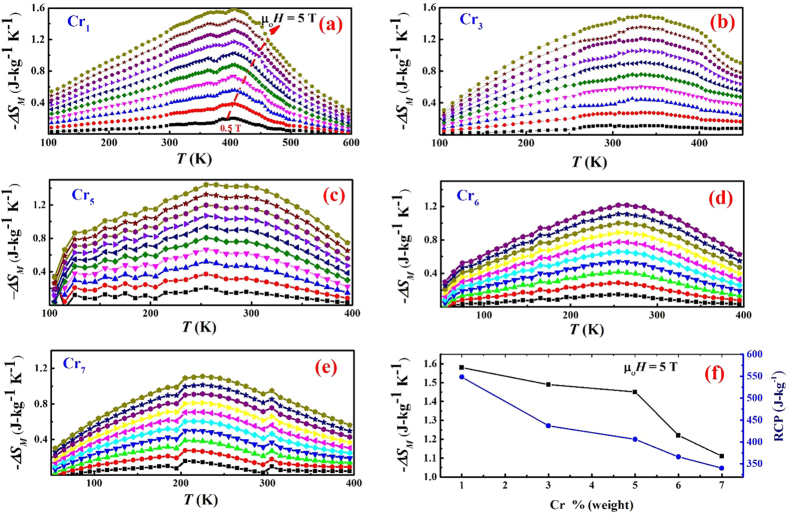
Figure 5(a,b,c,d,e) show the temperature dependence of the magnetic entropy change (−∆SM) under a range of magnetic fields, ranging from 0.5 T to 5 T for Cr1, Cr3, Cr5, Cr6 and Cr7 alloy, respectively. In all cases, the −∆SM versus T curves are very broad, exhibiting a table-like shape. There are several reports of the desirability of such table-like shape in magnetocaloric materials for real applications47,48. Comparing our data to the literature, the −∆SM and RCP values were calculated at TC. For 1 T applied magnetic field, ∆SM for Cr1, Cr3, Cr5, Cr6 and Cr7 at their TC was found to be 0.38 J-kg−1K−1, 0.27 J-kg−1K−1, 0.37 J-kg−1K−1, 0.29 J-kg−1K−1 and 0.28 J-kg−1K−1, respectively. When the field was increased to 5 T, ∆SM for Cr1, Cr3, Cr5, Cr6 and Cr7 was found to be 1.58 J-kg−1K−1, 1.49 J-kg−1K−1, 1.45 J-kg−1K−1, 1.22 J-kg−1K−1 and 1.11 J-kg−1K−1, respectively.

Figure 5.

Figure 5

Open in a new tab

Temperature dependence of magnetic entropy change (−∆SM) under magnetic field ranging from 0.5 T to 5 T for (a) Cr1, (b) Cr3, (c) Cr5, (d) Cr6 and (e) Cr7 alloy. (f) Dependence of −∆SM (left axis, black square) and RCP (right axis, blue circle) on chromium content in (Fe70Ni30)100−xCrx nanoparticles at applied magnetic field of 5 T.

Figure 5(f) shows the magnetic entropy change (left axis) and RCP (right axis) vs Cr % (weight) in (Fe70Ni30)100−xCrx alloy nanoparticles at an applied field of 5 T. Both ∆SM and RCP decrease with increasing Cr % in (Fe70Ni30)100−xCrx, which can be attributed to antiferromagnetic interactions associated with Cr atoms.

Relative cooling power (RCP) is an important performance metric, it is defined as the product of the maximum change in entropy (∆SM) and the full width at half maximum (δTFWHM) of the entropy versus temperature curve, i.e., RCP = ∆SM × δTFWHM. Figure 6(a) shows the variation of δTFWHM, also known as working temperature span, with applied magnetic field.

Figure 6.

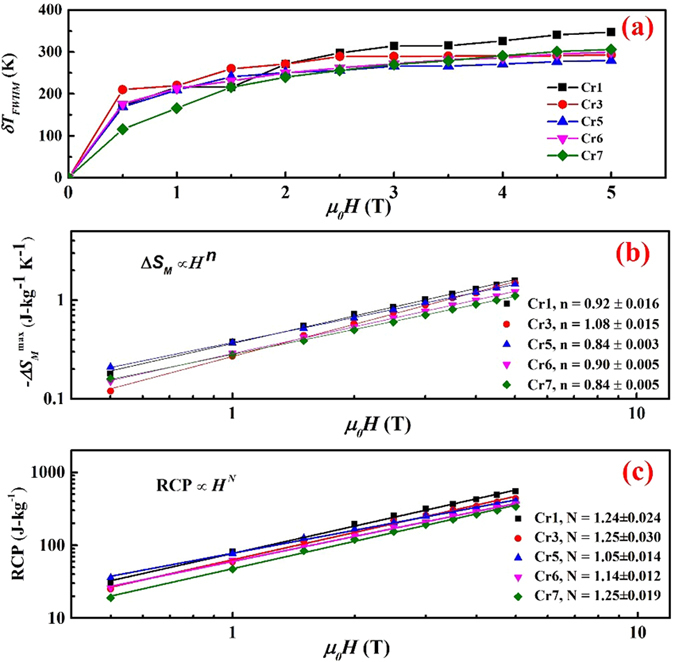
Figure 6

Open in a new tab

(a) Field dependence of working temperature span (δTFWHM) for Cr1, Cr3, Cr5 Cr6 and Cr7 alloys. (b) Variation in relative cooling power (RCP) and (c) maximum change in entropy (−∆SMmax) as a function of applied field. The plots (b) and (c) are in log-log scale.

The δTFWHM for Cr1, Cr3, Cr5, Cr6 and Cr7 was found to be 216 K, 220 K, 209 K, 213 K and 166 K at magnetic field of 1 T, respectively. Our δTFWHM values are higher than those of Gd (~35 K)49, Pr2Fe17 (~78 K)36, Nd2Fe17 (~95 K)36, (Fe70Ni30)89Zr7B4 (133 K)18 at an applied magnetic field of 1 T. Single and multiphase alloys of (Fe70Ni30)89B11 have δTFWHM value of 174 K and 322 K, respectively13. Our high working temperature span results in high RCP, which quantifies the magnitude of the heat extracted in a thermodynamic cycle. Fig. 6(c) shows the field dependence of RCP on the log-log scale and the corresponding linear fit. The RCP for Cr1, Cr3, Cr5, Cr6 and Cr7 increased from 82 J-kg−1, 59 J-kg−1, 77 J-kg−1, 62 J-kg−1 and 47 J-kg−1 to 548 J-kg−1, 436 J-kg−1, 406 J-kg−1, 366 J-kg−1 and 306 J-kg−1 as the field increases from ΔH = 1 T to ΔH = 5 T, respectively.

From the Arrott-Noakes equation of state, the magnetic entropy change at TC can be expressed by the relation ∆SM α Hn, where n = 1 + [(β − 1)/(β + γ)]. The field dependence of RCP can be expressed by the power law RCP α HN, with N = 1 + 1/δ. β, γ and δ are critical exponents50. The linear fit of field dependence of ∆SM(Fig. 6(b)) and RCP (Fig. 6(c)) at TC results in values of local exponents “n” and “N”. The values of local exponent “n” at TC for Cr1, Cr3, Cr5, Cr6 and Cr7 were 0.92, 1.08, 0.84, 0.90 and 0.84 respectively, and the values of local exponent “N” at TC for Cr1, Cr3, Cr5, Cr6 and Cr7 were 1.24, 1.25, 1.05, 1.14 and 1.25, respectively. The variation in local exponent can be attributed to different microscopic interactions due to different Cr % in the alloys.

Ferrofluid based magnetic cooling

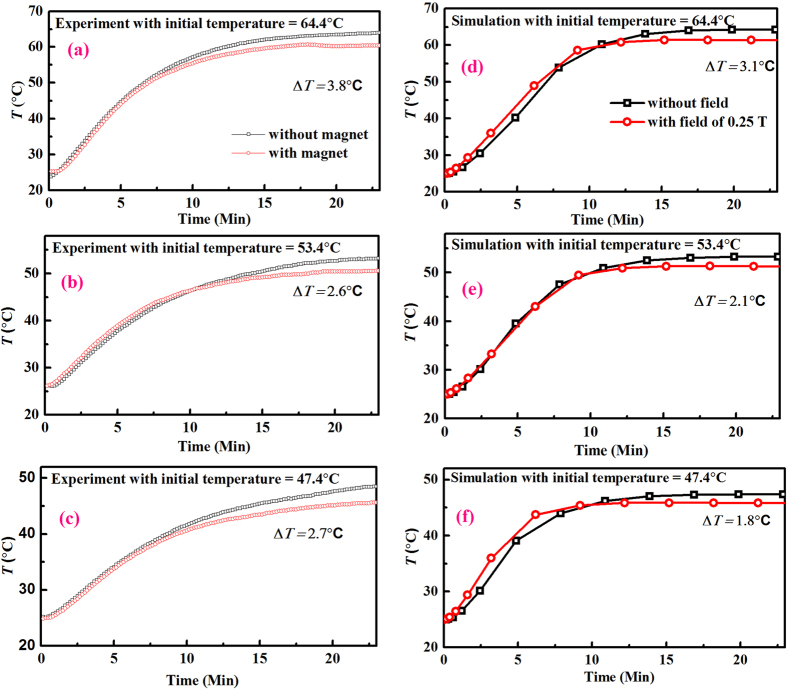
As mentioned in methods, we prepared a ferrofluid based on our nanoparticles which were synthesized by ball milling. To determine the effect of initial temperature of heat load on cooling, the initial heat load temperatures of 64.4 °C, 53.4 °C and 47.4 °C were used. A magnetic field of 0.25 T was applied near the heat load. Figure 7 shows the temperature profiles for heat load for different initial temperature with a magnetic field of 0.25 T and without magnetic field. The results from experiments and simulation show an obvious reduction in temperature (∆T) in all cases. The value of ∆T increases from 2.7 °C to 3.8 °C when load temperature increases 47.4 °C to 64.4 °C, respectively.

Figure 7.

Figure 7

Open in a new tab

Temperature v/s time for initial temperature of heat load of (a) 64.4 °C, (b) 53.4 °C and (c) 47.4 °C, respectively, without and with magnetic field of 0.25 T. Simulated temperature profiles without and with magnetic field of 0.25 T for corresponding temperature of heat load of (d) 64.4 °C, (e) 53.4 °C and (f) 47.4 °C.

These results show that ferrofluid based magnetic cooling is feasible. Our experimental results were in good agreement with the simulations for the same magnetic field, other parameters are the same as those used in the experiments.

Discussion

The (Fe70Ni30)100−xCrx (x = 1, 3, 5, 6 and 7) exhibits a second order magnetic phase transition that is tunable from ~438 K to ~215 K. The wide Curie temperature distribution and therefore high RCP, is consistent with the asymmetric nature of 111 diffraction peak in XRD, which implies that the alloys exhibit a range of lattice parameters due to the process of ball milling51. This lattice distribution gives high distribution of exchange interaction, which leads to a distribution of TC. The reduction in TC and ∆SM with increasing Cr% is related to the reduction of total exchange energy due to the antiferromagnetic nature of Cr. The Curie temperature and magnetic entropy change of the amorphous alloys Fe74−xCrxCu1Nb3Si15.5B6.5 (with x = 2, 8, 10, 12, 13, 14 and 20) were also found to decrease with increasing Cr content52.

Engelbrecht et al. reported that for practical cooling systems, a material with a broad peak in entropy change (large δTFWHM) provides significantly higher cooling power than a material with a sharp peak53. The cooling power for a material with low ΔSM and high δTFWHM is greater than that of a material with high ΔSMand low δTFWHM. Thus, for a magnetic regenerator, a broad temperature distribution of MCE is more attractive than sharp ΔSM peaks.

One of the main factors for the commercial exploitation of a magnetic material is its cost. Ucar et al., reviewed the RCP in terms of Joule/$ of various magnetocaloric materials and it was found that transition metal based materials have a critical advantage over rare earth based materials23. We have estimated the cost of our materials and other relevant magnetocaloric materials. The materials cost of our Fe-Ni-Cr nanoparticles is only about 2% of the cost of pure Gd. Very recently, a transition metal based high entropy alloy NiFeCoCrPdX was introduced as a promising magnetocaloric material. The materials cost of our Fe-Ni-Cr is only about 0.3% of the cost of NiFeCoCrPd0.50. In addition, our (Fe70Ni30)95Cr5 exhibit higher ΔSM (123%) and RCP (180%) compared to NiFeCoCrPd0.25; the TC is almost the same. Table 1 shows the values of ∆SM, RCP and cost of our alloys and other magnetocaloric materials.

Table 1. Curie temperature (T C ), change in magnetic entropy (ΔS M ), relative cooling power (RCP) and cost for selected magnetocaloric materials.

Nominal Composition TC (K) ∆SM (J-kg−1K−1) (μoH = 5T) RCP (J-kg−1) (μoH = 5T) Cost per 100 gm ($) Ref.
(Fe70Ni30)99Cr1 398 1.58 548 7.6 This work
(Fe70Ni30)97Cr3 323 1.49 436 8.1 This work
(Fe70Ni30)95Cr5 258 1.45 406 8.6 This work
(Fe70Ni30)94Cr6 245 1.22 366 8.8 This work
(Fe70Ni30)93Cr7 215 1.11 306 9.1 This work
NiFeCoCrPd0.25 (as rolled/annealed) ~210 0.9/0.82 170/150 1526 17
NiFeCoCrPd0.50 (as rolled/annealed) ~290 0.87/0.83 — 2984 17
(Fe70Ni30)95Mn5 338 1.45 470 7.3 31
(Fe70Ni30)92Mn8 340 1.67 466 7.3 5
(Fe70Ni30)89 Zr7B4 353 2.8 330 62.1 18
(Fe70Ni30)89B11 381 2.1 640 129 13
(Fe70Ni30)96Mo4 300 1.67 432 8.3 21
Gd 295 7.2 ~400 450 49
Gd5Ge1.9Si2Fe0.1 300 7.1 630 409.4 56
Open in a new tab

The cost of the materials was calculated using pure element cost.

The RCP values for our alloy nanoparticles are comparable with other key magnetocaloric materials, the better corrosion resistance would enhance their suitability for magnetic fluid applications. As mentioned earlier, nanoparticles exhibit additional advantages compared to the bulk, e.g. they can be dispersed in a suitable liquid and used as a ferrofluid for active cooling40. Ferrofluid-based self-pumping has novel applications, e.g., for cooling of microelectronic devices and power electronics system5,54. Alloy based ferrofluid was used for the first time for magnetic cooling application55. The stability of the ferrofluid needs to be improvement for long term application.

Conclusions

The magnetocaloric properties of Fe-Ni-Cr nanoparticles were studied. Cr was used to tune the TC of Fe-Ni alloy from more than 400 K to below room temperature. The RCP for Cr1, Cr3, Cr5, Cr6 and Cr7 increased from 82 J-kg−1, 59 J-kg−1, 77 J-kg−1, 62 J-kg−1 and 47 J-kg−1 to 548 J-kg−1, 436 J-kg−1, 406 J-kg−1, 366 J-kg−1 and 306 J-kg−1 J-kg−1 as field increases from ΔH = 1 T to ΔH = 5 T, respectively. The cost of our nanoparticles is only ~2% of the cost of pure Gd and Gd5Ge1.9Si2Fe0.1 magnetocaloric materials. The magnetocaloric properties, good corrosion resistance and low cost of these nanoparticles makes them attractive for magnetic fluid applications.

Methods

High energy ball milling is a suitable technique for producing large-scale, nano- and micro sized materials. This technique is based on mechanical energy transfer created by the collision of hard phase materials with the reactants. Mechanical alloying consists of flattening, welding, fracturing and re-welding of the powder by hard grinding balls. Therefore, alloying of nanostructured powders with defined stoichiometry and crystalline order can be achieved. the high energy ball milling of Fe-Ni-Cr alloy particles was performed.

Nanoparticles of (Fe70Ni30)100−xCrx alloy were prepared by high energy planetary ball milling (FRITSCH) at 600 rpm under Ar atmosphere from elemental Fe (99.99%, Sigma Aldrich), Ni (99.998%, Fisher ChemAlert Guide) and Cr (>99%, Sigma Aldrich) powders. The ball to powder ratio was 10:1. The vials and balls were made of zirconium oxide, and the volume of the vial was 125 ml, which contains 15 balls (10 mm in diameter). To prevent oxidation during heat treatment, the magnetic nanoparticles were sealed under high vacuum (10−5 torr) in a quartz tube. The sealed tube was heated at 700 °C (γ- phase region) for 2 h and quenched in water13. The rate of quenching was ~125 °C/sec. The structure and phase were determined by X-ray diffraction (XRD) using a Bruker D8 Advance diffractometer (CuKα radiation). The composition was confirmed by energy dispersive X-ray spectroscopy using a JEOL JSM-7600F scanning electron microscope. To determine particle size, transmission electron microscopy (TEM) of nanoparticles was carried out on a JEOL 2010 TEM with an operating voltage of 200 kV. Samples for TEM were prepared by ultrasonically dispersing a small amount of powder in hexane, followed by putting a drop of the suspension on a holey carbon-coated copper grid, the sample is then dried overnight in vacuum. The magnetic properties were measured using a physical property measuring system (PPMS) (EverCool-II, Quantum Design), equipped with a vibrating sample magnetometer probe and an oven (model P527). The M (H) isotherms with field from 0 to 5 T in steps of 5 K (near TC) and 10 K (elsewhere) were recorded for ΔSM measurements. The isothermal magnetic entropy change due to application of magnetic field was calculated using a numerical approximation to the Maxwell equation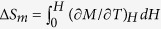Inline graphic, where ΔSM is the magnetic entropy change, T is the temperature, M is the magnetization.

These Fe-Ni-Cr nanoparticles were used to prepare the ferrofluid. (Fe70Ni30)95Cr5 nanoparticles were functionalized with oleic acid and ammonium hydroxide and subjected high energy ball milling. Subsequently, these coated nanoparticles were dispersed in oleic acid. This ferrofluid of Fe-Ni-Cr nanoparticles and oleic acid was used as the heat transfer medium to perform magnetic cooling.

A 5.2 mm inner diameter, 60 cm circumference polymer tube was used for circular flow. A heat load (electric heater made by Kanthal wires) and a heat sink (cold water) were placed opposite each other. A permanent magnet, which can provide a maximum field of 0.25 T, was placed close to the heat load. A temperature data logger with SD card was used to record temperature v/s time. The initial temperature was tuned by changing current through the Kanthal wire using a Keithley power supply (Model: 2231 A-30-3). For modelling, COMSOL Multiphysics simulation software version 4.4 was used with finite element method and normal mesh.

Additional Information

How to cite this article: Chaudhary, V. and Ramanujan, R.V. Magnetocaloric Properties of Fe-Ni-Cr Nanoparticles for Active Cooling. Sci. Rep. 6, 35156; doi: 10.1038/srep35156 (2016).

Acknowledgments

This Research is conducted by NTU-HUJ-BGU Nanomaterials for Energy and Water Management Programme under the Campus for Research Excellence and Technological Enterprise (CREATE), that is supported by the National Research Foundation, Prime Minister’s Office, Singapore.

Footnotes

Author Contributions V.C. conducted the experiments, and V.C. and R.V.R. wrote the manuscript. All authors reviewed the manuscript.

References

  1. Dudek M. R., Wojciechowski K. W., Grima J. N., Caruana-Gauci R. & Dudek K. K. Colossal magnetocaloric effect in magneto-auxetic systems. Smart Mater. Struct. 24, 085027 (2015). [Google Scholar]
  2. GschneidnerJr K. A., Pecharsky V. K. & Tsokol A. O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 68, 1479 (2005). [Google Scholar]
  3. Crossley S., Mathur N. D. & Moya X. New developments in caloric materials for cooling applications. AIP Advances 5, 067153 (2015). [Google Scholar]
  4. Moya X., Kar-Narayan S. & Mathur N. D. Caloric materials near ferroic phase transitions. Nat Mater 13, 439–450 (2014). [DOI] [PubMed] [Google Scholar]
  5. Chaudhary V. & Ramanujan R. V. Magnetic and structural properties of high relative cooling power (Fe70Ni30)92Mn8 magnetocaloric nanoparticles. J. Phys. D: Appl. Phys. 48, 305003 (2015). [Google Scholar]
  6. Zhang H. et al. Giant rotating magnetocaloric effect induced by highly texturing in polycrystalline DyNiSi compound. Scientific Reports 5, 11929 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Li L. W. et al. Magnetic properties and large magnetocaloric effect in Ho2Cu2In and Ho2Au2In compounds. Journal of Materials Science 51, 5421–5426 (2016). [Google Scholar]
  8. Li Z. et al. Two successive magneto-structural transformations and their relation to enhanced magnetocaloric effect for Ni55.8Mn18.1Ga26.1 Heusler alloy. Scientific Reports 5 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ursic H. et al. A multicaloric material as a link between electrocaloric and magnetocaloric refrigeration. Scientific Reports 6, 26629 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Zhukov A. Novel Functional Magnetic Materials: Fundamentals and Applications. (Springer International Publishing, 2016). [Google Scholar]
  11. BASF, Premiere of cutting-edge cooling appliance at CES (2015). Available at https://www.basf.com/cn/en/company/news-and-media/news-releases/2015/01/p-15-100.html.
  12. Aprea C., Greco A., Maiorino A. & Masselli C. Magnetic refrigeration: an eco-friendly technology for the refrigeration at room temperature. Journal of Physics: Conference Series 655, 012026 (2015). [Google Scholar]
  13. Chaudhary V., Maheswar Repaka D. V., Chaturvedi A., Sridhar I. & Ramanujan R. V. Magnetocaloric properties and critical behavior of high relative cooling power FeNiB nanoparticles. J. Appl. Phys. 116, 163918–163926 (2014). [Google Scholar]
  14. Durga P., Pecharsky V. K. & & Gschneidner J. Origins of ferromagnetism and antiferromagnetism in Gd5Ge4. J. Phys.: Condens. Matter 20, 235235 (2008). [Google Scholar]
  15. Pecharsky V. K. & Gschneidner J. K. A. Giant magnetocaloric effect in Gd5Ge2Si2. Phys. Rev. Lett. 78, 4494–4497 (1997). [Google Scholar]
  16. Nekuda Malik J. A. China eliminates rare-earths quotas. MRS Bull. 40, 206–207 (2015). [Google Scholar]
  17. Belyea D. D., Lucas M. S., Michel E., Horwath J. & Miller C. W. Tunable magnetocaloric effect in transition metal alloys. Scientific Reports 5, 15755 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ipus J. J., Ucar H. & McHenry M. E. Near room temperature magnetocaloric response of an (FeNi)ZrB Alloy. IEEE Trans. Magn. 47, 2494–2497 (2011). [Google Scholar]
  19. Jones N. J., Ucar H., Ipus J. J., McHenry M. E. & Laughlin D. E. The effect of distributed exchange parameters on magnetocaloric refrigeration capacity in amorphous and nanocomposite materials. J. Appl. Phys. 111, 07A334–337 (2012). [Google Scholar]
  20. Ucar H. Metastable gamma-iron nickel nanostructures for magnetic refrigeration near room temperature. PhD Thesis, Carnegie Mellon University, (2013).
  21. Ucar H., Craven M., Laughlin D. E. & McHenry M. E. Effect of Mo addition on structure and magnetocaloric effect in γ-FeNi nanocrystals. J. Electron. Mater. 43, 137–141 (2014). [Google Scholar]
  22. Ucar H., Ipus J. J., Laughlin D. E. & McHenry M. E. Tuning the Curie temperature in gamma-FeNi nanoparticles for magnetocaloric applications by controlling the oxidation kinetics. J. Appl. Phys. 113, 17A918–921 (2013). [Google Scholar]
  23. Ucar H., Ipus J. J., McHenry M. E. & Laughlin D. E. Overview of amorphous and nanocrystalline magnetocaloric materials operating near room temperature. Journal of Metals 64, 782–788 (2012). [Google Scholar]
  24. Wu R. et al. Critical dependence of magnetostructural coupling and magnetocaloric effect on particle size in Mn-Fe-Ni-Ge compounds. Scientific Reports 6, 20993 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Chen X., Maheswar Repaka D. V. & Ramanujan R. V. Structural investigation of the crossover in the magnetic transition of Mn–Fe–P–Ge magnetocaloric powders. J. Alloys Compounds 658, 104–109 (2016). [Google Scholar]
  26. Chen X. & Ramanujan R. V. The magnetic phase transition in Mn1.1Fe0.9P1−xGex magnetocaloric alloys. J. Appl. Phys. 117, 063909 (2015). [Google Scholar]
  27. Gschneidner K. A. Jr, Mudryk Y. & Pecharsky V. K. On the nature of the magnetocaloric effect of the first-order magnetostructural transition. Scripta Mater. 67, 572–577 (2012). [Google Scholar]
  28. Chaudhary V. & Ramanujan R. V. Iron Oxide-based Magnetic Nanoparticles for High Temperature Span Magnetocaloric Applications. MRS Online Proceedings Library 1708, vv10–08 (2014). [Google Scholar]
  29. Franco V., Blázquez J. S., Ingale B. & Conde A. The magnetocaloric effect and magnetic refrigeration near room temperature: materials and models. Annu. Rev. Mater. Res. 42, 305–342 (2012). [Google Scholar]
  30. Romero Gómez J., Ferreiro Garcia R., De Miguel Catoira A. & Romero Gómez M. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renewable and Sustainable Energy Reviews 17, 74–82 (2013). [Google Scholar]
  31. Chaudhary V., Chaturvedi A., Sridhar I. & Ramanujan R. V. Fe-Ni-Mn nanoparticles for near room temperature magnetic cooling. IEEE Magn. Lett. 5, 6800104–6800108 (2014). [Google Scholar]
  32. Chaudhary V. et al. High relative cooling power iron based magnetocaloric Nanoparticles. 6th IIF-IIR International Conference on Magnetic Refrigeration THERMAG VI, Victoria, BC, 7–10 Sept 2014 (2014).
  33. Chaudhary V. & Ramanujan R. V. High relative cooling power in a multiphase magnetocaloric FeNiB alloy. Magnetics Letters, IEEE 6, 6700104–6700108 (2015). [Google Scholar]
  34. Law J. Y., Franco V. & Ramanujan R. V. Direct magnetocaloric measurements of Fe-B-Cr-X (X = La, Ce) amorphous ribbons. J. Appl. Phys. 110, 023907 (2011). [Google Scholar]
  35. Chaudhary V., Chaturvedi A. & Ramanujan R. V. In Magnetics Symposium 2014 - Celebrating 50th Anniversary of IEEE Magnetics Society (MSSC50)1–2 (2014).
  36. Alvarez-Alonso P. et al. On the broadening of the magnetic entropy change due to Curie temperature distribution. J. Appl. Phys. 115, 17A929–932 (2014). [Google Scholar]
  37. Pablo Á. et al. Nanocrystalline Nd2Fe17 synthesized by high-energy ball milling: crystal structure, microstructure and magnetic properties. J. Phys.: Condens. Matter. 22, 216005 (2010). [DOI] [PubMed] [Google Scholar]
  38. Pedro G. et al. Relative cooling power enhancement in magneto-caloric nanostructured Pr2Fe17. J. Phys. D: Appl. Phys. 41, 192003 (2008). [Google Scholar]
  39. Rosensweig R. E. Refrigeration aspects of magnetic particle suspensions. Int. J. Refrig. 29, 1250–1258 (2006). [Google Scholar]
  40. Rosenweig R. E. Ferrohydrodynamics (Cambridge University Press, 1985). [Google Scholar]
  41. Mandal S., Panda J. & Nath T. K. Investigation of the critical behaviour and magnetocaloric effect in γ-Fe49Ni29Cr22 disordered austenitic stainless steel alloy by using the field dependence of magnetic entropy change. J. Alloys Compounds 653, 453–459 (2015). [Google Scholar]
  42. Men’shikov A. Z., Kuz’min N. N., Kazantsev V. A., Sidorov S. K. & Kalinin V. N. Exchange interaction in Fe-Ni-Cr alloys. Physics of Metals and Metallography 40, 174–177 (1975). [Google Scholar]
  43. Fukamichi K., Shirakawa K., Kaneko T. & Masumoto T. Pressure effect on the Curie temperature and high‐field susceptibility of FeCrB amorphous Invar alloy. J. Appl. Phys. 53, 2246–2248 (1982). [Google Scholar]
  44. Pardo A. et al. The influence of Cr addition on the corrosion resistance of Fe73.5Si13.5B9Nb3Cu1 metallic glass in marine environments. Corros. Sci. 44, 1193–1211 (2002). [Google Scholar]
  45. Pardo A. et al. The influence of Cr addition on the corrosion resistance of Fe73.5Si13.5B9Nb3Cu1 metallic glass in SO2 contaminated environments. Corros. Sci. 43, 689–705 (2001). [Google Scholar]
  46. Chen C.-W. Magnetism and Metallurgy of Soft Magnetic materials (North Holland Publishing Company, 1977). [Google Scholar]
  47. Fu H. et al. Table-like magnetocaloric effect in the Gd-Co-Al alloys with multi-phase structure. Appl. Phys. Lett. 104, 072401 (2014). [Google Scholar]
  48. Chaturvedi A., Stefanoski S., Phan M.-H., Nolas G. S. & Srikanth H. Table-like magnetocaloric effect and enhanced refrigerant capacity in Eu8Ga16Ge30-EuO composite materials. Appl. Phys. Lett. 99, 162513 (2011). [Google Scholar]
  49. Mathew S. P. & Kaul S. N. Tuning magnetocaloric effect with nanocrystallite size. Appl. Phys. Lett. 98, 2505–2508 (2011). [Google Scholar]
  50. Franco V., Blazquez J. S. & Conde A. Field dependence of the magnetocaloric effect in materials with a second order phase transition: A master curve for the magnetic entropy change. Appl. Phys. Lett. 89, 2512–2515 (2006). [Google Scholar]
  51. Groma I. & Monnet G. Analysis of asymmetric broadening of X-ray diffraction peak profiles caused by randomly distributed polarized dislocation dipoles and dislocation walls. J. Appl. Crystallogr. 35, 589–593 (2002). [Google Scholar]
  52. Moreno-Ramirez L. M. et al. Magnetocaloric response of amorphous and nanocrystalline Cr-containing Vitroperm-type alloys. J. Magn. Magn. Mater. 409, 56–61 (2016). [Google Scholar]
  53. Engelbrecht K. & Bahl C. R. H. Evaluating the effect of magnetocaloric properties on magnetic refrigeration performance. J. Appl. Phys. 108, 123918 (2010). [Google Scholar]
  54. Love L. J., Jansen J. F., McKnight T. E., Roh Y. & Phelps T. J. A magnetocaloric pump for microfluidic applications. NanoBioscience, IEEE Transactions on 3, 101–110 (2004). [DOI] [PubMed] [Google Scholar]
  55. Ramanujan R. V. & Chaudhary V. Self pumping magnetic cooling, 10201606447V (2016)
  56. Provenzano V., Shapiro A. J., Shull & Robert D. Vol. 429 Nature 5 (Nature Publishing Group, London 2004). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES