Abstract
Enumeration of elements differs as a function of their range. Subitizing (quantities 1–4) is considered to be an accurate and quick process with reaction times minimally affected by the number of presented elements within its range. In contrast, small estimation (range of 5–9 elements exposed briefly) is a less precise linear process. Subitizing was consider to be a pre-attentive process for many years. However, recent studies found that when attentional resources were occupied elsewhere, the subitizing process was impaired. In the current study, we examined whether subitizing can be facilitated by improving engagement of attention. Specifically, brief alerting cues that increase attentional engagement were presented in half of the trials during enumeration tasks. In Experiment 1, participants were required to enumerate dots presented in random arrays within the subitizing or small estimation range. Alerting facilitated enumeration of quantities in the subitizing range, but not in the small estimation range. We suggested that the benefit of alerting on the subitizing process was achieved via enhancement of global processing, a process that was previously associated with both alerting and subitizing. In Experiment 2, we provided direct evidence for this hypothesis by demonstrating that when global processing was used for items in the small estimation range (i.e., presenting quantities in a canonical array), a subitizing-like pattern was revealed in quantities beyond the subitizing range.
Keywords: Enumeration, Subitizing, Alertness, Global processing, Pattern recognition
Highlights
-
•
We examined the influence of an alerting cue on enumerating 1–9 quantities.
-
•
The alerting cue appeared in 50% of trials before random/canonical arrays of dots.
-
•
Alerting facilitated enumeration in the subitizing range in both types of arrays.
-
•
Alerting facilitated enumerating more than 4 dots only when presented canonically.
-
•
We conclude that alerting facilitates subitizing by enhancing global processing.
1. Introduction
Is enumeration modulated by attention? Recent reports suggested that the answer is positive. In the current study, we examined if and how one specific aspect of attention—alertness, the mechanism responsible for achieving and maintaining an optimal level of arousal during task performance—modulates enumeration processes.
1.1. Enumeration processes and the mechanisms underlying them
Enumeration is one of the building blocks of math ability. The ability to enumerate 1–4 elements has been referred to as subitizing (Kaufman, Lord, Reese, & Volkmann, 1949)—a fast and accurate process. In contrast, if more than 4 elements are presented, enumeration is serial, much slower, and is termed counting. A third process is estimation, which was described by Dehaene (1992) as the ability to determine the approximate numerosity of elements that cannot be efficiently subitized or counted. Estimation is required when elements are presented for short exposures and therefore cannot be counted. If the number of elements presented is in the counting range, but for a short exposure duration, the elements are considered to be in the small estimation range.
Throughout the past decades, a lot of research has been devoted to investigating the underlying mechanisms of enumeration processes. While there is an agreement that the enumeration process in the small estimation range requires attentional resources and is conducted serially, less is clear regarding the involvement of attentional processes in enumeration within the subitizing range. Several studies suggested that subitizing does not require attention at all (Atkinson et al., 1976, Trick and Pylyshyn, 1994). These studies argued that subitizing is a pre-attentive process because there are no differences in response latency between quantities in the subitizing range (i.e., as opposed to the small estimation range), and because subitizing can be performed in parallel with other processes. However, other more recent studies suggested otherwise.
Egeth, Leonard, and Palomares (2008), and Olivers and Watson (2008) conducted experiments using the attentional blink task combined with an enumeration task. Their results indicated that when attentional resources were captured by a letter identification task, the subitizing process was impaired in a parallel enumeration task (for similar results see also Railo et al., 2008, Vetter et al., 2008). The authors concluded that subitizing requires attentional resources.
Overall, previous evidence suggested that subitizing is impaired when attentional engagement in the enumeration task is reduced. An interesting complementary question, which has not been examined previously, is whether enhancement of attention during an enumeration task can improve the subitizing process.
Alerting is an attentional system that regulates the intensity of attention to a given stimulus and responding to it (Petersen and Posner, 2012, Posner and Petersen, 1990). Alerting can be manipulated by introducing brief warning cues (e.g., an auditory beep sound) that exert a state of high arousal (Posner, 1978). The warning cues do not deliver any information regarding the identity of the subsequent target or its spatial location. Nonetheless, reaction time (RT) is faster in trials with a warning cue compared with a no-cue condition. In the present study, we examined the impact of such warning cues on the subitizing process.
Cumulative evidence indicates that alerting might have a specific role in the subitizing process by modulating processing of spatial configurations. Mandler and Shebo (1982) argued that arrays of 1 to 4 items create familiar shapes, such as a line (2 items), a triangle (3 items), or a square (4 items). Namely, items in the subitizing range are recognized by their spatial configuration. That is, arrangement of several small elements can create a whole familial figure (i.e., hierarchical figure). Navon (1977) suggested that such figures could help dissociate between global perceptual processing (i.e., attention to the whole figure) and local perceptual processing (i.e., attention to the details that comprise the whole).
It should be noted that a familiar pattern can be created for quantities above the subitizing range (above 4). Indeed, canonical arrangements of dots can create familiar shapes (like on a dice) for quantities in the small estimation range. Studies revealed that when applying a canonical arrangement, adults and children presented a subitizing-like pattern of results, even for the quantities in the small estimation range (Ashkenazi et al., 2013, Kaufmann and Nuerk, 2008). Such results hint that attention to a global figure might play a crucial role in the subitizing process.
Interestingly, alerting was found to enhance global processing. Weinbach and Henik (2011) used a variation of Navon's task in which participants were presented with a large arrow (i.e., global level) made of small arrows (i.e., local level). Participants were required to indicate the direction of the small or large arrow in different blocks. The small and large arrows could point in the same direction (i.e., congruent condition) or in opposite directions (i.e., incongruent condition). The mean difference in RTs between the incongruent and congruent conditions was used as a measure of interference by the irrelevant dimension. Auditory alerting cues were presented in half of the trials prior to the arrow target. It was found that alerting increased the global interference (i.e., the interference from the big arrow was larger in the alerting compared to the no-alerting condition) when participants had to respond according to the local level (small arrows), but did not affect local interference when participants had to respond according to the global level. The authors suggested that alerting acts to enhance global processing. Other studies used this task to show that alerting can improve global processing in populations that are known for having deficient global processing abilities such as those with attention deficit hyperactive disorder (Kalanthroff, Naparstek, & Henik, 2013) and congenital prosopagnosia (born with difficulty in recognizing faces; Tanzer, Weinbach, Mardo, Henik, & Avidan, accepted for publication). In addition, Van Vleet and colleagues showed that a short training procedure aimed to increase alertness level induced a bias towards global processing of attention and reduced local processing (Van Vleet, Hoang-duc, DeGutis, & Robertson, 2011). To conclude, there is much support that alerting facilitates global processing. If the subitizing process relies on the spatial configuration of small elements into a familiar pattern (Mandler & Shebo, 1982), alerting should also facilitate processing of elements in the subitizing range, but not elements in the small estimation range (which do not create a familiar global pattern).
1.2. The current study
As was described in the introduction, alerting acts to increase attentional engagement in a given task, and was found to enhance attentional bias towards global elements. Since arrays of element in the subitizing range create a familiar global configuration, we hypothesized that the subitizing process would benefit from alerting cues. This hypothesis was examined in two experiments.
In both experiments, participants were presented with an array of dots and were instructed to report the quantity of the dots. The number of dots presented was either in the subitizing range (quantities 1–4) or in the small estimation range (quantities 5–9). In half of the trials, an alerting warning cue was presented prior to the array. In Experiment 1, the arrangement of the dots was random, and the influence of the alerting cues was examined in both the subitizing and small estimation ranges. We hypothesized that only the subitizing range would benefit from the alerting cue. In Experiment 2, two different arrangements of arrays were compared: canonical vs. random. Importantly, a canonical arrangement is symmetrical and relies on pattern recognition. Namely, small local elements create a larger global element that enables participants to grasp all the presented dots at once rather than count the dots one by one (for discussion of canonical arrangements see Ashkenazi et al., 2013, Piazza et al., 2002). In Experiment 2, we examined the influence of alerting cues on performance for each quantity separately. Because under a canonical arrangement participants can engage in global processing even in the small estimation range, we hypothesized that quantities above the subitizing range would also benefit from an alerting cue, supporting the role of alerting in facilitating global processing when involved in enumeration.
2. Experiment 1: The interaction between enumeration and alertness
2.1. Method
2.1.1. Participants
Twenty-four undergraduate students from Ben-Gurion University of the Negev (aged 21–30 years old) took part in this experiment in return for monetary payment (about $7) and were naïve as to the purpose of the study. They reported normal or corrected-to-normal vision, with no diagnosed attention disorder or learning disabilities. All participants gave their informed consent prior to their participation in the study.
2.1.2. Apparatus
The experiment was run on an IBM-PC with a 17-inch color screen monitor. E-Prime version 2.0 software was used for programming, presentation of stimuli, and timing operations. A headphone set was used to deliver an alerting cue. A microphone was used to register vocal input. RT was recorded electronically by a response box controlled by E-Prime software and was measured from onset of the stimulus to onset of the vocal response. The content of the subject's vocal response in each trial was input into the computer by the experimenter's key-press.
2.1.3. Stimuli
The number of dots varied from 1 to 9 per array. The dot arrays (white on a black background) were created with MATLAB™ code created by Gebuis and Reynvoet (2011). MATLAB code was also used to program the computer to record the absolute values of five different continuous properties, as were used and reported in Leibovich and Henik (2014). These properties included 1) average diameter (the dots in the array differed in size, therefore, the average diameter of the dots in an array was computed); 2) total surface area (i.e., the sum of the surface area for the dots in each array); 3) area extended (i.e., the smallest contour that included all of the dots, as if an elastic band was wrapped around the dots); 4) density (i.e., area extended divided by total surface); and 5) total circumference (i.e., the sum of the circumferences of all dots in an array). As far as we know, this is the first time that this kind of stimuli has been used in an enumeration task (specifically, when no comparison is required). The importance of controlling the continuous properties is so that these factors will not affect enumeration in any way (for review see Leibovich & Henik, 2013). From a viewing distance of 60 cm, the stimulus subtended a visual angle of 8.5o. Each number of dots had 18 different arrays. Each array was presented with or without an alerting cue before it appeared. For the alerting cue, a 50 ms, 2000 Hz sound was used.
2.1.4. Procedure
Participants were instructed to say aloud the number of dots that were presented on the screen, as fast and accurately as possible. Participants did not know what the maximum quantity of dots that could appear would be. A fixation point (a plus sign) was presented for 2500 ms before the target appeared. The fixation point was kept in view during the trial to maintain fixation. In half of the trials, an auditory tone was heard through headphones 500 ms before the target appeared. The target replaced fixation and remained in view for 200 ms. After a vocal response, the experimenter recorded the number that was said and then a blank screen appeared for 1000 ms until the fixation point of the next trial appeared (see Fig. 1).
Fig. 1.
A) Examples of stimuli in Experiments 1 and 2. Left column - random arrangement (used in Experiments 1 and 2); right column: canonical arrangement (used in Experiment 2). B). Example of a typical trial.
2.1.5. Design
Each block was composed of 54 trials: 2 (alerting cue) × 9 (quantity of dots) × 3 (repetitions of each trial). The alerting cue had two levels: presence or absence of a 2000 Hz, 50 ms beep sound. The quantity of dots had nine levels, 1–9, divided into two ranges: the subitizing range (1–4) and the small estimation range (5–9). A practice block of 9 trials, selected randomly from the full set of trials, was carried out. The practice block was followed by 6 blocks of randomly presented trials. Overall, each participant conducted 324 experimental trials.
2.2. Results
The analysis was carried out for correct responses only (1465 error trials were excluded, 19% of the original data). For each participant in each condition, RTs that were 2.5 SD below or above average were excluded (115 trials were excluded, 1.5% from the original data). Errors were relatively rare in the subitizing range (about 2% of the trials). In the small estimation range, the error rates increased with the quantity of dots as follows: 5 dots - 9.6%, 6 dots - 28.6%, 7 dots - 37.2%, 8 dots - 47.3%, and 9 dots - 60.7%. Due to the very high error rate, the quantity of 9 dots was not analyzed in the small estimation range. Therefore, the subitizing range included quantities of 1–4 dots, and the small estimation range included quantities of 5–8 dots. A 2 (alertness) × 2 (range) analysis of variance (ANOVA) was carried out with RT as a dependent variable.
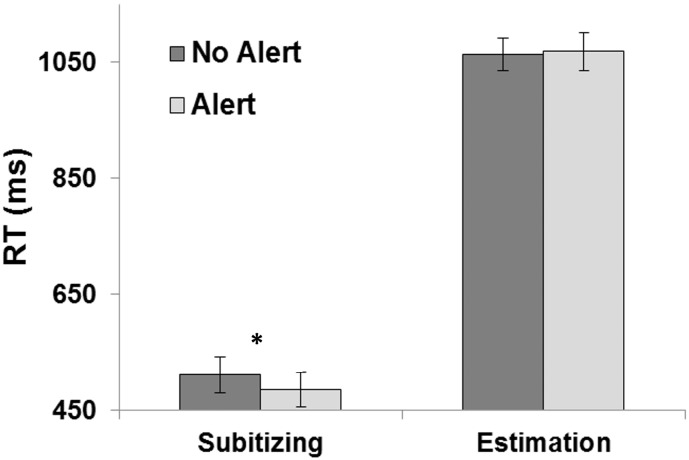
The analysis revealed a main effect for range, as RTs in the small estimation range were slower than in the subitizing range, F(1, 23) = 95.61, p < 0.01, ηp2 = 0.81. No main effect was found for alertness, F(1, 23) = 2.47, p = 0.13, ηp2 = 0.10, but the interaction between alertness and range was found to be significant, F(1, 23) = 5.68, p = 0.03, ηp2 = 0.20. A planned comparison of the effect of alertness, separately for trials with and without an alerting cue revealed that there was a benefit in RTs when an alerting cue preceded the target only in the subitizing range, F(1, 23) = 15.92, p < 0.01, ηp2 = 0.41. Results of the interaction are presented in Fig. 2.
Fig. 2.
Experiment 1 results: RT as a function of range and alertness. The error bars represent within-participants confidence intervals. The results demonstrated that in the subitizing range, responding was faster for alert than no-alert trials. In the small estimation range, alerting cues did not modulate task performance. * significant difference.
Planned comparisons of the alerting cue, separately for each quantity of enumeration, were carried out. They revealed that there was an alertness effect for the quantities of two, three and four: F(1, 23) = 23.94, p < 0.01, ηp2 = 0.51; F(1, 23) = 4.68, p = 0.04, ηp2 = 0.17; and F(1, 23) = 15.59, p < 0.01, ηp2 = 0.40, respectively. No alertness effect was found when one dot was presented, F(1, 23) = 1.36, p = 0.26, ηp2 = 0.01; but the same trend was found, that is, RT in the alert condition (464 ms) was shorter than in the no-alert condition (489 ms). Quantities in the small estimation range did not show an alertness effect: 5 dots - F(1, 23) < 1, p = 0.97, ηp2 = 0.00; 6 dots - F(1, 23) = 2.45, p = 0.13, ηp2 = 0.10; 7 dots - F(1, 23) = 0.01, p = 0.91, ηp2 = 0.00; and 8 dots - F(1, 23) = 0.25, p = 0.62, ηp2 = 0.01).
2.2.1. Further analysis
The interaction between alertness and range indicated that the subitizing range, but not small estimation range, could be modulated by global processing. However, a few cautions should be applied to this conclusion. First, one can argue that alertness could only modulate short RTs. It is possible that alertness contributed to speeding up of responding and not to the enumeration process per se. If this was true, then an alertness effect should appear for very fast responses and not for long responses even in the subitizing range. To rule out this possibility, 2 quartile analyses were conducted. RTs were allocated to quartiles from the fastest to the slowest (i.e., 4 quartiles: 25, 50, 75, 100), for each participant in each of the four conditions (i.e., 2 ranges × 2 alertness conditions). The average of each quartile was calculated and a three-way ANOVA (4 quartiles × 2 alertness × 2 ranges) was carried out. The results showed no significant interaction between alertness and quartiles, F(3, 66) = 1.6, p = 0.07, ηp2 = 0.10. The interaction between range and quartiles was significant, F(3, 66) = 50.45, p < 0.01, ηp2 = 0.71. This interaction showed that the variability in the small estimation range was larger than in the subitizing range; namely, the difference between percentile 25 and 100 was smaller in the subitizing range. The interaction between alertness, range and quartiles was not significant, F(3, 66) < 1, p = 0.90, ηp2 = 0.02.
In the second analysis, we compared RTs of the largest amount in the subitizing range (i.e., arrays with 4 dots) and the smallest amount in the small estimation range (i.e., arrays with 5 dots). RTs for the amounts of 4 and 5 were allocated to quartiles. The average RT of each quartile was calculated for each participant in each condition. A three-way ANOVA (2 quartile × 2 alertness × 2 amounts) was carried out. The results showed no significant interaction between alertness, quartile and amount, F(1, 23) = 1.12, p = 0.30, ηp2 = 0.18. Planned comparisons revealed an alerting effect in the slowest RTs for the amount 4, F(1, 23) = 7.49, p = 0.01, ηp2 = 0.25; and no alerting effect in the fastest RTs for the amount of 5, F < 1, ηp2 = 0.02 (the results are presented in Fig. 3). Because the average RT for the fastest amount of 5 (small estimation range) was faster than for the slowest amount of 4 (subitizing range), and an alerting effect was found only in the subitizing range (i.e., the slower RTs in this comparison), it can be concluded that the alerting effect only modulated the subitizing range and that the alerting effect could not be attributed to short RTs only.
Fig. 3.

RT as a function of quartile and alertness. The error bars represent within-participants confidence intervals. The results demonstrated that for the slowest trials, having 4 dots, responding was faster for alert than no-alert trials, while in the fastest trials, having 5 dots, there wasn't an alerting effect. * significant difference.
A third analysis was applied to the error rates. This analysis was important because the error rates for some of the quantities were very high (e.g., 8 dots - 47.3%). Therefore, it was important to explore whether we could find different patterns in the subitizing and the estimation ranges as a function of alerting. Specifically, we tested whether the effect of the alerting cue in the small estimation range would be reflected in the error rate; namely, whether alertness interrupted the process of enumeration in the small estimation range, which required local processing. A two-way ANOVA was carried out with independent variables of range and alertness, and with accuracy as a dependent measure. The results were as follows: the main effect of alertness was significant, as error rates were lower with an alerting cue compared to a no-cue condition, F(1, 23) = 9.82, p < 0.01, ηp2 = 0.33. The main effect of range was significant, as the error rates were lower in the subitizing range compared to the small estimation range, F(1, 23) = 113.11, p < 0.01, ηp2 = 0.83. However, the interaction between alertness and range was not significant, F(1, 23) < 1, p = 0.34, ηp2 = 0.04.
2.3. Discussion
Results of Experiment 1 showed that the presentation of an alerting cue modulated RTs only in the subitizing range. Specifically, a significant alerting effect was found in 3 out of 4 of the quantities in the subitizing range, and was not found in any of the quantities in the small estimation range. Analysis of RT quartiles indicated that the effect could not be explained by general differences in RTs between the subtilizing and small estimation ranges.
The absent alerting effect for quantity 1 under the condition of an alerting cue could be a false negative error. However, it should be noted that other studies also failed to find effects of attention for the quantity of 1. Egeth et al. (2008) and Olivers and Watson (2008) found that the subitizing range is effected by an attentional manipulation in the subitizing range for the quantities of 2, 3 and 4, and not for the quantity of a single item. These authors suggested that a single quantity is a special case that does not require attentional resources and therefore may not be influenced by attentional manipulations.
We hypothesized that alerting might modulate the subitizing process due to enhancement in global processing. As noted, global processing is inherent in the subitizing range, but not in the small estimation range. While the results of Experiment 1 hint towards this direction, they do not provide direct confirmation for the hypothesis, since the global properties of the stimuli were not directly manipulated. If alerting modulates the subitizing process via enhancement of global processing, then when arranging quantities in the small estimation range to create a familiar global figure, alerting should benefit performance, even for quantities in the small estimation range. Experiment 2 was designed to test this hypothesis.
3. Experiment 2: enumeration and alertness in random vs. canonical arrangements
A canonical arrangement of dots creates a hierarchical figure (a global figure made of small elements). Former studies used canonical arrays of dots in order to explore pattern recognition in adults (Mandler & Shebo, 1982) and children (Ashkenazi et al., 2013, Kaufmann and Nuerk, 2008). The typical pattern of results for a canonical array is that the subitizing range increases up to 6, as expressed in small changes in RTs between quantities 1–6. In Experiment 2, enumeration in subitizing and small estimation ranges was examined in a random or canonical arrangement. The influence of alerting cues was evaluated in both conditions. If alerting modulates the subitizing process by enhancing global processing, then alerting should improve performance even in the small estimation range, if the quantities are arranged in a canonical array. This should result in a three-way interaction between alerting, arrangement (canonical vs. random) and quantity. Namely, RTs in the random arrangement would be affected by alerting in the subitizing range only (as in Experiment 1). In contrast, for canonical arrangements, alerting should modulate both the subitizing and small estimation range.
3.1. Method
3.1.1. Participants
Twenty-one students from Ben-Gurion University of the Negev, who did not take part in Experiment 1, participated in this experiment for monetary compensation (about $7). They were naïve as to the purpose of the study, reported normal or corrected-to-normal vision, with no diagnosed attention disorder or learning disabilities. All participants gave their informed consent prior to their participation in the study.
3.1.2. Apparatus
The apparatus was the same as in Experiment 1.
3.1.3. Stimuli
The number of dots varied from 1 to 9 per array. In the random arrangement, the stimuli were the same as in Experiment 1. In the canonical arrangement, we rearranged the dots from each random array into a canonical array. Therefore, each number of dots had 36 different arrays (18 in a random arrangement and 18 in a canonical arrangement). Each array could have presented with or without an alerting cue before it appeared. The visual angle of the stimulus and the alerting cue was the same as in Experiment 1 (see Fig. 1).
3.1.4. Procedure
The procedure was the same as in Experiment 1.
3.1.5. Design
Each block was composed of 72 trials: 2 (alerting cue) × 2 (arrangement) × 9 (quantity of dots) × 2 (repetitions of each trial). Because we expected that alertness would modulate RT outside the subitizing range, the analysis was carried out for each quantity separately. A practice block of 9 randomly selected trials from the full set of trials was carried out and followed by 10 blocks of 72 randomly presented trials per block. Each array was presented with or without an alerting cue before it appeared.
3.2. Results
Three subjects were excluded from analysis due to very slow RTs (more than 2.5 SD from the average). The analysis was carried out for correct responses only (1638 error trials were excluded, 13% of the original data). For each participant in each condition, RTs that were 2.5 SD below or above average were excluded (285 trials were excluded, < 1% of the original data). Error rates were as follows: 1 dot - 1.4%, 2 dots - 0.6%, 3 dots - 1.2%, 4 dots - 1.7%, 5 dots - 6.3%, 6 dots - 16.4%, 7 dots - 18.4%, 8 dots - 27.3%, and 9 dots - 36.3%. A 2 (alertness cue) × 9 (quantities) × 2 (arrangements) ANOVA was carried out with RT as a dependent variable. The analysis revealed 3 main effects: alertness, as RTs with an alerting cue were faster than with no-cue, F(1, 16) = 33.84, p < 0.01, ηp2 = 0.67; arrangement, as RTs were faster in the canonical than the random arrangement, F(1, 16) = 51.21, p < 0.01, ηp2 = 0.76; and quantity, as RTs were slower as the quantity of dots increased, F(8, 128) = 57.31, p < 0.01, ηp2 = 0.78. The interaction of alertness × arrangement was not significant, F(1, 16) < 1, p = 0.82, ηp2 = 0.00. The interaction of arrangement × quantity was significant, F(8, 128) = 24.23, p < 0.01, ηp2 = 0.61. However this different was more robust in quantities 5–9 (small estimation) compared to that for quantities 1–4 (subtilizing range), F(1, 17) = 42.88, p < 0.01, ηp2 = 0.72. Most importantly, the triple interaction between alertness, arrangement and quantity was significant, F(8, 128) = 2.43, p = 0.02, ηp2 = 0.13. Planned comparison between trials with and without an alerting cue in the different arrangements revealed that in the canonical arrangement there was a benefit in RTs when an alerting cue preceded the target compared to the no-cue condition for the quantities of 1–6 and 8. As expected, in the random arrangement the alerting cue modulated RTs for the quantities of 1–5 and replicated the pattern of results of Experiment 1. The results of the three-way interaction are presented in Fig. 4. Planed comparisons of the benefit of the alerting cue for each quantity in each arrangement are reported in Table 1.
Fig. 4.

RTs for the different arrangements and quantity of dots. The error bars represent within-participants confidence intervals. The x-axis represents the quantity of dots.
Table 1.
Planned comparison of the alerting-cue for each arrangement and each quantity in Experiment 2.
| Arrangement | Quantity | F value | P value | ηp2 |
|---|---|---|---|---|
| Canonical | 1 | 31.39 | < .01 | .66 |
| 2 | 28.52 | < .01 | .64 | |
| 3 | 11.77 | .00 | .42 | |
| 4 | 8.66 | .01 | .35 | |
| 5 | 31.83 | < .01 | .67 | |
| 6 | 33.45 | < .01 | .68 | |
| 7 | .92 | .35 | .05 | |
| 8 | 4.85 | .04 | .23 | |
| 9 | 2.56 | .13 | .14 | |
| Random | 1 | 27.02 | < .01 | .63 |
| 2 | 10.99 | .00 | .41 | |
| 3 | 4.66 | .04 | .23 | |
| 4 | 7.4 | .02 | .32 | |
| 5 | 8.39 | .01 | .34 | |
| 6 | 3.97 | .06 | .20 | |
| 7 | 3.9 | .07 | .2 | |
| 8 | 1.61 | .22 | .09 | |
| 9 | 2.3 | .15 | .13 |
3.2.1. Further analysis
A closer look at the results of Experiment 2 revealed that in the random condition, an alerting cue reduced the RTs in amounts which were bigger than 5, even though not significantly. This pattern was different from the pattern of results in Experiment 1. Analysis of both random conditions, namely all the trials in Experiment 1 and half of the trials in Experiment 2, was conducted. A 2 (alertness cue) × 2 (ranges) × 2 (experiments) ANOVA was carried out with RT as a dependent variable. The analysis revealed no interaction between alertness, range and experiment, F(1, 44) = 2.1, p = 0.15, ηp2 = 0.05. However, planned comparison of the alerting effect in the small estimation range (i.e., 5 dots and above) in each of the experiments revealed the absence of an alerting effect in Experiment 1 and a significant alerting effect in Experiment 2, F(1, 44) < 1, p = 0.79, ηp2 < 0.01; and F(1, 44) = 5.62, p = 0.02, ηp2 = 0.11, respectively.
3.3. Discussion
Experiment 2 provides clear evidence that alerting can benefit enumeration of quantities beyond the subitizing range, if these quantities create a global pattern. Specifically, alerting cues facilitated the subitizing process, irrespective of whether the arrangement was canonical or random. Additionally, alerting benefit enumeration in the small estimation range when their arrangement was canonical, in the quantities 5, 6 and 8. It should be noted that the quantities of 7 and 9 were not modulated by the alerting cue, even when arranged canonically. A possible explanation of the absent alerting effect in quantities 7 and 9 is that a canonical arrangement of these quantities does not create a familiar global pattern, unlike quantities 5 and 6, which were arranged similar to on a dice. The arrangement of 8 is easier to process than the arrangements of 7 or 9 because of its symmetrical.
For the random arrangement, two deviations from Experiment 1 should be discussed. First, the alerting effect for the quantity 1 was significant in Experiment 2, but not in Experiment 1 (despite a clear trend in RTs). Therefore, we believe that the lack of effect in Experiment 1 can be attributed to a false negative error. Second, in contrast to the hypothesis, and as opposed to Experiment 1, in Experiment 2 the alerting benefited enumeration in the small estimation range in the random arrangement for quantity 5, and a marginally significant alerting effect was found for the quantities of 6 and 7. It is possible that because Experiment 2′s design involved both random and canonical arrangements within the same block of trials, participants adopted a strategy of looking for a pattern, even in the random array. However, in order to firmly assert this, further research that directly compares mixed vs. fixed blocks of canonical and random arrays is required.
4. General discussion
The present study was aimed at examining the involvement of attention in enumeration processes. Previous studies reported that when attention is disengaged from an enumeration task, the subitizing process is impaired (e.g., Egeth et al., 2008, Olivers and Watson, 2008). Here, we examined whether presentation of alerting cues that increase attentional engagement in a given task can facilitate the subitizing process. Experiment 1 revealed that alerting cues facilitated enumeration of quantities within the subitizing range, but not in the small estimation range. We suggested that alerting could facilitate the subitizing process by enhancing global processing of attention. Since subitizing involved pattern recognition (Ashkenazi et al., 2013, Mandler and Shebo, 1982), quantities within the subitizing range can be identified as familiar global figures, comprised of smaller elements. There are strong evidences suggesting that alerting acts to increase a global processing bias (Kalanthroff et al., 2013, Van Vleet et al., 2011, Weinbach and Henik, 2011). In order to directly examine the hypothesis that alerting modulates subitizing by enhancing global processing, we conducted Experiment 2. In this experiment, all quantities were presented either in a random array or in a canonical array that created a global figure comprised of smaller elements. The results of Experiment 2 showed that alerting facilitated enumeration of quantities even within the small estimation range when the arrangement of dots was canonical. In contrast with our hypothesis and the results of Experiment 1, there was also some benefit of alerting (although to a lesser extent) for quantities 5–7 in the random arrangement. We suggested that when canonical and random arrangements are intermixed in a single block, participants will search for canonical depictions even in random arrays. However, this hypothesis should be studied directly in future research. Overall, the present study confirms previous findings indicating that the subitizing process relies on attentional resources. Our results extend previous studies by showing that subitizing can be facilitated when encouraging engagement of attentional resources during task performance. In addition, we addressed the mechanism that might underlie this effect, namely, the enhancement of global processing by the alerting network.
Interestingly, imaging studies that investigated subitizing, global processing and alerting, revealed involvement of a common brain region, that is, the right temporo-parietal junction (rTPJ). With respect to global processing, multiple neuropsychological studies showed that patients with a focal brain lesion in the rTPJ demonstrate impaired ability to engage in global processing (Lamb et al., 1989, Lamb et al., 1990). A study on the neural networks involved in alerting revealed that the only brain region that was common for both auditory and visual alerting cues was the rTPJ (Robertson et al., 1998, Thiel and Fink, 2007). Lastly, in an imaging study on basic enumeration processes, Ansari and colleagues reported that the rTPJ was activated during enumeration of quantities within the subitizing range, but it was suppressed while enumerating in the estimation range (Ansari, Lyons, van Eimeren, & Xu, 2007). Future studies need to examine whether manipulation of activity in the rTPJ influences the mentioned abilities.
The results of the current study, demonstrating the role of alerting in improving the subitizing process, can shed light on several previous findings. For example, video-game players were found to present a larger subitizing range than non-players, and intensive training in video games to non-players increased their subitizing range (Green & Bavelier, 2003). Action-game video games were found to induce elevated levels of arousal (Anderson & Bushman, 2001). Therefore, when trying to understand what component in the video-game training was responsible for later improvement in the subitizing process, our results hint towards increase in the levels of alertness. Additionally, developmental dyscalculia (DD; American Psychiatric Association, 2013), is a disorder characterized by poor abilities to acquire and use arithmetic. A previous study reported that the subitizing range in those with DD is smaller than in healthy controls and was not improved when quantities were presented in a canonical arrangement of dots (Ashkenazi et al., 2013). Interestingly, another study that examined attentional networks in DD revealed atypical effects within the alerting networks, suggesting dysregulation of alertness levels in DD (Ashkenazi & Henik, 2010). In light of the current study, it is possible that the deficit in the subitizing process in DD can be attributed to dysregulation in the alerting system. Further studies are required to examine this possibility directly. Note that DD is consider to be a heterogenic disorder (i.e., Rubinsten & Henik, 2009), and has a high comorbidity with attention disorders (i.e., attention deficit/hyperactive disorder; Shalev & Gross-Tsur, 2001), which are also known for dysregulation in alerting and global processing (Kalanthroff et al., 2013). Therefore, future studies that would better characterize dysregulation of alerting and global processing in DD should examine DD subtypes that are not characterized by comorbid attentional disorders.
To conclude, the present study revealed that the subitizing process could be facilitated by inducing a manipulation that increases attentional engagement during an enumeration task. We exposed the beneficial effects of alerting on subitizing and clarified the association between subitizing, alerting and global processing. Research focusing on a mechanism that can improve rather than impair enumeration processes could prove helpful when considering rehabilitation in conditions such as DD. Future research can examine whether existing training procedures that act to increase alertness and global processing (Van Vleet et al., 2011) can also improve enumeration in healthy individuals and in special populations such as those with DD.
Acknowledgements
This work was supported by the European Research Council (ERC) under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement 295644.
We thank Dr. Marinella Cappelletti for her insights and suggestions, which led us to think about this research.
References
- American Psychiatric Association . 5th ed. Author; Arlington, VA: 2013. Diagnostic and statistical manual of mental disorders. [Google Scholar]
- Anderson C.A., Bushman B.J. Effects of violent video games on aggressive behavior, aggressive cognition, aggressive affect, physiological arousal, and prosocial behavior: A meta-analytic review of the scientific literature. Psychological Science. 2001;12:353–359. doi: 10.1111/1467-9280.00366. [DOI] [PubMed] [Google Scholar]
- Ansari D., Lyons I.M., van Eimeren L., Xu F. Linking visual attention and number processing in the brain: The role of the temporo-parietal junction in small and large symbolic and nonsymbolic number comparison. Journal of Cognitive Neuroscience. 2007;19:1845–1853. doi: 10.1162/jocn.2007.19.11.1845. [DOI] [PubMed] [Google Scholar]
- Ashkenazi S., Henik A. Attentional networks in developmental dyscalculia. Behavioral and Brain Functions. 2010;6:2. doi: 10.1186/1744-9081-6-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashkenazi S., Mark-Zigdon N., Henik A. Do subitizing deficits in developmental dyscalculia involve pattern recognition weakness? Developmental Science. 2013;16:35–46. doi: 10.1111/j.1467-7687.2012.01190.x. [DOI] [PubMed] [Google Scholar]
- Atkinson J., Campbell F.W., Francis M.R. The magic number 4 ± 0: A new look at visual numerosity judgements. Perception. 1976;5:327–334. doi: 10.1068/p050327. [DOI] [PubMed] [Google Scholar]
- Dehaene S. Varieties of numerical abilities. Cognition. 1992;44:1–42. doi: 10.1016/0010-0277(92)90049-n. [DOI] [PubMed] [Google Scholar]
- Egeth H.E., Leonard C.J., Palomares M. The role of attention in subitizing: Is the magical number 1? Visual Cognition. 2008;16:463–473. [Google Scholar]
- Gebuis T., Reynvoet B. Generating nonsymbolic number stimuli. Behavior Research Methods. 2011;43:981–986. doi: 10.3758/s13428-011-0097-5. [DOI] [PubMed] [Google Scholar]
- Green C.S., Bavelier D. Action video game modifies visual selective attention. Nature. 2003;423:534–537. doi: 10.1038/nature01647. [DOI] [PubMed] [Google Scholar]
- Kalanthroff E., Naparstek S., Henik A. Spatial processing in adults with attention deficit hyperactivity disorder. Neuropsychology. 2013;27:546–555. doi: 10.1037/a0033655. [DOI] [PubMed] [Google Scholar]
- Kaufman E.L., Lord M.W., Reese T.W., Volkmann J. The discrimination of visual number. The American Journal of Psychology. 1949;62:498–525. [PubMed] [Google Scholar]
- Kaufmann L., Nuerk H.C. Basic number processing deficits in ADHD: A broad examination of elementary and complex number processing skills in 9- to 12-year-old children with ADHD-C. Developmental Science. 2008;11:692–699. doi: 10.1111/j.1467-7687.2008.00718.x. [DOI] [PubMed] [Google Scholar]
- Lamb M.R., Robertson L.C., Knight R.T. Attention and interference in the processing of global and local information: Effects of unilateral temporal-parietal junction lesions. Neuropsychologia. 1989;27:471–483. doi: 10.1016/0028-3932(89)90052-3. [DOI] [PubMed] [Google Scholar]
- Lamb M.R., Robertson L.C., Knight R.T. Component mechanisms underlying the processing of hierarchically organized patterns: Inferences from patients with unilateral cortical lesions. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1990;16:471–483. doi: 10.1037//0278-7393.16.3.471. [DOI] [PubMed] [Google Scholar]
- Leibovich T., Henik A. Magnitude processing in non-symbolic stimuli. Frontiers in Psychology. 2013;4:375. doi: 10.3389/fpsyg.2013.00375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leibovich T., Henik A. Comparing performance in discrete and continuous comparison tasks. Quarterly Journal of Experimental Psychology. 2014;67:899–917. doi: 10.1080/17470218.2013.837940. [DOI] [PubMed] [Google Scholar]
- Mandler G., Shebo B.J. Subitizing: An analysis of its component processes. Journal of Experimental Psychology: General. 1982;111:1–22. doi: 10.1037//0096-3445.111.1.1. [DOI] [PubMed] [Google Scholar]
- Navon D. Forest before trees: The precedence of global features in visual perception. Cognitive Psychology. 1977;9:353–383. [Google Scholar]
- Olivers C.N., Watson D.G. Subitizing requires attention. Visual Cognition. 2008;16:439–462. [Google Scholar]
- Petersen S., Posner M.I. The attention system of the human brain: 20 years after. Annual Review of Neuroscience. 2012;35:73–89. doi: 10.1146/annurev-neuro-062111-150525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M., Mechelli A., Butterworth B., Price C.J. Are subitizing and counting implemented as separate or functionally overlapping processes? NeuroImage. 2002;15:435–446. doi: 10.1006/nimg.2001.0980. [DOI] [PubMed] [Google Scholar]
- Posner M.I. Lawrence Erlbaum; Hillsdale, NJ: 1978. Chronometric explorations of mind. [Google Scholar]
- Posner M.I., Petersen S.E. The attention system of the human brain. Annual Review of Neuroscience. 1990;13:25–42. doi: 10.1146/annurev.ne.13.030190.000325. [DOI] [PubMed] [Google Scholar]
- Railo H., Koivisto M., Revonsuo A., Hannula M.M. The role of attention in subitizing. Cognition. 2008;107:82–104. doi: 10.1016/j.cognition.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Robertson I.H., Mattingley J.B., Rorden C., Driver J. Phasic alerting of neglect patients overcomes their spatial deficit in visual awareness. Nature. 1998;395:169–172. doi: 10.1038/25993. [DOI] [PubMed] [Google Scholar]
- Rubinsten O., Henik A. Developmental dyscalculia: Heterogeneity might not mean different mechanisms. Trends in Cognitive Sciences. 2009;13:92–99. doi: 10.1016/j.tics.2008.11.002. [DOI] [PubMed] [Google Scholar]
- Shalev R.S., Gross-Tsur V. Developmental dyscalculia. Pediatric Neurology. 2001;24:337–342. doi: 10.1016/s0887-8994(00)00258-7. [DOI] [PubMed] [Google Scholar]
- Tanzer M., Weinbach N., Mardo E., Henik A., Avidan G. Phasic alertness enhances global processing in congenital prosopagnosia — A possible paradigm for rehabilitation? Neuropsychologia. 2016 doi: 10.1016/j.neuropsychologia.2016.06.032. (Manuscript accepted for publication) [DOI] [PubMed] [Google Scholar]
- Thiel C.M., Fink G.R. Visual and auditory alertness: Modality-specific and supramodal neural mechanisms and their modulation by nicotine. Journal of Neurophysiology. 2007;97:2758–2768. doi: 10.1152/jn.00017.2007. [DOI] [PubMed] [Google Scholar]
- Trick L.M., Pylyshyn Z.W. Why are small and large numbers enumerated differently? A limited-capacity preattentive stage in vision. Psychological Review. 1994;101:80–102. doi: 10.1037/0033-295x.101.1.80. [DOI] [PubMed] [Google Scholar]
- Van Vleet T.M., Hoang-duc A.K., DeGutis J., Robertson L.C. Modulation of non-spatial attention and the global/local processing bias. Neuropsychologia. 2011;49(3):352–359. doi: 10.1016/j.neuropsychologia.2010.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetter P., Butterworth B., Bahrami B. Modulating attentional load affects numerosity estimation: Evidence against a pre-attentive subitizing mechanism. PloS One. 2008;3:9. doi: 10.1371/journal.pone.0003269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinbach N., Henik A. Phasic alertness can modulate executive control by enhancing global processing of visual stimuli. Cognition. 2011;121:454–458. doi: 10.1016/j.cognition.2011.08.010. [DOI] [PubMed] [Google Scholar]