Characterization of biomechanical properties of aged human and ovine mitral valve chordae tendineae

Abstract

The mitral valve (MV) is a highly complex cardiac valve consisting of an annulus, anterior and posterior leaflets, chordae tendineae (chords) and two papillary muscles. The chordae tendineae mechanics play a pivotal role in proper MV function: the chords help maintain proper leaflet coaptation and rupture of the chordae tendineae due to disease or aging can lead to mitral valve insufficiency. Therefore, the aim of this study was to characterize the mechanical properties of aged human and ovine mitral chordae tendineae. The human and ovine chordal specimens were categorized by insertion location (i.e., marginal, basal and strut) and leaflet type (i.e., anterior and posterior). The results show that human and ovine chords of differing types vary largely in size but do not have significantly different elastic and failure properties. The excess fibrous tissue layers surrounding the central core of human chords added thickness to the chords but did not contribute to the overall strength of the chords. In general, the thinner marginal chords were stiffer than the thicker basal and strut chords, and the anterior chords were stiffer and weaker than the posterior chords. The human chords of all types were significantly stiffer than the corresponding ovine chords and exhibited much lower failure strains. These findings can be explained by the diminished crimp pattern of collagen fibers of the human mitral chords observed histologically. Moreover, the mechanical testing data was modeled with the nonlinear hyperelastic Ogden strain energy function to facilitate accurate computational modeling of the human MV.

1. Introduction

The mitral valve (MV) is a complex yet elegantly structured cardiac valve that consists of an annulus, anterior and posterior leaflets, chordae tendineae (chords) and two papillary muscles. Normal MV function involves a proper, delicate force balance between each of its components throughout the cardiac cycle (Sun et al., 2014). For instance, the chords, which originate from either papillary muscles (on the anterolateral and posterolateral walls) or multiple small muscle bundles attaching to the ventricular wall and insert into the ventricular side of the leaflets, prevent the leaflets from billowing into the left atrium during systole (Sun et al., 2014).

Disease and rupture of the chordae tendineae can be caused by many reasons. Rupture of the chordae tendineae of the mitral valve was first described by Corvisart in 1806 (Oliveira et al., 1983). Studies have shown that sub-acute endocarditis and rheumatic heart disease were the most frequent causes of chordae rupture (54.4% and 42.1%, respectively) for the secondary chordae tendinae rupture as there was almost no awareness about the roles of mitral valve prolapse and myxomatous degeneration before 1985 (Gabbay and Yosefy, 2010), these two rates have decreased substantially (to 37.4% and 24.8%, respectively) since 1985, and MV prolapse became predominant cause (Gabbay and Yosefy, 2010). Other underlying causes, such as blunt chest trauma, generalized connective tissue disorder, ischemic heart disease, and other heart and valvular diseases, are possibly episodic. Chordae tendineae rupture can also occur in apparently healthy subjects having no atypical appearance and who may be unaware of carrying risk (Gabbay and Yosefy, 2010).

Surgical chordal repair procedures are challenging due to complexity of the MV and adjacent structures. Determining the artificial chordal insertion points to provide the appropriate length and elasticity to restore normal MV function is a non-trivial task. A better understanding of the mitral chordae tendineae mechanics will be essential for the development and refinement of chordal replacement and repair techniques (Wang and Sun, 2013), as well as for the modeling of mitral valve mechanics under normal and diseased conditions. Substantial research has been conducted in recent years to characterize the structure and function of porcine mitral chordae tendineae, including determination of the distinct roles of specific chordal types (Kunzelman and Cochran, 1990; Liao and Vesely, 2003; Ritchie et al., 2005; Padala et al., 2010; Millard et al., 2011). Data on the human mitral chordae, however, is limited (Clark, 1973; Lim and Boughner, 1975; Casado et al., 2012; Barber et al., 2001). Through these studies it has been shown that smaller chordae are less extensible than larger chordae (Lim and Boughner, 1975), the stiffness of myxomatous chordae is approximately 50% of normal chordae (Barber et al., 2001), and moderately calcified marginal chordae are between three and seven times more compliant than normal chordae (Casado et al., 2012). Yet, the distinct mechanical properties of aged (65 years and older) human chordae of differing sizes, types, and insertion points, have not been characterized.

Because the ovine model has similar chordal structure (Degandt et al., 2007) and is often used to study MV mechanics (Timek et al., 2002; Krishnamurthy et al., 2009; Rausch et al., 2011; Siefert et al., 2012), the ovine chordal structural and mechanical properties compared to human chordal properties are of interest. In this study, chords from ovine, 1–2 years old, with heart weight of 374.83±47.95 g were studied and compared to aged human ones. Although 1–2 years old ovine is equivalent to a young human, this age range is commonly used in most animal studies. Thus, the objectives of this study were to: (1) characterize the elastic and failure properties of the human chordae tendineae through uniaxial tensile testing and structural analysis, and (2) determine any mechanical or structural property differences between aged human and ovine chords.

2. Materials and methods

2.1. Materials and sample preparation

Eighteen fresh frozen ovine hearts (weight of 374.83±47.95 g, 1–2 years old) were obtained from the Animal Technologies, Inc. (Tyler, TX), from which a total of 115 chord specimens were dissected. Fourteen human cadaver hearts (weight of 558.21±200.30 g, 76±11.25 years old) were obtained from the National Disease Research Interchange (NDRI, Philadelphia, PA), from which a total of 106 chord specimens were prepared, see Table 1 for human specimen characteristics. The use of human tissues was approved by the Institutional Review Board at the University of Connecticut. All human hearts were fresh frozen within a post-mortem recovery interval of 15.32±6.51 h, and delivered on the following day. Each heart was placed in a plastic bag filled with 10% DMSO (Bia et al., 2006) and 90% saline, and it was completely frozen after 30 min in the −80 °C freezer. It has been shown that the structural architecture (Gerson et al., 2009) and mechanical properties (Bia et al., 2006; Rosset et al., 1996; Song et al., 1995) of connective tissues can be preserved when stored in a cryoprotectant agent at low temperature (−80 °C). The cryopreserved specimens were thawed using a four-step process (Bia et al., 2006) to remove cryoprotectant substances prior to testing. Each chord was stored in a 4 °C saline solution and tested within 24 h of thawing.

Table 1.

Medical history of all human patients.

Patient no.	Age (years)	Gender	Heart weight (g)	Cause of death	Heart related disease(s)
1	60	M	711	CA	AAA
2	56	M	554	PC	None
3	63	F	505	CPA	HTN, CHF, MI
4	76	F	527	BC	None
5	69	M	733	CPA	HTN
6	75	F	575	CPA	HTN
7	81	F	621	Alz	None
8	86	F	1100	Unk	HTN
9	81	F	330	Unk	None
10	87	F	490	Unk	None
11	98	F	303	RA	None
12	75	M	425	CA	Unk
13	79	F	545	RF	CHF
14	78	M	396	CPA	HTN
Mean±SD	76±11.25		558.21±200.30

AAA, Abdominal Aortic Aneurysm; Alz, Alzheimer’s; BC, bladder cancer; CA, cardiac arrest; CHF, congestive heart failure; COPD, chronic obstructive pulmonary disorder; CPA, Chronic pulmonary aspergillosis; HTN, hypertension; PC, prostate cancer; RA, respiratory arrest; RF, respiratory failure; unk, unknown.

2.2. Chordae classification

Studies on mitral chordae mechanics have often distinguished chordae by either insertion location (Kunzelman and Cochran, 1990) based on Lam’s chordal classification (Lam et al., 1970) and/or by leaflet type (Barber et al., 2001; Sedransk et al., 2002). In this study, we categorized the chordae into five groups based on their insertion locations on the leaflets, as illustrated in Fig. 1a of a human MV, for analysis. The five chordae groups included: (1) the anterior marginal chordae (AM) of the rough-zone region, constituted by abundant chordae insertions distributed from the belly to the free-edge of the leaflet, (2) the anterior strut chordae (AS), the two largest chordae (also referred to as secondary), connecting to the rough zone at the 4 and 8 o’clock positions on the anterior leaflet, (3) the anterior basal chordae (AB) that insert near the annulus and beyond the free edge and strut chordae, (4) the posterior marginal chordae (PM), similar to the AM, which insert into the rough zone and free edge of the posterior leaflet, and (5) the posterior basal chordae (PB) which insert into the basal portion of the posterior leaflet.

Fig. 1.

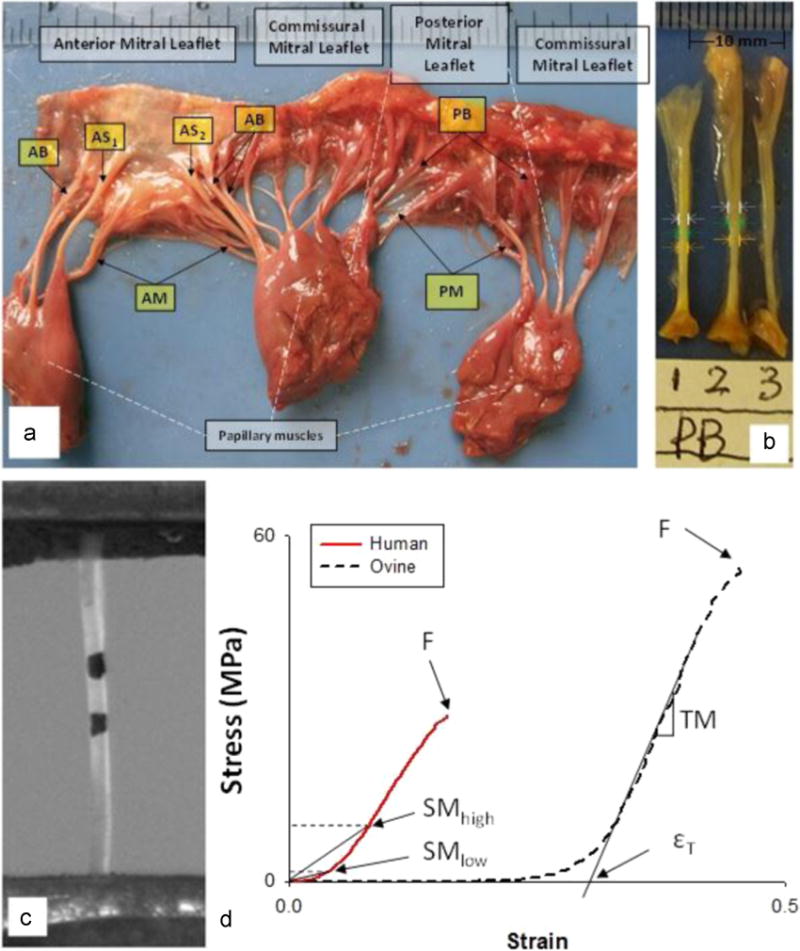
(a) A representative human mitral valve and identifications of five chordal types: Anterior Basal (AB), Anterior Marginal (AM), Anterior Strut (AS), Posterior Basal (PB) and Posterior Marginal (PM). (b) Diameter measurements along the chord using a digital camera. (c) A captured video image of a chord with markers used for strain measurement. (d) Representative stress–strain curves for human and ovine chordae and the calculated mechanical parameters: ε_T – Strain at transition point, or, TM – Tangent Modulus, F – Failure stress–strain, SM_low and SM_high – Secant Modulus at 1 MPa and at 10 MPa, respectively.

2.3. Experimental protocol

Uniaxial tensile testing was carried out on the chord specimens with a Tinius Olsen H50KS Universal Materials Testing system (Tinius Olsen, Inc., Horsham, PA) with some modifications as described below (Fig. 1c). The chordae diameters were measured at three locations near the center of its length from two digital images (front and back of a chord), as shown in Fig. 1b, the average diameter was recorded. Two black dots were marked around the central area of the chords using permanent marker for optical strain measurements. The chords were mounted between two specialized grips lined with sandpaper to prevent tissue slippage, and immersed in a tank of 0.9% saline solution throughout testing. A 250 N load-cell (Interface SMT1-250N, Interface Inc., Scottsdale, Arizona) was connected to the upper grip. The uniaxial tensile force measured from the load-cell was recorded using a National Instruments (NI) data acquisition/signal conditioning system that consists of a NI-PCI-6025E DAQ card connected to a NI-SCC-68 I/O Terminal Box and a NI-SCC-SG24 full-bridge signal conditioning module. A CCD camera (Sony XC-ST50, Sony Corporation of America, Park Ridge, NJ) was connected to a computer through a frame grabber card (NI-PCI-1405) to capture the locations of the markers throughout the duration of the test. A custom LabVIEW (National Instruments, Austin TX) program was developed to record video and load data simultaneously and synchronously at 30 frames per second. All specimens with length ranging from 10 to 15 mm were preconditioned by loading the tissue to a peak load of 2 N for 10 consecutive cycles at a rate of 50 mm/min. The specimens were then stretched to failure at the same loading rate. A post-processing LabVIEW image analysis program was developed to extract the coordinates of markers from all video frames for strain calculation.

2.4. Data analysis

The Green strain, ε in the axial direction was calculated as, ε = (λ²−1)/2, where the axial stretch is λ = L/L₀, and L₀ and L are the initial and current distances between the two markers, respectively. The chord tissues were assumed to be incompressible, hence, the deformed cross-sectional area, A, can be expressed as, A = A₀L₀/L, where A₀ is the initial cross-sectional area. The axial Cauchy stress, σ, was calculated as, σ= F/A, where F is the current load measured by the load-cell.

Two representative uniaxial stress-strain curves of human and ovine chordae are shown in Fig. 1d. The strain at the transition point (ε_T), Secant Modulus (SM), Tangent Modulus (TM), and failure strain (ε_max) and Ultimate Tensile Strength (UTS) were also calculated for each specimen. The post-transitional linear region of the stress-strain curve was fitted by the built-in least-square fitting function in MATLAB (Math-Works, Natick, MA). The TM represented the slope of the fitted line, and the chord extensibility was defined as the x-axis intercept of the fitted line. Since the stress–strain curve is known to be non-linear, the response cannot be characterized by either Young’s Modulus or a single SM. Therefore, the SM were calculated at two different stress levels (see Fig. 3) (a) at 1 MPa, which represents physiological loading prior to the transitional point in the stress–strain curve and (b) at 10 MPa, which represents the response at higher loads under complete recruitment of the collagen fibers. The UTS was measured and calculated at the rupture point, and ε_max was calculated from the last visible markers prior to rupture.

Fig. 3.

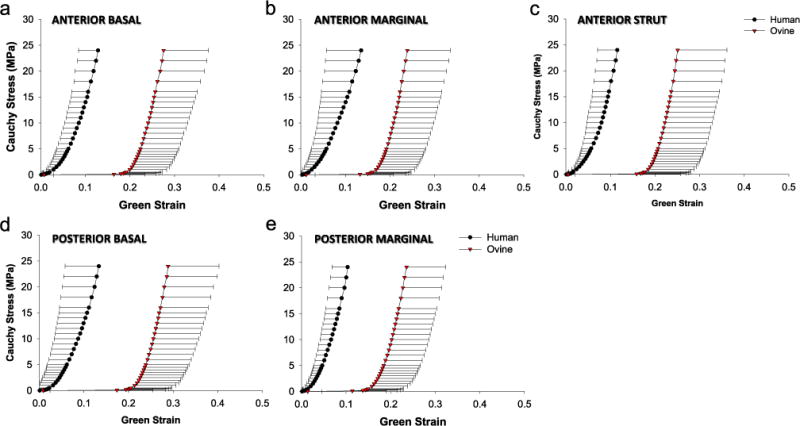
The mean and standard deviation of the stress–strain responses of human (circle) and ovine (down triangle) chordal types: (a) anterior basal, (b) anterior marginal, (c) anterior strut, (d) posterior basal, and (e) posterior marginal.

2.5. Constitutive modeling

The elastic portion of the chord stress–strain responses, prior to yielding, were fitted with the Ogden strain energy function (Ogden, 1997), W, given by

$$\mathrm{W}={\displaystyle \sum _{i=1}^N\frac{2{\mu }_i}{a_i^2}}({\lambda }_1^{a_i}+{\lambda }_2^{a_i}+{\lambda }_3^{a_i}-3)$$ (1)

where μ_i and a_i (i=1, 2, 3) are material constants and λ_j (j=1, 2, 3) are the principal stretches. The goodness of fit was determined by the R-squared value based on the Levenberg–Marquardt nonlinear regression algorithm using SYSTAT 10 (Systat Software Inc., Chicago, IL).

2.6. Microstructural analysis

Following mechanical testing, the chord tissues were fixed in 10% neutral buffered formalin for at least 24 h and dehydrated in a series of ethanol solutions of varying concentrations. The intact portion of each sample was processed in paraffin, sectioned into two 5-micron thick samples in both the radial and longitudinal directions, and then embedded in paraffin wax. Hematoxylin and Eosin (H&E) staining was carried out to visualize tissue integrity and orientation of the samples. Verhoeff–Van Giesson (VVG) staining was performed to visualize the collagen and elastin structures. Digital images of each slide were obtained utilizing a Zeiss Axio Scope.A1 microscope coupled with a Zeiss AxioCAM RMm microscope camera. The crimped structure of the collagen fibers were also assessed from the H&E stained samples and observed with a Zeiss Observer.D1 inverted microscope.

2.7. Statistics

All measurements were reported as a mean±standard deviation. Differences between the means of more than two groups were determined using the analysis of variance (ANOVA) test followed by the Holm–Sidak test and Dunn’s Method test for pair-wise multiple comparison. The independent two sample t-test was used to determine significant differences between two groups. Non-parametric tests, including the Wilcoxon signed-rank test and Mann–Whitney rank sum test, were used for non-normally distributed sample groups. Correlation between age and tissue properties was determined using Pearson’s correlation coefficient. A p-value less than 0.05 was considered to indicate a statistically significant event. Statistical analyses were performed with SigmaPlot (V11.0, Systat Software Inc., San Jose, CA).

3. Results

3.1. Chordal size

The diameter measurements for each chordal type are given in Table 2 and illustrated in Fig. 2. The AS was significantly larger than other chord groups (p<0.001) in both human and ovine models. A trend was observed when comparing chords by insertion location: the basal groups (AB and PB) were typically larger than the marginal groups (AM and PM), respectively; however, this trend was not significant between the ovine AB and AM groups. When comparing chordal diameter by leaflet types, there was no difference in the diameter of either the basal or marginal chords between the anterior and posterior leaflets. Human basal and strut chords were significantly larger than the ovine chords (AB: p=0.002, AS: p<0.001, and PB: p=0.027), yet there was no difference between the human and ovine marginal chords (AM: p=0.081 and PM: p=0.67).

Table 2.

Sample sizes (N), mean and standard deviation of the diameter, Secant Modulus (SM) at 0.4 and 10 MPa, and transition point or ε_T of each chordal group. Subsets of samples (n) were analyzed for failure properties expressed as breaking strain (ε_max) and Ultimate Tensile Strength (UTS). Samples were grouped by (A) chordal insertion and leaflet type, (B) leaflet type only, and (C) chordal insertion only.

A. Grouped by chordal insertion and leaflet type
	AB	N	Diameter (mm)	SM at 0.4 MPa (MPa)	SM at 10 Mpa (MPa)	Tangent Modulus (MPa)	εT	n	εmax	UTS (MPa)
HUMAN	AM	44	0.81±0.18	37.67±31.84	137.73±60.04	310.10±235.35	0.041±0.023	16	0.189±0.066	41.77±27.33
	AS	17	0.57±0.09	54.24±36.31	152.86±62.34	353.43±253.08	0.041±0.029	2	0.195±0.077	36.45±12.43
	PB	14	1.27±0.27	33.707±15.80	142.83±50.15	361.80±173.50	0.048±0.027	2	0.391±0.353	37.65±7.23
	PM	60	0.75±0.17	36.96±23.22	161.51±70.83	405.35±310.00	0.041±0.037	14	0.194±0.089	37.58±23.12
OVINE	AB	16	0.58±0.14	33.42±18.16	151.49±79.93	321.35±187.77	0.042±0.034	1	0.256	26.489
	AM	33	0.68±0.14	2.67±1.13	49.23±14.80	394.40±168.68	0.206±0.083	3	0.312±0.100	38.95±27.55
	AS	6	0.65±0.09	2.38±1.02	47.48±20.56	392.66±312.61	0.218±0.073	0	–	–
	PB	19	0.88±0.15	2.56±1.64	46.19±20.02	397.50±176.79	0.228±0.083	2	0.377±0221	23.64±4.99
	PM	35	0.67±0.15	2.05±0.63	42.07±11.28	440.69±218.37	0.237±0.071	8	0.314±0158	37.49±28.77
		13	0.54±0.11	2.73±1.33	49.36±20.36	384.18±215.91	0.218±0.078	3	0.406±0.069	42.28±13.70

B. Grouped by leaflet type
		N	Diameter (mm)	SM at 0.4 MPa (MPa)	SM at 10 Mpa (MPa)	Tangent Modulus (MPa)	εT	n	εmax	Ultimate Strength (MPa)
HUMAN	Anterior	75	0.847±0.29	40.68±31.22	142.29±58.47	329.57±227.76	0.042±0.025	20	0.210±0.119	40.82±24.58
	Posterior	76	0.71±0.18	36.20±22.17	159.37±72.41	387.67±289.55	0.041±0.036	15	0.198±0.087	36.84±22.46
OVINE	Anterior	53	0.75±0.17	2.60±1.29	48.00±17.07	395.25±186.92	0.215±0.081	5	0.338±0.136	32.83±22.50
	Posterior	40	0.64±0.15	2.22±0.89	43.94±14.22	426.56±216.40	0.232±0.073	11	0.367±0.103	42.20±22.78

C. Grouped by chordal insertion
		N	Diameter (mm)	SM at 0.4 MPa (MPa)	SM at 10 MPa (MPa)	Tangent Modulus (MPa)	εT		εmax	Ultimate Strength (MPa)
HUMAN	Basal	103	0.78±0.18	36.62±26.44	150.61±66.68	363.01±284.18	0.041±0.032	30	0.192±0.075	39.61±24.40
	Marginal	34	0.57±0.11	45.86±31.58	155.53±71.87	344.87±221.36	0.041±0.031	3	0.346±0.261	33.93±8.22
	Strut	14	1.27±0.27	33.70±15.80	142.83±50.15	361.80±173.50	0.048±0.027	2	0.195±0.077	36.45±12.43
OVINE	Basal	59	0.68±0.14	2.35±0.95	45.65±13.53	417.94±195.25	0.222±0.078	3	0.342±0.106	41.29±25.21
	Marginal	16	0.58±0.11	2.60±1.20	48.66±19.76	387.36±246.10	0.218±0.074	5	0.394±0.122	38.47±15.94
	Strut	18	0.88±0.15	2.56±1.64	46.19±20.02	397.50±176.79	0.228±0.083	0	–	–

Fig. 2. Overlaying boxplots and scatterplots of the diameter of the mitral chordae, showing the Anterior Strut (AS) is significantly thicker than other groups for both (a) human and (b) ovine. Basal chords are generally significantly thicker than marginal chords.

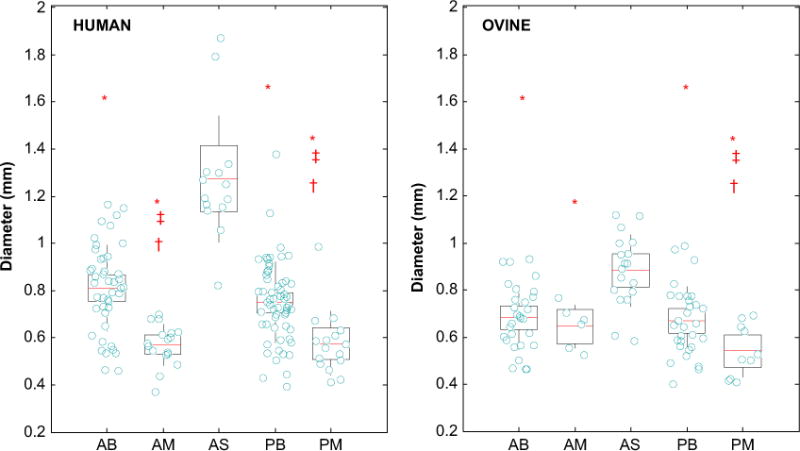
Anterior Basal (AB), Anterior Marginal (AM), Posterior Basal (PB) and Posterior Marginal (PM). *: is significantly smaller than AS; ‡: is significantly smaller than AB; †: is significantly smaller than PB.

3.2. Elastic and failure properties

The mean stress–strain responses of both human and ovine chords were non-linear with three distinctive regions (see Fig. 3), i.e. pre-transition compliant ‘toe’ region, transition region, and post-transition stiff regions. The two most noticeable differences between the two species are: (1) the ovine chords exhibited greater extensibility at low load during in the pre-transition region, whereas aged human chordae responses completed lacked this region; (2) the ovine chordae exhibited a sharp transition into the high load region compared to a more gradual transition region of the human chordae.

The SM at 1 and 10 MPa, ε_T, TM, ε_max and UTS, categorized by chordal insertions and leaflet types, are summarized in Table 2. For human chords, there was no significant difference in mechanical properties among the chordal groups, as shown in Fig. 4a and b. From Table 2, several general trends were observed: the human AM and PB chords were the stiffest at low and high loads, respectively; for the anterior chords, the marginal group was slightly stiffer than basal group, but not for the posterior chords. By comparing the insertion points, thinner marginal chords were stiffer than thicker basal and strut chords, while strut chords were relatively weaker. By comparing the leaflet types, the anterior chords, while being stiffer at low load, were weaker and more compliant at high load than posterior chords.

Fig. 4.

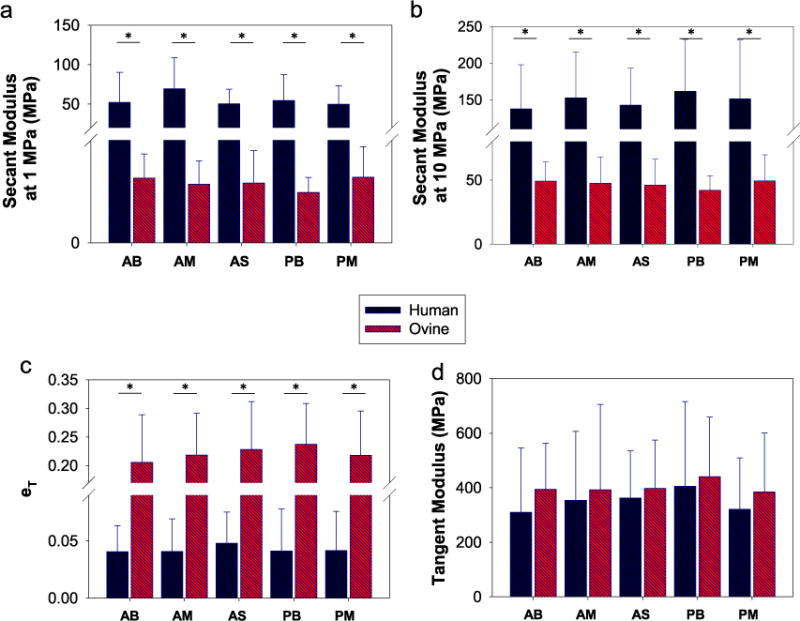
Comparison of the mean secant moduli at (a) 1 MPa, (b) 10 Mpa, (c) extensibility, and (d) tangent modulus among chordal groups and between human and ovine. Anterior Basal (AB), Anterior Marginal (AM), Anterior Strut (AS), Posterior Basal (PB) and Posterior Marginal (PM). (*) indicates a significant difference was detected between the two groups.

Similarly, the ovine chordal groups were not significantly different from each other. All human chordal types were consistently much stiffer than the ovine counterparts at low and high stresses, also see Figs. 4a and b (p<0.001 for all t-tests). The ε_T in Fig. 4c demonstrated that ovine chordae were highly extensible at low loads, and when comparing with the stiffer human chordae, the differences were significant (p<0.001 for all t-tests). Interestingly, the TM of human and ovine chordae were similar, the mean values were within the ranges of 310–405 MPa and 384–440 MPa for human and ovine, respectively (see Fig. 4d).

Due to the short length of the chordae, many of the chordae samples either slipped out from one of the grips or ruptured beyond the marker region, i.e. near the grips during testing. Thus, these data were not included in the data analysis. In general, human chords failed at lower strains than the corresponding ovine, but the UTS was comparable among the chordal groups and between the two species (Table 2). Among all parameters, a strong correlation between age and chordae UTS was observed with p-value less than 0.001, as shown in Fig. 5.

Fig. 5.

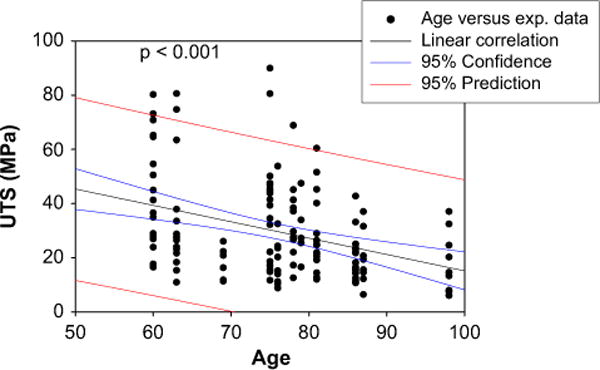
Correlation between age and Ultimate Tensile Strength (UTS) of all human chords.

3.3. Constitutive model

The Ogden model was able to capture the mechanical behavior of the chordae well with an average R-square value over 0.96. Illustrated in Fig. 6 are representative stress–strain curves of a human chordae and an ovine chordae, it can be seen that the Ogden model could capture the stress–strain curves of chordae testing data properly, except for the sharp transition region of the ovine data. The material constants of the fitted Ogden model for human and ovine chordae are summarized in Table 3.

Fig. 6.

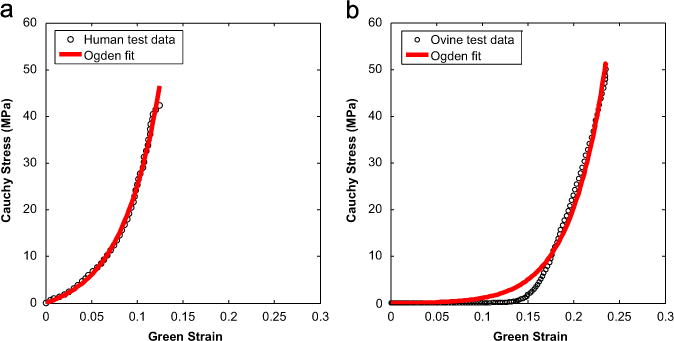
Representative stress–strain response curves with Ogden model fits of (a) human and (b) ovine anterior basal chordae. The model captures both responses well with mean R²>0.95.

Table 3.

The mean and standard deviation of Ogden model parameters for both human and ovine chordal groups categorized by chordal insertion and leaflet type.

		AB	AM	AS	PB	PM
HUMAN	μ1 (MPa)	8.39±8.96	8.91±9.21	9.61±9.52	9.43±10.23	9.57±12.59
	a1	22.04±9.50	27.02±16.52	30.86±19.70	25.48±13.55	22.78±8.29
	μ2 (MPa)	9.78±10.30	12.19±7.55	7.99±5.84	8.12±8.36	10.61±10.32
	a2	23.43±10.44	20.91±9.59	27.65±19.23	25.41±13.54	21.68±8.74
	μ3 (MPa)	9.26±8.96	12.78±10.14	7.81±7.93	12.33±16.11	10.65±13.07
	a3	25.44±18.03	20.89±9.62	30.00±19.20	26.03±12.96	21.35±8.83
OVINE	μ1 (MPa)	0.60±1.68	0.37±0.78	0.85±2.65	0.30±1.17	0.66±1.93
	a1	23.40±20.81	11.70±15.11	28.03±27.06	25.20±23.94	29.67±24.86
	μ2 (MPa)	0.02±0.09	1.79±2.82	0.21±0.64	0.38±1.55	1.37±2.48
	a2	3.91±10.35	5.00±13.50	5.47±12.31	2.42±9.00	18.25±23.29
	μ3 (MPa)	0.32±0.80	0.33±2.05	0.16±0.35	0.35±1.17	1.46±2.52
	a3	20.33±23.32	34.06±22.66	25.06±24.35	32.72±38.77	19.45±18.33

3.4. Histological analysis

Both human and ovine chordae are mainly composed of collagen fibers, which are densely packed in the innermost core. Ovine chordae exhibited a typical crimped collagen fiber structure, while this crimp pattern was almost diminished in human chordae (Fig. 7). The collagen structures in the central core, however, were normal with no sign of fiber disruption. Histological images in Fig. 8a and b show the microstructures of the representative five chordal types of two human hearts (Patients 1 and 2 according to Table 1) in the circumferential cross-section view. Some of the chords from both hearts appeared to be structurally normal with a large central core composed of compact collagen bundles and a thin spongiosa fibrous layer composed of elastic fibers (P1-AB, -AS, -PB, -PM and P2-AS, -PB, -PM), while several chords exhibited altered structures, P1-AM and P2-AB, -AM. The changes included multiple spongiosa layers consisted of unorganized collagen and fibrous tissues surrounding the central core and these spongiosa layers appeared irregular in thickness and frequently detached from the dense core.

Fig. 7.

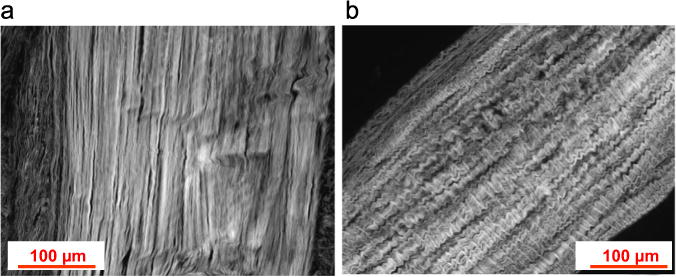
Representative longitudinal sections of (a) human and (b) ovine anterior basal chordae stained with H&E and visualized under an inverted microscope. Collagen crimped pattern is apparent in ovine chordae while almost diminished in human chordae.

Fig. 8.

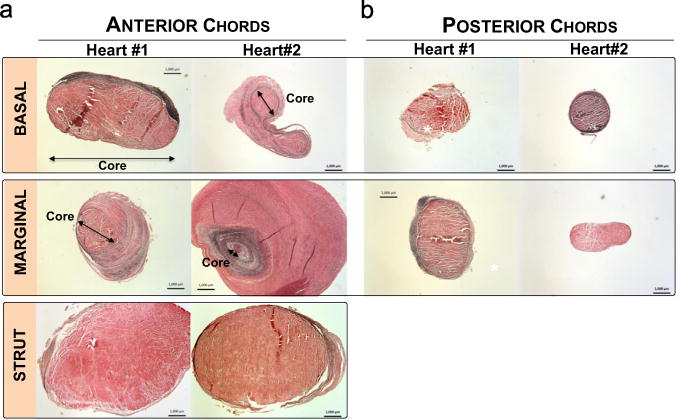
Circumferential cross-sections stained in Verhoeff–Van Gieson of (a) anterior basal (AB), anterior marginal (AM), anterior strut (AS), and (b) posterior basal (PB) and posterior marginal (PM) for two human hearts. Abnormal structure with excessive layer of fibrous tissues surrounding the core was found in AM of heart #1 and AB, AM of heart #2. Bar=1000 μm.

4. Discussion

In this study, the elastic and failure properties of aged human and ovine mitral chordae tendineae were quantified and compared. The five chordal groups had similar elastic and failure properties. The first study on human chordae mechanics was performed by Lim and Boughner (Lim and Boughner, 1975) in 1975 where they characterized the mechanical properties of human chordae of different sizes. For chordae with a cross-sectional area ranging from 0.1 to 0.8 mm², the mean secant modulus at 20 MPa was between 67.2 and 120.0 MPa. For a similar size range, the mean secant modulus at 10 MPa measured in this study, was 148±71.84 MPa. The ultimate strain for the human chordae in this study was 0.22±0.12 which falls within the range of that reported by Lim and Boughner (Lim and Boughner, 1975) (0.21±0.005), and the ultimate stress values were also comparable, 35.79±22.16 MPa in this study versus 30.87±19.20 MPa in (Lim and Boughner, 1975). Another study by Clark and Louis (Clark, 1973) found that the post-transition moduli and the elongation at transition point of all fresh human mitral chordae to be 8.83±4.67 MPa and 0.12±0.05, respectively. Overall, our chordae responses were relatively much stiffer (38.19±27.17 MPa at 1 MPa) and less extensible (0.042±0.03 elongation at transition point). Differences in stiffness could be due to age, as tissues in older patients are less extensible, weaker and stiffer as collagen content and characteristics (e.g., fibril diameter and crimp pattern) change with age (Natali et al., 2008). Note that the samples collected by Lim and Boughner were from humans aged between 5 and 66 years old, whereas our data were collected from humans aged 76.29±10.35 years old. The discrepancy between our data and those presented in the literature could also be due to differing testing methods. In studies (Clark, 1973; Lim and Boughner, 1975), the chordae deformation was measured using contacting strain gauges or approximated as the change in distance between the two grips of the uniaxial testing device (cross-head displacement). In this study, a marker tracking technique with a CCD camera was utilized to compute the Green strain at the middle region of the sample. Ritchie et al. Ritchie et al., (2006) have shown that the difference in the chord strain measurement using the marker tracking method (using high speed cameras) versus the cross-head displacement of the uniaxial system can be as high as 46.2%.

When comparing the mechanical properties of different chord types – by chordal insertion locations or leaflet types – no difference in elastic and failure mechanics between chordal types of either human or ovine was observed in this study. Most studies that compared chordae mechanics of different chordal types utilized porcine models (Kunzelman and Cochran, 1990; Liao and Vesely, 2003; Sedransk et al., 2002; Liao and Vesely, 2007). These studies found that thicker chordae were more extensible than thinner chordae (Liao and Vesely, 2003). Thus, marginal chordae were stiffer (Kunzelman and Cochran, 1990) with lower ultimate strain (Sedransk et al., 2002) than basal chordae. Although not statistically significant, our results showed a similar trend that thinner marginal chordae were stiffer and weaker than basal chordae.

Comparing between human and ovine models, the aged human chordae were much stiffer and less extensible. Such difference may be explained by the microstructural difference between these chordal groups. As shown in Fig. 7, the collagen fibers found in ovine basal chordae exhibited the crimp characteristic typical of collagen. Liao and Vesely (Liao and Vesely, 2003) found that the collagen fibril crimp characteristic determines overall chordae extensibility, and that more extensible chordae exhibited highly crimped collagen fibrils with smaller crimp period. This property is important for chordal functionality in the physiological state. The collagen fiber crimp and elastin fiber network allows for chordae elongation under low load to facilitate valve closure (Lim and Boughner, 1975; Shi and Vesely, 2004). While healthy and young human chordae exhibited wavy and crimp collagen structures (Lim and Boughner, 1975), this crimp pattern was almost diminished even at a relaxed, unloaded state, in aged human chords, which resulted in a substantial decrease in extensibility. Interestingly, the tangent modulus and UTS of the ovine chords was similar to that of human. This suggests that the mechanical response of fully-loaded chordae in aged human and 1–2 years old ovine is similar, and resembles the mechanical response of collagen fibers with an elastic modulus of 400 MPa (Freed and Doehring, 2005).

Several studies have reported chordae tendineae from degenerative mitral valves exhibited an increase in collagen and GAGs (Grande-Allen et al., 2003; Baker et al., 1988; Lis et al., 1987), accumulation of thickened layers of fibrosis tissues (Barber et al., 2001; Tamura et al., 1995), fragmentation of elastic fibers (Tamura et al., 1995; Fornes et al., 1999), and disruption of collagen core (Icardo et al., 2013), most of which associated with chordal rupture (Hickey et al., 1985; Jeresaty et al., 1985; McKay and Yacoub, 1973). Histological analyses of aged human chords in this study revealed some characteristics of degenerative changes: accumulation of thickened spongiosa layers surrounding the central core and these spongiosa layers were loosely detached from the dense core. Although the samples in this study were obtained from human with no valvular disease, according to Table 1, several patients had heart related diseases and cardiac arrest as a cause of death, in particular, Patient 1 had abdominal aortic aneurysm and cardiac arrest as a cause of death, and Patient 2 had no record of valvular disease. It was reported that histopathologic alternations in floppy myxomatous mitral valve chords were observed consistently from all attachment sites (Baker et al., 1988), however, in our study, we did not observe a consistency in microstructural changes among the chords within a valve. The mechanical properties were also not significantly different among the chordal groups. Thus, it appears that these layers of fibrous tissues did not support the central core nor contribute to the overall strength of the chord. Barber et al. Barber et al., (2001) compared the mechanical properties of normal and myxomatous chords, and they found that the fibrous overgrowth in the thickened myxomatous chords reduced the chordal strength by 4-fold, suggesting these tissues played little or no role in reinforcing the chordae or providing additional strength. Therefore, morphological changes observed in this study may be due to natural aging process. Further work is warranted to determine the relationship between degenerative changes and aging.

The hyperelastic Ogden model can capture the nonlinear, isotropic stress–strain behavior of human chordae tendineae properly. The data collected in this study could facilitate the development of more accurate computational models of the mitral valve. Several research groups have developed finite element models to study MV mechanics, particularly the effect of chordal distribution on leaflet stress, but such studies are limited by the use of simplified or animal mitral chordal properties (Rim et al., 2014; Wang and Sun, 2013; Stevanella et al., 2011; Prot et al., 2009; Votta et al., 2008; Kunzelman et al., 2007; Reimink et al., 1996). In this study, we showed that aged human chordae are stiffer than those of porcine models. Thus, these results suggest that the aged human mitral valve should be modeled using the aged human property data to obtain accurate simulation results, because the chordae, as well as other components of the mitral valve, may have undergone progressive remodeling in structure and function due to aging. Accurate computational models of the mitral apparatus will be powerful tools for evaluating mitral valve repair techniques to restore normal function.

5. Limitations

There are several limitations of this study. First, because the length of some testing samples were short, i.e., less than 15 mm long, rupture occurred outside of the optical markers during uniaxial failure testing. Therefore, sample size for failure properties were small. Second, although the cadaver hearts obtained for this study were considered to be healthy with no valvular diseases, patient medical records indicated that several patients had systemic HTN, abdominal aortic aneurysm, myocardial infarction, or congestive heart failure. There were subtle differences in the chord mechanics among these patients. Thus, a small sample size resulted in large deviation in the mean mechanical parameters. It is recommended that when performing a patient-specific mitral valve simulation the chordal material properties to be used should be matched with patient age and disease condition.

6. Conclusions

In this study, the mechanical and microstructural properties of aged human and ovine mitral chordae tendinae were characterized. Through the experimental testing, we obtained following key results and observations:

• Aged human and ovine mitral chords of different types exhibited similar elastic and failure properties.

• Among the human samples, the thinner marginal chordae were stiffer than the basal chordae, and the strut chordae were the weakest.

• The anterior chordae were slightly thicker than the posterior chordae, and were stiffer than the posterior chordae at low load, yet weaker and more compliant at high load.

• An increase in chordal thickness was due to the excess fibrous tissue layers surrounding the central core. However, these excess tissues but did not contribute to the overall strength of the chords.

• The human chordae of all types were significantly stiffer than the corresponding ovine chordae.

• The human chordae exhibited lower failure strains but similar failure stresses compared to the ovine chordae.

• Histopathological observations in this study indicated that the fibrous structure of the age human mitral chordae had been altered, i.e. diminished crimp characteristic of collagen fibers and excess fibrous tissue deposition surrounding the central core.

Collagen uncrimping may have contributed to the much greater stiffness of the aged human chords compared to the ovine chords tested in this study, as well as the porcine chord data presented in the literature. The chordae mechanical behavior was modeled with the Ogden strain energy function to facilitate finite element implementation. The presented data can be used in patient-specific computational models of the mitral valve to study the effects of chordae mechanics on the overall valvular structure and stress distribution, which may improve understanding of mitral valve function in the aged patient population, and may provide new insights for surgical repair techniques.