Abstract
In vivo studies allow us to investigate biological processes at the level of the organism. But not all aspects of in vivo systems are amenable to direct experimental measurements. In order to make the most of such data we therefore require statistical tools that allow us to obtain reliable estimates for e.g. kinetic in vivo parameters. Here we show how we can use approximate Bayesian computation approaches in order to analyse leukocyte migration in zebrafish embryos in response to injuries. We track individual leukocytes using live imaging following surgical injury to the embryos’ tail-fins. The signalling gradient that leukocytes follow towards the site of the injury cannot be directly measured but we can estimate its shape and how it changes with time from the directly observed patterns of leukocyte migration. By coupling simple models of immune signalling and leukocyte migration with the unknown gradient shape into a single statistical framework we can gain detailed insights into the tissue-wide processes that are involved in the innate immune response to wound injury. In particular we find conclusive evidence for a temporally and spatially changing signalling gradient that modulates the changing activity of the leukocyte population in the embryos. We conclude with a robustness analysis which highlights the most important factors determining the leukocyte dynamics. Our approach relies only on the ability to simulate numerically the process under investigation and is therefore also applicable in other in vivo contexts and studies.
1. Introduction
Many, if not most, open problems in biomedical research involve questions related to whole organism biology. Despite the wealth of insights provided by molecular and cell biology, genetics and genomics we still do not understand most of the tissue-level, physiological and organism-level processes underlying e.g. development, health and disease.
Mathematical models of biological systems are abstractions of much more complicated processes.1 Such models allow us to summarise our state of knowledge about biological systems and processes in a concise manner, to explore likely dynamics of biological systems, and to elucidate experimentally inaccessible aspects of the molecular machinery underlying complex phenotypes and the function of biological organisms more generally. In mathematical studies abstraction is not so much seen as a necessity but as a virtue, which enables us to focus on the principal underlying mechanisms. However, even most experimental analyses are performed under conditions that are very different from those encountered in natural systems. In vivo analyses are often performed under as close to realistic conditions as possible, but even here many interactions, e.g. with the environment, are controlled or suppressed. As biological research moves closer to clinical applications it becomes necessary to include more of these details in the analysis of biological systems. In principle it is straightforward to add detail to mathematical models, too. But in practice it then becomes more diffcult to calibrate (or “fit”) these more detailed models against complex and potentially highly resolved data.2
Here we introduce a statistical methodology that is able to estimate parameters of mathematical models from spatio-temporally resolved in vivo data. We employ a Bayesian framework, which also allows us to rank an arbitrary number of alternative models in light of data.2,3 Our approach does not require evaluation of the likelihood which is forgone in favour of a simulation-based approximate Bayesian computation procedure.4 Here simulated data are compared with observed data, and this way parameter (and model) posterior distributions can be constructed even for cases where conventional statistical approaches are currently unfeasible. We illustrate our approach in the context of leukocyte migration inside zebrafish embryos.5–7 These are optically transparent and allow us to track GFP marked leukocytes under different conditions and in response to different stimuli. The development of zpu.1:EGFP zebrafish enables this analysis of macrophage and neutrophil migration from life imaging data and reveals novel insights from leukocyte migration patterns.5,6 It was also shown that a hydrogen peroxide gradient is required for efficient recruitment of leukocytes to a wound site.8 By coupling the spatio-temporal dynamics with intra-cellular signal transduction models, true multi-scale analysis is coming within reach.9,10
Over the past decade several approaches for analysing and modelling leukocyte migration have been published.11 As early as 1980 Alt used mathematical descriptions of a biased random walk to model cell chemotaxis.12 In 1987 Tranquillo and Lauffenburger13,14 proposed a stochastic model for leukocyte chemotaxis, which is based on receptor binding fluctuations. They modelled the cell polarity based on noise in the cellular signal response mechanisms. Since then more experimental data about chemotaxis have become available, and Onsum and Rao15 constructed a mathematical model of neutrophil gradient sensing, which is based on the underlying biochemical mechanism. Using partial differential equations they showed how intracellular gradients can be generated from an external stimuli. This very complex model does not, however, describe the actual migration process of the neutrophils. A model that describes changes in the cellular morphology was proposed in the same year by Andrew and Insall.16 Recently Haastert described the movement of cells as a correlated random walk, also called persistent random walk, by modelling the extension of pseudopodia.17 These modelling approaches capture different levels of the response of leukocytes to external stimuli.
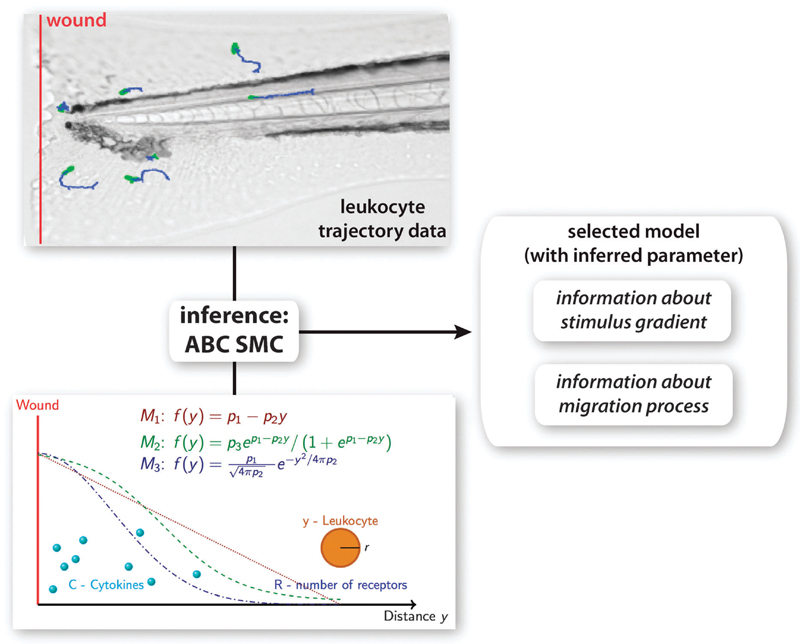
Here, we combine modelling of leukocyte migration in a living organism in response to wounding with intercellular signalling processes. We construct a model that describes the leukocyte dynamics. Our dynamical model depends on a stimulus gradient shape, which is unknown. We propose 3 different gradient shapes (M1–M3) and compare the combined model output to the leukocyte trajectories extracted from life imaging data (Fig. 1). We use approximate Bayesian computation (ABC) for model selection to infer the stimulus gradient shape. ABC allows us additionally to gain further details about the leukocyte dynamics during the migration process.
Fig. 1.
Overview of methodology. Leukocyte trajectory data were extracted from time lapse microscopy experiments and used for model selection and parameter inference using the ABC SMC framework. A model for leukocyte migration was constructed, which involves the production of a cytokine gradient after wounding (red line), the sensing of the gradient using receptor binding kinetics and the translation of the signal into movement of the leukocyte. 3 different models for the stimulus gradients (M1–M3) were proposed. From the model that explains the experimental data best information about the migration mechanism can be obtained as well as information about the stimulus gradient.
Here we outline a generic statistical framework that allows us to discriminate between different competing mechanistic models, estimate model parameters, and understand biological processes at a physiological/whole organism level. We illustrate the insights that can be obtained in this framework in the context of leukocyte migration patterns following injury to zebrafish embryos, and conclude with a discussion of how informative such data are about mechanistic models.
2. Results and discussion
2.1. Modelling leukocyte migration
The investigated biological system is illustrated in Fig. 1. In case of an injury to the zebrafish embryo a stimulus, e.g. cytokines, is released from the injured tissue and/or surrounding tissue, which leads to the establishment of a stimulus gradient. In our experiments we introduce the wound by tail transection so that the wound is orthogonal to the blood vessels of the zebrafish. Because of this simple wound geometry we can assume that the generated distribution of the stimulus is uniform in the direction parallel to the wound (here x direction), but changes with the distance to the wound, i.e. the direction orthogonal to the wound (here y direction). Now the concentration of the stimulus is a (unknown) function of the distance to the injury f(y,t), where t is the time passed after wounding. A leukocyte is here described by its centre at position y and its radius r (more detailed descriptions are possible, of course). Leukocytes move randomly until they are stimulated, e.g. when they sense a cytokine signal. This local external gradient will be translated into an internal cellular signal gradient of signalling molecules that activate F-actin polymerisation in areas with high gradient concentrations, and myosin aggregation in areas with low gradient concentrations, as well as microtubule assembly and disassembly, which lead to a movement of the leukocyte in the direction of the highest stimulus. Thus the direction of leukocyte movement depends on the slope of its internally generated gradient. We describe the behaviour of leukocytes as a sequence of steps, where each step includes: (i) sensing of the gradient by randomly protrusion of pseudopodia,17 (ii) collapsing pseudopodia in low gradient concentrations while keeping them in high gradient concentrations, and finally (iii) moving towards the high concentration. This discretisation of a in principle continuous process is motivated by the type of data we use for the analysis. The data contain leukocyte trajectories with values every 15 seconds. We computed the average distance between two consecutive steps (mean and variance of the step size) from the data and found that the overall step size is independent of the position of the leukocyte. Sampling from a normal distribution with the measured mean and variance allows us to simulate the step size in our model. Now the main part is to describe the direction of the cell, which combined with the step size will result in the absolute position of the cell. The direction of the cell depends on the directional bias and persistence. We do so by modelling the cell movement as a sequence of angles αt between consecutive steps t and t + 1, which is a weighted mean of two processes, persistence and bias:
| (1) |
with the first term describing the directional persistence of the leukocyte (i.e. its tendency to keep moving in the same direction) and the second term describing the directional bias of the leukocyte towards the direction of the highest stimulus, where wp and wb are the weights and Nc is the circular normal distribution with its mean and variance. Note that by using the weights wp and wb our model captures not only different levels of a biased persistent random walk, but also the more simple processes of only persistence random walk (if wb = 0) and only biased random walk (if wp = 0). Both directional persistence and bias were previously used to model leukocyte migration.11,12,17–20 However, in our model the level of the persistence and of the bias is not constant for a given cell, but instead depends on the gradient concentration the cell is sensing. The strength of the persistence and of the bias is here expressed as the variance of the two normal distributions in eqn (1). Since this model is mechanistic and we do not have much information about the biological parameters that regulate these dependencies, we aim to express our model with normalised parameters in as concise a form as possible. The variance of the two processes can be any positive number. To normalise it we introduce the concentration parameters ρp and ρb:
| (2) |
with ρ ∈ (0,1), to compute the variance for directional persistence and bias, respectively. If ρp and ρb are close to 1 a cell’s migratory behaviour will exhibit high persistence and high bias. We assume that both processes, directional persistence and bias, depend to some level on the external gradient such that we observe lower variance for high levels of persistence and bias. However, the (effective) gradient concentration is described by an unknown analytical function f(y). We prefer to use the term “effective gradient” as the real gradient will be more complex and presumably depend on a multitude of variables, as well as being more irregular/noisy than the forms considered here. This effective gradient subsumes these complications and describes the input that is sensed by the cell and translated into an internal gradient. The sensing happens via receptors responsive to the external stimuli, e.g. cytokine receptors, which are assumed to be uniformly distributed on the surface of the cell, i.e. Rfront ≈ Rrear ≈ R. Because of the wound geometry we assume that the leukocyte dynamics are dependent on the distance to the injury (y-direction) but not on the direction parallel to the injury (x-direction), the model of gradient sensing depends only on the y-direction. The leukocyte movement however is described in the x and y direction. Each binding event of a cytokine will lead to the activation of a signalling cascade to generate the internal gradient, which is here assumed to be linear. Therefore the internal gradient depends on ligand–receptor binding kinetics, i.e. on the amount of ligand–receptor complexes C:
| (3) |
with the number of receptors R, the receptor binding constant Kd and the ligand concentration f(y,t).
We assume that the level of persistence and bias depends to some level on the slope of the gradient regulated by the parameters dp and db. To normalise this dependency we divide the gradient slope C(f(y − r,t)) − C(f(y + r,t)) by the largest existing slope ΔCmax:
| (4) |
where r is the radius of the cell to describe front and rear. Now the parameters ρp and ρb can be expressed as:
| (5) |
| (6) |
where pmax and bmax describe the maximum possible persistence and bias, respectively, and r is the radius of a cell. To understand the relationship between the effective gradient concentration and the resulting variance as a function of y we plot eqn (3)–(6) for an example gradient f(y,t) (Fig. 2).
Fig. 2.
Dependencies between strength of persistence on the gradient shape. Shown is an example gradient shape f(y,t) and the resulting sensed internal gradient C(f), the concentration difference between front and back of a leukocyte ΔC, the concentration parameter ρ and the variance of the circular normal distribution according to eqn (2)–(6). The parameters R, Kd and pmax are fixed as an example. The parameter dp is ranged from 0 to 1 represented from dark to light.
2.2. Parameterisation of the leukocyte migration model
Here we discuss how the mathematical model can be calibrated against observed trajectories of leukocyte migration from life imaging data. As mentioned above, the leukocyte migration model includes an unknown function, f(y), which describes the spatial (and, implicitly, temporal) distribution of the stimulus with respect to the site of the injury. Several alternative phenomenological models have been proposed15,21 and three different distributions are considered here (Fig. 1),
| (7) |
| (8) |
| (9) |
where y is always the distance to the injury, p1, p2 and p3 are unknown parameters that define the effective gradient shape, and which here need to be inferred from the data. The models describe a linear gradient (M1), a sigmoidal gradient (M2) and a gradient generated by a standard diffusion process (M3).
In order to estimate the gradient shape that explains the leukocyte dynamics best, we apply an approximate Bayesian computation (ABC) approach as the likelihood for random-walk processes in unknown gradients is too cumbersome to evaluate exactly. ABC methods have been developed for just this case but where simulation of the (plausible) data generating process is still possible.
Typically observed, x, and simulated data, where θ is a parameter drawn from its appropriate prior distribution, π(θ), are compared via some distance measure, d(x,x′). Only when where ε is the desired tolerance level, is θ considered as a valid parameter drawn from the (approximate) posterior distribution, Pr(θ|x). When the data are detailed or have a complicated structure, then the probability of generating a simulated data set that resembles the observed data closely becomes vanishingly small if θ is drawn from the prior. In this case it is, with a number of caveats, possible to make some progress by only comparing summary statistics of real and simulated data, S(x) and respectively; especially when S(·) is a sufficient statistic of the data, this compression is loss-less and considerable speed-gains are obtained while still retaining a valid approximation to the posterior (subject to the tolerance level ε). Even if S(·) is not a priori suffcient it is possible to perform parameter estimation and a range of methods have been proposed that allow the construction of (approximately) suffcient statistics by pooling information captured by different summary statistics.22–24
ABC approaches can also be used for model selection, where we seek to evaluate Pr(Mi|x), i.e. the posterior distribution of a model (chosen from a set of candidate models, Here suffciency across models is also a problem, but here, too, methods to construct suffcient sets of statistics exist. As it turns out, the construction of suffcient statistics is straightforward for random-walk like processes using recent information on theoretical developments,24 especially if we care only about the directionality of the trajectories as a function of the gradient as is the case here. For each scenario we therefore compute the distribution of the straightness indices Di for the extracted trajectories,
| (10) |
where li is the total length of the trajectory and
| (11) |
is the Euclidian distance between the start and end points of each trajectory i. Because the straightness index is dependent on the length li of the trajectory we split all trajectories so that the resulting trajectories have all the same length l = 30 and eqn (10) can be written as
| (12) |
The precise value of l used for the analysis does not seem to matter but for l = 30 we are able to use the vast majority of trajectories.
In its simple rejection scheme ABC is too slow to cope with real-world problems and several computational improvements have been suggested, including regression–adaptation, Markov chain Monte Carlo (MCMC) and sequential Monte Carlo (SMC) approaches. We adopt the latter approach, in particular the ABC SMC procedure of Toni and Stumpf3,4 as implemented in the ABC-SysBio package25 which was adapted to allow for comparison between summary statistics for random walks and model simulation in R. This approach samples parameter combinations (particles) from a non-informative prior distribution, simulates the model and compares the simulation results with the experimental data using a distance function. For classical dynamical systems the distance function is usually the Euclidean distance between the simulated trajectories and the experimental measurements. However, as we deal with spatio-temporal data that have a considerable random component, the Euclidean distance between single trajectories does not contain suffcient information about whether different trajectories were generated from the same process. To distinguish between different forms of random walk behaviour we compare the distributions, , of Di. These distributions are generated by simulating 200 trajectories for each sampled particle and we process these in the same way as the experimental data set. Now we can compare the distribution using the Kolmogorov–Smirnov distance between their respective histograms. The resulting distance function is
| (13) |
where and * are the distributions of D for the experimental data and the simulated data, respectively, S is the number of spatial groups (here 3) and T is the number of temporal groups, and K is the Kolmogorov–Smirnov distance for pairs of empirical distribution functions. Details of the implementation are given in Materials and Methods.
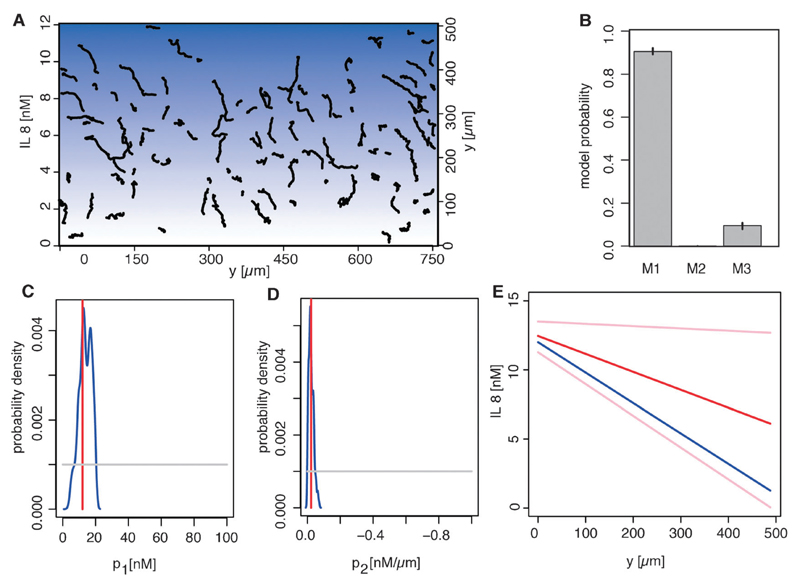
To validate this approach under controlled conditions we first applied it to leukocyte trajectory data extracted from migration patterns in a microfluidic device with a known linear interleukin 8 (IL 8) gradient. Fig. 3A shows the extracted trajectories. Our method identifies the experimentally applied linear gradient (model 1, eqn (7), has 89% of the posterior probability associated) correctly (Fig. 3B). The linear gradient has two parameters (p1 and p2). The estimates for these parameters are shown in Fig. 3C and D. The experimental parameter values are covered by the estimated posterior distribution and the resulting predicted gradient shape (Fig. 3E) is in good agreement with the actual experimental gradient. These results serve as a proof of principle for our model, our statistical approach and demonstrate the ability to extract hidden information from rather simple cell migration data. Purely in-silico analyses, where the true model is known by definition, result in similar credible intervals for the gradient parameters (data not shown).
Fig. 3.
Validation of the migration model and ABC approach. Trajectories of human neutrophils (black lines) in an interleukin 8 (IL8) gradient were extracted (A). The blue background visualises the IL8 gradient (from white to dark blue for 0 nM to 12 nM). All cells have a tendency to migrate towards high IL8 concentration. We used ABC SMC to obtain the posterior model probabilities (B). The prior distribution was uniform among all 3 gradient models. Shown are the mean probabilities over 5 runs, error bars are the lowest and highest probability of the 5 runs. Model 1 in the last population (population 22) has a probability of 0.89 to fit the experimental data best compared to the remaining two models (B). The estimates of the gradient parameters (red lines) (shift p1 and slope p2 of a line) are shown in the prior range (C and D). The prior distribution (grey lines) was for both parameters uniform. The experimentally measured parameters (blue lines) are in the posterior parameter range. The inferred gradient shape (red line) with 95 percentiles (pink lines) (interleukin concentration as a function of the distance from the source) and the experimentally measured gradient shape (blue line) are shown (E).
2.3. Spatio-temporal analysis of leukocyte migration
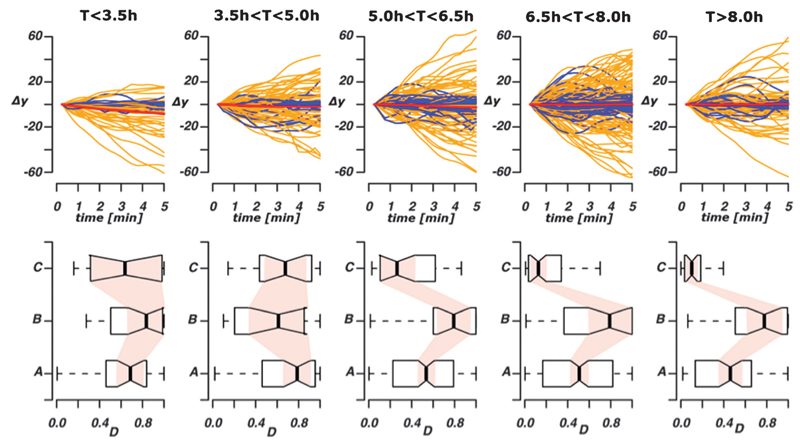
We tracked zpu.1:EGFP positive cells in living zebrafish embryos to study the spatio-temporal dynamics of leukocytes in response to wounding. We show that the dynamics of leukocyte movement is dependent upon the position of the cell in relation to the site of inflammation and on the time that has elapsed since the injury. Heterogeneity in spatio-temporal dependencies of leukocyte migratory behaviour is illustrated in Fig. 4. Each trajectory is presented as a line with the distance movement towards (Δy < 0) or away from (Δy > 0) the wound plotted on the Y-axis and time on the X-axis (Fig. 4, top row). Cells are migrating towards and away from the wound at all time points, which reflects the presence of retrograde chemotactic behaviour.6 The straightness index (see above) is indicated by the colour of the line: trajectories with a low straightness index (D < 0.5) are shown in blue and those that have high directionality (D > 0.5) in orange. At earlier time points post wounding (T < 3.5 hpw) more cells are traveling towards the wound (i.e. Δy < 0) than at later time points. Displaying each trajectory in this graphical form allows us to appreciate the diversity rather than merely the (not very informative) average behaviour of the immune cell population: while the average population behaviour may always suggest no net movement in the direction perpendicular to the wound (as indicated by the red lines in the top row), the individual migratory behaviour at the single cell level becomes most diverse between 3.5–6.5 hpw. We also plot the distributions of the straightness index of the trajectories at different times, divided into 3 classes according to their distance from the wound (Fig. 4, bottom row). At later time points (>5.0 hpw), the straightness index, D, is large for trajectories at intermediate distances and significantly higher than for leukocytes close or far away from the wound.
Fig. 4.
Spatio-temporal heterogeneity in chemotactic leukocyte migration behaviour. The top row shows the relative displacement of leukocytes following the start of the tracking (time measured in hpw); each trajectory was considered in non-overlapping 5 min intervals in order to capture any temporal effects acting over longer time scales. Blue trajectories have a straightness index directionality coefficient D < 0.5, orange trajectories have D > 0.5. The red line indicates the average behaviour across all trajectories shown in the panel. Values Δy > 0 indicates movement towards the wound, Δy > 0 indicates movement away from the wound. In the bottom row we show the distributions of the straightness index directionality coefficients divided into three different classes according to the distance from the wound ((A) y < 250 µm, (B) 250 µm < y < 500 µm, (C) y < 500 µm) and grouped according to time post-wounding (as top row).
Using different divisions of time results in qualitatively identical behaviour. The chosen partition, however, has the advantage of capturing both the biological phenomena of a dynamic gradient and resulting in good statistical power (similar numbers of trajectories) for the mechanistic analysis detailed next.
2.4. Spatio-temporal characteristics of stimulus gradients
In light of the spatio-temporal behaviour of the leukocytes in response to wounding we next infer the stimulus gradient, for which in general no direct measurements exist. Linking these extracted trajectories with our leukocyte migration model using the approach described above we gather not only information about the spatio-temporal dynamics of the stimulus gradient but also gain more detailed mechanistic insights into the leukocytes dynamics. The same models for the gradient shape were assumed and tested. The main difference between this data set and the microfluidic data set used in the validation of our approach is that the stimulus gradient is now a function of both the distance to the wound and of the time that has elapsed since the injury, f(y,t). Therefore the problem becomes far more complex due to the high dimensional parameter spaces for each of the three models. When we divide time into five intervals each model has now five times as many parameters which describe the gradient shape (resulting in 17 parameters for models 1 and 3, 22 parameters for model 2). The biophysical reaction parameters that describe the molecular processes inside leukocytes can be assumed to be constant over the time spans considered here.14
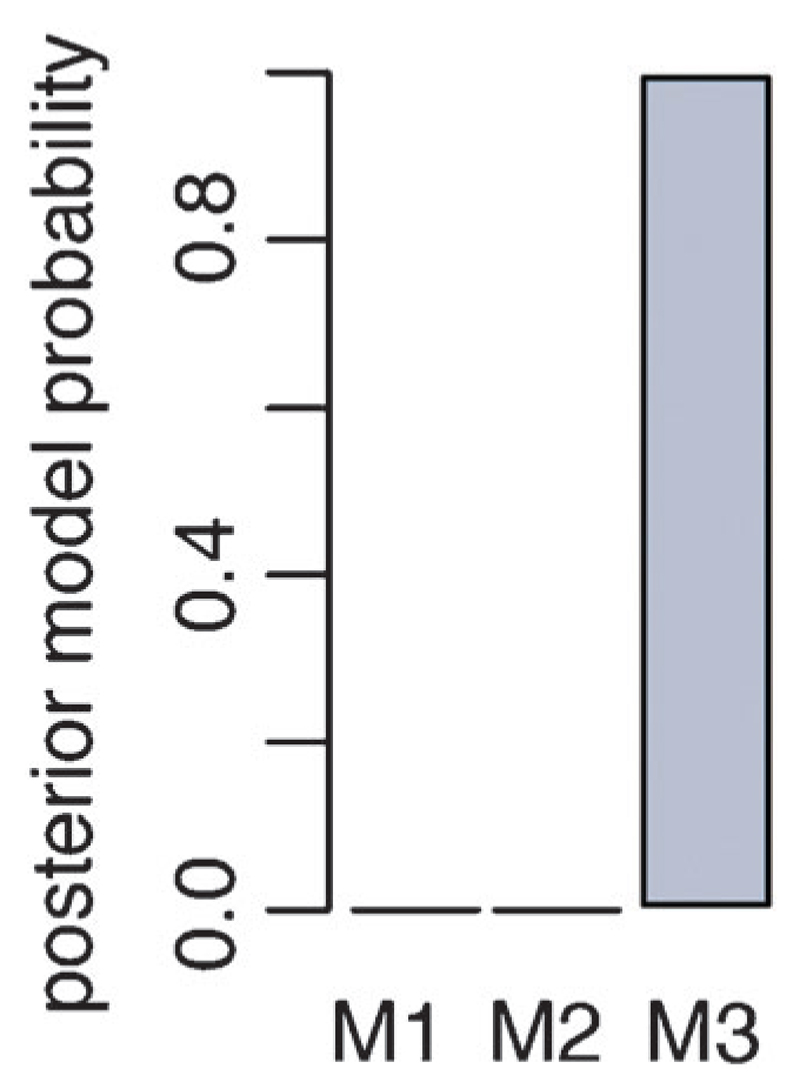
Using ABC SMC with a uniform prior model distribution we find that model 3, which uses a diffusion-process gradient, represents the available data sets best (Fig. 5). The posterior parameter distributions for model 3 reveal more details about the in vivo dynamics of leukocyte migration (Fig. 6A). Parameters db and dp are both higher than 0.5, which indicates that both bias and persistence are dependent on the gradient and therefore spatial characteristics. Parameters bmax and pmax describe the maximum level of bias and persistence, respectively. The posterior distribution shows that the level of persistence is higher than the level of the bias. This is also seen from parameter w (mean: 0.79), which is the relative weighting between bias and persistence. This parameter is clearly shifted towards 1, i.e. persistence is favoured over the bias. Parameters Kd and R are not inferable. These parameters describe the binding of the stimulus molecules to the surface receptors, i.e. the stimulus sensing. We can conclude that the trajectory data of the leukocytes do not carry information about these molecular details.
Fig. 5.
Posterior model probability distribution. Using a uniform prior distribution among the 3 models in the ABC SMC approach model 3 (M3) has a probability of 1 to represent the data best. Model 3 represents a diffusion type gradient that changes over time.
Fig. 6.
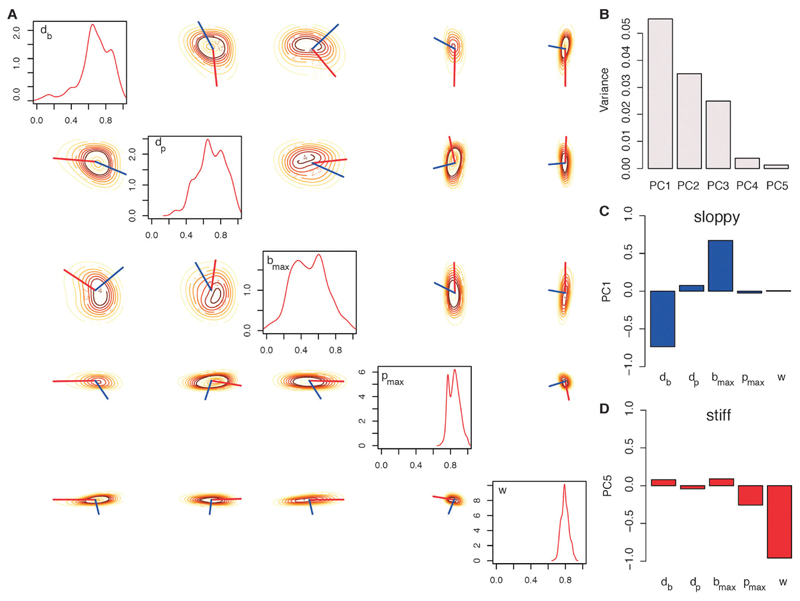
Robustness analysis. The marginalized density estimates for posterior parameter distributions related to chemotaxis are plotted on the diagonal in the range of the uniform prior distributions (A). The pairwise posterior density estimates are plotted on the off-diagonal. The red lines show the projection of the first principal component (PC), i.e. the robust direction. The “stiff” direction is displayed by the blue line and represents the vector of the fifth principal component (A). The variance of the principal components is shown in (B). PCA was performed on the correlation matrix of the posterior parameter distribution. The corresponding vectors of the first (C) and fifth (D) PCs are visualized by its projections onto the parameters (red bar plots for “sloppy” directions and blue bar plots for “stiff” directions are shown).
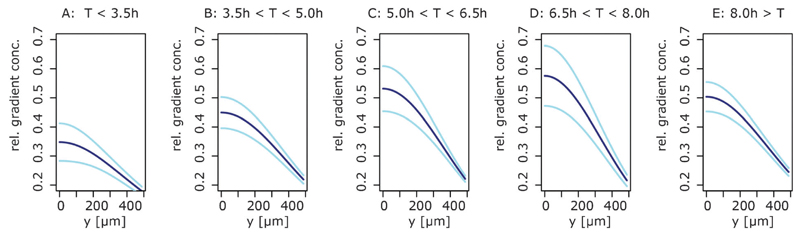
Finally, we can use the inferred 10 gradient specific parameters to investigate the gradient dynamics over time. Fig. 7 shows the inferred gradient shapes with their 95 percentiles for 5 time intervals after wounding. For all time points, we observe the classical diffusion shape gradient.26 Interestingly, the process that generates the stimulus gradient cannot result from the analytical form of the heat equation, because the concentration at the source (distance = 0 μm, wound) increases until around 7 hours after wounding. This shows an active production of the stimulus at the site of the injury. After around 7 hours this production decreases, which leads to a decreasing concentration at the wound; this shapes the temporal development of the effective stimulus gradient.
Fig. 7.
Spatio-temporal characteristics of chemokine gradients. Shown are the estimated chemokine gradients for 5 time intervals (A–E) using the mean estimate of the gradient parameters (dark blue lines) and the 5 and 95 percentiles (light blue lines). The gradient concentrations are plotted in relative units.
2.5. Analysis of leukocyte migration model
The models for leukocyte migration (eqn (1)–(3)) allow us to gain information about the stimulus gradient. Next we can use the same model and the corresponding parameter estimates to learn more about the characteristics of the leukocyte movement. Because the parameters, Kd and R, show flat posterior distributions, they are not inferable from the present data and we can exclude them from the following analysis. The posterior distribution including only the remaining 5 parameters (db, dp, bmax, pmax and w) was used to determine the relative dependencies of the migratory dynamics on the parameters. This in turn is related to how much information the data carry about the parameters and allows us to determine “stiff” and “sloppy” directions.27 We calculated the correlation matrix of the posterior distribution and used principal component analysis (PCA) to determine the directions with highest and lowest variance of the overall posterior.28,29 Fig. 6B shows the 5 principal components (PC) with their corresponding variances (upper row, left). PC1 has the highest variance, therefore the corresponding vector represents the “sloppiest” parameter combination (or the combination of parameters least constrained by the available data). The projections of PC1 onto the “raw” parameter vectors are shown in Fig. 6C. The two parameters db and bmax have the highest projection onto the first principal component, i.e. they are “sloppy” parameters and have thus comparatively minor influence over the leukocyte migration dynamics observed here. These two parameters determine the bias of leukocyte migration towards higher gradient concentrations. This suggests that the movement of leukocytes is not primarily regulated by directional bias. In contrast, the level of persistence is the dominating characteristic of the leukocyte movement. This results from PC5 (Fig. 6D), which represent the “stiffest” parameter combination, i.e. the combination of parameters for which the data exhibit the highest information content (and hence the collection of parameters that have the highest impact on system dynamics). The largest projections onto these two principal components are by w and pmax. The parameter w shows, as mentioned above, that persistence appears to be more pronounced than bias, while the parameter pmax quantifies the level of persistence and also suggests overall highly persistent leukocyte movement. Note that the level of persistence also depends on the slope of the local gradient (mean dp: 0.67). The importance of bias and persistence can also be seen in Fig. 6A. Here we show the pairwise posterior probability densities of the parameters. The red and blue lines indicate the “sloppy” and “stiff” directions, respectively. The “stiff” direction is almost parallel to w (representing the persistence), whereas the “sloppy” direction is almost parallel to bmax (representing the bias). This indicates that they affect the dynamics independently and that persistence exerts greater influence on the trajectories than bias.
2.6. Discussion
We used a flexible and powerful statistical framework—centred on ABC approaches—in order to calibrate spatio-temporal models of leukocyte migration during acute injury to live imaging data. We tested our approach on the trajectories of leukocytes migrating in an IL 8 gradient with a known shape. This test lent support to our approach and the assumed (and highly simplified) model of leukocyte migration and allowed us to tune our algorithmic setup for in vivo applications. Different models for the stimulus gradient emanating from the wound injury, in combination with experimental leukocyte trajectory data extracted from living zebrafish, enabled us to gain information about signalling processes on a tissue-wide scale: we were able to infer the stimulus gradient; experimentally this is nigh on impossible to measure experimentally at the same time as observing the processes inside the (optically transparent) fish embryos.8 In general there are a host of physiological problems where important characteristics (such as here the signal gradient) cannot be observed or measured directly. In such cases calibration methods such as the one used here are required to model or account for the missing information.
The application of the method on trajectory data extracted from living zebrafish leukocytes during acute injury provided us with detailed insights into the dynamics of the stimulus gradient. In particular we found evidence that the stimulus changes as a function of space and time. Biologically this is plausible but again current experimental setups cannot routinely overcome the technical diffculties in measuring such gradients let alone their change (even if all chemokines etc. involved in immune signalling were known). Our results suggest that the stimulus is produced at the site of injury until 7 hours post wounding (hpw). Because the stimulus concentration increases at the wound until that time, the diffusion of the stimulus is weaker than its production. This can also be seen from the increasing slope of the gradient until 7 hpw. This increased slope leads to a stronger persistence in the leukocyte movement at intermediate distances and allows a more effcient leukocyte recruitment to the site of injury, i.e. more cells are at the site of the injury.
We then performed robustness analysis on the leukocyte migration model: this reveals the most important characteristics of the leukocyte dynamics, but also safeguards against potential over-interpretation of the dynamics in light of the inferred parameters. From this analysis we learn that the persistence of leukocytes exerts the largest influence on the dynamical behaviour in vivo. On the other hand the leukocyte dynamics are robust to changes in the level of bias towards the wound. This means that even with low bias a leukocyte would still manage to migrate towards the wound as long as the level of persistence is high enough and dependent on the local slope of the gradient. This shows that persistent movement seems to be an optimal search strategy for leukocytes during inflammation. A migration pattern with a strong bias and low persistence would still lead the cell directly and quickly towards its target, however, the area the cell covers would be very small. In contrast, a random walk with a high level of persistence results in searching a large area of the tissue. An additional small bias will be enough to lead the cell towards its target while still covering large space. This is important because macrophages as well as leukocytes are not only required directly at the wound site, but also in the surrounding tissue to search for possible invaders.
The overarching problem as to how stimulus gradients change with space and time is hard to solve without some further assumptions: here we have partitioned both space and time into discrete intervals. Without this it would be impossible to achieve the statistical power required for the inference of the unknown gradient/model parameters. It may in principle be possible to use an explicitly spatio-temporal parametric model of the gradient but this will require much more detailed knowledge as to what are the actual signalling molecules than is presently known. Finally, with more knowledge available about specific signalling molecules it will eventually become feasible to use more detailed and truly multi-scale descriptions of immune signalling processes including for example specific signalling pathways known to be involved in leukocyte migration. In that case our approach could be used to infer molecular parameters, e.g. expression levels of specific genes or protein binding constants, or to determine specific protein functions. Inferential techniques such as ABC allow us to model immune-response processes by conditioning mathematical models on available data. In the present context, for example, the central finding of a spatially and temporally varying stimulus gradient is probably not surprising or unexpected. Without this type of modelling, however, it would not be possible to determine the relative balance between e.g. persistence and bias in the migratory behaviour. Such mechanistic insights (or hypotheses) cannot be derived from verbal/qualitative models alone.
3. Materials and methods
3.1. Data acquisition and image processing
Two data sets were generated and analyzed. The first data set was used to validate the statistical approach and the simple model of leukocyte migration. This data set was provided by Daniel Irimia (Harvard Medical School, Boston) and was generated using a microfluidic device, as described in ref. 30. It contains trajectory data of human neutrophils in a linear interleukin 8 gradient. The second data set describes the migration of zpu.1:EGFP+ + cells in a living zebrafish embryo after tail transection. zpu.1:EGFP transgenic zebrafish embryos at 5 or 6-days-postfertilization (dpf) were anesthetized by immersion in system water with 4.2% tricaine (Sigma). Transection of the tail was performed with a sterile scalpel. zpu.1:EGFP transgenic embryos used in time lapse imaging experiments were wounded at time 0 and transferred to 0.8% low melt agarose (Flowgen, Lichfield, UK) for imaging after 2 hours. Images captured using a Zeiss Axiovert 200 inverted microscope controlled by C-Imaging Simple-PCI acquisition software. The time gap between two consecutive images was 15 seconds. The images analysed contained fluorescent zpu.1:EGFP+ + cells. All images were processed in R using the package EBImage.31 Cells were detected with an edge detection method using a manually set threshold for the light intensity. The cells were tracked over time using a surface-tracking algorithm that is not based on any prior knowledge about the dynamical behaviour, but on the shortest distance of cells from two consecutive images.
3.2. Statistical analysis of data sets
The ABC SMC algorithm is implemented in the Python package ABC-SysBio25 and was adapted to allow for comparison between summary statistics and model simulation in R. ABC SMC was applied to both data sets. The inference on the second data set was applied to all 5 temporal groups simultaneously, resulting in 5 different gradient shapes for the 5 time points, and one set of model parameters. The model parameters and their prior distributions are summarised in Table 1. The gradient specific parameters for the 3 models are: p1 = U[0,100], p2 = U[−1,0] (M1); p1 = U[−100,100], p2 = U[−1000,1000], p3 = U[0,100] (M2) and p1 = U[0,1000], p2 = U[0,1000] (M3), where U[a,b] is the uniform prior distribution with minimum a and maximum b.
Table 1.
Leukocyte migration model parameters
| Parameter | Prior | Posterior mean (1st data set) | Posterior mean (2nd data set) |
|---|---|---|---|
| db | U[0,1] | 0.42 [9.6 × 10−4, 0.84] | 0.60 [0.05, 0.92] |
| dp | U[0,1] | 0.41 [1.3 × 10−3, 0.92] | 0.67 [0.26, 0.93] |
| bmax | U[0,1] | 0.45 [1.6 × 10−2, 0.93] | 0.53 [0.03, 0.82] |
| pmax | U[0,1] | 0.92 [0.84, 0.97] | 0.86 [0.71, 0.95] |
| Kd | U[0,10 000] | 4831.9 [151.2, 9345.5] | 5329.03 [39.2, 8939.4] |
| R | U[0,10 000] | 5086.3 [53.1, 9408.4] | 5052.25 [226.3, 8612.5] |
| w | U[0,1] | 0.81 [0.58, 0.98] | 0.79 [0.69, 0.88] |
List of parameters specific to the leukocyte migration model with priors used in the Bayesian framework (U—uniform prior).
The first in vitro data set contains (122) trajectories that are spatially distributed in the microfluidic device (Fig. 3A). The IL 8 gradient is known and constant over the measurement time. The second in vivo live-imaging data set contains (341) trajectories extracted from 18 zebrafish embryos, which are spatially distributed in the zebrafish tail (Fig. 1). The data were captured from 2 to 10 hours after wounding. For this data set the gradient is unknown and cannot be assumed to be constant over time. Because of that we group the trajectories in 5 equally distributed intervals over time to account for the temporal resolution. To analyse the spatial effects we group the trajectories according to their distance from the gradient source and wound for the first and second data sets, respectively. We use again equally distributed intervals. Compared to the first data set we have now 5 temporal groups in data set 2 (instead of 1) and each of them contains 3 spatial groups.
The following analysis is the same for both data sets. Since we are interested in the characteristics of the cells that describe the dynamics in dependence to the distance from the gradient source/wound, we analyse the motion parallel to the y-axis only. For each spatio-temporal group we compute the distribution of the straightness indices Di for the extracted trajectories accordingly to eqn (10)–(12). As a result we obtain 3 spatial distributions for the first data set and 5 times 3 spatio-temporal distributions for the second data set (Fig. 4 bottom row).
3.3. Robustness analysis
To understand how the dynamical behaviour depends on simultaneous changes to model parameters we perform a robustness analysis on the posterior distributions. The posterior parameter distribution allows us to evaluate the Fisher Information matrix,32 and the eigenvalues and the corresponding eigenvectors correspond to the information content. To determine so called “stiff” and “sloppy” parameter/parameter combinations27 we performed a principal component analysis (PCA) on the posterior parameter distributions, focusing on those parameters that are relevant for leukocyte migration (Table 1). The marginalised posterior distributions for parameters Kd and R are very close to their prior distributions, which means that they are not inferable given the provided data sets. Because of that we exclude these two parameters from the robustness analysis. The PCA was done on the correlation matrix of the remaining five parameter distributions. We can use the correlation matrix here, because all parameters can have values between 0 and 1 only. The 1st principal component (PC1) shows the “sloppiest” parameter vector, i.e. the parameter combination that carries the least information. We contrast this with the 5th principal component (PC5), which provides the “stiffest” parameter vector and therefore the parameter combination for which the data exhibit the highest information content (Fig. 6B–D). These vectors can be visualised as in Fig. 6A, where the pairwise probability density of the parameters is plotted with the vector for the “sloppy” (red line) and the “stiff” (blue line) direction. The length of the vector represents the inverse of the information content.
4. Conclusions
We present a statistical framework that allows us to calibrate mathematical models of biological systems against in vivo data. Here we study leukocyte dynamics in zebrafish embryos following injury to their tail-fin. We show that this response is mediated by a stimulus gradient, which emanates from the wound site and changes with space and time. While this change is not directly observable in experiments, we can infer the spatio-temporal behaviour of the stimulus using an approximate Bayesian computation framework, which is able to reliably infer an experimentally validated in vitro stimulus gradient. By coupling the in vivo migratory patterns of the leukocytes to a simple model of cellular response we explain the rich behaviour exhibited by the leukocyte population following the injury.
We expect that the ability to elucidate experimentally unobservable mechanisms will increase in importance as we start to study biological processes at the whole organism level and under physiological conditions. As we show the statistical inferences drawn here can greatly aid in our understanding of otherwise seemingly complex and diverse behaviour exhibited by e.g. populations of cells of the innate immune system in an in vivo setting.
Insight, innovation, integration.
Immune signalling depends on the interplay of molecular, cellular and tissue-wide processes. Here we develop a framework for the integrative statistical analysis of leukocyte migration data in vivo in zebrafish embryos. We show how our statistical framework, which builds on recent developments in approximate Bayesian computation, allows us to understand the spatial and temporal dependence of leukocyte migratory patterns on the unobserved but inferable, chemokine gradient emanating from an injury to the zebrafish tail fin. This methodology opens up the possibility to analyze spatiotemporally resolved in vivo data and combine experimental data obtained using different modalities and across different scales.
Acknowledgements
We would like to thank Daniel Irimia who provided the movie of migrating human neutrophils in an IL8 gradient using a microfluidic device. This work was funded by grants from the BBSRC, The Wellcome Trust and GlaxoSmithKline. MPHS is a Royal Society Wolfson Research Merit Award holder.
5. Appendix
5.1 Ligand–receptor binding kinetics
The internal gradient depends on the total number of receptors R and the number of ligands L, which is here the chemokine concentration f(y,t). The system can be described as follows:
| (14) |
where C is the ligand–receptor complex, R* and L* are the free receptor and ligand concentrations, respectively, and k1 and k2 are the reaction rates. We are interested in the ligand–receptor complex as a function of the total receptor and ligand concentration in the steady state. The total receptor and ligand concentrations are
| (15) |
| (16) |
We can formulate write down the rate equation as
| (17) |
In the steady state we have We can define the receptor binding constant Kd during the steady state as
| (18) |
Substitution of R* and L* in eqn (19) with eqn (15) and (16) as well as using eqn (18) results in
| (19) |
The solution of this quadratic equation is eqn (3).
References
- 1.May RM. Science. 2004;303:790–793. doi: 10.1126/science.1094442. [DOI] [PubMed] [Google Scholar]
- 2.Vyshemirsky V, Girolami MA. Bioinformatics. 2008;24:833–899. doi: 10.1093/bioinformatics/btm607. [DOI] [PubMed] [Google Scholar]
- 3.Toni T, Stumpf MPH. Bioinformatics. 2010;26:104–110. doi: 10.1093/bioinformatics/btp619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Toni T, Welch D, Strelkowa N, Ipsen A, Stumpf MPH. J R Soc Interface. 2009;6:187–202. doi: 10.1098/rsif.2008.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Renshaw SA. Blood. 2006;108:3976–3978. doi: 10.1182/blood-2006-05-024075. [DOI] [PubMed] [Google Scholar]
- 6.Mathias JR. J Leukocyte Biol. 2006;80:1281–1288. doi: 10.1189/jlb.0506346. [DOI] [PubMed] [Google Scholar]
- 7.Redd MJ, Kelly G, Dunn G, Way M, Martin P. Cell Motil Cytoskeleton. 2006;63:415–422. doi: 10.1002/cm.20133. [DOI] [PubMed] [Google Scholar]
- 8.Niethammer P, Grabher C, Look AT, Mitchison TJ. Nature. 2009;459:996–999. doi: 10.1038/nature08119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Martins ML, Ferreira SC, Jr, Vilela MJ. Curr Opin Colloid Interface Sci. 2010;15:18–23. [Google Scholar]
- 10.Schnell S, Grima R, Maini PK. Am Sci. 2007;95:134–142. [Google Scholar]
- 11.Beltman JB, Maree AF, de Boer RJ. Nat Rev Immunol. 2009;9:789–798. doi: 10.1038/nri2638. [DOI] [PubMed] [Google Scholar]
- 12.Alt W. J Math Biol. 1980;9:147–177. doi: 10.1007/BF00275919. [DOI] [PubMed] [Google Scholar]
- 13.Tranquillo RT, Lauffenburger DA. J Math Biol. 1987;25:229–262. doi: 10.1007/BF00276435. [DOI] [PubMed] [Google Scholar]
- 14.Tranquillo RT, Lauffenburger DA, Zigmond SH. J Cell Biol. 1988;106:303–309. doi: 10.1083/jcb.106.2.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Onsum M, Rao CV. PLoS Comput Biol. 2007 Mar 16;3(3):e36. doi: 10.1371/journal.pcbi.0030036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Andrew N, Insall RH. Nat Cell Biol. 2007;9:193–200. doi: 10.1038/ncb1536. [DOI] [PubMed] [Google Scholar]
- 17.Van Haastert PJM. PLoS Comput Biol. 2010;6:e1000874. doi: 10.1371/journal.pcbi.1000874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Codling EA, Plank MJ, Benhamou S. J R Soc Interface. 2008;5:813–834. doi: 10.1098/rsif.2008.0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li L, Nørrelykke SF, Cox EC. PLoS One. 2008;3:e2093. doi: 10.1371/journal.pone.0002093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Campos D, Méndez V, Llopis I. J Theor Biol. 2010;267:526–534. doi: 10.1016/j.jtbi.2010.09.022. [DOI] [PubMed] [Google Scholar]
- 21.Endres RG, Wingreen NS. Proc Natl Acad Sci U S A. 2008;105:15749–15754. doi: 10.1073/pnas.0804688105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Joyce P, Marjoram P. Stat Appl Genet Mol Biol. 2008;7 doi: 10.2202/1544-6115.1389. year. [DOI] [PubMed] [Google Scholar]
- 23.Nunes MA, Balding DJ. Stat Appl Genet Mol Biol. 2010;9:34. doi: 10.2202/1544-6115.1576. [DOI] [PubMed] [Google Scholar]
- 24.Barnes C, Filippi S, Stumpf MP, Thorne T. arXiv. stat.CO; 2011. year. [Google Scholar]
- 25.Liepe J, Barnes C, Cule E, Erguler K, Kirk P, Toni T, Stumpf MPH. Bioinformatics. 2010;26:1797–1799. doi: 10.1093/bioinformatics/btq278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.BERG HC. Princeton University Press; 1983. pp. 164–165. [Google Scholar]
- 27.Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. PLoS Comput Biol. 2007;3:1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Secrier M, Toni T, Stumpf M. Mol BioSyst. 2009;5:1925–1935. doi: 10.1039/b908951a. [DOI] [PubMed] [Google Scholar]
- 29.Erguler K, Stumpf MPH. Mol BioSyst. 2011;7:1593–1602. doi: 10.1039/c0mb00107d. [DOI] [PubMed] [Google Scholar]
- 30.Li Jeon N, Baskaran H, Dertinger S, Whitesides G, Van de Water L, Toner M. Nat Biotechnol. 2002;20:826–830. doi: 10.1038/nbt712. [DOI] [PubMed] [Google Scholar]
- 31.Pau G, Fuchs F, Sklyar O, Boutros M, Huber W. Bioinformatics. 2010;26:979–981. doi: 10.1093/bioinformatics/btq046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Plyasunov S, Arkin AP. J Comput Phys. 2007;2:724–738. [Google Scholar]