Stimulation of PPC Affects the Mapping between Motion and Force Signals for Stiffness Perception But Not Motion Control

Abstract

How motion and sensory inputs are combined to assess an object's stiffness is still unknown. Here, we provide evidence for the existence of a stiffness estimator in the human posterior parietal cortex (PPC). We showed previously that delaying force feedback with respect to motion when interacting with an object caused participants to underestimate its stiffness. We found that applying theta-burst transcranial magnetic stimulation (TMS) over the PPC, but not the dorsal premotor cortex, enhances this effect without affecting movement control. We explain this enhancement as an additional lag in force signals. This is the first causal evidence that the PPC is not only involved in motion control, but also has an important role in perception that is disassociated from action. We provide a computational model suggesting that the PPC integrates position and force signals for perception of stiffness and that TMS alters the synchronization between the two signals causing lasting consequences on perceptual behavior.

SIGNIFICANCE STATEMENT When selecting an object such as a ripe fruit or sofa, we need to assess the object's stiffness. Because we lack dedicated stiffness sensors, we rely on an as yet unknown mechanism that generates stiffness percepts by combining position and force signals. Here, we found that the posterior parietal cortex (PPC) contributes to combining position and force signals for stiffness estimation. This finding challenges the classical view about the role of the PPC in regulating position signals only for motion control because we highlight a key role of the PPC in perception that is disassociated from action. Altogether this sheds light on brain mechanisms underlying the interaction between action and perception and may help in the development of better teleoperation systems and rehabilitation of patients with sensory impairments.

Introduction

Our hands are fascinating organs that we use to sense and interact with our environment. Early studies of sensory processing advanced our understanding of the type of information available to the sensorimotor system during and after generating movements (Adams, 1987; Swinnen, 1996). Information such as position (Gandevia et al., 1992) and force (Jones, 2000; Mileusnic and Loeb, 2009) travels back to the brain and is combined with an efference copy of motor commands to adjust movements online and to provide us with a sense of the environment (Kawato, 1999). For some actions, we clearly rely on one of these signals more than the other. For example, we rely on position feedback when reaching for a pen, but on force feedback when putting pressure on the nib to write. However, in a number of other cases, such as when estimating an object's stiffness, the sensorimotor system integrates online information about position and force signals. How these two sensory signals are weighted to control actions and form a perception of object stiffness is still debated.

One way to disambiguate the contribution of position and force information to stiffness perception is to change the relationship between them by means of programmable robotic devices. For example, in a perceptual task of stiffness discrimination between pairs of linear elastic force fields, it is possible to introduce a time delay between position and force. Previous studies (Nisky et al., 2008, 2010) have shown that, if force information is delayed during movements probing an elastic force field, then subjects will underestimate stiffness. The less those probing movements break contact with the elastic force field, the more they will underestimate stiffness. To explain this, it has been suggested that a position control strategy is used for coordinating probing movements. In this case, the sensorimotor system obtains an estimate of stiffness by controlling a change in position while measuring the resulting force field and calculating a regression between the two to obtain a stiffness estimate. However, without an effort to probe the underlying neural mechanisms, this mechanistic explanation was necessarily speculative.

There is already evidence that a position controller exists in the brain. The posterior parietal cortex (PPC) has been shown to be associated with such a controller for reaching movements in free space (Chib et al., 2009; Davare et al., 2012). However, there is no evidence of the PPC integrating force and position information, as in the case of forming perception of stiffness or other forms of impedance. We hypothesize that the PPC is used to generate a regression-based stiffness estimator. Therefore, we expect that inducing a “virtual lesion” of PPC by applying continuous theta-burst stimulation (cTBS) (Huang et al., 2005) should alter stiffness judgment. We postulate two possible outcomes after PPC stimulation: (1) if the stimulation affects the position and force signals that serve as input of the estimator, then our regression model predicts a bias in perception without a change in discrimination sensitivity, and (2) if stimulation affects the output of the estimator, then a change in discrimination sensitivity is expected without a bias. Our results support the former hypothesis.

Materials and Methods

Experiments 1 and 2: PPC and dorsal premotor cortex (PMd) cTBS

Participants and experimental design.

Eleven participants (5 males, 6 females between 22 and 34 years of age) participated in the experiment after providing informed consent. Participants were seated in front of a semi-silvered mirror in which they viewed the reflection of an LCD computer screen placed above it (Fig. 1A). Participants held the stylus of a Touch X haptic device (Geomagic Technologies) with their right hand. We instructed participants to move only their wrist and ensured this by using orthopedic splints to prevent participants from using other joints during probing movements. As explained in Nisky et al. (2010), constraining the forearm generates slightly curved and tilted natural movements around the wrist. Therefore, we implemented a virtual environment at a 45° angle and participants were asked to interact with this environment. An opaque screen was fixed under the glass to block vision of the hand and participants were given visual feedback of their hand position in the X–Y (tilted) plane while information about the Z direction was blocked (Fig. 1B). Real-time force feedback was rendered at 1 kHz according to sampled hand position. Participants were instructed to probe two virtual force fields, represented by two distinct background colors, and report which one was stiffer by verbally indicating the color corresponding to the stiffer force field. By pressing on a virtual button, participants could switch between the two force fields as many times as they wished until they were ready to answer. The total probing time was not restricted and participants could perform as many movements as they wanted.

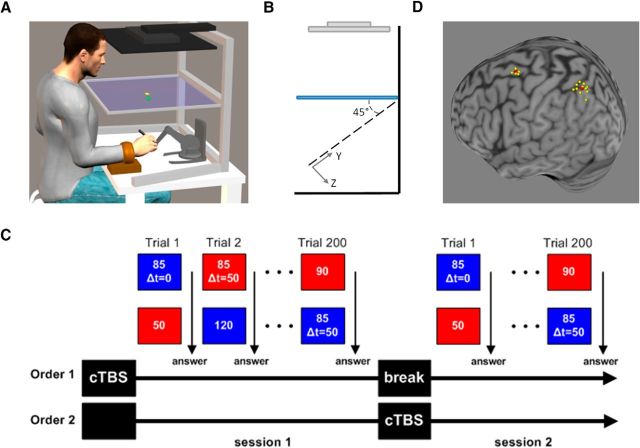
Figure 1.

A, Experimental setup. Participants held the stylus of the robot used to generate virtual force fields while looking at the projected image from an LCD screen placed above their head. Participants' arms were constrained using orthopedic splints so that they could only move the wrist. The virtual environment consisted of a yellow square cursor representing the end point of the stylus and a green square that was used as a button to switch between force fields. The force fields were distinguished by their background color (red or blue). Participants were allowed to perform multiple probing movements and change between the two force fields as many times as they wished. B, Side view of the virtual reality environment. The X–Y plane was rotated by 45°. C, Experimental protocol. The experiment consisted of two sessions. Each session consisted of 200 comparisons between pairs of force fields. In each pair, the stiffness value of one force field was always 85 N/m (standard field) and the second was drawn out of 10 possible stiffness values (comparison field). In half of the trials, the force feedback of the standard field was delayed by 50 ms. After each comparison, participants were asked which field was stiffer. Each participant had PPC cTBS before one of the sessions. D, TMS neuronavigation. Location of each participant's stimulation point (yellow) over the PPC or PMd after normalization into the MNI coordinate system. The average MNI coordinate for each region is indicated in red.

In each trial, participants were presented with two force fields, the standard and the comparison force fields. The standard force field could have consisted of either a linear force field in which force feedback is calculated according to the following equation: F(t) = K_standard(x_hand(t) − x₀) or a delayed force field in which force feedback is calculated according to past hand position, as follows: F(t) = K_standard(x_hand(t − τ) − x₀). The stiffness value (K_standard) was set to 85 N/m while the time delay value (τ) was set to 50 ms. The comparison force field was always linear with stiffness values (K_comparison) chosen out of 10 equally distributed stiffness levels between 40 N/m and 130 N/m with intervals of 10 N/m between them. We eliminated the possibility of participants breaking contact with the force field by preventing them access to the boundary point x₀. To do so, we set the boundary point beyond the reachable area at x₀ = 1/K[m] where K was either the standard or the comparison stiffness value. The switch button was placed at x_hand = 0, so subjects always felt a force of 1 N at the beginning of the probing movement. In addition, to prevent participants from pressing too hard on the force fields and reaching force saturation levels of the haptic device, a sound was played after penetration beyond 4.5 cm.

The experiment consisted of two sessions carried out on the same day (Fig. 1C). Each session began with 20 practice trials in which participants compared each of the two standard fields with each of the 10 comparison fields to allow acquaintance with the system. After the training session, participants performed 180 trials in which they compared each of the two standard force fields with each of the 10 comparison force fields (eight repetitions of each for the nondelayed standard field and 10 repetitions for the delayed standard field). The pair of force fields compared in a given trial was randomly chosen. The entire session lasted ∼40 min.

Transcranial magnetic stimulation.

We asked participants to perform two sessions of the stiffness judgment task on the same day. Before one of the sessions, we applied cTBS over the left PPC and the second session was used as a control for cTBS effects (Experiment 1). In addition, we repeated this experiment while targeting the left PMd as a control site (Experiment 2). Participants who also received cTBS on the control site (PMd) performed a total of 4 sessions, 2/d and 1 week apart.

For applying cTBS, we used a 70 mm standard figure-of-eight coil connected to a Magstim Rapid magnetic stimulator. Single-pulse TMS was initially delivered over the left M1 to determine the optimal coil position to induce motor evoked potentials (MEPs) in the contralateral first dorsal interosseous (FDI). We then measured the active motor threshold (aMT), defined as the minimum single pulse intensity required to produce an MEP >200 microVolts on more than five out of 10 trials from the contralateral FDI while the participant was maintaining a voluntary contraction of approximately 20% of maximum using visual feedback. The average aMT was 49 ± 6% (n = 11, mean ± SD) of the maximal stimulator output. We used BrainSight neuronavigation software (Rogue Research) to locate the left PPC and PMd. Anatomical landmarks were used to guide coil placement: PPC was located over the medial portion of the intraparietal sulcus, near the caudal part of the angular gyrus (Davare et al., 2012; Davare et al., 2015). PMd was located as the most caudal portion of the superior frontal gyrus at the level of its intersection with the precentral gyrus. The mean normalized MNI coordinates of our stimulations points were −33, −62, 56 for left PPC (x, y, z, n = 11; Fig. 1D) and −25, 0, 67 for left PMd (x, y, z, n = 5; Fig. 1D). For six participants who only received cTBS over left PPC, because the participants' structural MRI was not available at the time of the experiment, the left PPC was located as the P3 electrode placement according to the 10–20 EEG (electroencephalogram) coordinate system (Hilgetag et al., 2001; Herwig et al., 2003; Sparing et al., 2009). For anatomical reference, the exact TMS locations were then confirmed a posteriori by coregistering each participant's P3 location onto their structural MRI using BrainSight. Each participant's MRI was normalized using the MNI (ICBM152) template space. The average P3 MNI coordinates were −32.8, −61.5, 56 (x, y, z, n = 6). We used SPM8 (http://www.fil.ion.ucl.ac.uk/spm) anatomy toolbox (Eickhoff et al., 2005) to confirm these coordinates overlay the left dorsal PPC including the intraparietal sulcus adjacent to Broadman area 7a and 40.

After TMS site localization, we applied 40 s of cTBS (cTBS600 protocol; Huang et al., 2005) at an intensity of 80% aMT. The order of cTBS application in the experiment was counterbalanced across the 11 participants: Five had cTBS before Session 1 and six had cTBS before Session 2. The order for each participant is summarized in Table 1. When cTBS was applied before Session 1 (Order 1 in Fig. 1C), we made sure that stimulation effects did not carry over Session 2 by introducing a break period separating the start of Session 2 by at least 70 min from cTBS application (Huang et al., 2005).

Table 1.

Order of cTBS application across the 11 participants

Participant	Experiment 1		Experiment 2
	Session 1	Session 2	Session 1	Session 2
P1	cTBS of PPC	No stim	cTBS of PMd	No stim
P2	No stim	cTBS of PPC	No stim	cTBS of PMd
P3	No stim	cTBS of PPC	No stim	cTBS of PMd
P4	cTBS of PMd	No stim	cTBS of PPC	No stim
P5	No stim	cTBS of PMd	No stim	cTBS of PPC
P6	cTBS of PPC	No stim
P7	cTBS of PPC	No stim
P8	cTBS of PPC	No stim
P9	No stim	cTBS of PPC
P10	No stim	cTBS of PPC
P11	No stim	cTBS of PPC

Experiment 3: added delay

We conducted an additional experiment consisting of two sessions similar to Experiment 1 and 2. In this experiment, we did not apply any cTBS, but instead, in one out of the two sessions, we introduced an extra 50 ms delay to all the standard and comparison force fields. In one of the sessions, the force fields were similar to the other two experiments; that is, the participants compared between linear force fields (comparison) and linear or delayed force fields (standard). In the other session, participants compared between comparison fields with 50 ms delay in force feedback and standard fields with either 50 or 100 ms delay in force feedback. To match the sample size of the PPC cTBS experiment, 11 new subjects (seven males, four females, aged between 19 and 26) participated in this experiment. The experimental setup was similar to Experiments 1 and 2. The two sessions were carried out over 2 consecutive days and their order was counterbalanced across participants: five had the additional delay during Session 1 and six had the additional delay during Session 2.

Data analysis

We fitted psychometric functions to the probability of answering that the comparison force field was stiffer as a function of the difference between the comparison and standard force fields. We fitted the following equation to the data:

where Δk is the difference between the stiffness levels of the standard and comparison fields. The shape of the curve is determined by the parameters α, ζ, γ, and λ and the choice of a two-parameter function S, here a logistic function. γ and λ are the rates of subjects' lapse—an incorrect response regardless of the intensity of the difference between stiffness levels. α and ζ determine the shift and the slope of the sigmoid function, respectively.

We then computed the point of subjective equality (PSE) and the just-noticeable difference (JND) (Nisky et al., 2008). PSE was defined as the difference between the two force fields (ΔK = K_comparison − K_standard; x-axis) for which the participant did not perceive any difference as evidenced by a probability of 0.5 to answer that the comparison force field is stiffer (P(K_comparison > K_standard) = 0.5; y-axis). JND was calculated by subtracting the stiffness difference at 0.25 threshold value from the stiffness difference at 0.75 threshold value and dividing the result by 2. The psychometric function, the PSE, and the JND were calculated using the psignifit toolbox version 2.5.6 for Matlab (Wichmann and Hill, 2001). Briefly, the psychometric curve quantifies the participant's overall performance in a discrimination task. PSE and JND are useful parameters in describing the probability distribution of the participant's responses (Nisky et al., 2008). Intuitively, whereas PSE shows the mean of the stiffness judgments, JND quantifies the level of uncertainty in perceiving two force fields as different. For example, a decrease in PSE will indicate an overall underestimation of the standard force field stiffness, whereas an increase in JND will highlight a decrease in the sensitivity to discriminate between the two force fields.

Due to the blocked nature of our approach, we never compared the judgment of stiffness of force fields with and without cTBS within the same trial. As a result, we cannot determine whether cTBS had an absolute effect on stiffness perception. Nevertheless, different PSE values between the standard and the comparison force fields mean that, regardless of whether cTBS induces a general bias in perception, the participants judge the stiffness of the comparison fields as not equal to the standard fields.

To test whether the stimulation altered the metrics of probing movements, we analyzed the force and position trajectories of the participants as a function of time. For each trial, we estimated the following metrics (Nisky et al., 2010):

1. Mean probing movement time: by identifying the position reversal points where hand velocity equals zero; that is, the start and end points of each probing movement, we computed the duration of each probing cycle and averaged it for each condition and participant.

2. Mean movement amplitude: using the reversal points, we extracted the penetration distances for each trial and calculated the mean for each condition and participant.

3. Mean peak absolute velocity: for each pressing and releasing motion into the force fields, we extracted the peak velocity value. Because pressing and releasing have different movement directions, we considered the absolute value of peak velocity.

4. Mean force amplitude: to determine whether the amplitude of the forces acting on the participants' hands were different after stimulations, we calculated the mean value of forces for each trial.

5. Mean area reaching deviation: because motion was performed at 45° while participants had their forearm constrained, this led to slightly curved movements and we verified that the curvature of probing movements was not affected by cTBS. The amount of curvature was calculated as the area between the actual trajectory participants performed and the straight line connecting the start and end points of each probing cycle.

In addition to the characteristics of probing movements, we determined the number of probing movements that each participant made during interactions with the comparison and standard force fields. The number of probing movements indicates how difficult it was for the participants to make a decision in each trial. This metric may provide additional insights to the decision uncertainty based on the amount of information that was needed to make a decision. To do so, we counted the number of probing movements as the number of position reversal points when penetration into the field was at maximum value. Each reversal point indicated one probing motion. For each trial, we calculated the number of probing movements for the comparison and for the standard force fields.

Stiffness perception models

To explain the participants' perception of stiffness, we tested two computational models for stiffness estimation using the hypothesis of position and force control (Nisky et al., 2008). These estimations are based on the position and force information available while probing the force field. The first method is based on a position controller that estimates stiffness using a regression line with position as the independent variable and force as the dependent variable (marked as FOP, force over position). The second method is based on a force controller that estimates stiffness using a regression line with force as the independent variable and position as the dependent variable (marked as POF, position over force).

To calculate the models' stiffness estimation, we analyzed the data recorded during probing movements using the trajectories of the participants in the force–position plane; that is, a 2D space with one coordinate for the participant's hand position along the field direction (x) and the other coordinate for the force exerted by the haptic device (F). For the first method, we fitted a regression line by minimizing the squared residuals between the force data and the regression line. From this procedure, we used the fitted slope in F = K̂ · X as the estimated stiffness generated by this model. For the second model, we fitted a regression line by minimizing the squared residuals between the position data and the regression line. From this procedure, we used the inverse of the fitted slope in X = $\frac{1}{\widehat{K}}$ · F as the estimated stiffness generated by this model. For each method, we fitted the estimation to the standard (K̂_standard) and comparison (K̂_comparison) force fields and repeated this for each trial. Using the slopes values of the two regression lines as inputs, a decision model generated the answer to the question of which force field was stiffer within each trial pair. For example, if the slope of the regression line for the standard force field was greater than the one for the comparison force field, then the decision model would answer that the standard force field was stiffer or vice versa.

To test the ability of each of the models to predict participants' answers, we calculated a score based on the agreement between the participant's and model's answers. For each standard type force fields, that is, linear or delayed force fields, we counted all trials with an agreement and divided by the total number of test trials. A model will generate a perfect score of 1 if there is a full agreement between the model's and participants' answers. In reality, because we did not include decision noise in the model, we expected some disagreement between the model prediction and participants' actual decisions due to decision noise in participants' answers (for details about this aspect of model assessment, see Nisky et al., 2008).

To model the cTBS effect, we again used the two regression based models and tested different signal or estimation manipulations. We added white Gaussian noise to the position data, altered the alignment between the force and position signals by temporal shifting the force signal, and added noise to the two estimations that serve as inputs of the decision model. We used these manipulations only for trials performed after the cTBS sessions.

Statistical analysis

To test the effects of delay and cTBS on stiffness perception, we used two-way repeated-measures ANOVA with delay (0, 50 ms), cTBS (yes, no), and their interaction as independent factors and PSE values as a dependent variable. To test the effects of delay and cTBS on discrimination sensitivity as measured by the JND, we used the same procedure but with JND as a dependent variable. To test differences in movement metrics, we used a similar procedure but with each movement feature as the dependent variable (except for the number of probing movements). The number of probing movements was analyzed separately for the delayed and linear standard force fields. We used three-way repeated-measures ANOVA with type of force field (comparison, standard), cTBS (yes, no), and stiffness (10 levels 40–130 N/m) as independent factors. For the added delay experiment analysis, we used repeated-measures ANOVA similar to the analysis of the PPC cTBS experiment replacing the cTBS factor with the added delay factor (0,+50 ms). Post hoc tests with Bonferroni correction for multiple comparisons were performed when interactions were found to be statistically significant. Statistical significance was determined at the 0.05 threshold in all tests.

The models' scores are bounded between [0, 1] and thus are not distributed normally (especially for models with high agreement with participants' answers). Therefore, we used a Friedman ANOVA test to compare the scores of the different models.

Results

Participants underestimated the stiffness of the elastic fields with delayed force feedback compared with the linear and this relative underestimation was enhanced after PPC cTBS by an average of 16.2 ± 8.27 N/m. Applying cTBS did not change the minimal difference in stiffness values that participants were able to detect nor the movement kinematics.

PPC cTBS increased underestimation of delayed force field stiffness

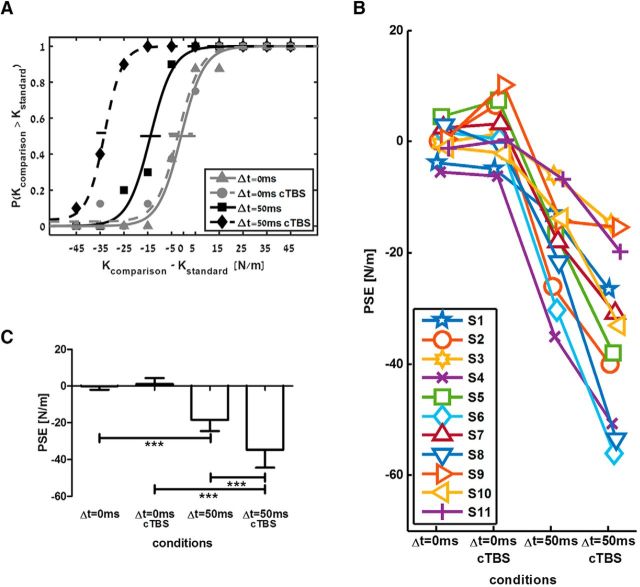
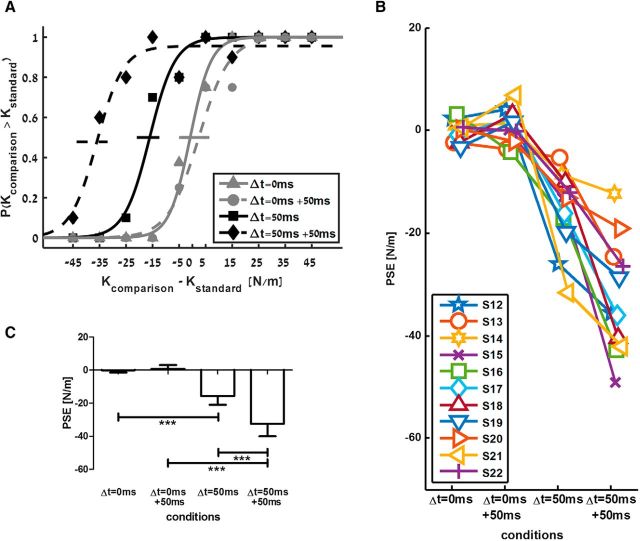
Based on participants' answers, we constructed psychometric curves that describe the probability to answer that the comparison force field had a higher level of stiffness than the standard force field. Figure 2A shows an example psychometric curve of a single participant. Perception was unbiased for the linear standard force field, as evident from a curve centered on a PSE equal to zero. In addition, there was an underestimation of the delayed force field, as shown by a leftward shift of the entire psychometric curve, so the PSE was negative. Importantly, PPC cTBS caused an additional shift in perception of the delayed force field, as indicated by an even lower PSE value. The individual response and group analysis of all participants are depicted in Figure 2, B and C, where the individual PSE and mean PSE of all participants is represented in the four conditions: (1) linear force field, (2) linear force field after PPC cTBS, (3) delayed force field, and (4) delayed force field after PPC cTBS. We found that delay caused a significant shift of PSE (F_(1,10) = 61.508, p < 0.001, η_p² = 0.86), that cTBS also led to a significant difference in PSE values (F_(1,10) = 19.736, p = 0.001, η_p² = 0.664), and that the interaction between delay and cTBS was statistically significant (F_(1,10) = 91.150, p < 0.001, η_p² = 0.901). Post hoc analyses clearly showed that the PSE values of delayed force fields were significantly smaller than PSE values of linear force fields (in the control session: t₍₁₀₎ = 6.45 p < 0.001; in the cTBS session: t₍₁₀₎ = 8.85 p < 0.001). Importantly, PSE values of delayed force fields after PPC cTBS were significantly smaller than PSE values of delayed force field in the control condition (−34.6 ± 14.57 vs −18.4 ± 9.13; t₍₁₀₎ = 6.49, p < 0.001). It is noteworthy that our experimental paradigm of comparing perception between delayed and linear force fields provides an internal control for nonspecific TMS effects.

Figure 2.

Increased underestimation of perceived stiffness after PPC cTBS. A, Psychometric curves fitted to the answers of a typical participant in the control (solid lines) and cTBS (dashed lines) sessions. Based on the participant's answers, we extracted the probability to answer that the comparison force field was stiffer than the standard force field. Gray lines represent the standard linear force field and black lines represent the standard delayed force-field conditions. Horizontal lines indicate 95% confidence intervals for the PSE, estimated using bootstrap (Wichmann and Hill, 2001). B, Individual PSE values of all participants for the four conditions. C, Mean PSE values across all participants for the four conditions. Error bars are 95% confidence intervals estimated using t distribution. ***p < 0.001.

No change in motion metrics and discrimination sensitivity after PPC cTBS

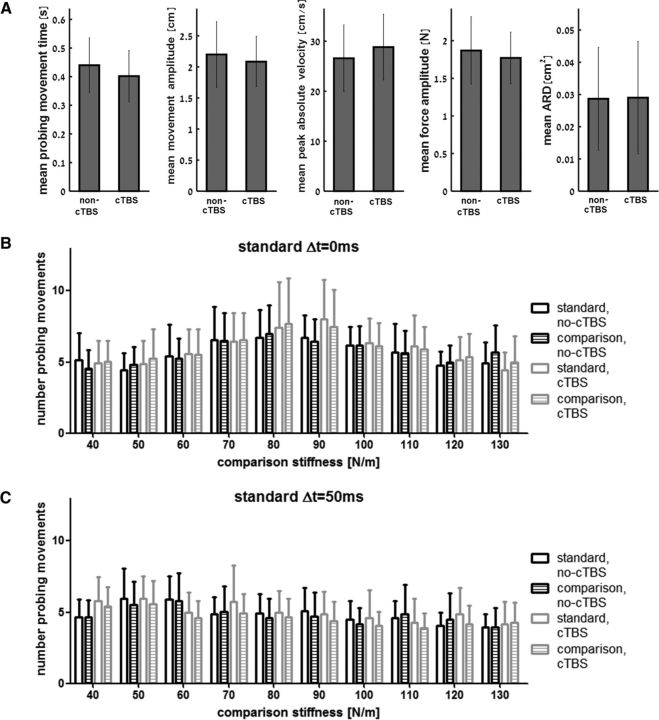
When we targeted the PPC, cTBS increased stiffness underestimation of a delayed force field without altering the kinematics or dynamic features of probing movements. We compared different movement metrics for both the control and cTBS sessions and for both the linear and delayed standard force fields; namely, the duration of probing motion, penetration amplitude, velocity, force amplitude, and movement curvature (Fig. 3A). There was no significant main effect of cTBS (all F_(1,10) < 0.82, all p > 0.38, η_p² < 0.076), delay (all F_(1,10) < 2.53, all p > 0.14, all η_p² < 0.202) nor interaction between cTBS and delay factors (all F_(1,10) < 1.26, all p > 0.28, all η_p² < 0.112), indicating that cTBS had no significant effect on any of these metrics for either delayed or nondelayed force fields.

Figure 3.

No change in kinematic or dynamic features of probing movements. A, There were no statistically significant differences in any of the tested movement parameters when probing the delayed force fields in the non-cTBS and cTBS sessions. Error bars are 95% confidence intervals estimated using t distribution. ARD, Area reaching deviation. B, Mean number of probing movements during trials in which the standard force field was nondelayed. Bars represent the number of probing movements during interaction with the nondelayed standard and comparison force fields as a function of the comparison force field stiffness values. The count of probing movements was similar between the cTBS and no-cTBS sessions for both force fields. Bar color and fill pattern distinguish between the results for force-field type (standard or comparison) and PPC cTBS condition (cTBS or no-cTBS). C, Same as in B but for trials in which the standard force field was delayed. Similar to the trials in which the standard force field was nondelayed, we found no PPC cTBS effect on the number of probing movements during trials in which the standard force field was delayed.

In addition, cTBS did not change the sensitivity in stiffness discrimination per se. This is evident in the slope of the psychometric curve and is quantified by calculating the JND in stiffness levels. The ANOVA_RM did not show any main effect of cTBS (F_(1,10) = 0.156, p = 0.7, η_p² = 0.015), delay (F_(1,10) = 0.451, p = 0.51, η_p² = 0.043) nor the interaction between cTBS and delay (F_(1,10) = 0.295, p = 0.59, η_p² = 0.029) on JND values.

This suggests that PPC cTBS changed the overall participants' stiffness judgment, making the delayed force fields feel more compliant (as measured by the PSE) than their actual stiffness without affecting participants' ability to discriminate that force fields with stiffness values higher than the PSE are stiffer and force fields with stiffness values lower than the PSE are more compliant.

Analyzing the number of probing movements also supported the result that cTBS did not increase the difficulty to judge force field stiffness. The cTBS factor did not have a statistically significant effect on probing movement number while interacting with the nondelayed standard (Fig. 3B, F_(1,10) = 0.113, p = 0.743, η_p² = 0.011) or the delayed standard (Fig. 3C, F_(1,10) = 1.236, p = 0.292, η_p² = 0.11) force fields. The interaction between cTBS and field type factors was also not found to be statistically significant (nondelayed: F_(1,10) = 0.03, p = 0.866, η_p² = 0.003, delayed: F_(1,10) = 1.13, p = 0.313, η_p² = 0.102). As depicted in Figure 3, B and C, there is some increase in the mean number of probing movements around the mean PSE of each standard force field. For the nondelayed force field, we found a high number of probing movements for stiffness values of 80–90 N/m, whereas, for the delayed force field, we found a high number of probing movements for stiffness values of 50–60 N/m during the no-cTBS session and for stiffness values of 40–50 N/m during the cTBS session. This result implies that around the PSE participants needed additional information to make their decisions.

PMd cTBS did not alter estimation of delayed force-field stiffness

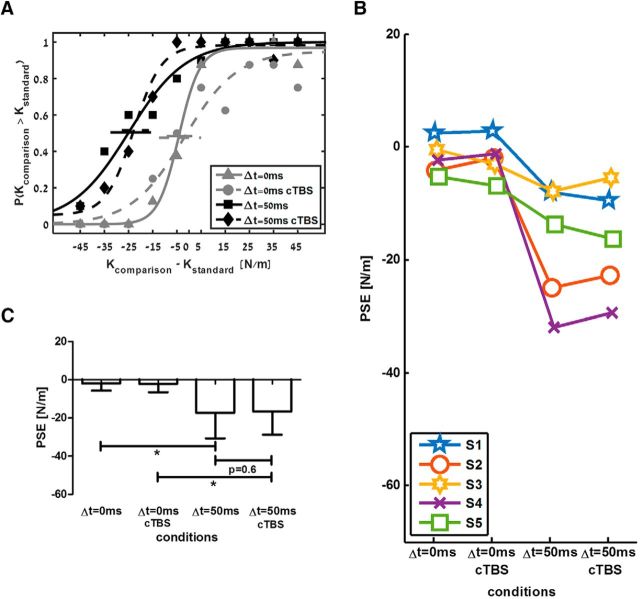
In addition to the stimulation of PPC, some participants repeated the experiment with PMd as target area (see Table 1). In contrast to the results for PPC stimulation, PMd cTBS did not affect perception of either the linear or the delayed standard force fields. Perception of linear force fields was unbiased and there was an underestimation of the delayed force fields for both cTBS and non cTBS sessions. In the example that is depicted in Figure 4A, the psychometric curve that was fitted to the answers about the linear force field remained unbiased with and without PMd cTBS. For the delayed force field, there was no change in the leftward shift after PMd cTBS, meaning that the participant underestimated the delayed force field, and this underestimation remained the same for both sessions. This was consistent across all participants (Fig. 4B). Group analysis (Fig. 4C) showed a statistically significant effect of delay on PSE values (F_(1,4) = 11.8, p = 0.026, η_p² = 0.748). However, there was no statistically significant effect of cTBS (F_(1,4) = 0.089, p = 0.78, η_p² = 0.022) or the interaction between delay and cTBS factors (F_(1,4) = 0.39, p = 0.56, η_p² = 0.091). Post hoc analysis showed that the PSE was lower for the delayed force field compared with the PSE for the linear force field for the cTBS session (t₍₄₎ = 3.24, p = 0.032) and for the control session (t₍₄₎ = 3.58, p = 0.023). We found no statistically significant difference in PSE values for the delayed force field when comparing between the cTBS and the control sessions (t₍₄₎ = 0.56, p = 0.6).

Figure 4.

No change in perceived stiffness after PMd cTBS. A, Psychometric curves fitted to the answers of a typical participant in a similar way as presented in Figure 2A. B, Individual PSE values across all participants for the four conditions. C, Mean PSE values across all participants for the four conditions in the experiment. Error bars are 95% confidence intervals estimated using t distribution. *p < 0.05.

In addition, we found no statistically significant effect of PMd cTBS on JND values. Performing the ANOVA_RM test did not show an effect of the cTBS factor (F_(1,4) = 1.88, p = 0.24), the delay factor (F_(1,4) = 1.34, p = 0.31), or their interaction (F_(1,4) = 1.28, p = 0.32).

Affecting the alignment between position and force signals used for the FOP regression-based model predicts the increase of underestimation of delayed force field stiffness

To explain the perceptual stiffness underestimation, Nisky et al. (2008) suggested two regression-based models: a regression line calculated using position as the independent variable and force as the dependent variable (FOP) and a regression line calculated using force as the independent variable and position as the dependent variable (POF). Here, we demonstrate that the FOP model can explain the underestimation of delayed force field. We further show that changing the alignment between the signals used as inputs for the FOP model can explain the increase of underestimation of stiffness. This suggests that cTBS affects the alignment between these inputs by delaying force signals sensed by the participants and used for stiffness estimation.

As shown analytically in Nisky et al. (2013), the FOP regression model estimates the stiffness of a spring with delayed force feedback as smaller than the nominal spring value. Assuming a discrete computation based on sampled vectors of position, x, and force, f, we can rewrite the stiffness estimation as the ratio of two sums:

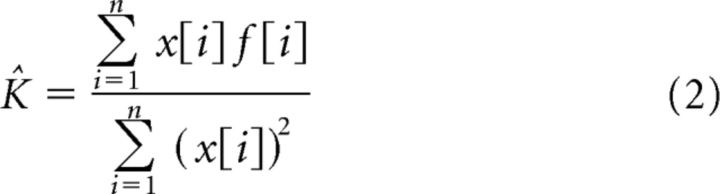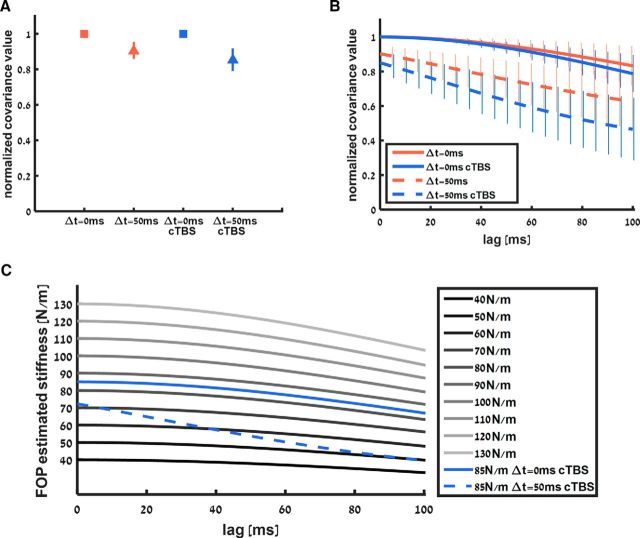
This expression shows that the estimated stiffness is calculated by dividing the covariance between hand position and sensed force by the variance of the hand position. For the linear spring case, the sensed force increases and decreases simultaneously with hand position, so the covariance between the two signals has a maximum value and the estimated stiffness is equal to the actual stiffness. Delaying the force decreases the value of this covariance because the temporal changes in the force signal are no longer simultaneous with the temporal changes in position signal. As a result, the estimated stiffness is reduced compared with the nominal stiffness value. This reduction in estimated stiffness value can explain why participants underestimated the stiffness of the delayed force field. To confirm this prediction with the actual covariance between force and position signals, we calculated the covariance values from the probing movements. Figure 5A shows the normalized covariance values that we calculated from the probing movements for the standard linear field and standard delayed field cases during the no-cTBS and cTBS sessions. The covariance values for the delayed field are lower than the covariance values for the linear field in both the no-cTBS and cTBS sessions. This difference in covariance values between the linear and delayed fields can explain why participants underestimated the delayed field compared with the linear field. In addition, this difference between linear and delayed fields was larger under the effect of cTBS. This can explain the increase in underestimation of delayed fields during the cTBS session; however, this difference is not large enough to create the difference in PSE values that we observed. To increase the difference between covariance values, we suggest that cTBS affected the force signal by lagging it further compared with the position signal.

Figure 5.

A, Normalized covariance value between force and position signals during the non-cTBS and PPC cTBS sessions. Covariance value for the linear force field was at maximum value since force increased and decreased according to hand position. This value was lower for probing the delayed force field because the simultaneity between the signals was affected by the delay. Error bars represent 95% confidence intervals. B, Cross-covariance function between force and position signals during the non-cTBS and PPC cTBS sessions as a function of introducing a lag in the force signal. Solid and dashed bold lines represent mean covariance values for linear (solid lines) and delayed (dashed lines) force fields for the no-cTBS (red) and cTBS (blue) sessions with 95% confidence intervals. For zero lag, that is, no manipulation of the recorded force signal, we have the same values of covariance as in A. Adding lag to the force signal reduced the cross-covariance value. The difference between covariance values of the linear spring and the delayed spring increased as a function of lag value under cTBS effect (difference between blue lines) compared with this difference during the no-cTBS session in which the difference in covariance value remained similar as a function of lag value (difference between red lines). Modeling cTBS effect by increasing the lag between the signals while using the FOP model can explain the increased stiffness underestimation exhibited during the experiment. C, Stiffness estimation of the standard and comparison force fields as a function of lag between force and position signals. Each line represents the FOP mean stiffness estimation as a function of added lag between signals for the PPC cTBS session. Although the stiffness estimation for the 85 N/m linear standard force field remains between 80 and 90 N/m as a function of the covariance lag, the stiffness estimation for the 85 N/m delayed standard force field decreases as a function of the same lag, explaining why the underestimation of stiffness for the delayed force field increased while leaving the stiffness estimation of the linear field the same.

To demonstrate how further delaying the force signal increases the underestimation of stiffness in the model, we calculated the covariance between hand position and sensed force when we added time lag between these signals; that is, we change the force signal to be f[i − Δ] where Δ is the lag that we added. In other words, we calculated the cross-covariance function between the force and position signals. Consistent with the previous explanation, when further delaying the force signal, the covariance between force and hand position is reduced. As shown in Figure 5B, the additional lag of the force signal sensed by the participants during the cTBS session decreased the covariance between the hand position and force signal. This decrease in covariance value was greater during interaction with the delayed field than during interaction with linear field. As a result, both stiffness estimations were reduced, but the model's stiffness estimation for the delayed field was reduced more than that of the linear field, so the delayed field was even more underestimated after cTBS.

Based on this analysis of signals covariance, we calculated the FOP stiffness estimation for the comparison and standard force fields. As shown in Figure 5C, increasing the lag between the signals decreases the absolute stiffness estimation of each force field. For the delayed force field, this decrease is larger than for the linear force field. We suggest that the cTBS increases the lag between signals such that it causes the delayed force field to be perceived as more compliant. For example, if we add no lag between the signals, then the stiffness estimation of the delayed force field falls between the stiffness estimation of force fields that have a stiffness value of 70 and 80 N/m. If we set the lag to 50 ms, then the stiffness estimation of the delayed force field falls between the stiffness estimation of force fields that have a stiffness value of 50 and 60 N/m. The additional lag can explain the decrease in participants' PSE as measured from the psychometric curves.

In contrast to the rapid decrease in FOP stiffness estimation for the delayed force field, the decrease for the linear force field is consistent with the decrease in estimation value for the comparison force fields. This means that the estimation of the standard linear force field always falls between the stiffness estimation of force fields that have 80–90 N/m stiffness values. Therefore, the perceived stiffness of the linear force field will always be between the perceived stiffness of these two values even if cTBS increases the lag between signals.

Regression-based model can explain the behavioral results

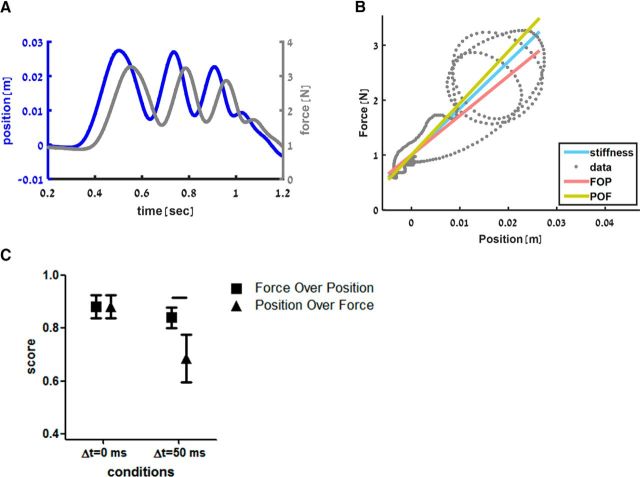
For each probing sequence that the participant performed (i.e., when sensing the standard and comparison force fields), we fitted two regression lines (FOP and POF) to the movement trajectory in the force–position plane (see example in Fig. 6A,B). We tested the agreement between the models' and the actual participant's answers in each trial. Figure 6C shows the proportion of trials in which each model predicted the participants' answers correctly during the control session; that is, without PPC cTBS. For the linear and delayed force fields, the FOP model could predict the participants' answers with a probability >0.8. The POF model, however, was able to predict participants' answers only for the linear force field with a statistically significant decrease in prediction capabilities for the delayed force field (Wilcoxon signed-ranks test, z = 2.934, p = 0.001). Comparing the prediction capabilities of the FOP and POF models for the delayed force field, we saw a clear advantage of the FOP model (Wilcoxon signed-ranks test, z = 2.805, p = 0.002).

Figure 6.

A, Example of probing trajectory as a function of time. Hand position (blue line) and sensed force (gray line) during a typical trial while probing a delayed force field. B, Example of model fitting. The stiffness of the linear standard force field is represented by the blue line in the force-position diagram (slope = 85 N/m). When the subject probed a delayed standard force field, the typical force–position trajectory is elliptical, as shown by the gray dots representing the example in A. Multiple ellipses can be seen because the participant probed the force field multiple times in this trial. By fitting the FOP regression model to these points, we get a lower stiffness slope as shown by the red line (71.9 vs 85 N/m in this trial). In contrast to the FOP, when fitting the POF regression model to the data points, the stiffness slope increased as shown by the yellow line (94.3 vs 85 N/m). C, Scores of the models predicting participants' answers during the control session calculated based on the probability of the model to predict the participants' answers correctly. Symbols indicate the average score of the FOP (square) and POF (triangle) for the delayed and linear force fields with 95% confidence interval. Although, for the linear field, there is no difference between the score of the models, for the delayed field, the FOP model better predicted participants' answers (horizontal line indicates statistically significant difference, p = 0.002).

For the cTBS condition, the prediction probability of both models did not change for the linear force field, but decreased significantly for the delayed force field, indicating that the models were not able to account for the additional cTBS-induced shift in perception.

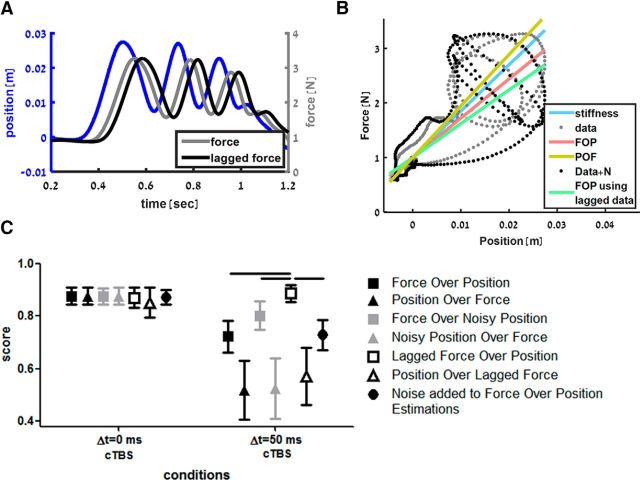
To account for the increase in stiffness underestimation in the PPC cTBS session, we suggest that the effect of cTBS can be modeled by altering the synchronization between the force and position signals used for stiffness estimation in the PPC. To alter the synchronization, we temporally lagged the force signal while keeping the position signal intact (see example in Fig. 7A,B). We tested two other signal manipulations. The first one was adding Gaussian noise to the position signal of all probing movements before performing the regression. The second manipulation was adding noise at the level of the decision model; that is, adding Gaussian noise to the stiffness estimations of the standard and comparison force field in each trial before choosing which one is stiffer. Overall, we compared seven models for the cTBS session. We fitted FOP and POF regression lines to the original data recorded during each trial for each participant, to the force and noisy position data, to the position and lagging force data and, by adding noise to the FOP-based stiffness estimations used by the decision model.

Figure 7.

A, Example of lagging the recorded force signal. Same example as in Figure 6A in which the gray line represents the delayed force sensed by the participant and the black line represents a lagged version of this force used to explain the cTBS effect (lag = 40 ms). B, Example of FOP model fitting to original data and lagged data. All the notations are similar to Figure 6B. Black dots represent the lagged force–position trajectory of the example in A. When the FOP model is fitted to the lagged data points (green line), the stiffness slope decreases even further (61.9 vs 85 N/m in this trial). This mimics the increased underestimation of the delayed force field stiffness after PPC cTBS. C, Score of the models predicting participants' answers during the PPC cTBS session. Similar to Figure 6C, the average score of each model is represented by different symbols and colors. For the linear force field, the scores of all models were similar. However, for the delayed force field, we found that the FOP model fitted to the lagged force and hand position data is statistically significantly better than all the other models. This suggests that the cTBS effect can be modeled as a desynchronization between the force and position information. Horizontal lines indicate statistically significant difference (p < 0.05).

While calculating the models, we searched for the optimal parameter for each subject that would maximize the proportion of trials in which the model answer predicted the participant's answer correctly. For the noise-based models, the noise added to each hand position data point was drawn from a Gaussian probability function with zero mean and optimized SD. For the models in which we added noise to the position signal, we found that, across subjects, the mean optimized noise SD for the FOP model was 0.82 ± 0.32 cm (n = 11) and, for the POF model, it was 0.12 ± 0.1 cm. For the model in which we added noise to the stiffness estimation values, we found that, across subjects, the mean optimized noise SD was 6.8 ± 9.8 N/m. In a similar way, for the temporal-lag-based models, we searched for the optimal lag between the force and position signals. Across subjects, the mean optimized lag for the FOP model was 61 ± 40 ms and for the POF model it was 22 ± 45 ms.

Across all subjects (Fig. 7C), we found that all models were able to predict participants' answers while comparing the standard linear force field with the comparison force fields. In this case, while comparing two linear force fields, the different possible cTBS effects that we examined affect the stiffness estimation of the these force fields in a similar way. Because the difference between the two estimations remains similar, the decision which of the two fields is stiffer remains the same as well regardless of whether the model captures the estimation of the participants. However, for the delayed force-field case, we found statistically significant differences between models' score (Friedman test, χ₍₆₎² = 50.67, p < 0.001). The FOP regression line fitted to the position and lagged force signals was the best model in predicting participants' answers compared with other models for (all post hoc comparisons z > 2.6, p < 0.05), suggesting that the effect of cTBS may be successfully explained as an additional lag of force sensory inputs.

Introducing additional external delay increased underestimation of delayed force-field stiffness in a similar way to PPC cTBS

In this section, we demonstrate how the FOP model with added delay between force and position signals can account for the increased underestimation of the delayed force field stiffness after PPC cTBS. We first explain analytically the increase in stiffness underestimation using the FOP model and then we test these predictions using the stiffness perception experiment in which we added an additional delay to the force feedback of both linear and delayed force fields.

Considering Equation 2, for a spring with force lagging hand position by τ samples; that is, f[i] = Kx[i − τ], we can write an expression for the estimated stiffness as follows:

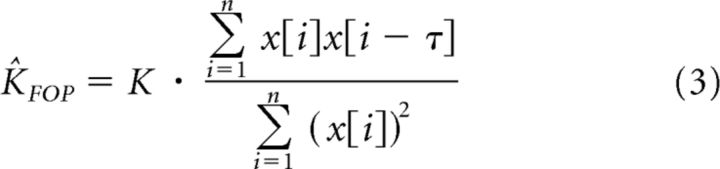Assuming that the probing motion can be represented using a sinusoidal function (e.g., see Fig. 6A), we can rewrite Equation 3 as follows:

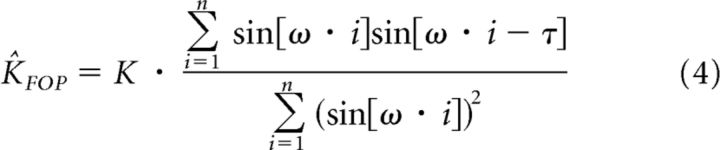As explained previously, the stiffness estimation changes according to the covariance function in the numerator. For the sine wave we can replace this expression by 0.5 · cos(ω · τ). This function has a value of 1 when there is no lag between force and position signals, that is, τ = 0, and its value decreases in a nonlinear fashion as the lag increases. Because the covariance in the numerator decreases with increased lag value, the stiffness estimation decreases as well when the lag increases.

According to this model, the delay that we introduced during the experiment decreased the value of the covariance between force and position signals, which resulted in underestimation of stiffness. This stiffness underestimation was larger after PPC cTBS. We suggest that the effect of cTBS introduces an additional lag between the signals. For example, if movement frequency is equal to 2 Hz, for the non-cTBS session, the FOP stiffness estimation for the comparison force fields is equal to the nominal stiffness value, 40–130 N/m, and the stiffness estimation for the delayed standard force field will be equal to 85 · cos(2π · 2 · 0.05) = 68.7 N/m. This means that the delayed force field will be perceived as stiffer than the comparison force field with a stiffness value of 60 N/m, but more compliant than the one with a stiffness value of 70 N/m. For the cTBS session, assuming just for the sake of illustration an additional lag of 20 ms, the estimated stiffness value for a comparison linear force field with stiffness K is K · cos(2π · 2 · 0.02) = K · 0.968 and the estimated stiffness for the delayed force field will be equal to 85 · cos(2π · 2 · (0.05 + 0.02)) = 54.18 N/m. In this case, the delayed force field will be perceived as stiffer than the comparison force field with a stiffness value of 50 N/m, but more compliant than the one with a stiffness value of 60 N/m (50 · 0.968 < 54.18 < 60 · 0.968). This example shows how added lag can decrease the PSE of the delayed force field.

To test our suggested model for the cTBS effect, we conducted Experiment 3, in which, instead of a cTBS session, participants performed an added delay session in which additional lag was introduced between force and position signals in the linear and in the delayed force fields. To do so, we delayed the force feedback in all force fields by 50 ms (+50 ms condition). This means that participants compared between the comparison and standard force fields while the force feedback was delayed by 50 ms for all or between the comparison force fields that were delayed by 50 ms and the standard force field that was delayed by 100 ms. We used this condition in addition to the original condition in which participants compared nondelayed comparison force fields with either a linear or delayed standard force field (control condition). We chose to add 50 ms based on the mean optimized lag for the FOP model explaining the cTBS effect: 61 ± 40 ms. We avoided introducing >50 ms of additional delay that would lead to an overall delay larger than 100 ms and thus potential instability of the haptic rendering.

The results of Experiment 3 (added delay) were similar to the results of Experiment 1 (cTBS), providing further support to our model of cTBS effect (Fig. 8). We found that the delay factor caused a significant shift of PSE (F_(1,10) = 75.822, p < 0.001, η_p² = 0.883), that additional delay also led to a significant difference in PSE values (F_(1,10) = 19.953, p = 0.001, η_p² = 0.666), and that the interaction between delay and added delay factors was statistically significant (F_(1,10) = 29.851, p < 0.001, η_p² = 0.749). Post hoc analyses showed that, when force feedback delay was not identical between the comparison and standard force fields, PSE values were significantly smaller than PSE values when force feedback was not delayed or identically delayed in both the standard and the comparison force fields (in the control condition: t₍₁₀₎ = 6.45, p < 0.001; in the +50 ms condition: t₍₁₀₎ = 8.85, p < 0.001). Although we found negative PSE values for the delayed standard force field in the control session, the PSE value of this force field became smaller when we delayed the force feedback of both the comparison and standard force fields (−32.48 ± 7.55 vs −15.76 ± 5.19; t₍₁₀₎ = 5.29, p < 0.001).

Figure 8.

Increased external delay between force and position signals mimics the effect of cTBS. A, Psychometric curves fitted to the answers of a typical participant in the control session (solid lines) and in the session with the added delay (+50 ms; dashed lines). B, Individual PSE values across all participants for the four conditions. C, Mean PSE values across all participants for the four conditions. Error bars are 95% confidence intervals estimated using t distribution. ***p < 0.001.

Discussion

Stiffness perception is a high-level process requiring the integration of position and force signals. To date, it is still unknown how the brain combines these different inputs to generate a percept of stiffness. In the present study, we show for the first time that the PPC has a causal role in integrating position information to sensed force feedback for estimating stiffness. Consistently with prior studies, participants underestimated the stiffness of delayed force fields compared with linear force fields (Nisky et al., 2008; Nisky et al., 2010). Importantly, we showed that a virtual lesion of PPC increases the underestimation of stiffness during perceptual judgments of delayed force fields. This cTBS effect was a pure perceptual bias because we did not find any change in the pattern of probing movements or in the discrimination sensitivity.

We modeled perceptual cTBS effects as a distortion of the processing of sensory inputs within the PPC. By increasing the phase between force and position signals, our model could replicate the increased underestimation of stiffness and fully predict the participants' discrimination performance in the task. Thus we could explain the mechanism by which cTBS acts on the PPC by quantifying the lag between the sensory inputs and relating cTBS effects to measured behavioral deficits.

Pressman et al. (2007) showed that the bias in stiffness perception of a delayed force field depends on the value of delay that was used in the virtual reality environment. In this study, we show that the same effect may be achieved using offline brain stimulation. In addition, we present a novel, quantifiable measure of the amount of distortion in neural processing of sensory inputs. Neuronal recordings of TMS effects in an anesthetized cat showed that the differential firing rate of V1 neurons during visual stimulus presentation versus rest was affected, altogether leading to a disorganized phase locking between spikes and brain oscillations (Allen et al., 2007). However, the causal link between distortion in neural activity and behavioral performance is still missing. Here, we demonstrate a link between distorted processing of position and force signals in the PPC and its effect on perceptual behavior. This new approach is important to assess the level of TMS-induced interference in brain areas other than M1, for which motor evoked potentials cannot serve as a readout of TMS effects.

The PPC has classically been linked to object orientated actions (Castiello, 2005; Grafton, 2010; Davare et al., 2011). While posteromedial regions of the intraparietal sulcus (IPS) contribute to the planning of reaching movements toward an object (Davare et al., 2012), anterolateral parts of the IPS integrate grasp-related information about the object (Tunik et al., 2005; Davare et al., 2007; Davare et al., 2010), with a gradient or interactions among these areas likely to reflect the degree of online control required by the action (Grol et al., 2007; Verhagen et al., 2013). Conversely, perception of an object's visual or tactile properties is classically thought to rely on areas located in the occipitotemporal pathway, termed the lateral occipital complex (Amedi et al., 2001). However, it has also been found that the PPC underlies perception of an object's multimodal features by processing both visual and haptic object attributes (Grefkes et al., 2002). As suggested by Dijkerman and de Haan (2007), the specificity of the PPC in guiding skilled hand actions toward objects provides this brain region with powerful neural tools for processing inputs related to visual or haptic object recognition. Object manipulation requires processing of both finger positions and contact forces exerted on the object (Davare et al., 2007; Fu et al., 2010); therefore, haptic object exploration may rely on the same neural resources for integrating position and force signals.

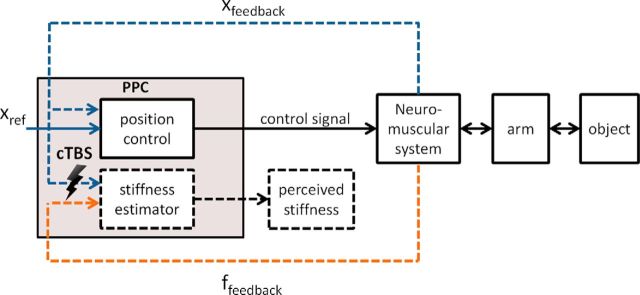
Here, we provide new evidence that the PPC has a role in encoding mechanical properties of objects, in particular stiffness. By mapping force readout onto position data, the PPC can extrapolate the slope of this relationship, which defines the object's stiffness. In our model, the mapping of force onto position implies that the PPC may act as a “position control-based estimator,” thus assuming position as an independent variable and force as a measured dependent variable. Although this model suggests that the PPC is regulating position signals for the purpose of stiffness estimation, we did not find distortion of movement characteristics. This is in contrast to the results of Chib et al. (2009), who reported that, during object manipulation, the PPC was causally responsible for controlling position. However, it is noteworthy that the PPC may only contribute to encoding kinematic parameters when movements are performed toward a target object (e.g., encoding of movement direction and digit positioning for reaching and grasping, respectively; see Davare et al., 2012, 2007). The role of PPC in encoding the kinematics of goal-directed movements might be different from how the PPC controls probing movements, the purpose of which is merely collecting and integrating sensory information. Importantly, our findings suggest that the PPC also houses a stiffness estimator or at least changes the alignment between position and force signals before an estimator located further downstream computes the stiffness. This highlights a significant role of PPC for perception in addition to its already established role in controlling actions.

These results provide the first causal evidence for the neural mechanism underlying stiffness judgment. We suggest that a regression-based model that assumes increased lag between position and force signals in the PPC can explain the effect of TMS on stiffness perception in the presence of delay (Fig. 9). An alternative explanation of the effect of TMS may suggest a distortion of the stiffness estimator per se (e.g., adding noise to the output of the estimator rather than to the position input). In such a case, we would expect a decrease in stiffness discrimination sensitivity. However, such a decrease was not observed here: the JND measurement was similar across our experimental conditions.

Figure 9.

Schematic diagram of the implementation of stiffness estimation. The PPC is responsible for generating arm movements by controlling arm position based on a reference position signal (X_ref) (Chib et al., 2009). In the current study, we demonstrate that the PPC is causally involved in stiffness perception, which can be modeled as an estimation based on the slope of a force over position regression. We suggest that TMS distorts the synchronization of position and force signals used by the stiffness estimator.

We examined TMS effects on a brain area involved in processing position using a task context known to rely on a position control scheme. As Nisky et al. (2008) showed, when frequently crossing the boundary of the elastic field and experiencing abrupt changes in the force fed back to the hand, effects on stiffness perception may rather depend on a force control scheme. Prior studies support the existence of a force controller in the motor system (Favilla et al., 1989; Mugge et al., 2009; Mugge et al., 2010; Squeri et al., 2010), but a specific area in the brain that may house such controller has not been clearly identified to date. Some studies suggested candidate brain areas in the primary sensorimotor and premotor cortices (Floyer-Lea and Matthews, 2004). Identifying such location will allow further TMS studies to explore causal force control in stiffness perception tasks and conditions in which the force control policy is dominant, such as probing with frequent boundary crossing (Nisky et al., 2008).

Conclusion

We provide a computational model for stiffness perception and show a causal relationship between neural processing in the PPC and the formation of a stiffness percept. Using offline TMS, we were able to enhance stiffness underestimation for delayed force fields and model this effect as being consequent to desynchronization between the force and position signals. Understanding of the neural mechanisms that underlie estimation of stiffness in the sensorimotor system and the effects of delay on stiffness perception formation is important for practical applications such as teleoperation (Nisky et al., 2013), as well as for advancing the general understanding of how perceptual mechanisms integrate multiple sensory inputs for estimating mechanical properties of objects in our environment.