Spatiotemporal Distribution of Location and Object Effects in Primary Motor Cortex Neurons during Reach-to-Grasp

Abstract

Reaching and grasping typically are considered to be spatially separate processes that proceed concurrently in the arm and the hand, respectively. The proximal representation in the primary motor cortex (M1) controls the arm for reaching, while the distal representation controls the hand for grasping. Many studies of M1 activity therefore have focused either on reaching to various locations without grasping different objects, or else on grasping different objects all at the same location. Here, we recorded M1 neurons in the anterior bank and lip of the central sulcus as monkeys performed more naturalistic movements, reaching toward, grasping, and manipulating four different objects in up to eight different locations. We quantified the extent to which variation in firing rates depended on location, on object, and on their interaction—all as a function of time. Activity proceeded largely in two sequential phases: the first related predominantly to the location to which the upper extremity reached, and the second related to the object about to be grasped. Both phases involved activity distributed widely throughout the sampled territory, spanning both the proximal and the distal upper extremity representation in caudal M1. Our findings indicate that naturalistic reaching and grasping, rather than being spatially segregated processes that proceed concurrently, each are spatially distributed processes controlled by caudal M1 in large part sequentially. Rather than neuromuscular processes separated in space but not time, reaching and grasping are separated more in time than in space.

SIGNIFICANCE STATEMENT Reaching and grasping typically are viewed as processes that proceed concurrently in the arm and hand, respectively. The arm region in the primary motor cortex (M1) is assumed to control reaching, while the hand region controls grasping. During naturalistic reach–grasp–manipulate movements, we found, however, that neuron activity proceeds largely in two sequential phases, each spanning both arm and hand representations in M1. The first phase is related predominantly to the reach location, and the second is related to the object about to be grasped. Our findings indicate that reaching and grasping are successive aspects of a single movement. Initially the arm and the hand both are projected toward the object's location, and later both are shaped to grasp and manipulate.

Introduction

Reaching and grasping typically have been considered to be two parallel processes that proceed concurrently in time but are segregated in both musculoskeletal and neural space (Jeannerod, 1984, 1986; Rizzolatti et al., 1998; Cavina-Pratesi et al., 2010; Cisek and Kalaska, 2010; Grafton, 2010; Davare et al., 2011). One's arm reaches for a cup controlled by a more dorsal stream of neural activity from the posterior parietal cortex to the dorsal premotor cortex to the primary motor cortex (M1). At the same time, one's hand preshapes to grasp the cup controlled by a more ventral stream from the anterior intraparietal area to the ventral premotor cortex to M1. Within M1, the reaching arm is controlled from the proximal upper extremity representation, while the grasping hand is controlled from the distal upper extremity representation. Because of this dual-stream view, studies of the neural activity underlying reaching and grasping by and large have focused either on reaching to various locations while grasping the same (or no) object (Georgopoulos et al., 1986; Fu et al., 1995; Moran and Schwartz, 1999a; Sergio et al., 2005; Churchland et al., 2012), or else on grasping a variety of objects, all presented at the same location (Mason et al., 2002; Spinks et al., 2008; Hendrix et al., 2009; Saleh et al., 2010).

Neural control of reaching and grasping from M1 may not be as spatially segregated as commonly thought, however. Generalized linear models that incorporate both arm and hand kinematics indicate that single M1 neurons can encode information on the kinematics of both the arm and the hand (Saleh et al., 2012). Moreover, the reach-to-grasp kinematics of both the arm and the hand can be decoded from populations of rostral M1 neurons recorded from the crown of the macaque precentral gyrus (Vargas-Irwin et al., 2010), even though distal representation on the crown of the gyrus is small compared with proximal representation (Kwan et al., 1978; Park et al., 2001). Though the distribution of neurons contributing to encoding or decoding of proximal versus distal aspects of combined reach-to-grasp movements has not been examined explicitly, these findings raise the possibility that control of reaching and of grasping each might be distributed widely in M1.

Furthermore, although many encoding and decoding models assume consistent relationships between some particular subset of movement and/or muscle parameters and the activity of a given M1 neuron (Moran and Schwartz, 1999b; Morrow and Miller, 2003; Griffin et al., 2008), other studies have suggested that these relationships might change over the time course of single movements. During reaching, for example, target direction, position, and distance were found to be encoded sequentially in the firing rate of many single M1 neurons (Fu et al., 1995). Other studies indicate that M1 neurons encode temporally extended movement fragments (Hatsopoulos et al., 2007), rather than continuously representing a subset of parameters with fixed weightings.

We recently found that during naturalistic reach–grasp–manipulate movements, both joint angles and muscle activity from the shoulder to the hand varied with location and with object (Rouse and Schieber, 2015b, 2016). Furthermore, rather than proceeding in parallel, two sequential phases were evident: an early phase of larger location-related variation followed by a later phase in which object-related variation predominated. We therefore examined the temporal evolution and the spatial distribution of location-related and object-related variation in the activity of M1 neurons as monkeys performed a reach–grasp–manipulate task that dissociated location and object.

Materials and Methods

Subjects and behavioral task.

Two rhesus monkeys—L and X (both males weighing 9–11 kg)—were subjects in the present study. All procedures for the care and use of these nonhuman primates followed the Guide for the Care and Use of Laboratory Animals and were approved by the University Committee on Animal Resources at the University of Rochester, Rochester, New York.

Each monkey performed a behavioral task—described in detail previously (Rouse and Schieber, 2015b)—that dissociated the location to which the monkey reached from the object the monkey grasped and manipulated. Four objects—a coaxial cylinder, a perpendicular cylinder, a button, and a sphere—were arranged at 45° intervals on a circle. Each of these peripheral objects was positioned at a 13 cm radius from a fifth, center object, another coaxial cylinder. Between blocks of trials, the entire apparatus was rotated about the center object such that different peripheral objects were located at up to eight locations, spanning a range from 0° (to the monkey's right on the horizontal meridian) to 157.5° (to the left, 22.5° above the horizontal meridian) in steps of 22.5°. Of the 32 possible location–object combinations (eight locations × four objects), we used only 24 because of three factors (described in detail previously): visual occlusion of some locations by the primate chair, biomechanical limitations of the arm, and mechanical constraints of the apparatus.

The monkey initiated each trial by grasping and pulling on the central object, positioned 32 cm in front of the shoulder. After a variable initial hold period (1500–2000 ms for monkey L and 1000–1500 ms for monkey X), blue LEDs were illuminated around the base of the horizontal rod supporting one of the four peripheral objects, instructing the monkey to reach to, grasp, and manipulate that object. The onset of movement was identified from motion-capture data as the monkey released the center object. Peripheral object contact was detected with semiconductor strain gauges mounted on the horizontal supporting rods. Upon grasping, the monkey pulled the perpendicular cylinder, pulled the coaxial cylinder, pushed the button, or rotated the sphere, closing a separate microswitch by manipulating each object appropriately. Green LEDs at the base of the horizontal rod supporting the manipulated object were illuminated as long as the microswitch was closed. The monkey then was required to hold the switch closed for 1000 ms before receiving a water reward. Trials of different objects were presented in a pseudorandom block design.

Errors occurred if the monkey failed to release the center object within 1000 ms of the blue LED instruction onset, failed to contact the instructed peripheral object within 1000 ms of releasing the center object, contacted the wrong peripheral object, or failed to maintain the static, final hold position for 1000 ms. Following any error, the trial was aborted immediately and the same object was presented on subsequent trials until the trial was performed successfully. Because the monkey thus knew which type of trial would follow an error trial, both error trials and successful trials immediately preceded by an error trial were excluded from analysis. All aspects of the behavioral task were controlled by custom software running in Tempo (Reflective Computing), which also sent behavioral event markers into the collected data stream.

Neural recordings.

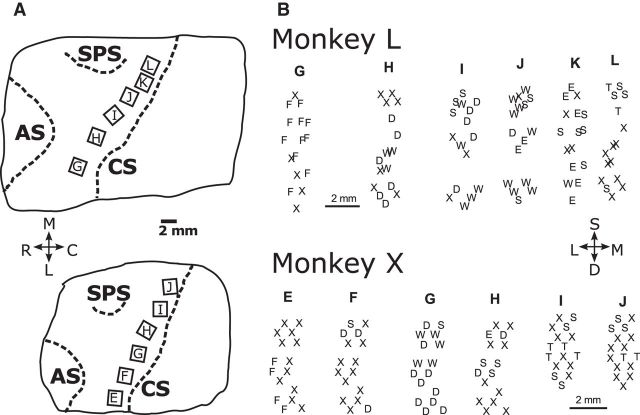
Floating microelectrode arrays (FMAs; MicroProbes for Life Sciences) were implanted in the cerebral cortex of each monkey, using procedures described in detail previously (Mollazadeh et al., 2011). Six FMAs, each with 16 recording electrodes (impedance, 0.5 MΩ; 70% Pt, 30% Ir), were implanted in M1 along the anterior bank of the central sulcus so as to span the upper extremity representation (Fig. 1A). All FMAs had electrodes of various lengths, in monkey L ranging from 1.5 to 8.0 mm on each array, and in monkey X from 1.5 to 6.0 mm on arrays E through H and from 1.5 to 4.5 mm on arrays I and J. After recovery, movements evoked by conventional trains of intracortical microstimulation (ICMS; consisting of 12 biphasic, cathodal first, 0.2 ms per phase, pulses at 3 ms intervals) at currents ≤100 μA were observed for each electrode. Plotting the threshold movement at the location of each electrode tip—estimated from intraoperative photographs of the implanted FMAs (Fig. 1A) and the known length of each microelectrode—demonstrated that in each monkey, trunk movements were evoked from some of the most medial electrodes and facial movements from some of the most lateral, with upper extremity movements of the shoulders, elbow, wrist, and digits evoked in between (Fig. 1B).

Figure 1.

A, Location of arrays in the anterior bank of the central sulcus for monkeys L and X. Array locations were determined from intraoperative photographs relative to the cortical sulci. CS, Central sulcus; AS, arcuate sulcus; SPS, superior precentral sulcus. Orientation crosshairs: M, medial, up; L, lateral, down; R, rostral, left; C, caudal, right. B, Spatial map of twitch movements evoked by threshold intracortical microstimulation delivered through each individual electrode. S, Shoulder; E, elbow; W, wrist; D, digits; F, face; T, trunk; X, no response with currents ≤100 μA. The three-dimensional location of each electrode tip was estimated from the location and orientation of the array (indicated by the letter at the top of each column) in the intraoperative photograph and the known length of the individual electrodes on each array. Three-dimensional sites then were projected onto a two-dimensional plane approximately parallel to the anterior bank of the central sulcus. Orientation crosshairs: S, superficial, up; D, deep, down; L, lateral, left; M, medial, right.

In daily sessions, neural data was collected with a Plexon data acquisition system as the monkey performed the reach, grasp, and manipulate task described above. Signals from each FMA were amplified 20× by a head stage and then hardware filtered [100 Hz (two-pole) to 8 kHz (four-pole)]. Neuron spiking activity from each of the 96 recording electrodes was amplified to a final gain of 1000–32,000×, and spike waveforms crossing a threshold selected on-line by an investigator were sampled at 40 kHz and saved to disk by Sort Client (Plexon).

Off-line, the spike waveforms from each channel were sorted initially by manually identifying spike clusters with Offline Sorter (Plexon). Then a custom algorithm was used to refine the sorting. After this sorting process was complete, two criteria were used to assess the quality of isolation for each sorted unit. First, the number of interspike interval (ISI) violations (<1 ms), v_ISI, was used to estimate the fraction of false-positive spikes, f_F, that might have originated from another neuron or noise source (Meunier et al., 2003; Hill et al., 2011; Eq. 1):

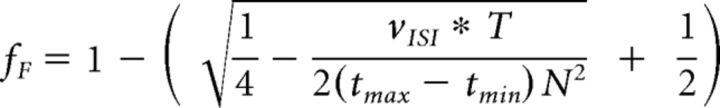where N is the total number of sorted spikes, T is the total duration of the recording session, t_max is the chosen refractory period (1 ms), and t_min is the waveform sort width following threshold crossing during which no new spikes can be detected (0.675 ms). Second, a signal-to-noise ratio (SNR) was calculated as follows: SNR = $\frac{A}{2{\sigma }_{noise}}$, where A is the peak-to-peak amplitude of the mean waveform across all spike waveforms in the cluster and σ_noise is the SD of the residual noise after subtracting the mean at each of the 32 sampled waveform time points. After sorting was complete, we considered those sorted units with an SNR ≥3 and no ISI violations (v_ISI = 0, f_F = 0) to be “definite” single units. Sorted units with an SNR ≥2.5 and an estimated ≥90% true spikes (f_F ≤ 0.1) were considered to be “probable” single units. Sorted units with 2.5 > SNR ≥ 1.5 and/or f_F > 0.1 were considered “multiunits.” Any sorted units with SNR <1.5 were discarded from further analysis.

Data analysis.

The firing rate of each definite single unit, probable single unit, or multiunit was estimated from its recorded spike times using Gaussian smoothing to focus on temporal trends rather than precise spike timing (Cunningham et al., 2009). Each spike train binned at 1 ms intervals was convolved with a Gaussian kernel (σ = 50 ms) in 1 ms time steps, providing a smooth firing rate profile with the temporal resolution needed to assess transitions during the present reach–grasp–manipulate movements.

Binned firing rates tend to resemble counts of a Poisson process and thus have higher trial-to-trial variance when the firing rate is higher. After convolution with the Gaussian kernel, we therefore applied square-root transformation to the smoothed firing rates (Kihlberg et al., 1972; Snedecor and Cochran, 1980; Ashe and Georgopoulos, 1994). The square-root transformation renders variance similar from low to high firing rates, making comparison of different rates more reliable. Moreover, square-root transformation makes a Poisson distribution closer to the normal distribution assumed in ANOVA (see below).

Because the duration of trials varied, for analysis the spike times and firing rates in each trial were aligned separately on four behavioral events: appearance of the instruction (I), onset of movement (M), peripheral object contact (C), and beginning of the final hold (H). To analyze as much data as possible around each event while minimizing overlap between sequential epochs, for each monkey we first calculated the median time between alignment events in each session, and then found the minimum median times across all sessions. For monkey L, the minimum median times were as follows: I–M, 243 ms; M–C, 228 ms; and C–H, 82 ms. We then split these durations before and after each event, analyzing the following: 122 ms after I, 122 ms before and 114 ms after M, 114 ms before and 41 ms after C, and 41 ms before and 100 ms after H, for a total of 658 time points. For monkey X, the minimum median times were as follows: I–M, 280 ms; M–C, 209 ms; and C–H, 113 ms. In monkey X, we therefore analyzed the following: 140 ms after I, 140 ms before and 105 ms after M, 105 ms before and 57 ms after C, and 57 ms before and 100 ms after H, for a total of 708 time points.

Two-way ANOVA then was performed on the firing rate of each unit using the two factors of location (eight categories from 0° to 157.5° in 22.5° steps) and object (four categories: perpendicular cylinder, coaxial cylinder, button, and sphere) as well as their interaction (location × object). At each 1 ms time step, t, the ANOVA model was used to quantify effect size, η_i²(t), the fraction of the total variance explained by each main factor and by their interaction as follows (Eq. 2):

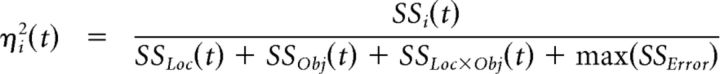where i is location (Loc), object (Obj), or their interaction (Loc × Obj), and SS_i(t) is the sum of squares from ANOVA. We observed that the error (unexplained) variance often fluctuated considerably at different time points. In particular, some units had very low firing rates during particular temporal epochs of the present task, causing the total sum of the squares to be close to zero and thus making calculation of η² unstable. Rather than including the error sum of squares from the ANOVA at each time point, SS_Error(t), as a term in the denominator, we chose instead to normalize η_i²(t) by using the maximum error sum of squares observed across all time points during the trials, max(SS_Error). This choice of a single, constant SS_Error value rather than a time-varying SS_Error effectively compares how effect sizes vary across time rather than how effect sizes compare to noise at each time point. This normalization thereby enabled more straightforward examination of effect sizes as a function of time. Moreover, for the population of units in each monkey, we found (1) that the times of the max(SS_Error) for different units were distributed relatively evenly across all trial time points, and (2) that the ratio SS_Error(t)/max(SS_Error) averaged across all units was similar for all time points (data not shown). Hence the time courses of effect sizes reported below are unlikely to result from the max(SS_Error) occurring consistently at some particular time in the trials.

We evaluated the significance of each effect at each time point with an ANOVA F test, Bonferroni corrected for multiple comparisons [i.e., using a significance threshold of p < 0.05 divided by the number of tests performed, which here was the number of time points × 3 factors (Loc, Obj, and Loc × Obj), resulting in 658 ms × 3 factors = 1974 tests for monkey L, and 708 ms × 3 factors = 2124 tests for monkey X]. Hence the result of each F test was considered significant only for p < 0.05/1974 = 0.000025 in monkey L, and p < 0.05/2124 = 0.000024 in monkey X. Only those sorted units that showed at least one significant effect at one point in time were included in subsequent analyses (we note, however, that of units with any significant effect, <10 units in each monkey showed <20 significant tests).

We also used the ANOVA model to compute a quotient, Q_m(t), that compared the relative sizes of the location and object effects as follows (Eq. 3):

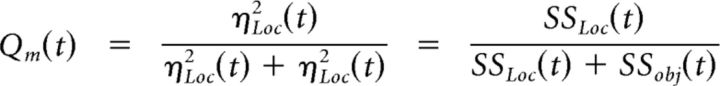Note that because the same denominator was used to calculate the η_i²(t) for both location and object (Eq. 2), the same Q_m(t) could be calculated simply using SS_Loc(t) and SS_Obj(t). Hence Q_m(t) is independent of our choice of the particular error term used in calculating effect sizes. Q_m will be close to 1 when the location effect is much larger than the object effect, close to 0.5 when the two effects are similar in size, and close to 0 when the object effect is much larger than the location effect.

Results

We analyzed sorted units in 14 sessions from monkey L and 8 sessions from monkey X. Table 1 lists the number of definite single units, probable single units, and multiunits obtained in each session. In each monkey, approximately a third of the sorted units were definite single units, a quarter were probable single units, and the remainder were multiunits. Although many of our results below are shown for all three types of units pooled together, we note here that more than half of the overall results in each monkey probably reflected the modulation of individual neurons.

Table 1.

Recording sessions and sorted units^a

Recording sessions	Definite single units	Probable single units	Multiunits	Total	Unique single units
Monkey L
L20120924	31	22	43	96	27
L20120926	13	19	37	69	12
L20120927	19	25	39	83	16
L20120928	35	22	41	98	29
L20121003	15	15	17	47	8
L20121004	17	17	14	48	11
L20121005	26	10	24	60	16
L20121009	12	12	26	50	6
L20121010	24	23	27	74	18
L20121012	27	13	22	62	22
L20121016	10	16	19	45	6
L20121017	13	9	26	48	7
L20121022	12	9	17	38	9
L20121024	13	15	21	49	11
Totals (%)	267 (31%)	227 (26%)	373 (43%)	867 (100%)	198
Monkey X
X20121206	17	9	23	49	12
X20121207	14	12	26	52	5
X20121210	18	14	28	60	9
X20121212	21	10	25	56	9
X20121213	18	21	25	64	6
X20121214	22	19	20	61	14
X20121218	29	10	21	60	16
X20121219	19	17	27	63	9
Totals (%)	158 (34%)	112 (24%)	195 (42%)	465 (100%)	80
Grand totals (%)	425 (32%)	339 (25%)	568 (43%)	1332 (100%)	278

^aIn the first four sessions from monkey L, recordings were made from all six M1 arrays, whereas in the remainder of the sessions from monkey L, recordings included only the four central arrays: H, I, J, K. In monkey X, all six arrays were recorded in all sessions.

We also examined definite single units across sessions to identify cases in which the same unit had been recorded in multiple sessions. For each definite single unit, we applied an algorithm that compared a number of features—the unit's waveform shape, mean firing rate, and autocorrelogram, as well as its pairwise cross-correlograms with other units from the same session—across different sessions to determine whether the same unit was recorded from the same electrode in multiple sessions (Fraser and Schwartz, 2012). Of the 267 definite single units in the 14 sessions from monkey L, we identified 198 unique single units, 37 of which had been recorded in multiple sessions. Likewise, of the 158 definite single units in the 8 sessions from monkey X, we identified 80 unique single units, 31 of which had been recorded in multiple sessions. For those unique single units recorded in multiple sessions, the Results below are reported only from the session in which each unique single unit had its largest SNR (numbers from each session are given in Table 1).

Firing rate variation with location and object

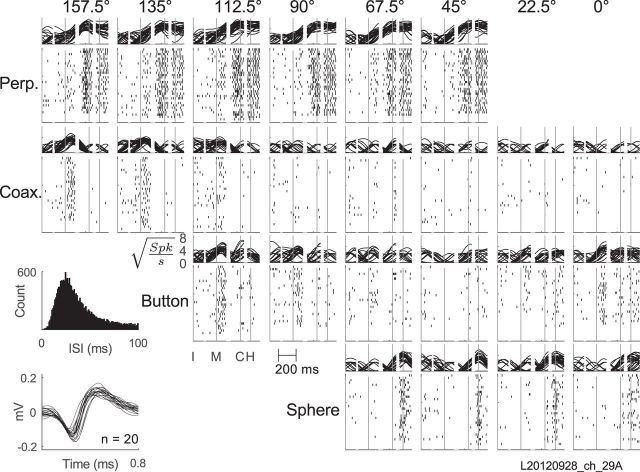
The activity of a definite single unit recorded from array H in monkey L is shown in Figure 2. For each of the 24 combinations of location and object, sweeps of smoothed firing rate in all trials have been overlapped above and spike rasters have been formed below, with activity aligned separately around each of the four behavioral events: appearance of the instruction, onset of movement, peripheral object contact, and beginning of the final hold. This example unit was most active around the time of peripheral object contact and final hold for movements involving the perpendicular cylinder. Further inspection also shows a small burst of firing just after the onset of movements, particularly those involving the coaxial cylinder and button when these objects were in relatively counterclockwise locations (e.g., 112.5–157.5° for the coaxial cylinder). The firing rate of this single unit thus increased both around the time of movement onset and around the time of peripheral object contact and final hold, though not necessarily for the same location–object combinations.

Figure 2.

Activity of an example single unit. For each of the 24 location (columns)–object (rows) combinations, overlapped square-root-transformed firing rates are shown above and spike rasters below, all aligned separately on the four behavioral events indicated by vertical lines. I, Instruction; M, movement onset; C, contact with the peripheral object; H, beginning of the final hold. Insets at lower left show (1) the unit's ISI histogram, and (2) 20 overlapped waveforms. With no ISIs <1 ms and an SNR of 5.95, this example unit was classified as a definite single unit. Perp., Perpendicular cylinder; Coax., coaxial cylinder.

Detailed inspection of Figure 2 shows that the firing rate of this example neuron also varied depending on both location and object, and furthermore that these dependencies changed over time. To illustrate this variation in greater detail, the firing rate of this example neuron sampled in individual trials at two different time points—movement onset and peripheral object contact—has been plotted in Figure 3, A and B respectively. The location to which the monkey reached in each trial has been plotted on the abscissae and different objects have been plotted as different symbols and colors. At the time of movement onset (Fig. 3A), the neuron's firing rate varied predominantly with location, being highest around 112.5° and lowest around 45°, but showed little systematic variation in relation to object. Figure 3B shows firing rates of the same neuron at the time of peripheral object contact. At this time the same neuron's firing rate showed little systematic variation with location, and instead variation depended predominantly on object, being generally highest for the perpendicular cylinder and lowest for the coaxial cylinder. The activity of the same neuron thus depended on location early and on object later in the same set of movements.

Figure 3.

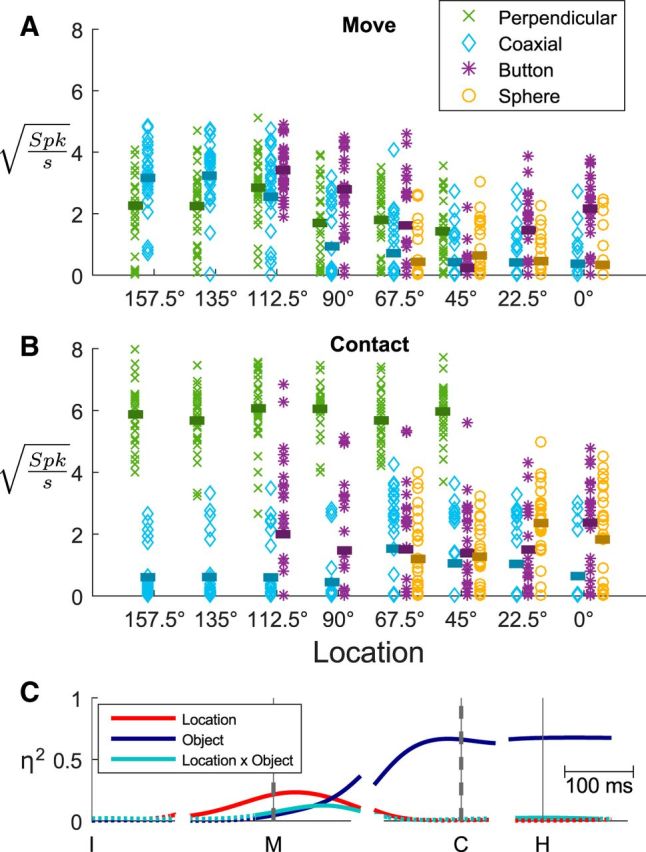
Variation in firing rates. A, For each successful trial, the firing rate of the neuron illustrated in Figure 2 at the time of movement onset has been plotted against location, with different objects represented by different symbols as indicated in the legend. Horizontal bars indicate the mean firing rate for each location–object combination. At movement onset, this unit's firing rate varied predominantly with location. B, The same neuron's firing rate has been plotted in the same fashion as A, but here using firing rates from the same trials at the time of peripheral object contact. At this time the neuron's firing rate varied predominantly with object. C, The sizes (η²) of location, object, and location × object interaction effects each have been plotted as a function of time around each behavioral event (vertical lines). Dashed vertical lines at M and C emphasize the times for which the firing rates from individual trials are shown in A and B, respectively. Solid lines indicate statistically significant effects; dotted lines indicate when effects were not significant.

To quantify the effects of location, of object, and of location × object interaction, η² values from two-way ANOVA as defined in Equation 2 were calculated at each 1 ms time point. Plotting these η² values as a function of time (Fig. 3C) revealed that the firing rate of this neuron, while low in amplitude, varied significantly in relation to location starting 115 ms after the appearance of the instruction, >122 ms before the onset of movement. Object effects and location × object interaction effects then became significant 26 and 27 ms before movement onset, respectively. As the time of contact with a peripheral object approached, the location and interaction effects both waned while the object effect waxed. The large object effect persisted after peripheral object contact and into the final hold, with a very small interaction effect reappearing. The activity of this example neuron thus showed an early phase of location-related variation and a later phase of object-related variation, with relatively small location × object interactions.

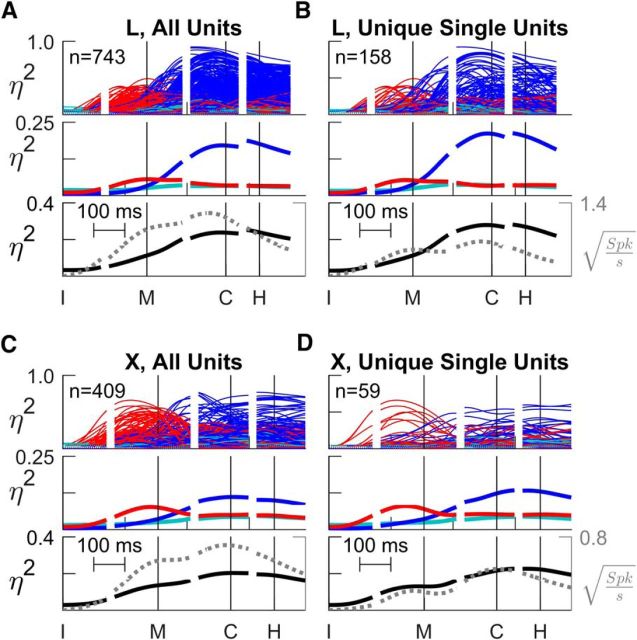
In both monkeys, a large majority (>70%) of sorted units of all types showed some significant effect (Table 2). The minority of sorted units with no significant effect were discarded from further analysis. Figure 4 shows plots of time-resolved η² values for all those sorted units that showed significant effects of any kind. Recordings from monkey L are shown above (A and B) and from monkey X below (C and D). The plots in the left column (A and C) include all sorted units from all sessions, whereas those in the right column (B and D) show only unique single units. In each panel, three frames show (1) overlapped traces of individual η² values (top), (2) averages across all units for each type of effect—location, object, and interaction (middle), and (3) total variance explained (black) plotted together with grand average firing rate (gray; bottom). The plots from both monkeys demonstrate that, like the example neuron described above, the firing rates of M1 neurons individually and on average showed a transition from location effects that began well before movement onset to object effects that began near movement onset and increased during the movement, becoming predominant by the time of peripheral object contact. Moreover, the same was true for all sorted units considered together (A and C) or unique single units only (B and D).

Table 2.

Units with significant effects^a

	Definite single units	Probable single units	Multiunits	Total	Unique single units
Monkey L
Significant	226 (85%)	203 (89%)	314 (84%)	743 (86%)	158 (80%)
Not significant	41 (15%)	24 (11%)	59 (16%)	124 (14%)	40 (20%)
Total	267 (100%)	227 (100%)	373 (100%)	867 (100%)	198 (100%)
Monkey X
Significant	123 (78%)	107 (96%)	179 (92%)	409 (88%)	59 (74%)
Not significant	35 (22%)	5 (4%)	16 (8%)	56 (12%)	21 (26%)
Total	158 (100%)	112 (100%)	195 (100%)	465 (100%)	80 (100%)

^aPercentages refer to the numbers of neurons with significant effects versus no significant effects for each type of sorted unit in each monkey.

Figure 4.

Time-resolved ANOVA. A, All sorted units from monkey L. B, Unique single units from monkey L. C, All sorted units from monkey X. D, Unique single units from monkey X. In each of these four panels (A–D), the top frame shows overlapped traces of location (red), object (blue), and location × object interaction (cyan) effect size (η²) as a function of time for each unit individually. The middle frame shows mean η² values across all individual traces from the top frame, averaged separately for location, object, and interaction effects. The bottom frame shows the sum of the three mean η² values, i.e., the total fraction of variance explained by the task factors (solid black line, left vertical axis), along with the mean change in firing rate from baseline (dashed gray line, right vertical axis). The baseline square-root firing rate for each unit was calculated in the 10 ms immediately following the instruction across all trials and subtracted from the square-root firing rate at all time points. All data have been aligned separately on the times of four behavioral events— instruction (I), movement onset (M), peripheral object contact (C), and beginning of final hold (H)—indicated by the vertical lines in each plot.

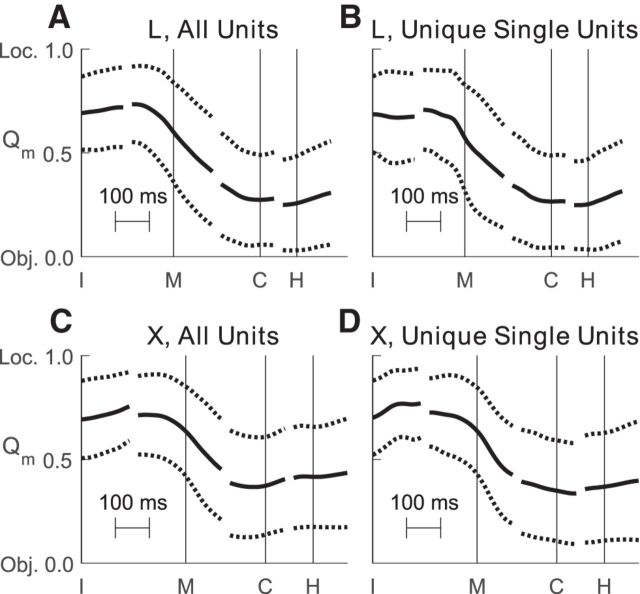
This transition from predominantly location-related firing rate variation to predominantly object-related variation was captured quantitatively by the ratio Q_m (Eq. 3). To examine the time course of this transition we calculated Q_m(t) for each unit shown in Figure 4, and then averaged separately across all sorted units and all definite single units in each monkey. Figure 5 shows the time course of these Q_m averages. Mean Q_m values for all sorted units at the onset of movement were 0.60 and 0.63 for monkeys L and X, respectively, indicating larger location effects than object effects. By the time of peripheral object contact, however, mean Q_m values were 0.27 and 0.37 for the two monkeys, indicating larger object effects than location effects. These differences in Q_m at movement onset versus peripheral object contact were significant both for all sorted units and for unique single units (paired-sample t test, p < 0.001).

Figure 5.

Time course of Q_m. Each panel shows the average time course (mean ± SD) of Q_m, an index that quantifies the relative size of location versus object main effects. Q_m is 1 if all task-related, main-effect variance is related to location, is 0.5 if location-related and object-related variance are equal, and is 0 if all such variance is related to object. Q_m is independent of the variance attributed to error (noise). All data have been aligned separately on the times of four behavioral events—instruction (I), movement onset (M), peripheral object contact (C), and beginning of final hold (H)—indicated by the vertical lines in each plot. A, All sorted units from monkey L. B, Unique single units from monkey L. C, All sorted units from monkey X. D, Unique single units from monkey X. In all four groups of units, average Q_m initially indicated larger location than object effects, but began to decrease before movement onset (M) and indicated larger object than location effects by the time of peripheral object contact (C).

In the bottom frame of each panel in Figure 4, we compare the total fraction of firing-rate variance explained by location, object, and their interaction (solid black line, left vertical axis) and the average firing rate (dotted gray line, right vertical axis). For both all sorted units and unique single units, the total variance explained and the average firing rate increased from before movement onset until approximately the time of peripheral object contact, after which they declined. In addition, we note that the average firing rate traces each showed two local peaks, one near the onset of movement, the other near peripheral object contact, consistent with two sequential phases of increased neural activity in M1.

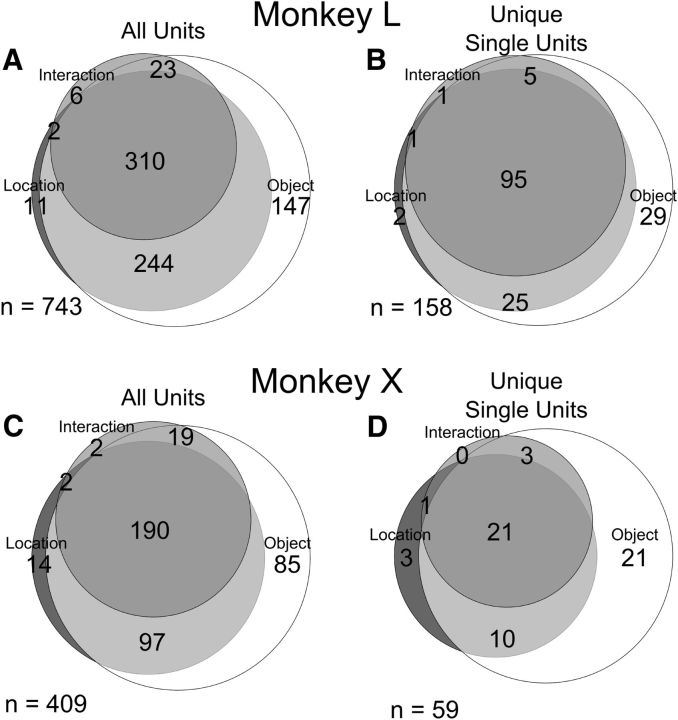
The example neuron illustrated in Figures 2 and 3 exhibited both location and object effects. But did location and object effects generally occur in the same neurons or in different neurons? Figure 6 shows Venn diagrams of the numbers of sorted units and of unique single units that showed significant effects at any time point. Substantial fractions of the unique single units varied with all three factors—location, object, and interaction—95 (60%) in monkey L and 21 (36%) in monkey X. An additional 25 (16%) unique single units in L and 10 (17%) in X varied with location and object but had no significant interaction term. The fraction of the unique single-unit population with both location and object effects (76% in L, 53% in X) thus was larger than either the fraction with location but not object effects (2% L, 7% in X) or that with object but not location effects (19% L, 41% X). Such was the case not only for unique single units (right column) but also for all sorted units in each monkey (left column), the largest fraction of the population being related both to location and to object rather than one or the other. While location effects occurred early and object effects later, substantial fractions of units had both types of main effects.

Figure 6.

Venn diagrams illustrating the numbers of units having various combinations of significant location, object, and interaction effects. A, All sorted units from monkey L. B, Unique single units from monkey L. C, All sorted units from monkey X. D, Unique single units from monkey X.

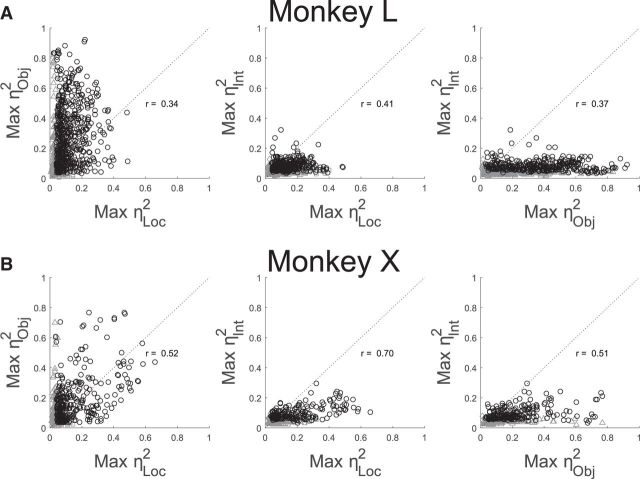
To examine the relative size of location, object, and interaction effects, we formed pairwise scatterplots of the maximal location, object, and interaction effect occurring at any trial time versus one another for each sorted unit (Fig. 7). The leftmost plot for each monkey shows that many units had both substantial location and substantial object effects. Maximal location and object effect sizes were positively correlated (r = 0.34 and 0.52 for monkeys L and X, respectively), indicating that units with larger location effects tended to have larger object effects as well, and vice versa (had there been two separate subpopulations of units—one with large location effects but small object effects, and the other with large object but small location effects—these correlation coefficients would have been negative). Positive correlations between maximal location and object effect sizes were found as well for the unique single units in each monkey (data not shown; L, r = 0.23; X, r = 0.48). Although maximal location and object effects were correlated, object effects tended to be somewhat larger than location effects overall, reflected by the fact that most sorted units fell above the line of unity slope (monkey L: 612 of 737 = 83%; monkey X: 261 of 407 = 64%; both p < 0.001, Wilcoxon signed-rank test). Similar percentages of unique single units fell above the line of unity slope (data not shown; monkey L: 126 of 157 = 80%, p < 0.001; monkey X: 35 of 59 = 59%, p < 0.05).

Figure 7.

Pairwise scatterplots of maximal location, object, and interaction effect sizes. A, All sorted units from monkey L. B, All sorted units from monkey X. Black circles indicate that the maximum η² was significant for both plotted factors. Gray symbols indicate that only one of the two factors was significant: Squares, Significant location effect; triangles, significant object effect; diamonds, significant interaction effect. Clusters of gray points close to the origin in each plot represent units for which neither plotted factor was significant at any analyzed time. Note that the sum of the maximum η² for two factors can exceed 1 because the two were not simultaneous values.

The middle and rightmost frames of Figure 7 show scatterplots of maximal location and object effect sizes, respectively, versus maximal interaction effect sizes. Interaction effects tended to be smaller than either location or object effects, with the large majority of points falling below the line of unity slope. Nevertheless, interaction effect size was positively correlated with both location effect size (monkey L, r = 0.41; monkey X, r = 0.70) and object effect size (L, 0.37; X, 0.51), indicating that units with larger location and/or object effects tended to have larger interaction effects as well. Again, similar trends were found for the unique single units from each monkey both for location (L, r = 0.30; X, r = 0.67) and object (L, r = 0.33; X, r = 0.42).

Spatiotemporal distribution of location and object effects

To begin to examine the spatial distribution of location and object effects, the same traces compiled together in the top frame of each panel in Figure 4 have been replotted in Figure 8, now separated according to the microelectrode array from which each sorted unit was obtained. These plots for individual arrays demonstrate that early location-related variation and later object-related variation both were widespread in the firing rates of M1 neurons from medial to lateral along the anterior bank of the central sulcus in both monkeys. In monkey X, location effects began earlier and became larger in the more medial arrays than in the more lateral arrays, but no such trend was evident in monkey L. The plots in the right column (B and D) show that these features of the distribution of both location and object effects along the central sulcus did not result solely from multiunit recordings, but were similar in unique single units as well.

Figure 8.

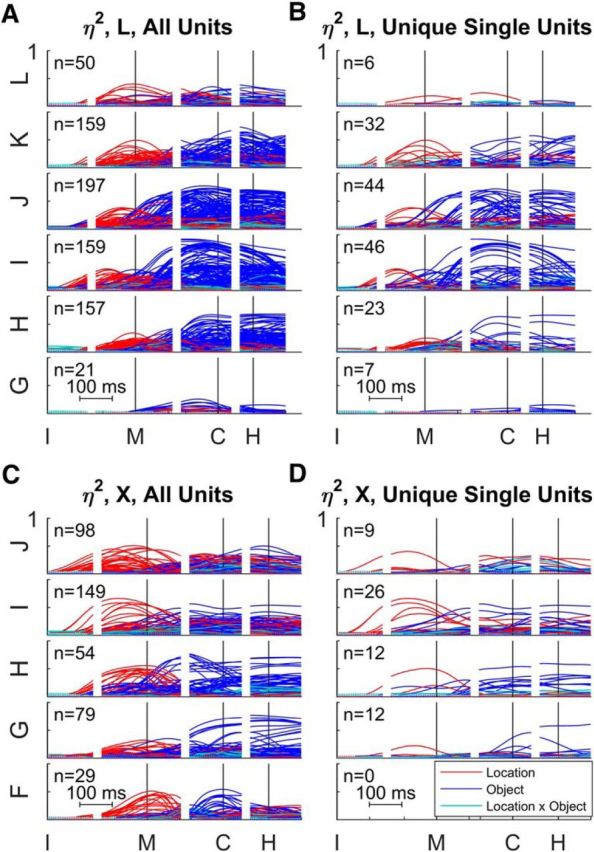
Time-resolved ANOVA by array. A, All sorted units from monkey L. B, Unique single units from monkey L. C, All sorted units from monkey X. D, Unique single units from monkey X. For each monkey, the arrays have been arranged in reverse alphabetical order from most medial above to most lateral below: L–G for monkey L, J–F for monkey X. Each plot shows the time-varying location (red), object (blue), and location × object interaction (cyan) effect size (η²) for each unit. All data have been aligned separately on the times of four behavioral events: instruction (I), movement onset (M), peripheral object contact (C), and beginning of final hold (H). Note that in monkey X no definite single units were obtained from the most lateral array, F.

To examine the distribution of effects from superficial to deep in the central sulcus as well as from medial to lateral, we projected the estimated position of each recording electrode tip onto a two-dimensional plane approximately parallel to the anterior bank of the central sulcus, as shown in Figure 1B. We then plotted each significant effect from each sorted unit as a filled circle at the two-dimensional position from which the recording was obtained. The preview image for Movie 1 shows such plots—for location (A), object (B), and interaction (C) effects, as well as the corresponding Q_m values (D)—at the time of peripheral object contact, incorporating the data from all sorted units obtained in all sessions from monkey L. Where multiple units were collected from the same electrode, the centers of the corresponding circles have been displaced slightly from one another to allow all the circles to appear in the displays. Both the diameter of each circle and the color saturation have been scaled to represent the size of each effect in A–C. In D, the color represents the Q_m values and the diameter of each circle is based on the summed main effect sizes, η_Loc² + η_Obj².

Movie 1.

Spatiotemporal distribution of location, object, and interaction effects in caudal M1. A–D, The colored circles in each panel represent location (A), object (B), and interaction effect sizes (C), as well as Q_m values (D), for all sorted units across all sessions from monkey L, each plotted at the two-dimensional location of the electrode tip from which it was recorded, as shown in Figure 1B. Crosshairs: S, superficial, up; D, deep, down; L, lateral, left; M, medial, right. Video frames step at 10 ms intervals. The sliding bar at the top indicates the time of the current video frame relative to four behavioral events: instruction (I), movement onset (M), peripheral object contact (C), and beginning of final hold (H). The preview (still) frame is taken at the time of peripheral object contact. In A–C, both the color saturation and diameter of each circle have been scaled proportional to the η² values from time-varying ANOVA. In D, the color of each circle represents the Q_m value (red indicating a larger location effect; blue a larger object effect), while the diameter of the circle has been scaled according to the sum of the location and object η² values. In each panel, the colored circles have been offset slightly when needed to permit display of >1 unit recorded from the same electrode. Black and white crosses indicate the centroid of all recording sites weighted by the magnitude of the η² values for location, object, or interaction.

Movie 1 illustrates the spatiotemporal progression in caudal M1 of location, object, and interaction effects, as well as Q_m values, over the time course of the present reach–grasp–manipulate movements. Few if any significant effects were present before 100 ms after the instruction. By 100 ms after the instruction, a handful of small effects were present. The Q_m values indicate that location effects generally were larger than object effects and were distributed medially to laterally along the central sulcus, though somewhat more superficially than deep. By 100 ms before movement onset, substantial effects had appeared, with location effects distributed throughout the field both mediolaterally and from superficial to deep, while some object effects and a few small interaction effects had appeared near the center of the field. By the time of movement onset, all three types of effects had increased in size and spread throughout the field, both mediolaterally and from superficial to deep. The Q_m values at movement onset indicate that location effects generally remained larger than object effects. By 100 ms after movement onset, however, though location and interaction effects showed small additional increases, object effects had increased substantially, becoming generally larger than either location or interaction effects. Only at the medial edge of the field did Q_m values indicate that location effects still were comparable in size to object effects. This spatial distribution of all three types of effect throughout the field, with object effects larger than location or interaction effects except at the medial edge of the field, then continued through the time of peripheral object contact and into the final hold. Similar spatiotemporal distributions of location, object, and interaction effects, though not shown here, were evident in the equivalent plots using only unique single units from monkey L and using either all sorted units or unique single units from monkey X.

Centroids also were calculated separately for the location, object, and interaction η² values at each time point (black-and-white “+” marks in Movie 1). In monkey L, the sampled territory spanned an area of 20.5 mm from medial to lateral × 6.5 mm from superficial to deep. The centroids for all three effects appeared near the center of the sampled territory and remained relatively stationary, drifting only 1.4 mm for location, 0.7 mm for object, and 1.1 mm for interaction over all the trial time points. In monkey X (data not shown), the sampled territory spanned 15.6 × 5.0 mm. The centroids for location were found a few millimeters medial of center, whereas those for object and interaction effects were close to the center. The range of drift over all trial time points was 2.5 mm for location, 1.1 mm for object, and 1.2 mm for interaction. These observations indicate that location, object, and interaction effects all were distributed widely throughout the sampled territory in both monkeys over the entire time course of the trials.

Although the spatial distribution of location and object effects was virtually coextensive by the time of movement onset in both monkeys, before movement onset, monkeys L and X showed somewhat different spatiotemporal spread of location effects in the mediolateral dimension, which can be appreciated by referring back to Figure 8. In monkey L, effects were present in the more central arrays ∼100 ms after the instruction appeared, and thereafter spread both medially and laterally. In monkey X, however, location effects began to appear in the most medial array shortly after the instruction and then spread laterally, though remaining larger in the more medial arrays.

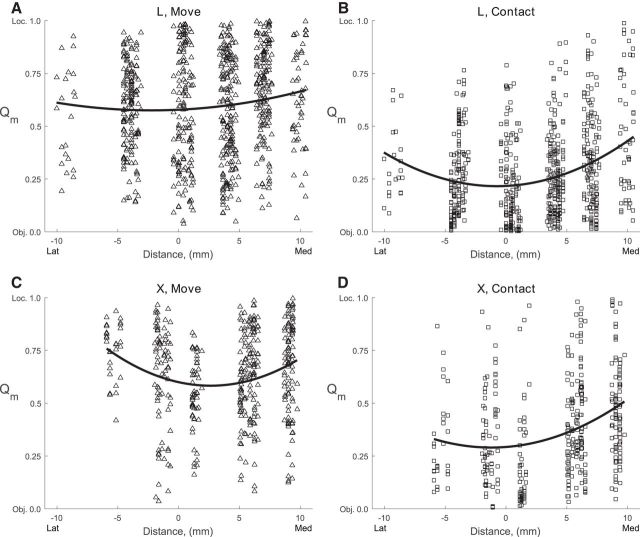
These observations suggest that while location effects had appeared relatively evenly throughout the field by the time of movement onset, object effects were strongest centrally, particularly in the mediolateral dimension. To evaluate this possibility quantitatively, we plotted the Q_m value of each sorted unit at the mediolateral location of the electrode along the central sulcus for two time points: movement onset and peripheral object contact (Fig. 9) and performed quadratic least-squares regression of these data for these two time points in each monkey. The best-fit parabola for each regression is also shown in Figure 9. The coefficient of the quadratic term was >0 for all quadratic fits and all were significant (p < 0.01) except at movement onset in monkey L (p = 0.09), confirming the observation that compared with location effects, object effects were stronger centrally. From movement onset to peripheral object contact, the Q_m values at the vertices of the fitted parabolas decreased from 0.58 to 0.22 for monkey L and from 0.58 to 0.29 for monkey X, reflecting the overall increase in object effect sizes relative to location effects. So although location and object effects were coextensive and widespread throughout the mediolateral extent of the M1 upper extremity representation, we detected a slight tendency for object effects to be stronger at the center of field, particularly at the time of peripheral object contact.

Figure 9.

Q_m as a function of mediolateral location. The Q_m ratio has been plotted for all sorted units from each monkey (L, top row; X, bottom row) at the time of two behavioral events (movement, left column; peripheral object contact, right column). Q_m values could range from 0 (only object effect) to 1 (only location effect), and have been plotted here as a function of mediolateral recording site location [lateral (left) to medial (right)]. The parabolas represent the quadratic best-fit to Q_m values versus mediolateral location for each monkey at each time point.

This observation raises the possibility that neurons located where digit movements were evoked by threshold ICMS might have larger object effects, whereas neurons located where shoulder movements were evoked might have larger location effects. To examine this possibility, we took the data that had been sorted by microelectrode array in Figure 8 and resorted the same data in Figure 10 according to the body part moved by threshold ICMS at each electrode—face (F), digits (D), wrist (W), elbow (E), shoulder (S), trunk (T), or no movement evoked with currents ≤100 μA (X). Small but significant effects were present in a few units recorded at F and T sites, possibly reflecting three factors: (1) movements evoked by threshold ICMS do not reveal the nature of all neuronal activity at a given site, (2) some upper extremity neurons are intermingled with face and trunk neurons at the lateral and medial edges of the upper extremity representation respectively, and/or (3) small face and trunk movements were made in conjunction with the present upper extremity movements (Schieber, 2001). In addition, substantial location and object effects were present in many units recorded at X sites, where no movement was evoked with ICMS, again reflecting differences between ICMS-evoked movements and neuronal activity. Overall, units recorded at D and W sites did have some of the largest object effects, whereas units recorded at S sites had some of the largest location effects. Remarkably, however, many units recorded at D sites had significant location effects, and many units recorded at S sites had substantial object effects. Although location and object effects thus were most prominent at S and D sites, respectively, S, E, W, and D sites all had local units with both location and object effects.

Figure 10.

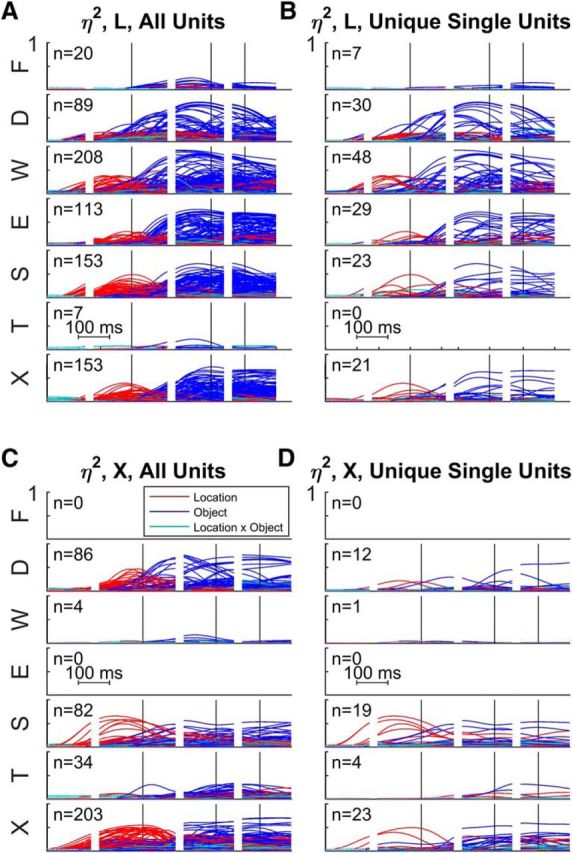
Time-resolved ANOVA sorted by ICMS-evoked movement. A, All sorted units from monkey L. B, Unique single units from monkey L. C, All sorted units from monkey X. D, Unique single units from monkey X. Using the same data shown in Figure 8 for each monkey, units here have been sorted according to the electrode sites where ICMS at threshold evoked movement of the face (F), digits (D), wrist (W), elbow (E), shoulder (S), trunk (T), or no movement was evoked with currents ≤100 μA (X). Each plot shows the time-varying location (red), object (blue), and location × object interaction (cyan) effect size (η²) for each unit. All data have been aligned separately on the times of four behavioral events: instruction (I), movement onset (M), peripheral object contact (C), and beginning of final hold (H).

Discussion

During the present reach–grasp–manipulation movements, we found that the activity of caudal M1 neurons depended both on the location to which the subject reached and on the object the subject grasped, with location effects predominating earlier and object effects later in the same movements. Interaction effects, while significant, were generally smaller than the main effects of location and object. All three types of effect were distributed widely throughout the caudal M1 upper extremity representation in the anterior bank of the central sulcus. Our findings do not necessarily pertain to rostral M1 on the crown of the precentral gyrus, which may be a separate motor area (Rathelot and Strick, 2009).

Many of the present sorted units were not definite single units with large SNRs and no ISI violations. But in both monkeys, similar observations consistently were made on the smaller but substantial subpopulation of unique single units, many of which showed both location and object effects. Furthermore, given that the units recorded from the same electrode all would have been within a few hundred micrometers of one another, even multiunit recordings provide valid information on the spatiotemporal distribution of M1 activity on the millimeter scale.

Temporal dynamics of location and object effects

Although reaching and grasping commonly are thought to proceed in parallel (see Introduction), the effects observed in M1 activity during the present reach–grasp–manipulate movements were in large part sequential. Location effects first appeared and then became both larger and more common than object effects up to the time of movement onset. After movement onset, however, location effects decreased somewhat as object effects grew, quickly becoming larger than location effects overall. Object effects continued to be larger while the monkey contacted and manipulated the peripheral objects. Indeed, the present task did not dissociate the shape of the hand and arm used to grasp each object from the forces applied to manipulate the object immediately after contact. The object effects described here therefore may reflect both the shape of the hand and arm used in grasping and the forces applied in manipulating the object.

In the same monkeys performing the same task, we previously have described similar temporal sequences of location and object effects in upper extremity EMG activity and in joint angle kinematics (Rouse and Schieber, 2015b, 2016). Not surprisingly, M1 neurons led muscle activity in time, which in turn led kinematics. Location effects appeared in M1 neurons >100 ms before and peaked near the time of movement onset, while in EMG activity location effects appeared ∼50 ms before movement onset and peaked during the first half of the movements. Object effects were substantial in M1 neurons before movement onset and typically became maximal well before peripheral object contact, while in EMG activity object effects generally peaked shortly before peripheral object contact. Joint angles began to change only at movement onset (by definition), with location effects rising faster than object effects initially, after which object effects increased and became larger than location effects through the time of peripheral object contact and final hold. During the present reach–grasp–manipulate task, an early phase of predominant location effects thus was followed by a later phase of predominant object effects in M1 neurons of the upper extremity representation, then in the activity of upper extremity muscles, and then in joint angles.

Spatial distribution of location and object effects

Classical studies of the macaque motor cortex using electrical stimulation at the pial surface indicated that the digits of the hand were represented in the anterior bank of the central sulcus with the more proximal upper extremity represented on the crown of the precentral gyrus (Woolsey et al., 1952). More recent studies using ICMS have shown that the digits are represented in a central core surrounded by a “horseshoe” of more proximal representation, with a substantial zone of proximodistal overlap (Kwan et al., 1978; Park et al., 2001). The central core lies largely in the anterior bank and the surrounding horseshoe largely on the gyral surface, but both extend from the gyral surface down the anterior bank of the central sulcus. Though the present microelectrode arrays did not sample more than ∼3 mm anterior to the sulcus and provide only a limited spatial sampling, the ICMS-evoked movements we observed (Fig. 1B) were consistent with such a core-horseshoe organization.

One therefore might have expected that in the present recordings, location effects would have been distributed around a central core of object effects. Some findings were consistent with such a spatial distribution. Many units from the more medial arrays, where ICMS evoked predominantly shoulder and elbow movement, showed Q_m quotients >0.5, indicating larger location than object effects even late in the movements (Movie 1). And fitting quadratic functions to the Q_m values showed minima near the mediolateral midpoint of the sampled territory in both monkeys, indicating that object effects were somewhat stronger near the center of the field (Fig. 9). This spatial variation was relatively minor, however, with location, object, and interaction effects widely distributed throughout a similar territory in caudal M1.

The coextensive distribution of location and object effects in M1 neurons again is consistent with our recent findings on muscle activity and joint angle kinematics during the present task. The EMG activity of many muscles that act about the shoulder or elbow showed both location and object effects, as did many wrist and extrinsic finger muscles. Only the intrinsic muscles of the hand showed object effects almost exclusively, with few location effects. Similarly, joint angles from the shoulder to the proximal interphalangeal joints showed both location and object effects, with location effects generally being somewhat larger proximally and object effects larger distally. The wide and coextensive spatial distribution of location and object effects in M1 neurons thus is consistent with the presence of location and object effects in muscle activity and joint angles from proximal to distal in the upper extremity.

Spatiotemporal spread in M1

Detailed spatiotemporal analysis of neural activity in rostral M1 on the crown of the precentral gyrus has shown that during reach-to-grasp movements neither local field potentials nor spiking activity appear simultaneously throughout M1; rather, neural activity spreads rapidly across M1 (Riehle et al., 2013; Best et al., 2016). Moreover, the pattern of spread may differ between individual subjects. Though we have not analyzed spatiotemporal spread in caudal M1 in the same way, our findings suggest that location and object effects likewise spread in the anterior bank of the central sulcus. In the two monkeys studied here, both location and object effects appeared initially in the superficial part of the sampled territory and then spread deeper by the time of movement onset, consistent with previous observations that using more superficial units provides high decoding accuracy of such movements earlier than using deep units (Mollazadeh et al., 2011). Spatiotemporal spread in the mediolateral dimension differed somewhat between the two monkeys, however. In monkey L, both location and object effects first appeared centrally and then spread both medially and laterally. But in monkey X, whereas object effects spread in a similar fashion, location effects appeared first at the medial aspect of the sampled territory and then spread laterally. Although such interindividual differences in part may result from variation in the placement of microelectrode arrays, the possibility remains that spatiotemporal spread of activity in caudal M1 differs among individuals.

Implications for motor control and neuroprosthetics

Our findings—at the levels of M1 neuronal activity, muscle activity, and joint angle kinematics—suggest that reaching and grasping are not controlled simply as parallel processes that evolve simultaneously, the former in the proximal parts of the extremity and the latter in the distal parts. Instead, the entire extremity from shoulder to fingers initially is projected toward an appropriate location, and subsequently the entire extremity is shaped to grasp and manipulate the object. Neural activity in other naturalistic movements might also have similar temporal segmentation.

M1 activity thus may be viewed as a dynamical process in a high-dimensional neural space that initially projects the intended reach location on to the muscles and joints of the upper extremity and then rotates to project the desired grasp (Churchland et al., 2012; Shenoy et al., 2013; Hall et al., 2014; Kaufman et al., 2014). Previous studies of M1 activity during reaching movements similarly found sequential representation of parameters—first direction, then target position, and then movement distance—that can be viewed as providing dynamically sequential control (Fu et al., 1993, 1995). What advantages might such sequential control offer, acting through the same neurons on the same muscles and joints? We speculate that in the present reach–grasp–manipulate movements, the two temporal phases may reflect differences in movement precision. In the early phase, the extremity is projected quickly toward the intended location with comparatively low precision. In the later phase, the extremity is shaped to grasp and manipulate the object with higher precision. Further studies will be needed to better understand the neural control of precision.

Our observations also have implications for neuroprosthetics. Though neural control of resting posture differs from control of movement per se (Velliste et al., 2014), modern decoding algorithms still typically rely on the assumption that once the limb is in motion, neural activity in the motor cortex provides a stationary, linear representation of muscle activity and/or movement kinematics. Our findings show, however, that during naturalistic reach–grasp–manipulate movements made with the native extremity, firing rates on average increase progressively, with initial variation that depends on location becoming supplanted by larger variation that depends on the object. A neural decoder trained on reaches to predict proximal arm movements would generalize poorly to the larger firing rates in the same neurons during object contact and manipulation. Decoding algorithms based on time-invariant models therefore may become inaccurate as reaching, grasping, and manipulation proceed (Wodlinger et al., 2015). Implementing decoding algorithms that vary nonlinearly in the course of a given movement might advance control of neuroprosthetic devices closer to that of natural human performance (Rouse and Schieber, 2015a).