Abstract
The mechanical behavior of eggshell was determined in terms of average rupture force and corresponding deformation. For the experiment, we selected goose eggs (Anser anser f. domestica). Samples of eggs were compressed along their x-axis and z-axis. The effect of the loading orientation can be described in terms of the eggshell contour curvature. Two different experimental methods were used: compression between two plates (loading rates up to 5 mm/s) and the Hopkinson split pressure bar technique. This second method enables achieving loading rates up to about 17 m/s. The response of goose eggs to this high loading rate was characterized also by simultaneous measurement of the eggshell surface displacements using a laser vibrometer and by the measurement of both circumferential and meridian strains.
Keywords: Eggs, Compression, Dynamic loading, HSPB technique, Rupture force
Introduction
The egg is a packaged food. One of the important quality aspects of packaged eggs is the mechanical strength of the egg shell [1]. Breaking of the eggshell is due to the forces acting on the eggs under static and/or quasi-static conditions, as at the bottom of the pile of loaded trays, but the greatest part occurs under dynamic conditions, e.g., when an egg falls on to the cage bottom at oviposition and in the many other events, which are collected by Carter [2]. The dynamic loading can also lead to the vibration of the egg liquid products. The eggs thus serve to dissipate the vibration energy rapidly to protect its contents. An uncooked hen egg’s capability to rapidly dissipate potentially harmful energy is due to sloshing of its contents. Sloshing is the oscillation of a liquid within a partially full container [3]. In a raw egg, the albumen and yolk are held separate by the vitelline membrane. The egg yolk is suspended within the albumen with the chalazae. Therefore, yolk and albumen are able to slosh out of phase from one another and/or out of phase from the oscillations of the eggshell. It can be possible that this type of the relative motion is responsible for the egg’s high mechanical damping [4]. Hence, there may be lessons to learn from the natural design of an egg, which could be employed in the engineered (artificial) design of a sloshing absorber.
Eggshell strength can be described using various variables such as eggshell thickness, eggshell stiffness, and/or rupture force [1, 5]. The rupture force of the whole egg depends on various factors such as the breeding conditions [6], the breed of poultry [7], the diet [8], egg shape [9], and microstructure of the eggshell [10]. The rupture force also depends on the temperature [11] and the value of loading rate. Influence of the loading rate was previously investigated using the most common technique for the measurement of the eggshell strength. In this case, the eggs are compressed between two plane plates. The eggs are placed on the fixed plate and pressed using a moving plate connected to the precise load cell until the egg ruptures. Two mutually perpendicular compression axes (x and z) corresponding to the main geometrical axes are used.
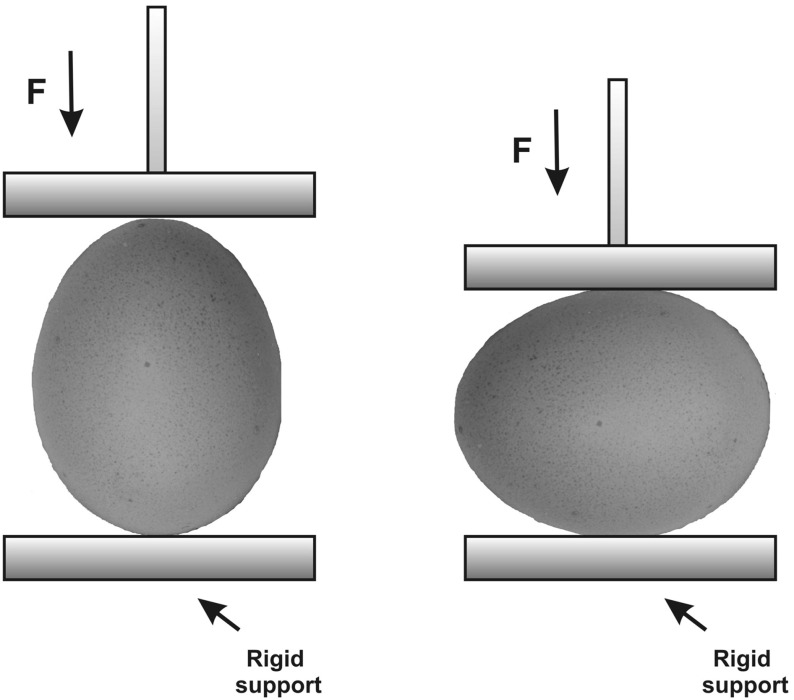
On the left side of Fig. 1 the loading along the x-axis is shown. Two more orientations were considered in case of the x-axis. If the egg’s sharp end is in contact with the moving plate, the symbol Xs is used. The symbol Xb corresponds to the orientation where egg’s blunt end is in contact with the moving plate. The loading along the z-axis is displayed on the right side of Fig. 1. This orientation is also termed as the loading in the equator plane of the egg.
Fig. 1.
Schematic of egg compression
It was found that eggshell strength is significantly dependent on the value of compression rate. The first data were obtained in the papers [1, 5] for hen eggs. The effect of loading rate on the eggshell rupture force has been also found for Japanese quail eggs [12] and for goose eggs [13]. This procedure enables studying of the influence of loading rate over a relatively narrow range of this quantity. The highest rate of the egg compression is mostly limited to about 5 mm/s. In order to achieve considerably higher values of loading rates, a new technique of eggshell strength evaluation under impact loading was developed [14]. In these experiments, the eggs are loaded by impact of a free-falling cylindrical bar (6 mm in diameter, 200 mm in length, and made from aluminium alloy). Impact velocity of the bar is changed (increased) up to the value at which the eggshell fracture occurred. This procedure enables reaching significantly higher values of loading rate than the method mentioned above.
In order to obtain higher loading rates under similar conditions as during egg compression between two plates, the Hopkinson split pressure bar (HSPB) seems to be a reasonable solution. For a review of the HSPB, see [15].
In the given paper, the HSPB technique is applied to the investigation of goose egg compression.
Materials and methods
For the experiments, exactly 30 fresh eggs from geese (Anser anser f. domestica) were chosen. Geese were kept in free-range technology at a commercial breeding farm in the Czech Republic (region South Moravia). The eggs were collected from 3-year-old geese.
A detailed description of the tested eggs’ geometry is presented in a previous paper [16]. This description enables also to evaluate the radii of curvature R. The radii were evaluated at the sharp end R 1, at the blunt end R 2, and for the equator circumference R 3. The knowledge of these radii is very useful, namely for the solution of contact problems (impact of bodies, etc.). The values of the main parameters describing the egg geometry together with the egg mass are given in [13]. In this paper, these data are presented only for goose eggs used in high-rate compression tests. These characteristics are given in Table 1.
Table 1.
Main characteristics of eggs used for the high-rate compression test (m mass of egg, L length of egg, W width of egg)
| Egg no. | m (g) | L (mm) | W (mm) | R 1 (mm) | R 2 (mm) | R 3 (mm) |
|---|---|---|---|---|---|---|
| 5 | 180.7 | 90.54 | 59.62 | 16.16 | 21.56 | 56.68 |
| 8 | 167.4 | 89.10 | 60.87 | 22.85 | 24.40 | 60.81 |
| 17 | 178.2 | 88.67 | 59.47 | 18.55 | 20.73 | 68.09 |
| 18 | 156.4 | 84.22 | 57.42 | 17.88 | 21.80 | 70.39 |
Two experimental approaches were used:
The eggs were compressed between the two plates using testing device TIRATEST 27025 (TIRA Maschinenbau GmbH, Germany). The tested eggs were placed on the fixed plate and loaded at the compression rates 0.0167, 0.167, 0.334, 1.67, and 5 mm/s until the egg ruptured. Two mutually perpendicular compression axes (x and z) corresponding to the main geometrical axes were used; see Fig. 1. Response of the egg to compression loading between two parallel plates is characterized by nearly linear increase in the loading force F with moving plate displacement p. At the moment of eggshell break, the loading force rapidly decreases. The maximum of the loading force is defined as the rupture force F m. Another parameter that described the eggshell rupture is the displacement at the point of rupture p m.
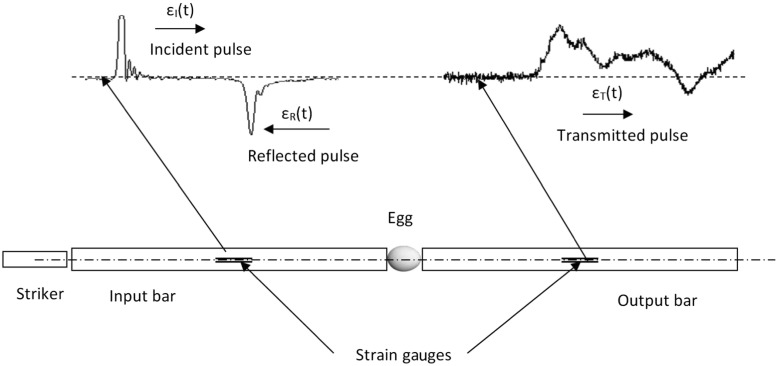
The higher compressive rates were achieved using the HSPB technique. A typical HSPB set up is shown in Fig. 2.
Fig. 2.
Schematic of the Hopkinson split pressure bar technique
The HSPB technique consists of striker, input and output bars, as well as a multi-channel strain acquisition system. A tested specimen is sandwiched between input and output bars.
The impact of the striker at the free end of the input bar develops a compressive longitudinal incident wave ε I(t). Once this wave reaches the bar specimen interface, a part of it, ε R(t), is reflected, whereas another part goes through the specimen and develops in the output bar the transmitted wave ε T(t). These three basic waves recorded by the gauges cemented on the input and output bars allow for the measurement of forces and velocities at the two faces of the specimen. According to wave propagation theory [17, 18], the forces and the velocities at both faces of the specimen are given by the following equations:
| 1 |
| 2 |
where A b is the bar’s cross-sectional area, E is Young’s modulus, and Z b is acoustic impedance of the bar. Z b = ρc, where ρ is the bar material density and c is the elastic wave speed, .
Instead of the strain, we can use incident σ I, reflected σ R and transmitted σ T stress pulses. The incident (loading) stress pulse is characterized by the following parameters:
Maximum of the stress (amplitude): σ Im.
Impulse: , where λI is the time of the stress pulse duration.
Energy of the stress pulse: , where Z is the acoustic impedance of the test bar.
These parameters are defined for the remaining stress pulses. The following symbols are used:
Amplitudes: σ Rm, σ Tm.
Impulses: I R, I T.
Energies: w R, w T.
We make use of polymethyl methacrylate (PMMA) bars instrumented with VTS AP 120-6-12/Au-Cu/BP semiconductor strain gauges, arranged in a diametrically opposed pair, positioned at around the mid-length. These gauges offer a gauge factor of around 120. Their resistance is dynamically measured using a potential divider circuit: the AC-component of the output voltage signal, representing the gauge response, was recorded using a DPO 2014B (Tektronix, Oregon, USA) digital oscilloscope. The bars were 15 mm in diameter and 1000 mm long. PMMA is a viscoelastic material. This means that additional dispersion and damping of the propagating waves occurs with viscoelastic bars due to their frequency-dependent and dissipative properties. When viscoelastic bars are employed, in general modeling the dispersion and attenuation must be involved in the evaluation of the stress and strain. This procedure is rather complicated; see e.g., [19, 20]. As was shown by Zhao [21] in the particular case of bars made of PMMA or nylon, the viscoelasticity induces only a negligible change in the usual local linear relations between the stress, the particular velocity, and the strain. This means that the use of the classical elastic formula (see Eqs. 1–2) can be used with no significant error.
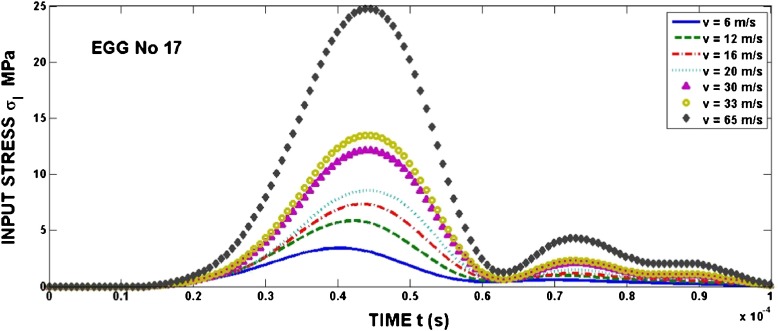
The material properties of the PMMA bars are: ρ = 1189 kg/m3, E = 3900 MPa, Z = 2.153 MPasm−1. A 30-mm-long beech striker (6 mm in diameter) is used to apply the dynamic loading at different striker speeds for duration of about 40 μs. The striker velocity v was increased up to about 72 m/s. Examples of incident stress pulses are shown in Fig. 3.
Fig. 3.
Incident stress pulses for different velocities of the striker bar v. Loading in the Xs direction
Similar results for the remaining eggs were obtained in Table 1. The eggs have been loaded along their x- and z-axes as during their compression between two plane plates. In Fig. 4, the detail of the egg loaded in the z direction is shown. A foam V-shaped edge supported the egg.
Fig. 4.
Egg placed between two PMMA bars
Simultaneous measurement of both circumferential and meridian strains was performed on egg no. 5. The position of the strain gauges is shown in Fig. 5.
Fig. 5.
View of the strain gauges on the eggshell surface – egg no. 5
All experiments were performed at the temperature of 20 °C.
Results and discussion
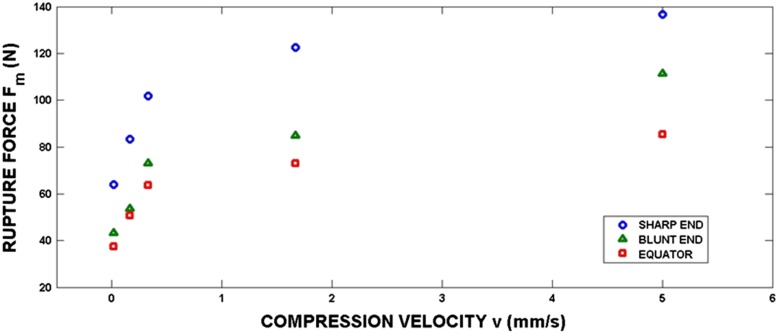
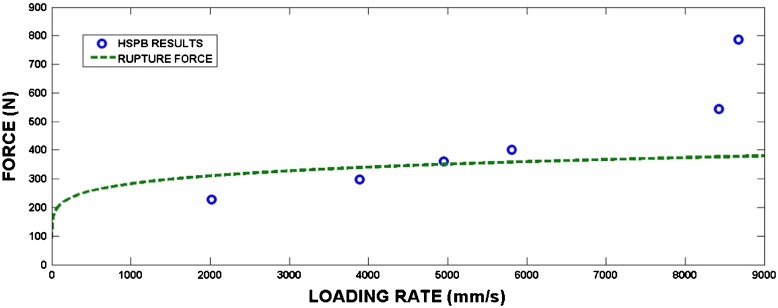
The results of goose egg compression between two plane plates are presented in Nedomová et al. [13]. The dependence of the rupture force on the compression velocity is displayed in Fig. 6. This dependence can be fitted by the function:
| 3 |
where F is given in N and v in mm/s. The maximum value of compression velocity was 5 mm/s.
Fig. 6.
Dependence of the rupture force on the compression velocity
The effect of the loading orientation on the rupture force can be described using of the mean curvature of the eggshell surface at the point of loading.
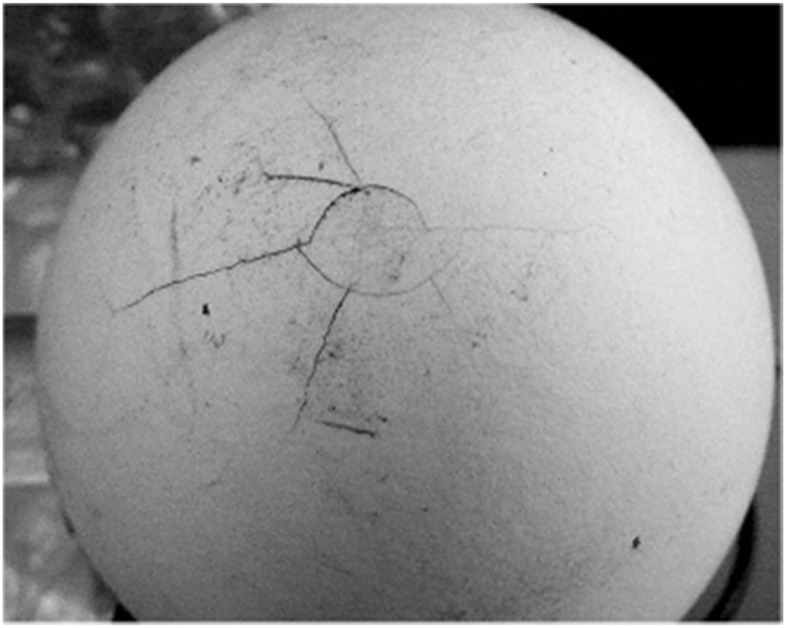
Higher velocities of the eggshell compression have been obtained using the HSPB technique. The velocity of the striker was increased up to the eggshell break. It has been found that the eggshell damage occurs at a striker bar velocity higher than 70 m/s. The typical form of this eggshell damage is shown in Fig. 7.
Fig. 7.
Cracks in the eggshell (egg no. 8 – loading in the Xs direction; striker bar velocity was 72 m/s)
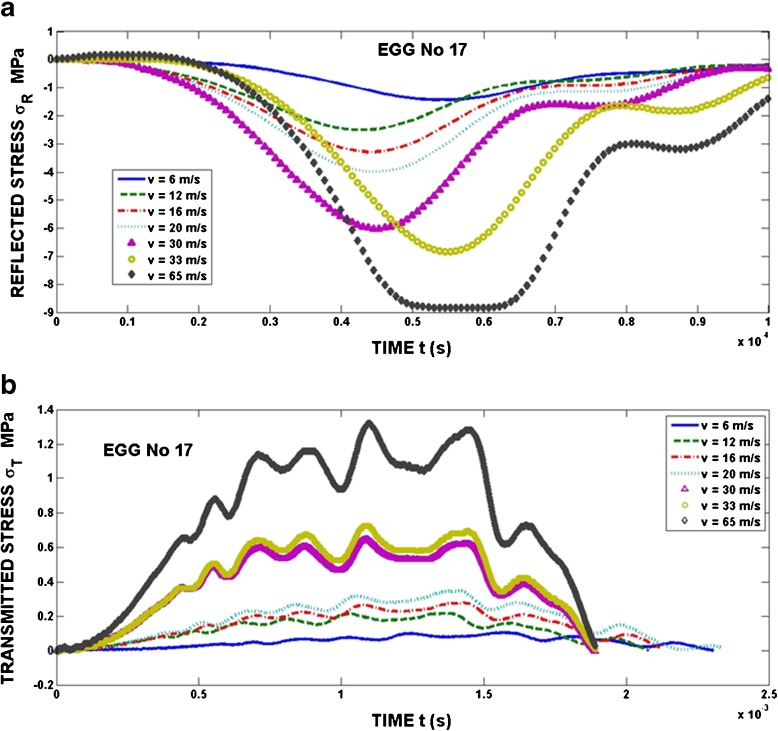
The response of eggs to loading by the incident stress pulse is given by reflected and transmitted stress pulses. The experimental records of these pulses are displayed in Fig. 8a, b.
Fig. 8.
a Reflected stress pulses for different velocities of the striker bar v (loading in the Xs direction). b Transmitted stress pulses for different velocities of the striker bar v (loading in the Xs direction)
The response of remaining eggs exhibited the same qualitative features as egg no. 17. The parameters of response functions σ Rm (MPa), σ Tm (MPa), I R (MPas), I T (MPas), w R (MJm−2), w T (MJm−2) depend on the incident stress pulse amplitude σ Im (MPa) or incident impulse I I (MPas) by the relations:
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
where R2 is the coefficient of determination.
The response of the egg can also be expressed in terms of compression velocity of the egg and by the whole egg shortening. The input and output velocities of the bar–egg contact are given by Eqs. (1–2). The velocity of compression v compression is than given as:
| 10 |
The egg shortening p is expressed as:
| 11 |
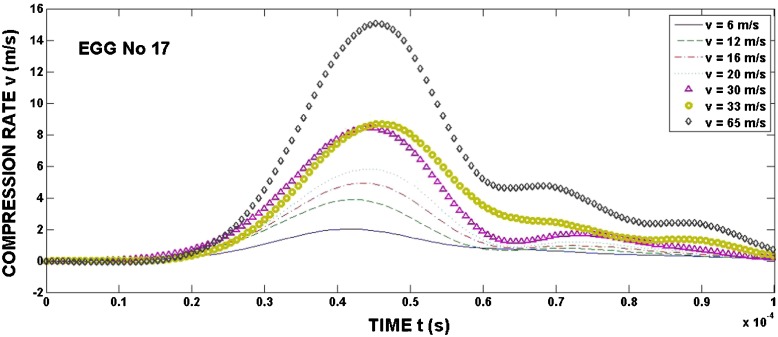
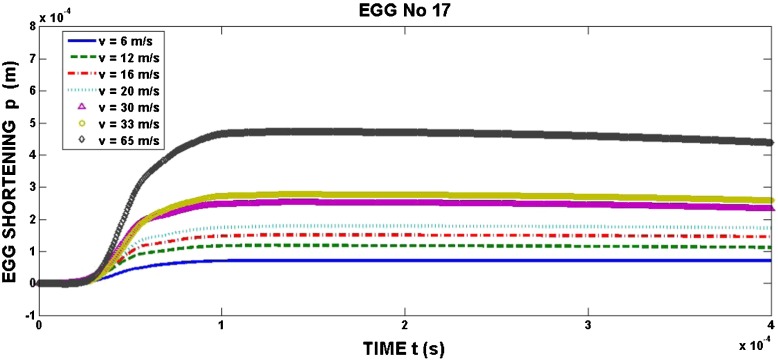
The time histories of egg compression rate and egg shortening are shown in Figs. 9 and 10. The compression rate increases to some maximum and then falls [22]. The shape of this dependence is very similar to the time history of the incident stress pulse. This situation is different from the compression between two plane plates (see Fig. 1) where the compression rate is constant [13]. The egg shortening increases to some maximum and then slowly decreases. This decrease corresponds to the egg unloading. After some time, the egg dimension in the loading direction returns to the initial value.
Fig. 9.
Egg compression rate (loading in the Xs direction)
Fig. 10.
Egg shortening (loading in the Xs direction)
The maximum of the compression velocity v compression (m/s) depends on the stress amplitude and can be fitted by:
| 12 |
The maximum of the egg shortening p max (m) also linearly increases with the input stress:
| 13 |
If the specimen has reached dynamic equilibrium and is deforming uniformly, force balance on the faces gives:
| 14 |
The egg does not reach equilibrium. The gradient of the force along the egg in the direction of loading may be described, e.g., by:
| 15 |
The time history of this force is very similar to that of σ I and/or σ R, respectively. The maximum value of this force F max (N) depends on the input stress amplitude σ Im (MPa) according to:
| 16 |
These parameters, which describe the egg response to the stress pulse loading, are not affected by the loading direction. The results for Xs, Xb and Z directions lie on the same curve. This conclusion is quite different from the results of the quasi-static compression, where the loading orientation significantly affects most of mechanical properties like rupture force, etc. In Fig. 11, the rupture force obtained under quasi-static compression and the experimental points (v compression , F max) are plotted.
Fig. 11.
Maximum of the force F max acting on the egg during the high rate of compression and egg rupture force loaded in the Xs direction
It is obvious that some values of F max lie well above the values of the rupture force. The values of F max presented in Fig. 11 correspond to the non-destructive loading of eggs. This means that it is impossible to use Eq. (3) for higher loading velocities.
The results suggest that the resistance of eggshell to fracture significantly increases under dynamic compression. Our results suggest that a force of about 800 N does not lead to eggshell damage at its compression. In order to obtain exact values of the rupture force it would be necessary to use bars from some stronger material than PMMA.
The shortening of the egg (see Fig. 10) describes the mutual movement of two opposite sides of egg. In order to obtain some view in the strain condition measurement of both circumferential and meridional strains was performed on egg no. 5.
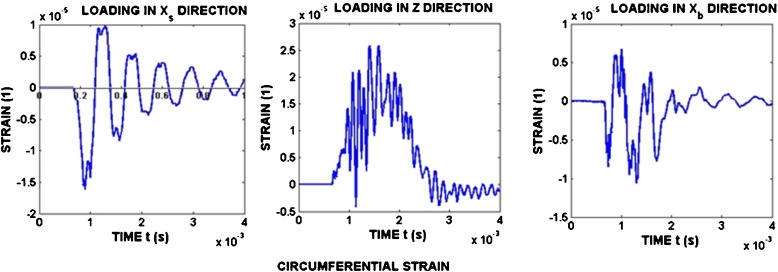
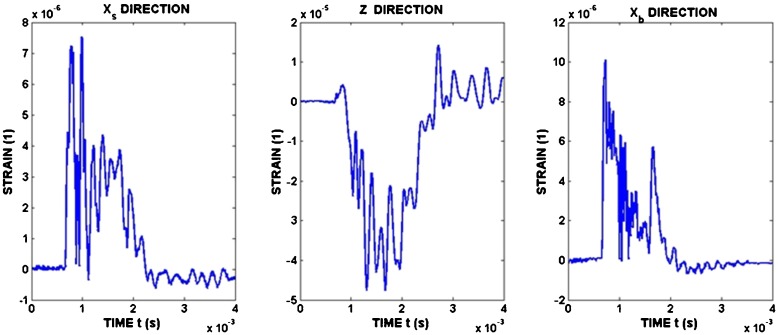
In Figs. 12 and 13, time histories of both circumferential and meridional strains are displayed. These data have been obtained for loading by nearly the same stress pulses σ I. These pulses are characterized by the stress wave amplitude σ Im.
Fig. 12.
Circumferential strain
Fig. 13.
Meridional strain
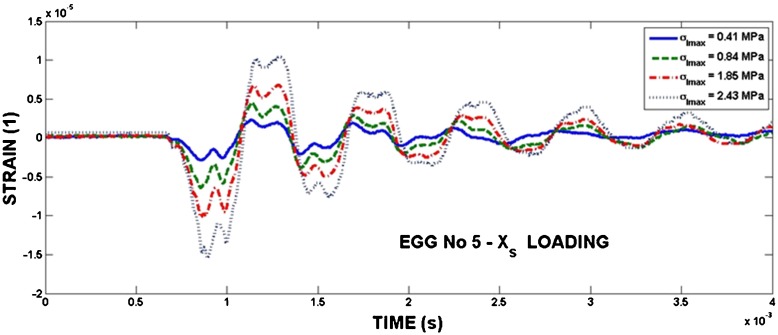
It is obvious that the strain is dependent on the loading direction. The circumferential strain during the loading in Xs and Xb directions exhibits characteristics of damping vibrations. Meridional strains also involve oscillations superimposed on the strain time history. The amplitude of these vibrations increases with the loading stress pulse amplitude, as is shown in Fig. 14. These vibrations probably correspond to sloshing, as mentioned in the introduction.
Fig. 14.
The influence of the loading intensity on the circumferential strain
Conclusions
The Hopkinson split pressure bar technique represents a very useful tool for studying egg behavior under dynamic compression. This method allows us to obtain many quantities, which describe the egg response to the compression at high rates. It has been found that the resistivity of goose eggs to fracture at very high loading rates is significantly higher than that found at quasi-static loading. The rupture force obtained at the high strain rate of compression is independent of the eggshell curvature at the point of contact between egg and loading (input) bar. This is quite a different result from that obtained at the quasi-static compression. Very valuable data on the stress wave propagation may be obtained using the strain gauges glued to the eggshell surface.
Acknowledgments
The authors would like to acknowledge the support of the Institute of Thermomechanics AS CR, c.v.v.i. of the Czech Academy of Sciences through project No. RVO: 61388998. This work was also supported by the project TP 6/2015, financed by Internal Grant Agency FA MENDELU.
References
- 1.Altuntaş E, Şekeroğlu A. Effect of egg shape index on mechanical properties of chicken eggs. J. Food Eng. 2008;85(4):606–612. doi: 10.1016/j.jfoodeng.2007.08.022. [DOI] [Google Scholar]
- 2.Carter TC. The hen’s egg: Shell forces at impact and quasi-static compression. Br. Poult. Sci. 1976;17(2):199–214. doi: 10.1080/00071667608416267. [DOI] [Google Scholar]
- 3.Marsh AP, Prakash M, Semercigil SE, Turan OF. An investigation and modelling of energy dissipation through sloshing in an egg-shaped shell. J. Sound Vib. 2011;330(26): 6287–6295. doi: 10.1016/j.jsv.2011.06.007. [DOI] [Google Scholar]
- 4.So G, Semercigil SE. A note on a natural sloshing absorber for vibration control. J. Sound Vib. 2004;269:1119–1127. doi: 10.1016/S0022-460X(03)00388-2. [DOI] [Google Scholar]
- 5.Voisey PW, Hunt JR. Effect of compression speed on the behaviour of eggshells. J. Agric. Eng. Res. 1969;14(1):40–46. doi: 10.1016/0021-8634(69)90065-1. [DOI] [Google Scholar]
- 6.Lichovnikova M, Zeman L. Effect of housing system on the calcium requirement of laying hens and on eggshell quality. Czech J. Animal Sci. 2008;53:162–168. [Google Scholar]
- 7.Machal L. The relationship of shortening and strength of eggshell to some egg quality indicators and egg production in hens of different initial laying lines. Arch. Anim. Breed. 2002;3:287–296. [Google Scholar]
- 8.Lichovnikova M, Zeman L, Jandasek J. The effect of feeding untreated rapeseed and iodine supplement on egg quality. Czech J. Animal Sci. 2008;53:77–82. [Google Scholar]
- 9.Nedomova S, Severa L, Buchar J. Influence of hen egg shape on eggshell compressive strength. Int. Agrophys. 2009;23:249–256. [Google Scholar]
- 10.Severa L, Nemecek J, Nedomova S, Buchar J. Determination of micromechanical properties of a hen’s eggshell by means of nanoindentation. J. Food Eng. 2010;101(2):146–151. doi: 10.1016/j.jfoodeng.2010.06.013. [DOI] [Google Scholar]
- 11.Voisey PW, Hamilton JR. Factors affecting the non-destructive and destructive methods of measuring egg shell strength by the quasi-static compression test 1. Br. Poult. Sci. 1976;17:103–124. doi: 10.1080/00071667608416254. [DOI] [Google Scholar]
- 12.Buchar J, Nedomova S, Trnka J, Strnkova J. Behaviour of Japanese quail eggs under mechanical compression. Int. J. Food Prop. 2015;18(5):1110–1118. doi: 10.1080/10942912.2013.862634. [DOI] [Google Scholar]
- 13.Nedomova S, Kumbar V, Trnka J, Buchar J. Effect of the loading rate on compressive properties of goose eggs. J. Biol. Phys. 2016;42(2): 223–233. doi: 10.1007/s10867-015-9403-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nedomova, S., Trnka, J., Dvorakova, P., Buchar, J.: Hen’s eggshell strength under impact loading. J. Food Eng. 94(3–4), 350–357 (2009). doi:10.1016/j.jfoodeng.2009.03.028
- 15.Gray, G.T.: Classic split-Hopkinson pressure bar testing. In ASM Handbook 8: Mechanical Testing an Evaluation, eds. Kuhn H, Medlin D. ASM International. Materials Park, pp. 462–476. Ohio (2000)
- 16.Nedomova S, Buchar J. Goose eggshell geometry. Res. Agric. Eng. 2014;60:100–106. [Google Scholar]
- 17.Follansbee PS, Frantz C. Wave propagation in the split Hopkinson pressure bar. J. Eng. Mater. Technol. (ASME) 1983;105(1):61–66. doi: 10.1115/1.3225620. [DOI] [Google Scholar]
- 18.Gorham D, Wu X. An empirical method of dispersion correction in the compressive Hopkinson bar test. J. Phys. 1997;7(C3):223–228. [Google Scholar]
- 19.Curry R, Cloete T, Govender R. Implementation of viscoelastic Hopkinson bars. EPJ Web of Conferences. 2012;26:01044. doi: 10.1051/epjconf/20122601044. [DOI] [Google Scholar]
- 20.Butt, H.S.U., Xue, P.: Determination of the wave propagation coefficient of viscoelastic SHPB: Significance for characterization of cellular materials. Int. J. Impact Eng. 74, 83–91 (2014). doi:10.1016/j.ijimpeng.2013.11.010
- 21.Zhao H, Gary G, Klepaczko JR. On the use of a viscoelastic split Hopkinson pressure bar. Int. J. Impact Eng. 1997;19(4):319–330. doi: 10.1016/S0734-743X(96)00038-3. [DOI] [Google Scholar]
- 22.Gama BA, Lopatnikov SL, Gillespie JW. Hopkinson bar experimental technique: a critical review. Appl. Mech. Rev. 2004;57(4):223–250. doi: 10.1115/1.1704626. [DOI] [Google Scholar]