A new definition and properties of the similarity value between two protein structures

Abstract

Knowledge regarding the 3D structure of a protein provides useful information about the protein’s functional properties. Particularly, structural similarity between proteins can be used as a good predictor of functional similarity. One method that uses the 3D geometrical structure of proteins in order to compare them is the similarity value (SV). In this paper, we introduce a new definition of the SV measure for comparing two proteins. To this end, we consider the mass of the protein’s atoms and concentrate on the number of protein’s atoms to be compared. This defines a new measure, called the weighted similarity value (WSV), adding physical properties to geometrical properties. We also show that our results are in good agreement with the results obtained by TM-SCORE and DALILITE. WSV can be of use in protein classification and in drug discovery.

Introduction

In a quantitative manner, comparing two protein tertiary structures to evaluate their similarity is a major challenge. A successful comparison can provide answers to some important questions in structural biology, cell biology, and biochemistry [1]. In particular, it is believed that functional similarity can be predicted from the structural similarity between proteins. The 3D structure of a protein is obtained by various experimental methods such as X-ray or electron crystallography and sometimes NMR [2]. If there is no crystallographic structure of a protein, computational structure prediction methods exist that use sequence similarity. In sequence similarity, a technique called homology modeling is used based on the structure of a known protein as a template to predict the structure of an unknown protein [3]. If structural information of the protein exists, there are methods that have been developed to compare the structures [4–13].

Examples of methods based on numerical techniques to predict structural information are: SCOP (Structural Classification of Proteins) [9, 10], CATH (Class, Architecture, Topology and Homologous superfamily) [13], TM-SCORE [14, 15], STRUCTAL software [16], FSSP (Families of Structurally Similar Proteins) [17] and DALILITE [18].

Recently, in Ref. [19], the similarity value (SV), as a geometrical-based structural property, was introduced as a new protein similarity measure. The SV is an alternative measure to the root-mean-square deviation (RMSD). ‘SV’ is defined as a normalized RMSD of the protein distances in reciprocal space so that the protein’s atomic coordinates are mapped into the corresponding Fourier space. There are theorems in mathematics that allow us to perform this task by using Wigner-D functions and then by using crystallography concepts to arrive at the structure factor [19]. The advantage of defining SV in the reciprocal space is that it solves the known problem of different sizes of two compared proteins. Thus, there is no need to use partial or local similarity tests. An example of using a method that relies on the partial RMSD for computing the similarity value is STRUCTAL software [16]. SV is also sensitive to protein topology (for a brief explanation regarding the differences between SV and other methods see [19]).

In this paper, we propose an improved SV definition, called the ‘weighted similarity value’ (WSV) in order to add some important physical properties required to adequately compare any two proteins. We define WSV by adding a lower limit on the reciprocal space dimension for the two proteins that are being compared. This constraint ensures that we do not lose any information in mapping from the protein’s spatial space to the reciprocal space. We also consider the masses of the atoms as a physical property in the protein shape function. The importance of adding mass to the shape function comes from the structure factors in X-ray scattering data [20]. Thus, adding the atomic masses to the shape function provides more reliable computed structure factors as we show later in this paper.

We compare the results regarding protein similarity obtained by WSV with NRMSD, DALILITE, and TM-SCORE, and we show that our results are in good agreement with these methods. DALILITE is a multiple alignment method, which is based on the alignment of the amino acid sequences and the secondary structure states (helix, sheet, coil) of the two proteins being compared [18]. Since DALILITE is a multiple alignment method, the results given by DALILITE have multi-valued z-scores and corresponding similarity values between two proteins [18].

The template modeling score (TM-SCORE) is a global fold similarity measure between two protein structures with different tertiary structures and it is independent of proteins sizes. The TM-SCORE is a normalized measure and has a value in the [0,1] range; when it is equal to 1, the two proteins are similar [21].

Methods

RMSD is defined as a dissimilarity parameter between two proteins as follows:

$$RMS{D}^2=\frac{2}{N\left(\mathit{N}-1\right)}{\displaystyle \sum _{\mathit{i}<j}^{\mathit{N}}}{\displaystyle \sum _{\mathit{j}=2}^{\mathit{N}}}{\left({\mathit{d}}_{\mathit{i}\mathit{j}}-{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}}\right)}^2=\frac{2}{\mathit{N}\left(\mathit{N}-1\right)}{\displaystyle \sum _{\mathit{i}<j}^{\mathit{N}}}{\displaystyle \sum _{\mathit{j}=2}^{\mathit{N}}}\left({\mathit{d}}_{\mathit{i}\mathit{j}}^2+{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}2}-2{\mathit{d}}_{\mathit{i}\mathit{j}}{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}}\right)$$ 1

where N is the number of proteins’ atoms and d _ij is defined as the elements of the distance matrix between the atoms’ positions of a given protein, as is the case for d ^'_ij. Here, we assumed that the two proteins in question have the same number of atoms. If the numbers of atoms of the two proteins are not equal, we should use a partial RMSD definition. RMSD is a semi-bounded parameter (between zero and infinity). We now define ‘normalized RMSD’ (NRMSD) as a bounded similarity parameter between two proteins. First, we introduce the following auxiliary parameter:

$${\mathit{D}}^2=\mathit{N}\left(\mathit{N}-1\right)\times RMS{D}^2=2{\displaystyle \sum _{\mathit{i}<j}^{\mathit{N}}}{\displaystyle \sum ^{\mathit{N}}}\left({\mathit{d}}_{\mathit{i}\mathit{j}}^2+{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}2}-2{\mathit{d}}_{\mathit{i}\mathit{j}}{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}}\right)$$ 2

and define:

$$\mathit{NRMSD}=\frac{1}{2}\left(1-\frac{{\mathit{D}}^2}{{\mathit{d}}_1^2+{\mathit{d}}_2^2}\right)$$ 3

where d ² = 2∑^N_i <j∑^N_j = 1 d ²_ij is the vector length (sum of the squares of arrays), as is the case for d ^' 2. If the two proteins are not correlated, we have D ² = d ² + d ^' 2 and NRMSD = 0. If we have a maximum correlation between these two proteins (two proteins are the same), i.e., D ² = 0, then, NRMSD = 1/2. In the next step we define WSV.

The SV was defined by using the Wigner-D function in conjunction with a series expansion of the protein’s shape functions [19]. The Wigner-D functions [22] describe the surface of a 4-sphere and they are an extension of spherical harmonic oscillators (SHO). The surface of a 4-sphere is a three-dimensional manifold, which can be explored by using a set of three angles, defined as Euler angles. On the other hand, Euler angles describe a motion in three-dimensional Euclidean space. Thus, we can project a three-dimensional Euclidean space onto the three-dimensional manifold (4-sphere surface). This means we project a body onto the surface of a 4-sphere. Adding atomic masses, M _atom to point coordinates gives gravitational attraction for a given projected point. Thus, we define the protein shape function as:

$$\mathit{f}\left({\mathit{\alpha }}_{\mathit{i}},{\mathit{\beta }}_{\mathit{j}},{\mathit{\gamma }}_{\mathit{k}}\right)=\left\{\begin{array}{c}\hfill {\mathit{M}}_{\mathrm{atom}},\mathrm{if}\mathrm{there}\mathrm{is}\mathrm{an}\mathrm{atom}\mathrm{with}\mathrm{mass}{\mathit{M}}_{\mathrm{atom}}\hfill \\ \hfill 0,\mathrm{else}\mathrm{where}\hfill \end{array}\right.$$ 4

where i, j, k = 1, 2, …, N (N is the number of protein’s atoms) and M _atom is the molar atomic mass in the atomic mass unit (in the definition of SV for all atoms we have M _atom = 1). Here, (α _i, β _j, γ _k) are three Euler angles corresponding to the position of this atom in the corresponding (x _i, y _j, z _k) PDB (Protein Data Bank) entry. We now expand a protein shape function in terms of the Wigner-D functions, D _lmn(α, β, γ), which span a basis set as follows:

$$\mathit{f}\left(\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\right)={\displaystyle \sum _{\mathit{l}=0}^{\infty }}{\displaystyle \sum _{\mathit{m}=-\mathit{l}}^{\mathit{l}}}{\displaystyle \sum _{\mathit{n}=-\mathit{l}}^{\mathit{l}}}{\mathit{C}}_{\mathit{l}\mathit{m}\mathit{n}}{\mathit{D}}_{\mathit{l}\mathit{m}\mathit{n}}\left(\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\right)$$ 5

where C _lmn s are the coefficients of the series expansion and they are unique for a given function, f(α, β, γ). Some theorems in mathematics allow us to use the coefficients of expansion of a function by the Wigner-D function as a three-dimensional Fourier transform of this function [23, 24]. Thus, in the above expansion, the C _lmn s corresponds to elements of the three-dimensional Fourier transform of f(α, β, γ). From crystallography considerations, it is readily recognized that these are the coefficients of the crystal shape function as a structure factor [25]. Thus, C _lmn s are the protein structure factors. Now, we can see why adding the masses of atoms is so important because in X-ray scattering the atomic masses play an important role in determining the corresponding structure factors [26]. C _lmn s can be obtained by the following relation:

$${\mathit{C}}_{\mathit{l}\mathit{m}\mathit{n}}=\frac{\left(2\mathit{l}+1\right)}{8{\mathit{\pi }}^2}{\displaystyle \int }{\displaystyle \int }{\displaystyle \int }\mathit{f}\left(\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\right){{\mathit{D}}_{\mathit{l}\mathit{m}\mathit{n}}}^{\mathit{*}}\left(\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\right)sin\mathit{\beta }d\mathit{\beta }d\mathit{\alpha }\mathit{d}\mathit{\gamma }$$ 6

where we have used the orthogonality relation between the Wigner-D functions as follows:

$${\displaystyle \int }{\displaystyle \int }{\displaystyle \int }{{\mathit{D}}_{{\mathit{l}}^{\mathit{\text{'}}}{\mathit{m}}^{\mathit{\text{'}}}{\mathit{n}}^{\mathit{\text{'}}}}}^{\mathit{*}}\left(\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\right){\mathit{D}}_{\mathit{l}\mathit{m}\mathit{n}}\left(\mathit{\alpha },\mathit{\beta },\mathit{\gamma }\right)sin\mathit{\beta }d\mathit{\beta }d\mathit{\alpha }\mathit{d}\mathit{\gamma }=\frac{8{\mathit{\pi }}^2}{\left(2\mathit{l}+1\right)}{\mathit{\delta }}_{\mathit{l}{\mathit{l}}^{\mathit{\text{'}}}}{\mathit{\delta }}_{\mathit{m}{\mathit{m}}^{\mathit{\text{'}}}}{\mathit{\delta }}_{\mathit{n}{\mathit{n}}^{\mathit{\text{'}}}}$$ 7

Now, in the reciprocal space, the two shapes (proteins) are described with the same dimensions [19], however, they have different numbers of atoms. This is due to the use of Wigner-D functions. The dimension of reciprocal space, N _R, is given by:

$${\mathit{N}}_{\mathit{R}}={\displaystyle \sum _{\mathit{l}=0}^{{\mathit{L}}_{\mathit{max}}}}{\left(2\mathit{l}+1\right)}^2=\frac{1}{3}\left({\mathit{L}}_{\mathit{max}}+1\right)\left(2{\mathit{L}}_{\mathit{max}}+1\right)\left(2{\mathit{L}}_{\mathit{max}}+3\right)$$ 8

where L _max is an arbitrary maximum value chosen in the computation of C _lmn.

The coefficients C _lmn s belong to the complex space and we can embed them in the (N _R × 2) -dimensional Euclidean space such that S≡(Real(C _lmn), Imaginary(C _lmn)) where S≡{S _ij}, (i = 1, 2, ⋯, N _R and j = 1, 2) is a matrix of structure factors. In this step, we can define an (N _R × N _R) -distance matrix for S and then, we define the SD parameter between two proteins as follows:

$$\mathit{S}{\mathit{D}}^2=2{\displaystyle \sum _{\mathit{i}<j}^{{\mathit{N}}_{\mathit{R}}}}{\displaystyle \sum _{\mathit{j}=2}^{{\mathit{N}}_{\mathit{R}}}}{\left(\mathit{s}{\mathit{d}}_{\mathit{i}\mathit{j}}-\mathit{s}{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}}\right)}^2=2{\displaystyle \sum _{\mathit{i}<j}^{{\mathit{N}}_{\mathit{R}}}}{\displaystyle \sum _{\mathit{j}=2}^{{\mathit{N}}_{\mathit{R}}}}\left(\mathit{s}{\mathit{d}}_{\mathit{i}\mathit{j}}^2+\mathit{s}{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}2}-2\mathit{s}{\mathit{d}}_{\mathit{i}\mathit{j}}\mathit{s}{\mathit{d}}_{\mathit{i}\mathit{j}}^{\mathit{\text{'}}}\right)$$ 9

where sd _ij and sd ^'_ij are the elements of the distance matrix in the reciprocal space of each of the two proteins that is defined by:

$$\mathit{s}{\mathit{d}}^2=\left(\begin{array}{cc}\hfill {\mathit{S}}_{11}\hfill & \hfill {\mathit{S}}_{12}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\mathit{S}}_{{\mathit{N}}_{\mathit{R}}1}\hfill & \hfill {\mathit{S}}_{{\mathit{N}}_{\mathit{R}}2}\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill {\mathit{S}}_{11}\hfill & \hfill \cdots \hfill & \hfill {\mathit{S}}_{{\mathit{N}}_{\mathit{R}}1}\hfill \\ \hfill {\mathit{S}}_{12}\hfill & \hfill \cdots \hfill & \hfill {\mathit{S}}_{{\mathit{N}}_{\mathit{R}}2}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill {\mathit{S}}_{11}^2+{\mathit{S}}_{12}^2\hfill & \hfill \cdots \hfill & \hfill {\mathit{S}}_{11}{\mathit{S}}_{{\mathit{N}}_{\mathit{R}}1}+{\mathit{S}}_{12}{\mathit{S}}_{{\mathit{N}}_{\mathit{R}}2}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\mathit{S}}_{11}{\mathit{S}}_{{\mathit{N}}_{\mathit{R}}1}+{\mathit{S}}_{12}{\mathit{S}}_{{\mathit{N}}_{\mathit{R}}2}\hfill & \hfill \cdots \hfill & \hfill {\mathit{S}}_{{\mathit{N}}_{\mathit{R}}1}^2+{\mathit{S}}_{{\mathit{N}}_{\mathit{R}}2}^2\hfill \end{array}\right)$$ 10

Here, we add a constraint on the definition of WSV by always making sure that N _R ≥ max(N ₁, N ₂) where N ₁ and N ₂ are the numbers of atoms of the two compared proteins. Then, we define $L_{\mathit{max}}=⌊N_R^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}-1⌋$ where ⌊.⌋ indicates the integer part of the number in the brackets. Now, we introduce a direct measure to characterize the similarity between two proteins, which depends on their geometries and physical properties (masses and positions of their atoms). Thus we define the weighted similarity values, WSV, as:

$$WSV=\frac{1}{2}\left(1-\frac{\mathit{S}{\mathit{D}}^2}{\mathit{s}{\mathit{d}}^2+\mathit{s}{\mathit{d}}^{\mathit{\text{'}}2}}\right)$$ 11

where $s{d}^2=2{\sum }_{i<j}^{N_R}{\sum }_{j=1}^{N_R}c{d}_{ij}^2$, is the vector length (sum of the squares of arrays), as is the case for sd ^' 2. If the two proteins are not correlated, we have SD ² = sd ² + sd ^' 2 and then, WSV = 0. If we have a maximum correlation between these two proteins (two proteins are the same), i.e., SD ² = 0, then, WSV = 1/2.

The range of atomic masses for the proteins is given in the following. The heaviest atom’s weight in a protein can be a sulfur atom, with a mass about 32.065 a.m.u. and the lightest atom mass is for hydrogen with a mass about 1.00794 a.m.u. We have also considered the atomic mass of some metal atoms in the liganded proteins.

We also wish to compare WSV with the other measures of protein similarity, namely (NRMSD, TM-SCORE, and DALILITE). We use these methods separately as targets and observe that WSV predicts the similarity or dissimilarity in close agreement with their predictions. To analyze it in this way, we compute ‘sensitivity’ (or the probability of prediction similarity between two proteins), ‘specificity’ (or the probability of prediction dissimilarity between two proteins), ‘accuracy’ (probability that the WSV measure is true or what it is supposed to measure), ‘precision’ (probability that if a test is repeated, it gives the same result), and ‘F-score’ (probability of giving a positive (similarity) prediction, or performance of higher sensitivity) [27] as explained below.

To compute sensitivity, specificity, etc., we first normalize TM-SCORE and DALILITE (referred to as M-score) to 0.5. Thus, when M = 0.5, the two proteins are completely similar and when it is 0, the two proteins are completely dissimilar. Then, we assume that a measure that predicts similarity between two proteins does so with any value greater than 0.251 and dissimilar proteins with a value less than 0.25. We have a true positive (TP) result when both measures predict similarity, true negative (TN) when both methods predict dissimilarity, false positive (FP) when WSV predicts similarity, and M-score predicts dissimilarity and false negative (FN) when WSV predicts dissimilarity and M-score predicts similarity. The definitions of sensitivity, specificity, etc., are given in Table 4.

Table 4.

The computation of sensitivity, specificity, accuracy, precision, and F-score for the 48 and 86 datasets

		Sensitivity1	Specificity2	Accuracy3	Precision4	F-Score5
NRMSD	48 dataset(i)	0.800	0.375	0.729	0.865	0.831
	86 dataset(ii)	0.857	0.625	0.814	0.909	0.882
TM-SCORE*	48 dataset(iii)	0.791	0.500	0.766	0.944	0.861
	86 dataset(iv)	0.771	0	0.762	0.985	0.845
DALILITE**	48 dataset(v)	0.756	0	0.723	0.944	0.839
	86 dataset(vi)	0.765	0.250	0.741	0.954	0.849

⁽ⁱ⁾ TP (true positive) = 32 TN (true negative) = 3 FP (false positive) = 5 FN (false negative)= 8

⁽ⁱⁱ⁾ TP = 60, TN = 10, FP = 6, FN = 10

⁽ⁱⁱⁱ⁾ TP = 34, TN = 2, FP = 2, FN = 9

^(iv) TP = 64 TN = 0 FP = 1 FN = 19

^(v) TP = 34 TN = 0 FP = 2 FN = 11

^(vi) TP = 62 TN = 1 FP = 3 FN = 19

^*Because there are no TM-SCORE values for some pairs we have compared 47 and 84 pairs of the 48 and 86 datasets, respectively

^**Maximum similarity values in DALILITE results are compared with WSV. Also, there are no DALILITE values for some pairs we have compared 47 and 85 pairs of the 48 and 86 datasets, respectively

¹ Sensitivity = TP/(TP+FN)

² Specificity = TN/(TN+FP)

³ Accuracy = (TP+TN)/(Num. of total population)

⁴ Precision = TP/(TP+FP)

⁵ F-Score = 2TP/(2TP+FP+FN)

We also compare WSV with the other scores by introducing a relative difference between WSV and M-score as:

$$\mathit{d}\mathit{i}\mathit{f}=\frac{\left|WSV-M\right|}{\left(WSV+M\right)}$$ 12

When dif = 0, the WSV and M-score have the same prediction values and when dif = 1, this means the WSV and M-score have totally different prediction values. In other words, one predicts that the two proteins are similar and the other predicts that they are totally dissimilar.

Results and discussion

In this paper, we defined WSV as a development of SV by including some physical properties of proteins in its definition and a constraint on the dimension of the reciprocal space. In Tables 1 and 2, we show a comparison of the WSV with SV [19], RMSD, NRMSD, TM-SCORE [14, 15] and DALILITE [18] values for 48 and 86 datasets, respectively, where both liganded and unliganded proteins are listed in the supplementary material of Li et al. [1] (these sets are reported in http://dragon.bio.purdue.edu/visgrid_suppl). We reported only minimum and maximum similarity values between two proteins predicted by DALILITE. The data acquisition for the TM-SCORE [14, 15] was obtained by the Zhang Lab’s server http://zhanglab.ccmb.med.umich.edu/TM-SCORE/ for 48 and 86 datasets (only 84 data of the 86 dataset and 47 data of the 48 dataset were used; because there are no TM-SCORE values) and for DALILITE [18] it was obtained by the Holm’s Lab’s server: http://ekhidna.biocenter.helsinki.fi/dali_lite/start) for 48 and 86 datasets (only 85 data of the 86 dataset and 47 data of the 48 dataset were used because there are no DALILITE values).

Table 1.

A set of 48 protein structures with WSV, SV [19], and RMSD from Li et al. [1], NRMSD, TM-SCORE [14, 15], and DALILITE [18]

First protein’s PDB ID	Second protein’s PDB ID	SV [8]	RMSD [1]	NRMSD	WSV	TM-SCORE [16, 17]*	DALILITE [18]*	L max
1A6W	1A6U	0.198	0.34	0.459	0.438	0.9958	100	11
1MRG	1AHC	0.401	0.43	0.325	0.416	0.9958	99	12
1RNE	1BBS	0.316	0.61	0.0706	0.284	0.9567	100-14	16
1RBP	1BRQ	0.108	0.62	0.49	0.0460	0.9865	100	10
1BYB	1BYA	0.499	0.43	0.499	0.497	0.9923	100	14
1HFC	1CGE	0.399	0.37	0.335	0.49	0.9636	100-5	10
3GCH	1CHG	0.070	1.10	0.427	0.328	0.0439	100-7	11
1BLH	1DJB	0.497	0.23	0.478	0.49	0.9984	100	11
1INC	1ESA	0.397	0.21	0.499	0.224	0.2633	100-4	11
1GCA	1GCG	0.499	0.32	0.498	0.499	0.9975	100-8	13
1HEW	1HEL	0.498	0.21	0.499	0.49	0.9975	100	9
1IDA	1HSI	0.083	1.07	0.497	0.449	0.9360	100	10
1DWD	1HXF	0.150	0.27	0.461	0.212	0.8795	100-2	12
2IFB	1IFB	0.382	0.37	0.499	0.468	0.9927	100-9	9
1IMB	1IME	0.498	0.22	0.499	0.499	0.9987	100	15
2PK4	1KRN	0.445	0.39	0.409	0.432	0.0802	100	7
2TMN	1L3F	0.266	0.62	0.497	0.09	0.9911	100	12
1IVD	1NNA	0.426	1.23	0.108	0.286	0.6688	49-4	18
1HYT	1NPC	0.332	0.88	0.470	0.107	0.9825 chain_1; 0.9795 chain_2	73	12
1PDZ	1PDY	0.499	0.66	0.499	0.49	0.9933	100-8	13
1PHD	1PHC	0.499	0.17	0.499	0.499	0.9994	100	13
1PSO	1PSN	0.499	0.33	0.49	0.499	0.9976	100-17	12
1SRF	1PTS	0.498	0.26	0.480	0.499	0.9694	100-1	11
1ACJ	1QIF	0.497	0.31	0.459	0.499	0.9908	100	15
1SNC	1STN	0.495	0.70	0.480	0.49	0.9741	100	9
1STP	1SWB	0.145	0.33	0.0284	0.362	0.9770	100-4	14
1ULB	1ULA	0.474	0.79	0.498	0.498	0.9674	94	12
2YPI	1YPI	0.165	1.27	0.499	0.0840	0.9727	100-5	14
2H4N	2CBA	0.498	0.20	0.465	0.499	0.9950	100	11
2CTC	2CTB	0.499	0.15	0.495	0.499	0.9995	100	12
5CNA	2CTV	0.034	0.40	0.0219	0.0063	0.9952	100	18
1FBP	2FBP	0.494	1.06	0.499	0.467	0.9600	100-5	17
2SIM	2SIL	0.499	0.14	0.499	0.499	0.9969	100-6	13
1MTW	2TGA	0.159	0.42	0.49	0.403	0.9837	100-5	10
1APU	3APP	0.498	0.40	0.498	0.499	0.9969	100-23	12
1QPE	3LCK	0.465	0.28	0.434	0.496	0.9984	2-4	12
5P2P	3P2P	0.480	0.42	0.49	0.457	0.9893	98	11
4PHV	3PHV	0.045	1.23	0.13	0.111	0.9268	99	10
3PTB	3PTN	0.122	0.26	0.499	0.292	0.9979	100	10
1BID	3TMS	0.499	0.24	0.499	0.499	0.9984	100	11
1OKM	4CA2	0.472	0.22	0.482	0.498	0.9986	100	11
4DFR	5DFR	0.496	0.82	0.0887	0.348	0.9725	99	12
3MTH	6INS	0.381	1.09	0.437	0.479	--	--	8
6RSA	7RAT	0.440	0.18	0.158	0.463	0.9981	100	11
1CDO	8ADH	0.403	1.34	0.101	0.161	0.8304	55-8	16
7CPA	5CPA	0.132	0.40	0.499	0.128	0.9956	100	12
1ROB	8RAT	0.469	0.28	0.490	0.491	0.9955	100	8
1IGJ	1A4J	0.411	0.80	0.47	0.0707	0.2793	78-4	17

^*For comparison, we have used TM-SCORE server at: http://zhanglab.ccmb.med.umich.edu/TM-SCORE/

^**The numbers reported here are the maximum and minimum sequence identity of aligned positions in percent. The data are given from the Dali server: http://ekhidna.biocenter.helsinki.fi/dali_lite/start/ .

-- No value reported by the site

Table 2.

A set of 86 protein structures with WSV, SV [8], and RMSD from Li et al. [1], NRMSD, TM-SCORE [16, 17], and DALILITE [18]

First protein’s PDB ID	Second protein’s PDB ID	SV [8]	RMSD [1]	NRMSD	WSV	TM-SCORE [16, 17]*	DALILITE [18]**	L max
1AD4	1AD1	0.499	0.50	0.463	0.498	0.9445	100-8	14
1AHX	1AHG	0.499	0.24	0.494	0.500	0.9989	100	17
1AUR	1AUO	0.499	0.20	0.499	0.499	0.9987	100-9	13
1AXZ	1AXY	0.498	0.12	0.499	0.500	0.9995	100	11
1GN8	1B6T	0.491	0.51	0.472	0.493	0.9904	100	12
1B9Z	1B90	0.494	0.54	0.499	0.500	0.9929	100-3	15
1LRI	1BEO	0.498	1.05	0.471	0.495	0.9317	99	8
1BUL	1BUE	0.499	0.18	0.482	0.500	0.9991	100	11
1BYD	1BYA	0.499	0.43	0.499	0.498	0.9923	100-5	14
1C3R	1C3P	0.202	0.39	0.11	0.141	0.9970	99	17
1C5I	1C5H	0.494	0.13	0.499	0.500	0.9993	100	10
1QJW	1CB2	0.498	0.63	0.495	0.495	0.9898	100-3	16
1CTE	1CPJ	0.499	0.29	0.492	0.500	0.9977	100	14
1SZJ	1CRW	0.499	0.33	0.499	0.498	0.9975	100	16
1ESW	1CWY	0.498	0.38	0.499	0.499	0.9978	100-4	14
1CY7	1CY0	0.155	1.12	0.45	0.085	0.9664	99-11	15
1DED	1D7F	0.481	0.26	0.364	0.499	0.9992	100-4	22
1P7T	1D8C	0.406	0.66	0.088	0.060	0.9827	97-4	21
1DMY	1DMX	0.499	0.19	0.499	0.500	0.9988	100	14
1DQY	1DQZ	0.052	0.75	0.0962	0.306	0.9494	99	15
1LP6	1DV7	0.471	0.56	0.126	0.443	0.9447	100-6	13
1E2S	1E1Z	0.499	0.13	0.492	0.500	0.9997	100	14
1ESE	1ESC	0.499	0.19	0.499	0.500	0.9991	100-8	12
6ALD	1EWD	0.477	0.44	0.434	0.435	0.9411	95-4	21
1NLM	1F0K	0.163	1.66	0.418	0.146	0.9454	15-6	16
1F4X	1F4W	0.488	0.25	0.499	0.500	0.9981	100-6	13
1JBW	1FGS	0.430	1.48	0.451	0.292	0.9286	100-3	13
1FR8	1FGX	0.498	0.54	0.490	0.493	0.9935	100	15
1LD8	1FT1	0.416	0.92	0.480	0.048	0.9852	96-6	17
1HVC	1G6L	0.345	0.46	0.12	0.428	--	97-96	13
1LSP	1GBS	0.360	0.26	0.499	0.483	0.9973	100	10
1LC3	1GCU	0.458	0.77	0.4	0.405	0.9774	13-7	12
1GJW	1GJU	0.499	0.29	0.499	0.500	0.9989	100-7	16
1N75	1GLN	0.422	1.47	0.49	0.095	0.9665	99	14
1GOY	1GOU	0.476	0.47	0.464	0.160	0.9727	100	11
1H46	1GPI	0.193	0.15	0.499	0.253	0.9996	100	13
1GUZ	1GV1	0.383	0.62	0.483	0.327	0.9908	13-7	19
1YDD	1HEA	0.491	0.18	0.499	0.500	0.9991	100	11
1YDA	1HEB	0.498	0.20	0.499	0.500	0.9989	100	11
1KIC	1HOZ	0.420	0.35	0.486	0.246	0.9911	100	16
1A80	1HW6	0.466	0.93	0.413	0.484	0.9540	100-11	11
1I3A	1I39	0.498	0.40	0.499	0.500	0.9946	100	10
4AIG	1IAG	0.494	0.26	0.494	0.500	0.9946	--	10
1JZS	1ILE	0.497	0.69	0.499	0.492	0.9952	100-7	17
1JQ3	1INL	0.493	0.35	0.480	0.500	0.9996	100-99	20
1JAY	1JAX	0.435	0.60	0.493	0.397	0.9884	100	13
1UEH	1JP3	0.499	0.67	0.451	0.499	0.9800	99	14
1JSO	1JSM	0.499	0.10	0	0.500	0.9998	100	14
1JYL	1JYK	0.208	0.94	0.0164	0.184	0.9724	99	18
1JVS	1K5H	0.351	1.16	0.253	0.067	0.7102	95-7	19
1K70	1K6W	0.497	1.08	0.499	0.499	0.9838	100-8	13
1M6P	1KEO	0.136	1.05	0.450	0.126	0.8779	100	12
3KIV	1KIV	0.467	0.30	0.458	0.478	0.9908	99	7
1KMP	1KMO	0.498	0.64	0.439	0.492	0.9393	97-1	16
2NGR	1KZ7	0.467	1.61	0.0536	0.233	--	97	19
2MIN	1L5H	0.084	0.55	0.103	0.234	0.9546	99-5	24
1LL2	1LL3	0.496	0.37	0.480	0.500	0.7234	100	11
1LMC	1LMN	0.499	0.10	0.49	0.500	0.9994	100	8
1EYN	1NAW	0.208	1.02	0.112	0.221	0.9855	100-8	17
1BHT	1NK1	0.033	0.58	0.465	0.044	0.9879	100	13
1PBO	1OBP	0.143	0.38	0.343	0.277	0.9062	99	13
1OPB	1OPA	0.295	0.68	0.129	0.471	0.9808	100	15
1I75	1PAM	0.499	0.13	0.499	0.499	0.9998	100	20
1NME	1PAU	0.499	0.29	0.45	0.500	0.0643	100	11
1KEV	1PED	0.281	0.81	0.499	0.374	0.9864	100-10	20
1PIG	1PIF	0.495	0.32	0.499	0.499	0.9985	100-8	14
1PJC	1PJB	0.498	0.61	0.499	0.499	0.9942	100-9	12
1KLT	1PJP	0.168	0.97	0.358	0.409	0.9555	98-3	11
1QHG	1PJR	0.499	0.23	0.473	0.500	0.9974	100-6	16
1CEB	1PKR	0.041	0.58	0.0925	0.183	0.6458	100	9
2PK4	1PMK	0.417	0.71	0.101	0.139	0.9566	100	9
1BK9	1PSJ	0.494	0.24	0.321	0.500	0.9967	100	9
1QBB	1QBA	0.497	0.11	0.499	0.489	0.9999	100-5	22
1PYY	1QME	0.157	0.59	0.38	0.271	0.9775	99-5	15
1OSS	1SGT	0.367	0.27	0.488	0.408	0.9976	99-0	10
1SWN	1SWL	0.497	0.31	0.467	0.492	0.9941	100-1	14
1LBT	1TCA	0.440	0.24	0.0796	0.356	0.9987	100	15
1WBL	1WBF	0.371	0.39	0.122	0.197	0.9955	100	18
1YDB	1YDC	0.491	0.12	0.499	0.498	0.9996	100	11
1H0S	2DHQ	0.499	0.26	0.485	0.500	0.9856	10-5	9
1LLO	2HVM	0.498	0.12	0.499	0.500	0.9996	100-5	11
43CA	43C9	0.491	0.23	0.495	0.499	0.9965	100-22	18
5BIR	4BIR	0.487	0.61	0.0932	0.193	0.9714	100	10
5EUG	4EUG	0.498	0.21	0.499	0.500	0.9986	100	11
5EAU	5EAS	0.064	0.40	0.38	0.019	0.9976	99-3	16
7TAA	6TAA	0.499	0.24	0.499	0.500	0.9990	100-7	14

^*For comparison we have used TM-SCORE server at: http://zhanglab.ccmb.med.umich.edu/TM-SCORE/

^** The numbers reported here are the maximum and minimum sequence identity of aligned positions in percent. The data are given from Dali server: http://ekhidna.biocenter.helsinki.fi/dali_lite/start/ .

-- No value reported by the site

A way to see how the mass of atoms and restriction on the space dimension perform the similarity criterion between two proteins is to compute the WSV and SV correlation with RMSD. The correlation between WSV and RMSD for the 48 dataset is 0.45 and for the 86 dataset is 0.55, which are better than the correlation between SV and RMSD for these two datasets, i.e., 0.32 and 0.36, respectively. In Ref. [19], a complete discussion is given to explain why we do not expect to see a high correlation between RMSD and SV (WSV). This is why we defined NRMSD for comparison with WSV. NRMSD is a bounded parameter that removes the inconvenience of semi-bounded RMSD. Also, both the parameters WSV and NRMSD are similarity criteria.

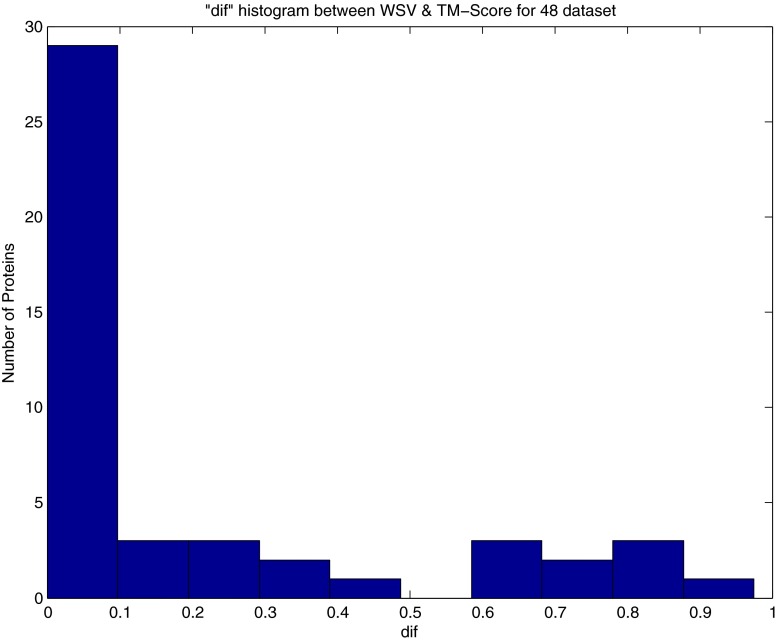
Figures 1 and 2 show the histogram of dif between WSV and NRMSD for the 48 and 86 datasets. We see that 60% of WSV and NRMSD prediction for the 86 dataset have less than 10% differences and 70% of their prediction values have less than 20% differences. The results for the 48 dataset also show a 60% agreement between WSV and NRMSD with less than 10% differences and 67% for 20% difference of prediction values. The disagreement between WSV and NRMSD by a 80% difference of prediction values for the 48 dataset is equal to 4.5% and for the 86 dataset is equal to 5.8% (a summary of these results is given in Table 3). Figures 3, 4, 5, and 6 show the histogram of dif computed between WSV and TM-SCORE and also DALILITE. These figures and also Table 3 show good agreement between WSV and these methods.

Fig. 1.

dif histogram between WSV and NRMSD for 48 dataset

Fig. 2.

dif histogram between WSV and NRMSD for 86 dataset

Table 3.

Differences between WSV and the other methods by using dif

	NRMSD		TM-SCORE		DALILITE
	48 dataset (48)*	86 dataset (86)*	48 dataset (47)*	86 dataset (84)*	48 dataset (47)*	86 dataset (85)*
Less than 10% differences	60.5%	59.3%	63.9%	63.1%	61.7%	63.5%
Less than 20% differences	66.7%	69.7%	68.1%	69.1%	68.1%	67.1%
More than 80% differences	4.1%	5.8%	8.5%	4.8%	6.4%	4.7%
More than 90% differences	0%	2.3%	2.1%	1.2%	4.3%	1.1%

^*Number of proteins pairs compared. TM-SCORE and DALILITE have not given values for all protein pair comparisons

Fig. 3.

dif histogram between WSV and TM-SCORE [14, 15] for 48 dataset

Fig. 4.

dif histogram between WSV and TM-SCORE [14, 15] for 86 dataset

Fig. 5.

dif histogram between WSV and DALILITE [18] for 48 dataset

Fig. 6.

dif histogram between WSV and DALILITE [18] for 86 dataset

Table 4 shows the sensitivity, specificity, accuracy, and precision of WSV compared with the other scores (NRMSD, DALILITE, TM-SCORE) as targets. In summary, as Table 4 shows, comparing WSV with NRMSD, the ‘sensitivity’ or the probability that two proteins are determined to be similar by WSV is about 85.7% (80.0%) for the 86(48) dataset and the ‘specificity’ or the probability that the two proteins are determined to be dissimilar by WSV is equal to 62.5% (37.5%). The accuracy of the method (WSV) for the 86(48) dataset is 81.4% (72.9%) and the precision is 90.9% (86.5%), which indicates that both measures show good agreement between WSV and NRMSD predictions. The F-score for the 86(48) dataset shows that the performance to give similarity prediction is about 88.2% (83.1%), which is an expected result because the two datasets for the proteins examined here are closely similar. These results show that WSV could be a good alternative parameter for RMSD (or NRMSD); it does not involve the protein size issue and provides a normalized similarity criterion between any two proteins. The results of the comparison between WSV and TM-SCORE [14, 15] and DALILITE [18], in the same manner as for WSV and NRMSD and reported in Table 4, show that a good agreement exists between WSV and these methods’ predictions and also good precision of WSV.

All of the above results show that WSV appears to be a reliable alternative parameter for RMSD (or NRMSD). WSV is a geometrical criterion while it also includes physical properties. Moreover, it does not suffer from the protein size problem and it provides a similarity criterion between two proteins as well as other criteria.

For computing WSV, we used an i7 laptop with 8 GB RAM. The time required to complete this computation depends on the proteins’ sizes and on average it takes about 3 min (for small proteins it takes about 1 min and for large proteins the computation takes about 6 min). In Tables 1 and 2, we also show the L _max used for each pair of proteins.

Conclusions

In this paper, we introduced WSV, which displays two major differences compared to SV. First, we weighted the shape function by atomic masses, which stresses the importance of the individual atoms in the computation. Second, we extended the dimensions of the reciprocal space at least up to the largest compared proteins’ sizes (measured by the number of atoms). This condition ensures that we do not lose any information about the proteins when we map them onto the reciprocal space. As discussed in the Results and discussion section, these two changes in SV improve the correlation between WSV with RMSD relative to SV. We compared WSV with NRMSD, TM-SCORE, and DALILITE by using statistical concepts such as sensitivity, specificity, etc. The results show good accuracy and precision for WSV. Also, we computed a relative difference (dif) between WSV and other methods, which also shows good agreement between WSV predictions and other scores. Our results confirm the reliability and usefulness of our method and show that WSV can be used alternatively with RMSD in helping to find protein similarity in various areas of protein science and in drug discovery.

WSV is now defined as a geometrical structural score. To develop this work in the future, it is suggested to define a score on both the WSV- and domain-based structural methods. Also, we wish to emphasize that WSV is a geometric-based method, sensitive to the protein's atoms positions and their masses. Thus, if one of these parameters changes, WSV will also change. Apparently, for two structurally similar proteins with dissimilar sequences, WSV does not give structural homologues as a result. This hypothesis will be examined in our future research and if it is indeed verified, this could present an advantage of WSV relative to SV or RMSD.