Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Oct 12;6:35313. doi: 10.1038/srep35313

Large spin-orbit coupling and helical spin textures in 2D heterostructure [Pb2BiS3][AuTe2]

L Fang 1,2,*, J Im 3,*, W DeGottardi 1,a, Y Jia 4, A Glatz 1,5, K A Matveev 1, W-K Kwok 1,b, G W Crabtree 1, M G Kanatzidis 1,2,c
PMCID: PMC5059675  PMID: 27731394

Abstract

Two-dimensional heterostructures with strong spin-orbit coupling have direct relevance to topological quantum materials and potential applications in spin-orbitronics. In this work, we report on novel quantum phenomena in [Pb2BiS3][AuTe2], a new 2D strong spin-orbit coupling heterostructure system. Transport measurements reveal the spin-related carrier scattering is at odds with the Abrikosov-Gorkov model due to strong spin-orbit coupling. This is consistent with our band structure calculations which reveal a large spin-orbit coupling gap of εso = 0.21 eV. The band structure is also characterized by helical-like spin textures which are mainly induced by strong spin-orbit coupling and the inversion symmetry breaking in the heterostructure system.

The motion of an electron through a lattice potential gives rise to a coupling between the electron’s momentum and its spin. This relativistic effect is known as spin-orbit coupling (SOC). SOC plays an important role in topologically nontrivial electronic structures1,2,3 as well as those which can realize Majorana fermions4,5,6. SOC also offers a unique route to tune the spin degree of freedom that has potential impact on spintronics devices7,8,9. Understanding SOC in confined systems such as interfacial boundaries and nanowires is particularly important in order to exert quantum control on electronic degrees of freedom in miniaturized devices. Extensive studies have been conducted in the 2D electron gas such as GaAs/Ga1-xAlxAs10 and HgTe/CdTe/HgTe quantum wells11. More emergent properties can be expected in similar systems with sufficiently strong SOC such as naturally formed crystalline heterostructures that adopt a structure similar to those of epitaxially grown heterostructure films. A strong advantage of naturally formed heterostructures is that a large number of organic and inorganic materials adopt this type of structure, for example the intergrowth chalcogenides12 and the inorganic-organic hybrid systems such as halides13. These crystal heterostructures provide a parallel platform to epitaxial films to uncover novel quantum phenomena derived from strong SOC and inversion symmetry breaking10,11.

Recent work on the naturally formed 2D mineral [Pb2BiS3][AuTe2] shows heterostructure electronic states featuring a conductive [AuTe2] layer sandwiched between two insulating [Pb2BiS3] sheets14. The building blocks [Pb2BiS3]+1 and [AuTe2]−1 are alternately stacked along the crystal’s c-axis to form an intergrowth structure, shown in Fig. 1a 14,15,16. A number of intriguing properties such as an extremely large electrical anisotropy, high mobility 2D carriers, and linear energy band dispersions were discovered14. The SOC strength in this material is expected to be strong, because many of the component materials are heavy elements. However, as we will discuss below, the SOC in [Pb2BiS3][AuTe2] is anomalous in that it lies beyond the expected scaling properties predicted by the Abrikosov-Gorkov model9. Furthermore, our calculations on atomically thin films unveil helical-like spin textures when the spin vectors traverse around the closed 2D Fermi surfaces. The helical-like spin textures could be an effect arising from the strong SOC and the unique heterostructure in [Pb2BiS3][AuTe2].

Figure 1.

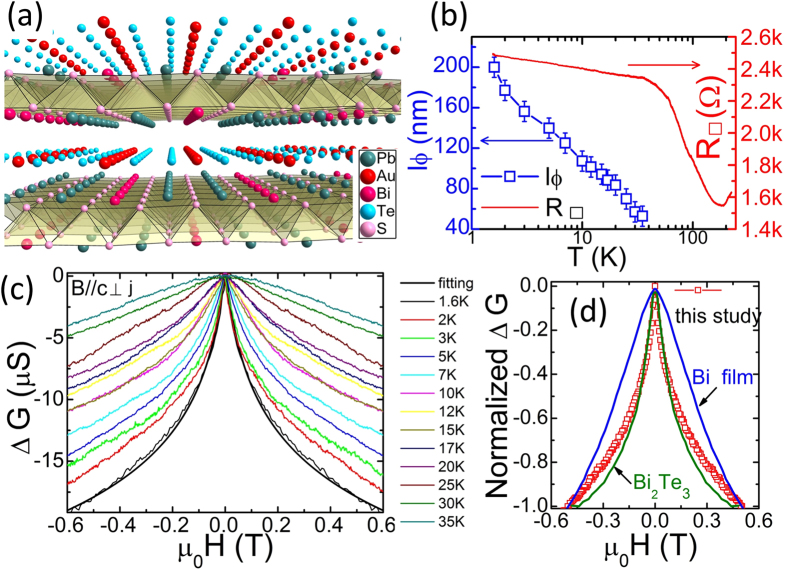
Figure 1

Open in a new tab

(a) The intergrowth structure of [Pb2BiS3][AuTe2] is constituted by two building blocks [Pb2BiS3]+ and [AuTe2]−, which stack alternatively along the c-axis. (b) Temperature dependent resistance and phase coherence length of a thin sheet crystal [Pb2BiS3][AuTe2]. (c) The field dependent conductance at elevated temperatures. The cusp shape curve at 1.6 K can be fitted with the 2D Hikami-Larkin-Nagaoka equation. (d) WAL of [Pb2BiS3][AuTe2] resembles that of Bi and TI Bi2Te3. The temperature is 2 K.

Results and Discussion

A direct measurement of a materials’ SOC strength is difficult because SOC is a relativistic effect. However, SOC manifests itself in quantum interference phenomena such as weak antilocalization (WAL)17,18. WAL provides an effective approach to quantitatively investigate the SOC strength of a material using standard electrical characterization. In the diffusion regime and in the case of self-intersecting electron scattering paths, the interference between the electron’s time reversed paths is pronounced and tends to localize electrons. This phenomenon is known as weak localization (WL). WAL occurs when strong SOC suppresses WL effects.

Figure 1b shows the temperature dependent resistance of a cleaved single-crystal thin layer. The resistance upturn below 150 K demonstrates the poor metallic property of the samples. Below 40 K, the resistance increases linearly with decreasing temperature. This behavior could be related to electron-electron interaction that has been extensively discussed in disordered semiconductors and topological insulators19,20. Our magnetoconductivity measurements focus on the low field regime, for example B < 0.6 T. In this regime, the Hall resistivity (ρxy) is far smaller than the longitudinal resistivity (ρxx) and the square conductance tensor takes the form 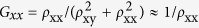Inline graphic. The magnetoconductance is defined as 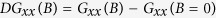Inline graphic. Figure 1c is the field dependent conductivity at different temperatures. Both its cusp shape and its negative sign are hallmarks of WAL. Due to thermal fluctuations, the cusp shape gradually broadens with increasing temperature and diminishes at 40 K.

We apply the 2D Hikami-Larkin-Nagaoka (HLN) equation21,22 to fit the data. Assuming that τφ is much longer than both τso and τe, the HLN equation [see equation (2)] can be written

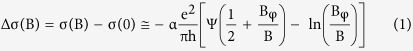graphic file with name srep35313-m3.jpg

where α = 1/2, e is the electron charge and h is the Planck constant. The parameters τe, τso, and τφ are the electronic elastic scatting time, spin-orbit scattering time and phase coherence time, respectively. The quantity Ψ(z) is the digamma function. We define a field strength Bφ  = ħ/(4e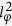Inline graphic) which is the characteristic field associated with the coherence length lφ, where 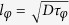Inline graphic and D is the diffusion constant. Figure 1c shows a fitting curve which virtually superposes on the experimental data. This fitting confirms that [Pb2BiS3][AuTe2] has strong SOC. At elevated temperatures (i. e. T = 35 K), lφ = 50 ± 10 nm, indicating robust quantum interference against thermal fluctuation in this system. Moreover, the agreement with a theoretical model of 2D transport confirms that the electronic degrees of freedom are confined to 2D in [Pb2BiS3][AuTe2]. Previous studies have shown large electrical anisotropy of Г~104 in this material14.

In Fig. 1d, we compare conductance data as a function of magnetic field of [Pb2BiS3][AuTe2] with that of Bi2Te323 and Bi24 at T = 2 K. For purposes of comparison, this data has been normalized to unity (see supporting information). The similarities among these various systems, especially between [Pb2BiS3][AuTe2] and Bi2Te3, is surprising. The topological insulator (TI) Bi2Te3 and semi-metal Bi are known for having unusually strong SOC among materials systems. This striking resemblance indicates that aspects of the SOC coupling in [Pb2BiS3][AuTe2] may be unusual. In order to gain a deeper understanding, we quantitatively investigated τso and τe of [Pb2BiS3][AuTe2] by analyzing the HLN equation that contains a form describing different scattering processes17,21,22.

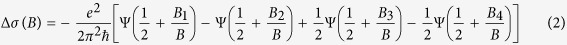graphic file with name srep35313-m6.jpg

where B1 = Be + Bso + Bs, B2 = 4/3Bso + Bφ + 2/3Bs, B3 = Bφ + 2Bs, B4 = B2. The characteristic fields Bn,n = 1–4 are connected with the characteristic relaxation times τn by the relation Bn = ħ/4eDτn. The parameter Bsis a characteristic field due to magnetic scattering and is zero in this case because [Pb2BiS3][AuTe2] is not a magnetic material with no magnetic impurities. It is worthy pointing out that Bergmann17 uses a special case of the formula derived by Hikami, Larkin, and Nagaoka21. Specifically, the corresponding decoherence times are the same for all three components of the spin. In addition, there is a typo in the HLN equation which has been corrected by Maekawa and Fukuyama22. Fitting data to equation (2) is challenging due to the large parameter space of Be, BSO and Bφ. This problem can be addressed by using the value of Bφ that was determined using equation (1), which assumes that τφ ≪ τso, τe still holds at low temperatures. Our fitting yields Bso = 0.5 ± 0.2 T and Be = 1 ± 0.2 T. The reported Bso of Bi is 0.25 T24. The reported value of Bso of Bi2Te3 is greater than 8 T25. In contrast, the Bso of material systems with moderate SOC are generally far less than 0.1 T (see supporting information). The large Bso for these three systems qualitatively explains their similar WAL data. Our fitting parameters are reasonable: a value of Be = 1 ± 0.2 T corresponds to a mean free path of ~10 nm which is consistent with the sample’s poor metallic properties as revealed by the resistivity measurement presented in Fig. 1b.

Materials with large SOC strength may have potential applications as platforms for spin-orbitronics7. Comparison of the SOC related carrier scattering in various systems is thus worthwhile. Here we use the model of Abrikosov and Gorkov which predicts τe/τso ≈ (αZ)4,9 where α ≈ 1/137 is the fine structure constant and Z represents the atomic number. This model reveals that the electrons’ spin-orbit scattering is not only determined by the atomic number, but also is influenced by the elastic scattering of electrons by impurities. This is particularly important for spin-orbitronics applications since it predicts that τso can be tuned by the material’s purity. Here, we use the weighted arithmetic mean to calculate the effective atomic number of materials composed of multiple elements. For [Pb2BiS3][AuTe2], only the elements Au and Te are accounted for in the effective Z since the density of states at the Fermi surface are mainly contributed by Au 3d electrons and Te p electrons14. Figure 2 summarizes the relations between τe/τso and the effective atomic mass of a variety of systems whose SOC strength has been investigated. Consistent with the Abrikosov-Gorkov prediction, a majority of the materials follow the trend that τe/τso is proportional to Z4, which is depicted by the red solid line in Fig. 2. The topological insulator Bi2Te3 is an exception due to its extremely large SOC26, the topology-related Berry’s phase and the backscattering immunity27 which always make τso extremely short and τe exceptionally long. In topological insulators, the elastic scattering rates can be weaker than the spin orbit scattering rates8,25, which results in τe/τso being greater than unity. The topological insulators are thus considered to be excellent spin-generator materials7. We categorize the TI material Bi2Te3 into the unconventional class of systems and the rest such as Au28 into the conventional class. Our [Pb2BiS3][AuTe2] sample falls between these two classes, suggesting the strong SOC, heterostructured systems may have potential for spin generation. The violation of the Abrikosov-Gorkov scattering model in our system is intriguing, and must be related to strong SOC.

Figure 2. τe/τso versus effective atomic number (Z) for different systems.

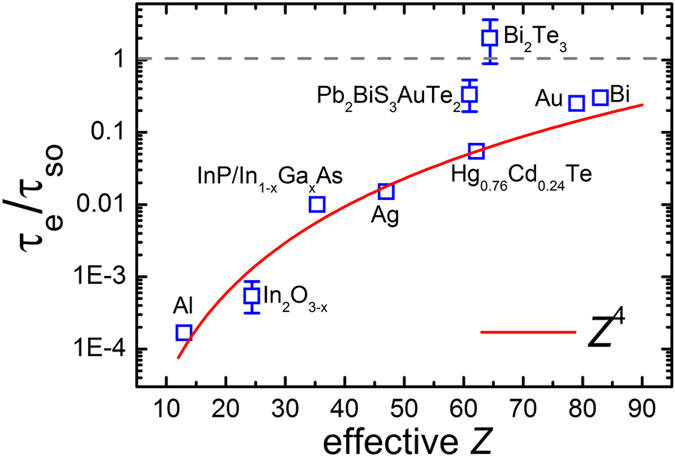
Figure 2

Open in a new tab

Weighted arithmetic mean is used to calculate the effective atomic number of materials composed of multiple elements. For [Pb2BiS3][AuTe2], only the elements Au and Te are accounted for the Z because the density of states at the Fermi surface are mainly contributed by Au 3d electrons and Te p electrons14. The red solid line is a simulation using the relation Z4. TI Bi2Te3 violates the Abrikosov and Gorkov’s prediction τe/τso~ Z4 due to the topology-related Berry’s phase and the extremely large SOC. [Pb2BiS3][AuTe2] does not follow the Z4 relation. The τso and τe of Al, InP/InGaAs, In2O3, Hg0.76Cd0.24Te, Au and Ag are from references28,35,36,37,38.

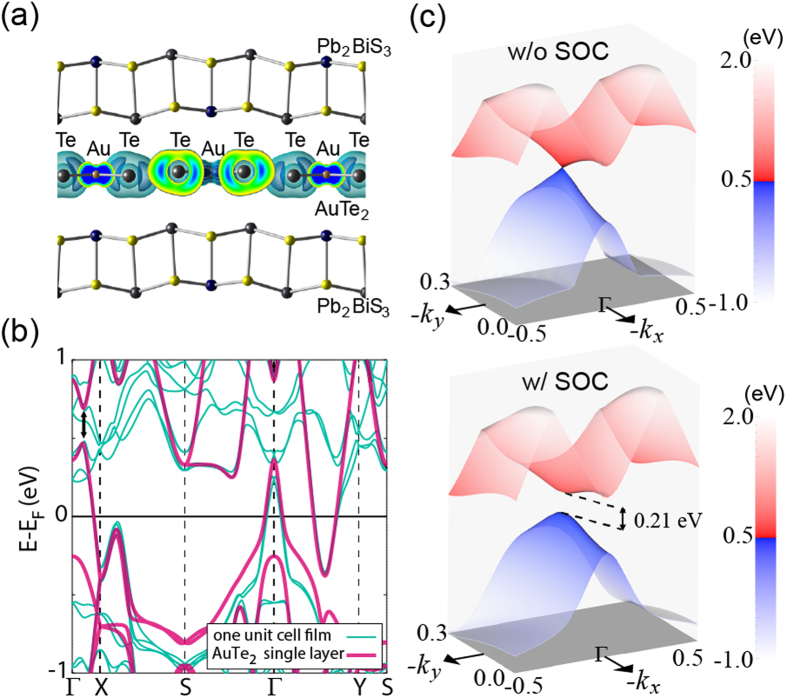
The large SOC can be understood by our ab initio calculations. The electronic structure near the Fermi level of [Pb2BiS3][AuTe2] purely originates from the [AuTe2]− layer. Figure 3a is a contour plot of the local density of state (LDOS) of [Pb2BiS3][AuTe2] near the Fermi level, which clearly shows that the electronic states are tightly confined to the [AuTe2]− layer. Figure 3b exhibits the energy band dispersions of the [AuTe2]− layer and the single-unit-thick films. The vertical arrow marks the gap opening due to strong SOC. Figure 3c shows the detailed information of the gap opening in 3D reciprocal space. Without SOC in the [AuTe2]− layer, a Dirac-like gapless state appears at the hole-band between the Г and X points. SOC opens the gapless Dirac-like state to form a spin-orbit gap of εSO = 0.21 eV. This value is comparable to the SOC-induced band inversion energy in TIs and the spin-orbit gap of the topology-nontrivial Sb-bilayer system26,29. The SOC gap in the [AuTe2]− layer also occurs at the Г point near the Fermi Energy (see the top panel of Figure S6 in supporting information). The large spin-orbit gap elucidates the large SOC and the violation of the Abrikosov-Gorkov scattering model. Since [Pb2BiS3][AuTe2] is not a TI, our studies thus suggest that materials can violate the Abrikosov-Gorkov scattering model as long as their SOC strengths are sufficiently large.

Figure 3.

Figure 3

Open in a new tab

(a) Contour plot of the local density of state (LDOS) of [Pb2BiS3][AuTe2] near the Fermi level. The [AuTe2]− layer dominates the electronic structure. (b) Energy bands dispersion of one-unit-cell [Pb2BiS3][AuTe2] film (light blue), and [AuTe2]− single layer (light red). A hole pocket lies at Г and an electron pocket is formed between Г-Y. (c) A Dirac-like gapless state appears at the hole-band without SOC (upper panel). SOC opens the Dirac-like gapless state with a spin-orbit gap of 0.21 eV (lower panel). The gap opening is denoted in (b) by the black arrow.

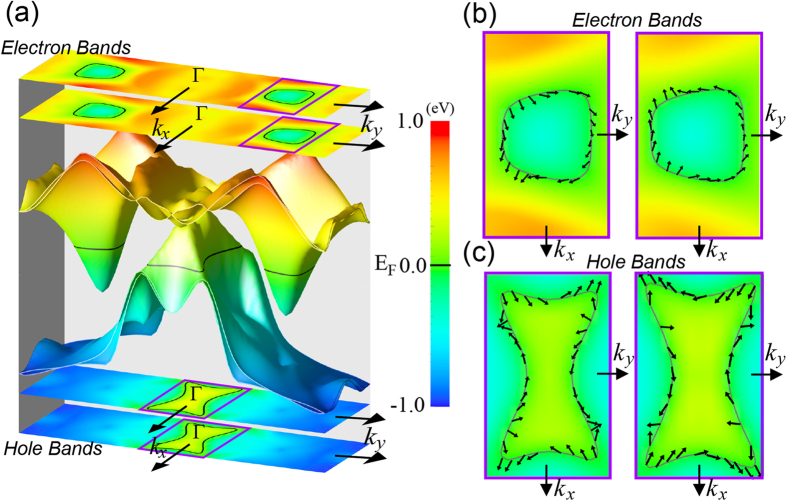
The large SOC, combined with the unique heterostructure in [Pb2BiS3][AuTe2], may lead to helical spin textures that have been observed in topological insulators and semiconductor heterostructure films27,30. We carried out theoretical investigations on the single-unit-cell film [Pb2BiS3][AuTe2] films where the twofold spin-degeneracy is lifted due to inversion symmetry breaking. Figure 4a presents the Fermi surfaces of the electron and hole bands and their projections at the Fermi level. The dual projection sheets are induced by broken inversion symmetry. Both electron bands and hole bands are found to have spin structures whose direction changes as a function of crystal momentum k. The spin textures of the electron and hole pockets exhibit different topological properties. For the electron pockets, the spin does not undergo a full winding as one traverses around the Fermi surface while for the hole pockets the spin winds around 3 times. The helical-like spin texture in the hole pocket can be attributed to the strong SOC and the inversion-asymmetry induced spin splitting in a heterostructure system. For example the Ga1-xInxAs/InP quantum well has shown helical spin texture in the presence of SOC30. The spin textures in the hole pocket exhibit spin-flip between the hole carriers with opposite momentum k and –k, as a consequence of time-reversal symmetry. The shape of the Fermi surface reflects the orthorhombic crystalline symmetry of [Pb2BiS3][AuTe2]. In addition, the spin-flip in the hole pocket may indicate a non-vanishing Berry’s phase. Direct detection of the Berry’s phase is beyond the scope of this study. However, the WAL in our sample is consistent with a nontrivial Berry’s phase which gives opposite signs to time-reversed electron paths. This type of destructive quantum interference can also result in WAL18,27,31. Our modeled helical spin textures in single-unit-cell films could be experimentally pursued as we demonstrate that single-unit-cell films naturally occur on the cleaved surfaces of a bulk crystal (Figure S1 in supporting information). Further experiments such as spin-resolved photoemission spectroscopy are needed to confirm our theoretical predictions of the helical spin textures.

Figure 4.

Figure 4

Open in a new tab

(a) A 3D plot of the electronic band structure of the one-unit-cell [Pb2BiS3][AuTe2] film near the Fermi level. The 2D projection of electron bands and hole bands are depicted on the top and at the bottom, respectively. Black solid lines indicate the Fermi level. The dual projected sheets are due to inversion symmetry breaking on the surfaces of the one-unit-cell film. (b,c) shows spin direction along the closed 2D Fermi surfaces for electron and hole bands, respectively. Left and right panels of (b,c) correspond to two non-degenerated bands due to inversion symmetry breaking in the one-unit-cell film. The area of (b,c) in momentum space are denoted by purple-colored rectangles shown in (a).

Conclusions

To summarize, large SOC strength was discovered in the 2D heterostructure [Pb2BiS3][AuTe2]. This large SOC is induced by a large spin-orbit gap εSO = 0.21 eV. More broadly, our work suggests that materials can violate the Abrikosov-Gorkov scattering model for sufficiently strong spin-orbit coupling. Ab initio calculations reveal helical-like spin textures and spin-flips at the Fermi surfaces. These predictions can be attributed to the effect of strong SOC and inversion symmetry breaking in the heterostructure as well as the constraint of crystalline symmetry in the AuTe2 layer. More generally, our work points out that naturally forming heterostructures made of heavy atoms provide a new direction for exploring novel quantum phenomena at the atomic scale. Given the large number of naturally formed organic and inorganic heterostructures and their hybrids12,13, more discoveries can be expected in this direction.

Methods

Bulk crystal synthesis follows a self-flux method by melting stoichiometric compositions of [Pb2BiS3][AuTe2]. Details of the crystal synthesis were reported in our previous paper14. Crystals were exfoliated on SiO2/Si wafers using the so-called scotch tape method and were post-annealed at 350 °C in argon gas to remove chemical residuals on the cleaved surface. The crystals’ thickness is determined by AFM (PSIA Corporation). Morphology studies on cleaved surfaces were conducted by a MultiMode scanning probe microscope (Veeco) operated in a peak-force tapping mode that has vertical spatial resolution up to 50 pm. Cleaved crystals with thickness 40 nm were selected for transport characterization. Standard photolithography (LaserWirter, MICROTECH) and magnetron sputtering were employed to pattern contacts on cleaved crystals. In-plane electrical characterization was conducted using the standard four probe method in a liquid 4He variable temperature cryostat equipped with a triple-axis vector magnet system (AMI).

Electronic structures of [Pb2BiS3][AuTe2] bulk, one-unit-cell thick [Pb2BiS3][AuTe2] film and the [AuTe2]− single layer were calculated within density functional theory using Projector Augmented Wave method32 implemented in the VASP code33. Perdew-Burke-Ernzerhof type34 generalized gradient approximation was utilized for the exchange correlation functional. Spin-orbit coupling was included in the non-collinear form. Experimentally resolved crystal structure was employed for [Pb2BiS3][AuTe2], and crystal structure of [AuTe2]− single layer was prepared from the bulk crystal structure of [Pb2BiS3][AuTe2] by removing [Pb2BiS3]+ layers. The crystal structure of the monolayer [Pb2BiS3][AuTe2] is calculated assuming a vacuum layer of 3 nm.

Additional Information

How to cite this article: Fang, L. et al. Large spin-orbit coupling and helical spin textures in 2D heterostructure [Pb2BiS3][AuTe2]. Sci. Rep. 6, 35313; doi: 10.1038/srep35313 (2016).

Supplementary Material

Supplementary Information
srep35313-s1.pdf (852.9KB, pdf)

Acknowledgments

The authors are grateful to Ivar Martin, Vivek Mishra, Ulrich Welp and Ralu Divan for useful discussions. Transport characterizations were supported by the US Department of Energy, Office of Science, Materials Sciences and Engineering Division. Synthesis and user facilities of the Center for Nanoscale Materials were supported by the Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Theoretical calculations were supported by the Korea Research Institute of Chemical Technology, under the project No. KN1502-I00(JI).

Footnotes

Author Contributions L.F. and M.G.K. synthesized the crystals. L.F., Y.J. and W.K.K. conducted the experiments. J.I. performed first-principles calculations. L.F., J.I., Y.J., W.D., A.G., K.M., M.G.K., W.K.K. and G.W.C. analyzed the data and wrote the manuscript.

References

  1. Kane C. L. & Mele E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005). [DOI] [PubMed] [Google Scholar]
  2. Bernevig B. A., Hughes T. L. & Zhang S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757 (2006). [DOI] [PubMed] [Google Scholar]
  3. Hor Y. S. et al. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010). [DOI] [PubMed] [Google Scholar]
  4. Mourik V. et al. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012). [DOI] [PubMed] [Google Scholar]
  5. Cho S. et al. Symmetry protected Josephson supercurrents in three-dimensional topological insulators. Nature Comms. 4, 1689 (2013). [DOI] [PubMed] [Google Scholar]
  6. Kurter C., Finck A. D. K., Hor Y. S. & Van Harlingen D. J. Evidence for an anomalous current–phase relation in topological insulator Josephson junctions. Nature Comms. 6, 7130 (2015). [DOI] [PubMed] [Google Scholar]
  7. Pesin D. & MacDonald A. H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 11, 409–416 (2012). [DOI] [PubMed] [Google Scholar]
  8. Manchonl A., Koo H. C., Nitta J., Frolov S. M. & Duine R. A.. New perspectives for Rashba spin–orbit coupling. Nat. Mater. 14, 871 (2015). [DOI] [PubMed] [Google Scholar]
  9. Abrikosov A. A. & Gor’kov L. P. Spin-Orbit interaction and the Knight Shift in superconductors. J. Exp. Theor. Phys. 15, 752–757 (1962). [Google Scholar]
  10. Klitzing K. V., Dorda G. & Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494 (1980). [Google Scholar]
  11. König M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007). [DOI] [PubMed] [Google Scholar]
  12. Rouxel J., Meerschaut A. & Wiegers G. A. Chalcogenide misfit layer compounds. J. Alloys Compd. 229, 144–157 (1995). [Google Scholar]
  13. Papavassiliou G. C. Three- and low-dimensional inorganic semiconductors. Prog. Solid. St. Chem. 25, 125–270 (1997). [Google Scholar]
  14. Fang L. et al. Two-Dimensional Mineral [Pb2BiS3][AuTe2]: High-Mobility Charge Carriers in Single-Atom-Thick Layers. J. Am. Chem. Soc. 137(6), 2311–2317 (2015). [DOI] [PubMed] [Google Scholar]
  15. Francis C. A. et al. Buckhornite, AuPb2BiTe2S3, a new mineral from Boulder County. Can. Mineral. 30, 1039−1047 (1992). [Google Scholar]
  16. Effenberger H., Culetto F. J., Tapa D. & Paar W. H. The crystal structure of synthetic buckhornite, [Pb2BiS3][AuTe2]. Z. Kristallogr. 215, 10−16 (2000). [Google Scholar]
  17. Bergmann G. Weak Localization in thin films a time-of-flight experiment with conduction electrons. Phys. Rep. 107, 1–58 (1984). [Google Scholar]
  18. Gantmakher V. F. Electrons and Disorder in Solids. Clarendon Press, Oxford, 2005). [Google Scholar]
  19. Altshuler B. L. & Aronov A. G. Zero bias anomaly in tunnel resistance and electron-electron interaction. Solid State Commun. 30, 115–117 (1979). [Google Scholar]
  20. Liu M. et al. Electron interaction-driven insulating ground state in Bi2Se3 topological insulators in the two-dimensional limit. Phys. Rev. B 83, 165440 (2011). [Google Scholar]
  21. Hikami S., Larkin A. I. & Nagaoka Y. Spin-orbit interaction and magnetoresistance in the two-dimensional random system. Prog. Theor. Phys. 63, 707 (1980). [Google Scholar]
  22. Maekawa S. & Fukuyama H. Magnetoresistance in two dimensional disordered systems: effects of Zeeman splitting and spin-orbit scattering, J. Phys. Soc. Jpn. 50, 2516–2524 (1981). [Google Scholar]
  23. He H.-T. et al. Impurity Effect on Weak Antilocalization in the Topological Insulator Bi2Te3. Phys. Rev. Lett. 106, 166805 (2011). [DOI] [PubMed] [Google Scholar]
  24. Sangiao S. et al. Quantitative analysis of the weak anti-localization effect in ultrathin bismuth films. EPL 95, 37002 (2011). [Google Scholar]
  25. Zhang S. X. et al. Magneto-resistance up to 60 Tesla in topological insulator Bi2Te3 thin films. Appl. Phys. Lett. 101, 202403 (2012). [Google Scholar]
  26. Zhang H. J. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438 (2009). [Google Scholar]
  27. Hsieh D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature, 460, 1101–1105 (2009). [DOI] [PubMed] [Google Scholar]
  28. Kawaguti T. & Fujimori Y. Magnetoresistance and inelastic scattering time in thin films of silver and gold in weakly localized regime. J. Phys. Soc. Jpn. 52, 722–725 (1983). [Google Scholar]
  29. Jin K.-H. & Jin S.-H. Quantum anomalous Hall and quantum spin-Hall phases in flattened Bi and Sb bilayers. Sci. Rep. 5, 8426 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Winkler R. Spin orientation and spin precession in inversion-asymmetric quasi-two-dimensional electron systems. Phys. Rev. B. 69, 045317 (2004). [Google Scholar]
  31. Lang M. et al. Competing weak localization and weak antilocalization in ultrathin topological insulators. Nano Lett. 13(1), 48–53 (2013). [DOI] [PubMed] [Google Scholar]
  32. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B. 50, 17953 (1994). [DOI] [PubMed] [Google Scholar]
  33. Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 59, 1758 (1999). [Google Scholar]
  34. Perdew J. P.; Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
  35. Santhanam P., Wind S. & Prober D. E. Localization, superconducting fluctuations, and superconductivity in thin films and narrow wires of aluminum. Phys. Rev. B, 35, 3188–3206 (1987). [DOI] [PubMed] [Google Scholar]
  36. Studenikin S. A., Coleridge P. T., Poole P. & Sachrajda A. Anomalous spin–orbit effects in a strained InGaAs/InP quantum well structure. J. Exp. Theor. Phys. Lett. 77, 311–316 (2003). [Google Scholar]
  37. Ben-Shlomo M. & Rosenbaum R. Transport properties of a 100-Å crystalline In2O3-x film. Phys. Rev. B. 39, 534–541(1989). [DOI] [PubMed] [Google Scholar]
  38. Hong J., Lee J., Joo S. & Rhie K. Control of the spin-orbit coupling by gate voltage in semiconductor FET structures. J. Korean Phys. Soc. 45, 197–201(2004). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep35313-s1.pdf (852.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES