Nanoindentation investigation of the stress exponent for the creep of dung beetle (Copris ochus Motschulsky) cuticle

ABSTACT

With the rapid development of bionic science, especially the progress that has been made in the fields of biomaterials and biomimetics, there is now great interest in the surface and internal mechanical properties of biological materials at the micro- and nanoscale. The study of micro- and nanoscale biomaterial mechanical properties could enable interdisciplinary applications in materials science, biological science and bionic science. Dung beetle (Copris ochus Motschulsky) cuticle is a viscoelastic material that is both viscous and flexible via elastic deformation under external forces; where stress σ, strain ε and elastic modulus E are related in the following way: σ = Eε. In addition, as σ is related to the rate of strain, time is also a factor. The stress-strain relationships of various parts of dung beetle cuticle were investigated in this paper. As time increased, the stress and strain of the material were found to decrease and increase, respectively, indicating that when the material was indented for a certain period, the interaction force between the indenter and the material gradually achieved a state of dynamic equilibrium. However, strain continued to occur until reaching a point of equilibrium because of the creep phenomenon. The stress-strain curves showed a strong character in each holding time condition: the longer the holding time, the more flattened the stress-strain curve. These findings will be useful in the advanced design of strong, lightweight, and biomimetic composites.

Introduction

Biomechanics is a discipline of quantitative physiology, which applies engineering principles and methods to biological systems.¹ The first consideration is the morphology of organisms, organs and microstructures and the establishment of a reasonable physical model, followed by measuring the mechanical properties of biological tissues or materials to determine the constitutive relations. Then, according to the basic principles of physics and the biological tissue, differential or integral equations are derived to describe the main constitutive relationship. Finally, according to the working environment of the organ, meaningful boundary conditions are obtained to solve for the boundary values. Physiological experiments are then used to verify the result, providing the basis for practical applications.

The insect cuticle has evolved to be protective, waterproof and wear-resistant. The cuticle is mainly composed of chitin fibers and a proteinaceous matrix.^2-4 For survival, the cuticle must be lightweight and function very efficiently,⁵ i.e., it must have superior mechanical properties, such as strength, stiffness and fracture toughness. The various arrangements of the chitin fibers, including cylindrical helicoidal, planar random, twisted orthogonal, 45° helicoid, and monodomain helicoidal,⁶ result in the light weight and lateral strength of the cuticle.

There some studies in the literature on the structures of beetle cuticles, including the surface wax layer chemical composition,⁷ ultrastructure,⁸ integument tissue structure,⁹ fiber configuration,¹⁰ and laminated characteristics of the cuticle, as well as related biomimetic designs.^4,11 The hydrophilic-hydrophobic composite structure of the desert beetle elytra, which can collect water from fog,¹² has been used in the design of bionic facilities. One study investigated the fractal characteristics of the surface of the dung beetle and its reaction to surface wetting, adhesion and friction against soil,¹³ which is helpful for the study of biomimetic surfaces with reduced drag. Another study found that bionic composites, which mimicked the dual helicoidal arrangement of plies and the continuity of fibers observed around holes in beetle cuticle, exhibited higher fracture toughness and strength than did conventional composite materials.¹⁴ The mechanical properties of insect cuticle may provide useful information for the design of advanced composites. While the cuticle of dung beetles is too thin for its mechanical characteristics to easily be measured using conventional techniques, nanoindentation technology provides an effective solution for this issue.

As nanoindentation can be used to measure hardness at the nano-scale, it has been widely used to study materials in the fields of surface engineering, microelectronics, microelectromechanical systems, biology and medicine, among others. Nanoindentation has also been used to study insect cuticles, the head-neck joint and wing-locking mechanism of beetles,¹⁵ the structure and mechanical properties of the mechanical interlocking of the elytral braking system,¹⁶ the microstructure and mechanical properties of the basilar membrane,¹⁷ and stiffness changes in a melanogaster during its larval, pupal, and early adult development in vivo.¹⁸ In addition, dynamic nanoindentation techniques have been used to investigate the energy-dissipation mechanisms of the beetle cuticle.¹⁹

In this paper, the stress-strain relationships of various parts of the dung beetle Copris ochus Motschulsky cuticle material were studied using nanoindentation. These results will be helpful in designing lightweight, high-strength, advanced composites.

Materials and methods

Samples

The test materials came from dung beetles (Copris ochus Motschulsky), as shown in Fig. 1A and 1B which were collected in Huajiao township, Huadian City, Jilin Province. The female dung beetles had an average body length of 27 mm, and the male dung beetles had an average body length of 25 mm. Three male and 3 female beetles were selected, and indentation testing was performed 10 times in a 0.075 mm × 0.01 mm area; the average of these values was considered the nanoindentation performance of the test part. The living dung beetle was anaesthetized, and then the test part was removed from the insect body. The removed part was attached to the stage using instant adhesive to ensure that the measured surface was vertical to the tip of the nanomechanical testing system.

Figure 1.

Dung beetle (Copris ochus Motschulsky) digital photo: (A) male and (B) female. (C) and (D) The fracture microstructures of cross section of dry and in-situ specimens of beetle elytra, respectively.

Field emission scanning electron microscopy (FESEM, JEOL JSM-6700F) was used to investigate the microstructure of a cross-section of the elytra (shown in Fig. 1C and 1D). The multilayer structure was clearly observed. Figure 1C and 1D show the general fracture microstructure of the elytral cuticle. The microstructures result in good interfacial strength because the thickness distributions of the epicuticle and the interfacial layers are well proportioned. All the fibers were well-proportioned and distributed in these cross-sections such that they would enhance the bending resistance of the elytral cuticle. The microfibers in each layer were parallel with each other, while the fibers were arranged in a spiral at a fixed angle (approximately 70°) in the adjacent layer. There is a distribution of many fracture dimples and traces of irregular, slender fiber pull-outs (Fig. 1D).

Nanoindentation

The mechanical properties of the samples were determined by using a nanoindenter with a Berkovich tip (TriboIndenter, Hysitron Inc.). This instrument offers precision staging for automated testing and sample positioning.

The theory of nanoindentation has been discussed extensively. The Oliver-Pharr method²⁰ for determining the nanoindentation modulus and hardness is well accepted in the literature. The initial unloading stiffness, or contact stiffness, S can be obtained from the slope of the unloading segment of the force-displacement curve.

Indentation creep testing is mainly used to study metal materials with low melting points to determine the creep properties of these materials at room temperature. However, not all experimental results agree with the traditional results; one important reason for this discrepancy is the impact of transient effects on the creep response.

If ${\displaystyle \dot{\epsilon }}$ denotes significant changes in the experiment, then at a high strain rate, the transient effect will affect the results. That is:

$${\displaystyle {\dot{\epsilon }}_u=C_1{\dot{\epsilon }}_i}$$ (1)

where in ${\displaystyle {\dot{\epsilon }}_u}$ is the uniaxial strain rate, ${\displaystyle {\dot{\epsilon }}_i}$ is the impression strain rate, and C₁ is the ratio constant related to the material structure.

Dynamic deformation in impression testing differs from that in uniaxial creep testing, as deformation of the material under the indenter continuously expands into the surrounding material, which was not previously deformed. The creep process is considered to depend on the progression rate of the elastic-plastic deformation region, while the progression of elastic-plastic deformation is related to the indentation radius.

Thus, the ratio Δ/A, of the transient change Δ to the instantaneous contact area A, is more suitable for defining the impression creep rate.

However, for an indenter with a geometrically similar cross-section, it is simpler to use the ratio ḣ/h, of the instantaneous displacement rate ḣ to the instantaneous displacement h, to express the strain rate; the impression strain rate ${\displaystyle {\dot{\epsilon }}_i}$ is defined as the following:

$${\displaystyle {\dot{\epsilon }}_i=\frac{\dot{h}}{h}}$$ (2)

From nano-mechanics, material hardness H is the ratio of maximum load P_max to the indenter contact area (projected area), namely:

$${\displaystyle H=\frac{P_{\text{max}}}{A(h_C)}}$$ (3)

The functional expression of contact depth h_C and the indenter area A(h_C) is the following:

$${\displaystyle A(h_C)=C_0{h}_C^2+C_1{h}_C+C_2{h}_C^{1/2}+C_3{h}_C^{1/4}+C_4{h}_C^{1/8}+C_5{h}_C^{1/16}}$$ (4)

For the Berkovich tip, C₀ is equal to 24.5,²¹ whereas for the 4-sided pyramid tip, C₀ is equal to 2.598;⁶ C₁- C₅ can be obtained via test iterations.

Substituting Eq. 4 into Eq. 3, the following is obtained:

$${\displaystyle H=\frac{P}{c{h}^2}}$$ (5)

Furthermore, substituting Eq. 5 into Eq. 2 yields the following:

$${\displaystyle \dot{\epsilon }=\frac{1}{2}(\frac{\dot{P}}{P}-\frac{\dot{H}}{H})}$$ (6)

To obtain reliable test results using Eq. 6, ${\displaystyle \dot{\epsilon }}$ must remain constant in the series of experiments. In the same loading system, it is necessary to maintain a constant normal loading rate Ṗ/P.²²

For creep-dominant materials, a nanoindenter can be used to quantitatively measure the creep parameters. When traditional creep parameters are calculated based on creep experiments of the uniaxial tensile stress state, the steady-state indentation strain rate is often described as the following ^23-28:

$${\displaystyle \dot{\epsilon }=\alpha {\sigma }^n\text{exp}(-Q_C/RT)}$$ (7)

where, α is a material constant, σ is the stress, n is the creep stress exponent, Q_c is the activation energy, R is the gas constant, and T is the temperature.

When a material undergoes creep experiments via the indentation method, σ of Eq. 7 corresponds to the contact pressure of the indentation experiments. Eq. 3 shows that the hardness is H = P/A = C₂σ; substituting H into Eq. 7, one can obtain:²⁶

$${\displaystyle \dot{\epsilon }=\mathrm{\alpha \prime }{H}^n\text{exp}(-Q_C/RT)}$$ (8)

When the temperature is constant, taking the logarithm on both sides of the equation yields:

$${\displaystyle \text{l}\text{n}\dot{\epsilon }=n\hspace{0.17em}\text{l}\text{n}\hspace{0.17em}H+C}$$ (9)

From here, ${\displaystyle n}$ can be obtained from the slope of the double logarithmic curve ${\displaystyle \dot{\epsilon }}$ and ${\displaystyle H}$, that is:

$${\displaystyle n=\frac{d\hspace{0.17em}\text{l}\text{n}\hspace{0.17em}\dot{\epsilon }}{d\hspace{0.17em}\text{l}\text{n}\hspace{0.17em}H}}$$ (10)

From ref. 29, the dung beetle cuticle creep power law is Δh = Kln(Mt + L); ${\displaystyle \dot{\epsilon }}$ can then be obtained by taking the derivative for t and dividing by the displacement.

The instantaneous H can be obtained from the ratio of the load to 24.5 h². The resulting data can be plotted on the double logarithmic curve, allowing the n value to be obtained.

Results and discussion

The stress-strain curves of all parts of the dung beetle were broadly similar. Figure 2 shows the stress-strain-time curves of the cuticle material of the femur of a dung beetle foreleg.

Figure 2.

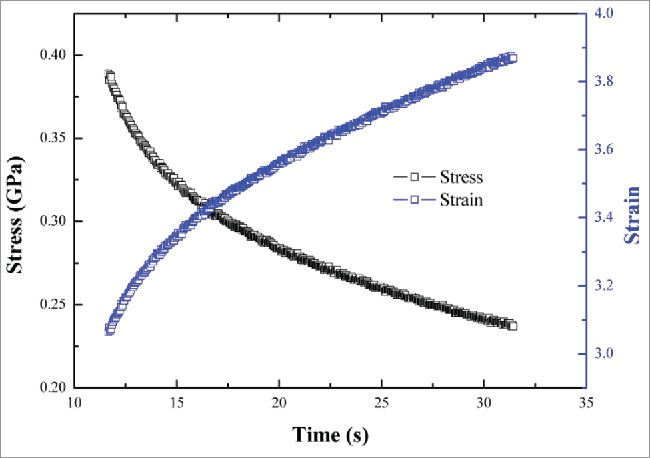
Stress-strain-time curve of the cuticle of a dung beetle foreleg femur.

As time increased, the stress decreased and the strain increased. These results showed that when the tip was pressed into the material for a certain amount of time, the interaction force between the indenter and the material gradually reached a state of dynamic equilibrium because the phenomenon of creep strain continued to change until reaching equilibrium.

When the holding time was 10–100 s, the stress value was high, and the stress change with time was not obvious. When the holding time exceeded 130 s, the stress was significantly reduced, and the rate of change of stress with time was more gradual.

When the holding time was 30–200 s, the strain changed little over time, but the holding time had a significant effect on the strain. The stress-strain curves showed a strong dependence on each holding time condition: the longer the holding time, the flatter the stress-strain curve.

It is well-known that the elytral cuticle is a multilayered structure that consists of an epicuticle, a procuticle and epidermal cells. The procuticle is subdivided into the exocuticle and the endocuticle and accounts for 1/3 of the entire thickness of the elytra, which is approximately 16 μm. The elytra are composite structures consisting of a multi-layered, fiber-reinforced matrix. The chitin fiber and the matrix form layers that are aligned in parallel with the surface of the elytra. Each chitin microfiber layer is parallel with the others, and the fibers in adjacent layers are rotated within a fixed angle (approximately 70°) relative to each other to form a spiral. The fiber-matrix layers in the inner epidermis are arranged orthogonally, and the fibers are long and thick, but relatively sparse.

Figure 3 shows the creep stress exponent under different holding times; ${\displaystyle n}$ ranged between 12.75 and 16.33. The stress exponent shows that the creep mechanism is the dislocation movement. The dislocation creep between the layers mainly occurs in higher temperatures and lower stress conditions; deformation of the material at room temperature is generated by 2 forms of slip and twins by dislocation sliding and climb generated simultaneously above a certain pressure. These mechanisms cause vertical dislocation movement when the material encounters obstacles.³⁰ Indentation creep is the result of dislocation slip and climb alternately occurring.

Figure 3.

Creep stress exponent under different holding times for the cuticle of a dung beetle foreleg femur.

One of the most important issues to test in biological systems is sample aging;³¹ when a portion of material is cut from the insect body for a test, water loss causes the structure of the sample material to vary. The moisture content of the cuticle is closely related to the hardness.³² According to the literature,¹⁶ when nanomechanically testing the heads and wings of live Geotrupes stercorarius beetles, one should ensure that the time from specimen preparation to the end of the experiment is less than 1 h.

Taking into account the influence of moisture on the hardness of the cuticle, the changes in the n of different parts of female and male dung beetle cuticles over time were determined (shown in Fig. 4 and Fig. 5, respectively).

Figure 4.

Creep stress exponent of different parts of a female dung beetle.

Figure 5.

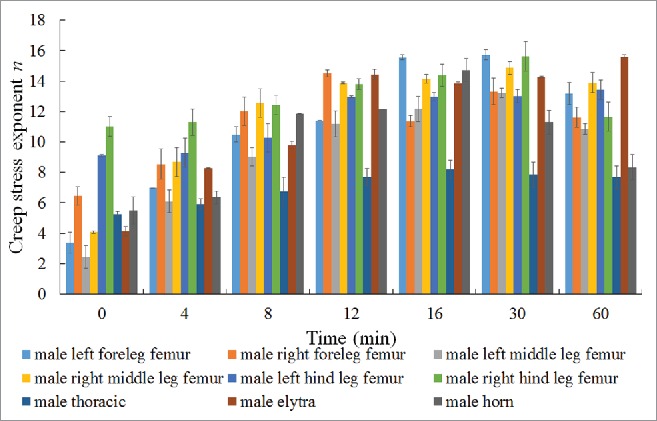
Creep stress exponent of different parts of a male dung beetle.

The creep of the female dung beetle hind leg femur cuticles was the highest, which indicates that this part of the material has a higher viscoelastic characteristic than the other tested areas. The rate of change of n was highest in the thoracic segment, followed by the left foreleg femur, clypeus, left hind leg femur, right foreleg femur, left middle leg femur, right middle leg femur, and right hind leg femur; the rate of change of n is lowest in the elytra.

As time increases, n will change; the variation law in different areas, except the clypeus, was broadly consistent with a slow upward trend, followed by a basically flat state within 1 h. The change of n of the clypeus was relatively large, with a maximum increase of 222%, indicating that the creep exponent is greatly influenced by the moisture content in this area. The moisture of the cuticle material of a dung beetle leg femur continuously decreases over time. As the cuticle moisture content decreases, the nano-hardness and elastic modulus increase, resulting in decreased indentation depth. After 25 h, the change in the mass of a dung beetle hind leg will stabilize, having been reduced by 53%, while this value is only reduced by 8% within 1 h. Thus, the change in n reaches a steady state within 1 h.

Hardness increases with decreasing moisture content. As hardness increases, so does the resistance to the dislocation motion. The resistance to creep is also larger; thus, the creep depth decreases as the hardness increases, i.e., the ability of the material to resist creep is stronger.³⁰

Similarly, the creep stress exponent of the male dung beetle right hind leg femur cuticle was the highest, indicating that this part of the material has a higher viscoelasticity than the other tested areas. The rate of change of n was highest in the left middle leg femur, followed by the left foreleg femur, elytra, right middle leg femur, horn, right foreleg femur, thoracic segment, and left hind leg femur; the rate of change of n was lowest in the right hind leg femur.

As time increases, n changes, and the variation law in different areas was roughly the same, with a gradual downward trend. Further physical, chemical, and microstructural research must be performed to determine the differences in the performance of male and female dung beetle cuticles.

Conclusion

Currently, along with the development of bionics, research on biological principles has become more quantitative than qualitative, research on biological surface morphology has developed from the macroscale to the micro- or nanoscale, and research on biological systems has shifted from the study of local materials and structures to comprehensively understanding entire systems. This study investigated the stress-strain relationships of various parts of the dung beetle cuticle material. Stress was found to decrease as time increased, whereas strain increased as time increased. These results indicated that when the material was indented for a certain time, the interaction force between the indenter and the material gradually reaches a state of dynamic equilibrium; however, because of the phenomenon of creep, strain continues to occur until reaching its point of equilibrium. When the holding time was 10–100 s, the stress value was high, and the changes in stress over time were not obvious. When the holding time exceeded 130 s, the stress was significantly reduced, and the rate of change of stress over time was more gradual. Although the strain changed little over time, it was significantly affected by the holding time. The stress-strain curves showed a strong character in each holding time condition: the longer the holding time, the flatter the stress-strain curve. The creep stress exponent ${\displaystyle n}$ of the dung beetle foreleg femur cuticle under different holding times ranged between 12.75 and 16.33. The moisture content also influenced the creep exponent. Our research will provide useful information for the design of lightweight, laminated, bionic composites and composite coatings.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.

Funding

This work was supported by the National Natural Science Foundation of China (31172144), by the National Science & Technology Pillar Program of China in the Twelfth Five-year Plan Period (2014BAD06B03), by the Development Program of Science and Technology of Jilin Province of China (201303040NY), and by “Project 985” of Jilin University.