Multiresolution Iterative Reconstruction in High-Resolution Extremity Cone-Beam CT

Abstract

Application of model-based iterative reconstruction (MBIR) to high resolution cone-beam CT (CBCT) is computationally challenging because of the very fine discretization (voxel size <100 µm) of the reconstructed volume. Moreover, standard MBIR techniques require that the complete transaxial support for the acquired projections is reconstructed, thus precluding acceleration by restricting the reconstruction to a region-of-interest. To reduce the computational burden of high resolution MBIR, we propose a multiresolution Penalized-Weighted Least Squares (PWLS) algorithm, where the volume is parameterized as a union of fine and coarse voxel grids as well as selective binning of detector pixels. We introduce a penalty function designed to regularize across the boundaries between the two grids. The algorithm was evaluated in simulation studies emulating an extremity CBCT system and in a physical study on a test-bench. Artifacts arising from the mismatched discretization of the fine and coarse sub-volumes were investigated. The fine grid region was parameterized using 0.15 mm voxels and the voxel size in the coarse grid region was varied by changing a downsampling factor. No significant artifacts were found in either of the regions for downsampling factors of up to 4×. For a typical extremities CBCT volume size, this downsampling corresponds to an acceleration of the reconstruction that is more than five times faster than a brute force solution that applies fine voxel parameterization to the entire volume. For certain configurations of the coarse and fine grid regions, in particular when the boundary between the regions does not cross high attenuation gradients, downsampling factors as high as 10× can be used without introducing artifacts, yielding a ~50× speedup in PWLS. The proposed multiresolution algorithm significantly reduces the computational burden of high resolution iterative CBCT reconstruction and can be extended to other applications of MBIR where computationally expensive, high-fidelity forward models are applied only to a sub-region of the field-of-view.

1. Introduction

Modern cone-beam CT (CBCT) systems utilize a variety of digital x-ray detectors, such as amorphous silicon flat panel detectors (a-Si FPDs), charge-coupled devices (CCDs) and complementary metal-oxide-semiconductors (CMOS). These sensors offer very fine pixel sizes (150 µm and less), enabling high resolution clinical and preclinical imaging at a level of detail not accessible to conventional CT. Examples of emerging high resolution applications include: (i) small animal imaging (Clark and Badea 2014, Boerckel et al 2014), (ii) breast CBCT (Boone et al 2001, Yang et al 2007, O’Connell et al 2010, Shen et al 2013), in particular for detection of micro-calcifications, (iii) otolaryngology, dental, and head and neck imaging (De Vos et al 2009, Hodez et al 2011, Xu et al 2012), and (iv) extremities imaging (Tuominen et al 2013, Nishiyama and Shane 2013, Carrino et al 2014, Marinetto et al 2016), with potential use in quantitative assessment of bone microarchitecture.

The small size of the sensing elements in high resolution detectors conventionally necessitates an increase in imaging dose to maintain the contrast-to-noise ratio sufficient for clinical tasks. This increase in patient exposure may be mitigated by model-based iterative reconstruction (MBIR), which was previously shown to yield improved resolution-noise tradeoffs as compared to conventional FBP at similar or even lower dose levels (Thibault et al 2007, Wang et al 2014). Application of MBIR to high resolution CBCT imaging is however challenged by the computational burden of iterative algorithms. Whereas analytical methods typically require only one backprojection operation, each iteration of MBIR generally requires at least one forward and one backprojection. Furthermore, since MBIR relies on a data fidelity term that matches image estimates to the measured data, a complete transaxial region of support for the image volume must be reconstructed to capture all contributions from the object for each ray path. Thus, region-of-interest (ROI) reconstructions that are often straightforward to implement using analytical methods cannot be realized in standard iterative algorithms. The requirement to reconstruct the entire field of view (FOV), typically as large as 20×20×20 cm³, using very fine voxels (≤ 75 µm), can make the application of MBIR to high resolution imaging prohibitively slow because the speed of the projection and backprojection operators is generally proportional to the number of voxels.

Projection operators can be accelerated by optimized implementation on parallel hardware using graphical processing units (GPUs) (Keck and Hofmann 2009, Brokish et al 2010, Papenhausen et al 2011, Pratx and Xing 2011) or distributed computing (Liu et al 2013). However, for large-FOV high resolution CBCT data, both approaches suffer from latency of data transfer – either between host computer and GPU or between computational nodes in a distributed network. Furthermore, while such methods improve the baseline speed of the projection operator, the performance gains remain dependent on the size of the FOV and resolution. The benefits of parallelization diminish when the number of required processes exceeds the number of available computational nodes due to e.g. very fine discretization of the FOV.

One approach to overcome the decreased performance of MBIR in high resolution applications relies on the observation that while iterative reconstruction of an isolated high resolution ROI is not possible, the model of the volume can be altered so that a fine parameterization is only used in the ROI. Some versions of such multiresolution schemes forego the traditional square voxel basis functions and employ a sparse representation of the volume using heterogeneous voxels, wavelets (Frese et al 2002, Degirmenci et al 2015) or meshes (Brankov et al 2004, Sitek et al 2006). Here we will focus on traditional voxel bases, where multiresolution reconstruction can be realized by using voxels of different size to parameterize different subvolumes (i.e. coarse grid regions and fine grid regions) in the image. These bases are straightforward and map well to physical memory in computing hardware.

Early examples of multiresolution methods include those that enable application of the iterative algorithm to a limited internal high resolution ROI and use an analytical method for the surrounding volume. The full FOV is first reconstructed with an analytical method. The ROI subvolume is set to zero and the surrounding volume is reprojected. The resulting sinogram is subsequently subtracted from the measured data to isolate the line integrals through the ROI. The line integrals of the ROI are then iteratively reconstructed (Ziegler et al 2008, Stearns et al 2007). An additional step consisting of smoothing of the reprojected coarse grid line integrals was found to yield reduced noise in the ROI reconstruction (Rashed et al 2007). However, artifacts attributable to edge degradation and beam-hardening artifacts in the initial FBP were found in the iteratively reconstructed ROI obtained using this general approach (Hamelin et al 2010).

A multiresolution approach where subvolumes with different levels of discretization are reconstructed using an iterative algorithm was proposed in (La Rivière 2007). The fine and coarse grids are jointly reconstructed using a maximum-likelihood (ML) algorithm applied in an alternating scheme, updating one grid while holding the other fixed. In contrast to this alternating optimization, simultaneous optimization of both coarse and fine grids using general purpose optimization algorithms was developed in (Hamelin et al 2007, Yu et al 2009). Similar to our work, this approach relies on a natural factorization of the line integrals into the projections of the fine and coarse grids, yielding a joint objective function for the entire volume. This formulation was also applied to reduce metal artifacts by applying high fidelity forward models (finer parameterization of metallic edges and polychromatic beam modeling) only in ROIs containing metallic objects (Van Slambrouck and Nuyts 2010, 2012).

This work investigates the application of multiresolution reconstruction in the context of extremity CBCT, in particular for visualization and quantitative assessment of bone microarchitecture. In this application, the fine trabecular detail (≤ 75 µm) needs to be reconstructed at very high resolution only over a relatively small ROI, covering e.g. the subchondral bone in the knee joint. The surrounding anatomy (cartilage, ligaments, muscle, fat, etc.) can be reconstructed at lower resolution over the larger FOV. We introduce a new multiresolution MBIR algorithm based on the penalized-weighted least squares (PWLS) framework (Sauer and Bouman 1993) with a separable paraboloidal surrogates (SPS) optimizer (Erdoğan and Fessler 1999b, Elbakri and Fessler 2002). We propose a penalty function specifically designed to provide regularization across the boundaries between fine and coarse voxel grids. We extend the multiresolution framework to include the possibility of regional binning of the projection images, resulting in variable pixel size in addition to the variable voxel size. We focus our evaluation on the tradeoffs between artifacts in the fine grid ROI and voxel size and regularization applied in the surrounding coarse grid region.

2. Methods

2.1. Multiresolution PWLS

The conventional forward model for a transmission tomography system, assuming a voxelized object representation, is given by:

$${ȳ}_l=g_i\text{ exp}(-{[\mathit{A}\mu ]}_{\mathit{i}})$$ (1)

where ȳ_i denotes the mean of the i^th measurement, g_i represents the system gain (including bare beam fluence and detector sensitivity for measurement i), μ is a vector of voxel attenuation values, and A is the forward projection operator. To formulate an objective function for model-based reconstruction, a noise model needs to be chosen. For quantum-limited projection data with negligible contribution of electronic noise, Poisson noise is often assumed. For systems with non-negligible contributions of electronic noise (such as the FPDs used in extremity CBCT) and when the projection data is post-processed with artifact correction algorithms prior to reconstruction (e.g. beam hardening and scatter correction), a more general Gaussian noise model is often more appropriate, leading to a weighted-least-squares objective. We adopt the Gaussian model and PWLS in this work as better suited for the statistics of FPD CBCT projection data. However, the multiresolution methodology presented here could be incorporated into any forward model and easily generalized to MBIR algorithms based on the Poisson noise model. PWLS reconstruction (Sauer and Bouman 1993) employs the following objective function:

$${\hat{\mu }}_{PWLS}=\underset{\mu >0}{\text{argmin}}\frac{1}{2}{\Vert \mathit{A}\mu -l\Vert }_{\mathit{W}}^2+\beta R(\mu )=\underset{\mu >0}{\text{argmin}}\frac{1}{2}{\Vert \mathit{A}\mu -l\Vert }_{\mathit{W}}^2+\beta \sum _{k\in K}\psi ({[\mathit{C}\mu ]}_k)$$ (2)

where l denotes the vector of line integrals l_i = −log y_i/ g_i. The traditional choice for W is a diagonal weighting by the inverse variance, approximated using the measurements: w_i = y_i. The second term (R) is a roughness penalty specified by the finite differencing operator C (Fessler 1997) and the potential function ψ. Here, C is a matrix and applies the 6 nearest-neighbor pairwise voxel difference (excluding diagonal neighbors). K is the total number of pairwise differences in the volume (K ~6 × number of voxels) and ψ is the quadratic penalty.

The above system model and reconstruction objective is general and permits many options for the parameterization of the image volume. We will use this framework and define forward projection and differencing operators for a multiresolution representation of the object. Specifically, we choose to represent the total volume μ as a union of a set of fine grid voxels μ_F and a set of coarse grid voxels μ_C:

$$\mu =\left[\begin{array}{c}\hfill {\mu }_C\hfill \\ \hfill {\mu }_F\hfill \end{array}\right]$$ (3)

The ratio of the coarse grid voxel size to the fine grid voxel size defines a downsampling factor η_μ. The linearity of the forward projection operator permits definition of the following multiresolution projector A, consisting of coarse and fine forward projectors A_C and A_F:

$$\mathit{A}\mu =[{\mathit{A}}_C\hspace{1em}{\mathit{A}}_F]\left[\begin{array}{c}\hfill {\mu }_C\hfill \\ \hfill {\mu }_F\hfill \end{array}\right]$$ (4)

Integrating (3) and (4) into (1), we may rewrite the forward model as:

$$ȳ=g\circ \text{exp}(-\mathit{A}\mathit{\mu })=g\circ \text{exp}(-{\mathit{A}}_C{\mu }_C)\circ \text{exp}(-{\mathit{A}}_F{\mu }_F)$$ (5)

where operator ∘ denotes the Hadamard (element-wise) matrix product. This forward model provides a convenient mathematical form for the development of iterative reconstruction algorithms that treat the reconstructed volume as a sum of non-overlapping regions, each with its own distinct forward model. In this work, we focus on forward models with different discretization of the image volume; however, this kind of decomposition has also been used in reconstruction methods that parameterize the object into known foreground components and an unknown background (Stayman et al 2012) for reconstruction in the presence of objects known to be in the FOV (eg, high-density surgical implants).

In addition to the large memory footprint of the reconstructed volume, projection datasets acquired with high-resolution flat-panel detectors can also be prohibitively large (up to ~3000×3000 pixels and ~1000 projections). Thus, we extend the multiresolution approach to include multiresolution binning of projection data. The binning ratio η_y is defined as the ratio of the coarse pixel size to fine pixel size. As illustrated in Figure 1, we assume that the binning is applied (via appropriate pre-processing) in such a manner that the fine grid regions of the volume are projected entirely onto the fine, natively sampled (unbinned) regions of the projection image. The forward projector now comprises A_FN (fine grid voxels to native pixels), A_CN (coarse gird voxels to native pixels) and A_CB (coarse grid voxels to binned pixels):

$$\hat{l}=\left[\begin{array}{c}\hfill {\hat{l}}_B\hfill \\ \hfill {\hat{l}}_N\hfill \end{array}\right]=\mathit{A}\hat{\mu }=\left[\begin{array}{cc}\hfill {\mathit{A}}_{CB}\hfill & \hfill 0\hfill \\ \hfill {\mathit{A}}_{CN}\hfill & \hfill {\mathit{A}}_{FN}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\hat{\mu }}_C\hfill \\ \hfill {\hat{\mu }}_F\hfill \end{array}\right]$$ (6)

where l_N and l_B denote the line integrals associated with native and binned pixels, respectively.

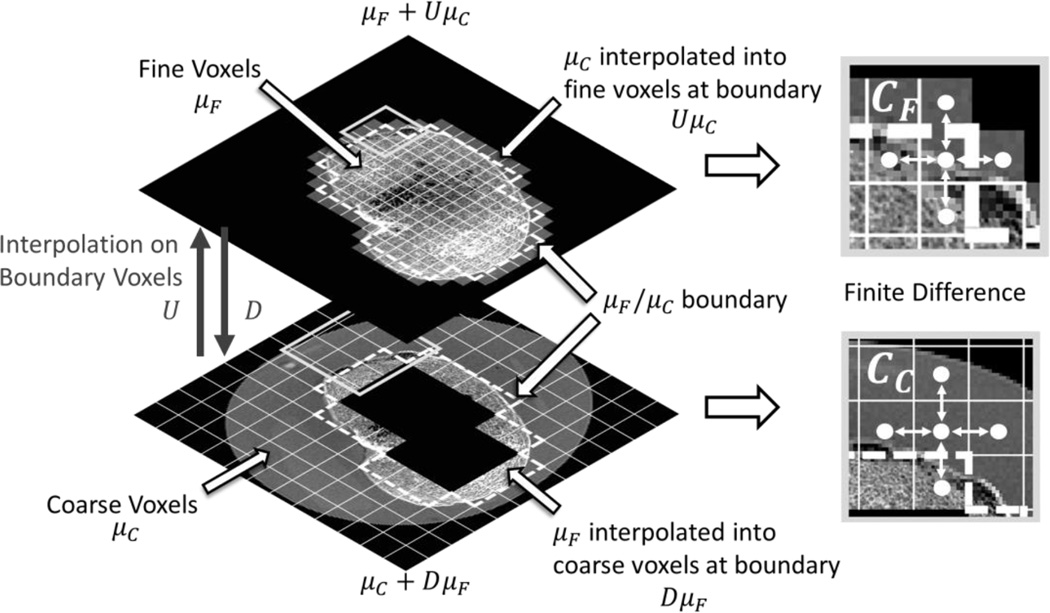
Figure 1.

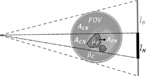
Schematic of multiresolution forward projection with detector binning. The estimated bone region parameterized using fine grid voxels (μ̂_F) is marked with a black dashed line. This region is projected onto native detector pixels (marked with l̂_N) using projection operator A_FN. The line integrals captured by the native projection pixels also include contributions from a subset of coarse voxels (μ̂_C), denoted by projection operator A_CN. Line integrals for binned projection pixels (marked as l̂_B) traverse only through coarse grid voxels, computed using projector operator A_CB.

Using the above multiresolution definitions, the data fidelity term in equation (2) is nearly complete. It remains to define the weighting matrix:

$$\mathit{W}=\left[\begin{array}{cc}\hfill {\mathit{W}}_B\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathit{W}}_N\hfill \end{array}\right]$$ (7)

with the corresponding diagonal inverse variance weights, W_B and W_N,which represent the measurement weights of the binned and native pixels, respectively. Such weighting can accommodate, for example, reduced noise in the binned measurements.

Implementation of the regularization term in the multiresolution PWLS of equation (2) requires specification of how the differencing operator C acts across the boundary between fine and coarse grid voxels. We propose the following general multiresolution penalty:

$${\tilde{\mu }}_c=\left[\begin{array}{c}\hfill {\mu }_C\hfill \\ \hfill \mathit{D}{\mu }_F\hfill \end{array}\right]\hspace{1em}{\tilde{\mu }}_F\left[\begin{array}{c}\hfill \mathit{U}{\mu }_C\hfill \\ \hfill {\mu }_F\hfill \end{array}\right]$$

$$R(\mu )={\beta }_C\sum _{k\in K_C}\psi ({\left[{\mathit{C}}_{\mathit{C}}{\tilde{\mu }}_c\right]}_k)+{\beta }_F\sum _{k\in K_F}\psi ({[{\mathit{C}}_{\mathit{F}}{\tilde{\mu }}_F]}_k)={\beta }_C{R}_C+{\beta }_F{R}_F$$ (8)

where we have defined augmented coarse and fine image vectors, μ̃_c and μ̃_F, respectively. These vectors include boundary voxel values from the adjacent ROI that have been resampled to the appropriate voxel grid. That is, we use D, an interpolating operator that downsamples fine grid voxels neighboring the μ_F/μ_C boundary to coarse grid voxels, to allow application of a coarse pairwise voxel difference operator (Fessler 1997), C_c, across the boundary of the coarse and fine ROIs (Figure 2). Alternately, we use U, an operator that upsamples the coarse grid voxels on the μ_F/μ_C interface, to apply a fine pairwise voxel difference operator, C_F, across the ROI boundary in the opposite direction. In this work, we choose D to be a binning operation that computes the mean over fine voxels, and U to upsample from coarse to fine voxels using linear interpolation. We have two regularization parameters, β_F and β_C, that control the penalty strengths for the fine and coarse grid ROIs, respectively. The sets, K_C and K_F, are rows of C̃μ̂ which enumerate all pairwise voxel differences contributing to the penalty terms for the coarse and fine ROIs, respectively.

Figure 2.

Schematic of multiresolution regularization scheme illustrating how the regularization over boundaries between the fine and coarse voxel grids is performed using interpolation operators.

Eq. (8) amounts to applying the conventional penalty to a region (fine or coarse grid) that was virtually expanded to include boundary voxels from the other region, which were appropriately resampled using interpolation. This procedure is general and can be applied to arbitrary boundaries, except perhaps for highly degenerate cases were interpolation is not applicable (e.g. ROIs consisting of a single voxel).

The objective function in (2) can be optimized using the SPS approach (Erdoğan and Fessler 1999b, Elbakri and Fessler 2002). We note that the same data-fit surrogate as in Eq. 17 of Elbakri and Fessler (2002) can be used here, with the standard projector operator replaced by the multiresolution projector. Crucially, the surrogate in the SPS algorithm is separable across voxels, i.e. the update for each voxel depends on the surrounding volume only through the line integrals of the previous iterate of the reconstruction. This yields a multiresolution algorithm that allows independent updates of the fine- and coarse-grid ROIs, as detailed in Table 1. Similarly, the separable surrogate for the penalty of (Erdoğan and Fessler 1999a) can be applied directly to the multiresolution objective, as the construction of the surrogate is independent of discretization. The algorithm presented in Table 1 can be easily generalized to an ordered subset form in a manner analogous to (Erdoğan and Fessler 1999b).

Table 1.

Glossary of terms and pseudocode of SPS optimization method for multiresolution PWLS. Ordered-subsets are omitted for simplification.

Definitions
l̂B, l̂N	forward-projected line integrals onto binned and native detector pixels
lB, lN	binned and native preprocessed line integral data
wB, wN	diagonal entries in weighting matrices WB and WN.
c	precomputed PWLS curvature, c = [W]+
1	volume covering the entire reconstruction FOV of all 1's.
L̇C, L̇F	derivatives of data-fit surrogates for voxels of μ̂C and μ̂F.
dC, dF	curvatures of data-fit surrogates for voxels of μ̂C and μ̂F.
ψ̇, ωψk	gradient and curvature of the penalty function ψ.
ṘC, ṘF	derivatives of penalty surrogates for voxels of μ̂C and μ̂F.
rC, rF	curvatures of penalty surrogates for voxels of μ̂C and μ̂F.

Algorithm
Precompute ${\mathrm{d}}_{\mathrm{C}}={\mathrm{A}}_{\mathrm{C}\mathrm{B}}^{\mathrm{T}}{[\mathrm{A}\mathbf{1}\circ \mathrm{c}]}_{\mathrm{B}}+{\mathrm{A}}_{\mathrm{C}\mathrm{N}}^{\mathrm{T}}{[\mathrm{A}\mathbf{1}\circ \mathrm{c}]}_{\mathrm{N}}$ for iteration n=1, …, N	${\mathrm{d}}_{\mathrm{F}}={\mathrm{A}}_{\mathrm{F}\mathrm{N}}^{\mathrm{T}}{[\mathrm{A}\mathbf{1}\circ \mathrm{c}]}_{\mathrm{N}}$
Coarse Grid Update	Fine Grid Update
l̂B = ACBμ̂C	l̂N = ACNμ̂C + AFNμ̂F
ḣB = wB ∘ (l̂B−lB)	ḣN = wN ∘ (l̂N − lN)
${\dot{\mathrm{L}}}_{\mathrm{C}}={\mathrm{A}}_{\mathrm{C}\mathrm{B}}^{\mathrm{T}}{ḣ}_{\mathrm{B}}+{\mathrm{A}}_{\mathrm{C}\mathrm{N}}^{\mathrm{T}}{ḣ}_{\mathrm{N}}$	${\dot{\mathrm{L}}}_{\mathrm{F}}={\mathrm{A}}_{\mathrm{F}\mathrm{N}}^{\mathrm{T}}{ḣ}_{\mathrm{N}}$
ṘCj = Σk∈KC ckjψ̇([C̃μ̂]k), j ∈ coarse voxels	ṘFi = Σk∈KF ckiψ̇([C̃μ̂]k), i ∈ fine voxels
${\mathrm{r}}_{{\mathrm{C}}_{\mathrm{j}}}={\mathrm{\Sigma }}_{\mathrm{k}\in {\mathrm{K}}_{\mathrm{C}}}{\mathrm{c}}_{{\mathrm{k}}_{\mathrm{j}}}^2{\mathrm{\omega }}_{{\mathrm{\psi }}_{\mathrm{k}}}({\left[\tilde{\mathrm{C}}\hat{\mathrm{\mu }}\right]}_{\mathrm{k}}),j\in \text{coarse voxels}$	${\mathrm{r}}_{{\mathrm{F}}_{\mathrm{i}}}={\mathrm{\Sigma }}_{\mathrm{k}\in {\mathrm{K}}_{\mathrm{F}}}{\mathrm{c}}_{\mathrm{k}\mathrm{i}}^2{\mathrm{\omega }}_{{\mathrm{\psi }}_{\mathrm{k}}}({\left[\tilde{\mathrm{C}}\hat{\mathrm{\mu }}\right]}_{\mathrm{k}}),i\in \text{fine voxels}$
${û}_{\mathrm{C}}=\text{max }({û}_{\mathrm{C}}-\frac{{\dot{\mathrm{L}}}_{\mathrm{C}}+{\mathrm{\beta }}_{\mathrm{C}}{Ṙ}_{\mathrm{C}}}{{\mathrm{d}}_{\mathrm{C}}+{\mathrm{\beta }}_{\mathrm{C}}{\mathrm{r}}_{\mathrm{C}}},0)$	${û}_{\mathrm{F}}=\text{max }({û}_{\mathrm{F}}-\frac{{\dot{\mathrm{L}}}_{\mathrm{F}}+{\mathrm{\beta }}_{\mathrm{F}}{Ṙ}_{\mathrm{F}}}{{\mathrm{d}}_{\mathrm{F}}+{\mathrm{\beta }}_{\mathrm{F}}{\mathrm{r}}_{\mathrm{F}}},0)$
end

2.2. Experimental Setup for Simulation Studies

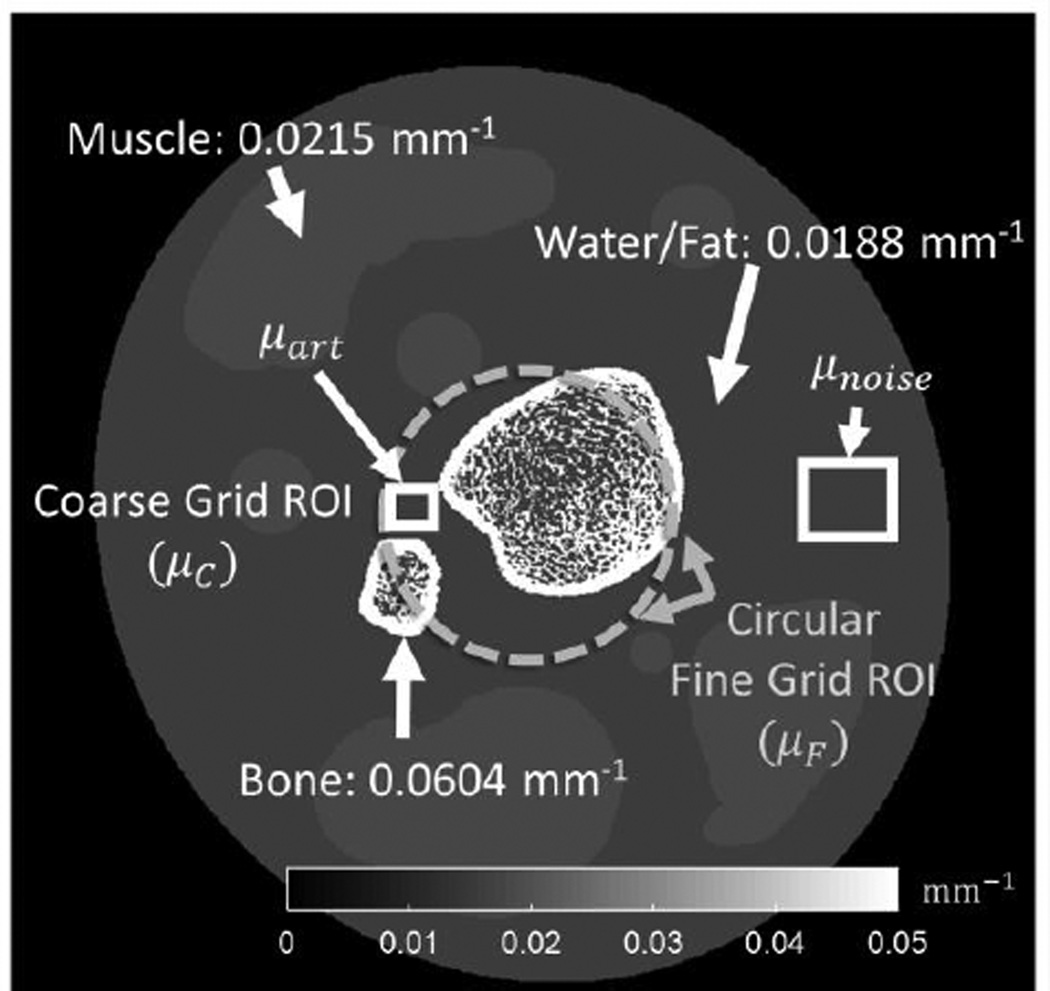
The proposed multiresolution approach was evaluated in a simulation study. The primary goal of the study was to evaluate the impact of different coarse voxel downsampling factors and the effect of regularization strength in the coarse and fine grid volumes on image artifacts in the fine grid region. Fig. 3 shows the digital phantom used in simulations. The phantom included soft tissues (emulating fat and muscle) and two bone regions. The bones consisted of a cortical shell and fine trabecular features based on a segmented micro-CT image. The attenuation values of the simulated tissues corresponded to effective beam energy of 60 keV, which approximates that of the 90 kVp (4 mm Al, 0.3mm Cu added filtration) spectrum of a dedicated extremity CBCT at our institution (Siewerdsen et al 2004, Zbijewski et al 2011). The digital phantom used 0.075 mm voxels and simulated projections were generated on a 0.194 mm pixel grid. A bare beam fluence of 10⁵ photons per detector pixel was assumed and Poisson noise was added to the projections. Simulated detector pixels had 100% efficiency. System geometry emulated the extremities CBCT scanner: source-axis distance (SAD) of 436 mm and source-detector distance (SDD) of 560 mm.

Figure 3.

Schematic of digital bone phantom with the boundary of a central fine voxel grid region marked with a thick dashed line. The ROIs used for measurement of artifacts in the fine grid region (μ_art) and noise (μ_noise) in the coarse grid region are indicated with boxes.

In the multiresolution reconstruction, the regularization strength of the interior fine grid ROI β_F was fixed at 10³ based on visual assessment of spatial resolution. 60 subsets were used. The reconstructed voxel size in the fine grid ROI was 0.15 mm, whereas the voxel size in the coarse grid region was varied by changing the downsampling factor η_μ from 1 (i.e., the same voxel size for μ_F and μ_C) to 10 (i.e., 10× larger voxels for μ_C). In cases where detector binning was considered in addition to a multiresolution volume representation, the binning factor (η_y) applied to the simulated projections was kept equal to the volume downsampling factor. The forward and back-projection operators in the simulation and reconstruction used an in-house GPU implementation of separable footprints algorithm using trapezoidal functions (Long et al 2010). The separable footprint algorithm is voxel-driven and thus can easily accommodate arbitrary ROI shapes. However, our current implementation of the projector relies on GPU texture memory and thus only handles rectangular volumes. Non-rectangular fine grid ROIs were simulated using a minimum bounding box and masking operations.

In addition to varying the coarse voxel size, the regularization strength β_C in the coarse region was also varied. Since image downsampling imparts a degree of smoothing, the effect of a specific β_C value will differ between reconstructions with different coarse voxel sizes. To facilitate comparison of the effects of regularization across a range of voxel sizes (downsampling factors), a normalization that accounts for the effects of sampling was applied to the quadratic penalty (Yu et al 2013). Following the derivation by Yu, for quadratic penalties:

$$\psi =\frac{t^2}{2}=\frac{{({\mu }_i-{\mu }_k)}^2}{2}\approx \frac{{[\nabla \mu ·{\mathrm{\Delta }}_{ki}]}^2}{2}={\mathrm{\Delta }}_{ki}^2\frac{\nabla {\mu }^2}{2}$$ (9)

where Δ_ki is the distance between neighboring voxels k and i. Eq. (9) implies that within a neighborhood where the change in underlying attenuation volume is smooth, the action of the penalty (for a fixed penalty strength) scales approximately as square of the voxel size or, equivalently, as square of η_μ. Henceforth, reconstructions are compared across a range of η_μ in a manner that accounts for additional blur due to downsampling by using the following normalized penalty strength, denoted as β:

$$\beta =(1/{\eta }_{\mu }^2){\beta }_C$$ (10)

In our studies we varied β from 0 (no regularization) to 10⁸ for each value of η_μ.

To assess the artifacts in the fine grid region, a small (3 mm × 3.8 mm) ROI, μ_art, was selected in a uniform area of soft tissue adjacent to two bone edges (Fig. 3), where initial evaluation indicated pronounced streaking in reconstructions with high downsampling and regularization of the coarse grid region. To quantify artifacts, reconstruction of noiseless projection data were generated for each set of parameters of the multiresolution reconstruction. Root mean squared error (RMSE) was calculated in the ROI between the noiseless multiresolution reconstruction and a truth image that was obtained by downsampling the digital phantom (0.075 mm voxels) to the voxel size of the fine grid region (0.15 mm):

$$RMSE=\sqrt{\frac{{\sum }_j{({\hat{\mu }}_{{\mathit{\text{art}}}_j}-{\mu }_{{\mathit{\text{art}}}_j})}^2}{N}}$$ (11)

where μ̂_artj are voxels in the artifact ROI of the noiseless multiresolution reconstruction, μ_artj are the corresponding voxels in the downsampled digital phantom and N is the total number of voxels in μ_art.

Increase in regularization strength and increase in voxel downsampling both impart resolution loss and noise reduction in the coarse grid region. The noise in μ_C (denoted as SD_c) was used as a metric quantifying the cumulative effect of coarse discretization and regularization. The noise was measured as RMSE between a flat region in the coarse grid subvolume of a noisy reconstruction, denoted as μ_noise (Fig. 3), and the same region in the truth image.

2.3. Physical Study using an Anthropomorphic Knee Phantom on a Benchtop CBCT

An anthropomorphic lower extremity phantom was scanned on a CBCT test bench (Zhao et al 2014) simulating a dedicated extremity CBCT (SAD=435.7 mm, SDD=559.2 mm). The detector was a PaxScan4030CB (Varian, Palo Alto, CA) operated at 1.5 fps and 0.194 mm pixel size. The x-ray source was a rotating anode DU694 x-ray tube with 14° anode angle, enclosed in EA10 housing (Dunlee, Aurora, IL). The scan consisted of 360 projections acquired over 360° at 90 kVp (+0.2 mm Cu, 2 mm Al), with 0.4 mAs per projection.

The total reconstructed volume was 18×18×18 cm³. The irregularly-shaped fine grid ROI contained a region of subchondral bone identified using an initial Feldkamp-Davis-Kress (FDK) analytical reconstruction and consisted of 31,623,168 voxels of 0.15 mm size. There were 26,505,888 voxels of 0.6 mm size in the coarse grid region (η_μ = 4). Multiresolution detector binning with η_y = 4 was applied, with the region of fine pixels in each view matching a forward projection of the subchondral bone mask. Regularization strengths were set to β_F = 10^−0.5 and β_C = 10⁴.

2.4. Analysis of Runtime and Memory Footprint

To estimate the savings in computation time and memory consumption provided by the multiresolution method, benchmarking was performed for a 12×12×12 cm³ volume. This volume is smaller than the one used in the anthropomorphic phantom experiments of Sec. 2.3. This is because a fine grid reconstruction of the entire grid was needed for benchmarking. The memory available on the GPU used in the experiments was not sufficient to fit a fine voxel grid larger than 12×12×12 cm³. Note however that this size of the volume is sufficient to cover a typical knee joint on the extremity CBCT system.

Fine grid ROIs with 0.15 mm voxels and varying volume (5×5×5 cm³ to 12×12×12 cm³) were considered. For each fine grid ROI, the remainder of the FOV was parameterized using a coarse grid over a range of upsampling factors (η_μ = 1,2,4). Since computation times for projection and backprojection vary and can be dependent on implementation, we considered the computational cost associated with projection-backprojection pairs. Average total projection-backprojection times were obtained separately for each fine grid volume (denoted as t_f) and for coarse grid volumes covering the entire FOV (t_c) at the various coarse grid voxel sizes. Furthermore, for each fine grid ROI, the projection-backprojection time for a volume equal in size to the fine grid ROI, but parameterized using coarse voxels was measured (t_Δ). The coarse grid projection-backprojection times were computed with and without projection binning. The estimate of projection-backprojection time for a given multiresolution parameterization (defined by a combination of fine grid volume size and upsampling factor) is t_f + t_c − t_Δ, assuming that projection and backprojection times are linear with the number of voxels. The validity of this assumption was confirmed for the range of volume discretizations considered here for both projection and backprojection operations. The reconstruction speedup was computed as the ratio of the average measured time for a projection-backprojection pair of our multiresolution implementation to the same average measured time using only the fine grid (η_μ = 1).

Each PWLS iteration requires storing the following variables: the current image μ, derivatives of data fit and regularization surrogates, L̇ and Ṙ, the curvatures of data fit and regularization surrogates, d_j and r, and the measured projections. (Here we ignored potential memory savings due to ordered subsets that may be offset by increased memory transfer times.) Memory footprint was thus calculated as the size of the projection dataset plus five times the size of the image volume, assuming all volumes are kept in memory. The memory footprint could be reduced by reusing the arrays associated with some of the variables, however at the expense of increased data transfer latency.

3. Results

3.1. Digital Phantom Study

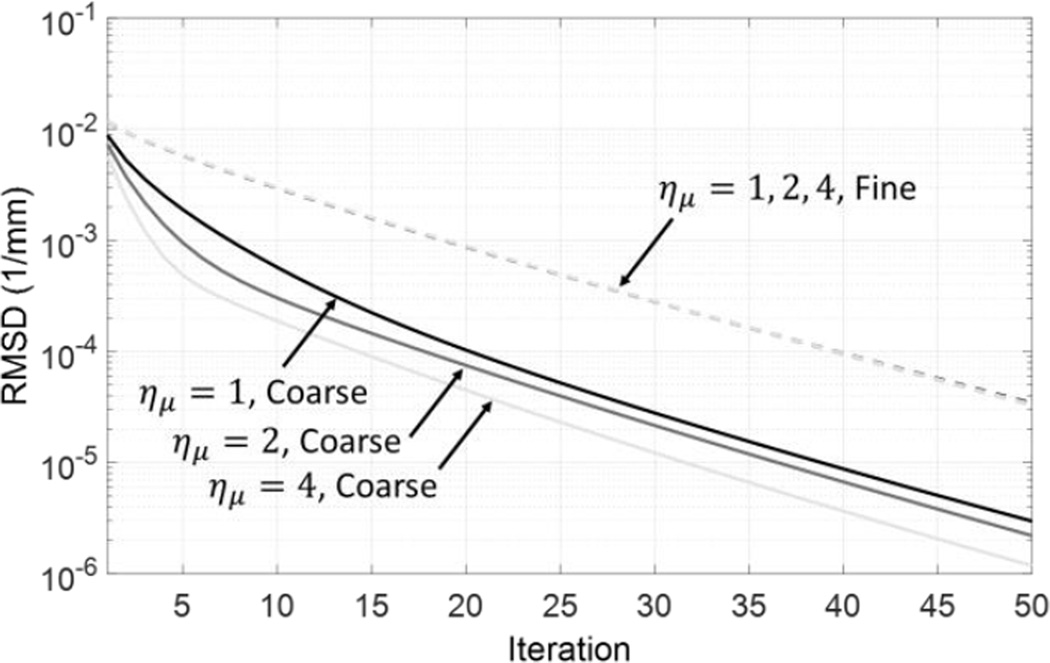
Figure 4 illustrates the convergence properties of multiresolution PWLS reconstruction as a function of the downsampling factor. For each value of η_μ, we computed root-mean-square difference (RMSD) between the volume estimate at the n^th iteration and a nearly converged estimate (approximated by the solution after 200 iterations). RMSD computed within the fine grid ROI (dashed line) and within the coarse grid ROI (solid lines) are shown separately. 50 iterations of multiresolution PWLS were sufficient to achieve an RMSD of less than 10⁻⁴ mm⁻¹ with this stable solution in both ROIs and across all values of η_μ. The RMSD behavior in μ_F was the same across all downsampling factors. Convergence was generally faster in μ_C than in μ_F, even at η_μ = 1 (equal voxel size in both grids), likely because the phantom contains fewer high-frequency structures in the coarse grid ROI. The convergence rate in μ_C increases with higher downsampling. This behavior is intuitive since coarser grids (with fewer parameters to estimate) generally have better condition numbers, leading to faster convergence. Overall, the number of iterations needed to arrive at a stable solution in multiresolution PWLS is determined by the convergence rate in fine grid ROI and is thus independent of η_μ. The crucial advantage of using higher downsampling is in improved time per iteration. Based on this analysis, 50 iterations of multiresolution PWLS were used throughout this study.

Figure 4.

Convergence profile measured in reconstructions of the digital phantom. The estimate at the current iteration is compared with a converged image at 200 iterations. β_F = 10^3.5; β_C = 10^4.5. The RMSD curves for the fie grid region (dashed line) overlap for all values of η_μ.

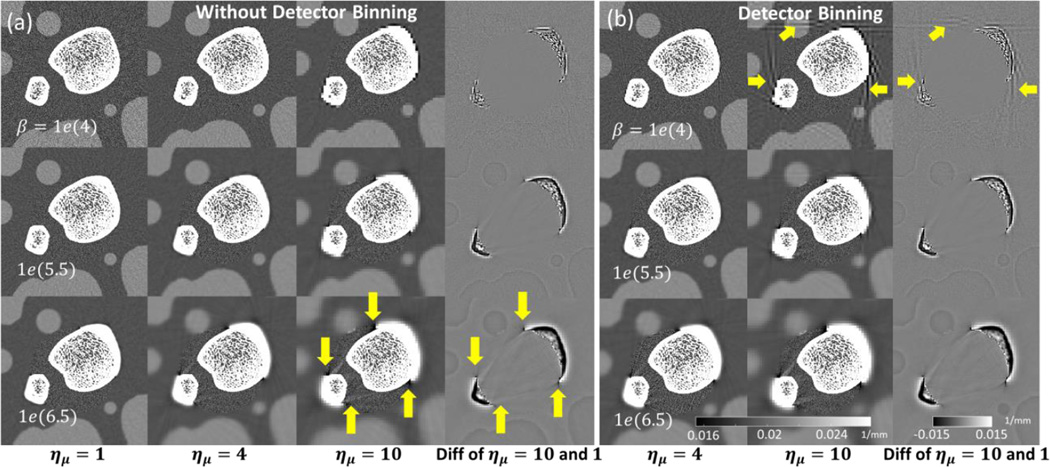
Figure 5 shows a comparison of multiresolution PWLS reconstructions [without projection binning in (a) and with projection binning in (b)] across a range of downsampling factors and normalized regularization strengths. Note that reconstructions with matched β but unmatched η_μ use different β_C, as given by Eq. 12. The case of η_μ = 1 corresponds to the same voxel size in μ_F and μ_C, but different values of β_F and β_C. A zoomed ROI is shown for each reconstruction that covers the fine grid ROI. Note that an increase in coarse grid regularization increases streak artifacts in the fine grid region. The artifacts become pronounced at large values of the downsampling factor. Additionally, when detector pixels are binned [Fig. 5 (b)], noticeable streak artifacts are apparent in the coarse grid near the ROI boundary in the case where η_μ = 10. The right-most column in Fig. 5 (a) and (b) shows a difference image computed between the case of η_μ = 10 and a reference image at η_μ = 1 (for this computation, the coarse grid voxels for η_μ = 10 were upsampled using nearest neighbor interpolation). Even for this high downsampling factor, there is no distortion in the trabecular features contained in the fine grid ROI μ_F (note that the same fine grid regularization strength β_F is applied in the downsampled and reference reconstructions).

Figure 5.

Multiresolution PWLS reconstructions for different downsampling factors and coarse grid regularization values. A central region of the digital phantom is shown for PWLS without detector binning (a) and with detector binning (b). The last column in each subfigure is a difference image between the case with maximal downsampling (η_μ = 10) and the case of no downsampling (η_μ = 1). Arrows indicate artifacts due to strong coarse grid downsampling and regularization.

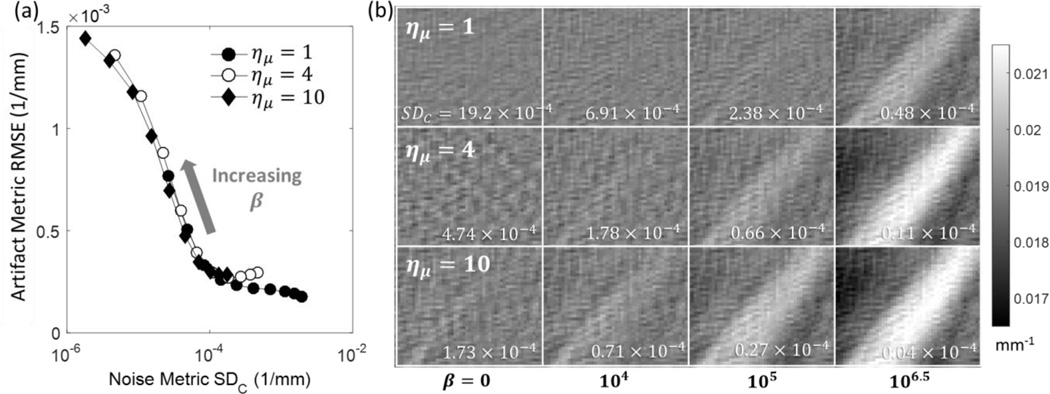
Figure 6a investigates the trade-off between the strength of artifacts in μ_F, measured using equation (11), and the cumulative effect of regularization and downsampling in μ_C, represented by the level of noise in the coarse grid region. The results are very similar for cases with and without detector binning; for clarity, results are shown only for reconstructions with detector binning.

Figure 6.

(a) Magnitude of the artifact in fine grid ROI (RMSE of μ_art in Fig. 3, given by Eq. 11) as a function of noise in the coarse grid region. The noise metric quantifies the cumulative effect of regularization and voxel downsampling in μ_C. (b) The artifact ROI (μ_art) in the fine grid region for a range of downsampling factors (rows) and normalized coarse grid regularization strengths β (columns).

For all downsampling levels, the artifact metric exhibits a plateau accross a range of low-to-moderate noise levels (standard deviations of 10⁻⁴ to 10⁻³ mm⁻¹ compared to muscle attenuation value of ~2×10⁻² mm⁻¹). In this regime, regularization strength in μ_C can be adjusted without introducing significant artifacts in the fine grid ROI. The RMSE rapidly increases at lower noise levels, corresponding to increased smoothing in μ_C. The graphs in Figure 6 (a) are largely overlapping, indicating that the magnitude of the artifacts is a function of the overall blur in the coarse grid ROI, regardless of whether the blur results from downasampling or regularization. Consequently, when a lower value of the downsampling factor is used, there is more room to adjust the regularization in the corase grid ROI, i.e. β_C can be varied over a broader range of values without introducing artifacts in the fine grid region. If the corase grid region is of clinical interest, this ablity to tune the resolution-noise tradeoff in μ_C when the downsapling factor is relatively low may be relevant for optimizing the performance of the reconstruction.

Figure 6 (b) illustrates the artifacts in the fine grid region using a zoom on the artifact ROI (μ_art). As the normalized penalty strength (β) and η_μ increase, streaking becomes apparent. The more downsampling, the lower the value of normalized β where the streaking becomes pronounced.

Further examination of Figure 6 (a) reveals a slight increase in RMSE at the lowest regularizations (highest noise levels) in the presence of downsampling (η_μ ≥ 4). This is attributed to bias in the forward projection of μ_C introduced by sharp edges in the coarse discretization of fat-muscle interfaces of the phantom. This effect is diminished when sufficiently high levels of regularization are applied in the coarse grid region, blurring the discretization-induced sharp intensity transitions. The artifact due to sharp edges in weakly regularized μ_C is visible as a pronounced cross-hatch pattern at η_μ ≥ 4 and low β values in Figure 6 (b). Note that a similar, but much less conspicuous pattern is visible at η_μ = 1, where it is likely to represent a combination of various discretization artifacts that are often present in noiseless reconstruction of digital phantoms with sharp edges.

3.2. Effect of the Location of the Fine Grid ROI

Examination of Fig. 5 suggests that the most pronounced artifacts in the fine grid ROI emerge from areas where the interface between μ_F and μ_C crosses regions of high contrast and sharp intensity transitions. The appearance and magnitude of the artifacts will depend on the location of the fine and coarse grid ROIs, as illustrated in Figure 7 for a case with both voxel downsampling and projection binning. Here, the boundaries of μ_F (marked with an orange dashed line) were designed to avoid cortical bone boundaries and other high contrast gradients. The downsampling factor was set to 10, which leads to severe artifacts in the reconstructions of Fig. 5 (5^th column). With the fine grid ROI conforming to the bone boundaries, however, no streaking artifacts are visible in the space between the two bones. A strong mismatch in the magnitude of noise in μ_C and μ_F is apparent at higher values of normalized regularization strength. Similarly to Fig. 5, the right-most column of Fig. 7 investigates a difference image between the downsampled case and the reference image at η_μ = 1 (equal voxel size in the coarse and fine grids). No visible distortions in the trabecular structure were introduced using multiresolution reconstruction.

Figure 7.

Multiresolution PWLS with fine grid ROI conforming to bone boundaries (marked with dashed line in the leftmost mage) for three values of the normalized penalty strength β. The downsampling factor η_μ is set to 10. The right-most subfigure shows a difference image between the downsampled case (β = 10^6.5) and the reference reconstruction with no downsampling. Projection binning is included.

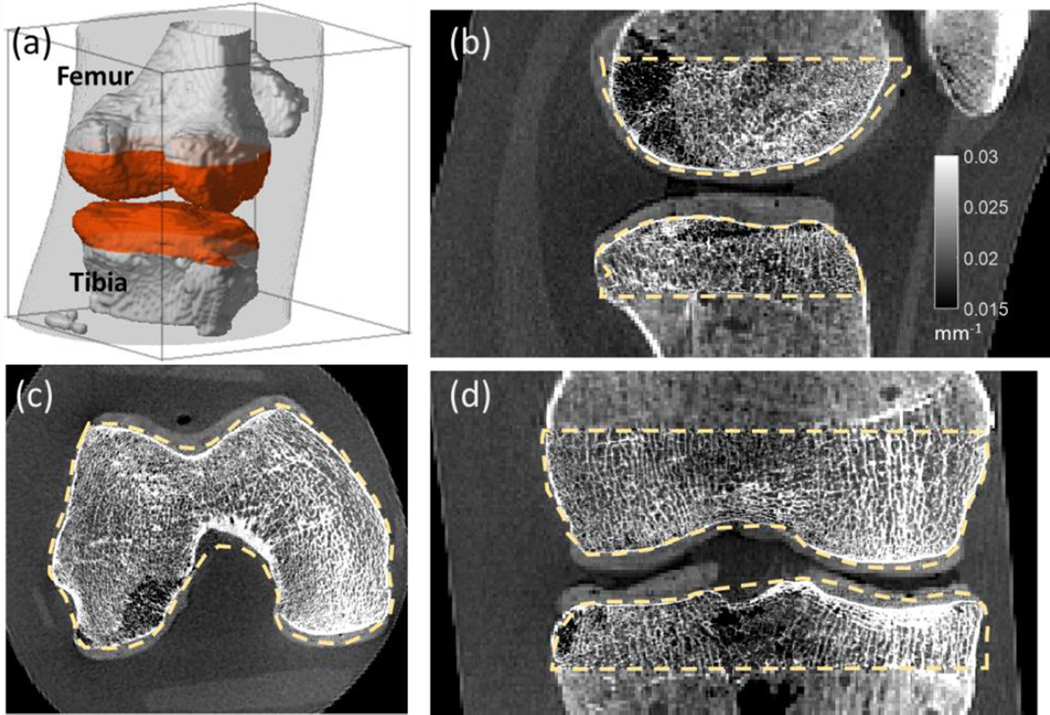
3.3. Multiresolution CBCT Reconstruction of an Anthropomorphic Knee Phantom

Figure 8 shows a reconstruction of an anthropomorphic knee phantom acquired on the CBCT test bench. Fig. 8 (a) illustrates the boundaries of the fine grid ROI. Four-fold downsampling of the volume and projections was employed. The multiresolution PWLS used 3.36% of the number of voxels and 17.7% of the number of detector pixels compared to a full FOV fine grid reconstruction. No artifacts arise from downsampling, and high-resolution trabecular features are visible in the fine grid ROI [outlined with orange dashed line in Fig. 8 (b)–(d)]. The resulting multiresolution image can be stored in less than 0.5 GB, whereas for the full-field fine grid image, approximately 7 GB would be required.

Figure 8.

Multiresolution PWLS reconstruction of an anthropomorphic knee phantom acquired on a CBCT benchtop. Fine and coarse grid regions are delineated in (a). (b)–(d) shows details of the high resolution trabecular ROI in the sagittal, axial, and coronal planes. Boundaries of the ROI are marked with a dashed line.

3.4. Computational Cost of Multiresolution PWLS

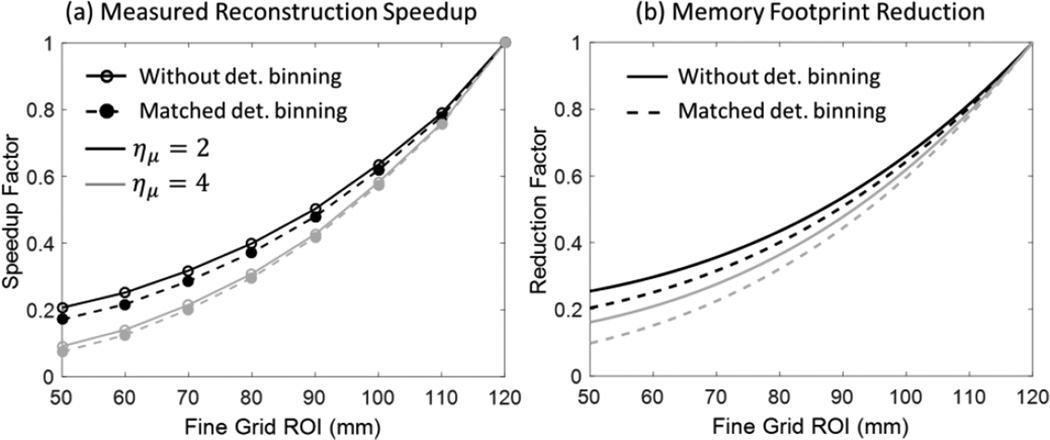
Figure 9 summarizes the investigation of computational savings provided by multiresolution PWLS. As expected, the speedup factor (compared to reconstruction using fine grid voxels throughout the entire FOV) can be as high as a 5× – 10× when the fine grid ROI is a relatively small fraction of the total size of the FOV. Most of the speedup is from image downsampling, rather than detector binning, which is to be expected with the voxel-driven forward projection method used here.

Figure 9.

(A) Measured reconstruction speedup of multiresolution PWLS as a function of the size of fine grid FOV (for total volume size of 120×120×120 mm³). (B) Total memory consumption of downsampled cases compared to fine grid cases.

Fig. 9 (b) examines the reduction in memory footprint provided by multiresolution PWLS. As anticipated, the memory savings are enhanced when projection binning is used in conjunction with volume downsampling. For a fine grid ROI of a similar size as the one used in the anthropomorphic knee phantom of Sec. 3.3, the memory footprint reduction is approximately 20% compared to reconstruction using only the fine grid voxels.

4. Discussion and Conclusions

We developed a PWLS reconstruction algorithm implementing a multiresolution voxelized parameterization of the object. The algorithm was evaluated for application in accelerated iterative reconstruction of finely sampled ROIs (voxel sizes <100 µm) from high resolution extremity CBCT projection data. It was assumed that the fine grid region is of the primary clinical interest and thus the investigation was focused on mitigation of artifacts in the fine grid region and quantification of the reconstruction speedup.

Streaking artifacts found in the fine grid ROI are likely caused by inconsistencies between the simulated forward projections of the coarsely and finely sampled ROIs. Artifact magnitude is thus a function of the cumulative blur due to downsampling and regularization of the coarse grid region. For example, downsampling factors as high as 10× were used without introducing visible streaking in the fine grid region by applying a relatively weak regularization in the coarsely sampled sub-volume. However, the tradeoff was that the μ_C exhibited a “blocky” appearance, which could limit the diagnostic utility of the coarsely sampled region. This may however be acceptable if the clinical interest is primarily in the fine grid ROI and achieving maximal speedup is a priority (and the coarsely sampled region may be reconstructed separately by other means using parameters suitable to soft-tissue visualization).

Additional memory savings can be attained when the multiresolution representation is augmented with binning of projection data. This work evaluated a scenario where projection binning was applied to pixels receiving the line integrals that traversed only through μ_C. This approach results in similar performance with respect to artifacts in the fine grid region as the method using only volume downsampling. In the coarse grid region, however, streaks tangential to the ROI boundary were found when using high levels of projection binning (η_y = 10) in conjunction with volume downsampling. The artifacts are hypothesized to emerge from mismatches in simulated projections of some of the coarse grid voxels located close to the ROI boundary. Such voxels are projected both on the binned and native pixels, depending on whether a given line integral traverses through μ_F for each projection angle. Since this inconsistency is not present for μ_F voxels, the fine grid ROI was unaffected.

The simulation study of Sec. 3.1 involves an ROI boundary that crosses through high contrast bone regions, resulting in a challenging scenario for multiresolution PWLS. Sec. 3.2 illustrates that both types of streaking artifacts discussed above can be effectively mitigated using a fine grid ROI that conforms to high contrast edges.

Overall, the optimal value of the downsampling factor will depend on the location of the fine and coarse grid regions and on the clinical application (i.e. whether both ROIs are of clinical interest, or only the finely sampled sub-volume). The results indicate that downsampling factors of ~4× are possible without perceptible artifacts in either of the ROIs. At this level of η_μ, the regularization strength in the coarsely sampled sub-volume can be adjusted over a relatively broad range without adversely affecting the fine grid region. For a typical knee volume, this downsampling corresponds to more than 5-fold acceleration of the iterative reconstruction. The current execution time for the multiresolution reconstruction of the knee phantom of Figure 8, obtained with η_μ = 4, is ~2 min per iteration (or ~100 min for the complete reconstruction of 50 iterations) using an un-optimized MATLAB-CUDA implementation. A naïve approach utilizing fine voxels throughout the whole volume would take ~10 hours for the reconstruction to complete and require ~15× more memory, and thus the multiresolution algorithm provided a significant step towards achieving clinically practical runtimes for iterative reconstruction of the trabecular detail in human studies. We anticipate that an additional 5× acceleration over the execution time stated here will be possible with an optimized implementation using a compiled executable with improved memory management on a multi-GPU workstation.

For certain configurations of the coarse and fine grid regions, downsampling factors as high as 10× can be used. For the typical knee CBCT (e.g. the sample reconstruction in figure 8), the 10× downsampling should yield ~52× speedup in PWLS, assuming a projection time that scales linearly with number of voxels. The acceleration factor will increase if the high resolution ROI is a smaller fraction of the total volume.

Similarly to the selection of the downsampling factor, the location, shape and the procedure for delineating the fine grid ROI will depend on the clinical application. The knee phantom reconstruction in Figure 8 represents a scenario where the scan parameters were selected to yield projection data that supports high-resolution reconstruction of the entire knee joint. In this case, a high fidelity FDK reconstruction could be obtained using the same projection data (thus at no additional dose), enabling precise definition of the fine grid ROI. However, such close adherence to bony boundaries is not always necessary. As shown in Figure 7, image artifacts due to downsampling will be minimized as long as the boundaries of the fine grid ROI do not cross high contrast edges. Detection of such high-contrast edges will typically be possible in an initial FDK reconstruction even if the projection data is noisy or sparsely sampled, as in low-dose imaging protocols intended for use with iterative reconstruction algorithms. In such cases, the initial analytical reconstruction may be non-diagnostic, but will likely be sufficient to delineate the fine grid ROI for the iterative algorithm. Furthermore, while the use of precisely defined fine grid ROIs (conforming with the object of interest) optimizes reconstruction time by minimizing the volume parameterized with fine voxels, the low dose applications are unlikely to yield data supporting reconstructions on very fine voxels. The use of sub-optimal fine grid ROIs (e.g. slightly larger than the object of interest) for low dose data will thus not be as detrimental for reconstruction performance as in the case of high resolution imaging.

Other factors to be considered in choosing the shape of the fine grid ROI involve computational burden and ease of implementation. In principle, the shape of the ROIs is only limited by the requirement that the fine grid voxel size must be an integer fraction of the coarse voxel size to ensure complete coverage of the volume. A fine grid ROI that is tightly matched to the shape of area of high resolution reconstruction has the advantage of minimizing the memory usage. At the same time, the execution speed may be hampered by non-contiguous memory access patterns that are likely to emerge when e.g. the fine grid ROI consists of multiple disjoint patches. Rectangular ROIs are easier to map to contiguous memory blocks and may thus yield improved computation speed compared to more complex ROI shapes when executed using general purpose software. In practice, the use of regular, rectangular or cylindrical fine grid ROIs loosely following the boundaries of the objects of interest (e.g. bones) and avoiding sharp tissue boundaries, combined with downsampling factors of 4–5, is likely to yield robust performance in typical clinical applications of multiresolution PWLS.

In conclusion, the proposed multiresolution algorithm for PWLS was tested in application to extremity CBCT. Artifact-free reconstructions of finely sampled ROIs were achieved at computation times that are 5× – 10× shorter compared to a brute force solution that applies fine voxel parameterization to the entire volume. The multiresolution framework can be further expanded to support other applications where computationally expensive forward models (e.g. modeling of detector blur (Tilley II et al 2015)) are applied only to a sub-region of the field-of-view. The algorithm permits application of different regularization strengths in the regions of coarse and fine grid, enabling reconstructions in which the sampling and regularization are individually optimized depending on the clinical task in each image region.