Abstract
Three ecotypes of killer whale occur in partial sympatry in the North Pacific. Individuals assortatively mate within the same ecotype, resulting in correlated ecological and genetic differentiation. A key question is whether this pattern of evolutionary divergence is an example of incipient sympatric speciation from a single panmictic ancestral population, or whether sympatry could have resulted from multiple colonisations of the North Pacific and secondary contact between ecotypes. Here, we infer multilocus coalescent trees from >1000 nuclear single-nucleotide polymorphisms (SNPs) and find evidence of incomplete lineage sorting so that the genealogies of SNPs do not all conform to a single topology. To disentangle whether uncertainty in the phylogenetic inference of the relationships among ecotypes could also result from ancestral admixture events we reconstructed the relationship among the ecotypes as an admixture graph and estimated f4-statistics using TreeMix. The results were consistent with episodes of admixture between two of the North Pacific ecotypes and the two outgroups (populations from the Southern Ocean and the North Atlantic). Gene flow may have occurred via unsampled ‘ghost' populations rather than directly between the populations sampled here. Our results indicate that because of ancestral admixture events and incomplete lineage sorting, a single bifurcating tree does not fully describe the relationship among these populations. The data are therefore most consistent with the genomic variation among North Pacific killer whale ecotypes resulting from multiple colonisation events, and secondary contact may have facilitated evolutionary divergence. Thus, the present-day populations of North Pacific killer whale ecotypes have a complex ancestry, confounding the tree-based inference of ancestral geography.
Introduction
Sympatric speciation is the evolution of reproductive isolation without geographic barriers (Mayr, 1963), in which the new species arise from a single randomly mating population (Gavrilets, 2003). Long-standing scepticism that this geographical mode of speciation was possible in nature (see, for example, Mayr, 1963; Felsenstein, 1981) remained even after theoreticians modelled the conditions and evolutionary processes under which sympatric speciation could take place. Most models of sympatric speciation evoke ecologically driven disruptive selection because of resource competition, that maintains polymorphisms that then segregate due to assortative mating (Dieckmann and Doebeli, 1999; Fry, 2003; Gavrilets, 2004; Bolnick and Fitzpatrick, 2007). The underlying assumptions of these models were thought by some not to be biologically realistic because of the seemingly low likelihood of maintaining linkage between loci associated with ecological variation and loci associated with mating preference in the face of even low levels of recombination, or of the evolution of ecological/mating preference pleiotropy (so-called ‘magic traits' see review by Bolnick and Fitzpatrick, 2007). However, a small number of empirical studies have identified monophyletic sister taxa in geographically isolated ‘islands', such as small crater lakes (Schliewen et al., 1994; Barluenga et al., 2006) or remote oceanic islands (Savolainen et al., 2006) in which sympatric divergence appears to be the most likely biogeographical scenario. The combination of support from theoretical models and empirical studies led to a widespread consensus that sympatric speciation is likely to have occurred in a few rare cases in nature (Coyne and Orr, 2004; Bolnick and Fitzpatrick, 2007). Yet, as predicted by Mayr (1963; and previously quoted by Bolnick and Fitzpatrick, 2007) ‘the issue will be raised again at regular intervals. Sympatric speciation is like the Lernaean Hydra which grew two new heads whenever one of its old heads was cut off' (p 451, Mayr, 1963).
The most recent resurgent interest in sympatric speciation has stemmed from the development and application of population genomic methods (see, for example, Keinan et al., 2007; Reich et al., 2009; Green et al., 2010; Pickrell and Pritchard, 2012) to better infer more complex evolutionary histories than the widely used phylogeographic approaches that simply infer monophyly from a point estimate of the majority-rule branching pattern (see, for example, Eaton and Ree, 2013; Malinsky et al., 2015; Martin et al., 2015). These population genomic methods typically identify asymmetry in the covariance of allele frequencies among populations that suggest introgression and indicate that the relationships among populations are not fully described by a simple bifurcating tree model. An elegant study by Martin et al. (2015) utilised such population genomic approaches to reveal a complex evolutionary history that included allopatric phases and secondary gene flow in arguably the best-supported empirical example of a sympatric radiation: that of Cameroon crater lake cichlids (Coyne and Orr, 2004). Here, in response to a phylogeographic study recently published in Heredity (Moura et al., 2015), we apply a population genomics approach to the genome-wide single-nucleotide polymorphism (SNP) data generated by restriction site-associated DNA sequencing (RAD-seq; Baird et al., 2008) to gain insights into the evolutionary history of a species for which the evidence for sympatric speciation is arguably equivocal: the sympatric ecotypes of killer whales inhabiting the waters of the Northeastern Pacific (Ford et al., 2000). We critically evaluate both the approach taken and the inferences drawn by this previous study.
The killer whale (Orcinus orca) is a globally distributed mammalian species, found from the Arctic to the Antarctic and all waters in between (Morin et al., 2015). As a species, killer whales have been observed feeding on a wide range of prey species; however, several studies have found that some lineages are specialised hunters and feed upon a narrower range of prey species (Ford et al., 1998, 2000, 2011a; Saulitis et al., 2000; Pitman and Ensor, 2003; Burdin et al., 2005; Matkin et al., 2007; Durban et al., 2016). Thus, the term ecotype has been widely used in the literature when referring to these ecologically specialised lineages (Ford et al., 2000). Killer whale ecotypes are found in sympatry in a number of locations (Ford et al., 1998; Pitman and Ensor, 2003; Foote et al., 2009), the most intensively studied being the partially sympatric ecotypes of the North Pacific (Ford et al., 1998, 2000). The mammal-eating ‘transient' ecotype occurs in partial sympatry in coastal waters with the fish-eating ‘resident' ecotype (Ford et al., 1998; Saulitis et al., 2000; Burdin et al., 2005; Matkin et al., 2007), whereas a third ‘offshore' ecotype is occasionally seen in the same waters, but most frequently encountered in waters further offshore (Dahlheim et al., 2008; Ford et al., 2011a). The resident and transient ecotypes thus satisfy the first criterion of Coyne and Orr (2004) for identifying sympatric speciation, that is, that species have largely overlapping geographic ranges.
No mitochondrial haplotypes are shared among these North Pacific ecotypes and estimates of FST based on allele frequencies of microsatellite loci and nuclear SNPs indicate that ecotypes are significantly genetically differentiated (Hoelzel et al., 1998, 2007; Barrett-Lennard and Ellis, 2001; Morin et al., 2010, 2015; Ford et al., 2011b; Parsons et al., 2013). Some studies have reported estimates of low-level, on-going, male-mediated gene flow between ecotypes (Hoelzel et al., 2007; Pilot et al., 2010). Others have found no evidence for contemporary male-mediated gene flow using many of the same approaches as Pilot et al. (2010) and sampling some of the same sub-populations (Ford et al., 2011b). It therefore appears to be unresolved whether killer whales meet the second criterion of Coyne and Orr (2004) for identifying sympatric speciation, that is, that reproductive isolation must be complete.
It is the failure to meet the third and fourth criteria of Coyne and Orr (2004) that we have previously argued makes the case for sympatric speciation (or divergence) of North Pacific killer whale ecotypes at best equivocal (Foote and Morin, 2015), namely, that clades thought to arise via sympatric speciation must be sister species or monophyletic endemic species flocks, and that ‘the biogeographic and evolutionary history of the groups must make the existence of an allopatric phase very unlikely'. A sparsely sampled nuclear DNA phylogeny based on RAD-seq data reconstructed a paraphyletic relationship (Moura et al., 2015). From their phylogeographic analysis of these RAD-seq data, Moura et al. (2015) infer the North Pacific as the most likely location of divergence for the three North Pacific ecotypes. However, mitochondrial DNA phylogenies reconstruct a polyphyletic relationship among North Pacific killer whales, clustering the residents and offshores together with lineages from the North Atlantic rather than with the transients (Barrett-Lennard and Ellis, 2001; Hoelzel et al., 2002; Morin et al., 2010, 2015; Foote et al., 2011; Moura et al., 2015). In addition, even if the inference that divergence took place in the North Pacific is correct, the size of this ocean does not make the existence of an allopatric phase very unlikely.
Given the failure to fully satisfy the criteria for sympatric speciation as noted above, we question the robustness of the inference of sympatric divergence drawn by the study of Moura et al. (2015). However, we also have concerns regarding the phylogenetic approach taken by these authors that we critically evaluate here. Moura et al. (2015) inferred a phylogenetic tree based upon concatenated RAD-seq data from five killer whale ecotypes/populations using MRBAYES (Ronquist and Huelsenbeck, 2003) and BEAST (Drummond and Rambaut, 2007). Such an approach may not be appropriate for analysing diploid markers for the timescales over which population splits occur within a species (Schierup and Hein, 2000; Kutschera et al., 2014; De Maio et al., 2015), as there is likely to be incomplete lineage sorting (ILS) of standing genetic variation that was present at the root of a phylogeny (De Maio et al., 2015). Accordingly, the number of fixed differences between the sampled killer whale populations (reported in Table 2 of Moura et al., 2014a) ranges from just 0 to 15. By sampling 1.7 Mb of the nuclear genome representing many genes, Hoelzel and Moura (2015) claim they have produced a reliable topology that accurately reconstructs the history of these populations. However, by concatenating the data they have ignored coalescent variance and assumed that all loci share the same genealogy (Knowles and Carstens, 2007; Kubatko and Degnan, 2007). Several processes can result in discordant gene trees and incongruence between individual gene trees and the true evolutionary history, with perhaps the best studied being ILS (Maddison and Knowles, 2006; Degnan and Rosenberg, 2009). Rapid radiations, such as have been inferred for killer whales (Hoelzel et al., 2002; Morin et al., 2015; Foote et al., 2016), can result in short branch lengths, the retention of ancestral polymorphisms in different populations and ILS because of the failure of lineages within a population to coalesce (Degnan and Rosenberg, 2009). Under such conditions, concatenation of genes can result in a consensus tree that is incongruent with the true evolutionary history, and simply adding and concatenating more data can exacerbate this discordance (Degnan and Rosenberg, 2009). In addition, the default settings of software used by Moura et al. (2015) treat sites that are heterozygous in an individual (and thereby classified as IUPAC (International Union of Pure and Applied Chemistry) codes) as ambiguous data. This is a known source of bias in the inference of topologies from diploid sequence data (Lischer et al., 2014; Potts et al., 2014). It is unclear whether Moura et al. (2015) accounted for this issue in their phylogenomic study. Lastly, inferring the relationship among populations as a single phylogenetic tree is only appropriate in population genomic studies if the amount of gene flow among populations can be shown to have a negligible effect on this reconstruction of a single evolutionary history (Schierup and Hein, 2000; Foote and Morin, 2015). A major limitation of using such an approach to infer ancestral states is that these tree-based methods do not consider the possibility that populations derived ancestry from multiple ancestral populations, for example, because of ancestral admixture events (Cavalli-Sforza, 1973; Cavalli-Sforza and Piazza, 1975; Felsenstein, 1982; Patterson et al., 2012). Thus, if each ecotype resulted from a distinct colonisation event followed by subsequent gene flow upon secondary contact, then the colonisation history will be obscured in a majority-rule phylogeny that will then wrongly infer that the previously allopatric ecotypes are sister taxa (Foote and Morin, 2015).
When considering evolutionary history within a species, the major processes underlying genetic differentiation among populations include genetic drift of allele frequencies that will in turn be constrained by gene flow between populations. Thus, genetic differentiation among populations primarily reflects differences in demographic processes and connectivity, at least until sufficient time has passed to allow accumulation of novel mutations and complete lineage sorting of ancestral alleles. In this study, we reconstruct the relationships among killer whale ecotypes based on methods appropriate for intraspecific comparisons that consider heterozygous sites and changes in allele frequencies and account for ILS and/or admixture. We focus on the assumption that the population history of killer whales conforms to a single, simple bifurcating tree unbiased by gene flow among populations that the phylogeographic inference of sympatric divergence within the North Pacific by Moura et al. (2015) relies upon. Recent studies have developed and applied explicit tests for the violation of a tree model and methods to infer more complex colonisation histories (see, for example, Reich et al., 2009; Green et al., 2010; Durand et al., 2011; Patterson et al., 2012; Pickrell and Pritchard, 2012). Here we apply some of these approaches to the published SNP genotypes generated by RAD-seq (Moura et al., 2014a, 2015), allowing us to explore more complex scenarios in the evolutionary history of North Pacific killer whale ecotypes.
Materials and methods
Quality control check of published SNP data
Moura et al. (2015) generated RAD-seq data from 43 samples, but concurrently published a larger genotype data set for 115 individuals generated using the same RAD-seq protocol (Moura et al., 2014a). These authors reported that 3281 SNPs were identified and confidently mapped to the killer whale genome (Moura et al., 2014a). We accessed this larger data set as a VCF file from the Dryad data depository (doi: 10.5061/dryad.qk22t), which included genotypes for 3678 sites.
As some of the models implemented in our analyses assume that loci are evolving under a Wright–Fisher model, that is, are evolving under neutrality, we filtered the data to remove loci identified as among the top outliers in an analysis of whole genome sequences (Foote et al., 2016) and in which alternative alleles resulting in nonsynonymous amino acid substitutions within protein coding genes were fixed in different ecotypes. Specifically, we removed two SNPs that fell within the GATA4 gene on scaffold KB316942.1 (positions 7 516 690–7 564 747). This contrasted with previous filtering of 365 SNPs inferred as evolving under selection by Moura et al. (2015) using the FDIST2 method (Beaumont and Nichols, 1996) implemented in LOSITAN (Antao et al., 2008). When used with the relatively limited number of SNPs available for the killer whale data set, and given the demographic shifts within this species (Foote et al., 2016), this method underestimates the range of neutral FST values, leading to false positive identification of loci evolving under selection (Lotterhos and Whitlock, 2014), thereby removing neutrally evolving loci that have greater phylogenetic informativeness.
Inspection of the data following filtering for putative loci under selection revealed that large numbers of SNPs were in close linkage; for example, >10% were ⩽10 bp apart on the same scaffold and approximately one-third of SNPs are ⩽100 bp from another SNP on the same scaffold (Supplementary Figure S1). The killer whale genome has low genetic diversity (π≈0.001–0.003), that is, one SNP on average every 300–1000 bp (Foote et al., 2016). Thus, a large proportion of the RAD-seq data have orders of magnitude higher genetic diversity than the genome-wide average, and the called SNPs in close physical linkage potentially result from sequencing reads being mapped to unmasked paralogous and/or repetitive regions, or other mapping artefacts. We therefore compared the coordinates of SNPs, which are given in the VCF file in respect to their position on the killer whale genome assembly, with the coordinates of putative repeat regions in the killer whale genome (Foote et al., 2015, 2016). We found that 447 of the SNPs in the VCF file were in repeat regions identified by RepeatMasker (Smit et al., 1996) using the Cetartiodactyl repeat library from Repbase (Jurka et al., 2005).
The removal of repeat regions identified by RepeatMasker did not remove all closely linked SNPs, and therefore we compared the unfiltered VCF coordinates with regions of the killer whale reference genome (Foote et al., 2015, 2016) with poor mappability (Q<30), excessive coverage (>twice the average coverage, as determined using angsd doDepth function; Korneliussen et al., 2014) or low coverage (less than a third of the average) as determined by the CallableLoci tool implemented in GATK (McKenna et al., 2010; DePristo et al., 2011). We found that 1172 SNPs in the VCF file fell into these regions, with the coordinates of 257 SNPs being identified as regions of poor mappability by both methods (RepeatMasker and CallableLoci). Thus, these two methods identified a combined total of 1360 SNPs in the VCF file that were mapped to putative repetitive elements. This constitutes 37% of the SNPs listed in the VCF file, consistent with repetitive elements constituting 41% of the killer whale genome (Foote et al., 2016). Thus, the number of SNPs retained after removing potential mapping artefacts was 2316.
Even after this filtering step several hundred of the retained SNPs were <10 kb from another SNP on the same scaffold and thus potentially linked (Supplementary Figure S1). Therefore, the SNP data set was further filtered to minimise the effect of linkage by including only SNPs that were spaced >100 kb apart on a scaffold, retaining 1346 putatively unlinked SNPs (Supplementary Figure S1). Data files for the filtering steps have been deposited in the Dryad data repository.
Coalescent species tree analyses of SNPs
To visualise uncertainty in the majority-rule topology, for example, if different genes have different evolutionary histories because of ILS, we used SNAPP v. 1.1.1 (Bryant et al., 2012) implemented in BEAST v2.3.1 (Drummond and Rambaut, 2007) to infer multilocus phylogenetic trees from nuclear SNPs based on the coalescent. SNAPP is a drift-based model that allows for a single new mutation per site and back mutations, assuming at most two alleles per site (Bryant et al., 2012). As this model assumes that loci are unlinked and evolving under the Wright–Fisher model, we therefore analysed the SNP data set filtered for putative repeats, linkage and loci evolving under selection. Because of the high computational intensity of running SNAPP on such a large number of markers and individuals, we followed the example of Stervander et al. (2015) and pruned our data set to include five randomly selected individuals from each population/ecotype. We used a burn-in of 10% and visualised the distribution of trees using DENSITREE v. 2.1 (Bouckaert, 2010). The maximum-clade-credibility tree was generated using TREEANNOTATOR v. 1.7.4 (Drummond and Rambaut, 2007). We repeated this process a further three times by randomly resampling without replacement different individuals than used for the first run (for populations with >5 genotyped individuals). To determine the effect of subsampling on theta-estimates, we then combined two of these subsets, so that for populations with ⩾10 genotyped individuals, we sampled 10 individuals. Details of which individuals were included in each subsample are given in Supplementary Table S1. We used the default prior and model parameters, including the defaults for u and v, and ran a single Markov chain Monte Carlo (MCMC) chain of 1 000 000 iterations with sampling every 1000 steps. Acceptable mixing (requiring effective sample size values to be >200) and convergence were checked by visual inspection of the posterior samples using Tracer (Rambaut and Drummond, 2007). Convergence rates of posterior split probabilities were also visualised using the online AWTY (Are We There Yet?) program (Nylander et al., 2008).
Tests for ‘treeness' and admixture
To further test for a violation of the tree model assumption (bifurcation) and to detect admixture/recombination events, we calculated the f4-statistic, which can provide robust evidence of admixture, even if gene flow events occurred hundreds of generations ago and under scenarios of ILS (Reich et al., 2009). Tests on simulated data have shown that the admixture proportions estimated using the f4-statistic are robust to ascertainment strategies and demographic history (Patterson et al., 2012).
The f4-statistic is based on the quantification of genetic drift (change of allele frequencies) between pairs of populations in a tree using variance in allele frequencies (Reich et al., 2009; Patterson et al., 2012; Peter 2016). For each set of four populations, there are three possible unrooted bifurcating trees that could describe the relationships among populations. For example, populations A, B, C and D could be described by trees ((A,B),(C,D)), ((A,C),(B,D)) and ((A,D),(B,C)). The differences in allele frequencies between the populations in each clade should be uncorrelated between clades if the topology is correct. Hence, if topology ((A,B),(C,D)) does accurately describe the relationship among these populations, then the allele frequency differences (drift) that have accumulated since population A split from population B should not be correlated with the allele frequency differences accumulated since population C split from population D, resulting in an f4-statistic that does not differ significantly from zero. For the incorrect alternate topologies, correlated drift should result in positive or negative correlation values. This would remain true under conditions of ILS, thus disentangling admixture from ILS.
We computed the statistic f4(A,B; C,D) for all possible combinations of populations using the fourpop function in Treemix (Pickrell and Pritchard, 2012). We used the data set of 2316 SNPs filtered to remove SNPs mapped to putative repetitive elements and the GATA4 locus, but not filtered for linkage. Instead, linkage disequilibrium was accounted for by jackknifing in windows of five adjacent SNPs, allowing the significance of each test to be assessed by calculating the standard error. The tests were replicated, jackknifing over blocks of 10 and 50 SNPs. The expected value of the f4-statistic was estimated visually by reconstructing the paths of allele frequency changes through the tree, first assuming the topology inferred in this study using SNAPP, and second assuming the topology inferred by Moura et al. (2015). The expected value of the statistic f4(A,B; C,D) would be zero if we see no overlap in the paths of allele frequency changes (drift) between A and B, and between C and D through the tree. The expected value of the statistic f4(A,B; C,D) and associated Z-score will be: negative and significantly different from zero if allele frequency changes between A and B and between C and D take paths in the opposite direction along a shared edge within the tree; or positive and significantly different from zero if the drift between A and B and between C and D share overlapping paths in the same direction along an edge within the tree. Thus by performing these tests, we identify when the relationship among four of our five populations are fully described by a simple tree model and if they are consistent with the topology inferred by SNAPP and/or the substitution-based tree model by Moura et al. (2015); or when the relationship among a combination of four populations is not fully described by a simple tree model, suggesting instead that some populations may derive from multiple ancestral populations due to admixture.
When a potentially admixed population is identified using this approach, the method can be extended to estimate admixture proportions using the ratio of f4-statistics. Patterson et al. (2012) defined the f4-ratio test as
where A and C are a sister group, B is sister to (A,B), X is a mixture of A and B and O is the outgroup. This ratio estimates the ancestry from A, denoted as α, and the ancestry from B, as 1−α (Supplementary Figure S2). We estimated the ancestry proportions of the offshore and transient ecotypes that were candidates for admixture from the Atlantic and Marion Island populations respectively (see below).
To further visualise ‘treeness', that is, how well relationships can be represented by bifurcations, we reconstructed the relationships between killer whale ecotypes in the form of a maximum likelihood graph using the unified statistical framework implemented in TreeMix v. 1.12 (Pickrell and Pritchard, 2012). TreeMix estimates a bifurcating maximum likelihood tree using population allele frequency data and estimates genetic drift among populations using a Gaussian approximation. The branches of this tree represent the relationship between populations based on the majority of alleles. Migration edges are then fitted between populations that are a poor fit to the tree model, and in which the exchange of alleles is inferred. The addition of migration edges between branches is undertaken in stepwise iterations to maximise the likelihood, until no further increase in statistical significance is achieved (Pickrell and Pritchard, 2012). The directionality of gene flow along migration edges is inferred from asymmetries in a covariance matrix of allele frequencies relative to an ancestral population as implied from the maximum likelihood tree. This is illustrated in the example tree ((X1,X2)(X3,X4)) given in Figure 1 of Pickrell and Pritchard (2012), in which a migration is inferred from the branch to population X2 to population X3 from the high covariance found between X1 and X3, but not between populations X2 and X4. We estimated the likelihood of graphs with from 0 to 5 migration events added in order to visualise the largest gene flow events and estimate their proportion and direction.
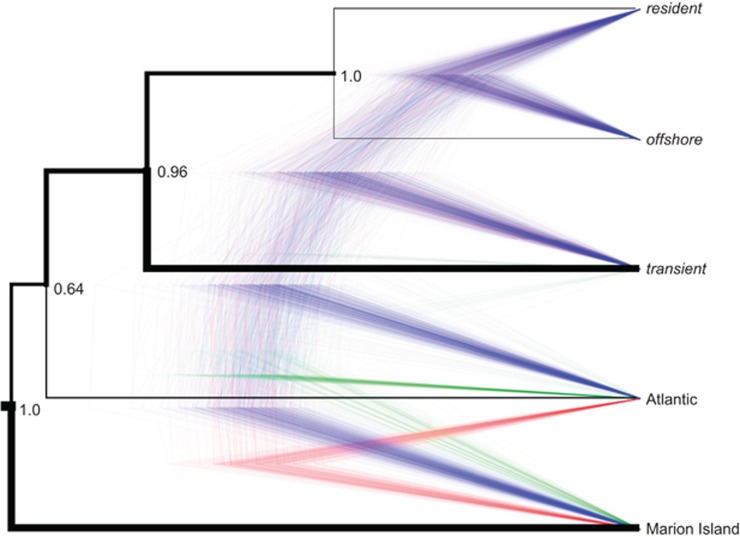
Figure 1.
Nuclear SNP phylogeny of 43 individuals assigned to 5 populations (10 resident, 10 transient, 7 offshore, 10 Marion Island and 6 North Atlantic) based on 1346 SNPs. Maximum-clade-credibility tree shown in the black right-angled tree with posterior probabilities at nodes. Branch width is proportional to theta. Tree cloud produced using DENSITREE of the last 50 trees (representing samples taken every 1000 MCMC steps from 500 000 iterations) from SNAPP analysis visualise the range of alternative topologies. For this subsample (5), a total of four topologies were found within the 95% HPD (see Supplementary Table S3).
Lastly, we visualised genetic structure among populations using Bayesian hierarchical clustering implemented in STRUCTURE v. 2.3.4 (Pritchard et al., 2000; Falush et al., 2003). To limit the effects of linkage disequilibrium, we used the filtered data set of 1346 SNPs. We used STRUCTURE to estimate proportions of admixture for every individual in the data set for k=5. Five independent runs were performed using a burn-in period of 50 000 iterations followed by 300 000 MCMC steps that were checked for acceptable convergence and mixing.
Results and discussion
Genomic methods are rapidly improving our ability to infer evolutionary and population genetics patterns and processes. In particular, by identifying variation in phylogenetic signal across genomic regions, these methods can infer processes such as introgression and ILS (Kutschera et al., 2014). A recently published phylogenomic study aimed at determining divergence patterns and processes in a rapid global radiation inferred ancestral geography assuming a tree-like relationship among five populations/ecotypes of killer whales (Moura et al., 2015). Here, we critically evaluate both the approach taken and the inferences drawn by this previous study. The analysis of concatenated RAD-seq loci by Moura et al. (2015) does not account for introgression or ILS, and concatenation is known to generate biases in the inference of a consensus tree (Kubatko and Degnan, 2007). Our re-analyses of the genome-wide SNPs presented by Moura et al. (2014a, 2015) find that their inferred topology is but one of several genealogical histories found for different independent loci, and is discordant with the genealogies of the majority of loci sampled here. Furthermore, by using methods that disentangle introgression from ILS, we find signatures of ancestral admixture with outgroups, but which are not equally shared among the three North Pacific ecotypes. Thus, our analyses argue against the North Pacific ecotypes arising from a single colonisation by a panmictic population and a vicariant split (that is, sympatric speciation).
Incomplete lineage sorting
We visualised the variation in the topology of gene trees using the multi-species coalescent model implemented in SNAPP (Bryant et al., 2012), thereby allowing each SNP to have its own genealogy (Figure 1). The MCMC chains showed stationarity and mixing (effective sample size >200 for all variables except for two theta-estimates at the root of the tree). The consensus tree topology and theta-estimates were relatively consistent across runs in which different individuals were sampled from each population (Figure 1, Supplementary Figure S3 and Supplementary Table S2), indicating that subsampling did not significantly bias the topology of the SNAPP trees. Two nodes were highly supported (highest posterior density (HPD)=1.0) in each consensus tree, but two nodes consistently showed weaker support; specifically, the nodes associated with the placement of the transient ecotype relative to both the Atlantic population and to the ingroup of the resident and offshore ecotypes. This topological uncertainty was visualised as a cloudogram of gene trees sampled from the posterior distribution inferred by SNAPP using DENSITREE (Bouckaert, 2010). The number of alternative topologies inferred per subsampling and within the 95% HPD ranged from 3 to 9 (Supplementary Table S3). In all inferred topologies within the 95% HPD the resident and offshore ecotypes consistently cluster together as the ingroup. However, the transient ecotype shifts position relative to this ingroup and the outgroups, in particular the Atlantic population (Figure 1, Supplementary Figure S3 and Supplementary Table S3). The topology inferred from the substitution model-based concatenated phylogenetic reconstruction of Moura et al. (2015), which constrains all sites to share the same evolutionary history, represents <11% of the SNAPP trees in the 95% HPD for each of the different subsamples (Supplementary Table S3).
The inference of ILS from the discordance of topologies inferred by SNAPP is supported by the high proportion of shared polymorphic sites and the low number of fixed differences among populations/ecotypes, and is expected for such a recent and rapid divergence as is the case in killer whales. The pattern of ILS among the Atlantic, Marion Island and Transient groups suggests that loci are coalescing in a large and structured ancestral source population. Low effective population size, as inferred from the theta-estimates (Figure 1,Supplementary Figure S3 and Supplementary Table S2), may have accelerated lineage sorting in the offshore and resident ecotypes. However, although the multilocus coalescence approach of SNAPP incorporates heterozygous sites and accounts for lineage sorting, the model does not consider gene flow among taxa. Therefore, the signal identified as resulting from ILS by SNAPP, could in fact be wholly or in part due to ancestral admixture events. Introgressive gene flow has long been acknowledged as a confounding factor in phylogenetic inference (see Schierup and Hein, 2000; Leaché et al., 2014). Introgression shortens branch lengths, reduces node support and results in populations being grouped together based on the extent of gene flow between them in substitution model-based phylogenetic trees (Schierup and Hein, 2000; Leaché et al., 2014). We therefore investigated whether historical gene flow between ancestral populations/ecotypes could be influencing gene tree topology using methods that can identify the extent and direction of introgression during recent and ancestral admixture events.
Evidence of shared substructure
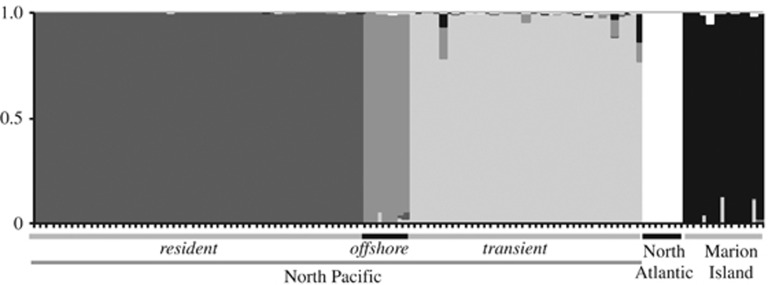
We estimated and visualised the proportions of shared ancestry among the two outgroups and the three North Pacific ecotypes using STRUCTURE. The highest likelihood run for k=5 is shown in Figure 2. The assignment probabilities indicated that the transient ecotype shared ancestry proportions with the Marion Island population, but the resident and offshore ecotypes did not. The transient ecotype also shared ancestry proportions with the offshore ecotype. Following an admixture event, recombination is expected to break up ancestry proportions over successive generations, and ancestry will be exchanged among individuals within the population, eventually resulting in homogenisation of ancestry proportions within a population. In contrast, we find relatively high proportions of ‘offshore' and ‘Marion Island' ancestry in just a few individuals of the transient ecotype. This variance in ancestry proportions among individuals is suggestive of relatively recent admixture that has not yet fully introgressed within the receiving transient ecotype.
Figure 2.
Population structure for a data set of 115 killer whales at k=5, as estimated by STRUCTURE 2.3.4. Each individual is represented by a column and the probability of that individual belonging to each population is indicated by coloured segments. The plot is based on the highest likelihood run (of five).
Although STRUCTURE is a powerful tool for detecting population substructure, it does not provide any formal tests for admixture. The genetic substructure shared by the outgroup Marion Island population and the North Pacific transient ecotype, but not the other two North Pacific ecotypes, could potentially be generated by multiple population histories: for example, introgression from an unsampled population into the transient ecotype and Marion Island population or shared ancestral variation that was lost in the resident and offshore populations or an artefact of rare alleles.
Evidence of ancestral admixture and a lack of ‘treeness'
In contrast to STRUCTURE, the f4-statistic and TreeMix are explicit tests for admixture that also provide some information about the directionality of gene flow (Patterson et al., 2012).
For most combinations of taxa our observed and our visual estimations of the expected f4-statistic were consistent with a tree-like relationship of the form ((outgroup, transient), (resident, offshore)) (see Table 1a and Supplementary Figures S4a and b) or ((outgroup, outgroup), (ecotype, ecotype)) (see Table 1b and Supplementary Figures S4c and d). However, our observed and our visual estimations of the expected f4-statistic were not consistent with a tree-like relationship in tests that included the North Pacific transient and offshore ecotypes and the Marion Island and Atlantic outgroups together (Table 1c and Supplementary Figure S4e). For this combination of taxa we expect that only the f4-statistic test f4(M,A; O,T) will be nonsignificant (Supplementary Figure S4e). However, the observed f4-statistic is not significant for either f4(M,A; O,T) or f4(M,O; T,A) and both trees appear to have approximately equal support (Table 1c). The f4-statistic test f4(M,O; T,A) was expected to be significant because of drift taking overlapping paths along the same edge e as for test f4(M,T; O,A). Yet, the f4-statistic are markedly different for the two tests, that is, we see less covariance of drift between the taxa forced in the clade (M,O) and the taxa forced into the clade (T,A) than expected. This indicates that drift is taking an alternative path in the tree because of introgressive admixture between two or more of these populations in different clades, but this admixture does not affect the covariance of drift as greatly as when comparing the clades (M,T) and (O,A). We observe discordance between the observed (nonsignificant) and the expected (significant) f4-statistics for this combination of populations whether we assume the consensus topology reconstructed from SNAPP or the topology inferred from concatenated RAD sequences by Moura et al. (2015). This combination of populations was not compared by Hoelzel and Moura (2015) in their tests of different topologies using DIY-ABC (Cornuet et al., 2014) presented as support for their earlier inference of sympatric evolution of North Pacific ecotypes (Moura et al., 2015), as they excluded the Atlantic population.
Table 1. The f 4 -statistic (±s.e.) results for comparisons of different topologies.
| Four-taxon tree | f4-statistic | Z-score | P-value | |
|---|---|---|---|---|
| (a) | (M,O; R,T) | −0.0070±0.0015 | −4.392 | <0.001 |
| (M,R; O,T) | −0.00611±0.0016 | −3.752 | <0.001 | |
| (M,T; O,R) | 0.0091±0.0011 | 0.840 | 0.401 | |
| (O,A; R,T) | 0.0064±0.0018 | 3.590 | <0.001 | |
| (O,T; R,A) | 0.0049±0.0018 | 2.751 | 0.006 | |
| (O,R; T,A) | −0.0015±0.0014 | −1.057 | 0.291 | |
| (b) | (R,A; O,M) | 0.0089±0.0022 | 3.992 | <0.001 |
| (R,M; O,A) | 0.0095±0.0022 | 4.255 | <0.001 | |
| (R,O; M,A) | 0.0006±0.0015 | 0.377 | 0.706 | |
| (M,T; R,A) | −0.0040±0.0014 | −2.785 | 0.005 | |
| (M,R; T,A) | −0.0034±0.0017 | −2.028 | 0.043 | |
| (M,A; R,T) | −0.0006±0.0015 | −0.414 | 0.679 | |
| (c) | (M,T; O,A) | −0.0031±0.0014 | −2.227 | 0.026 |
| (M,O; T,A) | −0.0019±0.0016 | −1.216 | 0.224 | |
| (M,A; O,T) | −0.0012±0.0014 | −0.851 | 0.395 |
A total of 461 jackknife blocks of 5 SNPs were used to estimate s.e. Two-tailed P-values are reported for each Z-score. (a) The f4-statistic test results for comparisons that include three Pacific ecotypes with one outgroup. Note that in each combination of four populations, one topology (bold) is clearly supported over the two rejected topologies. In each case it is the topology that groups the offshore and resident ecotypes. (b) The f4-statistic test results for comparisons that include two Pacific ecotypes with the two outgroups. The topologies that group the North Pacific ecotypes (bold) are supported over the two rejected topologies. (c) The f4-statistic test results for two Pacific transient and offshore ecotypes, with the two outgroups. Note that there is no one clearly supported topology. Further interpretation and visualisation of the drift paths are given in the Supplementary Material. Results over different jackknife block sizes are given in Supplementary Table S4.
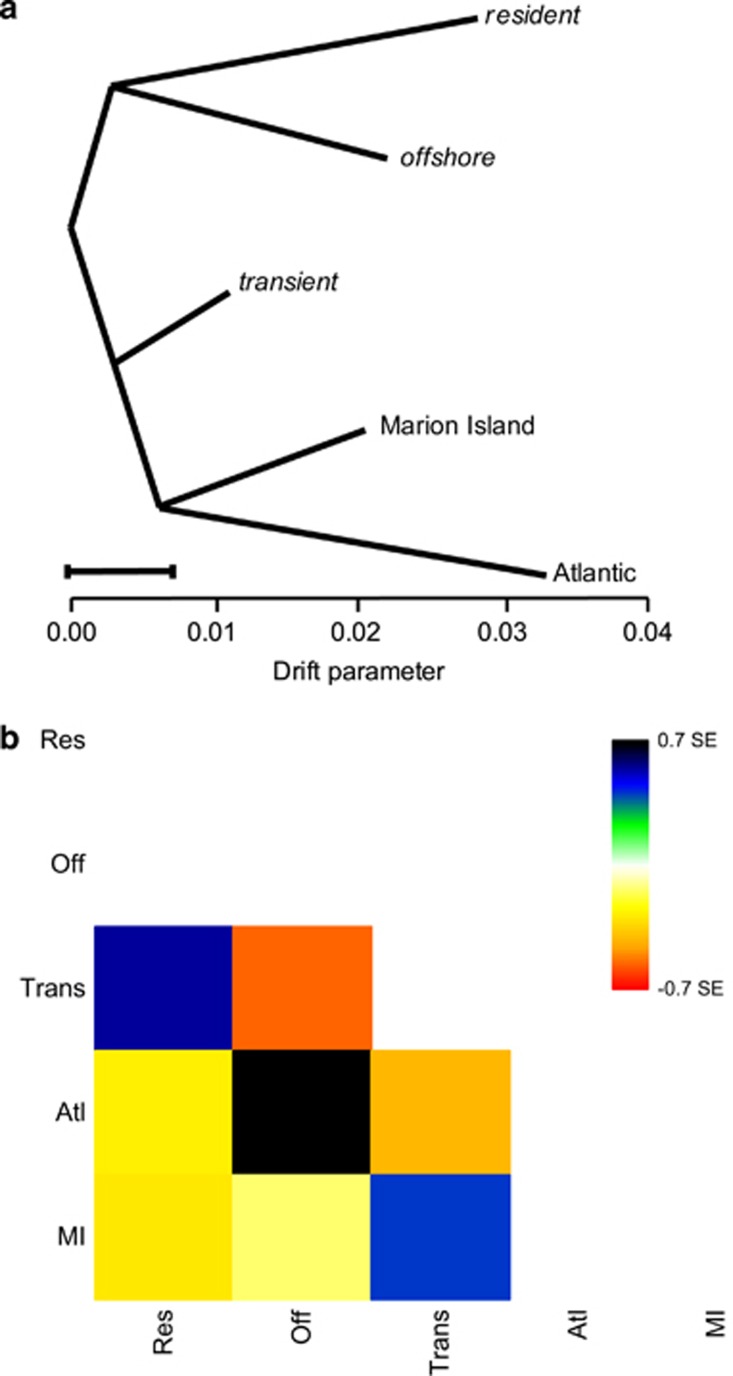
When no migration events are included, the drift-based model implemented in TreeMix infers a topology (Figure 3a) that is concordant with the consensus topology inferred by SNAPP (Figure 1). The resident and offshore ecotypes grouped together, as did the Marion Island and Atlantic populations, whereas the transient was intermediate between these two pairings (Figure 3a). Drift was higher in the resident and offshore ecotypes and Atlantic population (Figure 3a), consistent with the lower theta-estimates from SNAPP (Figure 1). Inspection of the matrix of residuals (Figure 3b) indicated how well this tree model fits the data, in which residuals above zero represent populations that are more closely related to each other than in the best-fit tree and are candidates for admixture, and negative residuals indicate that a pair of populations is less closely related than represented in the best-fit tree. Strongly positive residuals suggest candidate admixture events between the Marion Island population and transient ecotype, between the resident and transient ecotypes and between the Atlantic population and offshore ecotype. In contrast, we see a strongly negative residual suggesting that the covariance in allele frequencies between the offshore and transient ecotypes may be overestimated by the model.
Figure 3.
(a) TreeMix graph visualising the relationship among populations as a bifurcating maximum-likelihood tree. Horizontal branch lengths are proportional to the amount of genetic drift that has occurred along that branch. The scale bar shows 10 times the average s.e. of the entries in the sample covariance matrix. (b) Residual fit of the observed versus predicted squared allele frequency difference, expressed as the number of s.e. of the deviation. Colours are in the palette on the right. Residuals above zero represent populations that are more closely related to each other in the data than in the best-fit tree, and are candidates for admixture. Negative residuals indicate that a pair of populations are less closely related, based on the data, than represented in the best-fit tree.
TreeMix optimised the fit of the data to a tree by adding two migration events between populations (Supplementary Figure S5a). The likelihood was not further increased by adding additional migration edges. The TreeMix model makes a number of assumptions about, and simplifications of, the process of population splits and gene flow. First, migration is modelled as occurring at a single point in time, and in cases of on-going long-term gene flow this assumption will be violated and result in a poorly supported graph (Pickrell and Pritchard, 2012). For example, the covariance of allele frequencies between North Pacific resident and transient ecotypes could be a consequence of equilibrium demography, that is, populations are at a long-term stasis with a fixed low level of migration between them, and this could influence the topology of the maximum likelihood tree. Second, TreeMix also assumes that the history of the species is largely tree like, but in cases of complex structure, many graphs representing different histories may be equally supported by identical covariance matrices. Accordingly, we found that several different migration edges resulted in the same increase in likelihood of the fit of the data to the tree model. The two migration edges in the optimised admixture graph generated by TreeMix are consistent with the discordance between the observed and expected f4-statistic test f4(M,O; T,A). Supplementary Figures S5b and c illustrate how the expected covariance due to drift taking overlapping paths along the same edge e is reduced because of the migration edges. These migration edges have less influence on the covariance of drift in the f4-statistic test f4(M,T; O,A), and hence the observed and expected f4-statistic are relatively concordant for this test (see Supplementary Figure S5d).
Candidate admixed populations
The results presented here provide an indication of populations/ecotypes that might have ancestry derived from multiple populations. The consensus SNAPP and TreeMix topologies identified the North Pacific transient ecotype as being intermediate between the pairing of the resident and offshore ecotypes and the pairing of the Atlantic and Marion Island populations, with residuals from the TreeMix analysis suggesting potential admixture between the transient ecotype and Marion Island population and between the resident and transient ecotypes. STRUCTURE also identified shared substructure between the transient ecotype and Marion Island populations. Lastly, the f4-ratio estimator suggested that the transient ecotype shared roughly equal ancestry with the offshore ecotype (45%) and the Marion Island population (55%), dependent upon the timing of the admixture (see Supplementary Figure S2). The North Pacific offshore ecotype was also suggested by some analyses to be a candidate admixed population, with 22% shared ancestry with the Atlantic population inferred by the f4-ratio estimator (see Supplementary Figure S2). The residuals of the TreeMix analysis also suggested potential admixture between the offshore ecotype and Atlantic population. Finally, when the resident and offshore ecotypes were interchanged in the f4-statistic tests, the difference in the estimates were consistent with drift taking an additional path between the offshores and Atlantic population (Supplementary Figure S4a). Therefore, of the three North Pacific ecotypes, the offshores and the transients were candidates for having ancestry derived from more than one source population. It is important to note that the inferred source populations in these analyses may not be the actual donor of ancestry and instead admixture could be via intermediate and unsampled ‘ghost' populations; in fact, this is suggested by the positioning of the migration edges in the TreeMix graph (Supplementary Figure S5a). Interestingly, the offshore and transient ecotypes were found to group in mitochondrial genome clades with individuals sampled at low latitudes in the Eastern Tropical Pacific that Morin et al. (2015) inferred arose from episodic dispersal between high-latitude ecotypes and low-latitude populations. In contrast, the mitochondrial genomes of the resident ecotype did not group with any other populations (Morin et al., 2015). The relationship between high-latitude ecotypes and low-latitude populations and the influence on the inferences made here deserve further investigation.
Conclusions
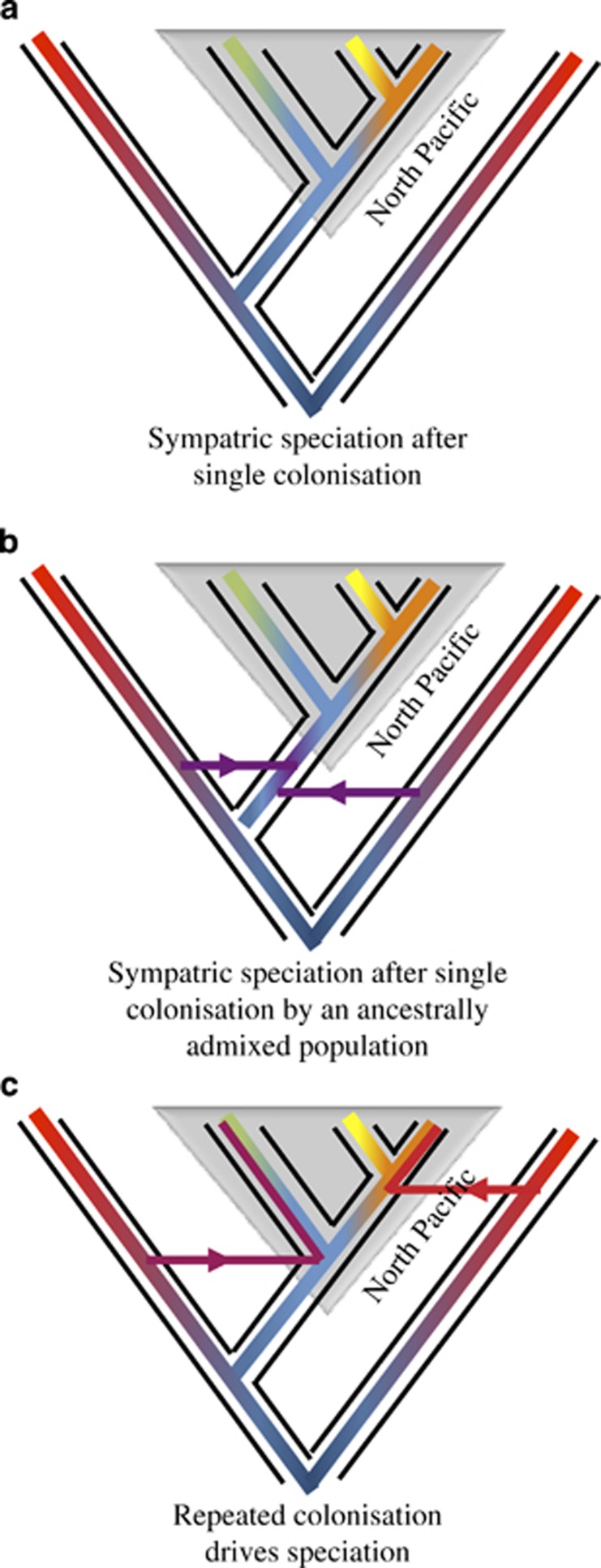
The analyses presented here do not provide unequivocal support for the argument that sympatry among the North Pacific killer whale ecotypes arose following secondary contact, nor do they argue unequivocally against a partially vicariant split within the North Pacific (as proposed by Moura et al., 2015). Our consensus topology does group the three North Pacific ecotypes together. Although this is not conclusive evidence of sympatric divergence, it is consistent with it. Therefore, the three North Pacific ecotypes may share ancestry tracts that coalesce in an ancestral North Pacific population that predates any additional colonisation, or evolutionary divergence, that is, primary contact. However, we find a signal of some ancestral admixture between the resident and transient ecotypes (or groups related to them), and potentially more recent admixture between the transient and offshore ecotypes (or groups related to them) in the STRUCTURE plot. Therefore, the three North Pacific ecotypes likely share ancestry tracts that postdate ecological and evolutionary divergence and result from more recent gene flow, that is, secondary contact. Teasing these two scenarios apart remains a challenge for future studies. Our analyses do however illustrate that multiple evolutionary histories can result in the same topology if modelled as a single bifurcating tree (Figure 4). Thus, we remain unconvinced by the claims of Moura et al. (2015) that their phylogeographic analysis of a single topology reconstructed from concatenated RAD-seq data, which included samples from just two populations outside of the North Pacific, is evidence for the divergence in sympatry of the North Pacific killer whale ecotypes. Instead, we believe that the mode of ecotypic divergence remains an open question and one that we hope will continue to be pursued.
Figure 4.
Three scenarios that could result in a majority-rule phylogeny consistent with sympatric speciation (adapted from Martin et al., 2015). (a) A single randomly mating population colonises the North Pacific and diverges during sympatry (i.e., sympatric speciation, sensu, Gavrilets, 2003). Under this scenario, the three North Pacific ecotypes would be expected to all share a similar proportion of their ancestry with outgroups. (b) colonisation of the North Pacific preceded by admixture with the outgroups followed by a period panmixia would also result in the three North Pacific ecotypes sharing a similar proportion of their ancestry with outgroups; alternatively, colonisation of the North Pacific by a structured meta-population or hybrid swarm (see, for example, Roy et al., 2015) would result in the amount of shared ancestry with outgroups differing among ecotypes. This second scenario would not satisfy the condition of Gavrilets (2003) for sympatric speciation. (c) Repeated colonisation of the North Pacific and episodic admixture upon secondary contact would also result in some North Pacific ecotypes sharing more of their ancestry with the outgroups most closely related to the source population of this secondary colonisation. This scenario would be consistent with the discordance of the mitochondrial and nuclear topologies if introgression was through male-mediated gene flow among matrilineal groups, as mitochondrial haplotypes would become fixed in the descendent lineage given that killer whale populations typically subdivide through matrilineal fission. These three examples are not meant to be exhaustive, but simply illustrative of how different evolutionary histories can result in the same majority-rule topology if evolutionary history is modelled as a single bifurcating tree.
These future studies should incorporate more markers (see, for example, Foote et al., 2016) and include a more representative global sample set (see, for example, Morin et al., 2015). The importance of complete taxon sampling for robust phylogeographical inference has been highlighted for killer whales by Morin et al. (2015) and other species (see, for example, Stervander et al., 2015). Studies on geographic origins of human population splits and ancestry, in particular those incorporating ancient genomes, have highlighted how the geographic distribution of present-day populations is often not indicative of their ancestral geographic distribution (Pickrell and Reich, 2014). Processes that include long-range dispersal followed by population replacement or admixture have greatly transformed the global distribution of human genetic variation (Alves et al., 2016). This complex geographic and genetic ancestry violates many of the assumptions made by simple tree-based phylogeographic approaches that sample the geography and genes of modern populations to infer their ancestral state (Pickrell and Reich, 2014). A focus for future work should be to better understand this complexity and particularly the role of long-range dispersal, secondary contact and subsequent gene flow among sympatric killer whale ecotypes. More broadly, our results strongly indicate that future work on this species, and others where complex ancestry due to long-range migration and ancient admixture are a possibility, can be best served by incorporating a population genomic framework, in addition to the more commonly applied phylogenetic framework.
In a recent review, the Marie Curie Speciation Network (2012) suggested that the classification of speciation mechanisms by geographical context into allopatric, parapatric and sympatry classes was no longer a satisfactory framework. Treating sympatric and allopatric speciation as a dichotomy may be biologically unrealistic, and instead the geographic context of speciation is perhaps best viewed as a graded continuum. The results presented here, although equivocal, hint at the North Pacific killer whale ecotypes falling somewhere along that continuum and their genomes appear to retain ancestry from both sympatric and allopatric periods of their evolutionary history. Whether these sympatric periods were the result of primary or secondary contact remains a challenging question for future studies.
Data archiving
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.803q8.
Acknowledgments
We thank Simon Ho, Martin Stervander, Vitor Sousa, Nagarjun Vijay and Jochen Wolf for helpful discussions on the methods applied here and in the original paper by Moura et al. We thank the two anonymous reviewers for their thoughtful and constructive feedback that greatly improved this manuscript. In this age where social media is playing an ever more important role in science, we also acknowledge the blog posting by Thomas Mailund on estimating admixture (www.mailund.dk) that was very helpful in highlighting how α can be underestimated in the f4-ratio test. Thanks also to Marie Louis and Benoit Simon-Bouhet for the R-script that was used to compare the coordinates of the SNPs in the VCF file with the repeat regions in the bed files.
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)
Supplementary Material
References
- Alves I, Arenas M, Currat M, Hanulova AS, Sousa VC, Ray N et al. (2016). Long-distance dispersal shaped patterns of human genetic diversity in Eurasia. Mol Biol Evol 33: 946–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antao T, Lopes A, Lopes RJ, Beja-Pereira A, Luikart G. (2008). LOSITAN: a workbench to detect molecular adaptation based on a FST-outlier method. BMC Bioinformatics 9: 323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baird NA, Etter PD, Atwood TS, Currey MC, Shiver AL, Lewis ZA et al. (2008). Rapid SNP discovery and genetic mapping using sequenced RAD markers. PLoS One 3: e3376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett-Lennard LG, Ellis GM. (2001) Population Structure and Genetic Variability in Northeastern Pacific Killer Whales: Towards an Assessment of Population Viability. Canadian Science Advisory Secretariat: Ottawa, Canada. [Google Scholar]
- Barluenga M, Stolting KN, Salzburger W, Muschick M, Meyer A. (2006). Sympatric speciation in Nicaraguan crater lake cichlid fish. Nature 439: 719–723. [DOI] [PubMed] [Google Scholar]
- Beaumont MA, Nichols RA. (1996). Evaluating loci for use in the genetic analysis of population structure. Proc R Soc Lond B Biol Sci 263: 1619–1626. [Google Scholar]
- Bolnick DI, Fitzpatrick BM. (2007). Sympatric speciation: models and empirical evidence. Annu Rev Ecol Evol Syst 38: 459–487. [Google Scholar]
- Bouckaert RR. (2010). DensiTree: making sense of sets of phylogenetic trees. Bioinformatics 26: 1372–1373. [DOI] [PubMed] [Google Scholar]
- Bryant D, Bouckaert R, Felsenstein J, Rosenberg NA, Roy-Choudhury A. (2012). Inferring species trees directly from biallelic genetic markers: bypassing gene trees in a full coalescent analysis. Mol Biol Evol 29: 1917–1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burdin A, Hoyt E, Sato H, Filatova O. (2005). Resident and transient-type killer whales, Orcinus orca, in Southeast Kamchatka, Russia. Report to Scientific Committee of the International Whaling Commission, Anchorage. SC/56/SM15.
- Cavalli-Sforza LL. (1973). Analytic review: some current problems of human population genetics. Am J Hum Genet 25: 82–104. [PMC free article] [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Piazza A. (1975). Analysis of evolution: evolutionary rates, independence and treeness. Theor Popul Biol 8: 127–165. [DOI] [PubMed] [Google Scholar]
- Cornuet JM, Pudlo P, Veyssier J, Dehne-Garcia A, Gautier M, Leblois R et al. (2014). DIYABC v2.0: a software to make approximate Bayesian computation inferences about population history using single nucleotide polymorphism, DNA sequence and microsatellite data. Bioinformatics 30: 1187–1189. [DOI] [PubMed] [Google Scholar]
- Coyne J, Orr H. (2004) Speciation. Sinauer Associates: Sunderland, MA, USA. [Google Scholar]
- Dahlheim ME, Schulman-Janiger A, Black N, Ternullo R, Ellifrit D, Balcomb III KC. (2008). Eastern temperate North Pacific offshore killer whales (Orcinus orca: occurrence, movements, and insights into feeding ecology. Mar Mamm Sci 24: 719–729. [Google Scholar]
- Degnan JH, Rosenberg NA. (2009). Gene tree discordance, phylogenetic inference and the multispecies coalescent. Trends Ecol Evol 24: 332–340. [DOI] [PubMed] [Google Scholar]
- De Maio N, Schrempf D, Kosiol C. (2015). PoMo: an allele frequency-based approach for species tree estimation. Syst Biol 64: 1018–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MA, Banks E, Poplin R, Garimella KV, Maguire JR, Hartl C et al. (2011). A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat Genet 43: 491–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dieckmann U, Doebeli M. (1999). On the origin of species by sympatric speciation. Nature 400: 354–357. [DOI] [PubMed] [Google Scholar]
- Drummond AJ, Rambaut A. (2007). BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol Biol 7: 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand EY, Patterson N, Reich D, Slatkin M. (2011). Testing for ancient admixture between closely related populations. Mol Biol Evol 28: 2239–2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durban JW, Fearnbach H, Burrows DG, Ylitalo GM, Pitman RL. (2016). Morphological and ecological evidence for two sympatric forms of Type B killer whale around the Antarctic Peninsula. Polar Biology. doi: 10.1007/s00300-016-1942-x.
- Eaton DAR, Ree RH. (2013). Inferring phylogeny and introgression using RADseq data: an example from flowering plants (Pedicularis: Orobanchaceae). Syst Biol 62: 689–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. (2003). Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. (1981). Skepticism towards Santa Rosalia, or why are there so few kinds of animals? Evolution 35: 124–138. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. (1982). How can we infer geography and history from gene frequencies? J Theor Biol 96: 9–20. [DOI] [PubMed] [Google Scholar]
- Foote AD, Liu Y, Thomas GWC, Vinař T, Alföldi J, Deng J et al. (2015). Convergent evolution of the genomes of marine mammals. Nat Genet 47: 272–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foote AD, Morin PA. (2015). Sympatric speciation in killer whales? Heredity 114: 537–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foote AD, Morin PA, Durban JW, Willerslev E, Orlando L, Gilbert MTP. (2011). Out of the Pacific and back again: insights into the matrilineal history of Pacific killer whale ecotypes. PLoS One 6: e24980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foote AD, Newton J, Piertney SB, Willerslev E, Gilbert MTP. (2009). Ecological, morphological and genetic divergence of sympatric North Atlantic killer whale populations. Mol Ecol 18: 5207–5217. [DOI] [PubMed] [Google Scholar]
- Foote AD, Vijay N, Ávila-Arcos M, Baird RW, Durban JW, Fumagalli M et al. (2016). Genome-culture coevolution promotes rapid divergence of killer whale ecotypes. Nat Commun 7: 11693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford JKB, Ellis GM, Balcomb KC. (2000) Killer Whales: The Natural History and Genealogy of Orcinus orca in British Columbia and Washington State, 3rd edn. UBC Press: Vancouver, BC, Canada. [Google Scholar]
- Ford JKB, Ellis GM, Barrett-Lennard LG, Morton AB, Palm RS, Balcomb KC III. (1998). Dietary specialization in two sympatric populations of killer whales (Orcinus orca in coastal British Columbia and adjacent waters. Can J Zool 76: 1456–1471. [Google Scholar]
- Ford JKB, Ellis GM, Matkin CO, Wetklo MH, Barrett-Lennard LG, Withler RE. (2011. a). Shark predation and tooth wear in a population of northeastern Pacific killer whales. Aquat Biol 11: 213–224. [Google Scholar]
- Ford MJ, Hanson MB, Hemplemann JA, Ayres KL, Emmons CK, Schorr GS et al. (2011. b). Inferred paternity and male reproductive success in a killer whale (Orcinus orca population. J Hered 102: 537–553. [DOI] [PubMed] [Google Scholar]
- Fry JD. (2003). Multilocus models of sympatric speciation: Bush vs Rice vs Felsenstein. Evolution 57: 1735–1746. [DOI] [PubMed] [Google Scholar]
- Gavrilets S. (2003). Models of speciation: what have we learned in 40 years? Evolution 57: 2197–2215. [DOI] [PubMed] [Google Scholar]
- Gavrilets S. (2004) Fitness Landscapes and the Origin of Species. Princeton University Press: Princeton, NJ, USA. [Google Scholar]
- Green RE, Krause J, Briggs AW, Maricic T, Stenzel U, Kircher M et al. (2010). A draft sequence of the Neandertal genome. Science 328: 710–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoelzel AR, Dahlheim M, Stern SJ. (1998). Low genetic variation among killer whales (Orcinus orca in the Eastern North Pacific and genetic differentiation between foraging specialists. J Hered 89: 121–128. [DOI] [PubMed] [Google Scholar]
- Hoelzel AR, Hey J, Dahlheim ME, Nicholson C, Burkanov V, Black N. (2007). Evolution of population structure in a highly social top predator, the killer whale. Mol Biol Evol 24: 1407–1415. [DOI] [PubMed] [Google Scholar]
- Hoelzel AR, Moura AE. (2015). Resource specialisation and the divergence of killer whale populations. Heredity 115: 93–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoelzel AR, Natoli A, Dahlheim ME, Olavarria C, Baird RW, Black NA. (2002). Low worldwide genetic diversity in the killer whale (Orcinus orca: implications for demographic history. Proc R Soc Lond B Biol Sci 269: 1467–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurka J, Kapitonov VV, Pavlicek A, Klonowski P, Kohany O, Walichiewicz J. (2005). Repbase Update, a database of eukaryotic repetitive elements. Cytogenet Genome Res 110: 462–467. [DOI] [PubMed] [Google Scholar]
- Keinan A, Mullikin JC, Patterson N, Reich D. (2007). Measurement of the human allele frequency spectrum demonstrates greater genetic drift in East Asians than in Europeans. Nat Genet 39: 1251–1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knowles L, Carstens B. (2007). Delimiting species without monophyletic gene trees. Syst Biol 56: 887–895. [DOI] [PubMed] [Google Scholar]
- Korneliussen TS, Albrechtsen A, Nielsen R. (2014). ANGSD: analysis of next generation sequencing data. BMC Bioinformatics 15: 356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubatko LS, Degnan JH. (2007). Inconsistency of phylogenetic estimates from concatenated data under coalescence. Syst Biol 56: 17–24. [DOI] [PubMed] [Google Scholar]
- Kutschera VE, Bidon T, Hailer F, Rodi JL, Fain SR, Janke A. (2014). Bears in a forest of gene trees: Phylogenetic inference is complicated by incomplete lineage sorting and gene flow. Mol Biol Evol 31: 2004–2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leaché AD, Harris RB, Rannala B, Yang Z. (2014). The influence of gene flow on species tree estimation: a simulation study. Syst Biol 63: 17–30. [DOI] [PubMed] [Google Scholar]
- Lischer HEL, Excoffier L, Heckel G. (2014). Ignoring heterozygous sites biases phylogenomic estimates of divergence times: implications for the evolutionary history of Microtus voles. Mol Biol Evol 31: 817–831. [DOI] [PubMed] [Google Scholar]
- Lotterhos KE, Whitlock MC. (2014). Evaluation of demographic history and neutral parameterization on the performance of FST outlier tests. Mol Ecol 23: 2178–2192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddison WP, Knowles LL. (2006). Inferring phylogeny despite incomplete lineage sorting. Syst Biol 55: 21–30. [DOI] [PubMed] [Google Scholar]
- Malinsky M, Challis RJ, Tyers AM, Schiffels S, Terai Y, Ngatunga BP et al. (2015). Genomic islands of speciation separate cichlid ecomorphs in an East African crater lake. Science 350: 1493–1498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marie Curie Speciation Network. (2012). What do we need to know about speciation? Trends Ecol Evol 27: 27–39. [DOI] [PubMed] [Google Scholar]
- Martin CH, Cutler JS, Friel JP, Dening CT, Coop G, Wainwright PC. (2015). Complex histories of repeated gene flow in Cameroon crater lake cichlids cast doubt on one of the clearest examples of sympatric speciation. Evolution 69: 1406–1422. [DOI] [PubMed] [Google Scholar]
- Matkin CO, Barrett-Lennard LG, Yurk H, Ellifrit D, Trites A. (2007). Ecotypic variation and predatory behavior among killer whales (Orcinus orca off the eastern Aleutian Islands, Alaska. Fish Bull 105: 74–87. [Google Scholar]
- Mayr E. (1963) Animal Species and Evolution. Belknap: Cambridge, MA, USA. [Google Scholar]
- McKenna A, Hanna M, Banks E, Sivachenko A, Cibulskis K, Kernytsky A et al. (2010). The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res 20: 1297–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morin PA, Archer FI, Foote AD, Vilstrup J, Allen EE, Wade P et al. (2010). Complete mitochondrial genome phylogeographic analysis of killer whales (Orcinus orca indicates multiple species. Genome Res 20: 908–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morin PA, Parsons KM, Archer FI, Ávila-Arcos M, Barrett-Lennard LG, Dalla Rosa L et al. (2015). Geographic and temporal dynamics of a global radiation and diversification in the killer whale. Mol Ecol 24: 3964–3979. [DOI] [PubMed] [Google Scholar]
- Moura AE, Kenny JG, Chaudhuri R, Hughes MA, Welch A, Reisinger RR et al. (2014. a). Population genomics of the killer whale indicates ecotype evolution in sympatry involving both selection and drift. Mol Ecol 23: 5179–5192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moura AE, Kenny JG, Chaudhuri RR, Hughes MA, Reisinger RR, de Bruyn PJ et al. (2015). Phylogenomics of the killer whale indicates ecotype divergence in sympatry. Heredity 114: 48–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nylander JAA, Wilgenbusch JC, Warren DL, Swofford DL. (2008). AWTY (are we there yet?): a system for graphical exploration of MCMC convergence in Bayesian phylogenetics. Bioinformatics 24: 581–583. [DOI] [PubMed] [Google Scholar]
- Parsons KM, Durban JW, Burdin AM, Burkanov VN, Pitman RL, Barlow J et al. (2013). Geographic patterns of genetic differentiation among killer whales in the northern North Pacific. J Hered 104: 737–754. [DOI] [PubMed] [Google Scholar]
- Patterson N, Moorjani P, Luo Y, Mallick S, Rohland N, Zhan Y et al. (2012). Ancient admixture in human history. Genetics 192: 1065–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter BM. (2016). Admixture, population structure and F-statistics. Genetics 202: 1485–1501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Pritchard JK. (2012). Inference of population splits and mixtures from genome-wide allele frequency data. PLOS Genetics 8: e1002967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Reich D. (2014). Toward a new history and geography of human genes informed by ancient DNA. Trends Genet 30: 377–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilot M, Dahlheim ME, Hoelzel AR. (2010). Social cohesion among kin, gene flow without dispersal and the evolution of population genetic structure in the killer whale (Orcinus orca. J Evol Biol 23: 20–31. [DOI] [PubMed] [Google Scholar]
- Pitman RL, Ensor P. (2003). Three forms of killer whales in Antarctic waters. J Cetacean Res Manage 5: 131–139. [Google Scholar]
- Potts AJ, Hedderson TA, Grimm GW. (2014). Constructing phylogenies in the presence of intra-individual site polymorphisms (2ISPs) with a focus on the nuclear ribosomal cistron. Syst Biol 63: 1–16. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. (2000). Inference of population structure using multilocus genotype data. Genetics 155: 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A, Drummond AJ. (2007). Tracer v1.4. Available from http://beast.bio.ed.ac.uk/Tracer.
- Reich D, Thangaraj K, Patterson N, Price AL, Singh L. (2009). Reconstructing Indian population history. Nature 461: 489–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronquist F, Huelsenbeck JP. (2003). MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics 19: 1572–1574. [DOI] [PubMed] [Google Scholar]
- Roy D, Lucek K, Walter RP, Seehausen O. (2015). Hybrid ‘superswarm' leads to rapid divergence and establishment of populations during a biological invasion. Mol Ecol 24: 5394–5411. [DOI] [PubMed] [Google Scholar]
- Saulitis EL, Matkin CO, Barrett-Lennard LG, Heise KA, Ellis GM. (2000). Foraging strategies of sympatric killer whale (Orcinus orca populations in Prince William Sound, Alaska. Mar Mamm Sci 16: 94–109. [Google Scholar]
- Savolainen V, Anstett M-C, Lexer C, Hutton I, Clarkson JJ, Norup MV et al. (2006). Sympatric speciation in palms on an oceanic island. Nature 441: 213–213. [DOI] [PubMed] [Google Scholar]
- Scheirup MH, Hein J. (2000). Consequences of recombination on traditional phylogenetic analysis. Genetics 156: 789–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schliewen UK, Tautz D, Paabo S. (1994). Sympatric speciation suggested by monophyly of crater lake cichlids. Nature 368: 629–632. [DOI] [PubMed] [Google Scholar]
- Smit A, Hubley R, Green P. (1996). RepeatMasker Open-3.0. Available from www.repeatmasker.org.
- Stervander M, Illera JC, Kvist L, Barbosa P, Keehnen NP, Pruisscher P et al. (2015). Disentangling the complex evolutionary history of the Western Palearctic blue tits (Cyanistes spp.)–phylogenomic analyses suggest radiation by multiple colonization events and subsequent isolation. Mol Ecol 24: 2477–2494. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.