Abstract
Purpose:
Clinical success of implant prosthodontics is dependent in part upon the type of implant thread design. The selection of implant thread design plays an important role in the outcome of the treatment. This study was undertaken to evaluate the pattern of stress distribution using a finite element analysis; hence, the area which would be bearing maximum load for a given design would be arrived.
Materials and Methods:
Three implants with different thread designs, namely V-thread, buttress, and reverse buttress thread designs were considered and dimensions were standardized. The site considered was the mandibular molar region with cortical and trabecular bone assuming to be isotropic and homogeneous. The implant modeling was done with the CATIA software. Vertical loads of 100N were applied. The stresses were calculated as Von Mises stress criterion.
Results:
Maximum stresses were seen at the cortical bone and were transferred to the implant. Minimum Von Mises stresses were seen with reverse buttress thread design at the cortical bone. The stresses were observed least at the cancellous bone and maximum at the implant.
Conclusion:
Hence, within the limitations of this study the results obtained can be applied clinically for appropriate selection of implant thread design for a predictable success of implant therapy.
Keywords: Finite element analysis, implant, thread designs
INTRODUCTION
Challenges in partial or complete edentulism have been met by the prosthodontic rehabilitation of the patient by different treatment options such as removable partial dentures, fixed partial dentures, and implant-based restorations. Implants offer brighter prospect owing to the advantages of improved functional efficiency, appearance, comfort, speech, and preservation of hard and soft tissues in the oral cavity.[1]
The significance of biomechanical aspects on the long term success of osseointegrated implants has been emphasized.[2] Assuming this, determining how implant thread designs contribute to stress distribution in the bone under an applied load might be relevant in adapting to suitable clinical decision. Hence, this study determines the contribution of three different thread designs on stress distribution in the bone using a three-dimensional (3D) finite element analysis (FEA).
Finite element method (FEM) is a numerical method of analyzing stresses and deformations in structures of any given geometry. The structure is discretized into the so-called “finite elements” connected through nodes.[3] The 3D FEA is considered as an appropriate method for investigation of stress throughout a structure.[4] 3D FEA is an accepted technique used in the solution of engineering problems and allows the researchers to predict the design feature optimizations.[5]
An important deciding factor for the success or failure of implant-based rehabilitation is the manner in which stresses are transferred through the implant to the surrounding bone, and this is influenced by macroscopic criteria such as the geometry of implant, structural metallurgy of implant, and variations in thread designs and microscopic criteria such as the surface chemistry and microtopography.[6]
Initially developed in the early 1960s to the aerospace industry, FEA was introduced in 1976 to implant dentistry.[3] It is showing overwhelming capability and versatility in its applications in dentistry. A thorough understanding of this phenomenon might lead to a reduction in the undesirable stresses assuring success in implantation.
MATERIALS AND METHODS
Three implants with different thread designs, namely V-thread, buttress, and reverse buttress thread designs with similar dimensions were considered. The site considered was the mandibular molar region with cortical and trabecular bone assuming to be isotropic and homogeneous.[2] ANSYUS program was used to solve the stress analysis problems.
Finite element method
A 3D quantitative analysis requires a mathematical method, making use of a geometric model accurate both in anatomical and physical characteristics, along with the use of a computer, which has become an indispensable aid as far as 3D analysis are concerned. This involves the subdivision or discretization of the structure under consideration into a number of finite sections or elements. These elements are connected at intersections called nodes.[1] A complex structure or continuum so discretized may contain many elements, which can be arranged in two or three dimensions in layers, rather like bricks in a wall. The methods in which the model was created and loads were applied are as follows:
-
Detailed geometry of the bone to be modeled: A 3D FE model was created to analyze the stress distribution in the bone around implants caused by an applied load. This includes application of specialized software for the direct transformation of 3D information in image data from computed tomography (CT) into FEA meshes[1]
In FEA, bone is modeled as isotropic, homogeneous, elastic, and linear material constants of Young's Modulus and Poisson's Ratio[1] listed in Table 1. In an isotropic model, the properties are the same in all directions. The situation was simulated by placing an implant in the first molar region. A layer of cortical bone of 2 mm is modeled around the implant neck, and the body is modeled as being embedded in the medullary bone.[7]
Implant to be modeled: Three implants with different thread designs, namely V-shaped, buttress, and reverse buttress thread designs were considered for the study. The implant modeling was done with the CATIA software. The other geometric variables such as implant length, diameter, and surface composition were not considered. The dimensions standardized were implant length being 12 mm,[6] diameter 4 mm,[6] thread length 0.5 mm,[8] thread pitch 1.2 mm,[9] thread depth 0.42 mm,[10] and thread angulations 45°[10] as depicted in Figure 1.
Boundary conditions: The boundary conditions modeling mandible were set to be fixed[11]
Bone-implant interface: FEA models assume a state of optimal osseointegration, meaning that cortical and cancellous bone is assumed to be perfectly bonded to the implant. The condition of osseointegration was simulated. The implant was rigidly anchored in the bone model along its entire interface.[12]
Table 1.

Figure 1.
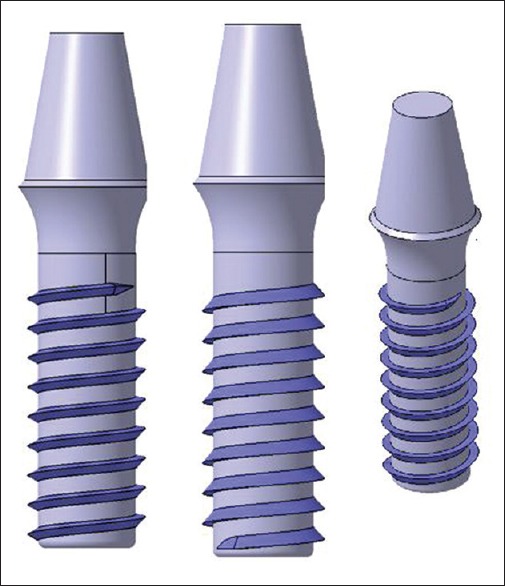
Schematic diagram of modeled V-thread, buttress, and reverse buttress thread designs
Elements and nodes[11]
The models were meshed with modeling software CATIA and the meshing used was Hypermesh. Table 2, represents the number of nodes and elements for each thread design. The modeled implants and modeled bone were meshed. The meshed implant was placed in the meshed bone as in Figure 2.
Table 2.
Number of nodes and elements meshed for each thread design

Figure 2.

Meshed implant, bone, and implant placed in the bone site
Constraints and loads
The software utilized for the study was ANSYS program. About 100N of vertical loads were applied.[8,11]
RESULTS
Results were presented in Von Mises stress criterion. The magnitude of stress distribution was represented with a color spectrum to better visualize mesh phenomena in the models. The colors in descending order are from red-orange-yellow-green-blue, i.e., the red depicts the highest stress and blue lowest. The stress distribution was evaluated within the cortical bone, cancellous bone, and the implant body. The stresses in MPa are listed in Table 3 and depicted in Figures 4–9.
Table 3.
Von Mises stresses on vertical loading

Figure 4.
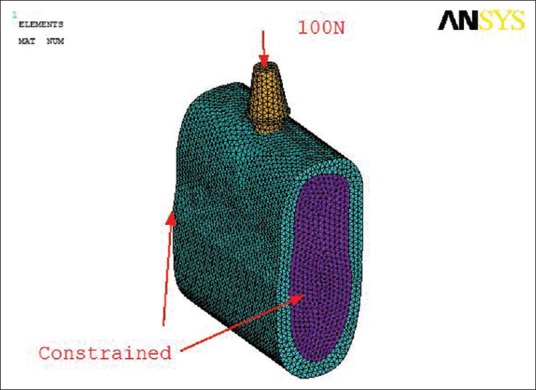
Vertical Loading with boundaries constrained
Figure 9.

Von Mises stress at reverse buttress thread design at the cancellous bone
DISCUSSION
Various methods such as brittle lacquer coatings, strain gauges, photoelasticity, holography, mathematical equations, and analysis using the FEA are used to study stress distribution in various fields.[13] FEA is a basic research tool and is used in dentistry as an initial step and as an aid for planning further laboratory tests and clinical projects that will reduce the inaccuracies.
The slices of a CT scan were assembled into a 3D model by means of the software CATIA modeling where the implants were also modeled according to the standardized parameters as in Figure 1. Then, the models created were hypermeshed with the nodes and elements as in Figure 2 and subjected to software ANSYS[14] for loading as in Figure 4.
Mesh density is another relevant parameter. As the surfaces are curved, increasing the mesh usually improves the results for the discrete model (increasing the accuracy in regions of high-stress gradients). There should be at least 30,000–200,000 elements and nodes. The size of elements must be 150–300 μm.[15]
The model used in this study implied several assumptions regarding the simulated structures. The structures in the model were all assumed to be homogeneous and isotropic and possess linear elasticity. The mechanical properties that are the Elastic Modulus and Poisson's ratio for the investigated materials was standardized. The corresponding elastic properties (E) and Poisson's Ratio were determined from the literature and were summarized in Table 1.
Implant bone interface was 100% that is a state of optimal osseointegration; meaning that cortical and trabecular bone were assumed to be perfectly bonded to the implant.
When the magnitudes of stress were compared between threaded and cylindrical implants, it was seen that maximum Von Mises stress was observed for the threaded implants in D4 bone.[16] The stepped or threaded implants induced greater stresses than the cylindrical shaped implants.[17] Both threaded and stepped designs showed an ability to dissipate interfacial stresses of bone.[18] The reason for this could be that the areas of threads would form the frontline of stress concentration due to sharp line angles located at the sides. The success rate of cylindrical implants in D4 bone was higher than that of the threaded implants. This was attributed to the fact that cylindrical implants generate less lateral force in spongy D4 bone than the threaded implants. The present study hence considers only D2 quality of bone generally seen in the mandibular first molar region and only the threaded implants.
Threads are designed to maximize initial contact, enhance the surface area, and facilitate dissipation of loads at the bone-implant interface. Functional surface area per unit length of the implant may be modified by varying three geometric thread parameters thread pitch, thread shape, and thread depth.[19]
Thread pitch is the distance measured parallel between adjacent thread form features of an implant. Distance from center of the thread to the center of next thread, measured parallel to the axis of a screw is defined as thread pitch.[9] The smaller or finer the pitch, the more threads on the implant body for a given unit length thus the greater surface area per unit length of the implant body if all other factors are equal. Restated, a decrease in the distance between threads will increase the number of threads per unit length. The thread pitch may be used to help resist the forces in poorer quality bone. Therefore, if force magnitude is increased, implant length decreased or bone density decreased, the thread pitch may be decreased to increase the thread number and increase the functional surface area. The functional surface area is defined as the area that actively serves to dissipate compressive loads to the implant-bone interface. Implant geometric body design, length, and bone density are related to the functional surface area.[19]
Thread depth is the distance between the major and minor diameter from the tip of thread to the body. The conventional implant provides a uniform thread depth throughout the length of the implant. Greater the thread depth, greater the surface area of the implant if all other factors are equal.[19] Hence, thread pitch and thread depth were standardized and kept constant.
In an FEA study, implants with 0.5 mm pitch had a more favorable stress distribution than those with a pitch of 1. 0 mm or 1.5 mm and maximum effective stress gradually decreased with decreasing thread pitch. In another FEA study, the thread pitch of 0.18–0.3 mm was considered as optimal from a biomechanical point of view.[10] Hence, in this study thread pitch of 1.2 mm and thread depth of 0.42 mm were standardized[9,10] as in Figure 3.
Figure 3.
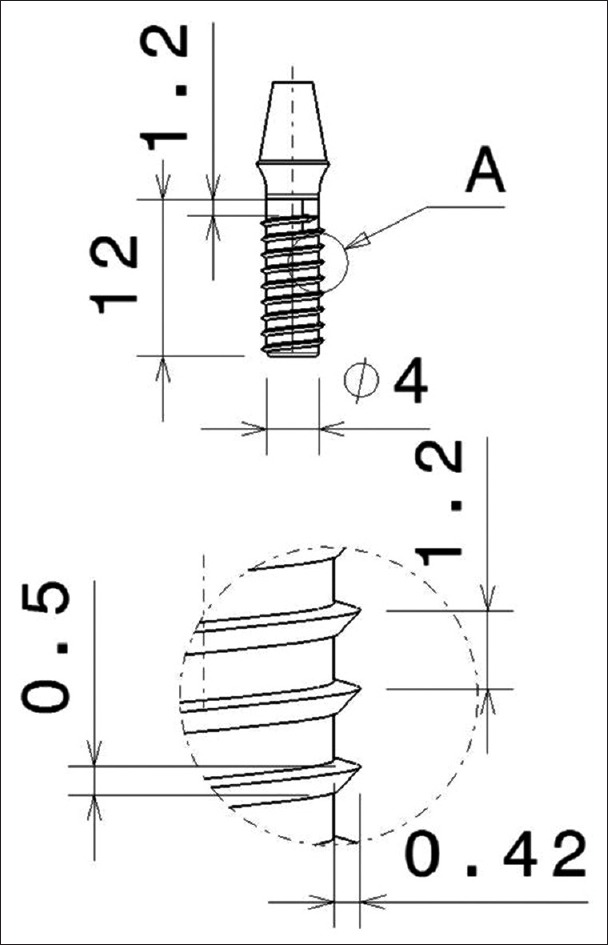
Schematic diagram of dimensions standardized for V-thread, buttress, reverse buttress thread design
As stated by Misch, the ideal implant diameter of 4 mm and implant length of 12 mm for the first mandibular molar was considered in the study.[6]
The thread shape is another characteristic of overall thread geometry. The thread shape in dental implant designs include square, V-shaped, buttress, and reverse buttress thread designs. The square or power thread provides an optimized surface area for intrusive, compressive load transmission. Most automobile jacks or engineering designs built to bear a load use some form of square design.[6]
In conventional engineering applications, the V-thread design is called a fixture and is primarily used for fixating metal parts together. The reverse buttress thread shape was initially designed for pull-out loads by Krupp. This screw design was used to secure cannons to concrete bunkers so that the discharge forces during firing of the cannon would not pull the screws out of the foundation.[6]
It was reported in the literature that stress (compressive) was more evenly distributed in the case when implant thread shape was square.[6] A study done by Mosavar demonstrated the superiority of square thread configuration as it showed the lowest stresses for all degrees of osseointegration in the implant-cortical bone transition region of the square threads.[20] Hence, this study does not consider the square thread and evaluates V-thread, buttress, and reverse buttress thread designs.
Misch states three functions for threads which are to maximize initial contact, enhance the functional surface area, and facilitate dissipations of stress at the interfacial area.[21] Interfacial stress analysis showed that threaded designs lower the stress near the valley of the thread. Moreover, two other clinical advantages can be counted for threaded types which are increased stability and stress-induced bone formation. Threaded designs show a wavy interfacial stress pattern along the implant's surface in the trabecular bone while the cylindrical straight model showed one large high-stress area.
Buttress and reverse buttress thread designs dissipate the stress transfer pathway from a single high-stress area into numerous disconnected areas of bone near the threads tips. Reasons for it being the stress concentration yielded by geometric discontinuity and stress shielding effect. The geometric discontinuity of the threaded designs results in high stress at the valley between the thread pitches. Moreover, in the valley between pitches, the radii were smaller than those on the tip of the thread which increases nonlinear stress on the implant surface. This is known as the stress shielding effect.[22]
High stress in buttress and reverse type of thread designs is primarily transferred through the implant surface of the valley of the thread reducing the stress in the bone near the interface which may improve osseointegration and benefit the threaded implants with greater bone-implant contact.[22]
The other parameters such as the ones mentioned thread pitch, depth, implant diameter, and length were all kept constant so that they do not affect the outcome of the study.
The conventional implant provides a uniform thread depth throughout. The stress was concentrated in the cervical cortical bone region and the highest stress concentration occurred at the region in jaw bone adjacent to the first thread of the implant explaining the high levels of crestal bone loss.[15] Thus, thread designs such as reverse buttress, which showed more compressive stresses, may be considered for bone stimulation.[23]
The study done by Eraslan O, Inan O demonstrated that different thread form designs did not affect the Von Mises stress concentration at supporting bone structure, the results of this study were variable because the loads applied were only axial static occlusal load.[8]
A study done by Anitua and Tapia concluded that maximum stress was located around the neck of the implant and the majority of the stress, independent of the parameter being studied, was distributed in the bone adjacent to the first six threads.[1] In the current study, the observation was that the maximum stress was located up to the first thread and at the neck of the implant.
Another study done by Gonsalves aimed to evaluate the influence of implant with and without thread representation on the outcome of a 2D FEA.[24] Stress distribution in each model as a whole and in cortical bone, trabecular bone, implant, and screw did not seem to be greatly influenced. The maximum Von Mises stress distribution at the cortical bone implant interfaces showed no differences in either model, also in trabecular bone. Showed that stress distribution in the cortical bone is also not greatly affected by implant shape, given similar implant necks and lengths unlike the results obtained in the present study which showed variations with the thread design.[25]
On vertical loading, maximum Von Mises stress was seen at Buttress thread design within the cortical bone as seen in Figure 5 which is not favorable for the bone. At the cancellous bone, maximum Von Mises stress was seen at V-thread design seen in Figure 6 and at the implant at the reverse buttress thread design transferring the stresses along the long axis of the implant seen in Figure 8. Least Von Mises stress at bone is with the reverse buttress thread and maximum at implant with reverse buttress thread design as seen in Figures 7–9 which is favorable for the bone and the implant.
Figure 5.

Von Mises stress at buttress thread design at cortical bone
Figure 6.
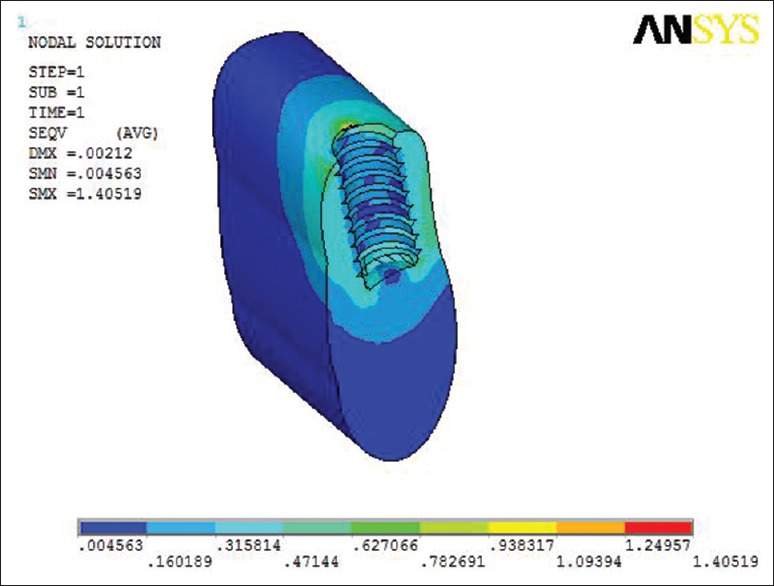
Von Mises stress at V-thread design at the cancellous bone
Figure 8.
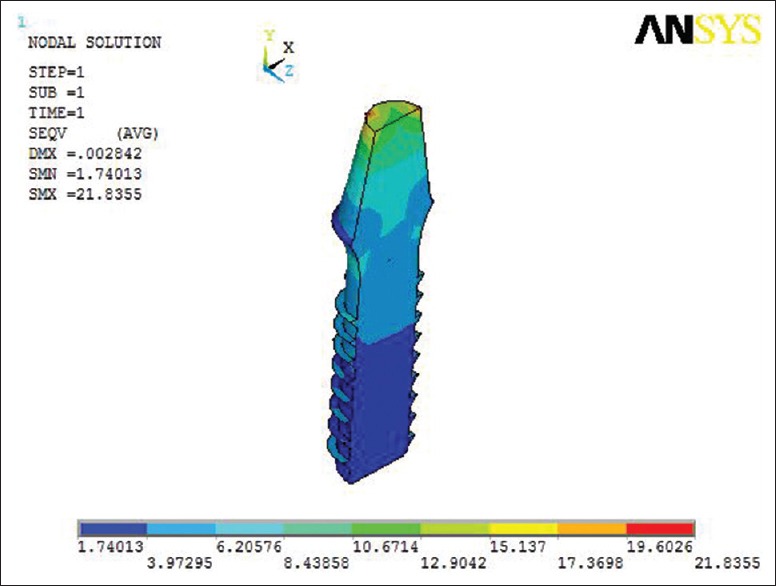
Von Mises stress at reverse buttress thread design at the implant
Figure 7.

Von Mises stress at reverse buttress thread design at the cortical bone
Hence, depending upon the available bone, the thread design can be chosen. Different implant thread forms can produce different stress intensities at the bone structure. Cortical bone and bone structure adjacent to the first thread bears most of the Von Mises stresses. Hence, the present study suggests that in case of good density bone a threaded implant may be considered. If the bone quality is poor than the thread design which will promote compressive stresses and minimize Von Mises stress as inferred the reverse buttress thread design can be chosen for better results. Within the limitations of the study, threads at neck region were not considered and other parameters can be varied and has scope for future research.
Limitations
The present study used the FEM to investigate the influence of implant thread designs on its stress distribution. FEA, originally used in solving engineering problems, is currently often applied in implant biomechanics analyses, contributing to improvements in implant design and prosthetic planning. While computer modeling offers many advantages over other methods in simulating the complexity that characterizes clinical situations, FEA is also sensitive to the assumptions made regarding model parameters, such as material properties and loading and boundary conditions.
FEA is a mathematical in vitro study and may not exactly simulate the clinical situation completely
A state of optimum osseointegration was assumed between cortical bone, cancellous bone, and implant in the model this may not occur clinically
All materials were assumed to be linearly elastic and homogeneous whereas natural bone is viscoelastic, isotrophic, and heterogeneous material
The resultant stress values obtained may not be quantitatively accurate but are generally accepted qualitatively
Chewing forces are dynamic in nature but the loads applied were static loads
In the present study, only a segment of mandible with implant was taken into consideration thus gives only a general insight into tendencies of stress/strain variations under average conditions, without attempting to simulate individual clinical situations
Due to the limitations pertaining to this study, further research regarding 3D FEA combined with long-term clinical evaluation is required.
CONCLUSION
FEA is becoming a common and valid method to advance dental technologies.[26] The outcome of this study will help the dental implant practitioners to predict the success or failure of the implant based on the thread designs for a given quality of bone. Within the limitations of the study it was observed that:
Maximum stresses were seen at the cortical bone compared to the cancellous bone
Stresses which were transferred more to the implant than to the bone promote bone preservation
Minimum Von Mises Stress concentration was seen with reverse buttress thread design at cortical bone which signifies bone preservation
Minimum Von Mises stresses were concentrated by reverse buttress thread design which is favorable for preserving the bone
Stress levels were observed maximum at implant and minimum at the cancellous bone
In view of the above conclusions, it may be inferred that the thread selection depending upon the conditions can bring better results.
This study offers a better understanding of the influence of various implant thread designs on stress distribution. Realistic geometries, material properties, loading conditions, and boundary conditions were considered in this study. The majority of stress characteristics were found to correlate well with the previous studies. Some findings were new and will further help in the appropriate selection of implant thread design.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
REFERENCES
- 1.Anitua E, Tapia R, Luzuriaga F, Orive G. Influence of implant length, diameter, and geometry on stress distribution: A finite element analysis. Int J Periodontics Restorative Dent. 2010;30:89–95. [PubMed] [Google Scholar]
- 2.Teixeira ER, Sato Y, Akagawa Y, Shindoi N. A comparative evaluation of mandibular finite element models with different lengths and elements for implant biomechanics. J Oral Rehabil. 1998;25:299–303. doi: 10.1111/j.1365-2842.1998.00244.x. [DOI] [PubMed] [Google Scholar]
- 3.Geng JP, Tan KB, Liu GR. Application of finite element analysis in implant dentistry: A review of the literature. J Prosthet Dent. 2001;85:585–98. doi: 10.1067/mpr.2001.115251. [DOI] [PubMed] [Google Scholar]
- 4.Clelland NL, Ismail YH, Zaki HS, Pipko D. Three-dimensional finite element stress analysis in and around the Screw-Vent implant. Int J Oral Maxillofac Implants. 1991;6:391–8. [PubMed] [Google Scholar]
- 5.Geng JP, Ma QS, Xu W, Tan KB, Liu GR. Finite element analysis of four thread-form configurations in a stepped screw implant. J Oral Rehabil. 2004;31:233–9. doi: 10.1046/j.0305-182X.2003.01213.x. [DOI] [PubMed] [Google Scholar]
- 6.Misch CE. Contemporary Implant Dentistry. 1st ed. St. Louis, MO: Mosby; 1999. Biomaterials for dental implants; p. 260. [Google Scholar]
- 7.Las Casas EB, Ferreira PC, Cimini CA, Jr, Toledo EM, Barra LP, Cruz M. Comparative 3D finite element stress analysis of straight and angled wedge-shaped implant designs. Int J Oral Maxillofac Implants. 2008;23:215–25. [PubMed] [Google Scholar]
- 8.Eraslan O, Inan O. The effect of thread design on stress distribution in a solid screw implant: A 3D finite element analysis. Clin Oral Investig. 2010;14:411–6. doi: 10.1007/s00784-009-0305-1. [DOI] [PubMed] [Google Scholar]
- 9.Lan TH, Du JK, Pan CY, Lee HE, Chung WH. Biomechanical analysis of alveolar bone stress around implants with different thread designs and pitches in the mandibular molar area. Clin Oral Investig. 2012;16:363–9. doi: 10.1007/s00784-011-0517-z. [DOI] [PubMed] [Google Scholar]
- 10.Tada S, Stegaroiu R, Kitamura E, Miyakawa O, Kusakari H. Influence of implant design and bone quality on stress/strain distribution in bone around implants: A 3-dimensional finite element analysis. Int J Oral Maxillofac Implants. 2003;18:357–68. [PubMed] [Google Scholar]
- 11.Cheng YY, Cheung WL, Chow TW. Strain analysis of maxillary complete denture with three-dimensional finite element method. J Prosthet Dent. 2010;103:309–18. doi: 10.1016/S0022-3913(10)60064-9. [DOI] [PubMed] [Google Scholar]
- 12.Silva GC, Mendonça JA, Lopes LR, Landre J Jr. Stress patterns on implants in prostheses supported by four or six implants: A three-dimensional finite element analysis. Int J Oral Maxillofac Implants. 2010;25:239–46. [PubMed] [Google Scholar]
- 13.Akça K, Iplikçioglu H. Finite element stress analysis of the influence of staggered versus straight placement of dental implants. Int J Oral Maxillofac Implants. 2001;16:722–30. [PubMed] [Google Scholar]
- 14.Nokar S, Baghai Naini R. The effect of superstructure design on stress distribution in peri-implant bone during mandibular flexure. Int J Oral Maxillofac Implants. 2010;25:31–7. [PubMed] [Google Scholar]
- 15.Caglar A, Bal BT, Aydin C, Yilmaz H, Ozkan S. Evaluation of stresses occurring on three different zirconia dental implants: Three-dimensional finite element analysis. Int J Oral Maxillofac Implants. 2010;25:95–103. [PubMed] [Google Scholar]
- 16.Himmlová L, Dostálová T, Kácovský A, Konvicková S. Influence of implant length and diameter on stress distribution: A finite element analysis. J Prosthet Dent. 2004;91:20–5. doi: 10.1016/j.prosdent.2003.08.008. [DOI] [PubMed] [Google Scholar]
- 17.Bevilacqua M, Tealdo T, Menini M, Pera F, Mossolov A, Drago C, et al. The influence of cantilever length and implant inclination on stress distribution in maxillary implant-supported fixed dentures. J Prosthet Dent. 2011;105:5–13. doi: 10.1016/S0022-3913(10)60182-5. [DOI] [PubMed] [Google Scholar]
- 18.Guan H, van Staden R, Loo YC, Johnson N, Ivanovski S, Meredith N. Influence of bone and dental implant parameters on stress distribution in the mandible: A finite element study. Int J Oral Maxillofac Implants. 2009;24:866–76. [PubMed] [Google Scholar]
- 19.Misch CE. Dental Implant Prosthetics. 1st ed. St. Louis, MO: Mosby; 2004. A scientific rationale for dental implant design; pp. 322–43. [Google Scholar]
- 20.Mosavar A, Ziaei A, Kadkhodaei M. The effect of implant thread design on stress distribution in anisotropic bone with different osseointegration conditions: A finite element analysis. Int J Oral Maxillofac Implants. 2015;30:1317–26. doi: 10.11607/jomi.4091. [DOI] [PubMed] [Google Scholar]
- 21.Misch CE. Dental Implant Prosthetics. 3rd ed. Philadelphia: Mosby; 2007. pp. 212–2. [Google Scholar]
- 22.Rismanchian M, Birang R, Shahmoradi M, Talebi H, Zare RJ. Developing a new dental implant design and comparing its biomechanical features with four designs. Dent Res J (Isfahan) 2010;7:70–5. [PMC free article] [PubMed] [Google Scholar]
- 23.Sevimay M, Turhan F, Kiliçarslan MA, Eskitascioglu G. Three-dimensional finite element analysis of the effect of different bone quality on stress distribution in an implant-supported crown. J Prosthet Dent. 2005;93:227–34. doi: 10.1016/j.prosdent.2004.12.019. [DOI] [PubMed] [Google Scholar]
- 24.Assunção WG, Gomes EA, Barão VA, de Sousa EA. Stress analysis in simulation models with or without implant threads representation. Int J Oral Maxillofac Implants. 2009;24:1040–4. [PubMed] [Google Scholar]
- 25.Pierrisnard L, Hure G, Barquins M, Chappard D. Two dental implants designed for immediate loading: A finite element analysis. Int J Oral Maxillofac Implants. 2002;17:353–62. [PubMed] [Google Scholar]
- 26.Chun HJ, Shin HS, Han CH, Lee SH. Influence of implant abutment type on stress distribution in bone under various loading conditions using finite element analysis. Int J Oral Maxillofac Implants. 2006;21:195–202. [PubMed] [Google Scholar]


