The Effects of Population Size Histories on Estimates of Selection Coefficients from Time-Series Genetic Data

Abstract

Many approaches have been developed for inferring selection coefficients from time series data while accounting for genetic drift. These approaches have been motivated by the intuition that properly accounting for the population size history can significantly improve estimates of selective strengths. However, the improvement in inference accuracy that can be attained by modeling drift has not been characterized. Here, by comparing maximum likelihood estimates of selection coefficients that account for the true population size history with estimates that ignore drift by assuming allele frequencies evolve deterministically in a population of infinite size, we address the following questions: how much can modeling the population size history improve estimates of selection coefficients? How much can mis-inferred population sizes hurt inferences of selection coefficients? We conduct our analysis under the discrete Wright–Fisher model by deriving the exact probability of an allele frequency trajectory in a population of time-varying size and we replicate our results under the diffusion model. For both models, we find that ignoring drift leads to estimates of selection coefficients that are nearly as accurate as estimates that account for the true population history, even when population sizes are small and drift is high. This result is of interest because inference methods that ignore drift are widely used in evolutionary studies and can be many orders of magnitude faster than methods that account for population sizes.

Introduction

Methods for inferring the selection coefficient at a single genetic locus from time series data have been employed extensively in evolutionary studies of simple traits. Such methods track the frequency of an allele or Mendelian trait over multiple generations and infer the selection coefficient that best explains the observed frequency changes. Studies of selective pressures conducted using time series approaches have provided evidence for selective forces in natural populations and have helped to characterize the ways in which environmental factors influence evolution through selection (Fisher and Ford 1947; Clarke and Murray 1962; Wall et al. 1980; Lynch 1987; Stine and Smith 1990; Goudsmit et al. 1996; Harrigan et al. 1998; Cook et al. 1999; Haubruge and Arnaud 2001; Bonhoeffer et al. 2002; Reimchen and Nosil 2002; Cook et al. 2005; Labbé et al. 2009).

Because random fluctuations in allele frequencies due to genetic drift are often small compared with changes due to selective pressures, it is common practice for studies to assume that allele frequencies change deterministically over time as they would in a population of infinite size according to well-known deterministic formulas of (Fisher 1922, p. 424) and (Haldane 1927, p. 840) or related expressions (Gillespie 1998; Hartl and Clark 2007). However, because allele frequency trajectories can be heavily influenced by genetic drift when population sizes or selection coefficients are small, many methods have been developed to account for drift by explicitly modeling finite population sizes when inferring selection coefficients from observed allele frequency trajectories (Manly 1985; O’Hara 2005; Bollback et al. 2008; Malaspinas et al. 2012; Mathieson and McVean 2013; Lacerda and Seoighe 2014; Steinrücken et al. 2014; Foll et al. 2015; Ferrer-Admetlla et al. 2015; Schraiber et al. 2016) and when testing hypotheses about selection versus drift (Fisher and Ford 1947; Schaffer et al. 1977; Wilson 1980; Nishino 2013; Feder et al. 2014).

Although it is commonly assumed that estimates of selection coefficients are likely to be improved by accounting for population size histories, the expected amount of improvement is not well characterized. Even in relatively small populations, allele frequencies and other evolutionary processes behave almost deterministically if the selection coefficient or allele frequency is sufficiently high (Rouzine et al. 2001), suggesting that methods that ignore drift might perform well under these conditions. Conversely, if drift is strong allele frequency trajectories can be noisy and the accuracy of methods that ignore drift may be comparable to that of methods that account for population size, as all methods are likely to perform poorly under these conditions (Gallet et al. 2012).

If computationally fast methods that ignore drift are accurate, they could dramatically reduce the time required to infer selection coefficients in data sets with many loci. In addition to their computational efficiency, methods that ignore drift by assuming that the population size is infinite do not require estimates of effective population sizes, which can be difficult to obtain accurately. Moreover, ignoring drift can lead to simple formulas and inference procedures under complicated scenarios involving multiple populations with migration or multiple loci with recombination (Illingworth et al. 2012). Therefore, in light of the beneficial properties of methods that ignore drift and assume deterministic allele frequency trajectories, it is of interest to compare their accuracy to that of methods that account for population size histories.

The theoretical accuracy of methods for inferring selection coefficients can be difficult to derive analytically. Thus, to explore differences between methods that ignore or account for drift, one can take the approach of empirically comparing inferences made by estimators that either account for the true population size history or ignore the size history by assuming that populations are large and drift is negligible. This is the approach we take here. For our analyses, we consider maximum likelihood estimators of selection coefficients because they are typically quite accurate and have desirable statistical properties. Moreover, the majority of recently developed methods for inferring selection coefficients from time series data are maximum likelihood estimators, making them an important category of methods to evaluate.

To draw conclusions about the accuracy of maximum likelihood estimators, it is important to consider estimators based on exact likelihoods rather than approximations, so that differences in estimates can be attributed entirely to whether a method ignores or accounts for drift. Although several approximate approaches have been developed for computing the likelihood of a selection model given time series allele frequency data, only three existing methods compute probabilities that are exact under a widely accepted model. In particular, the methods of Bollback et al. (2008) and Steinrücken et al. (2014) compute exact probabilities under the diffusion approximation of the Wright–Fisher process. However, these methods do not model time-varying population size histories. The third inference method based on an exact likelihood considers time-varying population size histories under the diffusion approximation of the Wright–Fisher process (Schraiber et al. 2016); however, it uses an MCMC algorithm to perform Bayesian inference that is not easily incorporated into a unified inference algorithm that allows us to directly compare inferences made by estimators that model the true population history with those that assume a population of infinite size without drift. No existing method computes the exact probability of an allele frequency trajectory under the discrete Wright–Fisher model, as the matrix powers required for such a method are considered to be computationally inefficient.

Here, we derive the exact probability of an allele frequency trajectory in a population of piecewise constant size under two classical models: the discrete Wright–Fisher model and the diffusion approximation of the Wright–Fisher process. We then use maximum likelihood estimators obtained using these probabilities to explore how ignoring or accounting for the true population history affects estimates of selection coefficients.

Our results are useful for understanding when point estimates obtained using estimators based on deterministic allele frequency trajectories are likely to be accurate and when accounting for the true population history could improve these estimates. Our results have implications for the interpretation of existing estimates of selection coefficients and for the use of deterministic estimators in future studies. The results can also help guide the development of demography-aware estimators of selection coefficients by identifying scenarios under which such estimators are likely to improve inference accuracy.

Results

To compare the performance of estimators that ignore or account for drift, we inferred selection coefficients from allele frequency trajectories simulated under a variety of population histories of time-varying size.

The Population Model

In all of our analyses, we considered a single biallelic locus with alleles labeled a and A evolving under selection and recurrent mutation in a panmictic population comprised of L different epochs $\ell =1,\dots ,L$, each with constant size $N_{\ell }$ diploid individuals (fig. 1). Epoch ℓ corresponds to the time interval $[{\tau }_{\ell -1},{\tau }_{\ell }]$, where time is measured continuously in units of generations and we define ${\tau }_0\equiv 0$. By varying the population sizes $N_{\ell }$ across epochs, it is possible to model a variety of size-change patterns including exponential growth, bottlenecks, and rapidly oscillating population sizes.

Fig. 1.

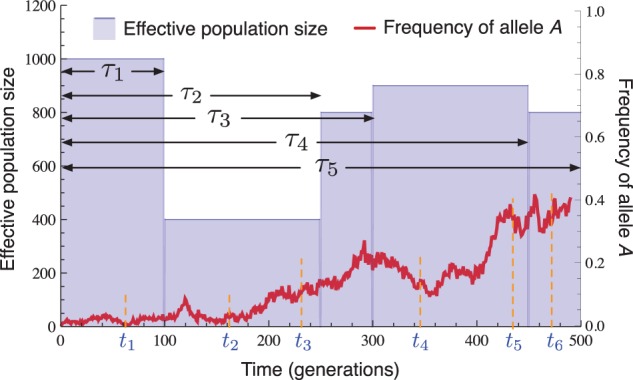
Diagram of the model. An allele at a single locus evolves in a population of piecewise constant size with $L=5$ epochs spanning the time periods $[{\tau }_0,{\tau }_1],\dots ,[{\tau }_{L-1},{\tau }_L]$, where ${\tau }_0\equiv 0$. Samples of sizes $n_1,\dots ,n_k$ haplotypes are taken at times $t_1,\dots ,t_K$.

Within epoch $\ell$, all mutation and selection parameters are assumed to be constant. In particular, we assume that the per-generation probability that allele a mutates to allele A is $u_{aA}^{(\ell )}$ and the per-generation probability that allele A to a is $u_{Aa}^{(\ell )}$. The three possible genotypes, aa, aA, and AA, have relative fitnesses given by $w_{AA}^{(\ell )}=1+s_{\ell },\hspace{0.17em}{w}_{aA}^{(\ell )}=1+h_{\ell }{s}_{\ell }$, and $w_{aa}^{(\ell )}=1$ in epoch $\ell$, where $s_{\ell }$ is the selection coefficient and $h_{\ell }$ is the dominance parameter.

We denote the collection of model parameters in epoch $\ell$ by ${\Theta }_{\ell }$ and the set of parameters across all epochs by Θ. It will also be convenient to denote the value of the model parameters at time t by N_t, $u_{aA}^{(t)},\hspace{0.17em}{u}_{Aa}^{(t)}$, s_t, and h_t, where t is measured continuously in units of generations. The epoch in which time t lies will be denoted by ${\ell }_t$ and the epoch in which sampling event k lies will be denoted by ${\ell }_k$. It will be clear from the context whether the subscript on $\ell$ refers to a time or a sampling event.

We denote the population-wide number of copies of allele A in generation t by c_t and the population-wide frequency of allele A by y_t. In practice, we do not observe the true population count of allele A. Instead, the data consist of observed counts $o_1,\dots ,o_K$ of the number of times allele A is observed in K different samples of sizes $n_1,\dots ,n_K$ haplotypes, taken at times $t_1<\cdots <t_K$. For simplicity, we assume that each sampling time t_k is an integer for $k=1,\dots ,K$. The consecutive observed counts $(o_k,o_{k+1},\dots ,o_{k\prime })$ will be denoted by $o_{[k:k\prime ]}$.

In general, we will denote random variables corresponding to observed quantities using capital letters (e.g., O_k, C_t, and Y_t). The goal is to compute the probability ${\mathbb{P}}_{\Theta }\{O_{[1:K]}=o_{[1:K]}\}$ of the observed data, conditional on the model parameters Θ.

Probabilities of Frequency Trajectories

Several different evolutionary models can be used to describe stochastic allele frequency changes over time in a population. Discrete changes in allele frequency are often modeled using the Wright–Fisher and Moran processes, whereas continuous changes are often modeled using the diffusion approximation of the Wright–Fisher process (Karlin and Taylor 1981; Ewens 2004; Wakeley 2008) or one of several approximations of the diffusion (Feder et al. 2014; Lacerda and Seoighe 2014).

Because it is unclear which model provides the most accurate description of biological evolutionary processes, we take the approach in this paper of deriving exact probabilities of allele frequency trajectories under two different evolutionary models: the discrete Wright–Fisher process and the continuous diffusion approximation.

Under the Wright–Fisher model, the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ of the observed allele counts can be obtained using the recursive formula presented in Procedure 1. Under the diffusion approximation, the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ can be obtained using the recursive formula presented in Procedure 2.

In the “Deterministic allele frequency trajectories under the Wright–Fisher model” and “Deterministic allele frequency trajectories under the diffusion model” sections, we show that if drift is ignored and allele frequencies evolve deterministically, then the probabilities ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ and ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ can be reduced to the simpler approximate probabilities ${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$ and ${\mathbb{P}}_{\Theta ,\mathcal{D}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$ which ignore the population history and which are computed using Procedures 3 and 4, respectively.

Different estimates of the model parameters Θ can be obtained using each of the different probabilities ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\},\hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\},\hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$, and ${\mathbb{P}}_{\Theta ,\mathcal{D}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$ by finding the value of Θ that maximizes the given probability of the observed allele counts $o_{[1:K]}$. In our analyses, we estimated the model parameters Θ separately using each of the different probabilities, yielding the estimators ${\hat{s}}_{\mathcal{W}},\hspace{0.17em}{\hat{s}}_{\mathcal{D}},\hspace{0.17em}{\hat{s}}_{\mathcal{W}}^{\infty }$, and ${\hat{s}}_{\mathcal{D}}^{\infty }$. The estimator ${\hat{s}}_{\mathcal{W}}$ accounts for drift under the discrete Wright–Fisher model, whereas drift in this model is ignored by the estimator ${\hat{s}}_{\mathcal{W}}^{\infty }$. Similarly, the estimator ${\hat{s}}_{\mathcal{D}}$ accounts for drift under the diffusion model, whereas drift in this model is ignored by the estimator ${\hat{s}}_{\mathcal{D}}^{\infty }$.

The degree to which accounting for drift can improve estimates of selection coefficients can be investigated by comparing ${\hat{s}}_{\mathcal{W}}$ to ${\hat{s}}_{\mathcal{W}}^{\infty }$ on trajectories simulated under the discrete Wright–Fisher model and by comparing ${\hat{s}}_{\mathcal{D}}$ to ${\hat{s}}_{\mathcal{D}}^{\infty }$ on trajectories simulated under the diffusion approximation.

Procedure 1. Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$

1: Define the quantities ${\mathbf{d}}_0=\left(\mathbb{P}\right\{C_0=0\},\mathbb{P}\{C_0=1\},\dots ,\mathbb{P}\{C_0=2N_{t_0}\left\}\right)$ and $\gamma \left(o_1\right)$, where $\gamma \left(o_k\right)=\left({\gamma }_0\right(o_k),{\gamma }_1(o_k),\dots ,{\gamma }_{2N_{t_k}}(o_k\left)\right)$ with ${\gamma }_i\left(o_k\right)=\left(\begin{array}{c}{n}_k\\ o_k\end{array}\right){(i/2N_{t_k})}^{o_k}{(1-i/2N_{t_k})}^{n_k-o_k}$.

2: Initialize ${\mathbf{v}}_1={\mathbf{d}}_0\left[\prod _{t=1}^{t_1}{\mathbf{T}}_{t-1,t}\right]\text{diag}\{\gamma (o_1\left)\right\}$.

3: For $k=2:K$, compute

$${\mathbf{v}}_k={\mathbf{v}}_{k-1}\left[\prod _{t=t_{k-1}+1}^{t_k}{\mathbf{T}}_{t-1,t}\right]\text{diag}\{\gamma (o_k\left)\right\}.$$

4: Compute ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}=\sum _{i=0}^{2N_{t_K}}{v}_{K,i}.$

______________________________________________________________________________________________

Modifications:

 If ${\mathbf{d}}_0$ is unspecified, omit Step 1and set ${\mathbf{v}}_1=\gamma \left(o_1\right)/2N_{t_1}$ in Step 2.

 If conditioning on the event S_K that allele A is segregating in the final sample, omit Step 4 and instead compute ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$ using equation(C.1).

Procedure 2. Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{O_{[1:K]}\right\}$

1: For an initial starting frequency y₀ initialize

$${\mathbf{b}}_0={\mathbf{C}}_{{\ell }_1}^{-1}{\mathbf{B}}_{{\ell }_1}\left(y_0\right),$$

where ${\mathbf{B}}_{\ell }\left(y_0\right)$ is the vector of eigenfunctions of the diffusion operator given inequation (A.14) and ${\mathbf{C}}_{\ell }=\text{diag}{\{\langle B_{\ell ,i},B_{\ell ,i}\rangle \}}_{i=0}^{\infty }$ is given in equation (A.18).

2: For $k=1:K$, compute

$${\mathbf{a}}_k = \{\begin{array}{cc}{\mathbf{b}}_{k-1}{\mathbf{E}}_{{\ell }_k}(t_k-t_{k-1})\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{k-1}={\ell }_k,\hfill \\ {\mathbf{b}}_{k-1}\mathbf{F}(t_{k-1},t_k;\zeta )\hfill & \hspace{0.17em}\text{otherwise},\hfill \end{array}$$

and

$${\mathbf{b}}_k={\mathbf{a}}_k{\mathbf{W}}_{{\ell }_k}{\mathbf{G}}_{{\ell }_k}^{o_k}{(1-{\mathbf{G}}_{{\ell }_k})}^{n_k-o_k}{\mathbf{W}}_{{\ell }_k}^{-1},$$

where the matrices ${\mathbf{E}}_{\ell }\left(t\right),\hspace{0.17em}\mathbf{F}(t_{k-1},t_k;\zeta ),\hspace{0.17em}{\mathbf{W}}_{\ell }$, and ${\mathbf{G}}_{\ell }$ are given byequations (A.17), (B.10), (A.15), and (A.11), respectively, and ζ is the set of Chebyshev nodes in the interval $[0,1]$. The matrix inverse ${\mathbf{W}}_{\ell }^{-1}={\mathbf{D}}_{\ell }{\mathbf{W}}_{\ell }^T{\mathbf{C}}_{\ell }^{-1}$ is computed easily using the diagonal matrices ${\mathbf{C}}_{\ell }$ and ${\mathbf{D}}_{\ell }$ in equations (A.18) and (A.19).

3: Compute

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}=\frac{c_{{\ell }_K,0}}{B_{{\ell }_K,0}\left(0\right)}{b}_{K,0},$$ (1)

where $c_{{\ell }_K,0}=\langle B_{\ell ,0},B_{\ell ,0}\rangle ={\left[C_{{\ell }_K}\right]}_{0,0}$ is the (0, 0) element of matrix ${\mathbf{C}}_{\ell }$ in equation (A.18) and $B_{{\ell }_K,0}\left(0\right)$ is the 0^th element of the vector ${\mathbf{B}}_{{\ell }_K}\left(0\right)$ in equation (A.14).

______________________________________________________________________________________________

Modifications:

 If y₀ is unspecified, omit Step 1 and initialize ${\mathbf{b}}_1$ using equation (B.17). Then iterate over $k=2:K$ in Step 2.

 If conditioning on the event S_K that allele A is segregating in the final sample, omit Step 3 and instead compute ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$ using equation (D.1).

Procedure 3. Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$

1: Starting with $y_0^{\infty }=y_0$, for $t=0,\dots ,t_K-1$,

Compute ${\tilde{y}}_t^{\infty }=u_{aA}^{(t)}+(1-u_{Aa}^{(t)}-u_{aA}^{(t)})y_t^{\infty }$.

Compute

$$y_{t+1}^{\infty }=\left[\frac{{({\tilde{y}}_t^{\infty })}^2(1+s_t)+{\tilde{y}}_t^{\infty }(1-{\tilde{y}}_t^{\infty })(1+h_t{s}_t)}{{\overline{w}}_t}\right],$$

where ${\overline{w}}_t={({\tilde{y}}_t^{\infty })}^2(1+s_t)+2{\tilde{y}}_t^{\infty }(1-{\tilde{y}}_t^{\infty })(1+h_t{s}_t)+{(1-{\tilde{y}}_t^{\infty })}^2$.

2: Compute

$${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}=\prod _{k=1}^K(\begin{array}{c}{n}_k\\ o_k\end{array}){(y_{t_k}^{\infty })}^{o_k}{(1-y_{t_k}^{\infty })}^{n_k-o_k}.$$

______________________________________________________________________________________________

Modifications:

 If y₀ is unspecified, set $△y=1/M$ for a large value M and repeat Steps 1 and 2 for the dense uniform grid of M + 1 values $y_0\in [0,△y,2△y,\dots ,1]$. Set ${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}=\frac{1}{M+1}\sum _{j=0}^M{\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]};y_0=j△y\}$.

Procedure 4. Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$

1: Fix a large integer n and set $\Delta t=1/n$.

2: Starting with $y_0^{\infty }=y_0$, for $j=0,\dots ,n{t}_K-1$, compute

$$y_{(j+1)\Delta t}^{\infty }=\{u_{aA}^{(j△t)}-(u_{aA}^{(j△t)}+u_{Aa}^{(j△t)})y_{j\Delta t}^{\infty } +y_{j\Delta t}^{\infty }(1-y_{j\Delta t}^{\infty })[(1-2y_{j△t}^{\infty })h_{j△t}{s}_{j△t}+y_{j\Delta t}^{\infty }{s}_{j△t}] \}\Delta t.$$

3: Compute

$${\mathbb{P}}_{\Theta ,\mathcal{D}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}=\prod _{k=1}^K(\begin{array}{c}{n}_k\\ o_k\end{array}){(y_{t_k}^{\infty })}^{o_k}{(1-y_{t_k}^{\infty })}^{n_k-o_k}.$$

______________________________________________________________________________________________

Modifications:

 If y₀ is unspecified, set $△y=1/M$ for a large value M and repeat Steps 1 and 2 for the dense uniform grid of M + 1 values $y_0\in [0,△y,2△y,\dots ,1]$. Set ${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}=\frac{1}{M+1}\sum _{j=0}^M{\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]};y_0=j△y\}$.

Overview of the Experimental Design

We simulated allele frequency trajectories under a variety of selection strengths and piecewise constant population histories reflecting demographic patterns such as exponential growth, bottlenecks, rapid population size oscillations, and constant histories. We then compared the demography-aware estimates ${\hat{s}}_{\mathcal{W}}$ and ${\hat{s}}_{\mathcal{D}}$ with the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{D}}^{\infty }$ that ignore drift to study the degree to which accounting for population size can improve the accuracy of inferences.

Expected Allele Frequency Trajectories

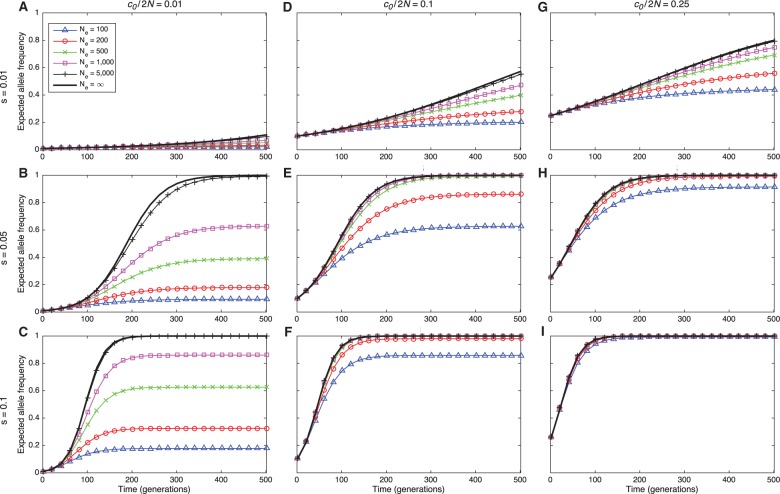
Before comparing the accuracy of the different estimators, we first explored the degree to which trajectories that ignore drift differ from trajectories that account for drift resulting from finite population sizes. Figure 2 shows the expected frequency of allele A in a discrete Wright–Fisher population of constant size for several different initial allele frequencies, selection coefficients, and effective population sizes. Figure 2 illustrates that, for any starting frequency and selection coefficient, the mean allele frequency trajectory approaches the mean trajectory in a population without drift (i.e., in a population of infinite size), as the true population size increases. Moreover, if the initial frequency is sufficiently high, the expected trajectory is close to its deterministic limit even when the population size is small and drift is high.

Fig. 2.

Expected Wright–Fisher trajectories of allele A for different initial starting counts c₀, selection coefficients s, and effective population sizes N. Columns correspond to different initial starting frequencies $c_0/2N$ with $c_0/2N=0.01,0.1,$ and 0.25. The dominance parameter is set to h = ½ in all panels. Because the effects of mutation are negligible during the time periods we consider, we set $u_{Aa}=u_{aA}=0$.

From figure 2, it can be seen that an effective population size of several thousand individuals is often sufficiently large to produce deterministic behavior, even when the selection coefficient and initial allele frequency are small. Thus, selection coefficient inference methods that ignore drift are likely to be accurate for a broad range of population sizes and selection coefficients. As we will see, methods that ignore drift can be almost as accurate as methods that account for drift, even within the small-parameter-value regime.

Inference Accuracy for Populations of Constant Size

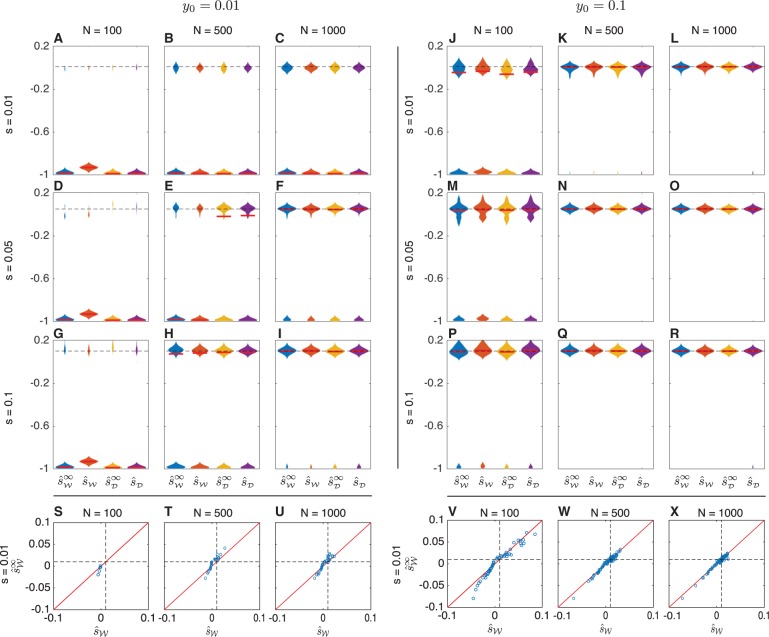
To explore how accounting for drift affects inference accuracy, we first considered the accuracy of inferring selection coefficients in a population of constant finite size. Figure 3 shows the maximum likelihood estimate (MLE) of the selection coefficient for three different effective population sizes (N = 100, 500, 1000), three selection coefficients $(s=0.01,0.05,0.1)$, and two initial allele frequencies $(y_0=0.01,0.1)$ for h = ½. In each of panels A-R, the violin plots summarize the maximum likelihood estimates for 100 different simulation replicates in which an allele frequency trajectory was simulated for 500 generations with samples of size n = 50 taken at generations $t=$50, 100, 150, 200, 250, 300, 350, 400, 450, and 500.

Fig. 3.

Maximum likelihood estimates of the selection coefficient s in populations of constant size. For each of three different selection coefficients ($s=0.01,0.05,0.1$) and effective population sizes (N = 100, 500, 1000), 100 allele frequency trajectories were simulated for 500 generations under the either the Wright–Fisher or diffusion models. Samples of 50 alleles were taken at times 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500 generations. Bars in panels A-R indicate medians. Dashed lines indicate true selection coefficients. The maximum width of each violin plot is scaled to the same value for all estimators. Scatter plots S, T, U, V, W, and X compare the estimates ${\hat{s}}_{\mathcal{W}}$ with the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ using the same data shown in the top modes of the distributions in Panels A, B, C, J, K, and L for the case s = 0.01. Diagonal lines in these scatter plots indicate the line ${\hat{s}}_{\mathcal{W}}^{\infty }={\hat{s}}_{\mathcal{W}}$. Bimodal violin plots are due to the fact that allele frequency trajectories typically fall into one of two categories: trajectories in which allele A is lost quickly, resulting in a strong negative estimate of the selection coefficient, and trajectories in which allele A remains segregating long enough to allow a more accurate estimate of the selection coefficient.

For the discrete Wright–Fisher model, allele frequency trajectories were simulated by sampling the allele frequency in each generation from the vector of transition probabilities, conditional on the frequency in the previous generation using Procedure 5. Under the diffusion model, trajectories were sampled using the approach in Procedure 6. Maximum likelihood estimates were obtained for the Wright–Fisher trajectories using the grid search described in Procedure 7 over the likelihoods computed using Procedures 1 and 3, and maximum likelihood estimates for the diffusion trajectories were obtained using the same grid search approach over the likelihoods computed using Procedures 2 and 4. In each panel in figure 3, the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{W}}$ were computed for the same set of 100 allele frequency trajectories simulated under the discrete Wright–Fisher model and the estimates ${\hat{s}}_{\mathcal{D}}^{\infty }$ and ${\hat{s}}_{\mathcal{D}}$ were computed for the same set of 100 allele frequency trajectories simulated under the diffusion model.

By comparing the estimates computed accounting for drift with the estimates obtained ignoring drift, it can be seen that all methods have similar accuracies. All methods perform well when the population size, selection coefficient, and initial frequency are sufficiently large (e.g., fig. 3I for the case $y_0=0.01$ and Panels 3K through 3R for the case $y_0=0.1$), and all methods have reduced accuracy, otherwise. To put this another way: the allele frequency trajectories for which selection coefficients are inferred accurately by demography-aware methods correspond to those for which the deterministic estimates are also accurate. Thus, methods that ignore or account for drift are likely to produce estimates with similar accuracy.

Moreover, it can be seen from the scatter plots (Panels 3S–3X), which compare the estimators ${\hat{s}}_{\mathcal{W}}$ and ${\hat{s}}_{\mathcal{W}}^{\infty }$, that the point estimates themselves are very similar for both the demography-aware and deterministic methods. Although this similarity may be expected given that the deterministic methods differ from the demography-aware methods only in that they ignore the additional variability in the allele frequencies arising from genetic drift, it is surprising that the point estimates are so similar, as the overall expected allele frequency trajectory in the deterministic case can differ considerably from the expected trajectory accounting for drift (fig. 2A–C).

As the magnitude of the selection coefficient decreases, the point estimates of the deterministic and demography-aware estimators remain well correlated, although the accuracy of all methods decreases. This can be seen in figure 3S–X and in supplementary fig. S1, Supplementary Material online in which the estimates by the different methods remain correlated, but become more variable as the selection coefficient s decreases and an increasingly large number of trajectories drift out of the population quickly, leading to strong negative estimates of selection coefficients by both methods.

Inference Accuracy in Populations of Piecewise Constant Size

We next explored the degree to which accounting for more complicated population histories can improve maximum likelihood estimates, focusing on three scenarios, a population with a bottleneck, a population undergoing exponential growth, and a population undergoing rapid oscillations in size. Under each scenario, we simulated 100 allele frequency trajectories for an allele with selection coefficient s = 0.05, dominance parameter h = ½, and initial frequency $y_0=0.1$ under the Wright–Fisher model and separately under the diffusion model. The parameter values in these simulations were chosen so that drift would be strong enough to affect allele frequency trajectories, but not strong enough to result in poor estimates of selection coefficients by the full-likelihood methods.

In addition to comparing estimates made by the deterministic estimators, ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{D}}^{\infty }$, with those of the exact estimators, ${\hat{s}}_{\mathcal{W}}$ and ${\hat{s}}_{\mathcal{D}}$, that account for the true time-varying population history, we investigated the effect on accuracy of using crude, yet reasonable estimates of the population history. In particular, we also inferred selection coefficients using likelihoods computed using variants of Procedures 1 and 2 in which the population was assumed to consist of a single epoch of constant size equal to the Watterson estimate (Watterson 1975, Eqn. 1.4a; Hein et al. 2005, p.62). The Watterson estimate was obtained by computing the expected site frequency spectrum (SFS) for the multi-epoch model for a sample size of 20 alleles using the method of Kamm et al. (2016) and then inferring the effective size of a single epoch using Watterson’s estimator (Computing the Watterson estimator of N_e from the expected SFS of a piecewise constant population). The discrete Wright–Fisher and diffusion estimators based on the Watterson estimate of effective size are denoted by ${\hat{s}}_{\mathcal{W}}^{N_e}$ and ${\hat{s}}_{\mathcal{D}}^{N_e}$, respectively.

The Case of a Bottleneck

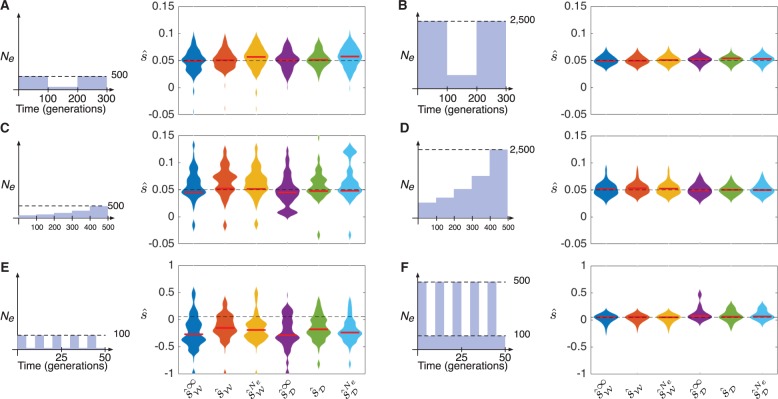
To model populations with bottlenecks, we considered populations composed of three epochs, each of length 100 generations, with sizes N₁, N₂, and N₃ satisfying $N_1=N_3=5N_2$. Samples of size 50 were taken at times $50,\hspace{0.17em}100,\hspace{0.17em}150,\hspace{0.17em}200,\hspace{0.17em}250$, and 300. Figure 4A and B shows the results for two different populations; in the population in figure 4A, we set $N_1=500$ and in the population in figure 4B we set $N_1=2500$.

Fig. 4.

Maximum likelihood estimates of the selection coefficient s in populations with a bottleneck, exponential growth, or rapidly oscillating population size. In each panel, the trajectory of an allele with selection coefficient s = 0.05, dominance parameter h = ½, and starting frequency $y_0=0.1$ was simulated 100 times under the Wright–Fisher and diffusion models. Bars indicate medians. Dashed lines indicate the true selection coefficient. The maximum width of each violin plot is scaled to the same value for all estimators.

From figure 4A and B, it can be seen that all methods performed similarly. However, the deterministic estimators had significantly lower bias than the full-likelihood estimators computed using the mis-specified population history for a bottleneck of size $N_2=100$ with $N_1=N_3=500$ (fig. 4A). In the case of the bottleneck in figure 4A, the means of the deterministic estimators ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{D}}^{\infty }$ were not significantly different from the true selection coefficient s (P = 0.59 and P = 0.93 for t-tests of the null hypotheses $\text{mean}({\hat{s}}_{\mathcal{W}}^{\infty })=s$ and $\text{mean}({\hat{s}}_{\mathcal{D}}^{\infty })=s$ versus the alternative hypotheses $\text{mean}({\hat{s}}_{\mathcal{W}}^{\infty })\ne s$ and $\text{mean}({\hat{s}}_{\mathcal{D}}^{\infty })\ne s$). In comparison, the means of the full likelihood estimators ${\hat{s}}_{\mathcal{W}}^{N_e}$ and ${\hat{s}}_{\mathcal{D}}^{N_e}$ with mis-specified histories were significantly different from s (P = 0.03 and P < 0.01, respectively). A similar trend was observed for the bottleneck history with larger sizes shown in figure 4B (P = 0.64 and P = 0.12 for t-tests of the null hypotheses $\text{mean}({\hat{s}}_{\mathcal{W}}^{\infty })=s$ and $\text{mean}({\hat{s}}_{\mathcal{D}}^{\infty })=s$, compared with P = 0.13 and P = 0.01 for t-tests of the null hypotheses $\text{mean}({\hat{s}}_{\mathcal{W}}^{N_e})=s$ and $\text{mean}({\hat{s}}_{\mathcal{D}}^{N_e})=s$). Note that, despite the tight bottleneck in figure 4A, inferences were still relatively accurate due to the larger sizes of epochs 1 and 3.

The Case of Exponential Growth

To model exponential growth, we considered populations composed of five epochs, each of length 100 generations, with effective population sizes chosen to represent 5-fold exponential growth across all five epochs. Specifically, the size in epoch ℓ was set to $N_{\ell }=N_0{e}^{\eta {\tau }_{\ell }}$, where we chose $N_0=100$ and the growth constant η was chosen such that $e^{\eta {\tau }_5}=5$. Samples of size 50 were taken in generations 100, 200, 300, 400, and 500. From the results in figure 4C and D, it can be seen that all methods performed with similar accuracy in the growth scenario.

The Case of Rapidly Oscillating Population Size

Figure 4E and F shows inferences of the selection coefficient in a population with rapidly oscillating size. Such demographic histories, which are often seen in insect populations like Drosophila, have moderate arithmetic mean sizes, but small harmonic mean sizes and experience episodes of extreme drift.

In the simulations shown in figure 4E, the population size oscillates rapidly between 10 and 100 diploids every five generations. In the simulations shown in figure 4F, the population size oscillates between 100 and 500 diploids every five generations. From figure 4, it can be seen that the methods that ignore drift have similar accuracy to the methods that account for drift. However, the methods that account for drift are slightly less biased when the population size oscillates between very small values (fig. 4E) (P = 0.017 and P = 0.012, respectively, for the one-tailed t-tests of the null hypotheses ${\hat{s}}_{\mathcal{W}}^{\infty }\ge {\hat{s}}_{\mathcal{W}}$ and ${\hat{s}}_{\mathcal{D}}^{\infty }\ge {\hat{s}}_{\mathcal{D}}$ versus the alternative hypotheses ${\hat{s}}_{\mathcal{W}}^{\infty }<{\hat{s}}_{\mathcal{W}}$ and ${\hat{s}}_{\mathcal{D}}^{\infty }<{\hat{s}}_{\mathcal{D}}$).

Conditioning on Segregation in the Final Sample

It is sometimes of interest to infer the selection coefficient of an allele, conditional on the event that the allele is segregating in the most recent sample. Such conditional inferences are useful if alleles are ascertained in present-day samples and their historical trajectories are subsequently investigated.

Conditioning on segregation in the final sample is also useful for estimating weak positive selection coefficients when initial allele frequencies are low. This is because a large fraction of weakly selected alleles with low initial frequencies will drift out of the population quickly resulting in large negative estimates of their selection coefficients. However, more accurate estimates can be obtained for the subset of alleles that are not lost quickly, which can be seen, for example, in figure 3B–I through I in which the part of the density corresponding to alleles that are not lost quickly from the population is localized around the true selection coefficient.

Considering only alleles that are segregating in the final sample can lead to biased estimates of selection coefficients if likelihood methods do not properly condition on segregation. For example, weakly selected alleles typically drift out of small populations quickly. Thus, weakly selected alleles that escape loss and ultimately fix generally exhibit faster-than-expected increases in frequency that are similar to the unconditional trajectories of alleles under stronger selection. Thus, if a likelihood method does not properly account for conditioning, weakly selected alleles that are segregating in the final sample will have inflated inferred selection coefficients.

Estimators that ignore drift cannot be modified to condition on the event of segregation in the final sample because they implicitly assume that alleles follow fixed trajectories whose long-term behavior in the absence of mutation is entirely determined by the selection coefficient: fixation for positively selected alleles and loss for negatively selected alleles. Thus, estimators that ignore drift are expected to produce biased estimates of selection coefficients when applied to conditioned trajectories.

In contrast, the allele frequency trajectories in likelihood methods that account for the population size are modeled stochastically, allowing likelihoods to be modified to condition on segregation in the final sample. It is expected that methods that account for the true population size can be modified to produce accurate estimates of selection coefficients, whereas methods that ignore drift will necessarily produce biased estimates.

Simulations Conditioning on Segregation

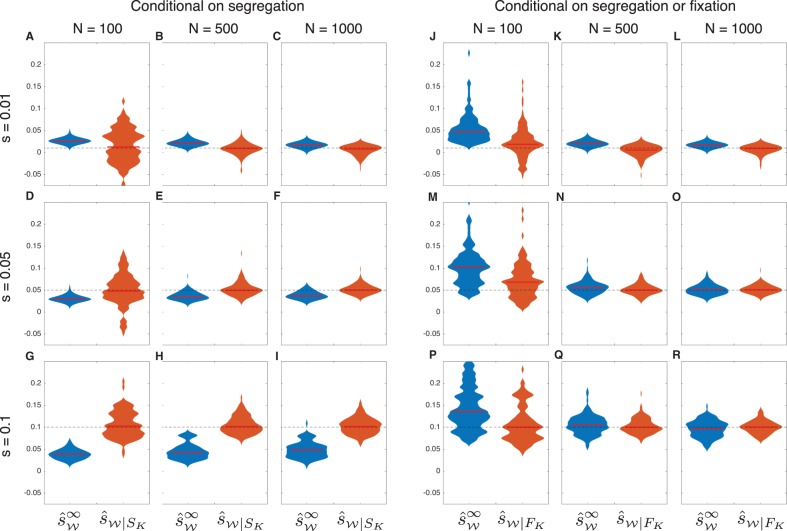
To investigate the degree to which accounting for drift can improve estimates of selection coefficients when allele frequency trajectories are conditioned on segregation in the final sample, we modified the discrete Wright–Fisher probability in Procedure 1 to compute the likelihood conditional on segregation in the final sample using results derived in the “Conditional Probabilities” section. Under a grid search, this modified likelihood yields the conditional maximum likelihood estimator ${\hat{s}}_{\mathcal{W}|S_K}$. We compared the estimates computed using the exact conditional estimator ${\hat{s}}_{\mathcal{W}|S_K}$ with estimates computed using the approximate estimator ${\hat{s}}_{\mathcal{W}}^{\infty }$ that ignores drift and cannot be modified to account for conditional allele frequency trajectories.

The effect of failing to account for conditioning is evident in the violin plots in figure 5A–I corresponding to the unconditional approximate maximum likelihood estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$. As expected, when the true selection coefficient is small ($s\le 0.01$), the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ are biased upward. Conversely, when the selection coefficient is larger ($s\ge 0.05$), the approximate estimator ${\hat{s}}_{\mathcal{W}}^{\infty }$ produces negatively biased estimates because alleles under strong positive selection that remain segregating in the final sample show slower-than-expected increases in frequency. In contrast to the estimator ${\hat{s}}_{\mathcal{W}}^{\infty }$, the bias is negligible in the estimator ${\hat{s}}_{\mathcal{W}|S_K}$, which accounts for drift and properly conditions on segregation in the final sample.

Fig. 5.

Estimates of selection coefficients, conditional on segregation. Each violin plot was computed using 100 frequency trajectories sampled over 500 generations for an allele with initial frequency $y_0=0.01$. As in figure 3, samples of size n = 50 were taken in generations 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500. In Panels A–I, trajectories were sampled conditional on the event that the selected allele was segregating in the final sample. In Panels J–R, trajectories were sampled conditional on the event that the selected allele was either segregating or fixed in the final sample. Red bars indicate medians. Dashed lines indicate the true selection coefficients. The maximum width of each violin plot is scaled to the same value for both estimators.

The results shown in figure 5A–I suggest that methods that account for drift are capable of significantly improving the accuracy of estimates of selection coefficients when allele frequency trajectories are conditioned on segregation. The differences in accuracy between methods that ignore or account for drift are visible for a range of selection coefficients and population sizes. However, the differences in accuracy between the methods diminish as the population size becomes larger.

Simulations Conditioning on Segregation or Fixation

The magnitude of the bias in the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ is due in part to the event on which trajectories are conditioned. In cases involving positive selection in populations of moderate or large size, most alleles will be fixed in the final sample (e.g., $>80\%$ fixation within 10 generations when s = 0.1, h = ½, $y_0=0.01$, and N = 1000). Thus, it may sometimes be more natural to condition on the event F_K that a selected allele is found (segregating or fixed) in the final sample. Under this conditioning scheme, the approximate estimator ${\hat{s}}_{\mathcal{W}}^{\infty }$ will not generally produce negatively biased estimates of selection coefficients because allele frequency trajectories will not be constrained to those which exhibit slower-than-expected increases in allele frequency.

In light of these considerations, we repeated the analysis shown in figure 5A–I, simulating allele frequency trajectories conditional on the event that the allele was segregating or fixed in the final sample. To compare the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ with maximum likelihood estimates that fully account for drift and the proper conditioning, we also modified the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ computed in Procedure 1 to condition on the event F_K of segregation or fixation in the final sample, yielding the conditional probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|F_K\}$ (eq. 21) with the associated estimator ${\hat{s}}_{\mathcal{W}|F_K}$.

By comparing figure 5J–R with figure 5A–I, it can be seen that the estimator ${\hat{s}}_{\mathcal{W}}^{\infty }$ has considerably less bias when conditioning on the event F_K than when conditioning on S_K. Although the bias is still high when the population size is small ($N\approx 100$), it decreases quickly as the population size increases and becomes comparable to the bias in the properly conditioned, demography-aware estimator ${\hat{s}}_{\mathcal{W}|F_K}$ when the population size is greater than approximately N = 500 diploids. In contrast to figure 5E–I, the bias in ${\hat{s}}_{\mathcal{W}}^{\infty }$ observed in figure 5M–R is positive because the trajectories on which these estimates are based exclude only those in which the allele is lost; thus, they exhibit faster-than-expected growth on average. The results in figure 5J–R suggest that under certain conditioning schemes, methods that ignore drift can produce similar estimates to methods that account for drift.

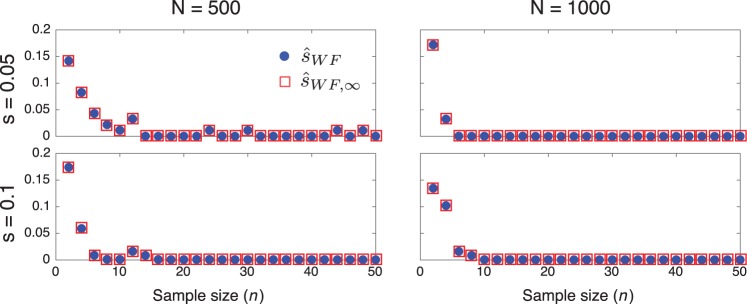
The Effect of Sample Size on Accuracy

When the sample size is small, the variance in estimates arising from sampling noise will tend to obscure small differences between estimators that ignore or account for population size. Thus, when comparing methods, it is important to sample a sufficiently large number of alleles to ensure that the differences between the methods due to ignoring or accounting for drift are visible.

To evaluate the effects of sample size on inference accuracy, we inferred the selection coefficient for a range of sample sizes for several different combinations of the population size and selection coefficient. Figure 6 shows a plot of the variance in selection coefficients inferred using Procedures 1 and 3 for sample sizes ranging from n = 2 to n = 50. For each combination of N_e, s, and n, the trajectories of 100 alleles were simulated under the Wright–Fisher process with an initial allele frequency of $y_0=0.1$. Samples were taken in generations 50 and 100.

Fig. 6.

The effect of sample size on inference accuracy. The variance of the estimates produced by the methods in Procedures 1 and 3 are shown for a range of sample sizes.

The plots in figure 6 suggest that variability due to small sample sizes has a strong effect on the variability in estimates only for sample sizes smaller than 10 alleles. Thus, in all of our simulations, we have used a sample size of n = 50 alleles so that differences between estimators are not likely to be obscured by the variance in estimates due to small sample sizes.

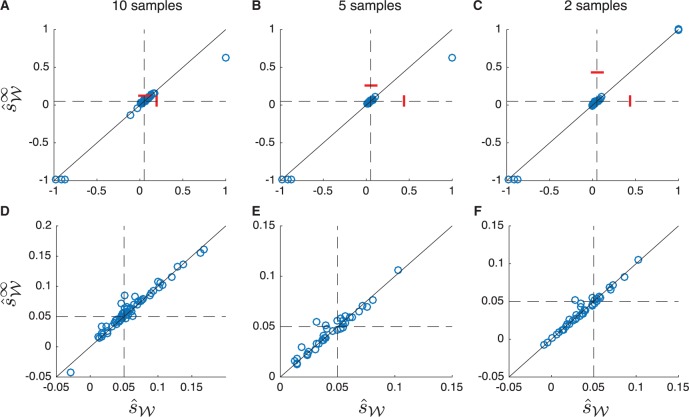
Unspecified Initial Allele Frequencies

In our simulations, we have assumed that the initial frequency y₀ of allele A at time t = 0 is known. Knowledge of the initial allele frequency provides approximately the same information as an informative sample taken at time t = 0. Although this information can improve the estimate of the selection coefficient if few samples are taken, it contributes relatively little information to the estimate of s when the number of samples is moderate. However, because a lack of knowledge of the initial frequency could potentially lead to greater errors in the deterministic estimators, we also compared versions of the estimators that assume a uniform prior distribution on the allele frequency at the time of the first sampling event, and which do not incorporate information about the initial allele frequency (Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ When ${\mathbf{d}}_0$ Is Unspecified, Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ When y₀ Is Unspecified, and Deterministic Estimators When the Initial Allele Frequency Is Unknown).

Figure 7 shows a comparison between the deterministic and exact Wright–Fisher estimates when the initial frequency is drawn uniformly from the interval $y_0\in (0,0.5]$ and the selection coefficient is inferred using Procedures 1 and 2 assuming no knowledge of the initial allele frequency. From figure 7, it can be seen that the deterministic and exact estimators produce similar results, even in the absence of knowledge of the initial frequency. Moreover, although the estimates produced by the two methods decrease in accuracy as the number of sampling events decreases, the accuracies of the two kinds of methods remain similar. In particular, From figure 7D–F, it can be seen that both the deterministic and exact methods are relatively accurate when allele frequency trajectories do not drift out or fix immediately due to random fluctuations.

Fig. 7.

Scatter plots comparing the estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{W}}$ when the initial allele frequency is unspecified during inference. One hundred allele frequency trajectories were simulated for 500 generations with s = 0.05, N = 100, and y₀ sampled uniformly from the interval $(0,0.5]$ as described in the “Simulations” section. Estimates ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{W}}$ were computed using Procedures 1 and 2 using the modified procedure taken when ${\mathbf{d}}_0$ and y₀ are unspecified. (A) Estimates computed using all ten samples of size n = 50 taken in generations $50,100,150,200,250,300,350,400,450$, and 500. (B) Estimates computed using the five samples taken in generations $50,150,250,350$, and 450. (C) Estimates computed using the two samples taken in generations 50 and 150. (D), (E), and (F) are zoomed-in versions of the plots in (A), (B), and (C). All panels correspond to the same 100 simulated trajectories. Dashed lines correspond to the true selection coefficient. Bars show means over all 100 estimates. The solid line is ${\hat{s}}_{\mathcal{W}}^{\infty }={\hat{s}}_{\mathcal{W}}$.

Violation of Model Assumptions

It is possible that violations of model assumptions in real data could increase the differences in accuracy between the deterministic and demography-aware estimators. To investigate this possibility we compared the performance of the deterministic and demography-aware discrete Wright–Fisher estimators using experimentally sampled allele frequency time series data that are thought to violate several model assumptions. In particular, we considered time series data for an allele at the medionigra locus in the species Panaxia dominula, which confers a darkened wing phenotype (Cook and Jones 1996). Although these samples are thought to represent a single population that is isolated from migration events, there is evidence for temporal fluctuations in the selection coefficient, frequency dependent selection, and assortative mating. These data are also useful for our analyses because they include estimates of population sizes obtained using mark, release, and recapture. The data set, which spans over 40 years, provided important evidence for natural selection resulting from environmental pressures.

We computed the log likelihood as a function of the selection coefficient s for three different values of the dominance parameter ($h=0,0.5$, and 1). Figure 8 shows the log likelihood for different values of h, along with asymptotic normal approximations of 95% confidence intervals. Figure 8 shows that the log likelihood surfaces computed using Procedures 1 and 3 are qualitatively similar, yielding similar point estimates for s. However, the confidence intervals for the deterministic estimator are considerably smaller than those of the demography-aware estimator. This result is expected, given that the deterministic estimator ignores the largely symmetrical variability arising from drift and considers only variability in the sampling frequency.

Fig. 8.

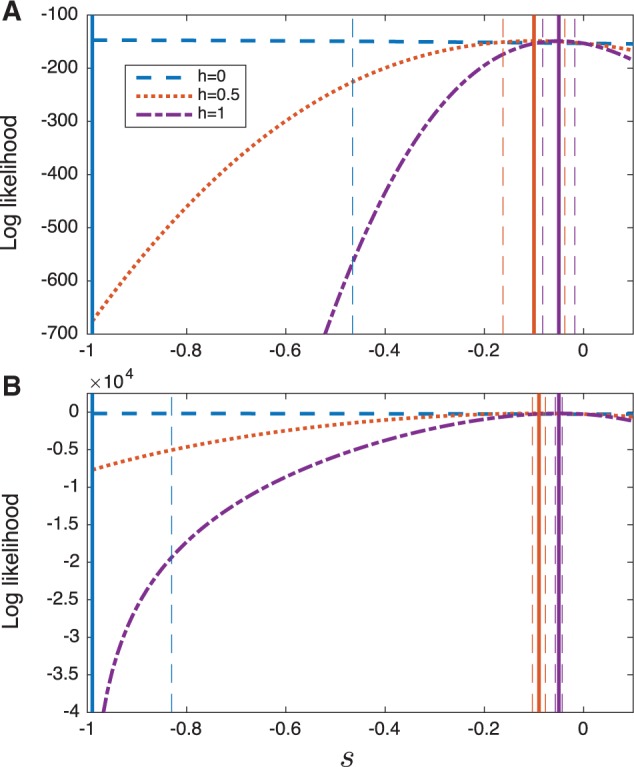
The log likelihood as a function of s computed using Procedures 1 and 3 for three different values of the dominance parameter h ($h=0,0.5,1$). Solid vertical lines show the maximum likelihood estimates, ${\hat{s}}_{\mathcal{W}}$ in (A) and ${\hat{s}}_{\mathcal{W}}^{\infty }$ in (B), for the curve of the corresponding color. Dashed vertical lines indicate asymptotic normal approximations of the 95% confidence intervals for s, for the curve of the corresponding color. (A) The demography-aware likelihoods (Procedure 1). (B) The deterministic likelihoods (Procedure 3).

Note that the point estimates presented in figure 8 are similar to those estimated previously in other studies. Using a model of additive selection (h = 0.5) Cook and Jones (1996) estimated $s\approx -0.16$ whereas Mathieson and McVean (2013) inferred $s\approx -0.12$. These estimates are close to the maximum likelihood estimates that we inferred under the same model of additive selection (${\hat{s}}_{\mathcal{W}}=-0.1$ and ${\hat{s}}_{\mathcal{W}}^{\infty }=-0.09$) (note that the estimates in Cook and Jones (1996) and Mathieson and McVean (2013) are reported using a different parameterization of the dominance model than the one we have used in this paper; thus, we have scaled the selection coefficients reported in these papers so that they are comparable with the ones reported here).

It is of interest to note that Mathieson and McVean (2013) found evidence that the medionigra allele is recessive, finding that the likelihood was maximized for a recessive model with a strong negative selection coefficient around $s\approx -1$, although they note that such a strong negative selection coefficient violates the assumptions of the Gaussian model under which their likelihoods were derived. In accordance with the result of Mathieson and McVean (2013), we find that both the deterministic and exact Wright–Fisher likelihoods we considered were also maximized for a recessive pattern of dominance (h = 0) with a large negative selection coefficient around $s\approx -1$.

Under a recessive model of dominance, the strongly negative selection coefficient that was inferred by the estimators in this study and by that of Mathieson and McVean (2013) is reasonable given that the allele frequency decreases rapidly, which would be unlikely under weak selection where alleles must combine in homozygotes for selection to act. Unlike the analyses of Mathieson and McVean (2013), a selection coefficient of $s\approx -1$ does not violate our model assumptions. Thus, our analysis provides further support that the medionigra variant is largely recessive, although there is evidence that the dominance of the variant can change over time (Cook and Jones 1996).

Computational Efficiency of Methods

As we have noted, methods that assume that allele frequency trajectories are deterministic can be considerably faster than methods that account for population size histories. Table 1 shows the average runtimes of the estimators ${\hat{s}}_{\mathcal{W}}^{\infty },\hspace{0.17em}{\hat{s}}_{\mathcal{W}},\hspace{0.17em}{\hat{s}}_{\mathcal{D}}$, and ${\hat{s}}_{\mathcal{D}}^{\infty }$ for the computations used to produce figure 3A–I.

Table 1.

Mean Runtimes of the Methods in figure 3A–I (seconds).

Ne	s	${\hat{s}}_{\mathcal{W}}^{\infty }$	${\hat{s}}_{\mathcal{W}}$	${\hat{s}}_{\mathcal{D}}^{\infty }$	${\hat{s}}_{\mathcal{D}}$
100	0.01	0.01	2.30	4.74	197.25
	0.05	0.01	2.36	4.23	204.66
	0.1	0.01	2.29	3.98	217.34
500	0.01	0.02	134.07	4.41	185.18
	0.05	0.01	132.45	4.41	496.83
	0.1	0.02	126.35	4.46	531.15
1000	0.01	0.02	175.27	4.64	196.90
	0.05	0.02	191.53	4.78	815.27
	0.1	0.02	199.32	4.67	1950.59

From the table, it can be seen that the runtimes are considerably faster for the estimators based on deterministic trajectories (${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{D}}^{\infty }$). Moreover, the runtimes for ${\hat{s}}_{\mathcal{W}}^{\infty }$ and ${\hat{s}}_{\mathcal{D}}^{\infty }$ do not depend on the population size or selection coefficient. In comparison, the runtimes for the estimators ${\hat{s}}_{\mathcal{W}}$ and ${\hat{s}}_{\mathcal{D}}$ increase with increasing N_e and s because these methods depend on eigenvalue decompositions or sparse matrix products, which require larger matrices or greater precision when N_e or s is large. Note that although the discrete Wright–Fisher estimator is considerably faster than the diffusion estimator for the scenarios we considered, the diffusion estimator can still be more efficient when samples are widely separated in time and the repeated matrix–vector products required by the discrete Wright–Fisher method become cumbersome.

Discussion

The results of our analyses suggest that accurate estimates of selection coefficients from allele frequency time series data can often be obtained by assuming that alleles evolve without drift in a population of infinite size. In the majority of our simulations, the estimates obtained using deterministic approximations were nearly as accurate as estimates obtained by explicitly modeling the true population history and they were sometimes more accurate than estimates obtained using crude but reasonable estimates of the population history. The latter result indicates that an overestimate of the population size, for example due to underestimation of the mutation rate or other factors, may have only small adverse effects on the accuracy of exact likelihood estimates of the selection coefficient from time series data, a result that is of interest because population size histories can be difficult to infer accurately.

Surprisingly, estimates made under the deterministic approximation were generally as accurate as estimates that accounted for drift, due to the fact that the exact maximum likelihood methods had low accuracy when drift was strong. Accounting for the true population history only resulted in significantly improved estimates of selection coefficients when conditioning on the event that the target allele was segregating in the final sample. Methods that modeled the true population history were more accurate in this case because they could be modified to model conditional trajectories, whereas methods that assumed infinite population sizes could not. These results suggest that methods that account for drift are likely to be preferable under circumstances in which conditioning on segregation is desirable. However, it is important to note that deterministic methods can perform well when population sizes are moderately large if allele frequencies are conditioned on a slightly different event: the event that an allele is found (segregating or fixed) in the final sample.

It is important to note that we have focused on estimates of the selection coefficient rather than the dominance parameter h, which is a more difficult task. However, in our analyses of the medionigra variant in the Panaxia dominula moth, we found that both the deterministic and exact likelihoods were qualitatively similar in both h and s and were both maximized for a recessive model of dominance. A comprehensive exploration of the effects of deterministic assumptions on the inference of h is deferred to future analyses.

It is also important to note that our analyses do not imply that the deterministic and exact estimators will produce exactly the same point estimate for a given allele frequency trajectory. Although the scatter plots in figures 3, 7, and supplementary figure S1, Supplementary Material online suggest that both deterministic and exact estimators often agree closely on the magnitude of the selective strength, the estimates for any given trajectory can differ by 100% or more. This result is consistent with the observation by Schraiber et al. (2016) that specifying different demographic histories led to different estimates of dominance and selection parameters for alleles affecting coat coloration in horses. Although specific point estimates can differ, our results demonstrate that deterministic and exact estimators have similar accuracies for estimating the strength of selection, even when the population size is small.

The idea that ignoring drift can lead to accurate estimates of selection coefficients is not new. In fact, inference methods based on deterministic allele frequency trajectories capitalize on exactly this idea. However, our comparison with estimators based on exact likelihoods makes it possible to characterize the relative loss in accuracy that is incurred when drift is ignored, as well as the demographic, evolutionary, and sampling scenarios under which accounting for drift is likely to be important.

The comparatively accurate estimates achieved by methods that assume deterministic allele frequency trajectories are encouraging for three primary reasons. First, a large number of studies have relied on the assumption that alleles evolve deterministically in order to infer selection coefficients from biological time series data. Our results suggest that these estimates are likely to be nearly as accurate as those obtained using the exact likelihood accounting for drift. Second, estimators based on deterministic trajectories can be considerably faster than estimators that account for drift, making them useful for inferring selection coefficients at large numbers of loci. Third, it may be easier to obtain analytical results under the assumption that allele frequencies change deterministically, simplifying the development of inference methods for inferring selection coefficients under more complicated scenarios; for example, inferring coefficients at linked loci (Illingworth et al. 2012). Finally, the ability to ignore the population size is useful in situations in which the true population history is unknown or difficult to infer.

In addition to characterizing the degree to which accounting for drift can improve estimates of selection coefficients, our results shed light on the accuracy of exact maximum likelihood methods for inferring selection coefficients from allele frequency trajectories. In accordance with predictions about the relative strengths of genetic drift and selection (Gillespie 1998, section 3.7) and experimental work (Gallet et al. 2012), our findings suggest that very small selection coefficients ($s\le 0.01$) are difficult to infer if the initial allele frequency and population size are not large. Moreover, even if the population size is large, the accurate inference of a small selection coefficient may require samples taken over hundreds of generations, during which time the selection coefficient could change considerably (Felsenstein 1976; Siepielski et al. 2009).

Despite the difficulties of inferring weak selection coefficients when the population size is small, coefficients of one percent or lower can be inferred accurately if the initial allele frequency is sufficiently high. It is important to note that the selection coefficient need not be high at the time of the very first sampling event, as long as the allele has reached a sufficiently high frequency at one of the intermediate sampling events, leading to quasi-deterministic behavior between some sampling time points that can be exploited by the maximum likelihood estimator.

Although we have only considered positively selected alleles in our simulation analyses, our results apply equally well to negatively selected alleles, as it is arbitrary whether we choose to track the trajectory of the allele with higher or lower fitness. We have also focused on low initial allele frequencies $(y_0\le 0.1)$ for selected alleles; however, it is clear from figure 2 that allele frequency trajectories become increasingly deterministic as the initial allele frequency increases. Thus, the accuracy of a method that assumes a deterministic trajectory will become more similar to that of a method that accounts for drift as the initial allele frequency increases. Conversely, for negatively selected alleles, the accuracy of the deterministic method will approach that of the exact likelihood as the initial allele frequency decreases. Thus, our analyses provide a characterization of inference accuracy for both positively and negatively selected alleles for a broad range of starting frequencies.

At first glance, our finding that the population size does not strongly influence estimates of selection coefficients might appear to be at odds with the fact that population size histories can be inferred from allele frequency time series data (O’Hara 2005; Bollback et al. 2008; Ferrer-Admetlla et al. 2015). However, this is not the case. Methods for inferring the population size capitalize on information in the short-term fluctuations of the allele frequency around its expected value, arising from drift; conversely, estimators of selection coefficients capitalize on the long-term changes in allele frequency due to selection, effectively averaging over the short-term fluctuations due to drift. Our results suggest that allele frequencies often change quasi-deterministically, even in small populations. Thus, deviations around the expected trajectory can be distinguished from long-term changes, allowing effective population sizes to be inferred accurately even in small populations.

We have conducted our analyses under two different models of evolution: the discrete Wright–Fisher model and the continuous diffusion model. Although the diffusion model was developed as an approximation to the Wright–Fisher process, it also captures the limiting behavior of a large class of evolutionary models, including the Wright–Fisher process, as the population size grows to infinity and mutation and selection parameters are scaled accordingly. Thus, it is reasonable to believe that our findings will generalize to maximum likelihood estimators derived under a wide range of evolutionary models.

Taken together, our results help to characterize the properties of maximum likelihood methods for inferring selection coefficients from time series data. Because of the accuracy and beneficial properties of maximum likelihood methods, it is reasonable to believe that our results provide insight into the accuracy with which it is possible to infer selection coefficients from biological data, and the degree to which accounting for the true population history can improve these estimates. Our results also provide justification for the use of fast inference methods based on the assumption that allele frequencies evolve deterministically. Such methods can be applied to infer selection coefficients efficiently on large genomic data sets with many loci. Finally, our results provide further justification for the use of deterministic approximations in the development of statistical approaches for studying time series data.

Methods

In this section, we compute the exact probability of an allele frequency trajectory in a population of piecewise-constant size under the discrete Wright–Fisher model and under the diffusion approximation. We also describe how drift can be ignored in these probabilities, yielding approximate estimators of selection coefficients that are similar to commonly used approaches that assume deterministic allele frequency trajectories.

Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ under the Discrete Wright–Fisher Model

To compute the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ under the discrete Wright–Fisher model, we make use of a hidden Markov model (HMM) similar to that presented in Steinrücken et al. (2014). However, the hidden state in our discrete model is the count c_t of the number of (unobserved) copies of allele A in the population at time t, rather than the continuous allele frequency y_t.

In our model, the count c_t of allele A evolves according to a Wright–Fisher process in which mutation occurs, followed by random mating, selection, and drift. Given that the count of allele A in generation t is c_t=i, let $f_{A|i}^t$ be the frequency of allele A in the gamete pool after mutation. Then

$$f_{A|i}^t=\left(\frac{i}{2N_t}\right)(1-u_{Aa}^{(t)})+\left(1-\frac{i}{2N_t}\right)u_{aA}^{(t)}=u_{aA}^{(t)}+(1-u_{Aa}^{(t)}-u_{aA}^{(t)})\left(\frac{i}{2N_t}\right).$$ (2)

After random mating, the fraction of zygotes with each of the genotypes AA, Aa, and aa is ${(f_{A|i}^t)}^2,\hspace{0.17em}2f_{A|i}^t(1-f_{A|i}^t)$, and ${(1-f_{A|i}^t)}^2$, from which it follows that the fraction of genotypes of each kind remaining after selection is given by

$$\begin{array}{l}{p}_{AA|i}^t=\frac{{(f_{A|i}^t)}^2(1+s_t)}{{\overline{w}}_{t,i}},\\ p_{Aa|i}^t=\frac{2f_{A|i}^t(1-f_{A|i}^t)(1+h_t{s}_t)}{{\overline{w}}_{t,i}},\\ p_{aa|i}^t=\frac{{(1-f_{A|i}^t)}^2}{{\overline{w}}_{t,i}},\end{array}$$ (3)

where ${\overline{w}}_{t,i}={(f_{A|i}^t)}^2(1+s_t)+2f_{A|i}^t(1-f_{A|i}^t)(1+h_t{s}_t)+{(1-f_{A|i}^t)}^2$ is the mean fitness of the population.

Immediately after selection and before drift occurs, the probability that a randomly chosen allele is of type A is given by $p_{A|i}^t=p_{AA|i}^t+\frac{1}{2}{p}_{Aa|i}^t$. Then, as the result of drift, the count of allele A in generation t + 1 is binomially distributed with mean $p_{A|i}^t$. Thus, the probability that allele A has count j in generation t + 1, given that it had count i in generation t is

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t+1}=j|C_t=i\}=\left(\begin{array}{l}2N_{t+1}\\ \mathit{j}\end{array}\right){\left(p_{A|i}^t\right)}^j{(1-p_{A|i}^t)}^{2N_{t+1}-j}.$$ (4)

The Wright–Fisher transition matrix ${\mathbf{T}}_{t,t+1}$ from generation t to generation t + 1 is the $(2N_t+1)\times (2N_{t+1}+1)$ matrix with entry i, j given by

$${[{\mathbf{T}}_{t,t+1}]}_{ij}={\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t+1}=j|C_t=i\},$$ (5)

which can be used to obtain the allele frequency distribution at each discrete generation t given the initial distribution at some time r < t. In particular, define ${\mathbf{d}}_t=(\mathbb{P}\{c_t=0\},\mathbb{P}\{c_t=1\},\dots ,\mathbb{P}\{c_t=2N_t\})$, to be the distribution of the count of allele A in generation t. Using equation (5), ${\mathbf{d}}_t$ can be computed recursively as

$${\mathbf{d}}_t={\mathbf{d}}_r\left[\prod _{g=r+1}^t{\mathbf{T}}_{g-1,g}\right]$$ (6)

for r < t.

Computing the Probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$

The probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ of the observed data is computed using the forward procedure for hidden Markov models. In particular, we define the vector ${\mathbf{v}}_k$ whose ith entry $v_{k,i}$ is the joint probability of the population-wide count of allele A at the kth sampling event and the observed sample allele counts up to sample k:

$$v_{k,i}={\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:k]}=o_{[1:k]},C_{t_k}=i\}.$$ (7)

To simplify calculations, we also define the conditional “emission probability”

$${\gamma }_i(o_k)={\mathbb{P}}_{\Theta }\{O_k=o_k|C_{t_k}=i\}=\left(\begin{array}{l}{n}_k\\ o_k\end{array}\right){(i/2N_{t_k})}^{o_k}{(1-i/2N_{t_k})}^{n_k-o_k}$$ (8)

of the observed allele count, conditional on the population allele count. The probability in equation (8) comes from the fact that the observed allele count at time t_k can be modeled as a binomial random variable with sample size n_k and probability $c_{t_k}$. Although the observed allele count is, strictly speaking, hypergeometric we use the binomial distribution to maintain consistency with the formulas for the diffusion model, which are often derived using a binomial sampling distribution. The binomial and hypergeometric distributions are very similar for the population and sample sizes we consider. We then construct the emission probability vector

$$\gamma (o_k)=({\gamma }_0(o_k),{\gamma }_1(o_k),\dots ,{\gamma }_{2N_{t_k}}(o_k)).$$ (9)

The probability of the data is then given by the forward procedure (Rabiner 1989), outlined in Procedure 1. In Procedure 1, the formula for ${\mathbf{v}}_1$ comes from the fact that

$$\begin{array}{l}{\mathbf{v}}_1=({\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_1=o_1,C_{t_1}=0\},\dots ,\hspace{0.17em}\\ {\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_1=o_1,C_{t_1}=2N_{{\ell }_{t_1}}\})=({\gamma }_0(o_1){\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t_1}=0\},\dots ,\\ {\gamma }_{2N_{{\ell }_{t_1}}}(o_1){\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t_1}=2N_{{\ell }_{t_1}}\})={\mathbf{d}}_{t_1}\text{diag}\{\gamma (o_1)\}\hspace{0.17em}\\ ={\mathbf{d}}_0\left[\prod _{t=1}^{t_1}{\mathbf{T}}_{t-1,t}\right]\text{diag}\{\gamma (o_1)\},\end{array}$$ (10)

where $\text{diag}(\gamma )$ denotes the square matrix whose diagonal entries are given by $\gamma$.

It has been noted by several authors that computing powers of the transition matrix is computationally prohibitive, providing one motivating factor for the use of approximations of the Wright–Fisher process, such as the diffusion and Gaussian approximations (Ewens 1963; Feder et al. 2014; Lacerda and Seoighe 2014). However, the products ${\prod }_{t=t_{k-1}+1}^{t_k}{\mathbf{T}}_{t-1,t}$ in Procedure 1 do not require products of the transition matrix ${\mathbf{T}}_{t-1,t}$ because it suffices to repeatedly compute vector–matrix products instead of multiplying full matrices together. In practice, this can be done very quickly, even for large population sizes. A similar fast procedure was carried out by Zhao et al. (2014) to simulate trajectories under the Wright–Fisher model.

Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ When ${\mathbf{d}}_0$ Is Unspecified

When the initial distribution ${\mathbf{d}}_0$ is unspecified, the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}\}$ can be obtained by assuming that the distribution ${\mathbf{d}}_{t_1}$ is uniform at the time of the first sampling event. Under this assumption, it follows directly from the second to last equality in equation (10) that the value of the joint density vector ${\mathbf{v}}_1$ is given by

$${\mathbf{v}}_1=\frac{1}{2N_{t_1}}1\text{diag}\{\gamma (o_1)\}=\frac{1}{2N_{t_1}}\gamma (o_1),$$ (11)

where 1 is the vector of length $2N_{t_1}$ with all entries equal to one. This form of ${\mathbf{v}}_1$ can then be substituted into Procedure 1.

Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ under the Diffusion Approximation

The diffusion approximation models the evolution of the continuous population frequency Y_t of allele A, rather than its count C_t. The time-evolution of the random frequency Y_t is governed by the diffusion transition density $p_{\Theta }(s,t;x,y)$ given by

$$p_{\Theta }(s,t;x,y)dy=\hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{D}}\{y\le Y_t<y+dy|Y_s=x\},$$ (12)

for an infinitesimal increment dy. The quantity $p_{\Theta }(s,t;x,y)$ specifies the density of the allele frequency at time t, conditional on the value of the allele frequency at an earlier time s. For more details about the transition density function of the diffusion approximation, see Appendix A.

Using the diffusion transition density $p_{\Theta }(s,t;x,y)$ Steinrücken et al. (2014) developed an HMM to compute the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ of the data in a single epoch of constant size by efficiently integrating over the hidden allele frequencies $\{y_{t_1},\dots ,y_{t_K}\}$ at the set of sampling times. Here, we extend this HMM to the case of piecewise-constant population size.

To compute the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ efficiently, Steinrücken et al. (2014) define the quantities $f_k(y)$ and $g_k(y)$ satisfying

$$f_k(y)dy:=\hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:k]}=o_{[1:k]},y\le Y_{t_k}<y+dy\},$$ (13)

and

$$g_k(y)dy:=\hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:k-1]}=o_{[1:k-1]},y\le Y_{t_k}<y+dy\}$$ (14)

for an infinitesimal increment dy. The quantity $f_k(y)$ is the joint density of the allele frequency at time t_k and the observed counts up to sampling event k. The quantity $g_k(y)$ is the joint density of the allele frequency at time t_k and the observed counts up to sampling event k – 1.

It follows from the definition of $f_k(y)$ that the probability of the data is given by

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}={\int }_{y=0}^1{f}_K(y)dy.$$ (15)

The quantity $f_K(y)$ can be obtained efficiently by recursion using the relationships

$$f_k(y)=g_k(y)(\begin{array}{l}{n}_k\\ o_k\end{array})y^{o_k}{(1-y)}^{n_k-o_k},$$ (16)

and

$$g_k(y)={\int }_{z=0}^1{f}_{k-1}(z)p_{\Theta }(t_{k-1},t_k;z,y)dz.$$ (17)

Equation (16) follows from the fact that the observed number of copies of allele A at sampling event k is binomially distributed with count n_k and probability $y_{t_k}$ and equation (17) follows from the law of total probability integrating over $Y_{t_{k-1}}$.

Let $B_{\ell ,i}(y)$ $(i=0,1,\dots )$ be the ith eigenfunction of the backward diffusion operator ${\ell }_{\ell }$ and let ${\pi }_{\ell }(y)$ be the speed density of ${\ell }_{\ell }$ in Epoch $\ell$ (Appendix A). Steinrücken et al. (2014) demonstrated that the recursive formulas in equations (16) and (17) can be evaluated efficiently by expressing $f_k(y)$ and $g_k(y)$ as series of the form

$$f_k(y)=\sum _{i=0}^{\infty }{b}_{k,i}{\pi }_{{\ell }_k}(y)B_{{\ell }_k,i}(y)={\mathbf{b}}_k{\pi }_{{\ell }_k}(y){\mathbf{B}}_{{\ell }_k}(y)$$ (18)

and

$$g_k(y)=\sum _{i=0}^{\infty }{a}_{k,i}{\pi }_{{\ell }_k}(y)B_{{\ell }_k,i}(y)={\mathbf{a}}_k{\pi }_{{\ell }_k}(y){\mathbf{B}}_{{\ell }_k}(y),$$ (19)

where ${\mathbf{B}}_{\ell }(y)=(B_{\ell ,0}(y),\hspace{0.17em}{B}_{\ell ,1}(y),\hspace{0.17em}\dots )$, and where ${\mathbf{b}}_k=(b_{k,0},b_{k,1},\dots )$ and ${\mathbf{a}}_k=(a_{k,0},a_{k,1},\dots )$ are vectors of constants that encode the densities $f_k(y)$ and $g_k(y)$. In Appendix B, we extend the results of Steinrücken et al. (2014) to derive recursive formulas for the coefficients ${\mathbf{a}}_k$ and ${\mathbf{b}}_k$, resulting in Procedure 2, which computes the probability of an allele frequency trajectory under the diffusion approximation in a population of piecewise constant size.

Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ When y₀ Is Unspecified

When the initial frequency y₀ is unspecified, the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ can be obtained by assuming that the distribution of the allele frequency $y_{t_1}$ at the time of the first sampling event is uniform. Under this assumption, we show in Lemma B.3.2 that the coefficients ${\mathbf{b}}_1$ encoding the distribution at the time of the first sampling event are given by equation (B.17). The form of ${\mathbf{b}}_1$ in equation (B.17) is then used in Procedure 2.

Conditional Probabilities

Sometimes it is desirable to compute the probability of the observed allele counts conditional on the event S_K that allele A is segregating in the final sample. In this section, we provide formulas for these conditional probabilities under the Wright–Fisher and diffusion models.

Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$

In the “Simulations Conditioning on Segregation” section, we consider the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$ of the data conditional on the event S_K that allele A is segregating in the final sample. In Appendix C, we show that in the case of the discrete Wright–Fisher model,

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|S_K\}\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}}\sum _{i=0}^{2N_{t_K}}{v}_{K,i},$$ (20)

where $v_{k,i}$ is defined in equation (7) and $\mathbb{P}\left\{S_K\right|O_K=o_K\}=1$ if $1\le o_K<n_K$, or 0 otherwise. The probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}$ is given in equation (C.3). Thus, if we wish to compute conditional probabilities under the Wright–Fisher model, we carry out Procedure 1, replacing step 3 with equation (20).

Computing ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|F_K\}$

Similarly, for the event F_K that allele A is segregating or fixed in the final sample, we show in Appendix C that

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|F_K\}\hspace{0.17em}=\frac{\mathbb{P}\left\{F_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{F_K\right\}}\sum _{i=0}^{2N_{t_K}}{v}_{K,i},$$ (21)

where $v_{k,i}$ is defined in equation (7) and $\mathbb{P}\left\{F_K\right|O_K=o_K\}=1$ if $1\le o_K\le n_K$, or 0 otherwise. The probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{F_K\right\}$ is given in equation (C.6). If we wish to compute the conditional probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|F_K\}$ under the Wright–Fisher model, we carry out Procedure 1, replacing step 3 with equation (21).

Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$

In the case of the diffusion approximation, we show in Appendix D that the conditional probability of the data given S_K can be computed as

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}|S_K\}\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}{c}_{{\ell }_K,0}{b}_{K,0}}{B_{{\ell }_K,0}\left(0\right)-c_{{\ell }_K,0}{\tilde{b}}_{K,0}\left(0\right)-c_{{\ell }_K,0}{\tilde{b}}_{K,0}\left(n_K\right)},$$ (22)

where $\mathbb{P}\left\{S_K\right|O_K=o_K\}=1$ if $1\le o_K<n_K$ or 0 otherwise, and

$${\tilde{\mathbf{b}}}_K\left(j\right)=\{\begin{array}{l}{\mathbf{b}}_0{\mathbf{E}}_{{\ell }_1}\left(t_K\right){\mathbf{W}}_{{\ell }_K}{\mathbf{G}}_{{\ell }_K}^j{(1-{\mathbf{G}}_{{\ell }_K})}^{n_K-j}{\mathbf{W}}_{{\ell }_K}^{-1},\hfill \\ \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{t_K}=1,\hfill \\ {\mathbf{b}}_0\mathbf{F}(0,t_K;\zeta ){\mathbf{W}}_{{\ell }_K}{\mathbf{G}}_{{\ell }_K}^j{(1-{\mathbf{G}}_{{\ell }_K})}^{n_K-j}{\mathbf{W}}_{{\ell }_K}^{-1},\hfill \\ \hspace{0.17em}\text{otherwise}\hspace{0.17em}.\hfill \end{array}$$ (23)

Thus, if we are interested in conditional probabilities under the diffusion model, we carry out Procedure 2, replacing step 3 with equation (22).

The Probability in the Absence of Genetic Drift

If we ignore genetic drift, the allele frequency changes deterministically over time, as it would in a population of infinite size. Here, we obtain versions of Procedures 1 and 2 in the case when the changes in allele frequency arising from genetic drift are negligible relative to the changes due to selection and recurrent mutation.

Deterministic Allele Frequency Trajectories under the Wright–Fisher Model

If there is no contribution to the change in allele frequency arising from genetic drift, the allele frequency in a given generation is equal to its expectation after mutation, random mating, and selection, conditional on its value in the previous generation. Because the expectation is not necessarily integer-valued, we no longer consider discrete integer allele counts c_t. Instead, we track the expected allele frequency in the absence of drift, which we denote by $y_t^{\infty }\equiv {\mathbb{E}}_{\infty }[Y_t]$, where the subscript ∞ denotes the expectation without drift as the effective population size tends to infinity.

The expected frequency $y_t^{\infty }$ in the absence of drift is obtained by combining equations (2) and (3), ignoring the drift step in equation (4), yielding

$$y_{t+1}^{\infty }=\left[\frac{{({\tilde{y}}_t^{\infty })}^2(1+s_t)+{\tilde{y}}_t^{\infty }(1-{\tilde{y}}_t^{\infty })(1+h_t{s}_t)}{{\overline{w}}_t}\right],$$ (24)

where

$${\tilde{y}}_t^{\infty }=u_{aA}^{(t)}+(1-u_{Aa}^{(t)}-u_{aA}^{(t)})y_t^{\infty }$$ (25)

and ${\overline{w}}_t={({\tilde{y}}_t^{\infty })}^2(1+s_t)+2{\tilde{y}}_t^{\infty }(1-{\tilde{y}}_t^{\infty })(1+h_t{s}_t)+{(1-{\tilde{y}}_t^{\infty })}^2$. Equations (24) and (25) are iterated to find the allele frequency in any generation t > 0.

Equation (24) is related to equation 3.1 of Gillespie (1998), which describes the dynamics of allele frequency change in a population of infinite size without drift. The frequency trajectories described by this formula are closely approximated by logistic curves that have closed formulas (Feder et al. 2014, equation 3), which can be used to increase the speed of deterministic approaches even further. However, we have chosen to implement the exact formulas for better comparison with the exact likelihoods.

Deterministic Allele Frequency Trajectories under the Diffusion Model

Under the diffusion model in an Epoch $\ell$ of constant size, the allele frequency Y_t obeys the stochastic differential equation (SDE)

$$d{Y}_t={\mathcal{M}}_{\ell }(Y_t)dt+\sqrt{Y_t(1-Y_t)}d{B}_t,\hspace{0.17em}t\in [{\tau }_{\ell -1},{\tau }_{\ell }],$$ (26)

with the initial condition $Y_{{\tau }_{\ell -1}}=y_{{\tau }_{\ell -1}}$, where time is measured in units of generations and ${\tau }_{\ell -1}$ is the time at which Epoch $\ell$ begins (Karlin and Taylor 1981, Section 15.14; Durrett 2008, Section 7.2). The quantity $\sqrt{Y_t(1-Y_t)}$ in equation (26) controls random fluctuations due to drift whereas the quantity ${\mathcal{M}}_{\ell }(y)$ describes the deterministic change in the mean frequency of the allele over time due to mutation and selection and is given by

$${\mathcal{M}}_{\ell }(y)=u_{aA}^{(\ell )}-(u_{aA}^{(\ell )}+u_{Aa}^{(\ell )})y+\hspace{0.17em}y(1-y)[h_{\ell }{s}_{\ell }(1-2y)+s_{\ell }y].$$ (27)

In equation (27), we have rescaled the usual form of ${\mathcal{M}}_{\ell }$ so that time is measured continuously in units of generations.

If the drift term in equation (26) is negligible compared with ${\mathcal{M}}_{\ell }(Y_t)$, then equation (26) can be approximated by the ordinary differential equation

$$\frac{d{y}_t^{\infty }}{dt}={\mathcal{M}}_{\ell }(y_t^{\infty }),$$ (28)

where we may write $y_t^{\infty }$ instead of Y_t because the evolution of the allele frequency is deterministic and follows its expectation in the absence of drift.

We can also suppress the explicit dependence on the epoch $\ell$ by defining ${\mathcal{M}}_t(y_t^{\infty })\equiv {\mathcal{M}}_{{\ell }_t}(y_t^{\infty })$, yielding

$$\frac{d{y}_t^{\infty }}{dt}={\mathcal{M}}_t(y_t^{\infty }),y_0^{\infty }=y_0,\hspace{0.17em}\hspace{0.17em}t\in [0,{\tau }_L],$$ (29)

which holds for the full population history across all epochs $\ell =1,\dots ,L$. Equation (29) can be solved numerically, for instance by choosing a sufficiently small time step $△t$ and iteratively computing $y_{t+△t}^{\infty }={\mathcal{M}}_t(y_t^{\infty })△t$.

Sample Probabilities Based on Deterministic Allele Frequency Trajectories

To compute the probability ${\mathbb{P}}_{\Theta }^{\infty }\{O_{[1:K]}=o_{[1:K]}\}$ under either the discrete Wright–Fisher or diffusion models when drift is negligible, we note that the observations $(O_1,\dots ,O_K)$ are conditionally independent of one another, given the underlying allele frequencies. Thus, in the absence of drift we have

$${\mathbb{P}}_{\Theta }^{\infty }\{O_{[1:K]}=o_{[1:K]}\}\hspace{0.17em}=\prod _{k=1}^K{\mathbb{P}}_{\Theta }\{O_k=o_k|Y_{t_k}=y_{t_k}^{\infty }\}$$ (30)

for both the diffusion and Wright–Fisher models, where $y_{t_k}^{\infty }$ is the deterministic allele frequency at time t_k, for $k=1,\dots ,K$. Using equations (24) and (30), the probability of the data under the Wright–Fisher model in a population without drift can be obtained using Procedure 3. Similarly, using equations (29) and (30), the probability of the data in the case of the diffusion model is given by Procedure 4.

Deterministic Estimators When the Initial Allele Frequency Is Unknown

If the initial allele frequency is unspecified, the selection coefficient can still be inferred using the deterministic estimators by integrating over the allele frequency $y_{t_1}$ at the time of the first sampling event, where we assume in these analyses that the initial allele frequency distribution is uniform. In practice, we perform this integration by specifying a dense grid of values $y_{t_1}\in [0,△y,2△y,\dots ,1]$, where $△y=1/M$ for some large predetermined value M. Defining the probability of the data when the initial allele frequency is y to be ${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]};y_0=y\}$, we compute the probability of the data as

$${\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]}\}\hspace{0.17em}=\frac{1}{M+1}\sum _{j=0}^M{\mathbb{P}}_{\Theta ,\mathcal{W}}^{\infty }\{O_{[1:K]}=o_{[1:K]};y_0=j△y\}.$$ (31)

Simulations

Allele frequency trajectories were simulated under two different models, the discrete Wright–Fisher model and the continuous diffusion model. All simulations were carried out by iteratively sampling the allele frequency at the time points $t_1,t_2,\dots ,t_K$ starting with a specified frequency y₀ or with the initial frequency y₀ sampled uniformly from the interval $(0,0.5]$ at time $t_0=0$.

Wright–Fisher simulations were carried out using Procedure 5. Specifically, for an initial allele frequency y₀, we took the initial distribution ${\mathbf{d}}_0$ to be the standard basis vector ${\mathbf{e}}_{\lceil y_0\rceil }$ of length $2N_0+1$ with element $\lceil 2N_0{y}_0\rceil$ set to unity and all other elements set to zero. We then sampled the population allele count $c_{t_k}$ at each sampling time t_k by iteratively propagating the allele frequency distribution $d_{t_k}$ forward, conditional on the population count $c_{t_{k-1}}$ at the previous sampling time using equation (6). The derived allele count o_k in each sample k was then chosen from a binomial distribution with sample size n_k and probability $c_{t_k}/2N_{t_k}$. For the results in the “Inference Accuracy for Populations of Constant Finite Size”, “Inference Accuracy in Populations of Piecewise Constant Size”, “Conditioning on Segregation in the Final Sample”, and “The Effect of Sample Size on Accuracy” sections, we fixed $y_0=0.01$ or $y_0=0.1$ in all simulations, as indicated in the results section. In the “Unspecified Initial Allele Frequencies” section, we simulated y₀ uniformly from the interval $(0,0.5]$.

Simulations under the diffusion model were carried out using Procedure 6. Specifically, for an initial frequency y₀, we computed the coefficients ${\mathbf{b}}_0$ of the expansion of the initial condition $\delta (y-y_0)$ in the basis functions ${\mathbf{B}}_{{\ell }_1}$ of the first epoch. In Appendix D, we show that the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_k=i\}$ of sampling i derived alleles at sampling event k (eq. D.3) can be obtained by computing a set of coefficients that we call ${\tilde{\mathbf{b}}}_k(i)$ (eq. D.7) that specify an expansion in the basis of eigenfunctions ${\mathbf{B}}_{{\ell }_k}$.

Thus, to sample the derived allele count o₁ in the first sample, we propagated the initial coefficients ${\mathbf{b}}_0$ to obtain ${\tilde{\mathbf{b}}}_1(i)$ and we used the fact that ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_1=i\}\propto {\tilde{\mathbf{b}}}_{1,0}(i)$ (eq. D.3) to sample $o_1=i$ with probability ${\tilde{\mathbf{b}}}_1(i)/\sum _{i=0}^{n_1}{\tilde{\mathbf{b}}}_1(i)$. Using the fact that ${\tilde{\mathbf{b}}}_k(o_k)$ is defined in Section D as the set of coefficients such that ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_k=o_k,y\le Y_{t_k}<y+dy\}={\tilde{\mathbf{b}}}_k(o_k){\pi }_{{\ell }_k}{\mathbf{B}}_{{\ell }_k}(y)$ for an infinitesimal increment dy, we then set ${\mathbf{b}}_1={\tilde{\mathbf{b}}}_1(o_k)$ and iterated this procedure to obtain the subsequent coefficient vectors ${\{{\tilde{\mathbf{b}}}_k(i)\}}_{i=2}^{n_k}$ and the full set of samples $o_{[1:K]}$. Simulated trajectories were checked for accuracy against those obtained using the software of Jenkins and Spanò (2015), personal communication.

Grid Searches to Infer Selection Coefficients

The same iterated grid search procedure, implemented as a wrapper function and outlined in Procedure 7, was used to infer selection coefficients using each of the methods described in Procedures 1–4. The grid search is initialized by specifying lower and upper bounds on a region $[s_{\ell },s_u]$ over which to search for a value of the selection coefficient s that maximizes the likelihood. Assuming that the likelihood surface is convex and smooth, the grid search iteratively refines the search to the region that contains the optimum until the width of the region is smaller than a specified tolerance ϵ. In our analyses, we chose the initial region to be $[s_{\ell },s_u]=[-0.99,1]$ and we set $\mathrm{ϵ}=2·{10}^{-4}$.

For each allele frequency trajectory simulated under the Wright–Fisher model, Procedure 7 was carried out using Procedure 1 and then subsequently for the same trajectory using Procedure 3, with or without conditioning. For each allele frequency trajectory simulated under the diffusion model, Procedure 7 was carried out using Procedure 2 and then subsequently for the same trajectory using Procedure 4, with or without conditioning. A gradient descent optimization approach produced nearly identical results and is available as an option in the software package we have released.

Computing the Watterson Estimator of N_e from the Expected SFS of a Piecewise Constant Population

In the “Inference Accuracy in Populations of Piecewise Constant Size” section, we obtain a crude constant estimate of the effective size N_e of a piecewise constant population by computing the expected unnormalized SFS for the true history and then inferring the effective size of a constant population with the same level of genetic diversity as the piecewise constant population using the Watterson estimator.

Under the assumption that any given base pair in a collection of n haplotypes from a population is at most biallelic, the unnormalized and folded SFS for the n haplotypes is a collection of counts ${\left\{{\xi }_{n,i}\right\}}_{i=1}^{n-1}$ in which ${\xi }_{n,i}$ is the number of sites with one or the other allele appearing in i out of n copies in the sample. When the expected number μ of new mutations occurring in a population within in a region of fixed length is specified, the expected SFS for n haplotypes spanning the region can be computed for a population of piecewise constant size using algorithms by Kamm et al. (2016).

The effective size of a population of constant size extending infinitely far back into the past with the same level of diversity as the piecewise constant population can be computed using the Watterson estimator (Watterson 1975, Eqn. 1.4a; Hein et al. 2005, p. 62). The information used by the Watterson estimator is the diversity in the n sampled haplotypes of specified length, combined with knowledge of the expected mutation rate μ. The Watterson estimator is given by

$${\hat{N}}_e=\frac{1}{4\mu }\frac{S}{\sum _{i=1}^{n-1}i},$$ (32)

where S is the total number of segregating sites observed in the sample. The total number of segregating sites can be computed as $S={\sum }_{i=1}^{n-1}{\xi }_{n,i}$, where ${\xi }_{n,i}$ is the ith entry of the un-normalized folded SFS.

Thus, given the expected SFS ${\left\{{\xi }_{n,i}\right\}}_{i=1}^{n-1}$ for a piecewise constant population computed using the algorithm of Kamm et al. (2016) and a specified mutation rate μ, we computed the Watterson estimate of the size N_e of a constant-sized population with similar diversity as

$${\hat{N}}_e=\frac{1}{4\mu }\frac{\sum _{i=1}^{n-1}{\xi }_{n,i}}{\sum _{i=1}^{n-1}i}.$$ (33)

When computing the expected SFS and the Watterson estimator, we arbitrarily chose a value of μ  = 1.

Procedure 5. Sampling Wright–Fisher trajectories

1: Optional: sample the initial population allele frequency y₀ uniformly from a predetermined interval $(y_{\ell },y_u]$, where $0\le y_{\ell }\le y_u\le 1$, and set $c_{t_0}=\lceil 2N_0{y}_0\rceil$.

2: Let ${\mathbf{d}}_0={\mathbf{e}}_{c_{t_0}}$ be the standard basis vector of length $2N_0+1$ with element $c_{t_0}$ equal to one.

3: For $k=1:K$,

Compute the conditional distribution ${\tilde{\mathbf{d}}}_k$ at sampling event k, conditional on the distribution ${\mathbf{d}}_{k-1}$ at time $t_{k-1}$ using

$${\tilde{\mathbf{d}}}_k={\mathbf{d}}_{k-1}\left[\prod _{t=t_{k-1}+1}^{t_k}{\mathbf{T}}_{t-1,t}\right].$$

Sample $c_{t_k}=i$ with probability ${\tilde{\mathbf{d}}}_k\left(i\right)$, for $i=0,1,\dots ,2N_{t_k}$.

Set ${\mathbf{d}}_k={\mathbf{e}}_{c_{t_k}}$, where ${\mathbf{e}}_{c_{t_k}}$ is the standard basis vector of length $2N_{t_k}+1$ with element $c_{t_k}$ equal to one.

4: For$k=1:K$, sample $O_k\sim \text{Binomial}(n_k,c_{t_k}/(2N_{t_k}\left)\right)$.

5: If conditioning on segregation in the final sample and o_K = 0 or o_K=n_K, return to Step 1. Otherwise, the sampled trajectory is $o_{[1:K]}$.

Procedure 6. Simulating diffusion model trajectories

1: Optional: sample the initial population allele frequency y₀ uniformly from a predetermined interval $(y_{\ell },y_u]$, where $0\le y_{\ell }\le y_u\le 1$.

2: For an initial starting frequency y₀ initialize

$${\mathbf{b}}_0={\mathbf{C}}_{{\ell }_1}^{-1}{\mathbf{B}}_{{\ell }_1}\left(y_0\right),$$

where ${\mathbf{B}}_{\ell }\left(y_0\right)$ is the vector of eigenfunctions of the diffusion operator given inequation (A.14) and ${\mathbf{C}}_{\ell }=\text{diag}{\{\langle B_{\ell ,i},B_{\ell ,i}\rangle \}}_{i=0}^{\infty }$ is given in equation(A.18).

3: For $k=1:K$,

Compute

$${\mathbf{a}}_k =\{\begin{array}{cc}{\mathbf{b}}_{k-1}{\mathbf{E}}_{{\ell }_k}(t_k-t_{k-1})\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{k-1}={\ell }_k,\hfill \\ {\mathbf{b}}_{k-1}\mathbf{F}(t_{k-1},t_k;\zeta )\hfill & \hspace{0.17em}\text{otherwise}.\hfill \end{array}$$

For $i=0,1,\dots ,n_k$, compute

$${\tilde{\mathbf{b}}}_k\left(i\right)={\mathbf{a}}_k{\mathbf{W}}_{{\ell }_k}{\mathbf{G}}_{{\ell }_k}^i{(1-{\mathbf{G}}_{{\ell }_k})}^{n_k-i}{\mathbf{W}}_{{\ell }_k}^{-1},$$

noting that ${\tilde{\mathbf{b}}}_{k,0}\left(i\right)\propto {\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_k=i\}$ (eq. D.3).

Sample o_k = i with probability ${\mathbf{b}}_{k,0}\left(i\right)/\sum _{i=0}^{n_k}{\mathbf{b}}_{k,0}\left(i\right)$.

Set ${\mathbf{b}}_k={\mathbf{b}}_k\left(o_k\right)$.

Here, the matrices ${\mathbf{E}}_{\ell }\left(t\right),\hspace{0.17em}\mathbf{F}(t_{k-1},t_k;\zeta ),\hspace{0.17em}{\mathbf{W}}_{\ell }$, and ${\mathbf{G}}_{\ell }$ are given by equations (A.17), (B.10), (A.15) and (A.11), respectively and ζ is the set of Chebyshev nodes in the interval $[0,1]$. The matrix inverse ${\mathbf{W}}_{\ell }^{-1}={\mathbf{D}}_{\ell }{\mathbf{W}}_{\ell }^T{\mathbf{C}}_{\ell }^{-1}$ is computed easily using the diagonal matrices ${\mathbf{C}}_{\ell }$ and ${\mathbf{D}}_{\ell }$ in equations (A.18) and (A.19).

4: If conditioning on segregation in the final sample and o_K = 0 or o_K=n_K, return to Step 1. Otherwise, the sampled trajectory is $o_{[1:K]}$.

Procedure 7. Grid search

1: Specify the bounds $s_{\ell }$ and s_u of an interval $[s_{\ell },s_u]$in which to search.

2: Specify the stopping tolerance ε.

3: While $s_u-s_{\ell }>\mathrm{\epsilon }$:

Evaluate the likelihood at the points $\{s^{(0)},s^{(1)},s^{(2)},s^{(3)},s^{(4)},s^{(5)}\}={\{s_{\ell }+i\delta \}}_{i=0}^5$, where $\delta =(s_u-s_{\ell })/5$.

Let $s_{\max \hspace{0.17em}}=\arg \hspace{0.17em}{\max \hspace{0.17em}}_i\left\{s^{(i)}\right\}$.

If $s_{\max \hspace{0.17em}}=0$, set $s_{\ell }=s^{(0)}$ and $s_u=s^{(1)}$.

Else, if $s_{\max \hspace{0.17em}}=5$, set $s_{\ell }=s^{(4)}$ and $s_u=s^{(5)}$.

Else, set $s_{\ell }=s^{(s_{\max \hspace{0.17em}}-1)}$ and $s_u=s^{(s_{\max \hspace{0.17em}}+1)}$.

4: Return $\hat{s}=(s_{\ell }+s_u)/2$.

Supplementary Material

Supplementary figure S1 is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Appendix A

Diffusion Transition Densities: Background

The equations in the “Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ under the Diffusion Approximation” section were derived under a model in which the selected allele A evolves under the diffusion approximation in a population of piecewise constant size. Given that allele A has frequency x at a fixed time s, the density at a later time t is given by the transition density of the diffusion approximation (eq. 12). Steinrücken et al. (2014) derived a formula for the density for the case of a single population of constant size. Here, we review this derivation to provide background and notation for the derivation of the diffusion model probability computed in Procedure 2.

The Diffusion Approximation in a Population of Constant Size

Let $p_{\ell }(s,t;x,y)$ denote the transition density restricted to a specific epoch $\ell$ of constant size with $s,t\in \ell$. The density $p_{\ell }(s,t;x,y)$ is the unique solution of the Kolmogorov backward equation,

$$\frac{\partial p_{\ell }(s,t;x,y)}{\partial t}=\frac{1}{2N_{\ell }}{\mathcal{L}}_{\ell }{p}_{\ell }(s,t;x,y)$$ (A.1)

satisfying the terminal condition ${\rho }_s(y)=\delta (y-x)$, where $\delta (·)$ is the Dirac delta distribution and ${\mathcal{L}}_{\ell }$ is the Kolmogorov backward operator in the epoch defined in equation (A.2). The factor $1/2N_{\ell }$ in equation (A.1) is introduced so that the time-scaling is the same in all epochs, and time is measured continuously in units of generations.

The Kolmogorov backward operator is defined in terms of the scaled mutation and selection parameters ${\beta }_{\ell }=4N_{\ell }{u}_{aA}^{(\ell )},\hspace{0.17em}{\alpha }_{\ell }=4N_{\ell }{u}_{Aa}^{(\ell )}$, and ${\sigma }_{\ell }=N_{\ell }{s}_{\ell }$ as

$${\mathcal{L}}_{\ell }=\frac{1}{2}{\xi }^2(x)\frac{{\partial }^2}{\partial x^2}+{\mu }_{\ell }(x)\frac{\partial }{\partial x},$$ (A.2)

where the quantity

$${\xi }^2(x)=x(1-x)$$ (A.3)

captures the contribution to the change in allele frequency arising from genetic drift and

$${\mu }_{\ell }(x)=\frac{1}{2}[{\beta }_{\ell }-({\beta }_{\ell }+{\alpha }_{\ell })x]+\hspace{0.17em}2x(1-x)[h_{\ell }{\sigma }_{\ell }(1-2x)+{\sigma }_{\ell }x]$$ (A.4)

captures the contribution from recurrent mutation and selection.

Song and Steinrücken (2012) showed that $p_{\ell }(s,t;x,y)$ can be expressed as an expansion in the eigenfunctions of ${\mathcal{L}}_{\ell }$ of the form

$$p_{\ell }(s,t;x,y)=\hspace{0.17em}\sum _{n=0}^{\infty }{e}^{-{\lambda }_{\ell ,n}(t-s)/2N_{\ell }}\frac{{\pi }_{\ell }(y)B_{\ell ,n}(x)B_{\ell ,n}(y)}{{\langle B_{\ell ,n},B_{\ell ,n}\rangle }_{{\pi }_{\ell }}},$$ (A.5)

where ${\{B_{\ell ,n}(x)\}}_{n=0}^{\infty }$ are the eigenfunctions of ${\ell }_{\ell }$ with associated eigenvalues ${\left\{{\lambda }_{\ell ,n}\right\}}_{n=0}^{\infty }$ and the function ${\pi }_{\ell }(y)$ is given by

$${\pi }_{\ell }(y)=e^{{\overline{\sigma }}_{\ell }(y)}{y}^{{\beta }_{\ell }-1}{(1-y)}^{{\alpha }_{\ell }-1},$$ (A.6)

where ${\overline{\sigma }}_{\ell }(y)=4h_{\ell }{\sigma }_{\ell }y(1-y)+2{\sigma }_{\ell }{y}^2$. The inner product ${\langle f,g\rangle }_{\omega }$ with respect to a weight function $\omega (x)$ in equation (A.5) is defined for two functions f and g on an interval $[a,b]$ by

$${\langle f,g\rangle }_{\omega }={\int }_a^{b}f(x)g(x)\omega (x)dx.$$ (A.7)

In equation (A.5), the inner product ${\langle ·,·\rangle }_{{\pi }_{\ell }}$ is taken over the interval $[0,1]$ with respect to ${\pi }_{\ell }(y)$.

Expressions for the Quantities in Equation (A.5)

Expressions for the eigenvalues ${\left\{{\lambda }_{\ell ,n}\right\}}_{n=0}^{\infty }$, eigenfunctions ${\{B_{\ell ,n}(y)\}}_{n=0}^{\infty }$, and inner products ${\{\langle B_{\ell ,n},B_{\ell ,n}\rangle \}}_{n=0}^{\infty }$ in equation (A.5) can be obtained using a matrix formulation developed by Steinrücken et al. (2014). In particular, the eigenfunctions ${\{B_{\ell ,n}(y)\}}_{n=0}^{\infty }$ can be expressed as

$$B_{\ell ,n}(y)=\sum _{m=0}^{\infty }{w}_{\ell ,n,m}{e}^{-{\overline{\sigma }}_{\ell }(y)/2}{R}_m^{({\beta }_{\ell },{\alpha }_{\ell })}(y),$$ (A.8)

where $R_m^{(\alpha ,\beta )}(y)=p_m^{(\beta -1,\alpha -1)}(2y-1)$ and $p_m^{(a,b)}(y)$ is the mth classical Jacobi polynomial (Abramowitz and Stegun 1972, Chapter 22). The vector ${\mathbf{w}}_{\ell ,n}=(w_{\ell ,n,0},w_{\ell ,n,1},\dots )$ is the nth left eigenvector of the infinite-dimensional matrix

$${\mathbf{M}}_{\ell }:=-({{\rm Y}}^{({\alpha }_{\ell },{\beta }_{\ell })}+\sum _{r=0}^4{q}_{\ell ,r}{\mathbf{G}}_{\ell }^r)$$ (A.9)

corresponding to the nth eigenvalue ${\lambda }_{\ell ,n}$, where ${{\rm Y}}^{(\alpha ,\beta )}=\text{diag}({\upsilon }_0^{(\alpha ,\beta )},{\upsilon }_1^{(\alpha ,\beta )},\dots )$ is the diagonal matrix with elements given by ${\upsilon }_n^{(\alpha ,\beta )}=\frac{1}{2}n(n+\alpha +\beta -1)$ and the quantities $q_{\ell ,r}$ are given by

$$\begin{array}{l}{q}_{\ell ,0}={\alpha }_k{h}_{\ell }{\sigma }_{\ell },\\ q_{\ell ,1}=-(2+3{\alpha }_{\ell }+{\beta }_{\ell }-2h_{\ell }{\sigma }_{\ell })h_{\ell }{\sigma }_{\ell }+(1+{\alpha }_{\ell }){\sigma }_{\ell },\\ q_{\ell ,2}=(2+2{\alpha }_{\ell }+2{\beta }_{\ell }+4{\sigma }_{\ell }-10h_{\ell }{\sigma }_{\ell })h_{\ell }{\sigma }_{\ell }-\hspace{0.17em}(1+{\alpha }_{\ell }+{\beta }_{\ell }){\sigma }_{\ell },\\ q_{\ell ,3}=16h_{\ell }^2{\sigma }_{\ell }^2+2{\sigma }_{\ell }^2(1-6h_{\ell }),\\ q_{\ell ,4}=-2{\sigma }_{\ell }^2{(1-2h_{\ell })}^2.\end{array}$$ (A.10)

The matrix ${\mathbf{G}}_{\ell }^r$ in equation (A.9) has elements given by

$${[{\mathbf{G}}_{\ell }]}_{n,m}=\{\begin{array}{l}\frac{(n+{\alpha }_{\ell }-1)(n+{\beta }_{\ell }-1)}{(2n+{\alpha }_{\ell }+{\beta }_{\ell }-1)(2n+{\alpha }_{\ell }+{\beta }_{\ell }-2)},\hfill \\ \hspace{0.17em}\text{if}\hspace{0.17em}m=n-1\hspace{0.17em}\text{and}\hspace{0.17em}n>0,\hfill \\ \frac{1}{2}-\frac{{\beta }_{\ell }^2-{\alpha }_{\ell }^2-2({\beta }_{\ell }-{\alpha }_{\ell })}{2(2n+{\alpha }_{\ell }+{\beta }_{\ell })(2n+{\alpha }_{\ell }+{\beta }_{\ell }-2)},\hfill \\ \hspace{0.17em}\text{if}\hspace{0.17em}m=n\hspace{0.17em}\text{and}\hspace{0.17em}n\ge 0,\hfill \\ \frac{(n+1)(n+{\alpha }_{\ell }+{\beta }_{\ell }-1)}{2(2n+{\alpha }_{\ell }+{\beta }_{\ell })(2n+{\alpha }_{\ell }+{\beta }_{\ell }-1)},\hfill \\ \hspace{0.17em}\text{if}\hspace{0.17em}m=n+1\hspace{0.17em}\text{and}\hspace{0.17em}n\ge 0,\hfill \\ 0,\hfill \\ \text{otherwise},\hfill \end{array}$$ (A.11)

which correspond to the coefficients of the three-term recurrence relation satisfied by the Jacobi Polynomials.

Matrix Expressions for the Transition Density

It is computationally and notationally simpler to express the eigenfunctions of ${\mathcal{L}}_{\ell }$ and the transition density as products of matrices. In particular, we can express equation (A.8) as

$$B_{\ell ,n}(y)=e^{-{\overline{\sigma }}_{\ell }(y)/2}{\mathbf{w}}_{\ell ,n}{\mathbf{R}}^{({\alpha }_{\ell },{\beta }_{\ell })}(y),$$ (A.12)

where

$${\mathbf{R}}^{(\alpha ,\beta )}(y)={(R_0^{(\alpha ,\beta )}(y),R_1^{(\alpha ,\beta )}(y),\dots )}^T$$ (A.13)

and we can express the vector ${\mathbf{B}}_{\ell }(y)$ of eigenfunctions as

$${\mathbf{B}}_{\ell }(y)={(B_{\ell ,0}(y),B_{\ell ,1}(y),\dots )}^T\hspace{0.17em}=e^{-{\overline{\sigma }}_{\ell }(y)/2}{\mathbf{W}}_{\ell }{\mathbf{R}}^{({\alpha }_{\ell },{\beta }_{\ell })}(y),$$ (A.14)

where

$${\mathbf{W}}_{\ell }=[\begin{array}{l}{\mathbf{w}}_{\ell ,0}\\ {\mathbf{w}}_{\ell ,1}\\ ⋮\end{array}]$$ (A.15)

is the matrix whose rows are the left eigenvectors of the matrix ${\mathbf{M}}_{\ell }$ in equation (A.9).

Using equations (A.5) and (A.14), the transition density in a single epoch ℓ can then be expressed as the matrix product

$$p_{\ell }(s,t;x,y)={\pi }_{\ell }(y){\mathbf{B}}_{\ell }^T(x){\mathbf{C}}_{\ell }^{-1}{\mathbf{E}}_{\ell }(t-s){\mathbf{B}}_{\ell }(y),$$ (A.16)

where

$${\mathbf{E}}_{\ell }(t)=\text{diag}\{e^{-{\lambda }_{\ell ,0}t/2N_{\ell }},e^{-{\lambda }_{\ell ,1}t/2N_{\ell }},\dots \}$$ (A.17)

and ${\mathbf{C}}_{\ell }=\text{diag}{\left\{{\langle B_{\ell ,n},B_{\ell ,n}\rangle }_{{\pi }_{\ell }}\right\}}_{n=0}^{\infty }$. Steinrücken et al. (2014) showed that the matrix ${\mathbf{C}}_{\ell }$ in equation (A.16) can be expressed as

$${\mathbf{C}}_{\ell }={\mathbf{W}}_{\ell }{\mathbf{D}}_{\ell }{\mathbf{W}}_{\ell }^T,$$ (A.18)

where

$${\mathbf{D}}_{\ell }=\text{diag}\{d_0^{({\alpha }_{\ell },{\beta }_{\ell })},d_1^{({\alpha }_{\ell },{\beta }_{\ell })},\dots \}$$ (A.19)

and

$$d_i^{({\alpha }_{\ell },{\beta }_{\ell })}=\hspace{0.17em}\frac{\Gamma (i+{\alpha }_{\ell })\Gamma (i+{\beta }_{\ell })}{(2i+{\alpha }_{\ell }+{\beta }_{\ell }-1)\Gamma (i+{\alpha }_{\ell }+{\beta }_{\ell }-1)\Gamma (i+1)}.$$ (A.20)

Thus, the transition density in a single epoch can be computed by constructing matrix ${\mathbf{M}}_{\ell }$, computing its eigenvectors ${\mathbf{W}}_{\ell }$ and eigenvalues $({\lambda }_{\ell ,0},{\lambda }_{\ell ,1},\dots )$, and plugging these into the components of equation (A.16). In practice, because the matrix ${\mathbf{M}}_{\ell }$ has infinite dimension, we approximate it by truncating its dimensions at some large integer M yielding approximate eigenvectors ${\left\{{\tilde{\mathbf{w}}}_{\ell ,n}\right\}}_{n=0}^M$ and eigenvalues ${\left\{{\tilde{\lambda }}_{\ell ,n}\right\}}_{n=0}^M$. We also truncate the length of the vector ${\mathbf{B}}_{\ell }(y)$ at a large integer N. Although these truncations lead to approximate values of the transition density, the approximation can be made arbitrarily precise by taking $N\le M$ to be sufficiently large.

Appendix B

Recursions for the Coefficients ${\mathbf{a}}_k$ and ${\mathbf{b}}_k$

Discussion of the Problem

Here, we extend the HMM of Steinrücken et al. (2014) to accommodate populations of piecewise constant size. As we noted in the “Computing ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ under the Diffusion Approximation” section, the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ of the data under the diffusion model can be obtained using the equation

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}={\int }_{y=0}^1{f}_K(y)dy,$$ (B.1)

where the quantity $f_K(y)$ is obtained by recursively evaluating equations (16) and (17). Because $f_k(y)$ and $g_k(y)$ can be expressed as the series $f_k(y)={\pi }_{{\ell }_k}(y){\mathbf{b}}_k{\mathbf{B}}_{{\ell }_k}(y)$ and $g_k(y)={\pi }_{{\ell }_k}(y){\mathbf{a}}_k{\mathbf{B}}_{{\ell }_k}(y)$ (eqs. 18 and 19), determining $f_k(y)$ and $g_k(y)$ amounts to determining the coefficients ${\mathbf{a}}_k$ and ${\mathbf{b}}_k$. Thus, it is useful to develop analogs of the recursions (15) and (16) that apply to the coefficients themselves.

Equations for Propagating Coefficients

From equation (16), it can be seen that obtaining $f_k(y)$ from $g_k(y)$ involves only multiplication by a polynomial in y. Thus, the formula for obtaining the coefficients ${\mathbf{b}}_k$ from the coefficients ${\mathbf{a}}_k$ does not depend on the population history and, therefore, it can be obtained from results in Steinrücken et al. (2014) who derived formulas for the recursion for the case of a population of constant size. However, the formula for obtaining $g_k(y)$ from $f_{k-1}(y)$ (eq. 17) involves the transition probability $p_{\Theta }(t_{k-1},t_k;z,y)$, which depends on the population parameters Θ. Thus, it is necessary to account for the population history when computing the coefficients ${\mathbf{a}}_k$ from the coefficients ${\mathbf{b}}_{k-1}$.

To obtain ${\mathbf{a}}_k$ from ${\mathbf{b}}_{k-1}$, we first consider the more general problem of obtaining the generalized vector of coefficients ${\mathbf{a}}_k(t)$ from ${\mathbf{b}}_{k-1}$, where ${\mathbf{a}}_k(t)$ is defined as the vector of coefficients of the expansion of the generalized density $g_k(y,t)$ defined by

$$g_k(y,t)dy\hspace{0.17em}:={\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:k-1]}=o_{[1:k-1]},y\le Y_t<y+dy\}\hspace{0.17em}={\pi }_{{\ell }_t}(y){\mathbf{a}}_k(t){\mathbf{B}}_{{\ell }_t}(y),$$ (B.2)

i.e., the joint density of the observed data up to sample k – 1 and the allele frequency at time t, where we assume $t_{k-1}\le t$ so that the time t at which $g_k(y,t)$ is evaluated occurs later than the time $t_{k-1}$ at which $f_k(y)$ is evaluated. The density $g_k(y)=g_k(y,t_k)$ defined in equation (14) is a special case of the generalized density $g_k(y,t)$ obtained when t = t_k.

To obtain ${\mathbf{a}}_k(t)$ from ${\mathbf{b}}_{k-1}$, there are two scenarios to consider: the case in which both $t_{k-1}$ and t lie within the same epoch $\ell$ and the case in which $t_{k-1}$ and t lie within distinct epochs. Our derivations of these separate cases provide the results necessary for step 2 of Procedure 2.

The Case ${\ell }_{t_{k-1}}={\ell }_t=\ell$

If both $t_{k-1}$ and t lie within the same epoch $\ell$, then the transition density is given by equation (A.16) and we have

$${\pi }_{\ell }(y){\mathbf{a}}_k(t){\mathbf{B}}_{\ell }(y)\hspace{0.17em}=g_k(y,t)\hspace{0.17em}={\int }_0^1{f}_{k-1}(z)p_{\ell }(t_{k-1},t;z,y)dz\hspace{0.17em}={\int }_0^1{\pi }_{\ell }(z){\mathbf{b}}_{k-1}{\mathbf{B}}_{\ell }(z){\pi }_{\ell }(y){\mathbf{B}}_{\ell }^T(z){\mathbf{C}}_{\ell }^{-1}\times \hspace{0.17em}{\mathbf{E}}_{\ell }(t-t_{k-1}){\mathbf{B}}_{\ell }(y)dz\hspace{0.17em}={\pi }_{\ell }(y){\mathbf{b}}_{k-1}[{\int }_0^1{\pi }_{\ell }(z){\mathbf{B}}_{\ell }(z){\mathbf{B}}_{\ell }^T(z)dz]\times \hspace{0.17em}{\mathbf{C}}_{\ell }^{-1}{\mathbf{E}}_{\ell }(t-t_{k-1}){\mathbf{B}}_{\ell }(y)\hspace{0.17em}={\pi }_{\ell }(y){\mathbf{b}}_{k-1}{\mathbf{E}}_{\ell }(t-t_{k-1}){\mathbf{B}}_{\ell }(y),$$ (B.3)

where the first equality follows from the definition of $g_k(y,t)$ (eq. B.2) and the second equality follows from equation (17). In the fifth equality we have used the fact that ${\int }_0^1{\pi }_{\ell }(y){\mathbf{B}}_{\ell }(y){\mathbf{B}}_{\ell }^T(y)dy={\mathbf{C}}_{\ell }$. Because the eigenfunctions ${\{B_{\ell ,n}(y)\}}_{n=0}^{\infty }$ form a complete basis of the Hilbert space defined with respect to the inner product ${\langle ·,·\rangle }_{{\pi }_{\ell }}$, the coefficients in the expansion on the left-hand side of equation (B.3) must equal those on the right-hand side. Thus,

$${\mathbf{a}}_k(t)={\mathbf{b}}_{k-1}{\mathbf{E}}_{\ell }(t-t_{k-1}),\hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{t_{k-1}}={\ell }_t.$$ (B.4)

The Case When ${\ell }_{t_{k-1}}\ne {\ell }_t$

If the times $t_{k-1}$ and t lie in different epochs, ${\ell }_{t_{k-1}}$ and ${\ell }_t$, then the transition density is no longer given by equation (A.16). Instead, we must use a formula for the transition density across multiple epochs of different sizes. Steinrücken et al. (2015) showed that if the allele frequency density ${\rho }_{\ell ,s}(y)$ at time s in epoch $\ell$ is given by the expansion

$${\rho }_{\ell ,s}(y)={\pi }_{\ell }(y){\mathbf{r}}_{\ell ,s}{\mathbf{B}}_{\ell }(y),$$ (B.5)

where ${\mathbf{r}}_{\ell ,s}=(r_{\ell ,s,0},r_{\ell ,s,1},\dots )$ are the coefficients encoding the density at time s in the basis of the eigenfunctions ${\{{\mathbf{B}}_{\ell ,n}(y)\}}_{n=0}^{\infty }$, then at time t in epoch $\ell +1$, the allele frequency density is given by ${\rho }_{\ell +1,t}(y)={\pi }_{\ell +1}(y){\mathbf{r}}_{\ell +1,t}{\mathbf{B}}_{\ell +1}(y)$, where the coefficients ${\mathbf{r}}_{\ell +1,t}$ are given by

$${\mathbf{r}}_{\ell +1,t}={\mathbf{r}}_{\ell ,s}{\mathbf{Z}}_{\ell }({\tau }_{\ell }-s;\zeta ){\mathbf{E}}_{\ell +1}(t-{\tau }_{\ell }),$$ (B.6)

where ${\tau }_{\ell }$ is the time of the terminating boundary of epoch $\ell$, and

$${\mathbf{Z}}_{\ell }(\tau ;\zeta )\hspace{0.17em}={\mathbf{E}}_{\ell }(\tau ){\mathbf{W}}_{\ell }{\mathbf{R}}_{\ell }(\zeta ){\mathbf{H}}_{\ell ,\ell +1}(\zeta ){\mathbf{R}}_{\ell +1}^{-1}(\zeta ){\mathbf{W}}_{\ell +1}^{-1}.$$ (B.7)

In equation (B.7), ${\mathbf{R}}_{\ell }(\zeta )$ and ${\mathbf{H}}_{\ell ,\ell +1}(\zeta )$ are given by

$${\mathbf{R}}_{\ell }(\zeta )=[{\mathbf{R}}^{({\alpha }_{\ell },{\beta }_{\ell })}({\zeta }_0),{\mathbf{R}}^{({\alpha }_{\ell },{\beta }_{\ell })}({\zeta }_1),\dots ],$$ (B.8)

where ${\mathbf{R}}^{\alpha ,\beta }(y)$ is defined in equation (A.13) and

$${\mathbf{H}}_{\ell ,\ell +1}(\zeta )\hspace{0.17em}=\text{diag }\{\frac{{\pi }_{\ell }({\zeta }_0)e^{-{\overline{\sigma }}_{\ell }({\zeta }_0)/2}}{{\pi }_{\ell +1}({\zeta }_0)e^{-{\overline{\sigma }}_{\ell +1}({\zeta }_0)/2}},\frac{{\pi }_{\ell }({\zeta }_1)e^{-{\overline{\sigma }}_{\ell }({\zeta }_1)/2}}{{\pi }_{\ell +1}({\zeta }_1)e^{-{\overline{\sigma }}_{\ell +1}({\zeta }_1)/2}},\dots \},$$ (B.9)

for an arbitrary collection of distinct values $\zeta =({\zeta }_0,{\zeta }_1,\dots )\in [0,1]$. In practice, we take $\zeta$ to be the Chebyshev nodes (Steinrücken et al. 2015).

By repeated application of equation (B.6), it follows that if the coefficients ${\mathbf{r}}_{{\ell }_s,s}$ encode the density ${\rho }_s(y)$ at time s in epoch ${\ell }_s$, then the coefficients ${\mathbf{r}}_{{\ell }_t,t}$ encoding the density ${\rho }_t(y)$ at time t in epoch ${\ell }_t>{\ell }_s$ are given by ${\mathbf{r}}_{{\ell }_t,t}={\mathbf{r}}_{{\ell }_s,s}\mathbf{F}(s,t;\zeta ),$ where

$$\mathbf{F}(s,t;\zeta )\hspace{0.17em}={\mathbf{Z}}_{{\ell }_s}({\tau }_{{\ell }_s}-s;\zeta )\left[\prod _{i={\ell }_s+1}^{{\ell }_t-1}{\mathbf{Z}}_i({\tau }_i-{\tau }_{i-1};\zeta )\right]\times \hspace{0.17em}{\mathbf{E}}_{{\ell }_t}(t-{\tau }_{{\ell }_t-1}).$$ (B.10)

Moreover, if we define ${\mathbf{r}}_{{\ell }_s,s}(x)$ to be the vector of coefficients encoding the density $\rho (y)=\delta (y-x)$, then it follows from equation (B.10) that the transition density $p_{\Theta }(s,t;x,y)$ for times s < t lying in distinct epochs ${\ell }_s<{\ell }_t$ is given by

$$\begin{array}{l}{p}_{\Theta }(s,t;x,y)={\pi }_{{\ell }_t}(y){\mathbf{r}}_{{\ell }_s,s}(x)\mathbf{F}(s,t;\zeta ){\mathbf{B}}_{{\ell }_t}(y),\\ \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_s<{\ell }_t.\end{array}$$ (B.11)

For the initial condition ${\rho }_{\ell ,s}(y)=\delta (y-x)$, it was shown in Proposition 1 of Steinrücken et al. (2014) that the coefficients ${\mathbf{r}}_{{\ell }_s,s}(x)$ are given by

$${\mathbf{r}}_{{\ell }_s,s}(x)=\left(\frac{B_{{\ell }_s,0}(x)}{{\langle B_{{\ell }_s,0},B_{{\ell }_s,0}\rangle }_{{\pi }_{{\ell }_s}}},\frac{B_{{\ell }_s,1}(x)}{{\langle B_{{\ell }_s,1},B_{{\ell }_s,1}\rangle }_{{\pi }_{{\ell }_s}}},\dots \right)\hspace{0.17em}={\mathbf{B}}_{{\ell }_s}{(x)}^T{\mathbf{C}}_{{\ell }_s}^{-1},$$ (B.12)

yielding

$$\begin{array}{l}{p}_{\Theta }(s,t;x,y)={\pi }_{{\ell }_t}(y){\mathbf{B}}_{{\ell }_s}{(x)}^T{\mathbf{C}}_{{\ell }_s}^{-1}\mathbf{F}(s,t;\zeta ){\mathbf{B}}_{{\ell }_t}(y),\hspace{0.17em}\\ \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_s<{\ell }_t,\end{array}$$ (B.13)

which is obtained by plugging equation (B.12) into equation (B.11).

We can now plug equation (B.13) into equation (17) to obtain a relationship between ${\mathbf{a}}_k(t)$ and ${\mathbf{b}}_{k-1}$ when times $t_{k-1}$ and t lie in different epochs:

$${\pi }_{{\ell }_t}(y){\mathbf{a}}_k(t){\mathbf{B}}_{{\ell }_t}(y)\hspace{0.17em}=g_k(y,t)\hspace{0.17em}={\int }_0^1{f}_{k-1}(z)p_{\Theta }(t_{k-1},t;z,y)dz\hspace{0.17em}={\int }_0^1{\pi }_{{\ell }_{k-1}}(z){\mathbf{b}}_{k-1}{\mathbf{B}}_{{\ell }_{k-1}}(z){\pi }_{{\ell }_t}(y){\mathbf{B}}_{{\ell }_{k-1}}{(z)}^T\hspace{0.17em}{\mathbf{C}}_{{\ell }_{k-1}}^{-1}\mathbf{F}(t_{k-1},t;\zeta ){\mathbf{B}}_{{\ell }_t}(y)dz\hspace{0.17em}={\pi }_{{\ell }_t}(y){\mathbf{b}}_{k-1}[{\int }_0^1{\pi }_{{\ell }_{k-1}}(z){\mathbf{B}}_{{\ell }_{k-1}}(z)\hspace{0.17em}{\mathbf{B}}_{{\ell }_{k-1}}{(z)}^{T}dz]{\mathbf{C}}_{{\ell }_{k-1}}^{-1}\mathbf{F}(t_{k-1},t;\zeta ){\mathbf{B}}_{{\ell }_t}(y)\hspace{0.17em}={\pi }_{{\ell }_t}(y){\mathbf{b}}_{k-1}\mathbf{F}(t_{k-1},t;\zeta ){\mathbf{B}}_{{\ell }_t}(y),$$ (B.14)

where we have again used the fact that ${\int }_0^1{\pi }_{\ell }(z){\mathbf{B}}_{\ell }(z){\mathbf{B}}_{\ell }{(x)}^{T}dy={\mathbf{C}}_{\ell }$. Finally, by the uniqueness of expansions in the Hilbert basis ${\left\{B_{{\ell }_t,n}\right\}}_{n=0}^{\infty }$, we have

$${\mathbf{a}}_k(t)={\mathbf{b}}_{k-1}\mathbf{F}(t_{k-1},t;\zeta ),\hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{t_{k-1}}\ne {\ell }_t.$$ (B.15)

The results derived in the “Equations for Propagating Coefficients” section provide the machinery necessary to propagate the coefficients ${\mathbf{a}}_k$ and ${\mathbf{b}}_k$ in the HMM over time. These results can now be used to compute the probability of observing a set of sampled allele frequencies under the diffusion model.

Derivation of Lemmas Necessary for Procedure 2

We now obtain three lemmas that provide the steps in Procedure 2.

Lemma B.3.1

If the initial frequency density ${\rho }_0(\mathit{y})$ at time ${\mathit{t}}_0=0$ is ${\rho }_0(\mathit{y})=\delta (\mathit{y}-\mathit{x})$, then the value of the initial vector ${\mathbf{b}}_0$ encoding the quantity ${\mathit{f}}_0(\mathit{y})$ is given by

$${\mathbf{b}}_0=\left(\frac{B_{{\ell }_1,0}(x)}{c_{{\ell }_1,0}},\frac{B_{{\ell }_1,1}(x)}{c_{{\ell }_1,1}},\dots \right)={\mathbf{C}}_{{\ell }_1}^{-1}{\mathbf{B}}_{{\ell }_1}(x),$$ (B.16)

where ${\mathbf{B}}_{\ell }(x)$ is given in equation (A.14) and ${\mathbf{C}}_{\ell }$ is the diagonal matrix given in equation (A.18).

Proof

Because ${\mathbf{b}}_0$ depends only on the parameters ${\Theta }_{{\ell }_1}$ in the first epoch, the proof of Lemma B.3.1 is the same whether we consider a population composed of a single epoch, or a population composed of multiple epochs. The equation for $f_k(y)$ (eq. 18) is the same as equation 2.14 of Steinrücken et al. (2014). Thus, the coefficients ${\mathbf{b}}_k$ in this paper correspond to the coefficients ${\mathbf{b}}_k$ in Steinrücken et al. (2014) who proved Lemma B.3.1 for the case of a population of constant size. Thus, the first equality in Lemma B.3.1 follows directly from Proposition 1 of Steinrücken et al. (2014). The matrix representation in the second equality follows directly from the definitions of ${\mathbf{C}}_{\ell }$ and ${\mathbf{B}}_{\ell }(x)$. □

Lemma B.3.2

If the initial frequency density ${\rho }_0(y)$ at time $t_0=0$ is unspecified and we instead assume a uniform prior on the allele frequency at the time of the first sampling event, then the coefficients ${\mathbf{b}}_1$ encoding the density at time t₁ are given by

$${\mathbf{b}}_1=\frac{1}{\text{Beta}(o_1+1,n_1-o_1+1)B_{(-{\sigma }_{{\ell }_1},o_1+1,n_1-o_1+1),0}(0)}\times \hspace{0.17em}{\mathbf{C}}_{({\sigma }_{{\ell }_1},o_1+1,n_1-o_1+1)}{\mathbf{W}}_{({\sigma }_{{\ell }_1},o_1+1,n_1-o_1+1)}\times \hspace{0.17em}{\mathbf{D}}_{({\sigma }_{{\ell }_1},o_1+1,n_1-o_1+1)}{\mathbf{W}}_{(-{\sigma }_{{\ell }_1},o_1+1,n_1-o_1+1)}^T\times \hspace{0.17em}{\mathbf{Z}}_{({\sigma }_{{\ell }_1},o_1+1,n_1-o_1+1),({\sigma }_{{\ell }_1},{\alpha }_{{\ell }_1},{\beta }_{{\ell }_1})}(0;\zeta ),$$ (B.17)

where ${\mathbf{C}}_{(\sigma ,\alpha ,\beta )},\hspace{0.17em}{\mathbf{D}}_{(\sigma ,\alpha ,\beta )}$, and ${\mathbf{W}}_{(\sigma ,\alpha ,\beta )}$ are obtained by replacing ${\sigma }_{\ell },\hspace{0.17em}{\alpha }_{\ell }$, and ${\beta }_{\ell }$ in equations (A.18), (A.19), and (A.15) with σ, α, and β. Similarly, ${\mathbf{Z}}_{(\sigma ,\alpha ,\beta ),(\tilde{\sigma },\tilde{\alpha },\tilde{\beta })}(\tau ;\zeta )$ is obtained by replacing ${\sigma }_{\ell },\hspace{0.17em}{\sigma }_{\ell +1},\hspace{0.17em}{\alpha }_{\ell },\hspace{0.17em}{\alpha }_{\ell +1},\hspace{0.17em}{\beta }_{\ell }$, and ${\beta }_{\ell +1}$ in equation (B.7) with σ, $\tilde{\sigma }$, α, $\tilde{\alpha }$, β, and $\tilde{\beta }$, respectively, $B_{(\sigma ,\alpha ,\beta )}(0)$ is the eigenfunction in equation (B.23) with ${\sigma }_{\ell },\hspace{0.17em}{\alpha }_{\ell }$, and ${\beta }_{\ell }$ replaced with σ, α, and β, and ${\mathbf{W}}_{(\sigma ,\alpha ,\beta )}$ is the matrix given in equation (A.15) whose rows are the left eigenvectors of ${\mathbf{M}}_{(\sigma ,\alpha ,\beta )}$, i.e., the matrix in equation (A.9) with ${\sigma }_{\ell },\hspace{0.17em}{\alpha }_{\ell }$, and ${\beta }_{\ell }$ replaced with σ, α, and β. Finally, $\text{Beta}(\alpha ,\beta )=\Gamma (\alpha )\Gamma (\beta )/\Gamma (\alpha +\beta )$ is the normalizing constant of the beta distribution with parameters α and β.

Proof

If the initial density ${\rho }_0(y)$ of the allele frequency is unspecified, then the density of $Y_{t_1}$ at the time t₁ of the first sampling event, conditional on the observed number o₁ of copies of allele A is given by Bayes Theorem:

$$f_{Y_{t_1}|O_1}(y|o_1)=\frac{\mathbb{P}\{O_1=o_1|Y_{t_1}=y\}{f}_{Y_1}(y)}{\mathbb{P}\{O_1=o_1\}}.$$ (B.18)

If we suppose that $f_{Y_{t_1}}(y)$ is uniform on the interval $[0,1]$ then equation (B.18) becomes

$$f_{Y_{t_1}|O_1}(y|o_1)\hspace{0.17em}=\frac{\left(\begin{array}{l}{n}_1\\ o_1\end{array}\right)y^{o_1}{(1-y)}^{n_1-o_1}}{{\int }_{y=0}^1\mathbb{P}\{O_1=o|Y_{t_1}=y\}{f}_{Y_{t_1}}(y)dy}\hspace{0.17em}=\frac{\left(\begin{array}{l}{n}_1\\ o_1\end{array}\right)y^{o_1}{(1-y)}^{n_1-o_1}}{{\int }_{y=0}^1\left(\begin{array}{l}{n}_1\\ o_1\end{array}\right)y^{o_1}{(1-y)}^{n_1-o_1}dy}\hspace{0.17em}=\frac{y^{o_1}{(1-y)}^{n_1-o_1}}{{\int }_{y=0}^1{y}^{o_1}{(1-y)}^{n_1-o_1}dy}\hspace{0.17em}=\frac{y^{o_1}{(1-y)}^{n_1-o_1}}{\text{Beta}(o_1+1,n_1-o_1+1)},$$ (B.19)

where, in the final equality, we have used the fact that $y^{o_1}{(1-y)}^{n_1-o_1}$ is the unnormalized beta distribution with parameters $o_1+1$ and $n_1-o_1+1$. Thus, conditional on the first observation o₁, we see that $Y_{t_1}|O_1$ has a beta distribution with parameters $o_1+1$ and $n_1-o_1+1$.

Steinrücken et al. (2014) showed in Appendix C of their paper that the distribution $\rho (y)=\frac{y^{\alpha -1}{(1-y)}^{\beta -1}}{\text{Beta}(\alpha ,\beta )}$ has coefficients given by

$${\mathbf{b}}_{\sigma ,\alpha ,\beta }=\frac{1}{\text{Beta}(\alpha ,\beta )B_{(-\sigma ,\alpha ,\beta ),0}(0)}\hspace{0.17em}{\mathbf{C}}_{(\sigma ,\alpha ,\beta )}{\mathbf{W}}_{(\sigma ,\alpha ,\beta )}\hspace{0.17em}{\mathbf{D}}_{(\sigma ,\alpha ,\beta )}{\mathbf{W}}_{(-\sigma ,\alpha ,\beta )}^T$$

in an epoch with selection parameter σ and mutation parameters α and β. Thus, using the change of basis in equation (B.6), we see that the distribution $\rho (y)=\frac{y^{\alpha -1}{(1-y)}^{\beta -1}}{\text{Beta}(\alpha ,\beta )}$ has coefficients given by ${\mathbf{b}}_{\sigma ,\alpha ,\beta }{\mathbf{Z}}_{(\sigma ,\alpha ,\beta ),({\sigma }_{\ell },{\alpha }_{\ell },{\beta }_{\ell })}(0;\zeta )$ in the basis of eigenfunctions ${\{B_{\ell ,n}(y)\}}_{n=0}^{\infty }$ corresponding to an epoch with parameters ${\sigma }_{\ell },\hspace{0.17em}{\alpha }_{\ell }$, and ${\beta }_{\ell }$, proving the result in equation (B.17). □

Lemma B.3.3

Let ${\mathbf{G}}_{\ell },\hspace{0.17em}{\mathbf{W}}_{\ell },\hspace{0.17em}{\mathbf{E}}_{\ell }(t)$, and $\mathbf{F}(s,t;\zeta )$ denote the matrices defined in equations (A.11), (A.15), (A.17), and (B.10), respectively, where $\zeta =({\zeta }_0,{\zeta }_1,\dots )$ is a set of distinct values arbitrarily chosen such that $\{{\zeta }_0,{\zeta }_1,\dots \}\in [0,1]$. Then the coefficient vectors ${\mathbf{a}}_k$ and ${\mathbf{b}}_k$ satisfy the recursive relationships

$${\mathbf{b}}_k={\mathbf{a}}_k{\mathbf{W}}_{{\ell }_k}{\mathbf{G}}_{{\ell }_k}^{o_k}{(1-{\mathbf{G}}_{{\ell }_k})}^{n_k-o_k}{\mathbf{W}}_{{\ell }_k}^{-1},\hspace{0.17em}$$ (B.20)

$$a_k=\{\begin{array}{ll}{\mathbf{b}}_{k-1}{\mathbf{E}}_{l_k}(t_k-t_{k-1})\hfill & if\hspace{0.17em}{\ell }_{k-1}={\ell }_k,\hfill \\ {\mathbf{b}}_{k-1}\mathbf{F}(t_{k-1},t_k;\zeta )\hfill & otherwise,\hfill \end{array}$$ (B.21)

where ${\mathbf{W}}_{\ell }^{-1}={\mathbf{D}}_{\ell }{\mathbf{W}}_{\ell }^T{\mathbf{C}}_{\ell }^{-1}$.

Proof

The relationship in equation (B.21) is obtained immediately by setting t = t_k in equations (B.4) and (B.15), which follows because ${\mathbf{a}}_k(t_k)={\mathbf{a}}_k$. The relationship in equation (B.20) does not depend on the population parameters Θ; therefore, equation (B.20) is the same as that derived in Steinrücken et al. (2014), who considered a population of constant size (see Steinrücken et al. 2014, Theorem 2). □

Lemma B.3.4

The probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}$ of observing the allele counts $o_{[1:K]}$, given the population parameters Θ is

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}=\frac{c_{{\ell }_K,0}}{B_{{\ell }_K,0}(0)}{b}_{K,0},$$ (B.22)

where $c_{\ell ,0}={[{\mathbf{C}}_{\ell }]}_{0,0}$ is element 0, 0 of the matrix ${\mathbf{C}}_{\ell }$ in equation (A.18) and

$$B_{\ell ,0}(0)=\sum _{m=0}^{\infty }{(-1)}^m{[{\mathbf{W}}_{\ell }]}_{0,m}\frac{\Gamma (m+{\alpha }_{\ell })}{\Gamma (m+1)\Gamma ({\alpha }_{\ell })}.$$ (B.23)

The quantity ${[{\mathbf{W}}_{\ell }]}_{i,j}$ in equation (B.23) is element i, j of the matrix ${\mathbf{W}}_{\ell }$ given in equation (A.15).

Proof

Equation (B.22) can be obtained by integrating over the joint density $f_K(y)$ of the data $O_{[1:K]}$ and the allele frequency $Y_{t_K}$ at the final sampling time:

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}\hspace{0.17em}={\int }_0^1{f}_K(y)dy\hspace{0.17em}={\int }_0^1\sum _{n=0}^{\infty }{b}_{K,n}{\pi }_{{\ell }_K}(y)B_{{\ell }_K,n}(y)dy\hspace{0.17em}=\sum _{n=0}^{\infty }{b}_{K,n}{\int }_0^1{\pi }_{{\ell }_K}(y)B_{{\ell }_K,n}(y)dy\hspace{0.17em}=\sum _{n=0}^{\infty }{b}_{K,n}{\int }_0^1{\pi }_{{\ell }_K}(y)B_{{\ell }_K,n}(y)\frac{B_{{\ell }_K,0}(y)}{B_{{\ell }_K,0}(0)}dy\hspace{0.17em}=b_{K,0}\frac{c_{{\ell }_K,0}}{B_{{\ell }_K,0}(0)},$$ (B.24)

where $c_{{\ell }_K,0}={[{\mathbf{C}}_{{\ell }_K}]}_{0,0}\equiv {\langle B_{{\ell }_K,0},B_{{\ell }_K,0}\rangle }_{{\pi }_{{\ell }_K}}$. In the fourth equality we have used the fact that $B_{\ell ,0}(y)=B_{\ell ,0}(0)$ is a constant function in y. To see why $B_{\ell ,0}(y)$ is constant, note that the eigenvalues ${\lambda }_{\ell ,0},{\lambda }_{\ell ,1},\dots$ are non-negative and strictly increasing. Thus, all terms in equation (A.5) must vanish in the limit $s\to -\infty$, except possibly the term n = 0. Because $p_{\ell }(s,t;x,y)$ approaches the stationary density in the limit $s\to -\infty$, it must be the case that ${\lambda }_{\ell ,0}=0$, so at least one term does not vanish. Thus, we have

$$\underset{s\to -\infty }{\lim }{p}_{\theta }(s,t;x,y)={\pi }_{\ell }(y)\frac{B_{\ell ,0}(x)\hspace{0.17em}{B}_{\ell ,0}(y)}{{\langle B_{\ell ,0},B_{\ell ,0}\rangle }_{{\pi }_{\ell }}}\propto {\pi }_{\ell }(y),$$ (B.25)

where we have used the fact that ${\pi }_{\ell }(y)$ is proportional to the stationary density of the diffusion equation in Epoch $\ell$. It follows from equation (B.25) that $B_{\ell ,0}(y)$ is constant. Thus, we obtain the result, proving equation (B.22). Equation (B.23) follows directly from the proof of Proposition 3 in Steinrücken et al. (2014). □

Appendix C

Conditional Probabilities: The Wright–Fisher Model

Under the Wright–Fisher model, the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$ of the observed allele counts, conditional on the event S_K that allele A is segregating in the final sample can be computed using the fact that

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|S_K\}\hspace{0.17em}=\sum _{j=0}^{2N_{t_K}}{\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]},c_{t_K}=j\left|S_K\right\}\hspace{0.17em}=\sum _{j=0}^{2N_{t_K}}\frac{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right|O_{[1:K]}=o_{[1:K]},c_{t_K}=j\}}{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}}\times \hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]},c_{t_K}=j\}\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}}\times \hspace{0.17em}\sum _{j=0}^{2N_{{\ell }_{t_K}}}{\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]},c_{t_K}=j\}\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}}\sum _{i=0}^{2N_{t_K}}{\mathbf{v}}_{K,i},$$ (C.1)

where the third equality in equation (C.1) follows from the fact that the conditional probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right|O_{[1:K]}=o_{[1:K]},c_{t_K}=j\}$ depends only on the allele count o_K and the final equality in equation (C.1) follows from the definition of ${\mathbf{v}}_k$. The probability $\mathbb{P}\left\{S_K\right|O_K=o_K\}$ in equation (C.1) is given by

$$\mathbb{P}\left\{S_K\right|O_K=o_K\}=\{\begin{array}{ll}1,\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}1\le o_K<n_K,\hfill \\ 0,\hfill & \hspace{0.17em}\text{otherwise}\hspace{0.17em}\hfill \end{array}$$ (C.2)

and the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}$ is given by

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{S_K\right\}\hspace{0.17em}=\sum _{i=0}^{2N_{t_K}}\mathbb{P}\left\{S_K\right|C_{t_K}=i\left\}{\mathbb{P}}_{\Theta ,\mathcal{W}}\right\{C_{t_K}=i\}\hspace{0.17em}=\sum _{i=0}^{2N_{t_K}}[1-\mathbb{P}\{O_K=0|C_{t_K}=i\}-\mathbb{P}\{O_K=n_K|C_{t_K}=i\}]\times \hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t_K}=i\}\hspace{0.17em}=\sum _{i=0}^{2N_{t_K}}\left[1-{\left(1-\frac{i}{2N_{t_K}}\right)}^{n_K}-{\left(\frac{i}{2N_{t_K}}\right)}^{n_K}\right]\times \hspace{0.17em}{\mathbb{P}}_{\Theta ,\mathcal{W}}\{c_{t_K}=i\},$$ (C.3)

where, as before, ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t_K}=i\}$ is given by the ith element of ${\mathbf{d}}_t={\mathbf{d}}_0{\prod }_{t=1}^{t_K}{T}_{t-1,t}$.

Note that it is easy to condition on other configurations of the final sample using a procedure similar to that used to derive equation (C.1). For example, for the event F_K that allele A is segregating or fixed in the final sample, which we consider in the “Simulations Conditioning on Segregation or Fixation” section, the probability ${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|F_K\}$ is given by

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\{O_{[1:K]}=o_{[1:K]}|F_K\}\hspace{0.17em}=\frac{\mathbb{P}\left\{F_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{F_K\right\}}\sum _{i=0}^{2N_{t_K}}{\mathbf{v}}_{K,i},$$ (C.4)

where

$$\begin{array}{l}\mathbb{P}\left\{F_K\right|O_K=o_K\}\\ =\{\begin{array}{ll}1,\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}1\le o_K\le n_K,\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (C.5)

and

$${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{F_K\right\}\hspace{0.17em}=\sum _{i=0}^{2N_{t_K}}\left[1-\mathbb{P}\{O_K=0|C_{t_K}=i\}\right]{\mathbb{P}}_{\Theta ,\mathcal{W}}\{C_{t_K}=i\}\hspace{0.17em}=\sum _{i=0}^{2N_{t_K}}\left[1-{\left(1-\frac{i}{2N_{t_K}}\right)}^{n_K}\right]{\mathbb{P}}_{\Theta ,\mathcal{W}}\{c_{t_K}=i\}.$$ (C.6)

Other probabilities can be obtained in a similar fashion.

Appendix D

Conditional Probabilities: Diffusion Model

Under the diffusion approximation, the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}|S_K\}$ of the observed allele counts conditional on the event S_K that allele A is segregating in the final sample can be computed using the fact that

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}|S_K\}\hspace{0.17em}={\int }_{y=0}^1{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]},Y_{t_K}=y\left|S_K\right\}dy\hspace{0.17em}={\int }_{y=0}^1\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{S_K\right\}}{f}_K(y)dy\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{S_K\right\}}{\int }_0^1{f}_K(y)dy\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{S_K\right\}}{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}\}\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}}{{\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{S_K\right\}}\frac{c_{{\ell }_K,0}}{B_{{\ell }_K,0}(0)}{b}_{K,0},$$ (D.1)

where the second equality follows from the fact that the conditional probability $\mathbb{P}\left\{S_K\right|O_K=o_K,Y_{t_K}=y\}$ depends only on the allele count o_K in the final sample, and the final equality follows from equation (B.22).

The probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{S_K\right\}$ can be computed as

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\left\{S_K\right\}\hspace{0.17em}=1-{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_K=0\}-{\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_K=n_K\}.$$ (D.2)

In equation (D.2), the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_K=j\}$ can be found easily by noting that if the only sampling time is t_K, at which O_K=j lineages are observed, then the probability computed using Procedure 2 is precisely the probability ${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_K=j\}$.

Consider the problem in which the only sampling occurs at time t_K and denote the coefficient vectors for this related problem by ${\tilde{\mathbf{a}}}_k$ and ${\tilde{\mathbf{b}}}_k$. Then, by equation (B.22), we see that

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_K=j\}=\frac{c_{{\ell }_K,0}}{B_{{\ell }_K,0}(0)}{\tilde{b}}_{K,0}(j),$$ (D.3)

where ${\tilde{b}}_K(j)$ is obtained by computing the steps in Procedure 2. In Step 1, we compute

$${\tilde{\mathbf{b}}}_0={\mathbf{b}}_0,$$ (D.4)

which follows because the initial vector ${\mathbf{b}}_0$ depends only on the initial frequency. In Step 2, we compute

$${\tilde{\mathbf{a}}}_K=\{\begin{array}{ll}{\tilde{\mathbf{b}}}_0{\mathbf{E}}_{{\ell }_1}(t_K),\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{t_K}=1,\hfill \\ {\tilde{\mathbf{b}}}_0\mathbf{F}(0,t_K;\zeta ),\hfill & \text{otherwise},\hfill \end{array}$$ (D.5)

which follows because the coefficients are propagated directly from time $t_0=0$ to time t_K. Finally, in Step 3 we have

$${\tilde{b}}_K(j)={\tilde{\mathbf{a}}}_K{\mathbf{W}}_{{\ell }_K}{\mathbf{G}}_{{\ell }_K}^j{(1-{\mathbf{G}}_{{\ell }_K})}^{n_K-j}{\mathbf{W}}_{{\ell }_K}^{-1}.$$ (D.6)

Combined together, equations (D.4), (D.5), and (D.6) yield

$${\tilde{\mathbf{b}}}_K(j)=\{\begin{array}{l}{\mathbf{b}}_0{\mathbf{E}}_{{\ell }_1}(t_K){\mathbf{W}}_{{\ell }_K}{\mathbf{G}}_{{\ell }_K}^j{(1-{\mathbf{G}}_{{\ell }_K})}^{n_K-j}{\mathbf{W}}_{{\ell }_K}^{-1},\hfill \\ \hspace{0.17em}\text{if}\hspace{0.17em}{\ell }_{t_K}=1,\hfill \\ {\mathbf{b}}_0\mathbf{F}(0,t_K;\zeta ){\mathbf{W}}_{{\ell }_K}{\mathbf{G}}_{{\ell }_K}^j{(1-{\mathbf{G}}_{{\ell }_K})}^{n_K-j}{\mathbf{W}}_{{\ell }_K}^{-1},\hfill \\ \text{otherwise}.\hfill \end{array}$$ (D.7)

Plugging equations (D.2) and (D.3) into equation (D.1) gives

$${\mathbb{P}}_{\Theta ,\mathcal{D}}\{O_{[1:K]}=o_{[1:K]}|S_K\}\hspace{0.17em}=\frac{\mathbb{P}\left\{S_K\right|O_K=o_K\}{c}_{{\ell }_K,0}{b}_{K,0}}{B_{{\ell }_K,0}(0)-c_{{\ell }_K,0}{\tilde{b}}_{K,0}(0)-c_{{\ell }_K,0}{\tilde{b}}_{K,0}(n_K)},$$ (D.8)

where

$$\mathbb{P}\left\{S_K\right|O_K=o_K\}=\{\begin{array}{ll}1,\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}1\le o_K<n_K,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (D.9)

Note that it is easy to condition on other configurations of the final sample by computing the probabilities $\mathbb{P}\left\{V_K\right|O_K=o_k\}$ and ${\mathbb{P}}_{\Theta ,\mathcal{W}}\left\{V_K\right\}$ for some other event V_K.