Clustering and Jamming in Epithelial-Mesenchymal Co-Cultures

Abstract

Collective behaviors emerge from coordinated cell-cell interactions during the morphogenesis of tissues and tumors. For instance, cells may display density-dependent phase transitions from a fluid-like “unjammed” phase to a solid-like “jammed” phase, while different cell types can “self-sort.” Here, we comprehensively track single cell dynamics in mixtures of sheet-forming epithelial cells and dispersed mesenchymal cells. We find that proliferating epithelial cells nucleate multicellular clusters that coarsen at a critical density, arresting migration and strengthening spatial velocity correlations. The addition of mesenchymal cells can slow cluster formation and coarsening, resulting in more dispersed individual cells with weak spatial velocity correlations. These behaviors have analogies with a jamming-unjamming transition, where the control parameters are cell density and mesenchymal fraction. This complex interplay of proliferation, clustering and correlated migration may have physical implications for understanding epithelial-mesenchymal interactions in development and disease.

Introduction

Self-organization and pattern formation arise from multicellular interactions during embryonic development, wound healing and cancer.^{1, 2} For example, motile cells can undergo “phase transitions” from a fluid-like state of isolated individuals to a solid-like “jammed” state of multicellular clusters with correlated motions.^3-12 Alternatively, mixtures of two different cell types have been observed to self-sort into their respective subpopulations.^13-19 These complex behaviors have intriguing analogies with self-propelled interacting particles in active matter systems.²⁰ These physical models are typically based on identical particles that undergo jamming-unjamming transitions near some critical packing density.²¹ In contrast, living cells are highly heterogeneous, proliferate and undergo dynamic changes in shape. Indeed, it has been proposed that dynamic shape changes can result in an unjamming transition, even at constant packing densities that approach 100%.^{11, 12} These emergent behaviors are challenging to resolve experimentally with limited sampling, population averages or endpoint measurements.²² In order to elucidate multicellular biological dynamics in the context of active matter, it is necessary to comprehensively measure all single cell behaviors in space and time.

An experimental system of interest is a mixture of epithelial and mesenchymal cell types, which interact during embryonic development to pattern tissues and organs.²³ Classically, epithelial cells display compact morphologies and are tightly anchored by cell-cell and cell-matrix junctions.²⁴ Epithelial cells in vivo are closely connected in multicellular layers that form the skin, airways, gastrointestinal tract etc.²³ Similarly, epithelial cells in vitro can organize into sheet-like architectures that display collective migration, which has been understood in the context of leader cells,²⁵ cryptic lamellipodia,²⁶ intercellular stresses^{27, 28} and boundary conditions (e.g. wound healing).^29-37 In contrast, mesenchymal cells display highly elongated morphologies with strong cell-matrix adhesions at the leading edge but minimal cell-cell attachments.³⁸ As a consequence, mesenchymal cells in vivo are unconnected and dispersed, particularly within connective tissue.³⁹ These mesenchymal cells coordinate their individual migration by avoiding cell-cell contact, known as contact inhibition of locomotion.⁴⁰ Mesenchymal cells in vitro may migrate and self-organize differently than epithelial cells, including orientational alignment at increasing density.⁹

Interconversion between epithelial and mesenchymal phenotypes can also occur in response to external stimuli. For example, the epithelial-mesenchymal transition (EMT) occurs when cells of epithelial origin in multicellular tissues disseminate as mesenchymal cells,⁴¹ effectively a transition from collective to individual migration.⁴² Instead, a mesenchymal-epithelial transition (MET) or condensation can occur at increased cell densities, forcing dispersed mesenchymal (stem) cells to differentiate and form cell-cell junctions.⁴³ This transient loss or gain of cell-cell contacts is associated with neural crest formation during embryonic development⁴⁴ as well as tumor invasion and metastasis.⁴⁵

Here, we comprehensively measure single cell dynamics in populations with varying ratios of epithelial and mesenchymal cells. We find that proliferating epithelial cells self-organize into multicellular clusters with characteristic nucleation, growth and coarsening, resulting in arrested migration with strengthening spatial velocity correlations. The addition of more motile and less proliferative mesenchymal cells frustrates clustering, maintaining constant migration dynamics with weak spatial velocity correlations. These collective behaviors have analogies with a jamming-unjamming transition in cell density and mesenchymal fraction, which may have intriguing implications for understanding morphogenesis in tissues and tumors.

Results

Clustering and Coarsening Diminish with Increasing Mesenchymal Fraction

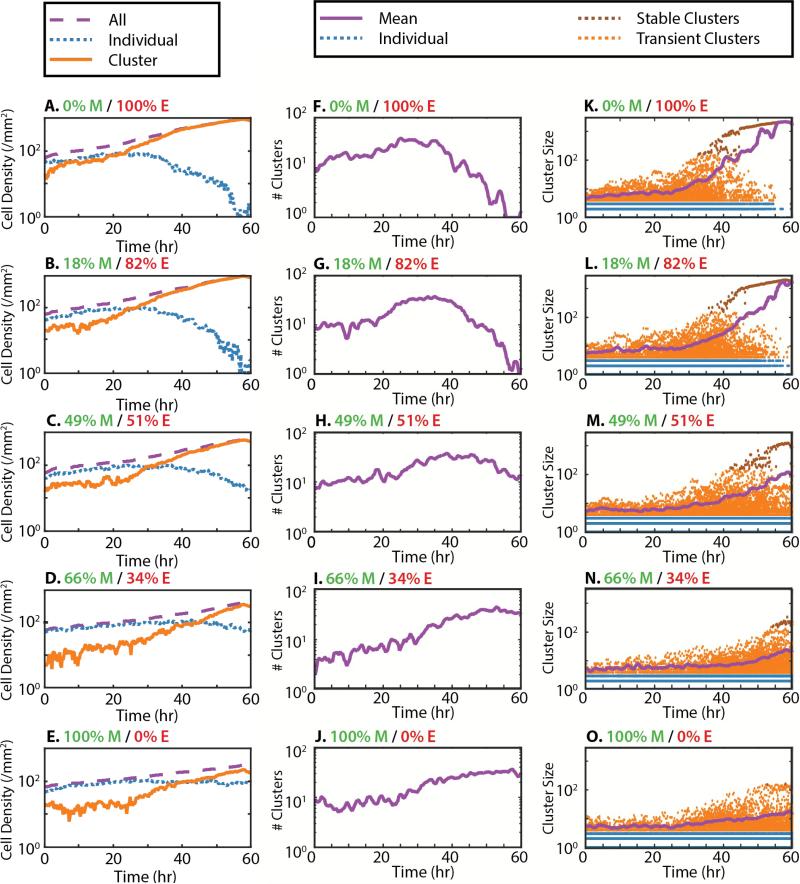
Epithelial (MCF-10A) and mesenchymal (MDA-MB-231) cells expressing red and green nuclear-tagged fluorescent proteins were plated in varying ratios on collagen I coated surfaces. Representative plots of experimentally measured cell positions over 60 h are displayed at varying initial mesenchymal percentage: %M = 0% to 100% in Figure 1 (time-lapse movies are available as Video S1-S5). Over time, cells aggregated into multicellular clusters (Figure 1, left to right). We defined clusters as four or more cell nuclei located in close proximity (<50 μm), a cutoff set from immunofluorescent staining of nuclei and cell-cell junctions (E-cadherin) (Figure S1). Subsequently, multicellular clusters grew in size and eventually merged together (coarsening). Moreover, cells migrated into unoccupied regions and became more uniformly distributed. As %M was increased, the overall cell numbers increased more slowly (Figure 1, top to bottom). Similarly, the formation of multicellular clusters occurred more slowly with increasing %M. For example, for mostly epithelial populations with low %M = 0% and 18%, the clusters spanned the entire field of view by ~50 h (Figure 1A, B). In contrast, at higher %M = 66% and 100%, more clusters formed with smaller sizes and the population remained subconfluent at 60 h (Figure 1D, E). For conditions where one subpopulation was significantly outnumbered (%M = 18% or 66%), the smaller subpopulation was often dispersed in small numbers and surrounded by the larger subpopulation by 60 h (Figure 1B, D).

Figure 1.

Representative snapshots of epithelial and mesenchymal cells mixed in varying ratios over time. Cell density increased over time (left to right). As the initial percentage of mesenchymal cells increased, the formation of clusters occurred with slower kinetics and smaller sizes (top to bottom). Mixtures shown by increasing mesenchymal percentage are 0% (A), 18% (B), 49% (C), 66% (D) and 100% (E).

Multicellular clustering dynamics were analyzed by classifying cells as individuals or clusters. For all %M, most cells were initially classified as individual, with a smaller number of cells in clusters. For mostly epithelial populations with low %M, the individual cell density began to decrease sharply at ~30 h, and continued to drop through 60 h (Figure 2A-C). In contrast, cluster cell density increased rapidly at ~20 h, overtaking the individual cell density and asymptotically approaching the total cell density. For higher %M, there was a smaller decrease in the individual cell density (Figure 2D,E). Indeed, for %M = 100%, the individual cell density actually increased slightly (Figure 2E).

Figure 2.

Cell densities, number of clusters and cluster size distribution as a function of time and initial mesenchymal percentage (top to bottom). (A-E) Total cell density (purple dashes) and clustered cell density (orange) increased over time, while individual cell density (blue dots) decreased. (F-H) For low initial mesenchymal percentage, the number of clusters initially increased (purple line), then decreased down to a single cluster. (I, J) For higher mesenchymal percentage, the number of clusters steadily increased over time. (K-M). For low mesenchymal percentage, the cluster size distribution remained roughly constant until ~30 h, when the average cluster size increased rapidly (purple line). Individual cells are colored blue, clustered cells are colored orange and stable clusters are colored brown. (N, O) For higher mesenchymal percentage, the average cluster size only increased slightly.

The number of clusters and cluster size distribution were further analyzed over time. For mostly epithelial populations with low %M, the number of clusters increased gradually up until ~30 h (Figure 2F, G), while the average cluster size remained relatively constant up until ~30 h (Figure 2K, L). A closer examination of the cluster size distribution indicated that ~30 h corresponded to outliers exceeding ~150 cells and continuing to grow over time, suggestive of a critical nucleation size. Indeed, clusters smaller than ~150 cells appeared to be unstable and fluctuated in size. For times longer than ~40 h, there was an apparent coarsening as stable clusters merged together. Subsequently, the number of clusters decreased rapidly to a single cluster (of ~2000 cells). For %M = 49%, the number of clusters slightly increased at ~25 h, reached a maximum of ~35 clusters at 40 h and then decreased back to ~10 clusters at 60 h (Figure 2H). The average cluster size increased at ~40 h, which is approximately when clusters of ~150 cells were observed (Figure 2M). By 60 h, the majority of the population was contained in one large cluster of ~1000 cells, but some scattered clusters of tens of cells were also present (Figure 2M), indicative of incomplete coarsening. Finally, for higher %M = 66% or 100%, the number of clusters increased monotonically over time from initial values of 2-10 to final values of ~30 (Figure 2I, J). This greater number of clusters also corresponded to smaller cluster sizes, with an average cluster size of ~10 cells and outliers of ~100 cells (Figure 2N, O). Altogether, increased densities of mesenchymal cells in the population appeared to decrease coarsening.

Clustering and Coarsening Depend on Cell Density and Proliferation

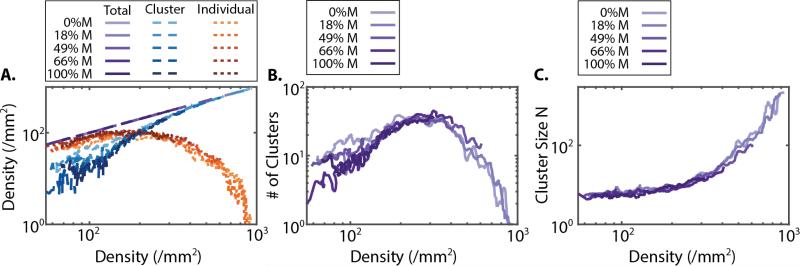
Cell density was observed to increase over 60 h from initial densities of 60-90 cells/mm² up to final densities of 300-900 cells/mm² (Figure 2A-E). Since epithelial cells proliferate faster than mesenchymal cells, increasing %M resulted in slower increases in cell density (Figure S2). In order to directly compare these cases, clustering metrics were replotted as a function of cell density. Remarkably, these different experimental conditions collapsed to similar curves as a function of density (Figure 3). In particular, the dropoff in individual cell density occurred consistently at a “critical” cell density ~250 cell/mm² (Figure 3A). Similarly, the number of clusters reached a maximum at this critical cell density, before decreasing due to coarsening (Figure 3B). Finally, cluster size began to rapidly increase at this cell density (Figure 3C). It should be noted that this critical cell density could arise from our definition of clustering based on a cutoff separation of ~50 μm. Nevertheless, we show in the next section that this cell density has physical significance independent of how clusters are defined.

Figure 3.

(A) Cell densities, (B) number of clusters and (C) cluster size distribution collapse together as a function of cell density. Across all mixture compositions, there is a “critical” cell density of ~250 cells/mm² corresponding to a decrease in individual cells, the onset of coarsening and an increase in cluster size.

Since clusters included both epithelial and mesenchymal cells, we evaluated the role of motility driven cell sorting. We quantified cell sorting using a segregation index for epithelial cells γ = 〈n_M / (n_E + n_M)〉,⁴⁶ where n_M and n_E are the number of nearest mesenchymal or epithelial neighbors, respectively. Essentially, γ represents the fraction of nearest neighbors that are mesenchymal. For perfect cell sorting in large systems, a given epithelial cell will be surrounded by a large number of epithelial cells, so γ → 0 over time. We found that γ decreased over time for all conditions, although it does not reach 0 (Figure S3). Instead, we found that this segregation index γ is consistent with the fraction of cells of each type measured at the population level.

Finally, the role of proliferation in clustering was verified by blocking proliferation with 25 μg/mL mitomycin-C, a DNA crosslinker. For treated cells, cell density remained constant over 60 h, even at increased initial seeding densities, and the relative proportions of epithelial and mesenchymal cells were unchanged (Figure S4). Moreover, cells remained almost entirely individual, with 10 or fewer cells observed in clusters over 60 h (Figure S4). Altogether, these results suggest that proliferation is crucial for clustering and dominates over motility-driven sorting.

Epithelial Migration Velocity Initially Increases, Then Decreases with Density

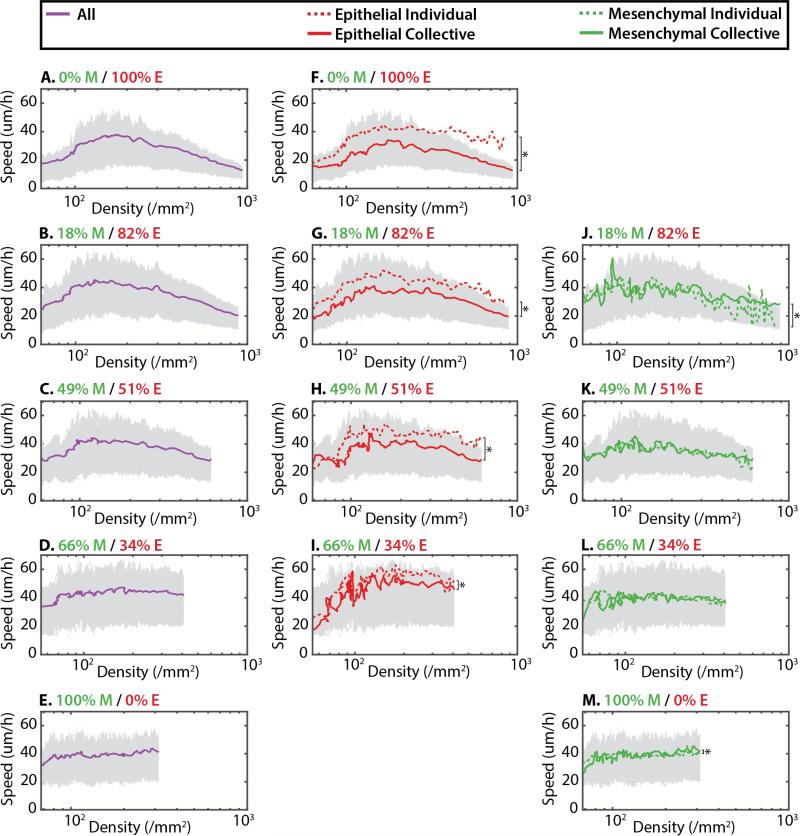
Cell migration velocities were then analyzed as a function of cell density. For mostly epithelial populations with low %M, a cell density of ~250 cell/mm² corresponded to a slowdown of migration (Figure 4A-C), comparable to the critical cell density previously observed for clustering (Figure 3). In general, the initial root mean squared average velocity <v_rms> was 20-30 μm/h, which steadily increased up to 40 μm/h at ~200 cells/mm², then decreased back to <20 μm/h at 700-1000 cells/mm² (Figure 4A-C). Instead, for mostly mesenchymal populations with high %M, <v_rms> remained roughly constant at ~40 μm/h up to ~300-400 cells/mm² (Figure 4D, E).

Figure 4.

Average root mean squared velocity is displayed as a function of cell density and initial mesenchymal percentage (top to bottom). Top and bottom quartiles (75%, 25%) are shown in gray for all plots. For low initial mesenchymal percentage, the overall velocity initially increased, then decreased with density (A-C). For high initial mesenchymal percentage, the overall velocity remained roughly constant with density (D-E). For all conditions, epithelial cells were significantly faster as individuals than in clusters (F-I). However, mesenchymal cells displayed similar average velocities as individuals and in clusters (J-M). * denotes statistically significant difference (p < 0.01)

To gain further insight into these dynamics, <v_rms> was calculated at the subpopulation level. Epithelial subpopulations displayed a qualitatively similar trend where <v_rms> initially increased at low densities, then decreased at higher density (Figure 4F-I). A visual inspection of the experimental data indicated that this initial increase in velocity was likely due to slower epithelial attachment and polarization relative to mesenchymal cells (Video S1-5). Moreover, within the epithelial subpopulation, individual cells displayed <v_rms> that was ~10 μm/h faster than cells in clusters, which was statistically significant (p < 0.01) (Figure 4F-I). In contrast, for the mesenchymal subpopulation, <v_rms> remained roughly constant with density and was comparable for individuals and clusters (Figure 4J-M).

One explanation for these results is that epithelial cells at low density can display a more mesenchymal phenotype. To test this hypothesis, cells were immunostained for the mesenchymal biomarker vimentin, which was compared with the cell type of origin based on the fluorescent protein expressed in the nucleus. As %M increased in the co-culture populations, there was increased vimentin expression and cellular elongation for cells of epithelial origin (Figure S5). These shape changes were further quantified using the shape index $p_i=P_i∕\sqrt{A_0}$ (where P is the perimeter and A is the area),¹² revealing that co-cultured epithelial cells displayed some elongation relative to epithelial cells alone (Figure S6). These results suggest that the epithelial cell type used here can undergo EMT when co-cultured with mesenchymal cells, resulting in increased velocities of individual cells. Interestingly, some co-cultured mesenchymal cells appeared more compact and expressed less vimentin, although the shape parameter does not display statistically significant differences as the population level. Overall, the increase and decrease in <v_rms> of the population with density is primarily driven by the epithelial subpopulation <v_rms>, while the mesenchymal subpopulation <v_rms> remains roughly constant. These results are suggestive of a critical cell density of ~250 cells/mm² where migration is impeded due to clustering and coarsening.

Spatial Velocity Correlations Decrease with Increasing Mesenchymal Subpopulation

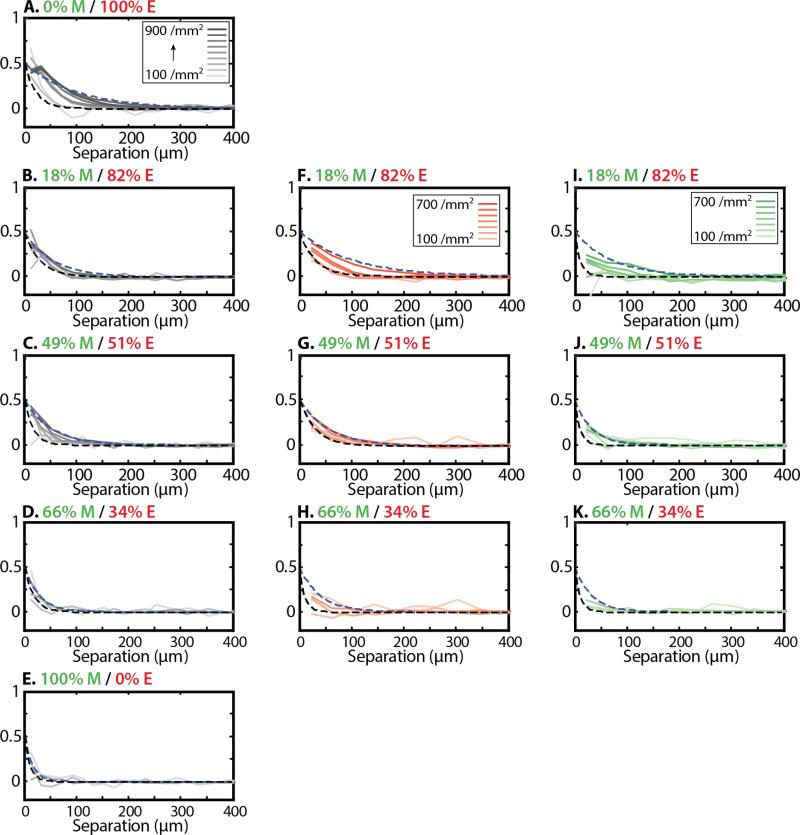
Spatial velocity correlations were then determined by averaging the scalar product of normalized velocity vectors v̂_i(t) and v̂_j(t) associated with cells i and j, respectively: C(|r_i – r_j|,t) = 〈v̂_i(t)·v̂_j(t)〉_i≠j, where brackets denote an average over all cell pairs i and j separated by a distance |r_i – r_j|. For all conditions measured, these spatial velocity correlations decayed roughly exponentially as a function of cell-cell separation and were fit to a function of the form C(|r_i – r_j|,t) = C₀ exp(–|r_i – r_j| / ξ) (Figure 5). For mostly epithelial populations with low %M, these correlations became stronger and longer ranged with increasing density, starting out with a characteristic length ξ = 21 μm at 100/mm² and increasing to ξ = 100 μm at ~700/mm² (Figure 5B). In contrast, for more mesenchymal populations with nearly equal %E and %M, these correlations displayed less of an increase over time, with a characteristic length ξ = 17 μm at 100/mm² and increasing to ξ = 52 μm at 400/mm² (Figure 5C, D). Indeed, for a purely mesenchymal population, the spatial velocity correlation was extremely short ranged and did not change appreciably, with a characteristic length ξ = 10 μm at 100/mm² h and ξ = 15 μm at 300/mm² (Figure 5E). It should be noted our analysis tracks the cell nuclei, which have a finite radius ~5 μm. For this reason, the spatial velocity correlation was cut off for small separations <5 μm, since these small separations may not be physically meaningful.

Figure 5.

Spatial velocity correlations are displayed as a function of cell-cell separation and initial mesenchymal percentage (top to bottom). Darker lines correspond to increasing cell density. Dashed black and blue lines correspond to exponential fits at 100/mm² and maximum observed densities, respectively. In general, spatial correlations became longer-ranged over time at the population level. However, spatial correlations became weaker with increasing initial mesenchymal percentage (A-E). In mixed populations, Spatial correlations tended to be longer ranged for epithelial cells (F-H) relative to mesenchymal cells (I-K).

Spatial velocity correlations were then recalculated for a subset of the population when cells i or j were epithelial or mesenchymal, respectively. Epithelial spatial correlations were longer ranged and increased with density (Figure 5F-H), while mesenchymal spatial correlations were shorter ranged (Figure 5I-K). For mostly epithelial populations with low %M = 18%, the mesenchymal spatial correlations were the largest and increased with density to an extent comparable to the epithelial spatial correlations. It should be noted that these subsets were selected if at least one cell in the pair was mesenchymal, so that this long-ranged effect could be a consequence of interactions between mesenchymal and epithelial cells. However, spatial correlation functions extracted explicitly for the same cell type, cells in clusters and individual cells did not yield statistically meaningful trends. Interestingly, negative (anti) correlations were occasionally observed at small separations, which may correspond to cell division events where daughter cells were moving apart. Altogether, increasing %M resulted in a decrease in ξ, indicating a shorter ranged spatial velocity correlation.

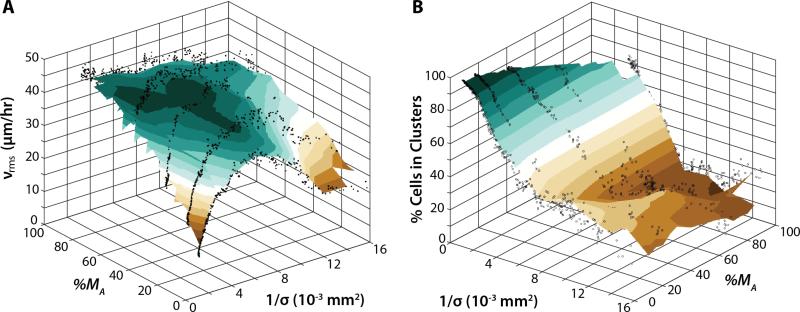
Phase Diagrams for Motility, Clustering, Mesenchymal Fraction and Reciprocal Density

To combine these results, a phase diagram was constructed where the average cell velocity v_rms was plotted as a function of reciprocal cell density 1/σ and actual mesenchymal percentage %M_A (Figure 6A). Approaching the origin, low average cell velocities corresponded to high cell densities and mostly epithelial populations. For reference, the critical cell density corresponding to a slowdown of migration was ~200 cells/mm², which corresponds to 1/σ ~ 5·10⁻³ mm². We estimated that a confluent monolayer was at least ~700 cells/mm² based on immunofluorescent staining of the cytoplasm (Figure S7). For a purely epithelial population with %M_A = 0, increasing 1/σ (decreasing cell density) resulted in an increase in v_rms from 11 μm/h to a maximum of 40 μm/h, then a decrease down to 17 μm/h. Instead, for small 1/σ, increasing %M_A from 0% to 100% corresponded to a consistent increase in v_rms up to ~40 μm/h. Finally, for a purely mesenchymal population with %M_A = 100%, increasing 1/σ from the origin corresponded to a slight decrease in v_rms from ~43 μm/h to ~32 μm/h. Overall, increasing %M_A at a given density had the effect of increasing cell motion.

Figure 6.

(A) Phase diagram of average cell velocity as a function of reciprocal cell density and actual mesenchymal percentage. Migration was arrested near the origin for mostly epithelial populations and high cell densities. Increasing initial mesenchymal fraction also increased average cell velocity. (B) Phase diagram of the percentage of cells in clusters as a function of reciprocal cell density and initial mesenchymal percentage. Almost complete clustering occurred near the origin for mostly epithelial populations and high cell densities. Increasing initial mesenchymal fraction also decreased the percentage of cells in clusters.

Alternatively, the percentage of cells in clusters can be displayed as a function of 1/σ and %M_A (Figure 7B). Near the origin, 100% of cells were associated with multicellular clusters. For a purely epithelial population with %M_A = 0, the percentage of cells in clusters dropped off from 100% to about 40% from small 1/σ ~ 10⁻³ mm² to 5·10⁻³ mm². This cluster percentage remained roughly constant from 1/σ = 5·10⁻³ mm² to 15·10⁻³ mm², before further decreasing to 20% at 1/σ = 16·10⁻³ mm². Instead, for small 1/σ, increasing %M_A from 0% to 100% corresponded to a more rapid decrease in percent clusters, down to 20% by 1/σ = 8·10⁻³ μm². Effectively, increasing mesenchymal percentage %M_A at high reciprocal cell density 1/σ (low cell density) decreased the percentage of cells clustered.

Finally, cells were treated with TGF-β to perturb clustering and density-dependent slowdown. TGF-β is a well-known inducer of EMT, although the downstream signaling mechanisms can depend on context.⁴⁵ After treatment, we found that both epithelial and mesenchymal cell types expressed increased vimentin levels, consistent with EMT (Figure S8). Epithelial cells also displayed some elongation based on shape parameter relative to a high density control (Figure S6). We found that the characteristic doubling times slowed to 28.2 h and 47.0 h for epithelial and mesenchymal subpopulations, respectively (Figure S9). Moreover, the individual cell density remained roughly consistent across all M, compared to the dramatic decrease observed previously in untreated conditions (Figure 3). Similarly, cluster cell density grew more slowly (Figure S10). Furthermore, the number of clusters grew continuously over time, with coarsening only observed for the purely epithelial population above 250 cells/mm² (M = 0) (Figure S10). Indeed, the corresponding cluster size distributions rarely exceeded the critical nucleation size of ~150. For all other populations with cells of mesenchymal origin (M > 0), the clusters remained relatively small and unstable, so that the average cluster size remained relatively constant over time (Figure S10). Despite cluster formation, v_rms remained relatively constant in density out to 400 cells/mm² (Figure S11), without the gradual decrease observed for untreated conditions starting at ~200 cells/mm² (Figure 5). Finally, the spatial velocity correlations increased slightly over time (~10-20 μm) in all conditions (Figure S12), but much less than the ~20-80 μm increase observed for untreated conditions (Figure 6). Consistent with these results, v_rms displayed a plateau for small 1/σ and %M_A (Figure S13), rather than the sharp dropoff observed beyond the critical reciprocal density 1/σ ~ 5·10⁻³ mm² for untreated conditions (Figure 7). Overall, TGF-β treatment appeared to maintain cells as dispersed individuals and suppress cluster coarsening, thereby permitting higher average velocities at elevated cell densities.

Discussion and Conclusion

Soft matter systems such as colloidal glasses or granular materials can display a density-dependent phase transition from a mobile fluid-like state to an arrested solid-like state.²¹ A “jamming phase diagram” can capture these transitions in the context of reciprocal density, temperature, and shear stress, with an arrested “jammed” state near the origin. For living epithelial monolayers, an analogous phase diagram has been proposed with control parameters based on reciprocal density, motility and reciprocal cell-cell adhesion.⁴⁷ Remarkably, we measure a qualitatively similar slowdown in motility above a critical cell density even in heterogeneous mixtures of epithelial (MCF-10A) and mesenchymal (MDA-MB-231) cell lines. We further show that this critical cell density corresponds to onset of multicellular cluster coarsening. These experimental results are qualitatively consistent with previous work by other groups in the limit of mostly epithelial populations (small numbers of mesenchymal cells).^3-11 Thus, reciprocal density and motility are appropriate control parameters to describe jamming in our heterogeneous cell population.

We demonstrate the fraction of mesenchymal cells can be used as a third control parameter. We found that increasing mesenchymal fraction (away from the origin) also resulted in an increase in motility (Figure 6). This behavior is analogous to increasing polydispersity in an inert soft matter system, which has been shown to frustrate jamming.⁴⁸ Indeed, the mesenchymal cell line used here (MDA-MB-231) may not form a jammed monolayer, since it has been malignantly transformed and does not display contact inhibition of proliferation.⁴⁹ It should be noted that cells are also capable of interconverting between epithelial and mesenchymal phenotypes, a biological phenomenon known as phenotypic plasticity. We show that treatment with TGF-β can also induce EMT and frustrate jamming. Moreover, the epithelial cell line used here (MCF-10A) can undergo an EMT at low densities,⁵⁰ which we observe through more individual migration as well as enhanced vimentin expression. This may also arise from the mesenchymal cell line used here (MDA-MB-231), which has been observed to secrete exosomes that reprogram epithelial cells (MCF-10A) to undergo EMT.^{51, 52} Finally, co-cultured primary liver hepatocytes have been observed to reprogram mesenchymal cell line (MDA-MB-231) to undergo MET.⁵³ We see some less elongation and vimentin expression in co-cultured MDA-MB-231 cells, but additional measurements of epithelial biomarkers are necessary to establish conclusively that MET is occurring. Altogether, various changes in mesenchymal fraction may correlate with changes in cell shape index, with a critical value of p₀ ~ 3.81 observed elsewhere for fully confluent airway epithelial cells.^{11, 12} Our preliminary measurements of cell shape index show qualitatively similar trends, but are consistently larger than 3.81 and would be considered unjammed (Figure S6). This disagreement may occur since our cell densities are not 100% confluent, so that cell morphologies are not fully described by a vertex model.

Mesenchymal fraction is also correlated with cell-cell adhesion, since mesenchymal cells display weak cell-cell contacts relative to epithelial cells. Nevertheless, cell-cell adhesion averages out the interactions between different cell types, which may obscure useful information. We anticipate that image correlation^{5, 9, 10, 30, 36, 37} and traction force microscopy^{4, 27, 28} could be utilized in future work to resolve cell orientation, cell-cell and cell-matrix adhesions with single cell resolution. Physically, these approaches may also reveal other signatures of jamming behavior, including the transient appearance of localized motion (dynamic heterogeneity), as well as cooperative rearrangements among neighbors.⁴⁷ Further analysis and theoretical modeling of these rich and complex behaviors is underway and will be described elsewhere.

One caveat is the MCF-10A and MDA-MB-231 cell lines used here do not fully recapitulate the complexity of epithelial-mesenchymal interactions in vivo. These two cell lines display pronounced genetic and phenotypic differences,⁵⁴ particularly in the context of their metabolism and media requirements. Thus, it is challenging to prolong these experiments while maintaining consistent conditions. Indeed, the interactions between distinct subpopulations may dynamically shift depending on the microenvironment. For instance, epithelial cells tend to outcompete the mesenchymal cells due to faster proliferation rates. Nevertheless, mesenchymal cells display enhanced resistance to stress caused by therapeutic treatments or resource-limited conditions.⁴¹ An intriguing prospect is to vary the physical microenvironment (e.g. matrix stiffness) or biochemical microenvironment (e.g. drugs) and measure the effect on single cell and collective dynamics. More generally, the physical hypothesis that increasing fractions of mesenchymal cells can unjam a solid tissue for more fluid-like multicellular motion will need to be tested with additional cell lines and types.

In summary, we have directly measured proliferation, clustering, single cell velocities and spatial correlations in mixtures of representative epithelial and mesenchymal cell lines. We find that mostly epithelial populations self-organize into multicellular clusters through a process of density-dependent nucleation, growth and coarsening. As a consequence, cell migration is arrested at elevated cell density, analogous to a jamming transition. However, increasing fractions of mesenchymal cells can impede clustering and jamming due to slower proliferation, faster migration and limited cell-cell adhesions. We also observe a qualitatively similar suppression of jamming when EMT is induced through TGF-β. Overall, we expect these single cell analyses can be applied to collective behaviors both in vitro and in vivo, with potential biophysical relevance for epithelial-mesenchymal interactions and transitions in human development and disease.

Materials and Methods

Cell Culture

Human mammary epithelial cells (MCF-10A) expressing H2B-mCherry were a generous gift from M.R. Ng and J.S. Brugge. Highly metastatic breast adenocarcinoma cells (MDA-MB-231) expressing H2B green-fluorescent protein (GFP) were a generous gift from R.J. Giedt and R. Weissleder. Cell culture reagents were obtained from Thermo Fisher Scientific (Waltham, MA), unless otherwise indicated. MCF-10A cells were cultured in growth media following Brugge et al. in Dulbecco's modified Eagle's medium F12 (DMEM/F12, Invitrogen 11330057) supplemented with 5% Horse Serum, 20 ng/mL human epithelial growth factor, 0.5 μg/mL hydrocortisone, 100 ng/mL cholera toxin, 10 μg/mL insulin and 1% penicillin/streptomycin.⁵⁶ MDA-MB-231 cells were cultured in Dulbecco's modified Eagle's medium (DMEM, MT-10-013-CV) containing L- Glutamine, 4.5 g/L Glucose and Sodium Pyruvate and supplemented with 10% fetal bovine serum (FBS) and 1% penicillin/streptomycin.

Half-area high content imaging 96-well plates from Corning Life Science Plastics (Thermo Fisher Scientific, Waltham, MA) were utilized for cell measurements. Each well was coated with 5 μg/cm² of rat-tail derived collagen-I (Corning). A single cell suspension was obtained by adding Accumax to culture flasks. Cells were subsequently counted using the Cellometer Auto 1000 Cell Viability Counter (Nexcelom Bioscience, Lawrence, MA) and plated at a low density (1500 cells/well) at specified ratios in MCF-10A growth media. Cells were allowed to settle and adhere for 3 hours before imaging.

To inhibit proliferation, cells were pretreated in culture with 25 μg/mL of mitomycin-C (Sigma; M4287) for 2 hours. Cells were subsequently counted and plated at a low density (2000 cells/well). Mitomycin-treated cells were imaged for a long duration (60 h) to examine clustering behavior at low density over time. To perturb cell clustering behavior and induce EMT, cells were suspended in 5 ng/mL of TGF-β (R&D systems), plated at a low density (2000 cells/well), allowed to adhere for 3 hours before imaging, and then imaged for the duration of a 48 h time course.

Time-Lapse Fluorescence Microscopy

Cell proliferation, clustering and migration were measured with an inverted epifluorescence microscope (Nikon TiE) with a light-guide coupled white light illumination system (Lumencore Sola) under environmentally controlled conditions (37°C, 5% CO₂, humidified). Using Nikon Elements software, images were acquired every 15 minutes with 14-bit resolution using a sCMOS camera (Andor Neo), 10x Plan Fluor objective (NA 0.3, long working distance), GFP/FITC Filter Set (Chroma 49002) or TRITC/DSRed Filter Set (Chroma 49004). Images were recorded under consistent acquisition parameters (e.g. exposure time, camera gain/gamma control and microscope aperture).

Immunofluorescence Staining

At the conclusion of time-lapse experiments, cells were washed with 1X Phosphate Buffered Saline (PBS) containing calcium chloride and magnesium chloride, and then fixed with 4% paraformaldehyde (Fisher Scientific) in PBS. Next, cells were permeabilized with Triton X-100 (0.1% in 1X PBS) for 5 minutes, washed with 1X PBS, blocked in goat serum (10% in PBS), washed with a sodium acetate buffer, and washed with nonfat dry milk (1% in PBS).

For mesenchymal cell biomarker staining, cells were then incubated overnight at 4° C with vimentin primary antibody (rabbit mAB, CST #5741) in 1% milk (1:200 dilution). The following day, cells were washed 3X with 1% milk, then incubated in the dark with Goat anti-Rabbit secondary antibody (Alexa Fluor 647, ThermoFisher). Alternatively, cells were stained with HCS CellMask Deep Red Stain (Thermo Fisher) to fluorescently label the entire cell. After several washes with PBS, fluorescent images were acquired using a 14-bit resolution sCMOS camera (Andor Neo), 20x Super Plan Fluor objective (NA 0.45, extra-long working distance), and a light-guide coupled Lumencore Sola white light excitation system. For throughput, an array of images was obtained for each multiwell plate, while acquisition parameters were held constant to maintain integrity across images and experiments.

Image Analysis and Cell Tracking

Time-lapse images in .nd2 format were converted to .ims format using the Imaris File Converter and imported into Bitplane Imaris for image analysis and nuclear tracking. Images were background subtracted to improve thresholding and nuclei were tracked using an autoregressive motion algorithm, then manually verified. Cell tracks shorter than 2 hours were discarded. The detection parameters utilized for tracking each cell type are shown in the table below:

Parameter	MCF-10A	MDA-MB-231
Estimated Nuclear Diameter	14 μm	15 μm
Classify Spots, “Quality” above	9.5	114
Tracking, MaxDistance	30.0 μm	50.0 μm

Cell Clustering and Population Growth Fits

At every time point, clusters were defined as groups of at least 4 cells where successive pairs of nuclei were separated by 50 μm or less, following the clustering algorithm by Lu.⁵⁵ Briefly, all cells were initially designated with a unique cluster index. If cells with cluster index i and j were less than 50 μm apart, they were both reassigned the lower cluster index of i or j. If either cell was already assigned to a cluster, all other cells within those clusters were also reassigned to the lower cluster index. This iterative process is able to determine spatial connectivity across multicellular clusters. Based on this approach, cells were classified into epithelial individuals or clusters as well as mesenchymal individuals or clusters. The growth or decay of the epithelial and mesenchymal subpopulations over time was fit to a single-term exponential function using the MATLAB function fit. Plots of the number of clusters and cluster size over time were smoothed using a moving average filter with the MATLAB function smooth. The segregation index γ = 〈n_M / (n_E + n_M)〉 was calculated by first constructing a Delaunay triangulation using the MATLAB function delaunay. For each cell, the nearest neighbors of each type were identified. This parameter was then averaged over all cells present at a particular time point.

Cell Shape Analysis

Phase images were imported into CellProfiler 2.1 (Broad Institute)⁵⁶ and selected cells were manually traced using the module IdentifyObjectsManually. Cell perimeter and area were then analyzed using the module MeasureObjectSizeShape, then exported to MATLAB to calculate the shape index $p_i=P_i∕\sqrt{A_0}$, where P is the perimeter and A is the area.¹²

Cell Velocity Analysis

For each cell i, the root mean squared velocity was calculated as $v_{i,rms}=\mid {\mathbf{v}}_i\mid =\mid \frac{{\mathbf{x}}_i(t+\Delta t)-{\mathbf{x}}_i\left(t\right)}{\Delta t}\mid$, where Δt = 1 h to reduce noise from nuclei detection. The average root mean squared velocity <v_rms> was calculated for by ensemble averaging over all cells or a selected subpopulation of cells present at a given time point. Before plotting, <v_rms> was smoothed using a moving average filter with the MATLAB function smooth.

Spatial Velocity Correlation Analysis

For each cell, the normalized velocity vector was computed as ${\widehat{\mathbf{v}}}_i\left(t\right)=\frac{{\mathbf{v}}_i\left(t\right)}{\mid {\mathbf{v}}_i\left(t\right)\mid }$ and the spatial correlation function was calculated by the averaged scalar product C(|r_i – r_j|,t) = 〈v̂_i(t)·v̂_j(t)〉_i≠j. This function was implemented for discretized data by ensemble averaging this scalar product for all cells within a particular separation interval, which was set to 20 μm for the entire population and 40 μm for the smaller subpopulation. For computational efficiency, spatial correlations were not computed for cells more than 500 μm apart. The decay of these subpopulations over time were fit to an exponential function C(|r_i – r_j|,t) = C₀ exp(–|r_i – r_j| / ξ) using the MATLAB function fit.

Jamming Phase Diagram

The reciprocal density was calculated as 1/σ = A/N_total, where the area of the field of view A = 1663 μm × 1403 μm and N_total was the total number of cells detected at that time point. A surface of the form <v_rms> = f(1/σ, %M) was interpolated from the discrete data points using the MATLAB function griddata. The resulting surface was displayed using the MATLAB function surf with interpolated shading.