Post-hoc Analysis for Detecting Individual Rare Variant Risk Associations using Probit Regression Bayesian Variable Selection Methods in Case-Control Sequencing Studies

Abstract

Rare variants have been shown to be significant contributors to complex disease risk. By definition, these variants have very low minor allele frequencies and traditional single-marker methods for statistical analysis are underpowered for typical sequencing study sample sizes. Multi-marker burden-type approaches attempt to identify aggregation of rare variants across case-control status by analyzing relatively small partitions of the genome, such as genes. However, it is generally the case that the aggregative measure would be a mixture of causal and neutral variants, and these omnibus tests do not directly provide any indication of which rare variants may be driving a given association. Recently, Bayesian variable selection approaches have been proposed to identify rare variant associations from a large set of rare variants under consideration. While these approaches have been shown to be powerful at detecting associations at the rare variant level, there are often computational limitations on the total quantity of rare variants under consideration and compromises are necessary for large-scale application. Here, we propose a computationally efficient alternative formulation of this method using a probit regression approach specifically capable of simultaneously analyzing hundreds to thousands of rare variants. We evaluate our approach to detect causal variation on simulated data and examine sensitivity and specificity in instances of high rare variant dimensionality as well as apply it to pathway-level rare variant analysis results from a prostate cancer risk case-control sequencing study. Finally, we discuss potential extensions and future directions of this work.

Introduction

With advancements in next-generation sequencing technologies, there has been a reinvigorated interest in the roles that rare variants (RVs) play in the genetic etiology of complex diseases [Cirulli and Goldstein 2010]. Due to low minor allele frequencies (MAFs), traditional single-variant risk association analysis methods on RVs suffer from low statistical power for even relatively large sample sizes, and specialized strategies are necessary to identify RV associations. This has led to the development of multi-marker aggregation strategies that are predicated on the notion that causal RVs may cluster in biologically relevant functional domains, such as genes [Bansal, et al. 2010]. There are a growing number of multi-marker omnibus methods available for RV association analysis that evaluate a priori defined target regions of interest (ROI) to localize clustering of causal RVs. These include various burden-based collapsing methods [Dering, et al. 2011], as well as variance component tests such as the C-alpha test [Neale, et al. 2011] and sequence kernel association test (SKAT) [Lee, et al. 2012; Wu, et al. 2011].

A notable caveat for these omnibus tests is that they do not provide any inference at the marker level as to which RVs may be driving a given multi-marker association. An alternative strategy is to simultaneously assess all of the RVs under consideration and apply some form of variable selection. One approach to identifying these RVs is to apply Bayesian variable selection procedures (for review, see [O'Hara and Sillanpaa 2009]). Use of these methods in marker association studies have the potential to be more powerful than other model selection procedures [Quintana and Conti 2013; Wilson, et al. 2010], and additionally provide relevant posterior quantities of interest for variable inclusion. Recently, Bayesian model uncertainty (BMU) strategies have been proposed for RV association analysis in case-control studies, referred to as the Bayesian risk index (BRI) [Quintana, et al. 2011]. The BRI method utilizes an aggregation and collapsing risk index parameterization of the selected RVs in a logistic regression framework, which we hereafter refer to as L-BRI. The authors' simulation results not only indicate increased power over traditional omnibus approaches for global association, but powerful detection of individual RVs driving an association signal through the derivation of marginal Bayes Factors (BFs).

A drawback of selecting the logit link function for the generalized linear model is that no closed-form solutions exist for the full conditional densities of the model parameters. Moreover, the Metropolis-Hastings (MH) algorithm for sampling from the model space in L-BRI applies a single-component proposal procedure to the variable inclusion vector. This can result in a computationally intensive algorithm requiring many hours to run to fully explore the model space for higher RV counts, reserving practical applications to smaller regions of the genome. Recent findings from large-scale sequencing studies indicate that, from a population-based perspective, RV sites can be quite common [Nelson, et al. 2012]. Consequently, sufficient sample size and sequence content could yield a computationally burdensome quantity of RVs for the L-BRI method. An illustrative example of potentially high RV dimensionality is a targeted sequencing study of the DISC1 locus investigating association with psychiatric traits [Thomson, et al. 2013], which identified over 2000 validated RVs (MAF < 1%) across the region of interest. Moreover, most sequencing studies are under-powered for gene-based analyses, prompting multi-genic analyses that aggregate rare variants across related genes in a given pathway[Wu and Zhi 2013]. Targeted analysis of multiple genes within a gene set could yield similarly extreme quantities of RVs. These applications may not be tenable for the L-BRI or similar approaches without application of strict exclusion criteria that could inadvertently filter out causal variation.

An alternative strategy to handling high dimensional rare variant analysis would be to apply Bayesian variable selection in a post-hoc fashion to identify potential causal variation driving an association finding from frequentist testing. One reformulation of the BRI approach would be to instead utilize the probit link function for the generalized linear model in combination with alternative MH algorithms that permit effective exploration of the model space. A key advantage of the Bayesian probit regression model is that closed forms of the full conditional distributions exist for appropriately selected conjugate priors using data augmentation techniques [Tanner and Wing 1987], resulting in efficient Gibbs sampling. The use of probit regression with Bayesian variable selection methods for high-dimensional modeling has been demonstrated to be quite powerful in the analysis of gene expression [Baragatti 2011; Lee, et al. 2003; Leon-Novelo, et al. 2012; Yang and Song 2010], capable of simultaneous consideration of hundreds to thousands of probesets. The utility of the probit regression approach relative to logistic regression for variant analysis in case-control sequencing studies was recently demonstrated by Kang et al. [Kang, et al. 2014].

Here we propose a fully Bayesian probit regression BRI (P-BRI) method for detection of individual RV risk associations and define strategies for instances of high variant dimensionality. We outline the basic sampling algorithm, which is an adaptation of existing Bayesian variable selection procedures for probit regression. We then evaluate the power of our approach at detecting causal rare variants via simulation studies, detailing sensitivity and specificity under varying conditions against L-BRI, as well as apply P-BRI to high dimensional variant scenarios. To illustrate our method using real data, we apply our P-BRI approach to a prostate cancer (PC) case-control whole-exome sequencing (WES) analysis of the previously detected rare variant pathway associations. Finally, we discuss the advantages of our approach and outline extensions and future research directions.

Methods

Model definition

Consider a case-control rare variation association study with N subjects consisting of N_D cases and N_C controls, and let Y be an N × 1 vector of corresponding binary responses indicating affected status, such that Y_i = 1 if the i^th subject is a case and Y_i = 0 if a control. Let Z be an N × p RV genotype matrix, where z_ij ≡ Z[i,j] represents the minor allele count for subject i at RV position j for j = 1, … p. We also define the N × q design matrix X consisting of q additional adjustment covariates, such as age or gender. In general, it is assumed that the proportion of truly causal RVs in Z is relatively small and that some form of model selection is desired to identify a subset of the total RVs that are associated with the trait of interest. For our approach we apply variable selection on the set of RVs in Z to characterize an RV load defined by the selected RVs. As such, each possible model ℳ_γ within the model space ℳ can be characterized through a variable inclusion vector γ, a p × 1 vector of indicators such that γ_j = 1 denotes that the j^th RV is included in the aggregation measure, yielding 2^p total possible models. For even moderate values of p, enumeration of all 2^p models ℳ_γ ∈ ℳ is not feasible.

To account for the effects of RVs on disease risk, we apply a risk index approach that considers the aggregate effect of multiple RVs by the collapsed measure $z_{\gamma ,i}={\mathit{Z}}_{\mathit{i}}^{\prime }\mathit{\gamma }$, where Z_i is a column vector corresponding to the i^th row of Z. The scalar quantity z_γ,i is the summation of minor alleles over the selected RVs in the model for subject i and indicates the subject-wise RV burden, and we denote Z_γ = (z_γ,1, …, z_γ,N)′. We define the binary regression model, such that

$$\begin{array}{c}Pr(Y_i=1|{\mathit{X}}_i{Z}_{\gamma ,i})=g^{-1}({\eta }_i)\\ {\eta }_i={\mathit{X}}_i^{\prime }\mathit{\beta }+{\mathrm{z}}_{\gamma ,i}{\beta }_{\gamma }\end{array}$$

where g(μ) is a link function and η_i denotes the linear predictor. For our approach, we select the probit link, such that g⁻¹(μ) = Φ(μ), where Φ(μ) represents the standard Gaussian cumulative probability distribution function. The model likelihood can then be written as

$${\mathrm{\Pi }}_i{[\mathrm{\Phi }({\eta }_i)]}^{y_i}{[1-\varphi ({\eta }_i)]}^{1-y_i},$$

which does not initially provide analytical solutions for the model parameter posteriors. However, Albert and Chib [Albert and Chib 1993] proposed a data augmentation solution to computing probit regression posterior distributions by introducing the additional vector of independent latent variables Ỹ corresponding to Y, such that

$$Y_i=\{\begin{array}{cc}1& \mathit{\text{if}}{\stackrel{\sim }{Y}}_{ı}>0\\ 0& \mathit{\text{if}}{\stackrel{\sim }{Y}}_{ı}\le 0\end{array}$$

and

$${\stackrel{\sim }{Y}}_{ı}|{\mathit{X}}_{\mathit{i}},Z_{\gamma ,i}~\mathcal{N}({\mathit{X}}_{\mathit{i}}^{\prime }\mathit{\beta }+Z_{\gamma ,i}{\beta }_{\gamma },1)$$

where 𝒩(μ,σ²) indicates a Gaussian distribution with mean μ and variance σ². Thus, the observed dichotomous variable Y is indicative of the sign of the latent random variable Ỹ, which is modeled via linear regression with fixed variance.

Prior distributions

We opt for traditional conjugate priors where applicable in order to attain full conditional distributions. We first define the prior distribution on the vector of design covariate parameters, β, to be a q-dimensional multivariate Gaussian distribution such that

$$\mathit{\beta }\sim {\mathcal{N}}_q(\mathbf{0},N{({\mathit{X}}^{\prime }\mathit{X})}^{-1})$$

which is a conventional g-prior distribution [Zellner 1983] in probit regression coefficients for blocked Gibbs sampling. We similarly place a standard Gaussian prior on the BRI coefficient β_γ, such that β_γ ∼ 𝒩(0,1).

We specify the prior probability of a given model ℳ_γ ∈ ℳ, Pr(ℳ_γ) through the individual variable prior inclusion probabilities Pr(γ_j = 1) = π_j, such that $Pr({\mathcal{M}}_{\gamma })={\mathrm{\Pi }}_{j=1}^r{\pi }_j^{{\gamma }_j}{(1-{\pi }_j)}^{1-{\gamma }_j}$. We define the model probability in this fashion via the assumption that the probabilities that given RVs are included in the model are independent, since low linkage disequilibrium is expected among RV sites [Pritchard 2001]. The vector π = (π₁, …, π_p)′ can either reflect no differential prior belief of inclusion, such that π₁= ⋯ =π_p= π, or may differ based upon available functional data that informs potential RV functionality in relation to the trait of interest. Similar to Quintana et al. [Quintana, et al. 2011], we specify the default prior on γ_j to be ${\pi }_j=(1-{\left(\frac{1}{2}\right)}^{\frac{1}{p}})$, such that the prior probability of the global null model $Pr({\mathcal{M}}_{\mathbf{0}})=Pr(\mathit{\gamma }={\mathbf{0}}_{\mathit{p}\mathbf{\times }\mathbf{1}})={\mathrm{\Pi }}_j(1-{\pi }_j)=\frac{1}{2}$ to account for the potential of a Type I error as well as render the models equitable in this regard.

Bayesian sampling algorithm

To obtain estimates of the posterior quantities of interest, we apply a Markov Chain Monte Carlo (MCMC) approach [Hastings 1970], whereby samples from the respective posterior distributions of the model parameters are iteratively drawn using Gibbs sampling (GS) and MH methods. To define our sampler, we first must characterize the full conditional distributions of the model parameters, which include f(Ỹ|Y,β,β_γ,γ), f(β|Ỹ, β_γ,γ), f(β_γ|Ỹ,β,γ), and f(γ|Ỹ,β,β_γ,). The full conditional distributions for the first three can easily be derived, such that

• ${\stackrel{\sim }{Y}}_{ı}|Y_i=1~\mathcal{N}({\mathit{X}}_{\mathit{i}}^{\prime }\mathit{\beta }+Z_{\gamma ,i}{\beta }_{\gamma },1)$ left truncated at 0

• ${\stackrel{\sim }{Y}}_{ı}|Y_i=0~\mathcal{N}({\mathit{X}}_{\mathit{i}}^{\prime }\mathit{\beta }+Z_{\gamma ,i}{\beta }_{\gamma },1)$ right truncated at 0

• $\mathit{\beta }|\stackrel{\sim }{\mathit{Y}},\alpha ,\mathit{\gamma }\sim \mathcal{N}({\mathit{V}}_{\mathit{\beta }}{\mathit{X}}^{\prime }(\stackrel{\sim }{\mathit{Y}}-{\mathit{Z}}_{\mathit{\gamma }}{\beta }_{\gamma }),{\mathit{V}}_{\mathit{\beta }})$ where ${\mathit{V}}_{\mathit{\beta }}=\frac{N}{N+1}{({\mathit{X}}^{\prime }\mathit{X})}^{-1}$

• ${\beta }_{\gamma }|\stackrel{\sim }{\mathit{Y}},\mathit{\beta },\mathit{\gamma }\sim \mathcal{N}({\nu }_{\gamma }{\mathit{Z}}_{\mathit{\gamma }}^{\prime }(\stackrel{\sim }{\mathit{Y}}-\mathit{X}\mathit{\beta }),{\nu }_{\gamma })$ where ${\nu }_{\gamma }=\frac{1}{{\sigma }_{\beta }^{-2}+{\mathit{Z}}_{\mathit{\gamma }}^{\prime }{\mathit{Z}}_{\mathit{\gamma }}}$

Since these distributions are properly defined, GS methods can be used for iterative updating. However, under our BMU procedure, the full conditional distribution of γ cannot be directly simulated easily, requiring a Metropolis-within-Gibbs approach. To sample from the distribution of γ, we adopt a marginalization strategy [Liu 1994], which is based upon the integrated distribution of the full conditional of γ over β_γ, f(γ|Ỹ,β). It can be shown using Bayesian linear model theory that f(γ|Ỹ,β) is proportional to

$$exp(-\frac{1}{2}({(\stackrel{\sim }{\mathit{Y}}-\mathit{X}\mathit{\beta })}^{\prime }({\mathit{I}}_{\mathit{N}}-\frac{{\mathit{Z}}_{\mathit{\gamma }}{\mathit{Z}}_{\mathit{\gamma }}^{\prime }}{{\sigma }_{\beta }^{-2}+{\mathit{Z}}_{\mathit{\gamma }}^{\prime }{\mathit{Z}}_{\mathit{\gamma }}})(\stackrel{\sim }{\mathit{Y}}-\mathit{X}\mathit{\beta })\left)\right)\times \prod _{j=1}^p{\pi }_j^{{\gamma }_j}{(1-{\pi }_j)}^{1-{\gamma }_j}$$

which we use to define a MH algorithm for updating γ, directly followed by simulation of β_γ from its full conditional distribution.

There are a number of options for proposing new values of γ in the MH step of the MCMC sampler. Quintana et al. [Quintana, et al. 2011] elected a single-step addition/deletion MH algorithm for model selection in L-BRI, whereby the proposed vector γ is generated by switching the binary value of a randomly chosen variable inclusion indicator γ_j. However, in instances of higher RV dimensionality, this approach requires a prohibitively large number of iterations to adequately explore the model space ℳ, resulting in relatively poor mixing. In contrast, updating each γ_i in a component-wise fashion can significantly improve mixing and convergence and may result in overall better performance [Johnson, et al. 2013]. Consequently, we apply a component-wise multistep MH algorithm, similar to that applied by Lee et al.[Lee, et al. 2014] for imaging data, that iteratively updates each element in γ. This is conducted in a modified metropolised Gibbs framework, such that the proposal for γ_i is always the opposite of the current state, yielding more efficient mixing[Liu 1996]. The unique formulation of the risk index as a product of a fixed design matrix Z and variable inclusion vector γ permits computationally efficient component-wise MH updating, which is generally infeasible for high dimensional problems. At each iteration of the MCMC algorithm we randomize the updating order of MH step for γ, and convergence to the stationary distribution may be checked by running multiple chains from different initial values and comparing posterior samples.

Given that the defined prior on the BRI parameter β_γ has positive support over the entire real line, it is possible for the sampler to draw negative values of β_γ despite it characterizing risk. One simple solution is to constrain the prior distribution to the positive real line by using a truncated normal prior. By Gelfand et al. [Gelfand, et al. 1992], we can accommodate this prior by adding a rejection step to the Gibbs sampler for β_γ, accepting new draws of β_γ, β_γ^(⋆), only if β_γ^(⋆) > 0.

Posterior measures of interest

Conditional on evidence against the global null model ℳ₀ (e.g., from a previously conducted test), a primary motivation is identifying an interesting subset of variants associated with the disease of interest for follow-up analyses. In the case of variable selection problems, the marginal posterior probabilities of inclusion are useful for such inference. Denote ζ_j = Pr(γ_j=1|Y) to be the marginal posterior probability of inclusion for j^th RV in Z. Quintana et al. [Quintana, et al. 2011] derive the marginal BFs to isolate RVs that may be driving an association, such that

$$\mathit{\text{BF}}[{\gamma }_j=1:{\gamma }_j=0]=\frac{Pr({\gamma }_j=1|\mathit{Y})}{Pr({\gamma }_j=0|\mathit{Y})}\times \frac{Pr({\gamma }_j=0)}{Pr({\gamma }_j=1)}=\frac{{\zeta }_j}{1-{\zeta }_j}\times \frac{1-{\pi }_j}{{\pi }_j}$$

We estimate ζ_j in a Monte Carlo fashion from the T posterior samples of γ, such ${\widehat{\zeta }}_j=\frac{{\sum }_r{\gamma }_j^{(t)}}{T}$. Decisions of relative importance of each RV can then be made with respect to common thresholds (e.g., >10 or 31.6) defined by Jeffreys' grades of evidence [Jeffreys 1961] using these marginal BFs.

Simulations

To evaluate the performance of P-BRI at identifying individual risk associated RVs, we considered a hypothetical case-control genetic association study with N = 1000 total subjects (N_D=N_C). To simulate the RV genotype data conditional on disease status, we employed the model developed by Li and Leal [Li and Leal 2008] and algorithmically defined by Zhou et al. [Zhou, et al. 2010]. This model is based upon the conditional Poisson-binomial whereby any of the v risk RVs can independently cause the disease status, defined though the MAFs, prevalence, and relative risks of RVs. The MAFs for all RVs were randomly generated uniformly on the interval (0.005,0.01), and all simulated RVs that resulted in an empirical MAF of zero were excluded from analysis. Prevalence was fixed at 0.01 and no additional covariates were included in the simulation model. Simulations under the null (i.e., no causal variation) simply involved random assignment of case-control status to randomly generated RV genotype vectors.

We first compared the performance of the P-BRI relative to the original L-BRI at detecting causal RVs in scenarios that were computationally reasonable for either method, fixing p = 50. Software implementation of the L-BRI method is available via the R package BVS, which we applied under default settings unless otherwise noted. For simulations involving causal variation, we considered the quantity of truly causal RVs, v, to range from 5 to 15, and applied both the P-BRI and L-BRI methods to detect the associated RVs. All causal RVs were attributed a relative risk (RR) of 1.5, 2.5, or 5, with all remaining RVs being neutral (RR = 1). Convergence of the L-BRI was evaluated by running two parallel chains and comparing output marginal BFs, as per the method's documentation, with convergence defined by the root mean square error between the two sets of BFs to be < 1. To evaluate convergence of P-BRI, the Gelman-Rubin diagnostic was applied to MCMC posterior samples of β_γ for two parallel chains with different starting values, with convergence declared if the upper 95% confidence limit was < 2. For the P-BRI method we sampled a total of 30,000 iterations, treating the first 15,000 as a burn-in, while for the L-BRI method we sampled 100,000 iterations and treated the first 50,000 as a burn-in. If convergence was not achieved at these iteration counts additional posterior samples were drawn until convergence criteria were met. Marginal BFs were also computed for P-BRI in order to compare the relative false positive (FPR) and true positive rates (TPR) based upon detection of causal variant status across all simulation iterations (50 × 500 = 25000 total variants). For P-BRI, instances where RVs had corresponding posterior inclusion probabilities (PIPs) estimates ζ̂_j = 1 were adjusted to ${\widehat{\zeta }}_j=\frac{T-1}{T}$ to avoid division by zero in the marginal BF. For purposes of comparing performance between L-BRI and P-BRI relative to TPR and FPR, we computed bootstrapped 95% confidence intervals on these metrics and/or their differential across methods using the R package fbroc, based upon 1000 bootstrap samples.

To additionally examine the performance of P-BRI under high RV dimensionality, we increased the total RV counts to p = 500 and p = 1000 and fixed the number of true deleterious RVs to v = 25, such that the causal RV proportions were 5.0% (p = 500 and 2.5% (p = 1000), respectively. Given the larger quantity of RVs under simultaneous consideration, we focused on identification of larger effect sizes and examined performance for RRs of 2.5, 5, and 10 for causal RVs. For these applications, the first 15,000 MCMC samples were discarded as a burn-in, resulting in a posterior sample size of 15,000.

Data Application: Prostate Cancer Risk

A whole-exome sequencing study of men with prostate cancer was conducted by the International Consortium of Prostate Cancer Genetics (ICPCG). The ICPCG has identified and sampled the most informative high-risk PC pedigrees known throughout the world. With the goal of identifying PC susceptibility loci utilizing this extraordinary collection of families, WES was performed on 539 familial cases of PC derived from 366 families all having at least three affected men with PC: 257 cases from 84 families (the majority having three sequenced/family) and 282 singleton cases. Whole-exome sequencing was performed using the Agilent 50Mb SureSelect Human All Exon chip or the Agilent SureSelect V4+UTR kit. Bioinformatics analysis was performed using GenomeGPS, a comprehensive analysis pipeline developed at Mayo Clinic which performs alignment using Novoalign (v.07.13), realignment and recalibration using the Genome Analysis Tool Kit (GATK,v3.3), germline single nucleotide and small insertion/deletion variant calling using GATK HaplotypeCaller, and Variant quality score recalibration (VQSR), following GATK best practices v3 [DePristo, et al. 2011; McKenna, et al. 2010; Van der Auwera, et al. 2013]. Population-based controls were selected from samples that were sequenced at Mayo Clinic using similar library preparation and sequencing to the cases. We identified 494 samples from four studies which met our inclusion criteria (germline sequencing using Agilent V2 or V4+UTR capture and with initial alignment performed using the same version of Novoalign. Samples included 89 unselected samples from the Mayo Clinic Community Biobank, 355 samples from two studies of cardiovascular phenotypes and 50 samples from a study of neuropathy. All samples were re-processed using the bioinformatics pipeline described above and underwent the same stringent quality control analyses.

We conducted a pathway-directed RV case-control study (see Supplemental Methods for details) to evaluate the role of RVs in risk of PC using 860 gene-set definitions from KEGG [Kanehisa 2002] and Reactome [Joshi-Tope, et al. 2005]. For our purposes, we restricted our analyses to unrelated subjects by randomly selecting single individuals from pedigrees with multiple sequenced subjects. After sample exclusions for quality control or relatedness, a total of 333 cases and 349 controls remained. In our analyses, we identified multiple highly overlapping gene-sets related to the Lands cycle (Reactome IDs R-HSA-1482922.1, R-HSA-1483226.1, R-HSA-1482788.1, R-HSA-1482839.1, R-HSA-1482925.1) to be significantly associated (P <5.8E-05) using SKAT-O[Lee, et al. 2012] and burden-based testing. The Lands cycle is involved in the acyl-chain remodeling of a variety of phospholipids, and the union of the associated pathways constitutes 26 genes involving 438 unique observed variants with empirical MAF < 0.05. To investigate which RVs may be driving the association, we applied the P-BRI approach to the data, including additional covariate adjustment for WES capture kit and five leading principal components derived from the complete genetic data. Similar posterior sampling procedures that were used in the simulations were applied and no additional information was used to alter the priors on γ.

Results

Simulation Analysis

The TPRs for RV associations declared at a marginal BF threshold of BF ≥ 10 are presented in Table I. Overall, we observed higher TPR as well as FPRs for L-BRI relative to P-BRI, indicating marginal BFs to be larger in general for the L-BRI approach and rendering performance comparisons difficult. When evaluating TPRs at a fixed FPR of 0.01 (Table II), we noted comparable performance. We additionally observed reduced TPR at fixed RR effect sizes as the proportion of causal variants increased, regardless of method. This is likely due to the fact that models encompassing a larger number of causal variants are less likely under the default prior distribution on the model space ℳ. In general, performance was comparable between the two approaches, with P-BRI tending to perform better under conditions of lower effect size and smaller proportion of causal variants and L-BRI under large effect sizes and higher causal variant proportion.

Table I.

Simulation results for empirical TPRs and FPRs and corresponding bootstrapped 95% confidence intervals for causal RV detection across simulation replications with fixed marginal BF threshold set to 10 (“strong” evidence).

		ν =5		ν =10		ν =15
Method	RR	TPR	FPR	TPR	FPR	TPR	FPR
P-BRI	1.5	0.341 (0.323,0.360)	0.012 (0.011,0.014)	0.331 (0.317,0.344)	0.014 (0.013,0.016)	0.313 (0.303,0.324)	0.015 (0.013,0016)
L-BRI		0.314 (0.295,0.333)	0.017 (0.015,0.019)	0.405 (0.391,0.417)	0.030 (0.028,0.033)	0.434 (0.423,0.445)	0.039 (0.036,0.042)
P-BRI	2.5	0.694 (0.677,0.713)	0.014 (0.012,0.015)	0.643 (0.630,0.656)	0.014 (0.013,0.016)	0.569 (0.558,0.581)	0.014 (0.012,0016)
L-BRI		0.761 (0.746,0.779)	0.035 (0.033,0.038)	0.806 (0.796,0.817)	0.058 (0.055,0.061)	0.784 (0.774,0.793)	0.070 (0.067,0.074)
P-BRI	5.0	0.972 (0.966,0.978)	0.013 (0.012,0.015)	0.929 (0.923,0,936)	0.014 (0.013,0.016)	0.867 (0.859,0.875)	0.014 (0.013,0016)
L-BRI		0.986 (0.981,0.990)	0.039 (0.036,0.041)	0.978 (0.974,0.982)	0.061 (0.058,0.064)	0.965 (0.961,0.969)	0.090 (0.086,0.095)

Table II.

Simulation results for empirical TPRs for causal RV detection across simulation replications at a fixed FPR of 0.01. For comparisons across methods, the difference in TPR (Δ) and corresponding bootstrap 95% confidence interval are reported.

		True Positive Rate
Method	RR	ν =5	ν =10	ν =15
P-BRI	1.5	0.324	0.288	0.265
L-BRI		0.253	0.262	0.250
Δ (95% CI)		0.070 (0.056,0.086)	0.026 (0.012,0.038)	0.015 (0.002,0.027)
P-BRI	2.5	0.660	0.603	0.523
L-BRI		0.638	0.612	0.560
Δ (95% CI)		0.022 (0.014,0.034)	-0.009 (-0.020,0.001)	-0.037 (-0.049,-0.022)
P-BRI	5.0	0.966	0.919	0.845
L-BRI		0.968	0.929	0.877
Δ (95% CI)		-0.002 (-0.006,0.001)	-0.010 (-0.015,-0.007)	-0.032 (-0.039,-0.024)

Marginal TPR and FPR results at BF thresholds of 10 and 31.6 for the high RV dimensionality simulations are presented in Table III. We observed similar patterns of performance with respect to underlying RR and causal variant proportions as observed in the low RV count simulations, with higher global TPRs for p = 500 relative to p = 1000 for a fixed causal variant effect size. Marginal RV detection evaluated by TPR and FPR was comparable across differing total number of evaluated variants at a fixed BF threshold, with increasing TPR at higher effect sizes with the FPR remaining relatively fixed.

Table III.

Simulation results for P-BRI in high RV dimensionality (p = 500, 1000) for marginal TPR and FPRs at traditional BF thresholds (10 and 31.6), along with bootstrap 95% confidence intervals.

	Marginal (BF>10)		Marginal (BF>31.6)
RR	TPR	FPR	TPR	FPR
	p =500
2.5	0.379 (0.368,0.385)	0.014 (0.014,0.015)	0.235 (0.228,0.241)	0.004 (0.004,0.004)
5.0	0.605 (0.596,0.613)	0.014 (0.013,0.014)	0.477 (0.468,0.486)	0.004 (0.004,0.004)
10.0	0.833 (0.826,0.840)	0.012 (0.012,0.013)	0.762 (0.754,0.770)	0.004 (0.004,0.004)
	p =1000
2.5	0.378 (0.369,0.386)	0.013 (0.013,0.014)	0.238 (0.231,0.245)	0.004 (0.003,0.004)
5.0	0.586 (0.577,0.594)	0.014 (0.014,0.014)	0.454 (0.445,0.461)	0.004 (0.004,0.004)
10.0	0.801 (0.794,0.808)	0.013 (0.012,0.013)	0.717 (0.709,0.725)	0.004 (0.004,0.004)

The above simulation results do not take into account the likely high degree of multiple testing that would likely occur prior to post-hoc evaluation, as the simulations only consider the case where true causal variation is present. Consequently, false positive rates may be higher than reported, depending upon how Type I error was controlled at the first stage of testing. To evaluate the behavior of P-BRI under false positive testing results, we conducted an additional 500 simulations for each of the high variant dimensionality conditions where none of the simulated variants were associated with case/control status. At a BF threshold of 10, variant-level false positive rates were commensurate with those reported in Table III (0.012 for p = 500; 0.013 for p = 1000).

Data Application

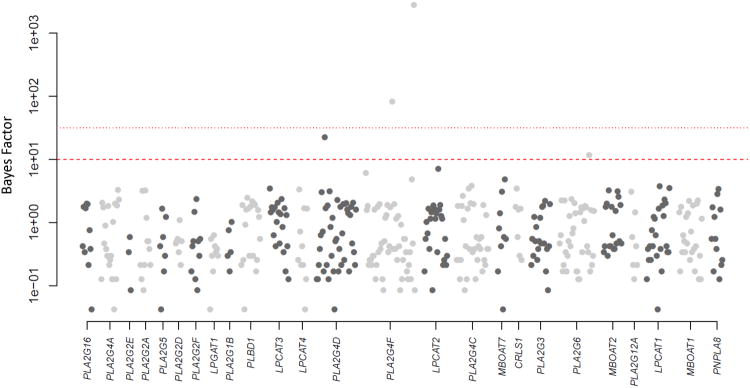
The marginal BFs for the 438 RVs analyzed in the PC risk analysis are presented in Figure 1. A total of four variants in three separate genes corresponded to a BF >10 (Table IV), including a splice-site variant in gene PLA2G4F (hg19 chr15:42448635A→T) with a corresponding marginal BF of 2787.7 and PIP of 0.815, occurring in 19 cases but only one control. Both PLA2G4D and PLA2G4F encode proteins that selectively hydrolyze glycerophospholipids, and dysregulation of lipid metabolism has been noted in many cancers[Huang and Freter 2015].

Figure 1.

Depiction of BFs (y-axis on log10 scale) for all 438 RVs within 26 genes related to pathways previously identified to have significant associations with PC risk in the data set. Colors of the points alternate by gene membership from dark gray to light gray, and the y-axis is annotated in the original scale. Horizontal lines depict BF thresholds of 10 and 31.6.

Table IV.

Annotation and marginal BFs for RVs with BF>10 in the post-hoc analysis of 438 RVs implicated in pathway RV analysis in prostate cancer risk.

Chr	Position	Gene	Ref	Alt	Effect	BF
15	42,364,046	PLA2G4D	T	C	Missense	22.5
15	42,439,921	PLA2G4F	G	C	Nonsense	82.9
15	42,448,635	PLA2G4F	A	C	Splice-site	2787.7
22	38,559,586	PLA2G6	G	C	Intronic	11.6

To evaluate the MCMC mixing for the data application, we computed the model mutation rate as the proportion of posterior samples that resulted in model state transitions (77.5%). Computational runtime for the full 30,000 iterations was approximately 20 minutes. Similar application of L-BRI resulted in only 188 accepted model transitions (mutation rate = 1.25%) for the same number of iterations. After 100,000 iterations (∼1 hour runtime) for two independent runs with a 50,000 burn-in, examination of the marginal BF output from L-BRI still indicated lack of convergence.

Discussion

In this paper, we have presented a regression-based Bayesian variable selection strategy for post-hoc analysis of aggregative RV associations in disease risk via a reformulation of the BRI method for case-control RV association analysis. By modeling the probability of affected status using a probit link function, in contrast to a logistic regression approach, we have demonstrated the method to be feasible for high dimensional applications. We have also proposed a component-wise MH algorithm for updating the variable inclusion vector γ, which results in rapid exploration of the model space. Our simulation results comparing L-BRI and P-BRI for moderate RV counts indicate that their ability to detect causal RVs is comparable for a variety of conditions, while P-BRI was also capable of detecting causal variation under very high RV dimensionality. This renders P-BRI a powerful method for dense post-hoc RV association analyses, as evidenced by both our large-scale simulations and our PC risk analysis of 438 RVs within genes involved in the Lands Cycle. The application of our approach indicates the significant associations previously detected by pathway-based analyses may be driven by variants within three phospholipase genes and additional targeted sequencing of these genes may be warranted in future research.

From a computational perspective, our probit approach benefits from a multi-step MH algorithm for updating variable inclusion vector γ. Execution runtimes for P-BRI in our simulation study under conditions where p = 50 and N = 1000 averaged 6.2 minutes, while runtimes for our larger simulations where p = 1000 and N = 1000 at 30,000 iterations were approximately 75 minutes on average. The latter analyses were not feasible for L-BRI in our simulations due to the high model space dimensionality and single-step updating of γ. These timings are based upon working code written in the R statistical language and executed on a modern workstation equipped with a Quad-Core AMD Opteron™ Processor and 16 Gb of RAM. We anticipate that computational burden for the P-BRI method may be further reduced substantially with alternative BVS methods, such as objective Bayes model selection [Leon-Novelo, et al. 2012] and particle stochastic search [Shi and Dunson 2011] approaches, as well as implementation of parts of the current MCMC algorithm in more computationally efficient computer languages such as C++.

A simplifying assumption of risk index methods in general is that each included RV contributes an equal effect to the RV burden, or rather that it models the mean effect of the selected RVs. While this assumption permits efficient sampling, it may not accurately reflect the effects of the individual RV associations. It is possible to utilize existing structural definitions, such as genes or exons, as a grouping mechanism and assign separate burden-based parameters, although careful consideration is necessary to avoid singular design matrices if the number of included elements exceeds the sample size. If protective RV's are present, they would not be appropriately modeled by our approach. However, the P-BRI method could be simply modified by increasing the support of γ to include negative indicators, as in the MixBRI approach by Quintana et al. [Quintana, et al. 2011].

Although the P-BRI method permits efficient exploration of high-dimensional model spaces, alternative MH algorithms for sampling from the model space ℳ may be useful in extreme scenarios where the RV dimensionality renders the component-wise MH algorithm computationally infeasible. One approach is to consider a subset of the model space ℳ, ℳ^b, by defining the MH transition kernel such that the number of included RVs in any model ℳ_γ ∈ ℳ^b is invariant and equal to an a priori defined quantity b. This approach is comparable to the MCMC algorithm outlined in Baragatti [Baragatti 2011] and preliminary simulations indicate feasibility for P-BRI with p ≥ 10,000, although further work is necessary to formally develop these methods. Adaptive algorithms designed for high-dimensional sampling in GWAS may also be of utility[Peltola, et al. 2012].

There are a variety of promising extensions from our development of the P-BRI method for post-hoc RV analysis. An added benefit of this work is that application to quantitative traits is trivial, since the algorithms are already in place through the latent variable Ỹ, although variational Bayesian methods have previously demonstrated high computational efficiency in this area[Logsdon, et al. 2014]. We could also extend the regression procedure to include common variants in the model selection for a comprehensive association analysis, as well as easily adopt the integrative variable selection procedures in Quintana et al. [Quintana and Conti 2013] for informed model selection based upon existing variant annotation. Finally, we are actively evaluating methods to estimate global null model posterior probabilities using sampling procedures implemented by Liang et al.[Liang and Xiong 2013] for association inference, as well as integrating P-BRI methods with curated pathway databases to facilitate genome-wide exploratory rare variant gene-set analysis.