Drug Concentration Thresholds Predictive of Therapy Failure and Death in Children With Tuberculosis: Bread Crumb Trails in Random Forests

Abstract

Background. The role of drug concentrations in clinical outcomes in children with tuberculosis is unclear. Target concentrations for dose optimization are unknown.

Methods. Plasma drug concentrations measured in Indian children with tuberculosis were modeled using compartmental pharmacokinetic analyses. The children were followed until end of therapy to ascertain therapy failure or death. An ensemble of artificial intelligence algorithms, including random forests, was used to identify predictors of clinical outcome from among 30 clinical, laboratory, and pharmacokinetic variables.

Results. Among the 143 children with known outcomes, there was high between-child variability of isoniazid, rifampin, and pyrazinamide concentrations: 110 (77%) completed therapy, 24 (17%) failed therapy, and 9 (6%) died. The main predictors of therapy failure or death were a pyrazinamide peak concentration <38.10 mg/L and rifampin peak concentration <3.01 mg/L. The relative risk of these poor outcomes below these peak concentration thresholds was 3.64 (95% confidence interval [CI], 2.28–5.83). Isoniazid had concentration-dependent antagonism with rifampin and pyrazinamide, with an adjusted odds ratio for therapy failure of 3.00 (95% CI, 2.08–4.33) in antagonism concentration range. In regard to death alone as an outcome, the same drug concentrations, plus z scores (indicators of malnutrition), and age <3 years, were highly ranked predictors. In children <3 years old, isoniazid 0- to 24-hour area under the concentration-time curve <11.95 mg/L × hour and/or rifampin peak <3.10 mg/L were the best predictors of therapy failure, with relative risk of 3.43 (95% CI, .99–11.82).

Conclusions. We have identified new antibiotic target concentrations, which are potential biomarkers associated with treatment failure and death in children with tuberculosis.

Tuberculosis affects >1 million children, and kills >140 000 of them, each year. In contrast to adult tuberculosis, in which >85% of patients manifest pulmonary disease that is predominantly cavitary in nature [1], children are more likely to have noncavitary pulmonary tuberculosis and extrapulmonary disease, involving a number of different anatomic sites. The cavitary pulmonary lesion presents specific barriers to therapeutics that differ from those in noncavitary pulmonary or disseminated tuberculosis or tuberculosis restricted to extrapulmonary sites. Antibiotics must reach each of the infected sites in children to exert effect [2–5]. This presents a therapeutic challenge in extrapolating from the treatment of adults with a regimen designed for drug penetration into the lung cavity, and activity against extracellular bacilli, to the treatment of disseminated tuberculosis, and even noncavitary pulmonary tuberculosis in children, in which the infecting bacilli are predominantly intracellular [4]. Furthermore, the paucibacillary and often extrapulmonary nature of childhood tuberculosis complicates diagnosis and risk stratification of patients, as sputum smears and cultures are traditionally used to diagnose tuberculosis and monitor response to treatment. These differences in the tuberculosis pathology in toddlers and babies compared with adult-type disease suggest that factors driving outcome may differ between children and adults [6].

Recently, there have been welcome efforts to design new doses and formulations of first-line antituberculosis drugs for children [1, 4, 5, 7]. New rifampin, isoniazid, pyrazinamide, and ethambutol doses have been proposed for use in children by the World Health Organization [8]. These recommendations have relied on the logic that optimal concentrations for treatment of tuberculosis in adults will be the same as those in children. However, optimal drug concentrations in adults still remain poorly defined. Commonly used targets for therapeutic drug monitoring (eg, 2-hour postdose concentrations of 3 mg/L for isoniazid, 8 mg/L for rifampin, and 20 mg/L for pyrazinamide) were derived from normal distributions in healthy volunteer adults and selected US adult patients receiving standard doses on the basis that they are predictably tolerated and expected to be efficacious [9, 10]. Here, we used a more agnostic and unbiased approach to identify threshold concentrations most predictive of clinical outcomes for both extrapulmonary and pulmonary tuberculosis in children, especially in toddlers and babies. We included 30 potential predictors, including patients' routinely collected clinical characteristics, measures of nutritional status, and drug pharmacokinetic measures (eg, peak concentration [“peak”], and 0- to 24-hour area under the concentration-time curve [AUC_0–24]), in machine learning algorithms. We used classification and regression tree (CART) analyses, boosted CART (TreeNet), and random forests to rank and identify the best predictors of outcome, as well as their cutoff values, in children with tuberculosis.

METHODS

Setting

Children were recruited from 6 separate tertiary institutions in Chennai, Madurai, Bengaluru, and Agra, in India. Ethical approval was obtained from all relevant institutional review boards. This was a noninterventional study.

Type of Study

The study was a prospective pharmacokinetic and pharmacodynamic study of an intermittent (thrice-weekly) regimen of first-line antituberculosis drugs in children. All children received supervised directly observed therapy at Revised National Tuberculosis Control Program (RNTCP) treatment centers. All doses were directly observed by healthcare workers and for those children who missed some doses but did not meet threshold for default (ie, missing >2 consecutive months' worth of doses), those missed doses were added at the end of 2 months or end of treatment after 6 months. Noncompartmental pharmacokinetic analyses for the 3 drugs, and impact of nutrition on outcomes for this study, have been published elsewhere [11–13]. Malnutrition was defined as weight-for-height, weight-for-age, or height-for-age z scores < −2 or >2. Here, compartmental pharmacokinetic analyses were performed for each drug for each child to identify their potential role in outcomes.

Treatment Regimens and Dosing

Diagnosis, initiation of therapy, clinical assessments on follow-up, and final evaluation at end of therapy were performed by specialist pediatricians at each institution according to RNTCP recommendations [8, 14]. The treatment regimens were according to category. Treatment category I comprised rifampin, isoniazid, pyrazinamide, and ethambutol and was given to new smear-positive cases or those with advanced disease, whereas category III did not include ethambutol and was reserved for less severe smear-negative tuberculosis. Category II included streptomycin plus ethambutol added to rifampin, isoniazid, and pyrazinamide during the intensive phase of therapy, after which the continuation phase was prolonged by a month. Category II therapy was given to children who had taken treatment for at least 4 weeks and had had treatment interruption plus active disease. Drug doses were based on body weight: 10 mg/kg for rifampin and isoniazid, 30–35 mg/kg for pyrazinamide, and 30 mg/kg for ethambutol. Whereas the entire therapy was intermittent in most instances, seriously ill children who were admitted were given daily supervised therapy during their stay in hospital. Fixed-dose combinations were given in blister packs according to weight bands of 4–6 kg, 7–10 kg, 11–14 kg, 15–19 kg, 20–24 kg, and >25 kg. Human immunodeficiency virus (HIV)–infected children were treated with a regimen of efavirenz and lamivudine plus either stavudine or zidovudine or tenofovir or abacavir [15].

Definition of Terms and Treatment Outcomes

The following standard terms were used to define tuberculosis disease site and clinical outcomes at end of therapy [14, 15]. The diagnosis of pediatric extrapulmonary tuberculosis was made on the basis recommended by RNTCP (http://tbcindia.nic.in/showfile.php?lid=2904). Radiological changes highly suggestive of intrathoracic tuberculosis such as hilar/paratracheal lymphadenitis with or without parenchymal lesion, miliary tuberculosis, or fibrocavitary pneumonia were designated as pulmonary tuberculosis. Completed treatment was reserved for children who attained bacteriologic cure or completed assigned therapy and did not demonstrate residual disease based on clinical assessments (weight gain, regression of fever). Failure was used to define children who deteriorated based on clinical (persistent fever, failure to thrive or weight loss) or radiological examination while on antituberculosis therapy, and the clinician would proceed to change treatments. Death while on therapy was also recorded as a separate outcome. We defined poor outcome as either therapy failure or death.

Pharmacokinetic Sampling

During the intensive phase of therapy, after at least 2 weeks on therapy, children were admitted to hospital for serial blood sampling for pharmacokinetic analyses. The study doses were administered by the study team after an overnight fast. Serial collection of 2 mL of blood predose and at 2, 4, 6, and 8 hours postdose was performed. Plasma drug concentrations were determined using well-described and validated methods [16, 17]. The assays were linear within the following ranges: 0.25–10.0 μg/mL for isoniazid, 0.25–15 ug/mL for rifampin, and 1.25–50.0 μg/mL for pyrazinamide in plasma. The within-day and between-day relative standard deviation for all drug standards were <10%. The average recoveries of isoniazid, rifampin, and pyrazinamide from plasma were 104%, 104% and 102%, respectively. All other assay characteristics have been described in detail in prior publications [16. 17].

Pharmacokinetic Modeling

All 805 concentrations of isoniazid, 795 of rifampin, and 720 of pyrazinamide were modeled in ADAPT software for each drug separately. We did not a priori assume the number of compartments for each drug. Instead, we analyzed each drug using 1-compartment and 2-compartment models, with first-order input and elimination. We used a 2-step approach: first, single 2-stage estimation to identify initial estimates for the Fortran model and parameter files, followed by a second analysis with maximum-likelihood solution via the expectation-maximization (MLEM) algorithm [6]. The best model was chosen from the MLEM output by comparing Akaike information criterion (AIC), Bayesian information criterion (BIC), and parsimony.

CART, Boosted CART (TreeNet), and Random Forests

We used CART, boosted CART, and random forest for variable selection because they have been successfully used in the past to solve “small n, large P” problems [18–20]. These artificial intelligence algorithms were developed by Breiman and Cutler in the late 1990s to improve model prediction accuracy using enhanced computing power. Pharmacokinetic/pharmacodynamic datasets like the current one are highly dimensional, and have repeated and correlated measures so that in some way they are “big data” from relatively fewer patients. A 3-step approach was used to identify and rank predictors of poor outcomes in children, as well as to identify the thresholds for those predictors, using both random forests and CART because of the unique attributes of each. First, we implemented random forests and boosted CART to identify and rank the most important variables predictive of outcomes. In both CART and random forests, variable importance measures were computed to assess the relevance of each variable in the model over all trees of the ensemble. Weighted mean “simple” improvement in the splitting criterion or improvement in the Gini gain was incorporated into computing the variable importance score [18, 21]. Two computer-generated variables, a positive and negative control, were included in the initial run. The positive control comprised numbers deliberately made to correlate 100% with outcome, while the negative control consisted of random generated numbers. The 30 potential predictors examined in the model were: age, sex, weight, height, body mass index, body surface area, height-for-age z score, weight-for-age z score, height-for-weight z score, HIV infection result, disease site, treatment category, rifampin dose, isoniazid dose, pyrazinamide dose, negative and positive control variables, and the drug pharmacokinetic measurements, including the 2-hour, peak, trough, AUC_0–24, and time to peak concentration for each drug. We then selected the top half (ie, 15 ranked variables and their scores) for each model based on the area under the receiver operating characteristic (ROC) curve value and prediction success rate. For the former, a cutoff value of 0.70 was arbitrarily applied, whereas the latter was tuned by varying the class weights so that a penalty of between 10% and 50% was applied for misclassifying death or failure of therapy. We used posttest or cross-validated values to limit overfit. All model building was examined for parsimony.

Second, we ran separate boosted CART models using only the significant predictors identified earlier. The purpose was to identify thresholds predictive of therapy failure, death, and the combined poor outcomes conditional on the ranking in importance and identified thresholds for the other covariates. Thresholds were obtained from the optimal tree. In addition, partial dependence plots were generated to give a graphical depiction of the marginal impact of 1 variable or the interaction of 2 variables on outcomes.

Third, to put the results in frequentist statistical perspective, more familiar to most clinicians, we took the predictors and thresholds identified by the 2 steps above and then computed relative risk and adjusted odds ratio from multivariate logistic regression plus their 95% confidence intervals (CIs). Additionally, we examined the utility of using the identified thresholds as biomarkers of outcomes by computing their sensitivity and specificity. Multivariate logistic regression analyses were performed with AIC, BIC, and ROC used for model selection with several biomarkers included in separate models. Adjusted odds ratios are reported.

Software

Compartmental pharmacokinetic models for each drug were identified using ADAPT 5 (Biomedical Simulations Resource, University of Southern California). CART, gradient-boosted CART in TreeNet, and random forests were run using Salford Systems Data Mining and Predictive Analytics Software version 8.0 (Salford Systems, San Diego, California). Standard statistical analyses were performed with Stata software version 13 (StataCorp, College Station, Texas).

RESULTS

Clinical and Pharmacokinetic Factors of Participants

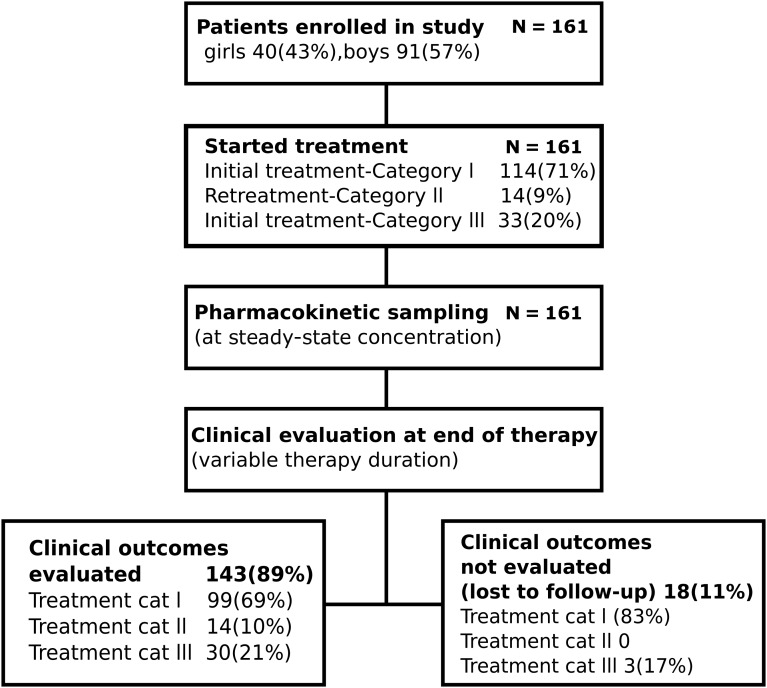
One hundred sixty-one children aged 1–15 years were enrolled (Figure 1). Fifty-seven percent of children had only extrapulmonary tuberculosis. Eighteen (11%) children did not have outcome known or ascertained. Table 1 summarizes the clinical and demographic factors in all 161 children, and compares those with ascertained outcomes to those with unknown outcomes. Table 1 shows that children with unknown outcomes were similar to those with known outcomes. The exception was that HIV-coinfected children were overrepresented among those with known outcomes.

Figure 1.

Study enrollment. Chart showing enrollment of study subjects, pharmacokinetic sampling, and evaluation for clinical outcomes at end of therapy.

Table 1.

Demographic and Clinical Characteristics of Study Patients

Characteristic	All Patients (N = 161)	Clinical Outcomes Evaluated (n = 143)	Clinical Outcomes Not Evaluated (n = 18)	P Valuea
Demographic features
Girls	70 (43)	62 (43)	8 (44)	.930
Boys	91 (57)	81 (57)	10 (55)
Age, years	7.81 (3.35)	7.86 (3.35)	7.42 (3.40)	.601
Clinical features
Extrapulmonary tuberculosis	91 (57)	79 (55)	12 (67)	.606
Pulmonary tuberculosis	68 (42)	62 (43)	6 (33)
Extrapulmonary plus pulmonary tuberculosis	2 (1)	2 (2)	0	.308
Treatment category I	114 (71)	99 (69)	15 (83)
Treatment category II	14 (9)	14 (10)	0
Treatment category III	33 (20)	30 (21)	3 (17)
HIV test positive	77 (48)	73 (51)	4 (22)	.021
HIV test negative	84 (52)	70 (49)	14 (78)
Isoniazid/rifampin mean dose, mg (SD)b	173 (67)	172 (65)	183 (86)	.495
Pyrazinamide mean dose, mg (SD)	582 (217)	578 (208)	611 (287)	.548
Measures of nutritional status
Mean weight, kg (SD)	18.45 (6.60)	18.55 (6.66)	17.65 (6.16)	.586
Mean height, cm (SD)	112.39 (19)	112.46 (18.71)	111.78 (21.76)	.886
Mean body mass index, kg/m2 (SD)	14.30 (2.27)	14.36 (2.30)	13.81 (1.97)	.337
Mean body surface area, m2 (SD)	0.75 (0.19)	0.76 (0.19)	0.74 (0.20)	.669

Data are presented as No. (%) unless otherwise indicated.

Abbreviations: HIV, human immunodeficiency virus; SD, standard deviation.

^a Indicates P-values < .05.

^b Given as a combined tablet.

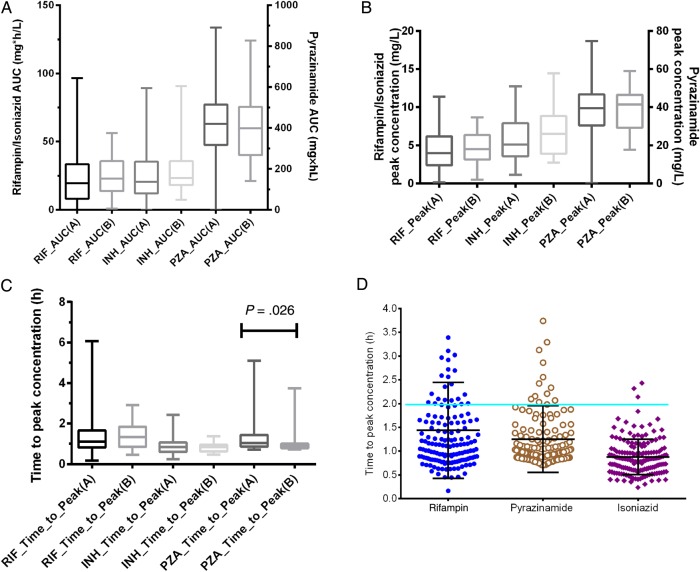
Isoniazid pharmacokinetics were best explained by a 2-compartment model, whereas rifampin and pyrazinamide concentrations were best explained by a 1-compartment model. The pharmacokinetic parameter estimates are shown in Table 2. The distributions of AUC_0–24, peak, and trough, as well as time to peak concentration, are shown in Figure 2. The ratio of highest to lowest (ie, span) peak and AUC_0–24 for rifampin was 69.47 and 1674, for pyrazinamide 9.64 and 9.13, and for isoniazid 12.42 and 36.19, respectively. The trough concentrations were dominated by zero values, making it impossible to calculate ratios; however, the ranges were 0–5.03 mg/L for rifampin, 0–6.09 for isoniazid, and 0–30.24 for pyrazinamide. Thus, there was wide between-child concentration variability. Figure 2D shows that the calculated times to peak concentration rarely fell at the 2-hour time point, which means the 2-hour systematically underestimates the peak concentration.

Table 2.

Pharmacokinetic Parameter Estimates of Antituberculosis Drugs in 161 Children

Parameter	Isoniazid		Rifampin		Pyrazinamide
	Mean	SD as %CV	Mean	SD as %CV	Mean	SD as %CV
Total clearance, L × h−1	7.8	67.8	11.0	130	1.3	41.9
Central compartment volume, L	5.2	34.3	21.8	17.0	12.8	48.4
Absorption constant, h−1	0.8	64.8	1.1	126	2.5	77.2
Intercompartmental clearance, L × h−1	15.4	16.9	…	…	…	…
Peripheral compartment volume, L	7.5	21.0	…	…	…	…
Half-life, h	1.7	48.2	2.3	88.12	7.8	50.35

Abbreviations:  …, not applicable for a 1-compartment model; CV, coefficient of variation; SD, standard deviation.

Figure 2.

Distribution of concentrations achieved in children with tuberculosis. Concentration distributions for rifampin (A), isoniazid (B), and pyrazinamide (C). “A” denotes those patients with outcomes ascertained, and “B” denotes those with outcomes unknown. D, Peaks rarely fell at the 2-hour time point. Abbreviations: AUC, area under the concentration-time curve; INH, isoniazid; PZA, pyrazinamide; RIF, rifampin.

Outcomes Ascertained at End of Therapy

Subsequent analyses were restricted to the 143 patients with known outcomes. A single outcome was unique to each child. One hundred ten (77%) children completed adequate therapy, 9 (6%) died, and 24 (17%) failed therapy. There was no significant difference (P = .738) in poor outcomes between those who received re-treatment because of initial default or prior treatment (ie, received category II regimen) and those who received category I/II (4/10 [40%] vs 29/129 [22%], respectively).

Factors Associated With Outcome Based on Standard Statistical Inferences

Table 3 shows the factors that were associated with poor outcomes, based on standard statistical approaches of comparing measures of central tendency. However, in standard multivariate analyses, none of the factors remained significant independent predictors of poor outcomes, suggesting presence of interaction or confounding effects. On the other hand, drug concentrations were significantly associated with outcome. However, the logistic regression assumptions precluded us from examining all 3 drug-concentration measures in the same model concurrently. In addition, this analytical approach could not be employed to rank the most important factors, nor obtain concentration thresholds associated with poor outcomes, important for clinical and drug development decision making; all it gave were comparisons of measures of central tendency.

Table 3.

Children Who Failed Therapy or Died Versus Completed Therapy in Standard Statistical Analysis

Characteristic	All Children (n = 143)	Completed Treatment (n = 110)	Failed Treatment (n = 24)	Died (n = 9)	P Value
Demographic
Girls	62 (43)	46 (42)	11 (46)	5 (56)	.701
Boys	81 (87)	64 (58)	13 (54)	4 (54)
Age, years	7.86 (3.35)	7.85 (3.30)	7.15 (3.70)	9.78 (2.54)	.110
Clinical
Extrapulmonary	79 (55)	64 (58)	14 (58)	1 (11)	.023
Pulmonary and extrapulmonary	64 (45)	46 (42)	10 (42)	8 (89)
Treatment category I	99 (69)	76 (69)	17 (71)	6 (67)	.090
Treatment category II	14 (10)	10 (9)	1 (4)	3 (33)
Treatment category III	30 (21)	24 (22)	6 (25)	0
HIV test positive	73 (51)	55 (50)	10 (42)	8 (89)	.049
HIV test negative	70 (49)	55 (50)	14 (58)	1 (11)
Isoniazid/rifampin dose, mg	172 (65)	178 (61)a	144 (73)a	169 (78)	.079
Pyrazinamide dose, mg	578 (208)	600 (190)b	475 (248)b	583 (250)	.022
Measures of nutritional status
Mean weight, kg (SD)	18.55 (6.66)	18.75 (6.84)	17.74 (6.77)	18.33 (4.21)	.796
Mean height, cm (SD)	112 (19)	113 (18)	109 (20)	120 (19)	.368
Mean height-for-weight z score (SD)	−1.16 (1.35)	−1.15 (1.28)	−1.19 (1.61)	−1.23 (1.70)	.989
Mean height-for-age z score (SD)	−2.19 (1.80)	−2.17 (1.84)	−2.00 (1.35)	−2.94 (2.41)	.399
Mean weight-for-age z score (SD)	−2.11 (1.16)	−2.07 (1.16)	−2.11 (1.14)	−2.61 (1.17)	.409
Mean BMI, kg/m2 (SD)	14.36 (2.30)	14.45 (2.29)	14.36 (2.04)	13.21 (3.58)	.296
Mean BSA, m2 (SD)	0.76 (0.19)	0.76 (0.20)	0.73 (0.20)	0.78 (0.14)	.727
Mean measures of drug exposures (SD)
Isoniazid
Peak, mg/L	5.58 (2.66)	5.76 (2.66)c	4.42 (2.64)c	6.42 (2.02)	.049
AUC0–24, mg/L × h	24.77 (16.03)	25.41 (15.94)d	17.23 (11.47)d	37.02 (19.48)	.004
Rifampin
Peak, mg/L	4.37 (2.48)	4.75 (2.41)e	3.08 (2.45)e	3.03 (1.70)	.003
AUC0–24, mg/L × h	22.81 (17.85)	24.71 (18.11)	18.63 (15.92)	9.32 (12.53)	.027
Pyrazinamide
Peak, mg/L	38.43 (13.32)	39.85 (12.73)f	30.80 (11.37)f	44.05 (17.45)	.004
AUC0–24, mg/L × h	421.54 (192.46)	438.11 (145.49)g	343.52 (163.35)g	456.48 (192.46)	.022

Data are presented as No. (%) unless otherwise indicated.

Italics values represent P-values <.05.

Abbreviations: AUC_0–24, 24-hour area under the concentration-time curve; BMI, body mass index; BSA, body surface area; HIV, human immunodeficiency virus; SD, standard deviation.

Between-group comparison: ^aP = .055; ^bP = .022; ^cP = .073; ^dP = .062; ^eP = .007; ^fP = .008; ^gP = .023.

Machine Learning Analyses of Outcomes in All Children

Random forests and boosted CART analyses identified our positive control variable as the primary predictor and also identified that the random number–generated parameter was not an important predictor for poor outcomes. The ROC score for all models examined was >0.75, which is reassuring. This was objective evidence that our analytic approach correctly selected predictors. The top half most important predictors for poor outcome for all 143 children are shown in Table 4. The ROC curve was 0.75 for the out-of-bag sample in random forests and 0.77 for test sample in boosted CART. Both modeling approaches identified pyrazinamide peak concentration at the apex followed closely by rifampin AUC_0–24, and peak concentration. Each of the z scores was within 5% points of each other, suggesting that one could be substituted for the other. Treatment category was not a significant predictor identified by either model. The difference in the value of the variable importance scores and ranking between the 2 models could be explained by their different approach to handling wide data (random forests) vs highly correlated variables (boosted CART). Thus, the ranking and scores from the 2 models in Table 4 represent different but important aspects about those predictors, which we further explored.

Table 4.

Top Half Predictors for Poor Clinical Outcomes Based on Boosted Classification and Regression Tree (TreeNet) and Random Forest Models

Variable	TreeNet		Random Forests
	Rank	Score	Rank	Rank	Score
Pyrazinamide peak	1	100	Pyrazinamide peak	1	100
Rifampin peak	2	81	Rifampin AUC0–24	2	61
Rifampin time-to-peak	3	57	Rifampin peak	3	59
Rifampin AUC0–24	4	53	Pyrazinamide AUC0–24	4	54
Pyrazinamide AUC0–24	5	49	Rifampin time-to-peak	5	26
Height	6	45	Isoniazid time-to-peak	6	22
Pyrazinamide time-to-peak	7	44	Isoniazid AUC0–24	7	21
Isoniazid AUC0–24	8	44	Pyrazinamide time-to-peak	8	21
Isoniazid time-to-peak	9	43	Rifampin-isoniazid dose	9	19
Disease site	10	41	Isoniazid peak	10	19
Weight-for-age z score	11	35	Height-for-age z score	11	18
Age	12	35	Weight-for-height z score	12	17
Height-for-age z score	13	35	Height (m)	13	15
Isoniazid peak	14	31	Weight-for-age z score	14	14
Gender	15	30	Pyrazinamide dose	15	13

Abbreviation: AUC_0–24, 24-hour area under the concentration-time curve.

Concentration Thresholds Associated With Poor Outcome

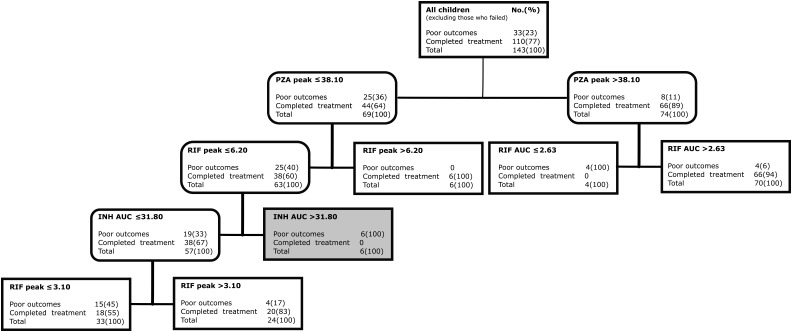
Next we used boosted CART models that included only ranked variables from Table 4 to identify drug concentration thresholds predictive of poor outcomes including failure of therapy. Figure 3 shows that when all 143 children were included, pyrazinamide peak <38.10 mg/L was identified as the main predictor for the composite poor outcome, followed by rifampin AUC_0–24 in those with pyrazinamide peak ≥38.10 mg/L and rifampin peak in those below the pyrazinamide threshold. The relative risk of poor outcomes below these peak concentration thresholds was 3.64 (95% CI, 2.28–5.83). Figure 3 shows that there was significant concentration-dependent antagonism driven by isoniazid. In children with pyrazinamide peak ≤38.10 and rifampin peak ≤6.20 mg/L, isoniazid AUC_0–24 >31.80 mg/L × h led to significantly higher proportions of children with poor outcomes (6/6 [100%] vs 19/57 [33%] with isoniazid <31.80 mg/L), which is a risk ratio for failure of 3.00 (95% CI, 2.08–4.33).

Figure 3.

Classification and regression tree (CART)–derived predictors of combined poor outcomes in all 143 children. CART tree from the optimal model for all children with combined poor outcomes (failure of therapy or death). Terminal nodes are shaped as sharp-edged rectangles; intermediate daughter nodes have rounded edges. Nodes shaded in light gray indicate antagonism where higher drug concentration led to higher proportions with poorer outcomes than lower drug concentrations. Abbreviations: AUC, area under the concentration-time curve; INH, isoniazid; PZA, pyrazinamide; RIF, rifampin.

Figure 4 shows results for the 134 children remaining after excluding 9 children who died (ie, therapy failure alone). The primary node was still pyrazinamide peak <38.10 mg/L. However, the daughter node threshold of rifampin peak was 3.01 mg/L. The isoniazid concentration–dependent antagonism was still evident among those with lower pyrazinamide peaks, this time at isoniazid peak concentration >4.77 mg/L.

Figure 4.

Predictors for failure of therapy in 134 children. Classification and regression tree (CART)–derived predictors of therapy failure only, excluding the 9 children who died. Abbreviations: INH, isoniazid; PZA, pyrazinamide; RIF, rifampin.

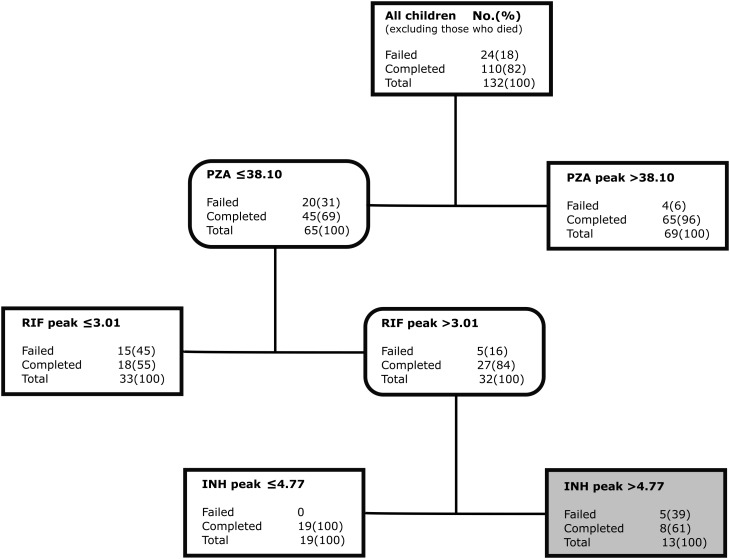
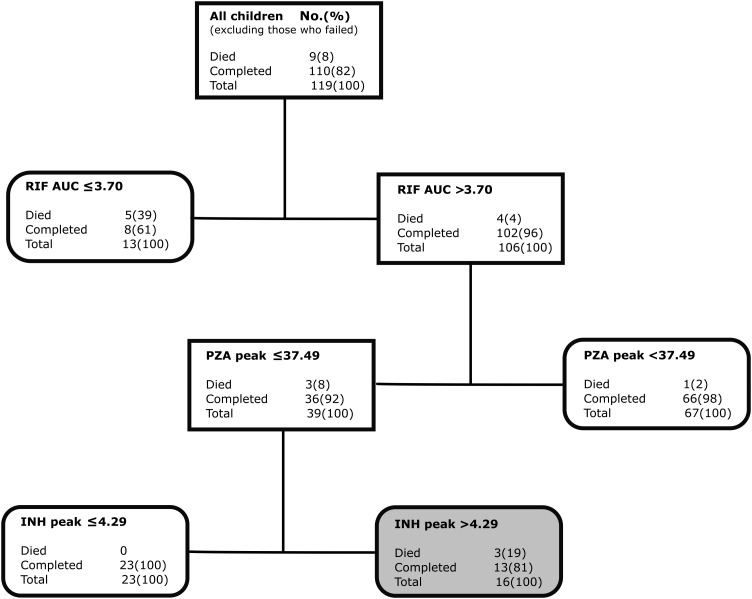
Figure 5 shows the most important predictors of death alone in 119 children after therapy failure was excluded from analysis. The most highly ranked predictors of death were rifampin AUC_0–24 ≤3.70 at the apex with a score of 100%, followed by pyrazinamide peak ≤37.49 mg/L with a score of 88%. The isoniazid peak ≤4.29 mg/L score was 49%, while that for the AUC_0–24 was 35%; however, for both parameters higher isoniazid concentration selected nodes with greater proportions of dead children, and in unpruned trees were ranked even higher. In other words, there was concentration-dependent antagonism that manifest in higher death rates. Figure 5 shows that 19% in the antagonism zone died compared to 0% of children (P = .061). Even though the majority (8/9) of children who died had HIV infection, 5 of 9 also had pyrazinamide peak concentrations below threshold prior to death. Indeed, in both boosted CART and random forests, drug concentration outranked HIV test results in separate analyses.

Figure 5.

Predictors of death in 119 children with tuberculosis. Classification and regression tree (CART)–derived predictors of death, excluding the 24 children who failed therapy. The CART tree was shallow, and identified 2 concentration-dependent predictors of death. Abbreviations: AUC, area under the concentration-time curve; INH, isoniazid; PZA, pyrazinamide; RIF, rifampin.

Machine Learning Analyses of Clinical Outcomes in Babies and Toddlers

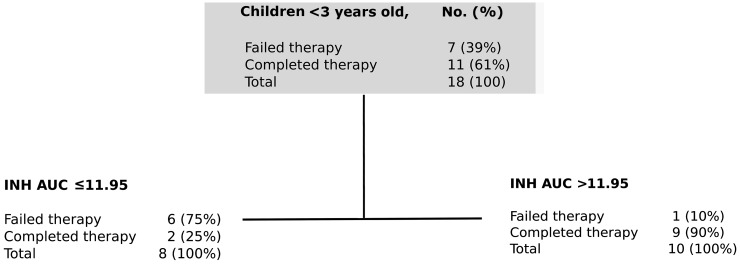
Age <3 years was a significant predictor of outcome (Table 4). There were no deaths observed in this age group, but 7 of 18 (39%) failed therapy. Therefore, predictors of therapy failure in children <3 years old were separately examined using CART, with results shown in Figure 6. The ROC for the test model was 89%, suggesting that the results would be highly reproducible in a separate sample. The primary node was isoniazid AUC_0–24 < 11.95 mg/L × h, followed closely by rifampin peak <3.10 mg/L. The relative risk for therapy failure was 3.43 (95% CI, .99–11.82).

Figure 6.

Classification and regression tree (CART) model of predictors of therapy failure in babies and toddlers. The optimal model and variable importance ranking together with the scores for children <3 years old with failure of therapy. Terminal nodes are shaped as sharp-edged rectangles; intermediate daughter nodes have rounded edges. Abbreviations: AUC, area under the concentration-time curve; INH, isoniazid.

Sensitivity and Specificity of Identified Thresholds as Biomarkers

Finally, we used standard statistical analyses to examine the impact of identified thresholds for decision making in the clinic, with results shown in Table 5. In all 143 children, for each 2-fold increase in pyrazinamide dose between 250 mg and 750 mg (which would increase proportions achieving threshold AUC_0–24), combined poor outcome fell by 43% (95% CI, 7%–66%) and failure of therapy fell by 54% (95% CI, 17%–75%). The multivariate logistic regression model in Table 5 reveals that isoniazid peak concentrations between 4.55 and 7.50 mg/L were associated with combined poor outcomes, indicative of antagonism (adjusted odds ratio, 3.08 [95% CI, .91–10.45]). The model was robust, with an ROC of 0.89. On the other hand, in children <3 years old, the relative risk for failure of therapy for those children with isoniazid AUC_0–24 < 11.95 mg/L × h was 5.73 (95% CI, .91–35.93).

Table 5.

Multivariate Logistic Regression Analysis of the Factors Associated With Poor Outcomes in All 143 Children

Variable	Concentration	No. of Patients	Adjusted OR (95% CI)	P Value
Pyrazinamide peak, mg/L	≤38.10	55 (43)	Referent
	>38.10	72 (57)	.15 (.05–.50)	.002
Rifampin peak, mg/L	<3.02	50 (36)	Referent
	3.02–6.20	57 (40)	.19 (.06–.56)	.003
	>6.20	34 (24)	.10 (.02–.55)	.008
Isoniazid peak, mg/L	≤4.55	61 (43)	Referent
	4.55–7.50	43 (30)	3.08 (.91–10.45)	.071
	>7.50	39 (27)	2.83 (.53–14.95)	.222

Italics values represent P-values <.05.

Abbreviations: CI, confidence interval; OR, odds ratio.

The identified rifampin, isoniazid, and pyrazinamide thresholds were used as biomarkers for poor outcome to reveal sensitivity and specificity results (Table 6). When pyrazinamide peak threshold <38.10 and rifampin peak <3.20 mg/L were used to screen for children who failed therapy, the specificity increased from 0.68 to 0.89 (Table 6).

Table 6.

Sensitivity and Specificity of Drug Concentration Thresholds in All Children and in Children Aged <3 Years

Biomarker Test Specifics	No. of Patients (%)	Sensitivity, % (95% CI)	Specificity, % (95% CI)	PPV, % (95% CI)	NPV, % (95% CI)	Likelihood Ratio	P Value
All children
Pyrazinamide peak <38.10 mg/L	127 (89)	76 (58–89)	68 (58–77)	45 (32–59)	89 (79–95)	2.374	<.001
Pyrazinamide peak <38.10 mg/L plus rifampin peak <3.20 mg/L	143 (100)	52 (34–69)	89 (82–94)	59 (39–76)	86 (78–92)	4.722	<.001
Children <3 y old
Isoniazid AUC0–24 < 11.95 mg/L × h	18 (13)	86 (42–100)	82 (48–98)	75 (35–97)	90 (56–100)	4.714	.041
Isoniazid AUC0–24 threshold plus rifampin peak <3.10 mg/L	18 (13)	86 (42–100)	75 (35–97)	75 (35–97)	86 (42–100)	3.429	.041

Italics values represent P-values <.05.

Abbreviations: AUC_0–24, 24-hour area under the concentration time curve; CI, confidence interval; NPV, negative predictive value; PPV, positive predictive value.

DISCUSSION

Standard statistical inferences are excellent for hypothesis testing, and in clinical sciences have the underlying assumption that the population studied is a good representation sample of the total population. With these standard approaches, we compare distributions and the measures of central tendency between groups, and use the P value to make sure that the differences observed are not due to chance. The underlying scientific philosophy is rejection of the null hypothesis. Machine learning algorithms, on the other hand, are governed by an entirely different philosophy [20, 22]. First, their main objective is prediction. Thus, they are not for hypothesis testing, but rather for hypothesis generation. The algorithms determine how likely the prediction is to be true or hold with different datasets. Once the hypothesis has been generated, it can be tested using standard statistical inferences. Second, these algorithms are distribution free. Third, the algorithms use nonparametric regression. Fourth, they simultaneously examine both linear and nonlinear analyses, as well as higher-order interactions between predictors and between predictors and the target response. Fifth, they are designed for pattern recognition, a difficult concept for standard statistical inferences. Here, we innovated an extra step to these algorithms, positive and negative controls (“known knowns”), in order to increase confidence in the identification of new predictors (the “unknown unknowns”). Random forest employs entropy and stochastic algorithm searches for each node and uses each separate variable to build trees, and allows the trees generated to vote and identify the best tree, which was useful for our wide data [19, 20]. On the other hand, boosted CART handles correlated variables better by incorporating both additive and interaction effects. Using both, findings from patients' data were ranked and thresholds identified, in a manner that allows straightforward clinical decision making. This allowed us to examine and rank all potential predictors without us prespecifying and biasing the importance with our favorite potential predictors, allowing us to accurately follow bread crumb trails home in a terrifying forest of many potential clinical, demographic, laboratory, and pharmacokinetic predictors [23].

Our first major finding was that pharmacokinetic variability is likely to be an important driver of therapy failure and death in children with tuberculosis [24, 25]. While the dosing schedule was based on intermittent therapy, the finding still remains and would be independent of that. There was a wide range of between-child variability in the absorption constant, systemic clearance, and volume of distribution. This, and the current dosing structure with weight bands, led to a wide variability in AUC_0–24 and peak concentrations in children on standard doses. This between-patient variability led to some patients having low drug concentrations, and those low concentrations were the highest-ranked predictors of therapy failure and death, accounting for 5 of 6 (83%) children <3 years old who failed therapy and 25 of 33 (76%) children who either failed therapy or died.

Second, we identified drug concentration thresholds predictive of poor outcomes. This means that there are specific drug concentrations and thresholds above which children are more likely to do well on therapy. These thresholds should be valid targets for developing optimal dosing for children. We previously observed that pyrazinamide concentrations, followed by rifampin concentrations, and then isoniazid concentrations were the best predictors of sputum culture conversion and long-term outcome in South African adults with tuberculosis. The pyrazinamide peak concentration threshold of ≥38.10 mg/L identified here in Indian children differed somewhat from that of 58.3 mg/L that we identified as the most important predictor of sputum culture conversion in adult pulmonary tuberculosis, but it remains roughly double the 20 mg/L 2-hour postdose concentration currently used to design doses for children. On the other hand, the rifampin peak ≥6.20 mg/L we identified as a predictor of improved outcome in children with lower pyrazinamide peaks is very close to the 6.60 mg/L threshold we identified as a predictor of favorable long-term outcome in adult pulmonary disease [6]. However, the isoniazid AUC_0–24 of 11.95 mg × h/L we identified as the most important predictor of outcome for children <3 years of age differs more from the value of 52 mg × h/L that we identified as a predictor of long-term outcome in adult pulmonary tuberculosis. The reasons are unclear, but could reflect differences in the pathophysiology of tuberculosis between adults and children, resulting in different drug partitioning between plasma and the site of infection and/or different contributions of individual component drugs to the overall activity of the regimen. In contrast, the pharmacokinetic/pharmacodynamic drivers (ie, pattern) appear remarkably concordant with the indices shown to drive outcomes in mice, the hollow fiber system model, and adult patients [5, 26].

Last, we identified a negative interaction between isoniazid and its companion agents, pyrazinamide and rifampin. This concentration-dependent antagonism has been described in murine tuberculosis, in the hollow fiber model, and in the sterilizing effects of the regimen on sputum cultures from adults with tuberculosis [5, 27–29]. We found that the antagonism occurred within certain concentration ranges. This perhaps points to the major limitation of extrapolating optimal pediatric doses from adult disease. In this case, that practice gave us doses whose resultant concentrations fall squarely in that zone of concentration-dependent antagonism, which was associated with higher death rates in children. It also illustrates another point, which is that optimal design of combination therapy must incorporate knowledge of full exposure-response surfaces for interactions of multiple paired concentrations to select doses that best avoid areas of antagonism [30–32].

There are several limitations to our findings. First, our models ranked and predicted important variables based on routinely collected data. This means that it cannot be excluded that unrecorded variables, outside the 30 potential predictors we examined, could also explain therapy failure and possibly be ranked highly. Second, typical of most pediatric tuberculosis, we did not isolate the infecting pathogen, which means that the role of minimum inhibitory concentration could not be investigated. For the same reasons, the impact of drug concentrations on acquired drug resistance was not examined. Moreover, therapy failure was not microbiologically defined, but was based on broad and perhaps more subjective clinical criteria. Third, a curious observation was that category assignment (ie, initial treatment compared to retreatment) did not contribute to significant difference in outcomes, either based on standard statistical analyses or artificial intelligence methods. Fourth, the incidence of HIV in this cohort was higher than is expected in the majority of Indian children with tuberculosis. However, this could be more consistent with the observation that places where recruitment took place are specialty care institutions, which could have skewed the population enrolled. We suspect that this would also explain the relatively higher proportion of children with extrapulmonary tuberculosis and low rate of bacteriologically confirmed tuberculosis. Thus, it is possible that some of these children did not have tuberculosis, were treated for tuberculosis, and did not get better—leading to a diagnosis of tuberculosis treatment failure. Finally, the impact of concomitant antiretroviral therapy in driving the variability of antituberculosis drugs could not be assessed directly because we did not measure antiretroviral drug concentrations. Nevertheless, HIV coinfection itself was not highly ranked as a predictor of therapy outcome. These limitations, which will need to be investigated in the future, however, do not deter conclusions from our findings.