Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Oct 14;6:35398. doi: 10.1038/srep35398

Line-scanning Brillouin microscopy for rapid non-invasive mechanical imaging

Jitao Zhang 1, Antonio Fiore 1, Seok-Hyun Yun 2,3, Hanyoup Kim 4, Giuliano Scarcelli 1,a
PMCID: PMC5064313  PMID: 27739499

Abstract

Brillouin spectroscopy probes the mechanical properties of material by measuring the optical frequency shift induced by photon-phonon scattering interactions. In traditional configurations, Brillouin spectrometers measure only one point of the sample at a time. This results in long acquisition times for mechanical imaging of large areas. In this work, we demonstrate a parallel detection configuration where the Brillouin shift of hundreds of points in a line can be measured simultaneously. In mm-sized samples, this novel configuration effectively shortens the acquisition time of two-dimensional Brillouin imaging from hours to tens of seconds, thus making it a powerful technology for label-free mechanical characterization of tissue and biomaterials.

Brillouin spectroscopy allows non-invasive measurement of material mechanical properties by measuring the frequency spectrum of acoustically-induced light scattering within a sample1. For this reason, for many years high-resolution Brillouin spectrometers based on Fabry-Perot interferometers have been widely used for material characterization and remote sensing2,3,4,5,6,7. In the past decade, the development of high-resolution spectrometers based on virtually-imaged phased array (VIPA) has greatly increased the spectral detection efficiency thus enabling mechanical characterization of biological tissue and biomaterials8,9,10. Further improvements in spectrometer performances11,12,13,14,15 have enabled in vivo measurements at safe power levels16,17 and 2D/3D imaging of biological cells18,19. However, despite the speed improvement enabled by VIPA spectrometers, Brillouin microscopy remains a slow technique compared to other imaging modalities. The optical signal of spontaneous Brillouin scattering is weak: about 100 ms are required with a few mW of illumination power focused on the sample to get sufficient signal-to-noise ratio (SNR) for accurate spectral measurements. Moreover, traditional Brillouin spectrometers can only measure one point of the sample at a time (Fig. 1a), therefore obtaining a 2D or 3D image can require a long time18,19,20,21,22. For many applications requiring imaging of large areas or volumes, reducing the time of data acquisition is critical. One avenue explored in recent years to address this issue has been to take advantage of nonlinear/stimulated Brillouin interactions rather than spontaneous scattering, as they potentially provide much higher energy conversion efficiency. Several techniques based on stimulated scattering phenomena have been recently demonstrated23,24,25,26,27,28; however, to date spontaneous-based protocols have remained faster than stimulated Brillouin imaging protocols in practice29,30. Considering also the added complexity and higher cost of stimulated-based setups, it is not clear whether in biological and clinical settings they will provide a net advantage.

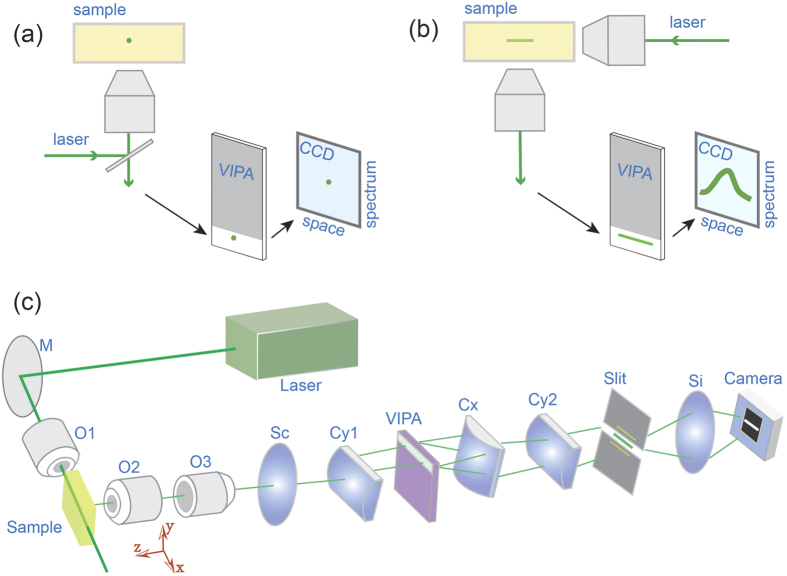
Figure 1. Comparison of point-scan vs line-scanning configuration of Brillouin microscopy.

Figure 1

Open in a new tab

(a) The traditional configuration couples a confocal microscope with a spectrometer. A spatial point of the sample is selected by the microscope and its spectrum is measured by the spectrometer. Thus, the images are formed by scanning the sample point-by-point. (b) In the new configuration, by arranging the illumination path and detection path at an angle (90 degree), many points along the line beam can be measured simultaneously and the images can be formed by scanning the line beam. (c) Schematic of the line-scanning Brillouin spectroscopy. M: mirror; O1,O2,O3: objective lens. Sc: spherical lens for beam collimation; Cy1, Cy2, Cx: cylindrical lenses; Si: spherical lens for imaging purpose.

In this work, we devised a novel configuration based on spontaneous Brillouin scattering that allows hundreds of points in a sample to be measured simultaneously using line-scanning parallel detection of scattering spectra. The schematic of this novel configuration is shown in Fig. 1b. Instead of collecting the backward scattering light as in Fig. 1a, the Brillouin scattering signal is collected with a 90-degree scattering geometry31,32. As input light, a line beam is created into the sample by focusing the incoming laser with a low-NA objective lens. This arrangement allows us to analyze multiple points along the beam line simultaneously by using a multiplexed VIPA-based spectrometer, described in Fig. 1c. With this setup, we reached the equivalent acquisition time of less than 1 ms per sample point, two orders of magnitude shorter than any previous protocols of Brillouin microscopy. A high-resolution two-dimensional Brillouin image can therefore be obtained in a matter of seconds by scanning the sample only in one dimension compared to ~hour required in traditional confocal configurations.

Results

Characterization of line-scanning Brillouin spectroscopy

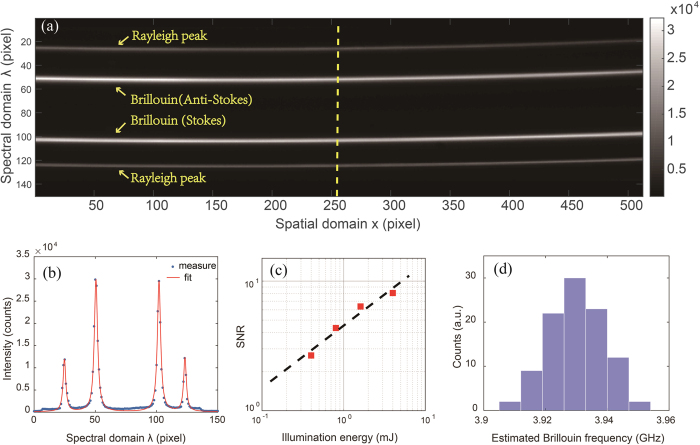
We used a homebuilt setup of line-scanning Brillouin spectroscopy (see Methods and Fig. 1c). The spectral dispersion of the novel spectrometer was characterized first. A plastic cuvette containing pure methanol was used as sample, and the dispersion pattern captured by the camera is shown in Fig. 2a. The spectral dispersion in the figure is along the vertical axis, while the horizontal axis represents the spatial domain within the sample. The two lines at the top and bottom are due to Rayleigh elastic scattering, and thus have the same frequency as the input laser. The other two lines in the middle are Brillouin peaks of adjacent dispersion orders. Because the sample is uniform, the Brillouin Stokes and anti-Stokes signatures are two continuous horizontal lines, in the center.

Figure 2. Spectral performances of line-scanning Brillouin microscopy.

Figure 2

Open in a new tab

(a) Raw dispersion pattern captured by camera. The color map is expressed in terms of CCD camera counts. (b) Spectral pattern at a single point. (c) SNR vs illumination energy on a log-log plot. Square: measured data; dotted line: linearly fitted data. (d) Distribution of the estimated Brillouin frequencies after acquiring the same point in the sample over time.

Figure 2b shows the Brillouin spectrum at the location indicated by the dotted line. The spectral dispersion (red solid line) was determined by fitting the measured data with Lorentz curve. The free spectral range of the VIPA etalon was 17 GHz, and the spectral dispersion factor (i.e., ratio of frequency shift to spatial dispersion distance) was around 0.18 GHz per pixel. We measured the spectrometer finesse to be ~36 by calculating the ratio of the distance between adjacent laser peaks and their full-width-at-half-maximum. We then characterized the SNR of the spectrometer at different illumination energy (Fig. 2c). The measured data showed near square root dependence, indicating shot-noise limited behavior. The accuracy of our Brillouin spectral estimation was calculated by repeated measurements of the same point in the sample. Figure 2d shows the representative distribution of the estimated Brillouin frequency for 100 measurements at input energy of 4 mJ. It has a Gaussian distribution of standard deviation of 8.5 MHz, which corresponds to the relative uncertainty of 0.22%. The Brillouin frequency of methanol (Fig. 2a,b) as well as several other liquids (Supplementary Fig. S1) was measured and is consistent with previously published results10,21,33,34.

In general, the spatial resolution of the line-scanning configuration is determined by both the illumination numerical aperture (NA) and detection NA. For our current setup, since the illumination NA (0.0175) was much smaller than detection NA (0.1), the lateral resolution (x- and y-direction) was determined by the detection NA and the axial resolution (z-direction) was determined by the illumination NA. In order to characterize the spatial performances of the setup, we placed a knife-edge right after the cuvette and in front of the detection objective lens. A translational stage carrying the knife-edge was moved in x-direction with step size of 25.4 μm, and the corresponding image of the knife-edge was monitored by the spectrometer’s camera. The result is shown in Fig. 3. The measured data was linearly fitted, and thus the spatial resolution (x-direction) was calculated as 3.29 μm per pixel close to diffraction limit. Our camera had 512 by 512 pixels in total, which corresponds to 1.68 mm field of view in the sample plane. Across the field of view, the spectral line was not perfectly straight but curved due to the deviation of the incident angles of off-axis points. This curvature may result in variation of the spectral dispersion factor at different points in the sample and reduce spectral extinction by making it difficult to block the elastic frequency using a spatial filter. To reduce the curvature, we used a high-NA tube lens in the microscope to minimize magnification before the spectrometer; then, we restored the desired image magnification with a cylindrical lens after the VIPA. In this way, we reduced the variation of the spectral dispersion factor to less than 3 MHz per pixel within more than 1-mm spatial field of view. For simplicity, we will ignore this effect and use the same spectral dispersion factor for all points in the following. For more accurate estimations, a characterization of the spectral dispersion at all points could be performed.

Figure 3. Spatial performance of the Brillouin microscopy.

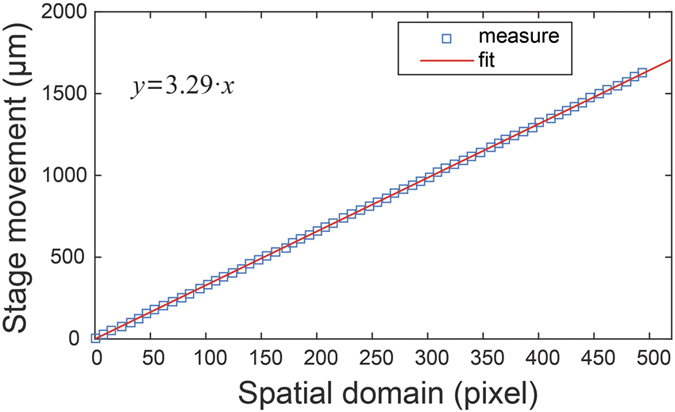
Figure 3

Open in a new tab

The step movement of the knife-edge at the sample plane (vertical axis) was monitored by the spectrometer’s camera (horizontal axis). The squares are measured data and the red line is linearly fitted data. The slope of the fitted line shows 3.29 microns per pixel.

Two-dimensional and three-dimensional imaging

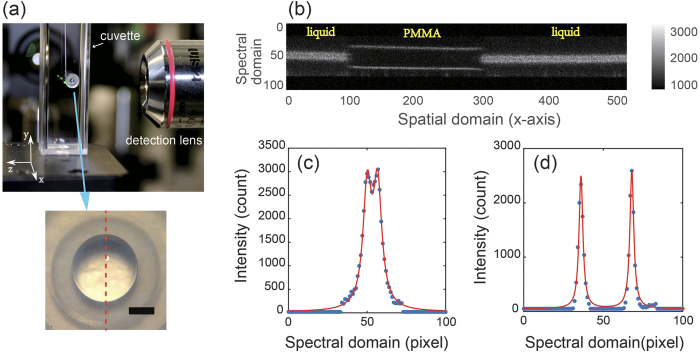
We measured the Brillouin shift of an aspherical lens made of PMMA in the setup shown in Fig. 4a. The PMMA lens was placed into a plastic cuvette filled with index-matching liquid. The laser power was 70 mW, and the exposure time of the camera was 0.1 second. When the sample was immersed into the liquid, it was almost invisible by naked eye because of the refractive index matching. However, since the stiffness of the sample and the matching liquid were different, we could easily distinguish them by their Brillouin signatures. Figure 4b is a snapshot of the representative signal acquired by the camera, in which only Brillouin frequency components were shown and the elastic frequencies were blocked by a slit. The Brillouin signatures of the matching liquid surrounding the PMMA lens are apparent. At the interface of different materials, there may be cross-talk between two Brillouin signatures corresponding to each material. This cross-talk effect will introduce an ambiguous region at the interface if the two materials have similar Brillouin shift. Because the PMMA and the liquid had distinct Brillouin shifts, we were able to quantify the ambiguous region to be within 2 pixels, i.e. 6.58 μm. Figure 4c,d showed the Brillouin spectra of the index-matching liquid and PMMA at single point, respectively. Using the characterization data of the spectral dispersion, the Brillouin frequency shifts of PMMA and the matching liquid were determined to be 11.32 GHz and 9.11 GHz, respectively. The measured PMMA data is consistent with published result35.

Figure 4. Experimental configuration and measurements.

Figure 4

Open in a new tab

(a) Picture of the PMMA lens. The picture was taken before filling cuvette with index-matching liquid. The lower panel shows a zoomed-in picture of the PMMA lens. Scale bar, 500 μm. (b) Snapshot of representative Brillouin pattern acquired by the camera during measurement. (c) Brillouin spectrum of PMMA. (d) Brillouin spectrum of index-matching liquid. The dots and solid curves are measured data and fitted data, respectively.

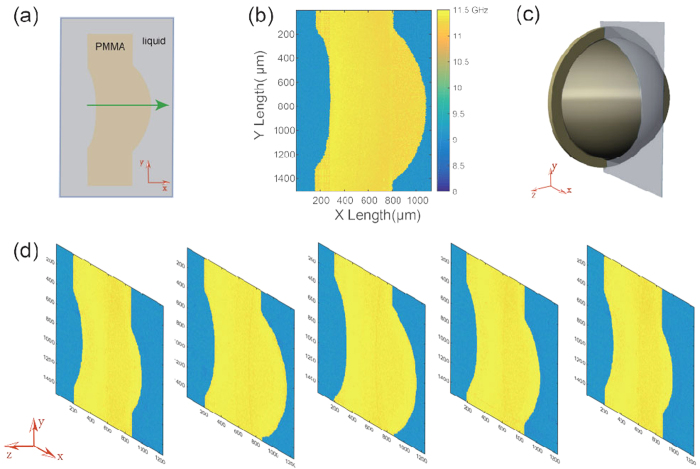
Figure 5 shows 2D and 3D Brillouin images of the PMMA lens. The cuvette containing the lens was carried by a vertical motorized translation stage, which enabled us to scan the sample in y-direction. A LABVIEW program was developed to synchronize the stage translation and camera acquisition so that the scanning could be carried out automatically. The speed of the stage was set as 50 μm/s and 300 frames were captured. Thus, within 30 seconds we acquired ~100,000 points of the sample within a field of view of 1.1 mm by 1.5 mm, a task that would require more than 1 hour in previous confocal Brillouin microscopes. Figure 5a indicates the scanned cross-section along the dotted line of Fig. 4a. The green line indicates the illumination beam. Figure 5b shows the 2D imaging of the PMMA lens immerged in the matching liquid based on the measured Brillouin frequency shift. The interface between the PMMA lens and the matching liquid could be clearly seen from the image, and the inner region of the PMMA lens was pretty uniform. We then demonstrated the capability of this spectrometer to do a rapid 3D imaging by use of the scanning method shown in Fig. 5c. Figure 5d shows five slices of obtained cross-section images as we moved the PMMA lens along z-axis using another translational stage.

Figure 5. 2D and 3D Brillouin images of the PMMA lens.

Figure 5

Open in a new tab

(a) Schematic of the cross-section that was scanned by the beam line. (b) Cross-sectional Brillouin image of the PMMA lens at the location indicated by the dotted line in Fig. 4a. The colorbar represents the Brillouin frequency shift with a unit of GHz. (c) Schematic of the 3D scanning of the PMMA lens. 3D images were obtained by scanning the cross-section in z-axis. (d) 3D Brillouin imaging of the PMMA lens. Each slice represents a cross-section image of the PMMA lens at a location along z-axis.

Discussion

To understand advantages and limitations of this new configuration, we started by comparing the spectral efficiency of angled geometries with traditional setups using confocal epi-detection configuration. If the illumination beam is vertically polarized and thus perpendicular to the scattering plane, the differential cross-section is not dependent on the scattering angle36, thus configurations with angled illumination-detection paths have the same differential cross-section as the epi-detection. However, the angled geometry will result in diminished geometrical efficiency per single point (i.e. not counting the advantage due to the massive parallelization of the measurement). The collected scattering power can be written as P = Iill · V · Ω · R, where Iill is the intensity of the illumination light, V is the interaction volume of the scattering, Ω is the collected solid angle, and R is the scattering coefficient, which has a unit of m−1 and can be considered as constant here. In orthogonal configuration, the interaction volume can be approximated by a cylinder with radius r = 0.61λ/NAcol and length l = 0.61λ/NAill, where NAill and NAcolare the NA of the illuminating objective lens and collecting objective lens, respectively. The collected solid angle depends on the collecting numerical aperture 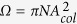Inline graphic. Therefore, the collected scattering power is 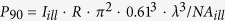Inline graphic. For epi-configuration, instead, the interaction volume is approximately 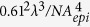Inline graphic, where NAepi is the NA of the objective lens, and the collected solid angle is 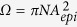Inline graphic. Thus, the collected scattering power is 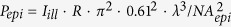Inline graphic. With same illumination intensity, the ratio of the collected power between two configurations turns out to be 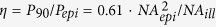Inline graphic. In orthogonal configurations, low NAill is usually preferred in order to generate a long illumination beam line uniformly across the field of view. For example, we used NAill = 0.0175 that corresponds to a 1.74 mm usable Rayleigh range. Comparing our particular experimental configuration with epi-configuration with NAepi = 0.1 (i.e. providing the same resolution in x-direction), the ratio is 34.8%. Our calculation is consistent with the prediction by other work37 where a different combination of objective lenses was used. Importantly, this calculation is consistent with the experimental results in Fig. 2 and with other epi-detection results18. The scattering efficiency in orthogonal and epi-detection is determined by the overlap between the illumination volume and detection volume, therefore one can design angled-geometries to be as efficient as epi-detection per single point measurement to maximize the parallelization advantage. Including the line parallel detection, the new method can accomplish the scan of a mm-sized sample with few-micron resolution within tens of seconds compared to >1 hour in epi-detection. Our method shares the same principles of light-sheet microscopy38 and 2D Raman spectroscopy39; In the orthogonal configuration of our current setup only samples accessible from both sides and with thickness of ~1 mm size (due to the limited Rayleigh range of the illumination beam) are measurable. This limitation can be solved with dual-beam illumination, which has been developed for light-sheet microscopy40.

In terms of background rejection, the angled configuration has inherently less background noise than epi-detection. In standard confocal configuration, back reflections of the illuminating light are easily coupled into the spectrometer and contribute to the background noise11. In the line-scanning configuration, the illumination and detection path are arranged orthogonally, thus the back reflection can be completely avoided. Furthermore, since only the region that is illuminated by the line beam produces Brillouin scattering signal, the line-scanning configuration enables optical sectioning as in the confocal configuration. On the other hand, in order to have parallel detection only one VIPA stage can be used; this limits the extinction ratio of the spectrometer to ~30 dB. This makes it challenging to measure interfaces or optically turbid samples, such as biological tissue. To improve the overall extinction ratio of the instrument, the line-scanning configuration can be combined with existing methods to suppress the background noise such as apodization18, narrow band-pass filtering41,42, and gas-chamber narrow absorption filtering13.

Methods

Brillouin scattering

Spontaneous Brillouin scattering is the scattering of light from sound waves (acoustic phonons). The elastic modulus E of an isotropic material is linked to the Brillouin frequency shift vB by the formula

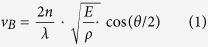graphic file with name srep35398-m7.jpg

where n is the refractive index of the ambient, λ is the wavelength of the light source, ρ is the density of the material, and θ is the scattering angle. By measuring the Brillouin frequency shift via a spectrometer, the mechanical properties of the sample can be determined.

Experimental setup

The light source was a single mode 532-nm cw laser (Torus, LaserQuantum). The beam from the laser head was focused by the objective lens O1 (NA = 0.0175) to generate a line beam and illuminated the sample. At 90 degree, the scattering light along the beamline was first imaged by a pair of objective lens O2 and O3 (both were 4X/0.1NA), and then collimated by a spherical lens Sc (f = 400 mm). The collimated light was then focused onto the entrance of a VIPA (FSR = 17 GHz, finesse = 36) by a cylindrical lens Cy1 (f = 200 mm). The dispersed light after the VIPA was imaged onto the plane of a slit by a pair of cylindrical lens Cx (f = 1000 mm) and Cy2 (f = 400 mm). This plane was re-imaged onto the camera (iXon, Andor) by a spherical lens Si (f = 60 mm). The slit works as a spatial filter in the measurement. By adjusting the aperture of the slit, we could block the undesired frequency and only let Brillouin frequency components pass (Fig. 1c).

Calibration

The calibration of the setup consists of two parts: spectral calibration and spatial calibration. The spectral calibration can be performed at each pixel (corresponding to one point of the sample) of the spectral line using measured spectral patterns of reference materials with known Brillouin shift (e.g., Supplementary Fig. S1). If Rayleigh peaks are cut by spatial filters, two unknown parameters need to be estimated: FSR and spectral dispersion factor. Therefore, the measurements of two samples of known Brillouin shifts are sufficient for calibration purposes. More reference materials will be needed if the spectral dispersion is not constant across the different spectral orders. The calibrated results can be further confirmed by comparing with the distance of two adjacent Rayleigh peaks by opening the slit. The calibrated FSR and spectral dispersion factor are then used to determine the unknown Brillouin shift of the samples under examination. The spatial calibration was carried out by translating a knife-edge with micrometric accuracy along the sample plane; the results are shown in Fig. 3, which indicates a good linear relationship.

Brillouin spectrum linewidth

The overall linewidth of the measured spectra is mainly determined by three contributions: intrinsic linewidth of the sample, limited finesse of the VIPA spectrometer, and spectral broadening from optical componenets (e.g. limited NA of the optics and other distortion effects). In our experiment, the limited finesse of the spectrometer is the largest broadening factor. For example, the intrinsic linewidth of methanol is about 0. 33 GHz33, and the linewidth of the spectrometer is about 0.47 GHz considering the FSR of 17 GHz and experimentally-measured finesse of ~36. Therefore, the minimum linewidth of the measurement is the convolution of intrinsic linewidth and finesse-limited linewidth, i.e., 0.557 GHz. In experiment, we measured 0.566 GHz at the center of the spectral line, very close to the expected limit. At the tail of the full field of view, small broadening effects due to optics elements are observed and the linewidth is ~3.5% broader than that at the center of the field of view.

Sample preparation

The PMMA lens was produced for cell phone’s camera and provided by an OEM supplier. The plastic cuvette had a size of 10 mm by 10 mm. To make the PMMA lens suspend in the central region of the cuvette, we first attached the margin of the PMMA lens to the tip of a syringe’s needle using optical adhesive, and then fixed the end of the needle to the wall of the cuvette. The liquid (Cargille Lab) had the refractive index of 1.4917 in order to match the PMMA. The motorized translational stage (T-LSM025A, Zaber) had a 25-mm traveling range and RS-232 control. The maximum speed can be as fast as 7 mm/s.

Additional Information

How to cite this article: Zhang, J. et al. Line-scanning Brillouin microscopy for rapid non-invasive mechanical imaging. Sci. Rep. 6, 35398; doi: 10.1038/srep35398 (2016).

Supplementary Material

Supplementary Information
srep35398-s1.pdf (216.2KB, pdf)

Acknowledgments

This work was supported in part by the National Institutes of Health (K25EB015885, R21EY023043, R01EY025454); National Science Foundation (CMMI-1537027, CBET-0853773); Human Frontier Science Program (Young Investigator Grant); and Canon Innovation Award. J.Z. would like to thank Mr. Qiannian Jiang from Dongguan Yu Guang Opt & Electronics Tech. Co., Ltd for providing the PMMA lens.

Footnotes

Author Contributions J.Z., S.-H.Y. and G.S. conceived idea. J.Z., A.F. and G.S. designed experiments. J.Z. performed experiments. J.Z., H.K. and G.S. analyzed and discussed data. J.Z. and G.S. wrote the manuscript. All authors reviewed the manuscript.

References

  1. Dil J. Brillouin scattering in condensed matter. Rep. Prog. Phys. 45, 285–334 (1982). [Google Scholar]
  2. Vaughan J. & Randall J. Brillouin scattering, density and elastic properties of the lens and cornea of the eye. Nature 284, 489–491 (1980). [DOI] [PubMed] [Google Scholar]
  3. Randall J. & Vaughan J. The measurement and interpretation of Brillouin scattering in the lens of the eye. Proc. R. Soc. Lond. B Biol. Sci. 214, 449–470 (1982). [DOI] [PubMed] [Google Scholar]
  4. Hickman G. D. et al. Aircraft laser sensing of sound velocity in water: Brillouin scattering. Remote Sens. Environ. 36, 165–178 (1991). [Google Scholar]
  5. Bailey S. T. et al. Light-scattering study of the normal human eye lens: elastic properties and age dependence. Biomed. Eng., IEEE Transactions on 57, 2910–2917 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ruta B., Monaco G., Scarponi F., Fioretto D. & Andrikopoulos K. Brillouin light scattering study of polymeric glassy sulfur. J. Non-Crystalline Solids. 357, 563–566 (2011). [Google Scholar]
  7. Koski K. J., Akhenblit P., McKiernan K. & Yarger J. L. Non-invasive determination of the complete elastic moduli of spider silks. Nat. materials 12, 262–267 (2013). [DOI] [PubMed] [Google Scholar]
  8. Xiao S., Weiner A. M. & Lin C. A dispersion law for virtually imaged phased-array spectral dispersers based on paraxial wave theory. Quantum Electron., IEEE Journal of 40, 420–426 (2004). [Google Scholar]
  9. Koski K., Müller J., Hochheimer H. & Yarger J. High pressure angle-dispersive Brillouin spectroscopy: A technique for determining acoustic velocities and attenuations in liquids and solids. Rev. Sci. Instrum. 73, 1235–1241 (2002). [Google Scholar]
  10. Scarcelli G. & Yun S. H. Confocal Brillouin microscopy for three-dimensional mechanical imaging. Nat. Photonics 2, 39–43 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Scarcelli G. & Yun S. H. Multistage VIPA etalons for high-extinction parallel Brillouin spectroscopy. Opt. Express 19, 10913–10922 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Reiß S., Burau G., Stachs O., Guthoff R. & Stolz H. Spatially resolved Brillouin spectroscopy to determine the rheological properties of the eye lens. Biomed. Opt. Express 2, 2144–2159 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Meng Z., Traverso A. J. & Yakovlev V. V. Background clean-up in Brillouin microspectroscopy of scattering medium. Opt. Express 22, 5410–5415 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Antonacci G., Lepert G., Paterson C. & Török P. Elastic suppression in Brillouin imaging by destructive interference. Appl. Phys. Lett. 107, 061102 (2015). [Google Scholar]
  15. Berghaus K., Zhang J., Yun S. H. & Scarcelli G. High-finesse sub-GHz-resolution spectrometer employing VIPA etalons of different dispersion. Opt. Lett. 40, 4436–4439 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Scarcelli G., Kim P. & Yun S. H. In vivo measurement of age-related stiffening in the crystalline lens by Brillouin optical microscopy. Biophysical Journal 101, 1539–1545 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Scarcelli G. & Yun S. H. In vivo Brillouin optical microscopy of the human eye. Opt. Express 20, 9197–9202 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Scarcelli G. et al. Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy. Nat. Methods 12, 1132–1134 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Antonacci G. et al. Quantification of plaque stiffness by Brillouin microscopy in experimental thin cap fibroatheroma. J. R. Soc. Interface 12, 20150843 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Traverso A. J. et al. Dual Raman-Brillouin microscope for chemical and mechanical characterization and imaging. Anal. Chem. 87, 7519–7523 (2015). [DOI] [PubMed] [Google Scholar]
  21. Koski K. & Yarger J. Brillouin imaging. Appl. Phys. Lett. 87, 061903 (2005). [Google Scholar]
  22. Berghaus K. V., Yun S. H. & Scarcelli G. High Speed Sub-GHz Spectrometer for Brillouin Scattering Analysis. J. Vis. Exp. 106, e53468 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Yan Y. X. & Nelson K. A. Impulsive stimulated light scattering. I. General theory. J. Chem. Phys. 87, 6240–6256 (1987). [Google Scholar]
  24. Kinoshita S., Shimada Y., Tsurumaki W., Yamaguchi M. & Yagi T. New high‐resolution phonon spectroscopy using impulsive stimulated Brillouin scattering. Rev. Sci. Instrum. 64, 3384–3393 (1993). [Google Scholar]
  25. Zhao L. et al. Impulsive stimulated scattering of surface acoustic waves on metal and semiconductor crystal surfaces. J. Chem. Phys. 114, 4989–4997 (2001). [Google Scholar]
  26. Ratanaphruks K., Grubbs W. T. & MacPhail R. A. CW stimulated Brillouin gain spectroscopy of liquids. Chem. Phys. Lett. 182, 371–378 (1991). [Google Scholar]
  27. Sonehara T. & Tanaka H. Forced Brillouin spectroscopy using frequency-tunable continuous wave lasers. Phys. Rev. Lett. 75, 4234–4237 (1995). [DOI] [PubMed] [Google Scholar]
  28. Grubbs W. T. & MacPhail R. A. High resolution stimulated Brillouin gain spectrometer. Rev. Sci. Instrum. 65, 34–41 (1994). [Google Scholar]
  29. Ballmann C. W. et al. Stimulated Brillouin Scattering Microscopic Imaging. Sci. Rep. 5, 18139 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Remer I. & Bilenca A. Background-free Brillouin spectroscopy in scattering media at 780 nm via stimulated Brillouin scattering, Opt. Lett. 41, 926–929 (2016). [DOI] [PubMed] [Google Scholar]
  31. Gross E. Change of Wave-length of Light due to Elastic Heat Waves at Scattering in Liquids. Nature 126, 201–202 (1930). [Google Scholar]
  32. Antonacci G., Foreman M. R., Paterson C. & Torok P. Spectral broadening in Brillouin imaging. Appl. Phys. Lett. 103, 221105 (2013). [Google Scholar]
  33. Faris G. W., Jusinski L. E. & Hickman A. P. High-resolution stimulated Brillouin gain spectroscopy in glasses and crystals. J. Opt. Soc. Am. B 10, 587–599 (1993). [Google Scholar]
  34. Goodwin R. D. Methanol Thermodynamic Properties from 176 to 673 K at Pressures to 700 Bar. J. Phys. Chem. Ref. Data 16, 799–892 (1987). [Google Scholar]
  35. Hayashi N., Mizuno Y., Koyama D. & Nakamura K. Dependence of Brillouin frequency shift on temperature and strain in poly(methyl methacrylate)-based polymer optical fibers estimated by acoustic velocity measurement. Appl. Phys. Express 5, 032502 (2012). [Google Scholar]
  36. Boyd R. W. in Nonlinear optics 3rd edn, Ch.8, 395–402 (Academic Press, London, 2008). [Google Scholar]
  37. Kim M. et al. Shear Brillouin light scattering microscope. Opt. Express. 24, 319–328 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mertz J. Optical sectioning microscopy with planar or structured illumination. Nat. Methods 8, 811–819 (2011). [DOI] [PubMed] [Google Scholar]
  39. Veirs D. K., Ager J. W., Loucks E. T. & Rosenblatt G. M. Mapping materials properties with Raman spectroscopy utilizing a 2-D detector. Appl. Opt. 29, 4969–4980 (1990). [DOI] [PubMed] [Google Scholar]
  40. Dodt H.-U. et al. Ultramicroscopy: three-dimensional visualization of neuronal networks in the whole mouse brain. Nat. Methods 4, 331–336 (2007). [DOI] [PubMed] [Google Scholar]
  41. Carolan P. G., Selden A. C., Bunting C. A. & Nielson P. A nanometer notch filters with high rejection and throughput. Rev. Sci. Instrum. 63, 5161–5163 (1992). [Google Scholar]
  42. Fiore A., Zhang J., Shao P., Yun S. H. & Scarcelli G. High-extinction virtually imaged phased array-based Brillouin spectroscopy of turbid biological media. Appl. Phys. Lett. 108, 203701 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep35398-s1.pdf (216.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES