Abstract
Interneurons (INs) of the hippocampus exert versatile inhibition on pyramidal cells by silencing the network at different oscillation frequencies. Although IN discharge can phase‐lock to various rhythms in the hippocampus, under high‐frequency axon firing, the boutons may not be able to follow the fast activity. Here, we studied Ca2+ responses to action potentials (APs) in single boutons using combined two‐photon microscopy and patch clamp electrophysiology in three types of INs: non‐fast‐spiking (NFS) neurons showing cannabinoid 1 receptor labelling and dendrite targeting, fast‐spiking partially parvalbumin‐positive cells synapsing with dendrites (DFS), and parvalbumin‐positive cells with perisomatic innervation (PFS). The increase in [Ca2+]i from AP trains was substantially higher in NFS boutons than in DFS or PFS boutons. The decay of bouton Ca2+ responses was markedly faster in DFS and PFS cells compared with NFS neurons. The bouton‐to‐bouton variability of AP‐evoked Ca2+ transients in the same axon was surprisingly low in each cell type. Importantly, local responses were saturated after shorter trains of APs in NFS cells than in PFS cells. This feature of fast‐spiking neurons might allow them to follow higher‐frequency gamma oscillations for a longer time than NFS cells. The function of NFS boutons may better support asynchronous GABA release. In conclusion, we demonstrate several neuron‐specific Ca2+ transients in boutons of NFS, PFS and DFS neurons, which may serve differential functions in hippocampal networks.
Keywords: axon terminal, calcium dynamics, GABAergic synapse, hippocampus, imaging
Introduction
In the hippocampus, there is a complex and multifaceted GABAergic network composed of more than 21 different types of interneurons (INs) (Freund & Buzsaki, 1996; Klausberger & Somogyi, 2008). Although the morphology and physiology of certain types of INs have been investigated, much less is known about the axonal properties and the heterogeneity of individual bouton responses. In particular, Ca2+ dynamics at the individual bouton level have not been studied in anatomically identified GABAergic INs. Based on discharge patterns in response to depolarizing currents at room temperature (23–26 °C), GABAergic INs can be subdivided into non‐fast‐spiking (NFS; < 50 Hz) and fast‐spiking (FS; > 50 Hz) groups. FS neurons can be further categorized by their target selectivity, i.e. whether they induce perisomatic or dendritic inhibition of pyramidal cells. Accordingly, in our study, INs were subdivided into three groups: (a) NFS neurons with cannabinoid 1 receptor labelling (CB1+) that target dendrites (i.e. Schaffer collateral‐associated, perforant path‐associated and apical dendritic‐innervating cells); (b) partially parvalbumin (PV)‐positive FS cells that make synapses in the dendritic domain (DFS neurons; PV− projection and PV+ bistratified cells); and (c) PV+ FS INs with exclusive perisomatic innervation (PFS neurons; i.e. axo‐axonic and basket cells).
It is generally accepted that the presynaptic terminal is one of the key players in plasticity. Although the function of axon terminals has been heavily discussed, axonal firing‐induced intracellular Ca2+ dynamics in the terminal, the prerequisite of GABA release, are not well understood. This study is the first attempt to analyse the details of Ca2+ dynamics in various post‐hoc identified INs in an acute rat hippocampal slice preparation in which morphological and functional integrity were maintained, estimating their unperturbed [Ca2+]i value, endogenous buffer capacity and decay time. Any information about the characteristics of the presynaptic GABAergic terminals that exclusively innervate the soma or the dendrites of pyramidal cells (Klausberger & Somogyi, 2008; Klausberger, 2009) might facilitate understanding of the input/output transformations, integration and synaptic plasticity that occur at these synapses (Zucker & Regehr, 2002; Eggermann & Jonas, 2012).
Morphology and intracellular signalling, especially the Ca2+ response evoked by action potentials (APs), vary greatly between different IN types. PFS INs (Somogyi, 1977) exert perisomatic inhibition and thereby control the output of pyramidal cells. In these PV+ INs, short Ca2+ transients and smaller Δ[Ca2+]i are generated, whereas INs expressing CB1 receptors, a characteristics of NFS cells (Katona et al., 1999; Bezaire & Soltesz, 2013), show unique decay dynamics with longer‐lasting increases in [Ca2+]i and larger Δ[Ca2+]i in response to single APs and train stimulations. In this paper, we provide the first demonstration of the local mechanisms in GABAergic boutons that potentially underlie asynchronous release, including the ability to maintain the high [Ca2+] evoked by APs in NFS INs, which enable terminals to release GABA for a longer period and tonically influence the integration of incoming impulses at the dendritic region of pyramidal cells. Our findings reveal remarkable IN type‐specific characteristics of axon terminals that underlie their different functional roles.
Materials and methods
Acute slice preparation and patch‐clamp recordings
The experiments in this study were performed in accordance with the Hungarian Act of Animal Care and Experimentation (1998, XXVIII. Section 243) and were approved by the Institutional Animal Care and Use Committee. These guidelines conform to the principles of UK regulations. Acute hippocampal slices were prepared from 14‐ to 20‐day‐old Wistar rats of either sex using isoflurane anaesthesia followed by swift decapitation. Transverse (300 μm) hippocampal slices were cut with a vibratome (Vibratome 3000; Ted Pella Inc., Redding, CA, USA). After 30 min of incubation at 32 °C, the slices were stored at room temperature in artificial cerebrospinal fluid (ACSF; in mm: 126 NaCl, 2.5 KCl, 2 CaCl2, 2 MgCl2, 1.25 NaH2PO4, 26 NaHCO3 and 10 glucose; chemicals were purchased from Merck, Darmstadt, Germany). The cell bodies of hippocampal GABAergic interneurons from the CA1 stratum radiatum (non‐fast‐spiking) and the oriens/pyramidale (fast‐spiking) were visualized using differential interference contrast (DIC) microscopy with an Olympus BX50WI microscope and a 40 × water immersion objective (LUMPLFLN 40 × WI, 0.8 NA; Olympus, Hamburg, Germany). Borosilicate glass pipettes (Harvard Apparatus, Edenbridge, UK) with tip diameters of approximately 1 μm were used for patch‐clamp recording. The pipettes were pulled with a Sutter P‐2000 micropipette puller (Sutter Instruments, Novato, CA, USA) filled with the morphological tracer Alexa Fluor 594 (40 μm), fluorescent Ca2+ indicators (Life Technologies, Eugene, OR, USA) and the following solution (in mm): 125 K‐gluconate, 20 KCl, 10 HEPES, 10 di‐Tris‐salt phosphocreatine, 0.3 Na‐GTP, 4 Mg‐ATP and 10 NaCl, purchased from Sigma‐Aldrich (St Louis, MO, USA) and Merck. Patch pipette resistance in the bath was approximately 4–7 MΩ. Current‐clamp recordings were obtained at 23–26 °C (Axopatch‐1 D, Digidata 1322A; Molecular Devices, Sunnyvale, CA, USA). The ACSF used for perfusion was continuously saturated with 95% O2 and 5% CO2. It was difficult to maintain the seal at 36 °C because of swelling that occasionally occurred during loading (> 1 h); therefore, the experiments were carried out at 23–26 °C. In addition, recording at a lower temperature reduces leakage of the dye to the extracellular medium (Malgaroli et al., 1987).
In the experiments, the holding potential ranged from −70 to −75 mV. APs were evoked by somatic current injection (2 ms, 1000–1300 pA). Firing patterns were studied using current steps of 1 s duration, which ranged from −100 to 450 pA in 50‐pA increments. Data acquisition was performed using pclamp 10.2 software (Axon Instruments, Foster City, CA, USA). Passive membrane properties were measured 5–10 min after break‐in at holding currents below −100 pA. Accommodation ratios were calculated from the current step at which the firing frequency was maximal and free of distortion. The time difference between the last two APs was divided by the time difference between the second and third APs. The peak amplitude, half‐width, rise time and decay time were calculated from the current train step at which at least three APs occurred, beginning with the second AP. Tetrodotoxin (TTX) was purchased from Alomone Labs (Jerusalem, Israel). EGTA, CdCl2 and MgCl2 were purchased from Sigma‐Aldrich and dissolved in ACSF on the day of the experiment.
Two‐photon Ca2+ imaging
We used a custom‐built two‐photon instrument based on a modified Olympus FluoView 300 laser scanning confocal microscope for two‐colour (green/red) fluorescence imaging. A tunable, femtosecond‐pulse Ti‐sapphire laser (Tsunami‐S with a 5‐W Millennia pump laser from Newport/Spectra Physics, Harwell, UK) generated nearly transform‐limited pulses with τFWHM values of approximatley 80 fs at a central laser wavelength of approximatley 810 nm. The repetition rate of approximatley 80 MHz ensured high two‐photon excitation efficiency for the fluorescent dyes (Oregon Green BAPTA and Alexa Fluor‐594). The average power reaching the sample was set by a reflective neutral density filter wheel to avoid thermal damage. Typical power levels past the objective were in the range 5–10 mW. We constructed two detection units (an upper and a lower unit) for highly efficient collection of the fluorescence signals from our samples. The imaging system was used in line‐scan mode, which provided high temporal resolution (3 ms). The scan duration was 3 s. Scans were repeated three times over the same bouton and were averaged. Starting 60 min before imaging, interneurons were loaded via the patch pipette with different high‐ and low‐affinity Ca2+‐sensitive dyes [Oregon Green BAPTA (OGB‐1, K D = 200 nm or OGB‐6F, K D = 3.0 μm] at concentrations of 56, 112, 224 or 336 μm, as indicated) and with the morphological tracer Alexa Fluor 594 (40 μm) to visualize cell morphology (red fluorescence) and to locate the boutons of interest at distances > 50 μm from the cell body. After this procedure, the GABAergic presynaptic boutons were easily identified as bead‐like swellings. Fluorophores were excited in two‐photon mode at approximatley 810 nm, and the laser power was optimized for emission detection at different depths in the slice without causing phototoxicity. To measure the Ca 2+ signals, green fluorescence was collected during the line scans across the axon terminals. The amplitude of the Ca 2+ transients was expressed as fractional change of the basal fluorescence ΔF/F, which is proportional to the change in [Ca2+]i (Kisfali et al., 2013). At the end of each experiment, a series of images across the depth of the volume encompassing the imaged neuron were collected. Analysis of the line scan data was performed in off‐line mode with custom‐made software in matlab 6.1 (The Mathworks, Inc., Natick, MA, USA).
Post‐hoc identification of the recorded cells
Cells were classified based on their localization/axonal arborization and electrophysiological properties. In particular, cells firing lower than 50 Hz in the stratum radiatum were identified as NFS cells, whereas cells firing above 50 Hz in the stratum oriens were identified as FS cells. FS cells were further classified as DFS and PFS cells based on their axonal arborization. In contrast to DFS cells, PFS cells show a preference for arborization in the pyramidal layer. To appropriately determine the morphological features of the studied cells, at the end of the two‐photon imaging and biocytin filling, the slices were fixed in 4% paraformaldehyde at 4 °C for at least 2 days and were then washed with 0.1 m phosphate buffer (PB) and Tris‐buffered saline (TBS). The slices were blocked with 10% normal goat serum (NGS; Vector Laboratories Inc., Burlingame, CA, USA) in TBS for 60 min and then incubated overnight in rabbit anti‐CB1 receptor primary antibody (Cayman Chemical, Ann Arbor, MI, USA) diluted to 1 : 1000 (cells from the stratum radiatum) or rabbit anti‐PV primary antibody (Swant, Marly, Switzerland) diluted to 1 : 1000 (cells from the stratum oriens/pyramidale) in TBS containing 2% NGS and 0.3% Triton X‐100 (Acros Organics, Geel, Belgium). The slices were then washed with TBS and incubated in TBS containing Alexa Fluor 568‐conjugated goat anti‐rabbit secondary antibody (Life Technologies) diluted to 1 : 500, Alexa Flour 488‐conjugated streptavidin diluted to 1 : 3000 (Life Technologies) and 0.3% Triton X‐100 for 4 h for visualization and cell recording. Finally, the slices were embedded in Vectashield mounting medium (Vector Laboratories). The examined cells were morphologically identified based on confocal images (Nikon A1R with 10 × and 60 × objectives; Nikon Europe, Amsterdam, The Netherlands). Next, for all of the cells pre‐classified as NFS based on morphology and electrophysiology, the classifications were further confirmed by CB1 immunoreactivity, whereas all pre‐classified FS cells were tested for PV immunopositivity. All NFS cells showed CB1 immunopositivity, supporting the finding that, with the exception of neurogliaform cells, all NFS interneurons in the hippocampus CA1 stratum radiatum possess CB1 receptors. However, PV positivity was not always evident, which might have been caused by dye elimination during the long washout. In the case of projection cells, members of the DFS group, PV positivity was not required. Thus, CB1 and PV immunoreactivity was used only as confirmatory information for the classification.
Analysis of fluorescence transients
To evaluate the features of the Ca2+ transients, the following equations were used:[Ca2+] at resting conditions ():
| (1) |
where K D is the dissociation constant of the applied dye, is the maximum change in fluorescence intensity following a saturating influx, and R f is the dynamic range of a given dye, which can be derived from: R f = F max/F min (Maravall et al., 2000). Saturation was established with a train of APs at 60 Hz. The number of APs applied varied from 15 to 150 according to the type of cell and the type of dye. Based on the highest recorded values of and our previous experiments with ionomycin (Kisfali et al., 2013), the R f of OGB‐1 was estimated to be 5.5.
Intracellular free ():
| (2) |
where ΔF/F is the actual change in fluorescence intensity (Helmchen et al., 1997).
Exogenous buffer capacity (κB):
| (3) |
where is the total concentration of dye in the pipette and [Ca2+]peak is the actual concentration of Ca2+ at the peak of the transients. Because the local concentration of the dye inside cells is not known, a correction factor was applied to compensate for the likely difference in dye concentration reached in the axon in some experiments.
Total [Ca2+] change () (Jackson & Redman, 2003):
| (4) |
where Δ[Ca2+]i = [Ca2+]i − [Ca2+]rest, and κE is the endogenous buffer capacity. [Ca2+]i is the actual concentration of Ca2+ calculated from Ca2+ transients evoked by somatic stimulation.
Under unperturbed conditions, where κB = 0:
| (5) |
where is in the absence of exogenous buffer.
Decay time constant (τ):
The decay times of the AP‐evoked transients were fit with either a single exponential or the sum of two exponentials. If the decay was biphasic, τ was calculated as follows:
| (6) |
where τ w is the amplitude‐weighted decay time constant, A 1 and A 2 are the amplitudes of the first and second exponential components, respectively, and τ 1 and τ 2 are the time constants of the first and second exponential components, respectively. Because accurate determination of τ at high was not always possible, the regression method could not be used to estimate τ under unperturbed conditions (τ 0). Therefore, the τ 0 values were calculated as follows (Jackson & Redman, 2003):
| (7) |
and
| (8) |
where τ e is the elementary decay time, which reflects removal in the complete absence of buffering. Exponential fits were performed with the Solver function of Excel.
Extrusion rate (γ):
| (9) |
Number of entering Ca2+ions ():
| (10) |
where V b is the volume of the bouton, and N A denotes the Avogadro constant. In the volume calculation, 20% (i.e. the volume of the presynaptic organelles) was subtracted (Ermolyuk et al., 2013). (Note: the boutons were interpreted as barrels.)
Number of extruded Ca2+ under unperturbed conditions (j) (Brenowitz & Regehr, 2007):
| (11) |
Statistical analyses
Statistical significance was tested using two‐sample t‐tests, one‐way anova with Tukey and non‐parametric Kruskal–Wallis tests with Dunn's post‐hoc test for independent samples and Wilcoxon signed‐rank or Friedman tests for dependent samples. Normality was established with the Shapiro–Wilk test. The error bars in the figures and ± values in the text indicate SEM (*P < 0.05, **P < 0.01 and ***P < 0.001).
Calculation of bouton volume (Vb)
The anatomical structure of axons and the volume of boutons are important factors that affect the diffusion and distribution of molecules (buffer) injected into a neuron. Boutons were taken as barrel‐shaped, and their volume was determined according to their fluorescence image.
Results
NFS cells with CB1 receptor immunopositivity were mainly located in the stratum radiatum, targeting the dendritic region of pyramidal cells (Fig. 1A). CB1 + basket cells were not included in our study. The axons of DFS neurons also innervated the dendritic domains of pyramidal neurons at both the apical and the basal regions to the same extent (Fig. 1B). In contrast, PFS axons typically innervated the soma and proximal dendrites or initial axon segment of pyramidal neurons (Fig. 1C). The cell bodies of the latter two types of INs are exclusively located in stratum oriens/pyramidale. In some cases, PV immunoreactivity was not observed in cells showing the perisomatic targeting phenotype, which might have been caused by washout of PV during longer dye loading. In response to current injection, the firing rate of NFS cells was less than half the rates observed in DFS and PFS cells (Table 1). Furthermore, in contrast to FS cells, AP firing in NFS neurons showed marked accommodation (Fig. 1E and Table 1). Based on their anatomical and electrophysiological features (input resistance and the peak amplitude, half‐width, rise and decay times of APs) (Fig. 1D–H), the INs could be classified as one of these cell types.
Figure 1.
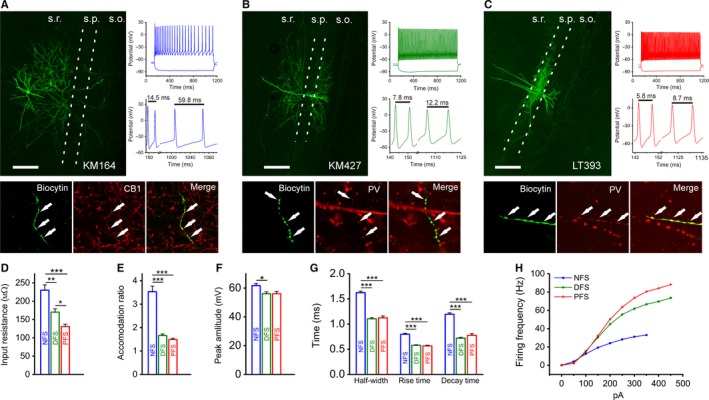
Identification of non‐fast‐spiking and fast‐spiking interneuron types in the hippocampus. (A–C) Confocal maximum intensity projection image (left), immunocytochemical staining (bottom) and firing pattern (top right) – highlighting the accommodation ability (middle right) – of a typical NFS (A), DFS (B) and PFS (C) IN. S.r.: stratum radiatum; s.p.: stratum pyramidale; s.o.: stratum oriens; scale bar, 200 μm. (D) Membrane resistance values at rest for NFS, DFS and PFS INs. (E) Accommodation ratios were determined from the maximal firing responses in which the AP shape was not distorted and calculated as the time elapsed between the last two APs divided by the time between the second and third APs. (F) AP amplitudes in the different groups, which were calculated from responses evoked by the step protocol. (G) Half‐width, rise time and decay time constants of APs in the different types of INs. (H) Average firing frequencies of the different cell populations, which were induced by 0–450 pA current steps with 50‐pA increments. The data shown in this figure are means and SEM. Tukey post‐hoc test after one‐way anova (half‐width, rise time, decay time) and Dunn's post‐hoc test after Kruskal–Wallis test (input resistance, accommodation ratio, peak amplitude from threshold); *P < 0.05, **P < 0.01 and ***P < 0.001.
Table 1.
Electrophysiological properties of the cell groups
| NFS | DFS | PFS | Significance | |
|---|---|---|---|---|
| Resting membrane potential (mV) | −53 ± 1 (n = 47) | −55 ± 1 (n = 26) | −56 ± 1 (n = 22) | NFS‐DFS n.s.; NFS‐PFS n.s.; DFS‐PFS n.s. |
| Input resistance (MΩ) | 230 ± 15 (n = 55) | 170 ± 9 (n = 30) | 131 ± 7 (n = 28) | NFS‐DFS**; NFS‐PFS***; DFS‐PFS*. |
| Accommodation ratio | 3.5 ± 0.2 (n = 29) | 1.7 ± 0.1 (n = 29) | 1.5 ± 0.1 (n = 29) | NFS‐DFS***; NFS‐PFS***; DFS‐PFS n.s. |
| Maximal firing frequency (Hz) | 35 ± 1 (n = 77) | 74 ± 2 (n = 31) | 91 ± 4 (n = 29) | NFS‐DFS***; NFS‐PFS***; DFS‐PFS n.s. |
| Peak amp. from threshold (mV) | 61.74 ± 1.47 (n = 29) | 56.10 ± 1.30 (n = 29) | 56.06 ± 1.66 (n = 29) | NFS‐DFS*; NFS‐PFS n.s.; DFS‐PFS n.s. |
| Half‐width (ms) | 1.62 ± 0.03 (n = 29) | 1.11 ± 0.02 (n = 29) | 1.12 ± 0.04 (n = 29) | NFS‐DFS***; NFS‐PFS***; DFS‐PFS n.s. |
| Rise time (ms) | 0.80 ± 0.02 (n = 29) | 0.58 ± 0.01 (n = 29) | 0.57 ± 0.02 (n = 29) | NFS‐DFS***; NFS‐PFS***; DFS‐PFS n.s. |
| Decay time (ms) | 1.2 ± 0.03 (n = 29) | 0.72 ± 0.02 (n = 29) | 0.78 ± 0.03 (n = 29) | NFS‐DFS***; NFS‐PFS***; DFS‐PFS n.s. |
Statistical analysis: Tukey's post‐hoc test after one‐way anova (half‐width, rise time, decay time); Dunn's post‐hoc test after Kruskal–Wallis test (resting membrane potential, input resistance, accommodation ratio, maximal firing frequency, peak amp. from threshold); n.s., non‐significant, *P < 0.05, **P < 0.01 and ***P < 0.001.
Characterization of bouton Ca2+ transients in hippocampal INs
One hour after break‐in, axons became visible as bead‐like swellings, and line scans were performed across individual boutons at 330 Hz (Fig. 2A). The maximum change in fluorescence (ΔF/F max) was determined in each bouton by the application of 60‐Hz trains of APs (Fig. 2B–D). Without AP generation, subthreshold depolarizations did not produce Ca2+ transients in the boutons of INs (data not shown). Interestingly, in the presence of OGB‐1 (applied at 112 μm) we observed a surprisingly large difference in single AP‐evoked Ca2+ responses; in the boutons of NFS INs, larger transients were evoked [46.5 ± 1.7% of (ΔF/F)max, n = 42] than in FS cells [24.8 ± 1.3 (n = 35) and 23.0 ± 1.1% (n = 26) of (ΔF/F)max for DFS and PFS cells, respectively] (Dunn's post‐hoc test after Kruskal–Wallis test; P < 0.001 comparing NFS vs. DFS and NFS vs. PFS, P > 0.05 comparing DFS vs. PFS) (Fig. 2B–D). However, with a larger number of invading APs, a difference in the evoked responses appeared as a longer decay of transients, indicating Ca2+ accumulation in NFS cells (Fig. 2B–D). Stimulation with five APs at 60 Hz resulted in a Ca2+ response far from saturation using OGB‐6F, and peak amplitudes were also greatly different [43 ± 2% (n = 23) in NFS cells, 29 ± 1% (n = 19) and 17 ± 1% (n = 18) for DFS and PFS] (Dunn's post‐hoc test after Kruskal–Wallis test; P < 0.001 comparing NFS/PFS, P < 0.01 comparing NFS vs. DFS and DFS vs. PFS). Then, we studied the source of Ca2+ elevation during the AP‐evoked local responses. Cd2+ (200 μm), a non‐selective blocker of voltage‐gated calcium channels, fully abolished these Ca2+ transients in boutons. Consistent with this observation, the application of 5 mm MgCl2 also reduced the amplitude of the transients (data not shown). When extracellular free Ca2+ in the perfusion solution was bound by 5 mm EGTA, APs failed to produce Ca2+ transients in NFS INs, whereas complete blockade of voltage‐dependent sodium channels by TTX (2 μm) was found to inhibit AP‐evoked responses in boutons (data not shown), showing the extracellular origin and local depolarization‐dependency of the Ca2+ response.
Figure 2.
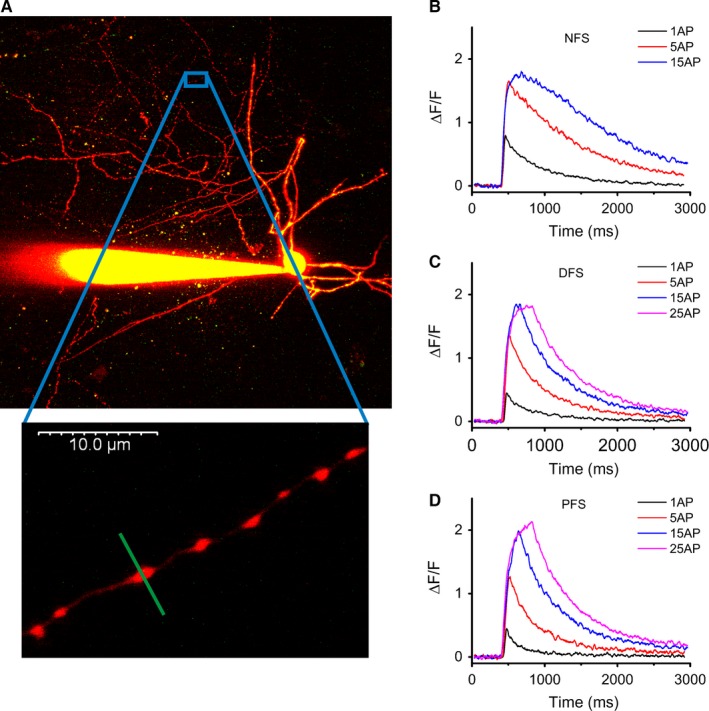
Characterization of local Ca2+ responses in individual boutons. (A) Two‐photon z‐stack image of an NFS cell (filled with Alexa Fluor 594 and Oregon Green BAPTA‐1) highlighting a short axon branch (bottom). (B–D) Averaged two‐photon fluorescence time‐lapse responses (single AP and five‐, 15‐ and 25‐AP‐evoked transients at 60 Hz) in NFS, DFS and PFS cells. Using the high‐affinity dye OGB‐1 (112 μm), fluorescence signals were most likely saturated at stimulation with 15 APs; n = 4–11 cells, 16–49 boutons.
Variability in the amplitude of Ca2+responses within axon branches
Single or trains of APs were able to pass branch points and invade into subsequent boutons, as shown by local Ca2+ responses following OGB‐1 (112 μm) loading irrespective of the IN type (Fig. 3A–C). In one case when 21 boutons located on six branches of the same PFS cell were recorded, all branches and most of the boutons responded to single APs, but one unresponsive bouton was also found (Fig. 3G–H), suggesting that the propagation of APs was not stopped even at the unresponsive bouton. In contrast, such unresponsive boutons were not found in an NFS cell recorded under similar settings (20 boutons, four branches). In rare cases, none of the boutons responded to APs; such unresponsive cells were found in each IN group. Responses evoked by a single AP typically showed relatively moderate variability within cells (Fig. 3A–C, right), whereas the variability was somewhat larger at the population level (Fig. 3D–F). The responses of NFS cells exhibited larger amplitudes than those of DFS and PFS INs, resulting in a rightward shift of their distribution (Fig. 3D–F). To precisely estimate variability, we used data sets recorded under conditions where the amplitudes fell within the linear range of the dye (10–30% of ΔF/F max) and the exogenous buffering was low (NFS: OGB‐6F 112 μm; DFS and PFS: OGB‐1 56 μm). Under these settings we found 4.1‐, 3.8‐ and 4.0‐fold cell‐to‐cell variability (variability within group) in NFS, DFS and PFS cells, respectively. The bouton‐to‐bouton variability (within individual cells), which was calculated with data from neurons from which at least five boutons were measured, was < 2.5‐fold for all cell types (NFS: 2.2; DFS: 2.4, PFS: 2.3). These variability levels did not differ significantly from each other, as revealed by the calculated coefficient of variation (CV) for bouton‐to‐bouton variability (Kruskal–Wallis test; P > 0.05 in each comparison) (Fig. 3I). Five‐AP‐induced transients (recorded with OGB‐6F) showed similar variability (cell‐to‐cell ≤ 3.5, bouton‐to‐bouton ≤ 2.0) for each type of IN. The relative amplitude of the evoked Ca2+ responses in en passant boutons around branch points was slightly larger than the amplitude in branch points irrespective of the IN type, as shown by the ratio of responses in the different locations (Fig. 3I).
Figure 3.
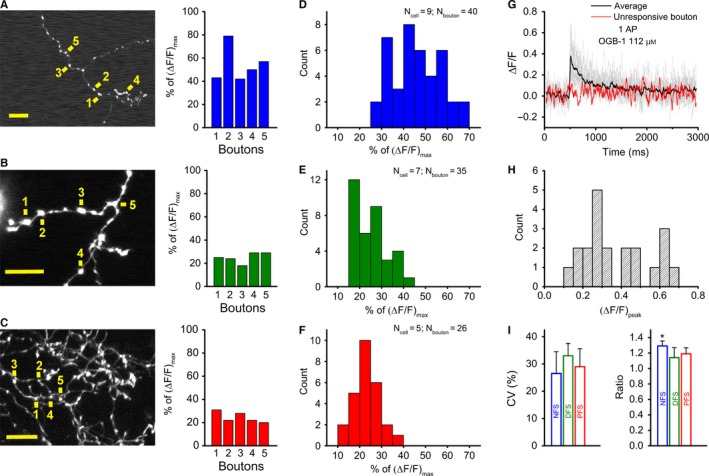
Low variability of individual bouton responses across interneuron types. (A–C) Two‐photon z‐stack images of axonal segments of NFS (A), DFS (B) and PFS (C) cells. Yellow signs next to numbers indicate the individual bouton where single AP‐evoked Ca2+ transients were measured; scale bar, 10 μm (left). The peak amplitude of the Ca2+ transients evoked in five boutons is expressed as a percentage of the saturation level using OGB‐1 (112 μm). (D–F) Bar charts of single‐AP‐evoked peak amplitudes for NFS (blue), DFS (green) and PFS (red) cells. Note that the NFS responses are of the order of approximately 50%, whereas the DFS and PFS responses are approximately 20–30% of the saturation using OGB‐1 (112 μm). (G) Single‐AP‐evoked Ca2+ responses in 21 boutons of the same PFS cell (grey lines denote responsive boutons, red line shows the unresponsive one) with their average (black solid line). (H) Bar chart of the peak amplitudes of the same PFS cell, given as ΔF/F. (I) Variability of single AP‐evoked Ca2+ responses in each IN type, which was calculated as the mean of the coefficients of variation (CVs) of multiple individual cells in which at least five boutons were imaged (left). Because this calculation was based on experiments in which the amplitudes fell in the linear range of the dye (10–30% of saturation), the data for NFS cells were derived from experiments using OGB‐6F (112 μm), whereas the data for DFS and PFS cells were measured with OGB‐1 (56 μm) (n = 3 cells, 16–19 boutons for NFS, DFS and PFS cells). The ratio of single‐AP‐evoked Ca2+ responses in en passant boutons and branching points in NFS (blue), DFS (green) and PFS (red) cells (right). To calculate the ratio, the average of the responses in 3–5 en passant boutons close to the branching points was used; n = 6–7 cells and 8–10 branching points for NFS, DFS and PFS cells. Dunn's post‐hoc test after Kruskal–Wallis test; *P < 0.05.
Ca2+ concentration and calculation of ion‐level dynamics in IN groups during AP propagation
During loading of a cell with Ca2+‐sensitive dye, the amplitude of the apparent Ca2+ elevation is being reduced by the increasing exogenous buffer capacity (κB), and the decay is slowing down, thereby perturbing the measured Ca2+ signal. To eliminate this effect of the dye, we applied OGB‐1 at different concentrations and estimated the Δ[Ca2+]i during unperturbed conditions (Δ[Ca2+]0). We also determined the endogenous buffer capacity (κE) for each group using a single compartment model (Neher & Augustine, 1992). The x‐axis intercept of the regression lines for the inverse of the individual Δ[Ca2+]i peak values (determined at 56, 112, 224 and 336 μm of OGB‐1) indicated the κE values (Fig. 4A). The [Ca2+]rest in the boutons of NFS and FS cells showed no remarkable differences ([Ca2+]rest equal to 67, 77 and 63 nm in NFS, DFS and PFS cells, respectively). Note that these [Ca2+]rest data recorded in boutons are very similar to spine and bouton data reported by others (Sabatini et al., 2002; Jackson & Redman, 2003; Rozsa et al., 2004; Aponte et al., 2008; Ermolyuk et al., 2013). Interestingly, the peak Δ[Ca2+]0 was substantially higher in NFS cells (2.5‐ and 4‐fold difference) than in DFS and PFS cells (Fig. 4A and B). In contrast, an inverse tendency was found for κE; NFS cells (κE = 63) showed a lower κE than DFS (κE = 96) and PFS (κE = 122) cells (Fig. 4A). Because κE refers to the ratio of endogenous buffer‐bound and buffer‐unbound [Ca2+], high values indicate that the majority of entered Ca2+ ions attain an endogenous buffer bound state and only a small portion remain free. Indeed, Δ[Ca2+]0, which indicates free [Ca2+] at unperturbed conditions, was 565 nm in NFS boutons from a single AP stimulation, whereas it was considerably lower in FS boutons (214 and 147 nm, for DFS and PFS cells, respectively). The single‐AP‐evoked Δ[Ca2+]T was approximately two times higher in the NFS than in the DFS and PFS groups (36.2 μm for NFS, 20.8 μm for DFS and 18.1 μm for PFS neurons). To determine the number of entering Ca2+ ions (N Ca 2+), we estimated the volume of boutons (V b) based on two‐dimensional fluorescence images. After determination of their minor and major diameters, boutons were modelled as barrel‐shapes with the restriction that the extension in the z‐direction was always equal to the minor diameter. The volume of boutons was observed to be smaller in NFS cells (0.72 ± 0.04 μm3, n = 60) and larger in DFS (0.85 ± 0.05 μm3, n = 43) and PFS (0.98 ± 0.04 μm3, n = 58) neurons. We estimated that in PFS and DFS cells, nearly the same amount of Ca2+ enters the bouton, whereas in NFS boutons, a higher number of entering Ca2+ ions can be calculated in response to a single AP stimulation (Table 2). These data revealed that differences in κE and V b might cause the 1.5‐fold difference in N Ca 2+ between the NFS and FS groups. Low‐affinity dyes can be used to uncover buffering effects and to reveal endogenous Ca2+ transients. Due to its high K D (3 μm), the perturbation effect of OGB‐6F is considerably lower than that of OGB‐1 (K D = 200 nm). To reach an appropriate signal‐to‐noise ratio, we applied five APs to evoke Ca2+ responses in the boutons of INs. Using OGB‐6F and five APs, the Δ[Ca2+]i remained significantly higher in NFS cells, and the difference between FS groups also became more pronounced (Fig. 4C and D). Thus, after minimizing the buffering effect, more Ca2+ influx in the boutons of NFS cells compared with FS cells was confirmed. Five APs increased the [Ca2+]i to 2451 ± 173 (n = 9 cells; 24 boutons), 1096 ± 65 (n = 6; 19) and 593 ± 34 nm (n = 4; 13) in NFS, DFS and PFS cells, respectively (Fig. 4C and D). When calculating the proportion of the response represented by a single AP, it was 486, 219 and 119 nm of the increase in the [Ca2+]i per AP in NFS, DFS and PFS neurons, respectively, which indicated that for up to five APs, the elevation of [Ca2+]i was proportional to the number of APs in each group.
Figure 4.
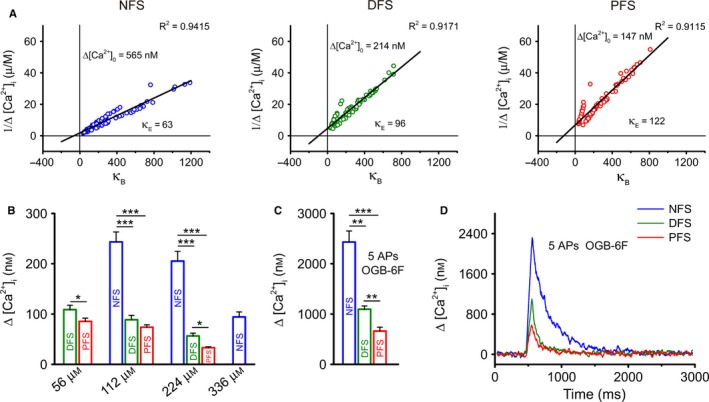
Cell‐type‐dependent buffering capacity and Δ[Ca2+]i in boutons. (A) Endogenous buffering capacity (κE) in NFS (blue), DFS (green) and PFS (red) INs. Linear regressions for single‐AP‐evoked Δ[Ca2+]i values were calculated at the individual bouton level. Values of 1/Δ[Ca2+]i were plotted as a function of the exogenous binding ratio (κB). The y‐axis intercepts denote the Δ[Ca2+]i in unperturbed conditions (Δ[Ca2+]0), and the x‐axis intercepts indicate κE values. All regressions were highly significant (least squares method; P < 0.001); n = 17–31 cells and 77–122 boutons for PFS, DFS and NFS cells. (B) Mean Δ[Ca2+]i values in response to single AP stimulation in each IN type at different exogenous buffering levels. (C) Mean Δ[Ca2+] values in response to five APs at 60 Hz, using n = 3–9 cells and 18–24 boutons for PFS, DFS and NFS cells. (D) Dynamics of five‐AP‐evoked Ca2+ transients in cells loaded with OGB‐6F (112 μm), expressed as Δ[Ca2+], calculated in different cell types. Dunn's post‐hoc test after Kruskal–Wallis test, except DFS vs. PFS comparison at 56 μm OGB‐1, where two‐sample t‐test was used; *P < 0.05, **P < 0.01 and ***P < 0.001.
Table 2.
Characteristic values of Ca2+ dynamics evoked by a single AP at unperturbed conditions calculated for boutons of GABAergic INs (based on data with OGB‐1); except τ there is no deviation of these derived values and therefore significance was not calculated
| NFS | DFS | PFS | |
|---|---|---|---|
| Δ[Ca2+]0 (nm) | 565 | 214 | 147 |
| Δ[Ca2+]T (μm) | 36.2 | 20.8 | 18.1 |
| Ca2+ entering the bouton (N Ca 2+) | 12 500 | 8500 | 8500 |
| Decay time (τ) (ms) | 207 ± 12 | 161 ± 14 | 180 ± 17 |
| Ca2+ extrusion rate (γ) (s−1) | 310 | 600 | 680 |
| No. of extruded Ca2+ (j) (s−1) | 60 400 | 52 500 | 47 200 |
Decay of Ca2+ transients in single boutons
Ca2+ indicator dyes are able to slow the apparent decay of Ca2+ transients due to their buffering capacity. At high κB, the majority of the responses showed biexponential decay, but the proportion of cases with biexponential decay could be reduced by decreasing the κB to 50% in NFS boutons but not in FS boutons. The apparent decay showed a tendency to be faster in NFS neurons using 224 μm OGB‐1, whereas at lower loading concentrations, the decay was somewhat faster in FS cells in response to a single AP stimulation (Fig. 5A). The elementary decay time constant (τe) (Jackson & Redman, 2003), which refers to Ca2+ removal in the complete absence of buffering, was 3.0 ± 0.2, 1.7 ± 0.1 and 1.5 ± 0.1 ms for NFS, DFS and PFS neurons, respectively. By multiplying these values by (1 + κE), we estimated ‘unperturbed’ time constants of decay (τ0) for single AP‐evoked transients, which were 207 ± 12 ms (n = 95) for NFS, 161 ± 14 ms (n = 48) for DFS and 180 ± 17 ms (n = 41) for PFS cells. There are no significant differences among these values (Dunn's post‐hoc test after Kruskal–Wallis test; P > 0.05 in each comparison). Although the contribution of the fast‐component differs among IN types (contribution of fast‐component: 33% for NFS, 52% for DFS and 67% for PFS INs) the total decay curves of INs revealed only minimal differences (Fig. 5B) (these curves were derived by extruding the buffering effect of OGB‐1). Using τ0 we determined the extrusion rate (γ) and the number of extruded Ca2+/s (j). Although FS INs can extrude many times more Δ[Ca2+]0 within 1 s (γ values) our calculation showed that NFS INs can extrude even more ions (j values) finally than FS cells (Table 2) consistent with their lower κE, which slow their decay to a lesser extent than that of FS INs. Not only can low‐affinity dyes reveal the magnitude of Ca2+ transients under less perturbed conditions, fine differences in the decay kinetics may also be uncovered. Five‐AP stimulation was used to study the decay with OGB‐6F (112 μm) to appropriately resolve decay time constants (Fig. 5C and D). The decay time constants (τ5AP) were 428 ± 35 (n = 8 cells; 19 boutons), 337 ± 60 (n = 4; 10) and 302 ± 58 (n = 3; 12) for NFS, DFS and PFS cells, respectively. Although the differences among these values were only tentative and non‐significant (Dunn's post‐hoc test after Kruskal–Wallis test; P > 0.05 in each comparison), when we calculated the fast‐component, sharp dissociation between the decay dynamics of NFS and FS cells became visible (Fig. 5C). In this set of experiments, decays were highly dominated by the fast‐component; its contribution to the full decay was between 80 and 90% in each group. The fast‐component of the decay was about three times slower in the NFS cells than in the FS groups (320 ms in NFS cells vs. 90 and 122 ms in DFS and PFS cells, respectively). The decline of the response to five APs was significantly more progressive in FS than in NFS cells, as revealed by the smaller amount of residual fluorescence at 100 ms after the time of the peak (Dunn's post‐hoc test after Kruskal–Wallis test; P < 0.001 comparing NFS vs. DFS and NFS vs. PFS) (Fig. 5D).
Figure 5.
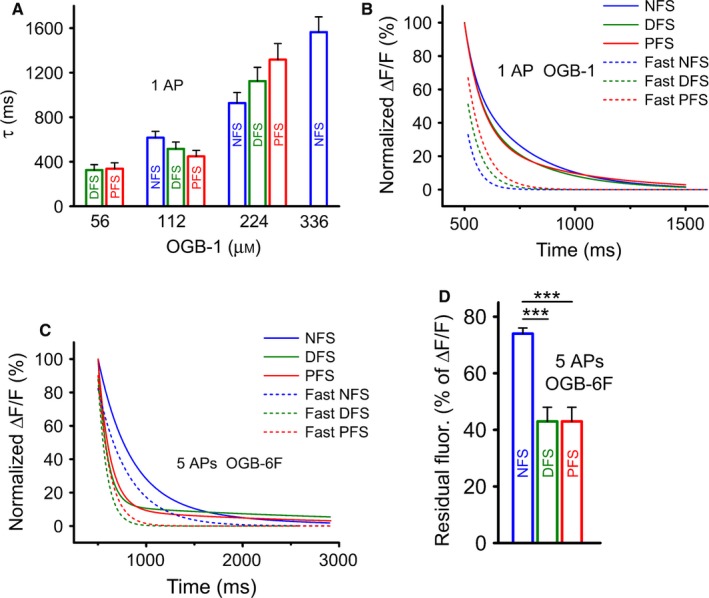
Phenotype‐dependent decay of Ca2+ transients in boutons. (A) Calculated decay time constants (τ values) in the different cell groups following a single AP under various buffering conditions. Decays were mono‐ or biexponential; for cases of biexponential decay, τ was calculated as the weighted mean of the two time constants. (B) The tails of the single AP‐evoked normalized Ca2+ transients excluded the buffering effect of OGB‐1. The figure shows the total decays and fast components of the decays for different INs. (C) Decay fitting for an average of five‐AP‐induced transients at 60 Hz. The data are shown as double component fitting (solid line) and the fast component of the biexponential decay. Note that the kinetics of the fast component (dashed line) of FS cells differ from those of NFS cells; n = 3–8 cells and 11–19 boutons for PFS, DFS and NFS cells. (D) Residual fluorescence calculated at 100 ms after the time of the peak amplitude, expressed as percentage of the peak amplitude. Note the marked difference between FS and NFS cells. Dunn's post‐hoc test after Kruskal–Wallis test; ***P < 0.001.
Possible functional role of the different Ca2+ dynamics in different IN types
The repeatability of Ca2+ transients in response to invading APs in anatomical compartments is a key issue because hippocampal field oscillations, which are especially important for INs, last for a longer time. Therefore, sustainable responses in the axon could be critical for creating a network‐level effect. Using the low‐affinity dye OGB‐6F (112 μm), three trials of 15 APs at 60 Hz separated by 30‐s intervals induced Ca2+ transients without saturation in each IN group (Fig. 6A). In these experiments, neither the amplitude nor the decay of the Ca2+ responses recorded during the third trial changed significantly from the responses recorded during the first trial (Friedman test; P > 0.05 in each group), indicating highly sustainable local Ca2+ transients. Based on the data shown in Fig. 5B and C, individual responses are well discriminated when evoked amplitudes decline to 90% of the initial value. Thus, each of the three IN phenotypes could discriminate between the first and second AP in a high‐frequency (90–100 Hz) train under unperturbed conditions (Fig. 5B). In contrast, when analysing the resolution of the fifth invading AP (Fig. 5C), the time to 90% Ca2+ response in the bouton is approximately 13–14 ms, so the maximal frequency sufficient for resolution is of the order of 70–76 Hz for FS cells. The corresponding values are 33 ms and approximatley 30 Hz for NFS cells, indicating that the functioning of NFS boutons makes them less likely to be capable of following high‐frequency hippocampal oscillations (gamma) appropriately. Therefore, we further investigated the characteristics of Ca2+ responses in boutons during high‐frequency and long train stimulation. The parameters of Ca2+ dynamics of INs remained distinct even after five APs (Fig. 6B). For NFS neurons, a train of 45 APs (60 Hz) was sufficient for saturation, while more than 100 APs at 60 Hz had to be applied to saturate local responses in FS neurons (Fig. 6B). This feature of FS neurons might make them capable of following higher frequency gamma oscillations for longer periods of time than NFS cells, at least at the bouton level, supporting the observations based on decay analysis of high‐frequency trains. At lower frequency AP stimulation, individual spikes were easily distinguished at the level of boutons during five‐AP trains. When comparing NFS and FS cells at 3 Hz (lower theta) and 10 Hz (higher theta) frequencies, individual APs evoked visible individual Ca2+ responses in the bouton on top of ongoing Ca2+ accumulation (Fig. 6C).
Figure 6.

System‐related characteristics of bouton Ca2+ transients. (A) Peak values of evoked transients in three consecutive trials in NFS, DFS and PFS cells. Stimulation trains (15 APs at 60 Hz) were applied three times at 30‐s increments. Each coloured line represents an individual bouton. Note that no tendency towards facilitation or depression is present in the peak values. (Amplitudes were normalized onto the peak of the first trial.) (B) Long‐train‐evoked Ca2+ responses in boutons of the three IN types using OGB‐6F (112 μm); n = 9–10 cells and 26–29 boutons for 15 and 45 APs (NFS cells); n = 3–6 cells and 8–18 boutons for 15 and 100 APs (DFS); and n = 2 cells and 5–7 boutons for 15 and 100 APs (PFS). (C) Ca2+ transients in boutons in response to stimulation with five APs at 3, 5 and 10 Hz. NFS and FS cells were loaded with OGB‐1 (224 μm); n = 2 cells and at least 4 boutons.
Discussion
GABAergic cells in the hippocampus are traditionally classified as the most important inhibitory INs involved in shaping pyramidal cell activity (Klausberger & Somogyi, 2008). Although convincing evidence indicates that increases in [Ca2+]i in response to somatic stimulation primarily arise from an influx of extracellular Ca2+ (Koester & Sakmann, 2000) into glutamatergic terminals, much less is known about the Ca2+ dynamics in the boutons of hippocampal INs. The importance of measuring Ca2+ responses in single boutons is highlighted by the finding that the amplitude of presynaptic Ca2+ influx is an indicator of the synaptic strength in a heterogeneous population of GABAergic terminals (Kirischuk & Grantyn, 2002). In this paper we show that INs of different phenotypes, which are responsible for specific functions in the hippocampal network, are equipped with axon terminals appropriate for specific functions using variable Ca2+ dynamics, whereas within the same cell type the Ca2+ transients are fairly robust and repeatable. Although other previous studies also detected differences among presynaptic transients of different anatomically distinct IN groups (Karayannis et al., 2010; Lenkey et al., 2015), here we performed more detailed analyses of IN groups, which were not included in the previous comparisons.
The variability of Ca2+ transients among the boutons of IN axons seems lower than dendritic variability
In the various anatomically identified GABAergic INs, no failures of APs were observed, which indicates reliable AP propagation from throughout the soma to the axonal arbour. This observation supports the finding that a supercritical density of Na+ channels in basket cell axons can compensate for the morphological properties of IN axons, ensuring that APs propagate to the distal axon with high reliability (Hu & Jonas, 2014). At the same time, the propagation of APs in IN axons is in contrast to the high variability of AP‐evoked Ca2+ transients that can be observed in dendrites (Maravall et al., 2000; Rozsa et al., 2004; Szabo et al., 2008); the amplitude and shape of the Ca2+ transients repeatedly induced in a given bouton by single pulses or trains varied surprisingly little in our hands. However, in agreement with observations in the boutons of granule (Brenowitz & Regehr, 2007) and pyramidal cells (Koester & Sakmann, 2000), there was relatively high (approximately four‐fold) cell‐to‐cell variability in the amplitude of bouton Ca2+ responses. Differences in the presynaptic Ca2+ transients recorded in neighbouring boutons that are part of the same collateral or that are located on different branches may contribute to the variation in transmission observed at different synapses (Scanziani et al., 1998). The low bouton‐to‐bouton variability we found in our experiments suggests strongly that the amount of endogenous buffer molecules was relatively uniform among boutons.
Differences in the Ca2+ dynamics of boutons between NFS and FS cells
For INs of all three phenotypes, we found that the [Ca2+]i in boutons at rest was within the concentration range (20–100 nm) reported by others for glutamatergic (Maravall et al., 2000) and GABAergic (Rozsa et al., 2004) dendrites. However, our findings in NFS, DFS and PFS INs revealed significant differences in the shape and duration of the Ca2+ transients evoked by somatic stimulation. We observed that the [Ca2+]peak evoked by single pulses or trains of stimulation was much smaller in PFS and DFS cells. In contrast, in CB1+ NFS cells, the [Ca2+]peak that was reached in response to a single AP was much higher, and the relatively high [Ca2+]i that was elicited by single or burst stimulation was maintained for a longer time. The studied neurons contained various amounts of endogenous Ca2+ buffer, but the κE values were highest in FS boutons, which are PV+. The two‐fold difference in κE between NFS and PFS cells (63 vs. 122) cannot account, by itself, for the remarkable differences in their measured [Ca2+]i/AP values (565 vs. 147 nm per AP). Further analysis revealed that in response to single stimulation in NFS INs more Ca2+ enters the bouton than in FS cells. This may be due to various mechanisms: for example, the AP was wider and its decay was longer in NFS than in FS INs, which allows longer opening of Ca2+ channels for the former type. However, a disparity in the number of Ca2+ channels is also conceivable. In response to single AP stimulation, the decay of the boutonal Ca2+ transients was not significantly different among the IN types using OGB‐1. Using five‐AP trains and OGB‐6F, FS cells exhibited highly different decay than NFS cells, suggesting higher potential for the recovery of Ca2+ transients in FS INs. Following burst stimulation, the contribution of the fast‐component was higher (> 80%) than in the case of single AP stimulation in all of the studied INs. Further analysis of the decay revealed that the fast‐component was approximately three times faster in FS cells than in NFS cells. As shown in the example of the single AP‐evoked transients the faster decay did not necessarily indicate more effective removal; the j value was higher for NFS INs. The removal of Ca2+ ions depends on the capacity of the endogenous buffers and the speed of the removal mechanisms. Current models assume that immobile endogenous buffers prolong the recovery so they function as ‘endogenous Ca2+ sources’, whereas mobile buffers can accelerate decay (Matthews et al., 2013). In our analysis, we cannot distinguish the contributions of the mobile and immobile endogenous buffers in the total endogenous buffer capacity. These features of bouton Ca2+ dynamics make FS neurons capable of reliably producing Ca2+ responses at higher frequencies, which is important for IN function in the hippocampus.
Potential functional implications of differential Ca2+ dynamics in INs
The time course and efficacy of transmitter release are determined by the rise time and transient nature of the [Ca2+]i produced by the arrival of the AP at the nerve terminal (Yamada & Zucker, 1992). Because presynaptic Ca2+ signalling plays a decisive role in the facilitation of transmitter release and in short‐term plasticity (Zucker, 1989), the longer duration of the increases in [Ca2+]i observed following burst stimulation in NFS INs is indicative of conditions that favour short‐term facilitation. This phenomenon has been previously described (Atluri & Regehr, 1996; Hefft & Jonas, 2005). We observed that in NFS INs, the [Ca2+]i evoked by APs displayed a longer decay. These INs seem to be primarily primed for the asynchronous release of GABA. Indeed, in the boutons of NFS INs, elevated [Ca2+]i can persist for longer periods and provide the opportunity for subsequent APs to accumulate [Ca2+]i. Higher local [Ca2+]i at the end of a longer train increases the release probability of that particular bouton. The fact that each AP generated in the soma in our experiments was able to invade virtually all varicosities of NFS INs and produce Ca2+ transients suggests that a substantial number of terminals release GABA non‐synaptically into the extrasynaptic space, increasing the ambient concentration of GABA and exerting a non‐synaptic effect (Paton & Vizi, 1969; Vizi et al., 2010) that manifests as a tonic influence on surrounding cells. In this manner, INs are able to tonically activate extrasynaptic high‐affinity GABAA receptors, which outnumber the synaptically located receptors (Nusser et al., 1995). In addition, we conclude that the PFS phenotype of GABAergic INs fits well with the function of these neurons; the Ca2+ dynamics responsible for their GABA release are fast, phasic and less likely to result in the accumulation of [Ca2+]i and are thus able to control the timing of spikes with respect to gamma oscillations in the hippocampus (Buzsaki & Chrobak, 1995). Indeed, Hefft & Jonas (2005) have shown that GABA release from PV+ INs is nearly exclusively synchronous in GABAergic IN‐granule cell synapses. Because NFS INs mainly innervate the dendritic region (Megias et al., 2001) of pyramidal cells, their function is focused on the domain where the incoming excitatory impulses (via receptors on dendritic spines) will be integrated. Network oscillations, which appear at different frequencies, are associated with the encoding, consolidation and retrieval of information (Jadhav et al., 2012). In the awake animal, the firing of different IN types exhibits preferential phase locking that is important for the functional organization of hippocampal circuits (Varga et al., 2012). In our experiments, even the characteristics of presynaptic Ca2+ dynamics were found to differ between NFS, DFS and PFS INs, and these differences might match the different network functions of these cells. Due to these features of GABAergic INs, these neurons play a pivotal role in controlling the activity of pyramidal cells, which are the major players in multiple central nervous system disorders (e.g. schizophrenia, memory deficits, epilepsy). PV+ FS INs, in particular, have been associated with the pathomechanisms of schizophrenia (Behrens & Sejnowski, 2009). These cells represent 5% of all cortical neurons and perisomatically innervate pyramidal cells, and they are involved in the generation of gamma oscillations (Cardin et al., 2009). Our data revealed several cell type‐specific determinants of bouton Ca2+ transients in NFS and FS cells that taken together can effectively shape the presynaptic functioning of these cells and probably contribute to the different positions they possess in hippocampal network operations. Therefore, we hope our findings might facilitate understanding of the cellular mechanisms of related diseases and assist in the development of new drugs for the treatment of these diseases.
Acknowledgements
We are grateful to Dr K. Svoboda and Dr Z. Nusser for comments on the manuscript and Dr Á. Mike for advice. The authors wish to thank the Nikon Microscopy Centre at the Institute of Experimental Medicine.
Abbreviations
- ACSF
artificial cerebrospinal fluid
- AP
action potential
- CB1
cannabinoid 1 receptor
- DFS
dendritic fast‐spiking
- EGTA
ethylene glycol tetraacetic acid
- FS
fast spiking
- IN
interneuron
- NFS
non‐fast spiking
- PFS
perisomatic fast‐spiking
- PV
parvalbumin
- TTX
tetrodotoxin
References
- Aponte, Y. , Bischofberger, J. & Jonas, P. (2008) Efficient Ca2+ buffering in fast‐spiking basket cells of rat hippocampus. J. Physiol., 586, 2061–2075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atluri, P.P. & Regehr, W.G. (1996) Determinants of the time course of facilitation at the granule cell to Purkinje cell synapse. J. Neurosci., 16, 5661–5671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens, M.M. & Sejnowski, T.J. (2009) Does schizophrenia arise from oxidative dysregulation of parvalbumin‐interneurons in the developing cortex? Neuropharmacology, 57, 193–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezaire, M.J. & Soltesz, I. (2013) Quantitative assessment of CA1 local circuits: knowledge base for interneuron‐pyramidal cell connectivity. Hippocampus, 23, 751–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenowitz, S.D. & Regehr, W.G. (2007) Reliability and heterogeneity of calcium signaling at single presynaptic boutons of cerebellar granule cells. J. Neurosci., 27, 7888–7898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki, G. & Chrobak, J.J. (1995) Temporal structure in spatially organized neuronal ensembles: a role for interneuronal networks. Curr. Opin. Neurobiol., 5, 504–510. [DOI] [PubMed] [Google Scholar]
- Cardin, J.A. , Carlen, M. , Meletis, K. , Knoblich, U. , Zhang, F. , Deisseroth, K. , Tsai, L.H. & Moore, C.I. (2009) Driving fast‐spiking cells induces gamma rhythm and controls sensory responses. Nature, 459, 663–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggermann, E. & Jonas, P. (2012) How the ‘slow’ Ca2+ buffer parvalbumin affects transmitter release in nanodomain‐coupling regimes. Nat. Neurosci., 15, 20–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermolyuk, Y.S. , Alder, F.G. , Surges, R. , Pavlov, I.Y. , Timofeeva, Y. , Kullmann, D.M. & Volynski, K.E. (2013) Differential triggering of spontaneous glutamate release by P/Q‐, N‐ and R‐type Ca2+ channels. Nat. Neurosci., 16, 1754–1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freund, T.F. & Buzsaki, G. (1996) Interneurons of the hippocampus. Hippocampus, 6, 347–470. [DOI] [PubMed] [Google Scholar]
- Hefft, S. & Jonas, P. (2005) Asynchronous GABA release generates long‐lasting inhibition at a hippocampal interneuron‐principal neuron synapse. Nat. Neurosci., 8, 1319–1328. [DOI] [PubMed] [Google Scholar]
- Helmchen, F. , Borst, J.G. & Sakmann, B. (1997) Calcium dynamics associated with a single action potential in a CNS presynaptic terminal. Biophys. J ., 72, 1458–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu, H. & Jonas, P. (2014) A supercritical density of Na+ channels ensures fast signaling in GABAergic interneuron axons. Nat. Neurosci., 17, 686–693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson, M.B. & Redman, S.J. (2003) Calcium dynamics, buffering, and buffer saturation in the boutons of dentate granule‐cell axons in the hilus. J. Neurosci., 23, 1612–1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav, S.P. , Kemere, C. , German, P.W. & Frank, L.M. (2012) Awake hippocampal sharp‐wave ripples support spatial memory. Science, 336, 1454–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karayannis, T. , Elfant, D. , Huerta‐Ocampo, I. , Teki, S. , Scott, R.S. , Rusakov, D.A. , Jones, M.V. & Capogna, M. (2010) Slow GABA transient and receptor desensitization shape synaptic responses evoked by hippocampal neurogliaform cells. J. Neurosci., 30, 9898–9909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katona, I. , Sperlagh, B. , Sik, A. , Köfalvi, A. , Vizi, E.S. , Mackie, K. & Freund, T.F. (1999) Presynaptically located CB1 cannabinoid receptors regulate GABA release from axon terminals of specific hippocampal interneurons. J. Neurosci., 19, 4544–4558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirischuk, S. & Grantyn, R. (2002) Inter‐bouton variability of synaptic strength correlates with heterogeneity of presynaptic Ca2+ signals. J. Neurophysiol., 88, 2172–2176. [DOI] [PubMed] [Google Scholar]
- Kisfali, M. , Lőrincz, T. & Vizi, E.S. (2013) Comparison of Ca2+ transients and [Ca2+]i in the dendrites and boutons of non‐fast‐spiking GABAergic hippocampal interneurons using two‐photon laser microscopy and high‐ and low‐affinity dyes. J. Physiol., 591, 5541–5553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausberger, T. (2009) GABAergic interneurons targeting dendrites of pyramidal cells in the CA1 area of the hippocampus. Eur. J. Neuorsci., 30, 947–957. [DOI] [PubMed] [Google Scholar]
- Klausberger, T. & Somogyi, P. (2008) Neuronal diversity and temporal dynamics: the unity of hippocampal circuit operations. Science, 321, 53–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koester, H.J. & Sakmann, B. (2000) Calcium dynamics associated with action potentials in single nerve terminals of pyramidal cells in layer 2/3 of the young rat neocortex. J. Physiol., 529, 625–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenkey, N. , Kirizs, T. , Holderith, N. , Mate, Z. , Szabo, G. , Vizi, E.S. , Hajos, N. & Nusser, Z. (2015) Tonic endocannabinoid‐mediated modulation of GABA release is independent of the CB1 content of axon terminals. Nat. Commun., 6, 6557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malgaroli, A. , Milani, D. , Meldolesi, J. & Pozzan, T. (1987) Fura‐2 measurement of cytosolic free Ca2+ in monolayers and suspensions of various types of animal cells. J. Cell Biol., 105, 2145–2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maravall, M. , Mainen, Z.F. , Sabatini, B.L. & Svoboda, K. (2000) Estimating intracellular calcium concentrations and buffering without wavelength ratioing. Biophys. J ., 78, 2655–2667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews, E.A. , Schoch, S. & Dietrich, D. (2013) Tuning local calcium availability: cell‐type‐specific immobile calcium buffer capacity in hippocampal neurons. J. Neurosci., 33, 14431–14445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megias, M. , Emri, Z. , Freund, T.F. & Gulyas, A.I. (2001) Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience, 102, 527–540. [DOI] [PubMed] [Google Scholar]
- Neher, E. & Augustine, G.J. (1992) Calcium gradients and buffers in bovine chromaffin cells. J. Physiol., 450, 273–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusser, Z. , Roberts, J.D. , Baude, A. , Richards, J.G. & Somogyi, P. (1995) Relative densities of synaptic and extrasynaptic GABAA receptors on cerebellar granule cells as determined by a quantitative immunogold method. J. Neurosci., 15, 2948–2960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton, W.D. & Vizi, E.S. (1969) The inhibitory action of noradrenaline and adrenaline on acetylcholine output by guinea‐pig ileum longitudinal muscle strip. Br. J. Pharmacol., 35, 10–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rozsa, B. , Zelles, T. , Vizi, E.S. & Lendvai, B. (2004) Distance‐dependent scaling of calcium transients evoked by backpropagating spikes and synaptic activity in dendrites of hippocampal interneurons. J. Neurosci., 24, 661–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatini, B.L. , Oertner, T.G. & Svoboda, K. (2002) The life cycle of Ca2+ ions in dendritic spines. Neuron, 33, 439–452. [DOI] [PubMed] [Google Scholar]
- Scanziani, M. , Gahwiler, B.H. & Charpak, S. (1998) Target cell‐specific modulation of transmitter release at terminals from a single axon. Proc. Natl. Acad. Sci. USA, 95, 12004–12009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Somogyi, P. (1977) A specific ‘axo‐axonal’ interneuron in the visual cortex of the rat. Brain Res., 136, 345–350. [DOI] [PubMed] [Google Scholar]
- Szabo, S.I. , Zelles, T. , Vizi, E.S. & Lendvai, B. (2008) The effect of nicotine on spiking activity and Ca2+ dynamics of dendritic spines in rat CA1 pyramidal neurons. Hippocampus, 18, 376–385. [DOI] [PubMed] [Google Scholar]
- Varga, C. , Golshani, P. & Soltesz, I. (2012) Frequency‐invariant temporal ordering of interneuronal discharges during hippocampal oscillations in awake mice. Proc. Natl. Acad. Sci. USA, 109, E2726–E2734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vizi, E.S. , Fekete, A. , Karoly, R. & Mike, A. (2010) Non‐synaptic receptors and transporters involved in brain functions and targets of drug treatment. Br. J. Pharmacol., 160, 785–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada, W.M. & Zucker, R.S. (1992) Time course of transmitter release calculated from simulations of a calcium diffusion model. Biophys. J., 61, 671–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker, R.S. (1989) Short‐term synaptic plasticity. Annu. Rev. Neurosci., 12, 13–31. [DOI] [PubMed] [Google Scholar]
- Zucker, R.S. & Regehr, W.G. (2002) Short‐term synaptic plasticity. Annu. Rev. Physiol., 64, 355–405. [DOI] [PubMed] [Google Scholar]


