Sphingolipids contribute to acetic acid resistance in Zygosaccharomyces bailii

ABSTRACT

Lignocellulosic raw material plays a crucial role in the development of sustainable processes for the production of fuels and chemicals. Weak acids such as acetic acid and formic acid are troublesome inhibitors restricting efficient microbial conversion of the biomass to desired products. To improve our understanding of weak acid inhibition and to identify engineering strategies to reduce acetic acid toxicity, the highly acetic‐acid‐tolerant yeast Zygosaccharomyces bailii was studied. The impact of acetic acid membrane permeability on acetic acid tolerance in Z. bailii was investigated with particular focus on how the previously demonstrated high sphingolipid content in the plasma membrane influences acetic acid tolerance and membrane permeability. Through molecular dynamics simulations, we concluded that membranes with a high content of sphingolipids are thicker and more dense, increasing the free energy barrier for the permeation of acetic acid through the membrane. Z. bailii cultured with the drug myriocin, known to decrease cellular sphingo­lipid levels, exhibited significant growth inhibition in the presence of acetic acid, while growth in medium without acetic acid was unaffected by the myriocin addition. Furthermore, following an acetic acid pulse, the intracellular pH decreased more in myriocin‐treated cells than in control cells. This indicates a higher inflow rate of acetic acid and confirms that the reduction in growth of cells cultured with myriocin in the medium with acetic acid was due to an increase in membrane permeability, thereby demonstrating the importance of a high fraction of sphingolipids in the membrane of Z. bailii to facilitate acetic acid resistance; a property potentially transferable to desired production organisms suffering from weak acid stress. Biotechnol. Bioeng. 2016;113: 744–753. © 2015 The Authors. Biotechnology and Bioengineering Published by Wiley Periodicals, Inc.

Introduction

The yeast Zygosaccharomyces bailii is considered to be one of the most troublesome food spoilage organisms due to its ability to withstand food preservatives (Zuehlke et al., 2013). Its toler­ance to weak organic acids has been extensively studied, as reviewed by (Piper et al., 2001), although the fundamental mechanisms underlying its exceptional resistance have yet to be elucidated. Apart from the development of methods to prevent food spoilage, understanding and harnessing the mechanisms behind Z. bailii's robustness is of the utmost importance if we are to identify the characteristics that can improve the performance of other industrial microorganisms grown under acid stress (Dato et al., 2010). For example, organic acids such as acetic acid and formic acid are released during the pretreatment of lignocellulosic raw material, prior to the production of fuels and chemicals in a biorefinery (Koppram et al., 2014). These acids represent a major obstacle to the fermenting microorganism, commonly Saccharomyces cerevisiae (Parachin et al., 2011). Inhibition occurs mainly by the undissociated form of weak acids, due to their ability to enter the cell in an uncontrolled fashion by passive diffusion across the plasma membrane (Warth, 1989). If the mechanisms and the genetic bases underlying the high tolerance of Z. bailii to organic acids were to be understood, it might be possible to transfer key characteristics to S. cerevisiae, or to other production organisms, through genetic engineering.

The high acetic acid tolerance of Z. bailii has previously been linked to three different factors. First, co‐consumption of glucose and acetic acid gives Z. bailii the ability to efficiently remove acetic acid from the intracellular environment (Sousa et al., 1996). This ability is unique, as acetic acid consumption is repressed in the presence of glucose in most other yeast species (Rodrigues et al., 2012). Second, Z. bailii exhibits population heterogeneity with a small subpopulation of cells exhibiting lower intracellular pH, which limits the acetic acid stress in these cells by reducing the accumulation of intracellular acetic acid (Stratford et al., 2013). Third, it has low acetic acid membrane permeability, as indicated by experiments in which Z. bailii retained its intracellular pH better than S. cerevisiae during short‐term (Arneborg et al., 2000) and long‐term (Fernandes et al., 1999) exposure to acetic acid. No direct comparison has been made of the acetic acid membrane permeability in Z. bailii and S. cerevisiae, but measurements of propionic acid uptake have shown that it is more than ten times faster in S. cerevisiae than in Z. bailii (Warth, 1989). In our previous study, we investigated the plasma membrane lipid profile of S. cerevisiae and Z. bailii, showing a strong difference in lipid profile between the two yeasts, with sphingolipids being several times higher in Z. bailii than in S. cerevisiae, supporting a potential difference in membrane permeability (Lindberg et al., 2013). In addition, Z. bailii showed a unique ability to remodel the composition of its plasma membrane upon acetic acid stress, so as to greatly increase the fraction of sphingolipids (two to nine times increase depending on sphingolipid class), at the expense of glycerophospholipids (overall level reduced by half and phosphatidyl inositol which is required for sphingolipid synthesis increased from 40 to 88% of the total glycerophospholipids in the membrane).

Based on the qualitative evidence discussed in the above section, we formulated the model illustrated in Figure 1, to provide a quantitative theoretical description of the effect of the rate of acetic acid translocation across the plasma membrane on the intracellular concentration of acetic acid in Z. bailii. Intracellular pH is the first critical determinant of intracellular acetic acid concentration (Stratford et al., 2013). Upon exposure of the cells to the acid, undissociated acetic acid will diffuse across the membrane until equilibrium is reached between the intracellular and extracellular sides of the membrane. The difference in pH between the intracellular and extracellular spaces will determine the difference in total concentration of the acid, whereby the commonly found higher intracellular pH will lead to an accumulation of acetic acid inside the cell. To counteract accumulation of acetic acid, Z. bailii has a great advantage over other yeasts, namely the ability to consume acetic acid (Fig. 1, v_Cons) in the presence of other carbon sources (Sousa et al., 1996). Z. bailii has also been shown to have proteins that remove acetic acid by active extrusion of anions and protons (Fig. 1, v_Ext), but their significance in this context is unclear. Entry of acetic acid into the cell occurs by passive diffusion across the plasma membrane (Fig. 1, v_Diff) and if required by a facilitated uptake mechanism (Fig. 1, v_Uptake) probably induced to allow faster acetic acid consumption when diffusion into the cell is not sufficiently high (Sousa et al., 1996, 1998). Accumulation of intracellular acetic acid and consequently acetic acid stress can thereby be avoided when v_Diff and, if relevant, v_Uptake is less than the sum of v_Cons and v_Ext. Indeed, a comparison of the acetic acid uptake rate (v_Diff and v_Uptake) measured by Stratford et al. (2013) and the acetic acid consumption rate (v_Cons) determined in our previous study (Lindberg et al., 2013) reveals that these rates are of the same order of magnitude, supporting our hypothesis that the diffusion rate is important in intracellular acetic acid accumulation and, hence, tolerance.

Figure 1.

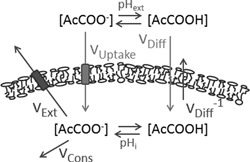
Proposed model of the mechanisms determining intracellular acetic acid concentration in Z. bailii. The pH determines the distribution between the undissociated and the dissociated form of acetic acid, based on the pKa value. The undissociated form enters the cell through passive diffusion (v_Diff) across the membrane, until equilibrium is reached between the two sides of the membrane. The dissociated form can also be taken up by the cell through a facilitated transport system (v_Uptake) (Sousa et al., 1996, 1998). Intracellular acetic acid is removed through consumption of the anion (v_Cons) (Sousa et al., 1996). Proteins removing acetic acid by active extrusion of anions and protons (v_Ext) exist in Z. bailii, but their significance in this context is unclear (Piper et al., 2001). The overall sum of all these rates and the intracellular pH determines the acetic acid concentration in the cell.

In this study, we hypo­the­size that the high fraction of sphingolipids in Z. bailii, and the membrane remodeling toward more sphingolipids upon acetic acid exposure could be linked to reduced permeability to acetic acid. In the light of this information, we have here investigated the importance of a high fraction of sphingolipids in the plasma membrane of Z. bailii in maintaining low acetic acid mem­brane permeability and high acetic acid tolerance by combining in silico molecular dynamics simulations with in vivo techniques.

Materials and Methods

In Silico Membrane Construction

Model membranes were constructed and subjected to molecular dynamics simulations to study their structural and dynamic properties. The membranes were made using inositol phosphoryl­ceramide (IPC) as the representative sphingolipid, 1,2‐dioleoyl‐sn‐glycero‐3‐phosphocholine (DOPC) and 1‐palmitoyl‐2‐oleoyl‐sn‐glycero‐3‐phospho‐(1′‐myo‐inositol) (POPI) as representatives of glycerophospholipids, and ergosterol. Seven membrane were simulated, with the sphingo­lipid content varying from 10 to 60% by varying the glycerophospholipid content correspondingly while keeping the ergosterol content constant at 15%, as outlined in Table I.

Table I.

Composition of simulated model membranes. 

Membrane	IPC a (%)	DOPC b (%)	POPI c (%)	ERG d (%)
# 1	10.0	37.5	37.5	15.0
# 2	15.0	35.0	35.0	15.0
# 3	20.0	32.5	32.5	15.0
# 4	30.0	27.5	27.5	15.0
# 5	40.0	22.5	22.5	15.0
# 6	50.0	17.5	17.5	15.0
# 7	60.0	12.5	12.5	15.0

^aInositolphosphoryl ceramide.

^b1,2‐dioleoyl‐sn‐glycero‐3‐phosphocholine.

^c1‐palmitoyl‐2‐oleoyl‐sn‐glycero‐3‐phospho‐(1'‐myo‐inositol).

^dErgosterol.

All membranes consisted of a total amount of 128 lipid molecules; 64 in each leaflet. The leaflets were symmetric with respect to lipid content. The Slipid force field (Jämbeck and Lyubartsev, 2012a, 2012b, 2013) was used to describe all lipids. The DOPC force field was already available (Jämbeck and Lyubartsev, 2012b), and force fields for IPC, POPI, and ergosterol were developed based on established protocols (Jämbeck and Lyubartsev, 2012a, 2012b, 2013). Bonded and van der Waals parameters were taken from the CHARMM lipid force field (Klauda et al., 2010), and the charges were derived as follows. The charges on the lipid tails were taken from the Slipid force field, as the alkyl chains of all lipids have the same charges. The charges on the inositol/phosphate head group and the ceramide backbone of IPC were determined by calculations using the restrained electro­static potential algorithm (RESPA) (Bayly et al., 1993) in which the conformations for the inositol/phosphate head group were taken from the CHARMM membrane builder (Wu et al., 2014a), while the conformations for the ceramide backbone were generated through a LowModeMD conformational search (Labute, 2010) with the MOE software (Chemical Computing Group Inc., 2015). The electrostatic potential (ESP) was then calculated at the B3LYP/cc‐pVTZ level of theory (Becke, 1993; Kendall et al., 1992; Lee et al., 1988), using a polarized continuum model (IEF‐PCM) of water (Tomasi et al., 1999) to mimic the effect of solvent. Finally, the charges were fitted to the ESP using the RESPA method. The charges on the ergosterol molecule were determined using RESPA on a single conformation optimized at the B3LYP/cc‐pVTZ level. The ESP was calculated at the B3LYP/cc‐pVTZ level of theory using the IEF‐PCM of hexa­decane to mimic the interior of the membrane. All quantum mechanical calculations were per­formed with the Gaussian09 software (Frisch et al., 2009). All force fields developed herein can be downloaded from the Supporting information, Dataset S1.

All bilayers were solvated by 5120 TIP3P water (Jorgensen et al., 1983), and neutralized with Na⁺ ions. Initial bilayer structures were assembled using the CHARMM Membrane Builder (Wu et al., 2014a). Unfortunately, this tool does not support the building of IPC, so all the bilayers were made of POPI instead of IPC and were, then, subsequently replaced by IPC using an in‐house script.

Force fields created for the IPC, POPI and ergosterol molecules are provided in supporting information in Gromacs file format.

In Silico Simulation of Membrane Properties

Model membranes were simulated with molecular dynamics methodology using the Gromacs software (version 4.6) (Hess et al., 2008). The membranes were equilibrated for 100–200 ns in the NPT ensemble (constant pressure and temperature), followed by a 100 ns production run where data were collected every 10 ps. The time step was 2 fs and all covalent bonds were constrained with the LINCS algorithm (Hess et al., 1997). Water molecules were constrained with the SETTLE algorithm (Miyamoto and Kollman, 1992). The pressure was maintained at 1 atm using a Parrinello–Rahman barostat (Parrinello and Rahman, 1981) with a 10 ps coupling constant and a compressibility of 4.5 × 10⁻⁵ bar⁻¹. The pressure in the membrane plane was independent of the pressure in the membrane normal. The temperature was kept at 298 K using a Nosé–Hover thermostat (Nosé, 1984) with a 0.5 ps time constant. Electrostatic interactions were treated with the particle‐mesh Ewald summation (Darden et al., 1993) with a 1 nm real‐space cut‐off, and van der Waals interactions were subjected to a 1 nm cut‐off with a long‐range continuum correction (Allen, 1987).

Membrane thickness was measured as the average distance between the phosphate groups in the different leaflets. Lipid tail order was calculated from the deuterium order parameter (S _CD) according to Equation (1):

$$S_{\text{CD}}=\frac{1}{2}〈3{\cos }^2\theta -1〉$$ (1)

where θ is the angle between a carbon–deuterium bond in the given acyl chain and bilayer normal, and the bracket indicates an average over the MD simulation. Averaging over identical molecules was also performed.

In Silico Simulation of Acetic Acid Membrane Permeability

The potential of mean force (PMF) of undissociated acetic acid along the membrane normal was calculated with umbrella sampling simulations, as described below (Torrie and Valleau, 1977). These calculations give the free energy of transferring acetic acid to different depths in the membrane.

The acetic acid molecule was described by the general Amber force field (Wang et al., 2004) with AM1‐BCC charges (Jakalian et al., 2002). Two acetic acid molecules were inserted at specific distances from the center of the bilayer. For the 20% IPC system, acetic acid was inserted at distances between 0 and 3.6 nm from the bilayer center, and for the 40% IPC system between 0 and 4.3 nm. The two acetic acid molecules were always placed in different leaflets, separated by 3.6 or 4.3 nm along the membrane normal, and by at least 0.5 nm in the membrane plane. The position in the membrane plane was randomized. Two independent sets of simulations were initiated by placing the acetic acid molecules at different positions in the membrane plane. Initially, the acetic acid molecules were assumed not to interact with the surrounding membrane, and the interactions were turned on gradually during a 5 ns simulation. This procedure allows the membrane to relax naturally around the acetic acid molecule. During these simulations, the two acetic acid molecules were fixed at their initial positions. The simulation parameters were otherwise identical to the procedure described above.

The systems prepared using this procedure were then subjected to umbrella sampling with the PLUMED plug‐in (Tribello et al., 2014) (version 2.1) of Gromacs (Hess et al., 2008). The distance between the acetic acid molecule and the center of the bilayer was restrained using a harmonic spring with a 1000 kJ mol⁻¹ nm⁻² force constant, and the instantaneous distance was recorded every 10 ps. The simulations with acetic acid molecules at different restrained distances were coupled, and exchange between neighbors was attempted every 4 ps to improve sampling (Neale et al., 2013). The umbrella sampling simulations were 30 ns in length at each point (simulation parameters as described above), and data from the initial 5 ns were throughout discarded as equilibration. The records of the instantaneous distances from the different simulations were combined into a PMF with WHAM (weighted histogram analysis method) (Grossfield; Kumar et al., 1992). Records from the acetic acid molecules in both leaflets, as well as the two independent simulations, were combined to give a single WHAM estimate. Thus, the WHAM estimate was based on a combined 100 ns sampling. The uncertainty in the PMF was estimated by block averaging with 20 blocks of 5 ns each.

The permeability coefficient, P, of acetic acid upon transport from the water phase to the center of the bilayer was calculated using the expression in Equation (2) (Marrink and Berendsen, 1994):

$$1/P=\int \frac{\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{\Delta }G(z)/RT)}{D(z)}\mathrm{d}z$$ (2)

where ΔG(z) is the free energy of transferring the acetic acid to depth z in the membrane, calculated by umbrella sampling, D(z) is the local diffusion along the membrane normal at depth z, R is the gas constant, and T is the absolute temperature. The integration runs from the water phase to the center of the bilayer.

An approximate estimate of the diffusion was calculated from the expression in Equation (3) (Issack and Peslherbe, 2015; Woolf and Roux, 1994):

$$D(z=〈z〉)=\frac{\mathrm{v}\mathrm{a}\mathrm{r}(z)}{{\tau }_z}$$ (3)

where <z> is the center of restraint in the umbrella sampling simulations, var(z) is the variance of z during the simulation, and τ_z is the correlation time of the time series of z. The largest error in the estimation of D(z) lies in the calculation of τ_z (Hummer, 2005; Issack and Peslherbe, 2015). To reduce the noise in the estimate of D(z), diffusion was estimated from the full simulation without any block averaging, and thus the uncertainty was calculated only from the series in the two leaflets. The uncertainty in P was estimated by computing the standard error from the two independent series of simulations.

Strains and Cultivation Media

Z. bailii strain CBS 7555 (Centraalbureau voor Schimmelcultures (CBS) Fungal Biodiversity Centre strain collection, the Netherlands) was used in this study. Cells were cultured in mineral medium (20 g L⁻¹ glucose, 5 g L⁻¹ (NH₄)₂SO₄, 0.5 g L⁻¹ MgSO₄× 7H₂O, 3 g L⁻¹ KH₂PO₄, 1 mL L⁻¹ vitamin solution, 1 mL L⁻¹ trace element solution). Vitamin solution and trace element solution were prepared as described previously (Verduyn et al., 1992). Potassium hydrogen phthalate buffer, 100 mM, was used to maintain the culture at pH 5, except in the case of the cultivation medium supplemented with L‐lactic acid, which had to be adjusted to pH 4 to increase the fraction of inhibitory undissociated acid in the total supplemented acid. It was not possible to achieve an inhibitory concentration of undissociated acid at pH 5 due to the low solubility of l‐lactic acid.

Media Supplements

The effect of myriocin on cell growth was evaluated at 0.8, 1.2, and 1.6 μM myriocin (Mycelia sterilia, Sigma–Aldrich). A 1 mM myriocin stock solution prepared in 40% ethanol was used. Acetic acid, formic acid, l‐lactic acid, sorbic acid, and benzoic acid were added to the medium as concentrated stock solutions adjusted to pH 5 with KOH, except for the l‐lactic acid stock solution, which was adjusted to pH 4.

Inoculum

Inoculum was prepared in Erlenmeyer flasks where the culture occupied a maximum of 10% of the flask volume. Cultures were grown under continuous shaking at 180 rpm at 30°C overnight. Exponentially growing cells were harvested by centrifugation at 3,000 g for 3 min at room temperature, resuspended in fresh medium and added to the Erlenmeyer flask cultures or microscale cultures at an initial optical density at 600 nm (OD₆₀₀) of 0.2.

Screening of Cell Growth

Cell growth was automatically monitored at 30°C in 150 μL aerobic microscale cultures using Bioscreen C MBR equipment (Oy Growth Curves Ab, Ltd, Finland) with 5–10 replicates per experimental condition to evaluate the effect of weak acids and myriocin. The cultures were shaken contin­uously, and cell density was measured optically every 15 min using a wideband 450–580 nm wavelength filter. Measured cell density values were converted to equivalent OD₆₀₀ values using Equation (4).

$${\mathrm{O}\mathrm{D}}_{600}=\frac{{\mathrm{O}\mathrm{D}}_{\mathrm{w}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{b}\mathrm{a}\mathrm{n}\mathrm{d}450-580}}{\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{h}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}\left(\mathrm{c}\mathrm{m}\right)\times 1.32}$$ (4)

The nonlinear correlation between optical density and cell density at high cell concentrations was corrected for using Equation (5) (Warringer and Blomberg, 2003).

$${\mathrm{O}\mathrm{D}}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}={\mathrm{O}\mathrm{D}}_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}+{\mathrm{O}\mathrm{D}}_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}^2\times 0.449+{\mathrm{O}\mathrm{D}}_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}^3\times 0.191$$ (5)

Intracellular pH Response After Acetic Acid Pulse

Cells were cultured in triplicate in 250 mL baffled Erlenmeyer flasks with 25 mL culture volume. To evaluate the effect of myriocin, it was added to the cell suspension to a final concentration of 1.6 μM at the start of cultivation, and the intracellular pH of myriocin treated cells was compared to that in control cultures with no added myriocin. Cells were harvested at an OD₆₀₀ of 2 by centrifugation at 21,100 g for 3 min at room temperature.

Carboxyfluorescein diacetate succinimidyl ester (CFDA‐SE) (Vybrant CFDA SE Cell Tracer Kit, Life Technologies, Thermo Fisher Scientific) was used as a probe to detect changes in intracellular pH as an indirect measure of acetic acid inflow. The non‐fluorescent CFDA‐SE enters the cell by passive diffusion, where a highly fluorescent molecule is formed when intracellular esterases cleave off the acetate groups. The dye is retained within the cell by conjugation with intracellular amines. A stock solution of 10 mM CFDA‐SE was prepared in DMSO, aliquoted under nitrogen gas, and stored at −20°C. A 20 μM CFDA‐SE solution was prepared in McIlvaine buffer (0.2 M K₂HPO₄/0.1 M citric acid) at pH 7 immediately before use. Harvested cells were resuspended in 1 mL CFDA‐SE solution to obtain an OD₆₀₀ of 0.2 and then incubated at 30°C, 800 rpm for 20 min. Stained cells were centrifuged at 21,100 g for 3 min at room temperature, and then diluted tenfold with McIlvaine buffer at pH 5.

Intracellular pH of cells was analyzed using a Guava easyCyte 8HT flow cytometry system (Merck Millipore) equipped with a 75 mW, 488 nm wavelength excitation laser. The emitted fluorescence was measured using a green 525/30 nm bandpass filter. As myriocin‐treated cells exhibited a higher staining efficiency, variations in dye loading were minimized by considering only relative changes in fluorescence between cell populations with comparable staining efficiency. More specifically, the reduction in green 525 nm fluorescence was detected 30 s after pulsing the stained cells with 50, 100, and 200 mM acetic acid (final concentration), and compared to the signal from cells not subjected to an acetic acid pulse. To evaluate the possible influence of staining efficiency on the reduction in green fluorescence, cells with 30–40% reduced staining efficiency were obtained using CFDA‐SE buffer solution prepared two hours before use, containing a lower amount of CFDA‐SE due to hydrolysis of the probe in the aqueous environment. Weaker stained cells only affected the percentage of 525 nm fluorescence reduction after the 50 mM acetic acid pulse to a minor extent, compared to the more strongly stained cells, indicating that the staining efficiency did not influence the reduction in pH after the acetic acid pulse (data not shown). The small amount of background fluorescence detected from non‐stained cells was subtracted from each measurement.

Results and Discussion

In this study, in silico techniques were used to investigate how sphingolipids affect the physicochemical properties of the membrane and the acetic acid membrane permeability. In vivo investigations were also performed to evaluate the effect of reduced sphingolipid content on acetic acid tolerance and acetic acid membrane permeability in Z. bailii.

A Higher Fraction of Sphingolipids Gives Thicker and More Dense Membranes

To understand how sphingolipids influence the physicochemical properties of the plasma membrane, seven different model membranes were simulated in silico (Table I). As it is not possible to recreate an exact copy of the yeast membrane, we constructed simplified membranes composed of IPC as the only sphingolipid, and DOPC and POPI as the glycerophospholipids, together with ergosterol. The choice and composition of lipids reflects the characteristics of Z. bailii and S. cerevisiae membranes in terms of composition, chain length, and bond saturation (Lindberg et al., 2013). However, absolute quantification of the lipids were not possible but by looking at the trends, and compare common levels in a previous study (Klose et al., 2012), the model membranes containing 10–20% sphingolipids were designed to represent the plasma membrane lipid composition in S. cerevisiae, while the membrane with 40–60% IPC better corres­ponds to the membrane composition of Z. bailii cultured with acetic acid.

The simulations predicted that a higher fraction of sphingolipids would give thicker and more dense membranes, i.e., a 26% increase in bilayer thickness and a 17% decrease in the area occupied by the simulated membrane, when comparing membranes with 10% and 60% sphingolipids (Fig. 2A). An increase in lipid tail order, which is a measure of the rigidity of the carbon bonds in the fatty acyl chains, provided further evidence of the condensation of membranes containing a higher fraction of sphingolipids. The lipid tail order increased on average by 55% for the saturated acyl chain of POPI, when the sphingolipid fraction was increased from 10% to 60% (Fig. 2B). Similar increases in lipid tail order were also observed for the DOPC and IPC lipid tails (Fig. S1A–F). Sphingolipids function in creating thicker and more dense bilayers has previously been predicted based on the molecular structure of sphingolipids, due specifically to the long, saturated acyl chain, in combination with amide carbonyls and hydroxyls capable of hydrogen bonding (Levine et al., 2000). However, in the present study, we performed simulations that allowed us to directly study the structure and dynamics of the membranes at atomic resolution, giving us additional information. For instance, the condensation effect can only be accurately predicted by observing interactions between lipids in the mem­brane. Similar modeling approaches have been used previously to study a range of phenomena such as the role of ergosterol in mitigating the effect of ethanol on the membrane structure (Dickey et al., 2009), the effect of cholesterol on the permeability of hypericin derivatives (Eriksson and Eriksson, 2011), and the orientation of different phosphoinositides (Wu et al., 2014b). A snapshot from the simulation of a membrane with 40% sphingolipids visualizes the dynamic interaction that occurs between lipids in the membrane (Fig. 3). Upon studying the very long fatty acyl chain on the sphingolipid molecule more closely, the simulations predicted the tail to be positioned in many positions in‐between protruding into the opposite leaflet, or bending so as to occupy space between the two leaflets.

Figure 2.

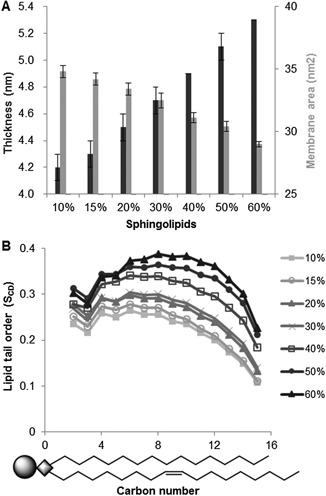
In silico membrane simulations predicting the properties of membranes containing 10% to 60% of the sphingolipid class IPC, 15% ergosterol and equal distributions of the glycerophospholipids DOPC and POPI. The results were obtained with a 100 ns simulation A. Simulated membrane thickness and the area occupied by the simulated membrane. The graph shows the mean over one simulation ± standard deviation. B. Mean lipid tail order for a saturated sn‐1 chain of POPI. Schematic drawing of POPI illustrates the carbon number position in the lipid molecule.

Figure 3.

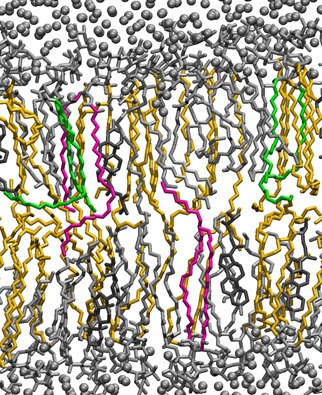
Snapshot of a simulated membrane with 40% sphingolipids. Water molecules are shown as gray spheres. The lipids are shown as lines and are colored according to lipid type; ergosterol in dark gray, POPI, and DOPC in silver and IPC in yellow. A few IPC lipids are colored green and pink. The green IPC lipids have long folded tails that lie between the two leaflets, while the pink IPC lipid tails protrude into the opposite leaflet. Only a slab of 0.1 nm of the membrane is visualized for clarity.

A Higher Fraction of Sphingolipids Reduces the Permeability Coefficient of Acetic Acid

Umbrella sampling was used to quantify the free energy barrier for the transport of undissociated acetic acid through the membrane. Simulations were performed at concentrations 20% and 40% of sphingolipids in the membranes, respectively. In the membrane with 20% sphingolipids, the free energy barrier for transport of undissociated acetic acid from the water phase to the middle of the membrane was approximately 15 kJ/mol, and in the membrane with 40% sphingolipids, approximately 20 kJ/mol, i.e., a difference of approximately 5 kJ/mol. Although there is a sizeable uncertainty in the PMF, as can be seen in Figure 4, it is clear that the difference between the PMFs is large at the center of the membrane. A two‐sided ­t‐test gave a P‐value of 0.025, indicating that the difference is statistically significant at the 95% confidence level.

Figure 4.

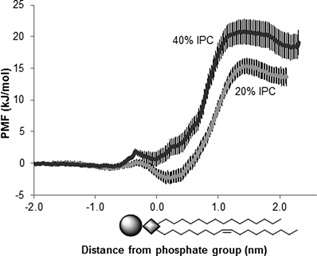
In silico simulations of membrane permeability to acetic acid with 20% and 40% sphingolipids. The graphs show the potential of mean force (PMF) of transferring the acetic acid over the membrane. Each trace represents the mean of 20 blocks from two simulations and two independent positions of the acetic acid molecules. The error bars indicate the standard deviation. Schematic drawing of POPI represents the lipid bilayer.

Using solubility‐diffusion theory (Marrink and Berendsen, 1994), we calculated a rough estimate of the permeability coefficient, P. The local diffusion coefficient, D(z), was particularly difficult to estimate in the 40% sphingolipid simulations due to the very dense bilayer, however, as the free energy is the dominating factor, the noise in D(z) should have only a minor effect on the relative value of P. The permeability coefficient of acetic acid was found to be 5.4 ± 1.0 × 10⁻⁹ cm s⁻¹ in the membrane with 20% sphingolipids, and 4.1 ± 1.9 × 10⁻¹⁰ cm s⁻¹ in the membrane with 40% sphingolipids, a reduction by an order of magnitude. A two‐side ­t­‐test gave a P‐value of 0.035, indicating that the difference is statistically significant at the 95% confidence level. This suggests that a higher level of sphingolipids in the membrane reduces the acetic acid membrane permeability.

Inhibition of Sphingolipid Synthesis Reduces Acetic Acid Tolerance

To investigate a possible correlation between a high sphingolipid fraction in Z. bailii and its high tolerance to acetic acid, sphingolipid synthesis was decreased by in vivo treatment with the drug myriocin, which binds irreversibly to serine palmitoyltransferase, inhibiting the first step of sphingolipid synthesis (Wadsworth et al., 2013). The use of myriocin is well established, and previous studies have demonstrated its ability to decrease the fraction of sphingolipids in various cell systems, including yeast (Breslow et al., 2010; Huang et al., 2012; Shimobayashi et al., 2013).

The addition of up to 1.6 μM myriocin in the absence of acetic acid had little or no effect on the growth rate of Z. bailii in mineral medium (Fig. 5A). However, in the presence of 200 to 400 mM acetic acid, the specific growth rate of cells was significantly reduced. Myriocin addition had a detrimental effect on cell growth at these acetic acid concentrations, and the effect increased with concentration. This demonstrates the requirement of a high sphingolipid fraction in the membrane to deal with acetic acid stress.

Figure 5.

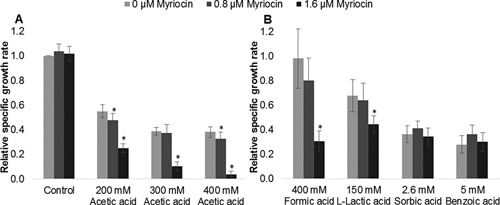
Growth of Z. bailii in the presence of acetic acid, formic acid, sorbic acid, benzoic acid (pH 5) and l‐lactic acid (pH 4) at 0–1.6 μM myriocin. The results are expressed as relative growth rate to the growth rate of cells without acid and myriocin added. The acid concentrations were chosen to give approximately 70% growth inhibition with the specific acid and 1.6 μM myriocin. The results were calculated from five to ten biological replicates. The bars represent the mean ± standard deviation. *Significant decrease compared to no myriocin addition, according to the t‐test (P < 0.05).

Inhibition of Sphingolipid Synthesis Reduces Tolerance to Other Weak Organic Acids

Passive diffusion across the plasma membrane is a major entry route for many weak organic acids (Piper et al., 2001). To investigate whether the high fraction of sphingolipids in Z. bailii is also involved in the mechanisms offering resistance to other weak organic acids, the effect of myriocin on the growth of Z. bailii in the presence of formic acid, l‐lactic acid, sorbic acid, and benzoic acid was investigated. The acid concentrations were chosen so as to give approximately 70% growth inhibition with each acid together with 1.6 μM myriocin. The chemical properties and experimental conditions are given in Table II. Cells cultured with myriocin and either formic acid or l‐lactic acid showed a reduction in growth comparable to that in the case of acetic acid (Figure 5B). However, cells cultured with myriocin and either sorbic acid or benzoic acid showed no reduction in growth (Fig. 5B). This apparent difference in the effect of myriocin in the presence of different weak acids could be explained by their difference in hydrophobicity, commonly expressed as log P, the partition coefficient between octanol and water (Table II). Higher hydrophobicity facilitates diffusion across the membrane, resulting in a higher diffusion rate. Formic acid and l‐lactic acid have relatively similar values of hydrophobicity to acetic acid, whereas sorbic acid and benzoic acid are both much more hydrophobic. Sorbic acid and benzoic acid were indeed found to inhibit cell growth at concentrations two orders of magnitude lower than acetic acid, formic acid, and l‐lactic acid. Therefore, the reduction of sphingolipid content by myriocin probably causes a larger relative increase in the diffusion rate (v_Diff in Fig. 1) of acetic acid, formic acid, and l‐lactic acid, which leads to intracellular accumulation of these acids. Sorbic acid and benzoic acid, on the other hand, already have a high diffusion rate and the reduction in sphingolipids caused by myriocin is probably not large enough to influence the overall balance of rates determining the intracellular acid concentration. Although it cannot be excluded that a higher myriocin concentration, creating larger membrane rearrangements, would have affected sorbic acid and benzoic acid tolerance in a comparable way as it did for the less hydrophobic weak acids. Tolerance of Z. bailii and S. cerevisiae to weak acids with different hydrophobicity has recently been investigated, showing that Z. bailii was approximately three times more tolerant than S. cerevisiae to the majority of the investigated acids independently of their degree of hydrophobicity (Stratford et al., 2013). The authors argued that if membrane permeability would have been a resistance mechanism of Z. bailii, there should be a larger difference in tolerance between the two yeasts to the more hydrophobic acids, and therefore rejected membrane permeability as a factor contributing to its tolerance. Taking into account our findings, we do not consider that the data presented by Stratford et al. rejects an involvement of membrane permeability in acetic acid tolerance, since for molecules with higher hydrophobicity, the inflow rate is already high, so a difference in membrane permeability will only slightly affect the inflow rate and consequently influence the overall intracellular acid concentration to a lesser extent (Fig. 1).

Table II.

Chemical properties of the weak organic acids investigated in this study and the experimental conditions. 

Chemical properties				Experimental conditions
Name	Structure	pKa a	Log P a	pH	Total acid (mM)	Undissociated acid c (mM)
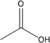
Acetic acid		4.76	−0.31	5	200, 300, 400	73, 110, 146
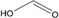
Formic acid		3.75	−0.42	5	400	21
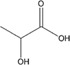
L‐lactic acid		3.86	−0.67	4 b	150	63
Sorbic acid		4.76	1.3	5	2.6	0.9
Benzoic acid		4.20	1.9	5	5.0	0.7

^aObtained from ChemBioDraw Ultra 14.0.

^bAdjusted to pH 4 in order to ensure a sufficiently high concentration of undissociated acetic acid to cause cell inhibition within the solubility range of the acid.

^cThe most inhibitory form of the acid due to its ability to enter the cell in an uncontrollable fashion by passive diffusion.

Inhibition of Sphingolipid Synthesis Increases Acetic Acid Membrane Permeability

To verify that the observed reduction in growth after the addition of myriocin to Z. bailii cultured with acetic acid was due to a difference in membrane permeability, the rate of inflow of acetic acid was measured indirectly using flow cytometry to monitor the change in intracellular pH shortly after an acetic acid pulse, by measuring the fluorescence of the pH‐dependent dye CFDA‐SE.

A first indication of increased membrane permeability in myriocin‐treated cells was the increase in fluorescence intensity. Cells cultured with myriocin displayed almost tenfold higher average emission than control cells at 525 nm (Fig. 6A). The increased emission probably originates from an increase in dye loading of the cells treated with myriocin, which is credible since CFDA‐SE enters the cell by passive diffusion, and the staining of Z. bailii without myriocin was relatively poor. The higher signal intensity could also have been due to a higher intracellular pH, but this appears unlikely as the difference in the signal corresponds to an increase of approximately two pH units, which is very high, and the increased emission was also observed at 586 nm, where the emission is less pH‐dependent (data not shown)(Stratford et al., 2013).

Figure 6.

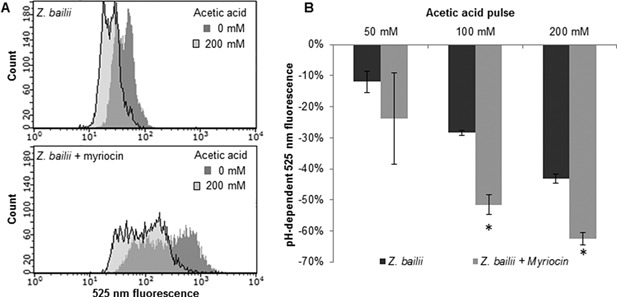
Single‐cell analysis of intracellular pH. Fluorescence signals from cells in buffer solution at pH 5, before and 30 s after acetic acid pulses. A. Overlaid cell distribution histograms of 525 nm fluorescence signals before (dark gray) and after 200 mM (pale gray) acetic acid pulse. Upper chart: Z. bailii cultured without myriocin, lower chart: Z. bailii cultured with 1.6 μM myriocin. Representative examples are given from one biological replicate of each condition. B. Percentage reduction in the pH‐dependent 525 nm fluorescence signal after acetic acid pulse compared to the signal without acetic acid addition. Each bar represents the mean of 3 biological replicates, and the error bars indicate the standard deviation. *Significant difference compared with Z. bailii, according to the t‐test (P < 0.05).

A second indication of increased membrane permeability in cells treated with myriocin was observed on the decrease in intracellular pH after acetic acid pulses. Pulses of 50–200 mM acetic acid led to an immediate decrease in the fluorescence emission at the pH‐dependent wavelength 525 nm, corresponding to a decrease in intracellular pH, both for cells cultured with myriocin and for control cells cultured without myriocin, indicating an inflow of acetic acid into the cell (Fig. 6B). In addition, after pulsing cells with 200 mM acetic acid, the fluorescence emission in myriocin‐treated cells decreased by 62%, while it fell by only 43% in the control cells, indicating a faster inflow of acetic acid in myriocin‐treated cells. A similar, although less marked trend was also seen following pulses of 50 and 100 mM acetic acid. Microscopic examination of cells cultured with myriocin alone showed no effect on morphology or viability (determined using methylene blue staining, data not shown) compared to control cells, further supporting the hypothesis that the observed reduction in acetic acid tolerance for Z. bailii cultured with myriocin was due to changes in membrane permeability caused by the sphingolipid reduction, rather than a general cellular response to myriocin.

Conclusions

Low acetic acid membrane permeability, due to a high fraction of sphingolipids in the membrane has been found in this study to be a key characteristic contributing to acetic acid resistance in Z. bailii. In silico molecular dynamics simulations showed the role of sphingolipid in increasing bilayer thickness and density, as well as suggested a reduction in the permeability coefficient for acetic acid diffusion. In vivo reduction of the fraction of sphingolipids in the plasma membrane increased acetic acid membrane permeability, resulting in reduced acetic acid tolerance, further strengthen our in silico predictions. In this work, we also placed acetic acid diffusion in relation to other factors influencing acetic acid tolerance, and concluded that the rate of diffusion into the cell is critical only when the counteracting rates removing acetic acid are larger. Yet, diffusion rate is concentration dependent, therefore, cell growth will occur at the acetic acid concentration that enables a diffusion rate which is lower than the rates removing acetic acid from the cell, thereby avoiding the toxic accumulation of acetic acid. Specific plasma membrane lipid composition is probably crucial for the tolerance to many lipid soluble molecules which currently stresses microbial cell factories. In this work, we provide sphingolipids as an example, and demonstrate the predictive power of molecular dynamics simulations in designing optimal plasma membrane lipid composition for the specific purpose.

Financial support from the Swedish Energy Agency, the Swedish Research Council, the Chalmers Energy Area of Advance, and the Wenner‐Gren foundations are gratefully acknowledged. We also acknowledge generous grants of computing time at the C3SE Supercomputing Center in Gothenburg, as provided via the Swedish National Infrastructure Committee (SNIC).

Supporting information

Supplementary Figure S1.

Supporting Information S1.

Supporting Information S2.

Supporting Information S3.

Supporting Information S4.

Supporting Information S5.