BCL::MP-Fold: membrane protein structure prediction guided by EPR restraints

Abstract

For many membrane proteins, the determination of their topology remains a challenge for methods like X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy. Electron paramagnetic resonance (EPR) spectroscopy has evolved as an alternative technique to study structure and dynamics of membrane proteins. The present study demonstrates the feasibility of membrane protein topology determination using limited EPR distance and accessibility measurements. The BCL::MP-Fold algorithm assembles secondary structure elements (SSEs) in the membrane using a Monte Carlo Metropolis (MCM) approach. Sampled models are evaluated using knowledge-based potential functions and agreement with the EPR data and a knowledge-based energy function. Twenty-nine membrane proteins of up to 696 residues are used to test the algorithm. The protein-size-normalized root-mean-square-deviation (RMSD100) value of the most accurate model is better than 8 Å for twenty-seven, better than 6 Å for twenty-two, and better than 4 Å for fifteen out of twenty-nine proteins, demonstrating the algorithm’s ability to sample the native topology. The average enrichment could be improved from 1.3 to 2.5, showing the improved discrimination power by using EPR data.

1 Introduction

Membrane protein structure determination continues to be a challenge. About 22 % of all proteins are membrane proteins and an estimated 60 % of pharmaceutical therapies target membrane proteins.¹ However, only 2.5 % of the proteins deposited in the Protein Data Bank (PDB) are classified as membrane proteins.^2,3 Protein structures are typically determined to atomic detail using X-ray crystallography or NMR spectroscopy. However, membrane proteins provide challenges for both techniques.⁴ It is difficult to obtain quantities of purified membrane proteins sufficient for both X-ray crystallography and NMR spectroscopy. The two-dimensional nature of the membrane complicates crystallization in a three-dimensional crystal lattice. In order to obtain crystals, the target protein is often subjected to non-native-like environments and/or modifications such as stabilizing sequence mutations.^5,6 Additional problems may evolve from post-translational modification such as phosphorylation.⁷ Many membrane proteins continue to be too large for structure determination by NMR spectroscopy.⁸ Even if the target itself is not too large, the membrane mimic adds significant additional mass to the system.⁹ Despite wonderful successes in determining the structure of high-profile targets, it is critical that the structural features observed with one technique are confirmed with an orthogonal technique.¹⁰

EPR spectroscopy in conjunction with site-directed spin labeling (SDSL) provides such an orthogonal technique for probing structural aspects of membrane proteins.^11–13 Advantages of EPR spectroscopy include that the protein can be studied in a native-like environment and that only a relatively small sample amount is required. In addition, EPR spectroscopy can be used to study large proteins. Although EPR is a versatile tool for probing membrane protein structure, it has its own challenges: at least one unpaired electron (spin label) needs to be introduced into the protein. Typically, this requires mutation of all cysteine residues to either alanine or serine, introduction of one or two cysteines at the desired labeling sites, coupling to the thiol-specific nitroxide spin label S-(1-oxyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methyl methanesulfonothioate (MTSL), and functional characterization of the protein. As a result, data sets from EPR spectroscopy are sparse containing only a fraction of measurements per residue in the target protein. EPR is not a high-throughput technique.

EPR provides two categories of structural information important to membrane protein topology: a) EPR can provide information about the local environment of the spin label.^14–16 The accessibility of the spin label to oxygen probe molecules indicates the degree of burial of the spin label within the protein in the transmembrane region. Accessibility measurements are typically performed in a sequence scanning fashion. This provides an accessibility profile over a large portion of the sequence.^17,18 The accessibility profile tracks the periodicity of SSEs as individual measurements rise and fall according to the periodic exposure and burial of residues. The exposed face of a SSE can be determined,¹⁹ a task that is difficult within the hydrophobic environment of the membrane. b) When two spin labels are introduced, EPR can measure inter-spin label distances, routinely of up to 60 Å through the double electron-electron resonance (DEER) experiment.^20,21 EPR distance measurements have been demonstrated on several large membrane proteins including MsbA,²² rhodopsin,²³ and LeuT.²⁴ Given the sparseness of data, EPR has been frequently used to probe different structural states of proteins.^25,26 Changes in distances and accessibilities track regions of the protein that move when converting from one state into another. Such investigations rely upon an already determined experimental structure to define the protein topology and provide a scaffold to map changes observed via EPR spectroscopy.

One critical limitation for de novo protein structure prediction from EPR data is that measurements relate to the tip of the spin label side-chain where the unpaired electron is located whereas information of the placement of backbone atoms is needed to define the protein fold. For distance measurements, this introduces an uncertainty in relating the distance measured between the two spin labels to a distance between points in the backbone of the protein. This uncertainty, defined as the difference between the distance between the spin labels and the distance between the corresponding C_β-atoms is up to 12 Å.^27,28 To address this uncertainty we previously introduced a motion-on-a-cone (CONE) model, which provides a knowledge-based probability distribution for the C_β-atom distance given an EPR-measured spin label distance.^27,29 Using the CONE model, just twenty-five or even eight EPR measured distances for T4-lysozyme, enabled Rosetta to provide models matching the experimentally determined structure to atomic detail including backbone and side-chain placement.²⁷ Further success was reported by Yang et al.,³⁰ who successfully determined the tertiary structure of a homodimer by using inter-chain restraints determined from NMR and EPR experiments. These studies demonstrate that de novo prediction methods can supplement EPR data sufficiently to allow structure elucidation of a protein.

De novo membrane protein structure prediction was demonstrated with Rosetta using twelve proteins with multiple transmembrane spanning helices.³¹ The method was generally successful for the membrane topology for small proteins up to 278 residues. The results of the study suggest that sampling of large membrane topologies requires methods that directly sample structural contacts between sequence distance regions of the protein.³²

For this purpose, we developed an algorithm that assembles protein topologies from SSEs termed BCL::Fold.³³ The omission of loop regions in the initial protein folding simulation allows sampling of structural contacts between regions distant in sequence and thereby rapidly enumerates all likely protein topologies. A knowledge-based potential guides the algorithm towards physically realistic topologies. The algorithm is particularly applicable for the determination of membrane protein topologies as transmembrane spans are dominated by regularly ordered SSEs.³⁴ Loop regions and amino acid side-chains can be added in later stages of modeling structure. The algorithm was tested in conjunction with medium-resolution density maps³⁵ achieving models accurate at atomic detail in favorable cases.³⁶ The algorithm was also tested in conjunction with sparse NMR data.³⁷

The present study combines EPR distance and accessibility restraints with the BCL::Fold SSE assembly methodology for the prediction of membrane protein topologies. In a first step, we introduce scores specific to EPR distances and accessibilities and demonstrate their ability to enrich for accurate models. In a second step, we describe the approach and results for assembling twenty-three monomeric and six multimeric membrane proteins guided by EPR distance and accessibility restraints. The results demonstrate that the inclusion of protein specific structural information improves the frequency with which accurate models are sampled and greatly improves the discrimination of incorrect models.

2 Materials and methods

2.1 Compilation of the benchmark set

Twenty-nine membrane proteins of known structure were used to demonstrate the ability of EPR specific scores to improve sampling during protein structure prediction as well as selecting the most accurate models. The proteins for the benchmark were chosen to cover a wide range of sequence length, number of SSEs, and percentage of residues within SSEs (Table 1 on the following page). Twenty-three of the proteins were monomers ranging in size from 91 to 568 residues. One protein (2L35) has two chains, with the second chain being a single transmembrane span. The remaining five proteins were symmetric multimeric proteins of two or three subunits containing up to 696 residues. 5000 independent structure prediction trajectories were conducted for each protein without restraints, with distance restraints only, with accessibility restraints only, and with distance and accessibility restraints. In order to achieve results that are independent of one specific spin labelling pattern, ten different restraint sets were used for each protein. Those trajectories were conducted with SSEs predicted from sequence and, to test the influence of incorrectly predicted secondary structure, with the SSEs obtained from the experimentally determined structure. In addition, rhodopsin (PDB entry 1GZM) was added to the benchmark set to demonstrate the algorithm’s ability to work with experimentally determined restraints.

Table 1.

Proteins used for benchmarking the structure prediction algorithm

Protein	#aas	#SSE	%resSSE	source	res.
1IWG	68	5	90%	X-ray	3.5 Å
1GZM	349	7	62%	X-ray	2.7 Å
1J4N	116	4	80%	X-ray	2.2 Å
1KPL	203	8	76%	X-ray	3.0 Å
1OCC	191	5	74%	X-ray	2.8 Å
1OKC	297	9	71%	X-ray	2.2 Å
1PV6	189	8	87%	X-ray	3.5 Å
1PY6	227	9	75%	X-ray	1.8 Å
1RHZ	166	5	65%	X-ray	3.5 Å
1U19	278	7	66%	X-ray	2.2 Å
1XME	568	18	79%	X-ray	2.3 Å
2BG9	91	3	87%	EM	—
2BL2	145	4	88%	X-ray	2.1 Å
2BS2	217	8	80%	X-ray	1.8 Å
2IC8	182	7	68%	X-ray	2.1 Å
2K73	164	5	62%	NMR	—
2KSF	107	4	64%	NMR	—
2KSY	223	7	78%	NMR	—
2NR9	196	8	75%	X-ray	2.2 Å
2XUT	524	16	72%	X-ray	3.6 Å
3GIA	433	15	81%	X-ray	2.2 Å
3KCU	285	10	67%	X-ray	2.2 Å
3KJ6	366	8	47%	X-ray	3.4 Å
3P5N	189	6	70%	X-ray	3.6 Å
2BHW	669	12	45%	X-ray	2.5 Å
2H8A	363	12	79%	EM	3.2 Å
2HAC	66	2	79%	NMR	—
2L35	95	3	81%	NMR	—
2ZY9	344	16	90%	X-ray	2.9 Å
3CAP	696	18	68%	NMR	2.9 Å

The twenty-nine proteins for the benchmark were chosen to cover a wide range of sequence length, number of SSEs as well as number and percentage of residues within SSEs while having a mutual sequence identity of less than 20 %. The columns denote the sequence length, the number of SSEs, the number of residues within SSEs, and the percentage of the residues is within SSEs. The proteins above the separating line are monomeric proteins; below the separating line are multimeric proteins. 2HAC, 2ZY9, and 3CAP are homodimers, 2BHW and 2H8A are homotrimers, and 2L35 is a heterodimer. 1GZM was additionally included to evaluate the protocol on experimentally determined data.

2.2 Simulation of EPR restraints

For 1GZM, EPR distance restraints were available,²³ whereas for the other proteins EPR distance and accessibility restraints were simulated to obtain data sets for each of the twenty-nine proteins. Accessibility restraints were simulated by calculating the neighbor vector value³⁸ for residues within SSEs of each protein. Unlike the neighbor count approximation of the solvent accessible surface area (SASA), the neighbor vector approach takes the relative placement of the neighbors with respect to the vector from the C_α-atom to the C_β-atom into account. It thereby becomes a more accurate predictor of SASA.³⁸ The resulting exposure value for each residue was considered an oxygen accessibility measurement. One restraint per two residues within the transmembrane segment of each SSE was simulated.

Distance restraints were simulated using a restraint selection algorithm,³⁹ which distributes measurements across all SSEs (see Section 6.1.1 on page 20 for details). It also favors measurements between residues that are far apart in sequence. One restraint was generated per five residues within the transmembrane segment of an SSE, if not indicated otherwise. Distances are calculated between the C_β-atoms; for glycine, the H_α2-atom is used. To simulate a likely distance observed in an actual EPR experiment, the distance is adjusted by an amount selected randomly from the probability distribution of observing a given difference between the spinspin distance (D_SL) and the back bone distance (D_BB).²⁸ In order to reduce the possibility of bias arising from restraint selection and spin labelling patterns, ten independent restraint sets were generated. For the five symmetric multimeric proteins, the same protocol was used, but only distance restraints between the same residues in the different subunits were considered.

2.3 Translating EPR accessibilities into structural restraints

EPR accessibility measurements are typically made in a sequence scanning fashion over a portion of the target protein. Although each individual accessibility measurement is difficult to interpret, the pattern of accessibilities over a stretch of amino acids within an SSE indicates reliably, which phase of the SSE is exposed to solvent/membrane versus buried in the protein core. We found accessibility restraints to have a limited impact on structure prediction for soluble proteins.²⁷ We concluded that this is the case as knowledge-based potentials on their own can distinguish the polar phase of an SSE that is exposed to an aqueous solvent from a hydrophobic phase buried in the protein core. However, we also hypothesized that the situation will be different for membrane proteins where it would be harder to distinguish the membrane-exposed from the buried phase of an α-helix as both of these tend to be apolar.

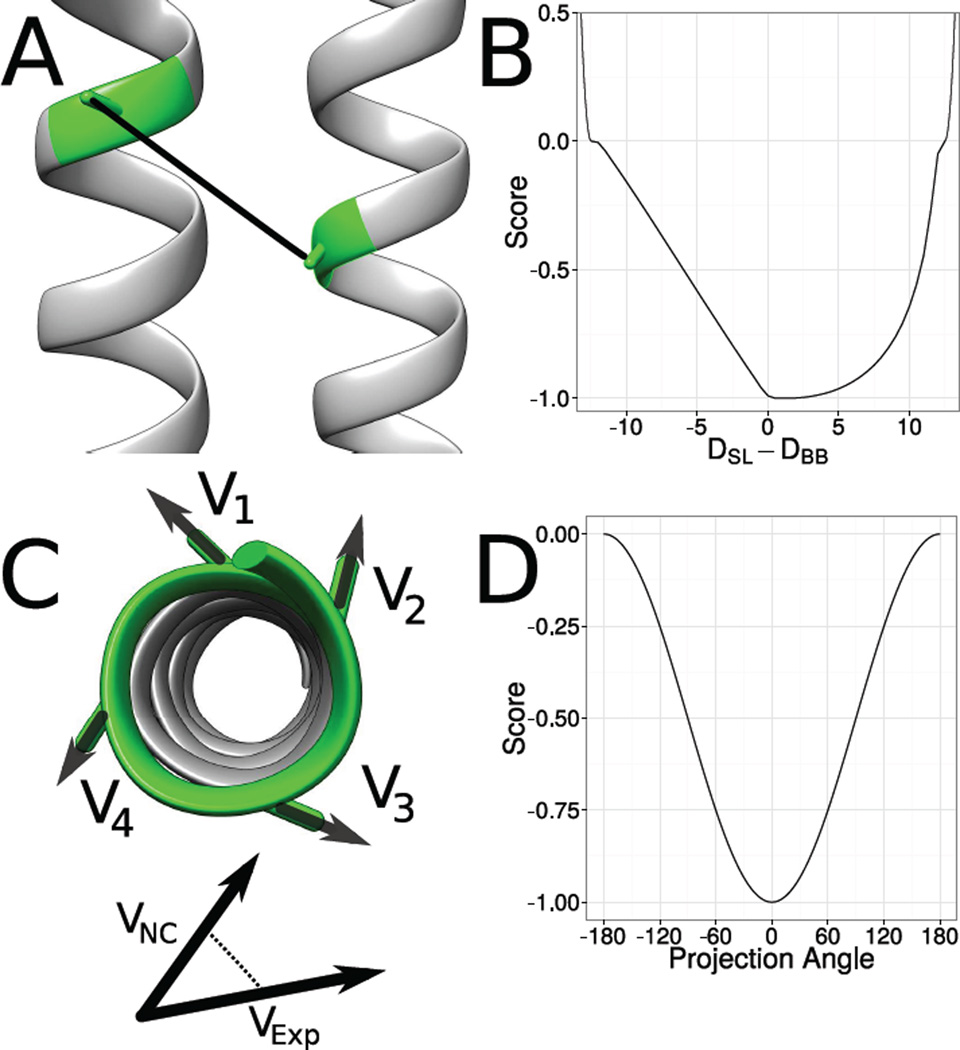
Our approach for developing an EPR accessibility score takes advantage of the regular geometry within the SSE: The exposure moment of a window of amino acids is defined as ${𝖤}_w={\sum }_{n=1}^{𝖭}{e}_n·s_n$, where 𝖭 is the number of residues in the window, e_n is the exposure value of residue n, and s_n is the normalized vector from the C_α-atom to the C_β-atom of residue n. This equation was inspired by the hydrophobic moment as previously defined.⁴⁰ The exposure moment calculated from solvent accessible surface area SASA has been previously demonstrated to approximate the moment calculated from EPR accessibility measurements.¹⁹

During de novo protein structure prediction, the protein is represented only by its backbone atoms hampering calculation of SASA. Further, calculation of SASA from an atomic detail model would be computationally prohibitive for a rapid scoring function in de novo protein structure prediction. Therefore, the neighbor vector approximation for SASA is used.³⁸ The exposure moment is calculated for overlapping windows of length seven for α-helices and four for β-strands. The score is computed as 𝖲_orient = −0.5 · cos(θ) where θ is the torsion angle between the exposure moments. This procedure assigns a score of −1 if θ = 0° and a score of 0 if θ = 180° (Figure 1 on the preceding page).

Figure 1. Translation from EPR data into structural restraints.

EPR distance measurements measure distances between residues in a protein indirectly. Whereas the experiment determined the spin-spin distance (D_SL), a distance between the backbone atoms (D_BB) is needed during the de novo protein structure prediction process. Therefore a translation from 𝖣_SL to 𝖣_BB is necessary. BCL::Fold uses a knowledge-based potential to evaluate the agreement of the distance between the C_β-atoms in the model with the experimentally determined spin-spin distances (B). EPR accessibility data is translated into structural restraints by summing up the hydrophobic moment vectors (C_α-atom to C_β-atom) of four consequtive residues (C). This is done twice: first the normalized C_α-C_β vectors are multiplied with the accessibility determined in the EPR experiment, the second time they are multiplied with the neighbor count of the residue in the model. The vectors are summed up for each approach and the projection angle between the two resulting vectors is scored, with an angle of 0° being the best and 180° being the worst agreement (D).

It has previously been demonstrated that the burial of sequence segments relative to other segments can be determined from the average accessibility values measured for that stretch of sequence.⁴¹ To capture this information, the magnitude of the exposure moment for overlapping residue windows is determined from the model structure and from the measured accessibility. The Pearson correlation is then calculated between the rank order magnitudes of the structural versus experimental moments. This gives a value between −1, which indicates the structural and exposure magnitudes are oppositely ordered, and 1, which means the structural and exposure magnitudes are ordered equivalently. The score S_magn is obtained by negating the resulting Pearson correlation value so that matching ordering will get a negative score and be considered favorable.

2.4 Translating EPR distances into structural restraints

The CONE model²⁷ yields a predicted distribution for the difference between D_SL and D_BB. This distribution was converted into a knowledge-based potential function, which is used to score the agreement of models with experimentally determined EPR distance restraints.²⁸ This score spans a range of D_SL − D_BB between −12 Å and 12 Å. D_SL is the EPR measured distance between the two spin labels; D_BB is the distance between the corresponding C_β- or H_α2-atoms on the residues of interest; D_SL − D_BB is the difference between these two distances (Figure 1 on the previous page).

In addition, we found it beneficial to add an attractive potential on either side of the range spanned by the scoring function to provide an incentive for the MCM minimization to bring structures within the defined range of the scoring function. These attractive potentials use a cosine function to transition between a most unfavorable score of 0 and a most favorable score of −1. The attractive potential is positive for 30 Å ≥|D_SL −D_BB|≥ 12 Å. It levels to 0 when the difference between D_BB and D_SL approaches 12 Å (Figure 1 on the preceding page).

2.5 Summary of the folding protocol

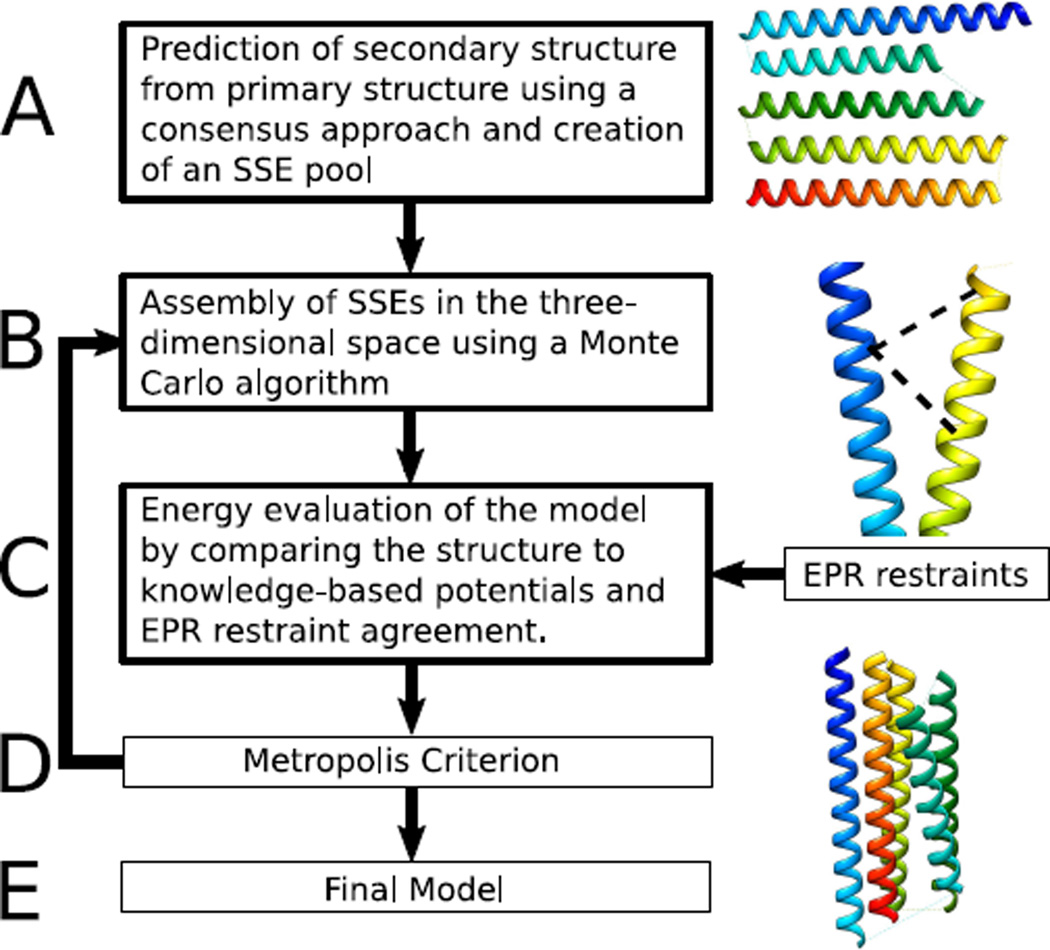
The protein structure prediction protocol (Figure 2 on the next page) is based on the protocol of BCL::Fold for soluble proteins.³³ The method assembles SSEs in the three-dimensional space, drawing from a pool of predicted SSEs. A MC energy minimization with the Metropolis criteria is used to search for models with favorable energies. Models are scored after each MC step using knowledge-based potentials describing optimal SSE packing, radius of gyration, amino acid exposure, and amino acid pairing, loop closure geometry, secondary structure length and content, and penalties for clashes.⁴²

Figure 2. Structure prediction protocol for using EPR data.

(A) SSEs are predicted using machine learning. (B) BCL::Fold arranges predicted glsplsse using an Monte Carlo (MC) algorithm in conjunction with knowledge-based potentials (C) and Metropolis criterion (D).

The algorithm was adapted for membrane protein folding by altering the amino acid exposure potential according to an implicit membrane environment.³⁴ Additional scores are used, which favor orthogonal placement of SSEs relative to the membrane and penalizing models with loops going through the membrane. All moves introduced for soluble proteins are used.³³ In addition, we include perturbations that optimize the placement of the protein in the membrane such as translation of individual SSEs in the membrane as well as rigid body translation and rotation of the entire protein.

The assembly of the protein structure is broken down into five stages of sampling with large structural perturbation moves that can alter the topology of the protein. Each of the five stages lasts for a maximum of 2000 MC steps. If an energetically improved structure has not been generated within the previous 400 MC steps, the minimization for that stage will cease. Over the course of the five assembly stages, the weight of clashing penalties in the total score is ramped as 0, 125, 250, 375 and 500.

Following the five stages of protein assembly, a structural refinement stage takes place. This stage lasts for a maximum of 2000 MC steps and will terminate sooner if an energetically improved model is not sampled within the previous 400 steps. The refinement stage consists of small structural perturbations, which will not drastically alter the topology of the protein model.

After 5000 models have been generated for each protein, the models are filtered according to EPR distance score. The top 10 % or 500 models resulting from the structure prediction protocol are selected for a second round of energy minimization. The second round occurs as described above, the only difference being that the minimization uses the SSE placements of a given protein as a starting point. For each starting structure, 10 models are created, resulting in 5000 models. This boot strapping approach, which re-optimizes structures that are in good agreement with the EPR restraints and with the knowledge-based potential was beneficial when combining BCL::MP-Fold with limited NMR data and is not applied when no experimental data are used.³⁷

2.6 Summary of the benchmark setup

To test the influence of EPR restraints, each protein besides 1GZM was folded in the absence of restraints, with just distance restraints, with just accessibility restraints, and with distance and accessibility restraints. To test the influence of secondary structure prediction accuracy (see section 6.1 on page 20), the experiment was repeated with optimal SSEs derived from the experimentally determined structure. 1GZM was only folded without restraints and with the experimentally determined distance restraints. 5000 models were created for each of the benchmark proteins in independent MCM folding trajectories. EPR distance and accessibility scores are used during the five assembly and one refinement stages of structure prediction protocol. The EPR distance scores have a weight of 40 during all assembly and refinement stages using either pool.

2.7 Structure prediction protocol

For each protein, two sets of SSE pools are generated for use during structure assembly. The first SSE pool consists of the transmembrane spanning helices as predicted by obtainer of correct topologies for uncharacterized sequences (OCTOPUS). The second SSE pool contains elements predicted by OCTOPUS as well as SSEs predicted from sequence by Jufo9D (see Section 6.1.2 on page 20 for details). Using these two SSE pools, the structure prediction protocol is independently conducted twice: a) once using the SSE pool containing predictions from OCTOPUS and Jufo9D (“full pool”) and b) once emphasizing the predictions by OCTOPUS (“OCTOPUS pool”). Emphasis is placed on OCTOPUS predictions by using only the OCTOPUS generated SSE pool during the first two stages of assembly. During last three stages of structure assembly, the SSEs predicted from Jufo9D are added to the pool. This allows for better coverage of SSEs within the structure, since OCTOPUS only predicts transmembrane spanning helices.

EPR specific scores are used during the five assembly and one refinement stages of structure prediction (see Section 6.1.2 on page 20 for details). The EPR distance scores have a weight of 40 over the course of the assembly and refinement stages.

2.8 Calculating EPR score enrichments

The enrichment value is used to evaluate how well a scoring function is able to select the most accurate models from a given set of models. The models of a given set are sorted by their RMSD100 values. The 10 % of the models with the lowest RMSD100 values put into the set 𝖯 (positive) the rest of the models will be put into the set 𝖭 (negative). The models of 𝖲 are then also sorted by their assigned scoring value and the 10 % of the models with the lowest (most favorable) score are put into the set 𝖳. The models, which are in 𝖯 and in 𝖳 are the models, which are correctly selected by the scoring function and their number will be referred to as TP (true positives). The number of models, which are in 𝖯 but not in 𝖳 are the models, which are not selected by scoring function despite being among the most accurate ones. They will be referred to as FN (false negative). The enrichment will then be calculated as $e=\frac{\#TP}{\#𝖯}·\frac{\#𝖯+\#𝖭}{\#𝖯}$. The positive models are in this case considered the 10 % of the models with the lowest RMSD100 values. Therefore, $\frac{\#𝖯+\#𝖭}{\#𝖯}$ is a constant value of 10.0. No enrichment would be a value of 1.0 and an enrichment value between 0.0 and 1.0 indicates that the score selects against accurate models.

3 Results

3.1 Using EPR specific scores during membrane protein structure prediction improves sampling accuracy

For each protein, the ten models sampled with the best RMSD100⁴³ values are used to determine ability to sample accurate models by taking their RMSD100 value average, μ₁₀. Using the best ten models by RMSD100 provides a more consistent measure of sampling accuracy compared to looking at the single best because of the random nature of the structure prediction protocol. Additionally, the percentages of models with an RMSD100 less than 4 Å and less than 8 Å, τ₄ and τ₈, were calculated.

By using EPR distance and accessibility scores, not only is the frequency increased with which higher accuracy models are sampled, but the best models achieve an accuracy not sampled in the absence of EPR data (Table 3 on page 22). Across all proteins, μ₁₀ is, on average, 6.0 Å when EPR distance and accessibility scores are not used. When adding restraints for distances and then both distances and accessibilities, the average μ₁₀ value drops to 5.1 Å and 5.0 Å, respectively (Table 3 on page 22). By only adding EPR accessibility restraints the average μ₁₀ over all proteins improves only slightly to 5.8 Å. This demonstrates that the accuracy of the models is primarily improved by using EPR distance restraints in the structure prediction process. With the exception of 1KPL and 2XUT, all proteins achieve a μ₁₀ value of less than 8.0 Å. This indicates the placement of the transmembrane spanning regions follow the experimentally determined structures and the correct fold could be predicted. Figure 3 on the next page compares the RMSD100 values of the average of the 1 % most accurate models with and without the usage of EPR distance restraints — an average improvement of 0.8 Å over the benchmark set is observed. The shift to lower RMSD100 values in distributions for selected benchmark proteins is shown in figure 3 on the following page. The average τ₄ and τ₈ values improve from 3 % and 13 %, when folding without EPR restraints, and to 6 % and 19 % when using EPR restraints, respectively.

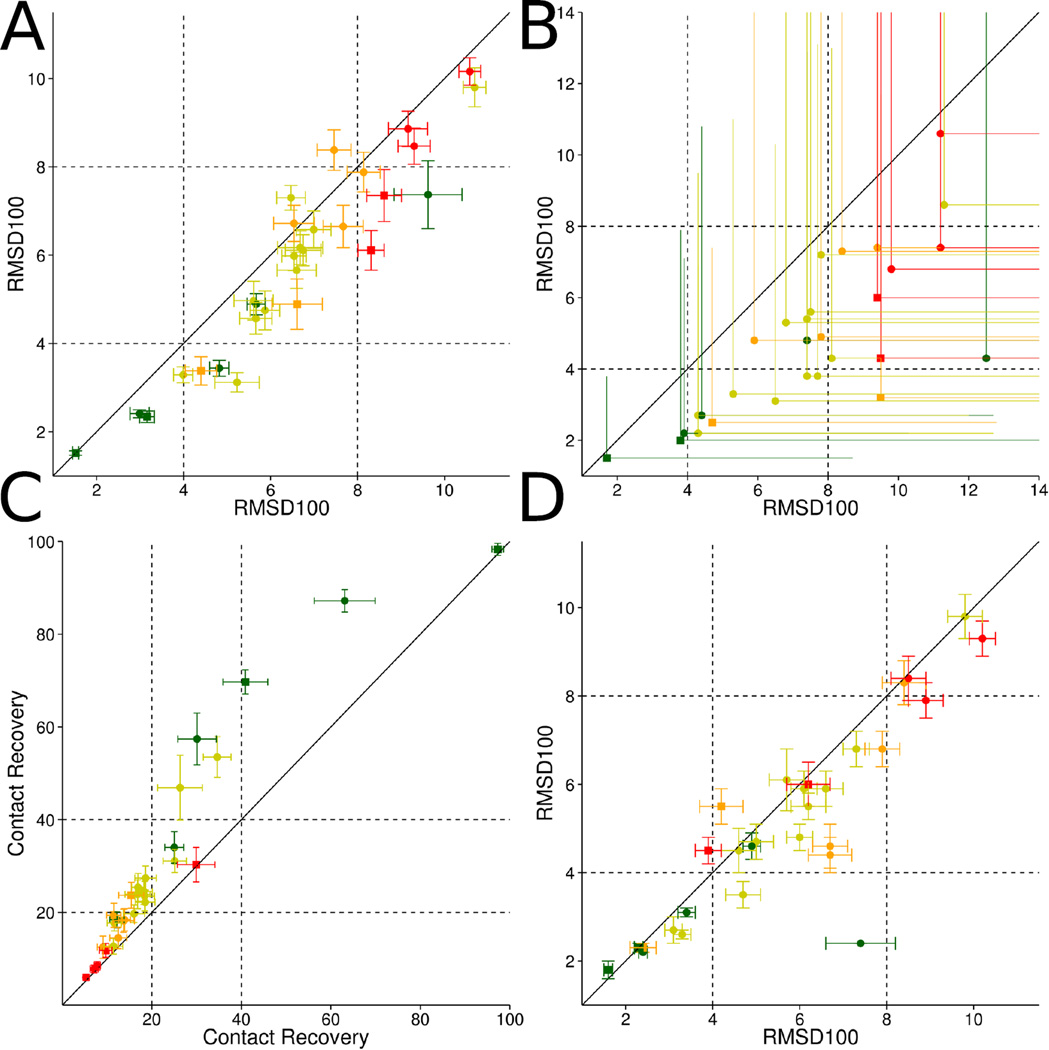
Figure 3. Sampling accuracy, contact recovery, and enrichment results when using EPR data.

By using EPR distance and accessibility data in the structure prediction process the sampling accuracy can be improved significantly for monomeric (circles) as well as oligomeric (squares) proteins (A). The sampling accuracy could be improved in twenty-five out of twenty-nine cases by using EPR distance and accessibility data, which is demonstrated by comparing the average RMSD100 values of the 1 % most accurate models predicted without (x-axis) and with EPR data (y-axis) in (A). Adding protein specific structural information in the form of EPR distance and accessibility restraints also improves our ability to select the most accurate models among the sample ones. In each of the twenty-nine cases EPR distance and accessibility restraints enable us to select more accurate models when compared to structure prediction without EPR data available. Shown are the average (line) and best (dot/square) RMSD100 values of the best 1 % models by BCL score with (y-axis) and without (x-axis) EPR restraints (B). By using EPR accessibility data only (y-axis) the Contact Recovery could be improved in twenty-two out of twenty-nine cases (C) when compared to structure prediction without EPR accessibility restraints (x-axis). Improvements in SSE prediction methods would also lead to improved sampling accuracies (D, see also table 6 on page 25). In twenty-one out of twenty-nine cases the average RMSD100 of the ten most accurate models could be improved by using SSE definitions obtained from the experimentally determined structure (y-axis) compared to using predicted SSEs.

The six multimeric proteins achieve an average μ₁₀ value of 5.0 Å when the structure prediction was conducted without using EPR restraints. By using EPR distance and accessibility restraints μ₁₀ could be improved to 2.9 Å. The τ₄ and τ₈ values could be improved from 13 % and 24 % to 21 % and 41 % when using EPR distance and accessibility restraints in the structure prediction process.

3.2 EPR accessibility scores are important for improving contact recovery

EPR accessibility scores were previously used in conjunction with the Rosetta protein structure prediction algorithm.²⁷ The scores were applied in a benchmark to predict the structures of the small soluble proteins T4-lysozyme and αA-crystallin. The improvement in sampling models that are more accurate was compared between prediction trajectories using an EPR distance score and trajectories using an EPR distance score coupled with an accessibility score. For T4-lysozyme and αA-crystallin, using the accessibility score did not result in a significant improvement in the accuracy of models sampled. This was attributed to the simple rule of exposure that is well captured by the knowledge-based potentials: polar residues tend to be exposed to solvent; apolar residues tend to be buried in the core of the protein.

Membrane proteins are subjected to a more complex set of possible environments. Any given residue can reside buried in the core of the protein or exposed to different environments ranging from the membrane center to a transition region to an aqueous solvent. If the protein fold contains a pore, a residue can be solvent-exposed deep in the membrane.⁴⁴ Such a complex interplay of environments will not be as easily distinguished by knowledge-based potentials. Here it has been demonstrated that using EPR accessibility information consistently improves the contact recovery for highest accurate models.

Although improvements regarding sampling accuracy and selection of the most accurate models by RMSD100 is mainly achieved by using EPR distance restraints, EPR accessibility restraints help determining the correct rotation state of SSEs and therefore improves the number of recovered contacts (Figure 3 on the previous page). A contact is defined as being between amino acids, which are separated by at least six residues and have a maximum Euclidean distance of 8 Å. We are measuring the percentage of the contacts in the experimentally determined protein structure, which could be recovered in the models. In order to be independent of huge deviations occurring when only looking at the best model sampled, we quantify the average contact recovery of the ten models with the highest contact recovery (ϕ₁₀) and the percentage of models, which have more than 20 % and 40 % of the contacts recovered (γ₂₀ and γ₄₀).

For folding without EPR restraints, the average ϕ₁₀ value over all twenty-three monomeric proteins was 23 % whereas with accessibility restraints it was 31 % (Table 4 on page 23). Using distance restraints additionally to the accessibility restraints ϕ₁₀ remains at 31 %. This is demonstrating that improvements in contact recovery are mainly achieved by using EPR accessibility restraints in the structure prediction process. The average γ₂₀ and γ₄₀ values over all twentynine proteins for structure prediction without EPR restraints were 5 % and 3 %. By using EPR accessibility restraints, the values could be improved to 12 % and 16 %, respectively.

For the six multimeric proteins, improvements in contact recovery by the usage of EPR accessibility restraints are observed as ϕ₁₀, γ₂₀, and γ₄₀ values could be increased to 46 %, 25 % and 16 % from the previous values of 38 %, 17 % and 14 % when performing protein structure prediction without EPR data. By complementing the accessibility with distance restraints ϕ₁₀, γ₂₀, and γ₄₀ values can be improved to 50 %, 30 % and 16 %.

3.3 EPR specific scores select for accurate models of membrane proteins

The ability of EPR specific scores to select for accurate models is tested by calculating enrichment values for structure prediction trials of twenty-nine membrane proteins (Table 5 on page 24). The enrichment of a scoring function indicates how well the score identifies a protein model that is accurate by a good score. It computed as the cardinality of the intersection 𝖨 = HS∩𝖯 with 𝖯 being the set of the accurate models and HS being the set of the 10 % of the models with the most favorable score (see section 2.5 on page 7).⁴² Accurate is defined as the 10 % of the models with the lowest RMSD100 when compared to the experimentally determined structure. Therefore, if a score correctly identifies all accurate models as being accurate, a perfect enrichment would result in a value of 10.0.

Enrichment values are computed for the protein models created without experimental restraints. For protein structure prediction without EPR data, the average enrichment value for just the knowledge-based potentials over all twenty-nine proteins is 1.3. By using EPR distance and accessibility data, the average enrichment is improved to 2.5. The enrichment for using EPR distance and accessibility restraints ranges from 1.1 to 6.2. In seventeen out of twenty-nine cases, the enrichment is greater than 2.0. In twenty-three out of twenty-nine cases the enrichment could be improved by at least 0.5 (Table 5 on page 24). By using EPR accessibility data only the average enrichment over all proteins is 1.6, demonstrating that improvements regarding the selection of the most accurate models are mainly caused by EPR distance restraints.

3.4 The number of restraints determines the significance of improvements in sampling accuracy

For four proteins, the influence of varying numbers of restraints was examined. In addition to the one restraint per five residues within SSEs setup used for all benchmark cases, the tertiary structure of 1OCC, 1PV6, 1PY6, and 1RHZ was predicted using one restraint per ten residues, one restraint per three residues, and one restraint per two residues within SSEs. For 1PY6, the sampling accuracy could be steadily improved with an increasing number of restraints demonstrated by τ₈ values increasing from 15 % to 20 % to 24 % to 28 % to 33 % and μ₁₀ values improving from 4.4 Å to 4.2 Å to 3.6 Å to 3.5 Å to 3.3 Å for structure prediction without restraints, one restraint per ten residues, one restraint per five residues, one restraint per three residues and one restraint per two residues (see table 2 and figure 6 on page 26). For 1OCC, 1PV6, and 1RHZ, a significant improvement in sampling accuracy is observed for using one restraint per three residues instead of one restraint per ten residues within SSEs, which is demonstrated by improvements in τ₈ values from 42 % to 53 %, from 8 % to 36 %, and from 6 % to 22 % and by improvements in μ₁₀ values from 3.2 Å to 1.9 Å, from 5.3 Å to 4.3 Å, and from 4.7 Å to 3.3 Å, respectively. Increasing the number of restraints to one restraint per two residues within SSEs fails to further improve the sampling accuracy. We attribute this observation to significant bends in some of the SSEs that are currently not sampled sufficiently dense by BCL::MP-Fold.

Table 2.

Sampling accuracy is improving with an increasing number of EPR restraints.

	1/10			1/3			1/2
Protein	μ10	τ4	τ8	μ10	τ4	τ8	μ10	τ4	τ8
1OCC	3.3 Å	2.0 %	42.4 %	1.9 Å	5.6 %	52.6 %	2.0 Å	5.4 %	51.0 %
1PV6	5.3 Å	0.0 %	8.3 %	4.3 Å	0.0 %	35.9 %	4.2 Å	0.0 %	34.6 %
1PY6	4.2 Å	0.0 %	19.8 %	3.5 Å	0.0 %	27.7 %	3.3 Å	0.6 %	32.7 %
1RHZ	4.7 Å	0.0 %	5.5 %	3.3 Å	0.7 %	22.2 %	3.5 Å	0.4 %	24.0 %

The percentages of models sampled with RMSD100 values less than 4 Å and 8 Å (τ₄and τ₈) are increasing with the number of restraints increase from one distance restraint per ten residues within SSEs to one restraints per three residues within SSEs to one restraint per two residues within SSEs. An upper limit is met at one restraint per three residues for 1OCC, 1PV6, and 1RHZ since the further accuracy improvements would require a more effective sampling of possible dihedral angle conformations.

3.5 Using experimentally obtained EPR distance restraints for rhodopsin

The benchmark was extended to also contain rhodopsin (PDB entry 1GZM) for which EPR distance measurements were available.²³ Although only sixteen EPR distance restraints were available, which amounts to less than one restraint per ten residues within SSEs, the sampling accuracy as well as the enrichment improve significantly. The μ₁₀ values improved from 4.9 Å for folding without restraints to 4.4 Å when using restraints. The enrichment values could be improved from 0.6 to 1.2 demonstrating that even a small number of restraints improves discrimination of incorrect models.

4 Discussion

EPR distance and accessibility restraints can aid the prediction of membrane protein structure. For this purpose, EPR specific scores were coupled with the protein structure prediction method BCL::MP-Fold. BCL::MP-Fold assembles predicted SSEs in space without explicitly modeling the SSE connecting loop regions. This allows for rapid sampling of complex topology that is not easily achieved when an intact protein backbone must be maintained. By adding EPR specific scores to the knowledge-based scoring function, sampling of accurate structures is increased. Additionally the selection of the most accurate models could be improved significantly.

However, it has to be clearly stated that — with the exception of bovine rhodopsin (PDB entry 1GZM) — all EPR restraints used in this study were simulated using the CONE model. Therefore, the relevance of our findings depends on how well the CONE model describes the nature of experimental DEER measurements and in particular the mobility of the spin label.

4.1 EPR distance scores improve the accuracy of topologies predicted for membrane proteins

EPR distance measurements are associated with large uncertainties in relating the measured spin label – spin label distance into backbone distances. In spite of this, EPR distance measurements provide important data on membrane protein structures.^23,24,45 In the present study, it has been demonstrated that EPR distance data can significantly increase the frequency with which the correct topology of a membrane protein is sampled (Figure 3 on page 11 and figure 4 on the next page). This is important because as the correct topologies are sampled with higher accuracy, models start to reach the point where they can be subjected to atomic detail refinement to further increase their accuracy.⁴⁶

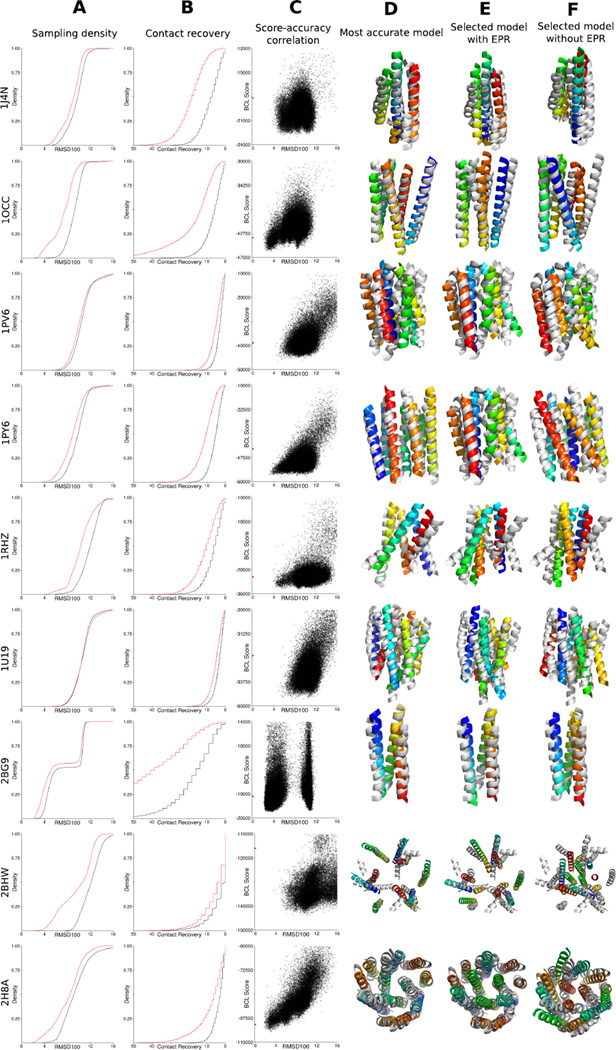
Figure 4. Gallery of the structure prediction results when using EPR data.

By using EPR distance and accessibility restraints, the sampling accuracy is significantly improved as the selection ability regarding accurate models. For selected proteins, a comparison of the RMSD100 (column A) and Contact Recovery (column B) distributions for sampling with (red) and without (black) EPR restraints is shown. The y-axis of column A shows the cumulative density of models with respect to the RMSD100. The y-axis of column B shows the cumulative density of models with respect to their contact recovery. Column C shows the correlation between the BCL score and the RMSD100 for the models sampled with EPR restraints (black dots) and the experimentally determined structure (red dot). The y-axis is the pseudo-energy score the algorithm assigned to the structure; the x-axis is the RMSD100 relative to the experimentally determined structure. The superimpositions show the best models by RMSD100 for folding with EPR restraints (column D), the best model by pseudo-energy score for folding with EPR restraints (column E), and the best model by pseudo-energy score for folding without EPR restraints (column F) superimposed with the experimentally determined structure (grey).

It is crucial to distinguish between the two major challenges in de novo structure prediction — sampling and scoring: The average improvement in sampling accuracy — i.e. the best model built among 5000 independent folding trajectories — of 0.8 Å is moderate but significant. However, inclusion of the EPR data does not only allow folding of models that are more accurate, it greatly improves discrimination of incorrect models with a scoring function that combines BCL knowledge-based potentials and EPR restraints. Without using EPR restraints the average enrichment is 1.3, i.e. 13 % of the most accurate models are in a sample of 10 % best scoring models, which is close to chance. By using EPR data in addition to the knowledge-based score enrichment increases to 2.5, i.e. one out of four models in the 10 % best scoring models also has the correct fold. This is important as it greatly improves the chance to identify correctly folded models, e.g. through clustering of good-scoring models. The combination of improved sampling and discrimination thereby significantly improves the reliability with which were able to predict the tertiary structure of a protein.

The EPR distance data used for the present study is simulated from known experimental structures. It will be interesting to repeat this benchmark once sufficiently dense experimental data sets for several membrane proteins become available. For now, considerable effort was put forth to ensure that the simulated data mimics what would be obtained from a true EPR experiment, so that any results are unbiased by the simulated data. The previously published method for selecting distance restraints was used to create ten different data sets per protein.³⁹ This ensures results are not biased by a particularly selected data set. Previously, the uncertainty in the difference between spin label distances and the corresponding C_β distance (D_SL − D_BB) was accounted for in simulated distance restraints by adding a random value between 12.5 Å and −2.5 Å.³⁹ Here, the probability of observing a given D_SL − D_BB is used to determine the amount that should be added to the C_β − C_β distance measured from the experimental structure.

Using a method developed for soluble proteins to select restraints for membrane proteins is not necessarily ideal. The constraints already imposed upon membrane proteins by the membrane geometry suggest that optimized methods for selecting restraints for membrane proteins should be developed. One such strategy could be to measure distances between transmembrane segments on the same side of the membrane, with the assumption that transmembrane helices are mostly rigid, parallel structures. Further, additional work is needed to account for topologically important SSEs that do not span the membrane, as well take into account the deviations of transmembrane segments from ideal geometries.

The improved sampling accuracy in the protein structure prediction process is primarily caused by the distance restraints. Whereas by using EPR accessibility restraints the average μ₁₀ value over all twenty-nine proteins drops from 6.0 Å to 5.8 Å, by using EPR distance restraints the average μ₁₀ value could be improved to 5.1 Å.

4.2 Why not use the membrane depth parameter as additional restraint?

Of note is that EPR-derived accessibility measurements have been also used to the determine membrane depth parameter Φ.^47–49 For this purpose, the accessibility ∏ of a single residue to two paramagnetic reagents are compared, the water-soluble (nickel-(II)-ethylenediaminediacetate — NiEDDA) and the membrane-soluble (molecular oxygen — O₂). The ratio of both values is used to compute the membrane depth parameter: Φ_n = ln(∏_O2/∏_NiEDDA). The present approach does not test effectiveness of a score that relies on the membrane depth parameter for membrane protein structure prediction for several reasons: a) we hypothesize that knowledge-based potentials will be capable of placing transmembrane SSEs at the right depth for this placement should again be dominated by polarity which is well captured in such potentials (read above), and b) the membrane depth parameter Φ_n is affiliated with a larger error margin for NiEDDA accessibilities become very small in the core of the membrane and they omit averaging over multiple residues. Nevertheless, testing if a membrane depth related score can improve BCL::MP-Fold could be a goal in a future experiment.

4.3 Improved secondary structure predictions will improve the accuracy of predicted structures

The SSE pools are created in order to reduce the possibility of missing a SSE, which is generally a successful approach as demonstrated previously for soluble proteins.³³ The helical transmembrane span prediction software OCTOPUS⁵⁰ is used in conjunction with Jufo9D.⁵¹ Jufo9D provides predictions for SSEs that do not necessarily span the membrane and therefore will not be predicted by OCTOPUS. Improved secondary structure prediction methods will benefit membrane protein structure prediction. In addition, it has been demonstrated that the pattern of accessibility values for measurements along a sequence follow the periodicity of the SSE on which they are measured.^17,22,45 Measured accessibility profiles could therefore be used to inform the pool of SSEs used for structure prediction.

The pool of SSEs used to assemble the membrane protein topologies is the most important determinant in successfully predicting the membrane proteins’ structure. This is seen for 1U19 and 2BL2. With predicted SSEs, the structure of the two proteins can be sampled to μ₁₀ values of 5.9 Å and 6.2 Å, respectively (Table 3 on page 22). By using SSE definitions extracted from the experimentally determined structure, the proteins can be sampled at μ₁₀ values of 4.4 Å and 2.6 Å, respectively. This is caused by secondary structure prediction methods breaking up transmembrane helices into several short helices making it harder to assemble the tertiary structure that does not have loop going through the membrane. The experiment was repeated with SSE definitions obtained from the experimentally determined structures of the proteins. Whereas with predicted SSEs average μ₁₀, τ₄, and τ₈ values of 5.0 Å, 6 %, and 19 % are achieved over all twenty-nine proteins, by using the SSE definitions from the experimentally determined structure we could improve them to 4.5 Å, 8 %, and 25 %. In twenty-one out of twenty-nine cases the average accuracy of the ten best models by RMSD100 could be improved by using SSE definitions obtained from the experimentally determined structure (Figure 3 on page 11). This demonstrates that further improvements of the secondary structure prediction will also lead to an improved sampling accuracy of BCL::Fold.

4.4 Limitations of the CONE model knowledge-based potential

The unknown label conformation is taken into account by the CONE model, which yields a D_SL − D_BB distribution. This wide probability distribution accounts for two inherently different aspects — a structural and a dynamical: The structural effect looks at the relative position of the unpaired electron with respect to the protein backbone. This positioning is dependent on the protein structure, specifically the direction in which the C_α − C_β vector project into space with respect to the C_α − C_α vector that links the two labeling site. As the CONE model is applied in a model-independent fashion, it does not consider these geometric features but expresses the resulting ambiguity as part of the probability distribution. Second, chemical environment and exposure cause variable levels of spin label dynamics. These result in distance distributions of variable tightness in EPR experiments. This information is currently not considered as parameter in the CONE model but absorbed by using a very wide D_SL − D_BB probability distribution. This approach has the advantage that it is very robust with respect to uncertainties within the EPR experimental parameters and very fast to compute. At the same time, the CONE model knowledge-based potential neglects important geometric parameters. Developing and testing approaches that take these parameters into account and lead to tighter distance distributions without losing the advantages of speed and robustness is an active area of our research.

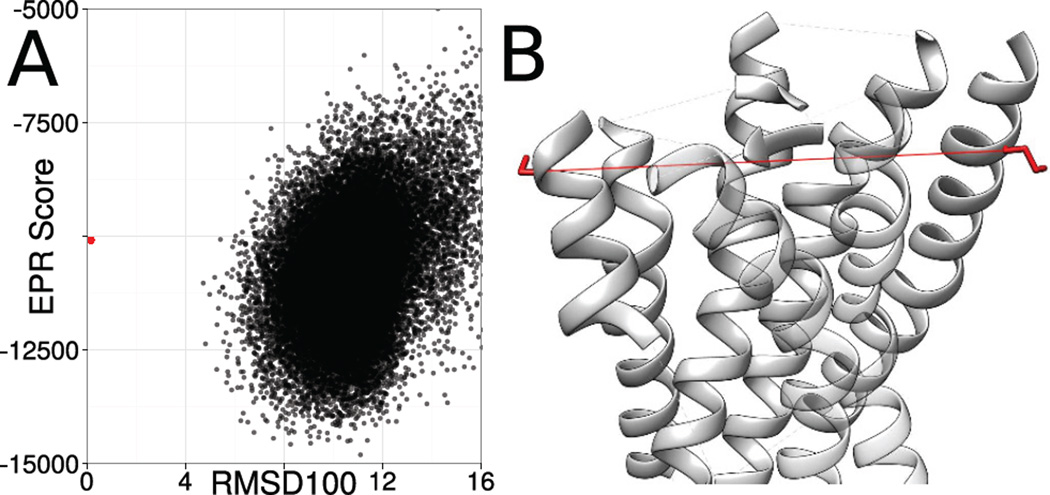
Not considering geometrical features hinders the selection of accurate models for 1U19. EPR distance restraints improved the sampling accuracy, but it is still not possible to reliably select accurate models (Figure 5). Although the distances observed in EPR experiments are typically long and therefore allow a broad range of topologically different models to fulfill them, inaccuracies in the translation from D_SL to D_BB also contribute to the selection problem. In the case of 1U19 the experimentally determined structure, which served as the template for the simulation of the EPR distance restraints, shows a worse agreement with the restraints than the best scoring models. The spin-spin distance between residue 7 and residue 170 is 43.6 Å, whereas the distance between the C_β-atoms is 35.7 Å resulting in an agreement score of 0.3 on a scale from 0 to 1. Following the EPR potential, a C_β − C_β distance of 41.1 Å is favorable, which is accomplished by the sampled models with the best score leading to the selection of models, which deviate significantly from the experimentally determined structure. Both spin labeling sites are exposed, indicating they are at the outside of the protein. The projection angle between the C_α − C_β vectors is greater than 160°, making it more likely that the spin labels are pointing away from each other. Those two properties allow the inference that we would expect a larger difference between D_SL and D_BB than 2.5 Å. By using a knowledge-based potential, which also takes the exposure of the spin labeling sites and additional geometrical information into account a better ranking of the sampled models would be possible.

Figure 5. Limitations of the CONE model.

For 1U19, the most accurate model cannot be reliably selected (A). One reason for that is, that the translation from the observed spin-spin distance to the backbone distance is inaccurate resulting in models which deviate topologically from the experimentally determined structure achieving a better agreement with the EPR distance restraints than the experimentally determined structure (B). This is demonstrated by the plot showing the correlation between the agreement with the EPR distance restraints (y-axis) and the RMSD100 relative to the experimentally determined structure (x-axis). The EPR potential does not take the exposure of the spin labeling site and the orientation of the C_α − C_β vectors into account leading to inaccuracies when translating D_SL into D_BB for the residues 7 and 170 of 1U19. Both spin labels are at the outside of the protein and on different sides of the structure leading to greater difference between D_SL and D_BB.

4.5 Ambiguities in the ranking of models remain

Although the usage of restraints obtained from EPR experiments significantly improves the discrimination of incorrect models, ambiguities in the ranking of the models remain for multiple proteins in the benchmark set. This observation was especially pronounced for the proteins 1J4N, 1PV6, 1PY6, and 1U19 (Figure 4 on page 15). In those cases, the best 10 % of the models by BCL score cover a wide range of topologies. For 1PV6, the best 10 % of the models by BCL score cover an RMSD100 range of 8 Å when compared to the experimentally determined structure. Multiple factors are contributing to this observation. First, the BCL::Fold scoring function is an inaccurate approximation of free energy, which limits its discriminative power.⁴² Although adding a term that measures agreement with experimental data will improve its discriminative power, it appears that sparse restraints from EPR data are sometimes insufficient to remove all ambiguities. This is also because, second, the translation of spin label distance distributions into a backbone structural restraint introduces a substantial uncertainty and therefore allows sometimes multiple topologies to fulfill the restraint. One side effect of these approximations is that — as shown in figure 4 on page 15 — the native structure is not always in the global minimum of the BCL scoring function. Relaxing the experimentally determined protein structures in the BCL force field indicate that the closest minimum in the scoring function is between 1.5 Å and 4.1 Å in RMSD100 separate relative to the experimentally determined structures.

5 Conclusion

The determination of membrane protein folds from EPR distance and accessibility data is within reach if these restraints aid protein folding protocols such as BCL::MP-Fold. The ability of EPR data to improve the sampling of native-like topologies and the importance of EPR accessibility data for obtaining highest contact recovery values was demonstrated. Further, the EPR specific scores allow the selection of close-to-native models, thereby overcoming a major obstacle in de novo protein structure prediction. Refining EPR distance potentials to also take the exposure of the spin labeling sites as well as relative orientation of the C_α − C_β vector might provide a more accurate translation from spin-spin distance into backbone distance, thereby further increasing model quality.