Augmented Beta rectangular regression models: A Bayesian perspective

Abstract

Mixed effects Beta regression models based on Beta distributions have been widely used to analyze longitudinal percentage or proportional data ranging between zero and one. However, Beta distributions are not flexible to extreme outliers or excessive events around tail areas, and they do not account for the presence of the boundary values zeros and ones because these values are not in the support of the Beta distributions. To address these issues, we propose a mixed effects model using Beta rectangular distribution and augment it with the probabilities of zero and one. We conduct extensive simulation studies to assess the performance of mixed effects models based on both the Beta and Beta rectangular distributions under various scenarios. The simulation studies suggest that the regression models based on Beta rectangular distributions improve the accuracy of parameter estimates in the presence of outliers and heavy tails. The proposed models are applied to the motivating Neuroprotection Exploratory Trials in Parkinson’s Disease (PD) Long-term Study-1 (LS-1 study, n=1741), developed by The National Institute of Neurological Disorders and Stroke Exploratory Trials in Parkinson’s Disease (NINDS NET-PD) network.

1 Introduction

In many clinical trials or biomedical studies, researchers often collect some outcomes in the form of percentages, proportions, fractions, and rates measured in the open unit interval (0, 1) (referred to as proportional data) (Kieschnick & McCullough, 2003). Examples include the Alzheimer’s disease assessment scale (range from 0–70, which can be transformed into the unit interval) (Rogers et al., 2012), microbial data expressed as percentages (Zhao et al., 2001), and proportion of parasitized eggs in a biological control assay (Vieira et al., 2000). Beta regression models (Ferrari & Cribari-Neto, 2004) are increasingly used by researchers from various fields to directly model the covariate effects on the proportional response through a generalized linear model (GLM) framework. When the outcomes are measured longitudinally, Beta regression models with random effects have been proposed to account for the within-subject correlation (Verkuilen & Smithson, 2012; Figueroa-Zúniga et al., 2013). However, because the support of the Beta distributions is between zero and one, boundary values zero and one are not allowed in Beta regression models. Several previous studies have discussed this issue through various approaches. Smithson & Verkuilen (2006) introduced a Lemon-squeezer (LS) transformation which first linearly transforms the variable from the original scale to the open unit interval (0, 1) and then compresses the range to avoids zeros and ones. The re-scaling might work nicely for small proportions of zeros and/or ones, but the parameter estimates can be sensitive with higher proportions (Galvis et al., 2014). Such inefficiency may be even worse with the presence of within-subject correlation or multi-level clustering in typical longitudinal data. Ospina & Ferrari (2010) proposed a mixed continuous-discrete distribution to capture the probabilities at zero and one, by using a continuous distribution on the open unit interval (0, 1) and a degenerate distribution that assigns values of zero and one with non-negative probabilities. This approach allows one to directly model the variable without transformation. Using the same idea, Galvis et al. (2014) proposed a generalized linear mixed model framework by augmenting the probabilities of zeros and ones to the Beta regression model via a zero-one-augmented Beta (ZOAB) model. They termed the model as “augmented” model rather than “inflated” model because the Beta distribution does not include zero and one in its support, similar in spirit to Hatfield et al. (2011, 2012).

The Beta regression models are based on Beta distributions, which can take on a variety of shapes to account for non-normality and skewness in proportional data by considering different values of its parameters (Johnson et al., 1994). However, as noted by Hahn (2008), García et al. (2011), and Bayes et al. (2012), the Beta distribution considers neither the tail area events nor the outlying events, fails to represent excess variability and over-occurrence of tail-area events, which could limit its applications for modeling the proportional data. Various methods have been proposed to address the issue of outlying and tail area events. Rigby & Stasinopoulos (2005) proposed a generalized additive models for location, scale and shape (GAMLSS) family and developed an R package GAMLSS (Stasinopoulos & Rigby, 2007), which allows all parameters of the response variable’s distribution to be modeled as linear and non-linear functions of the covariates. In the current context, the zero and one inflated Beta regression model (BEINF) in the GAMLSS family can be used for modeling proportional data in [0, 1]. Additionally, Hahn (2008) proposed a Beta rectangular distribution, which is a mixture distribution consisting of a Beta distribution and a uniform (rectangular) distribution between 0 and 1. The Beta rectangular distribution reduces to the Beta distribution when the mixture probability is 0. Comparing to the Beta distribution, the Beta rectangular distribution assigns more weight to extremal tail-area events, and more probability to the outliers and extremal events. Bayes et al. (2012) proposed a Beta rectangular regression model for cross-sectional data and obtained more robust inference against outlying observations than the Beta regression. However, the Beta rectangular model accounts for neither the within-subject correlation in longitudinal data nor the boundary values zeros and ones.

In this article, we generalize the model by Bayes et al. (2012) and develop an augmented Beta rectangular regression model to account for the occurrence of boundary values 0 and 1 in the closed unit interval [0, 1]. Moreover, we account for the within-subject correlation in the longitudinal data by introducing random effects under the generalized linear mixed model framework. The rest of the article proceeds as follows. In Section 2, we describe a motivating clinical trial, the proportional outcome variable of interest, and the issue of outlying observations. In Section 3, we briefly review the Beta and Beta rectangular distributions and their regression models, and develop the augmented Beta rectangular regression model. In Section 4, we discuss the Bayesian inference and Bayesian model selection criteria. In Section 5, we conduct an extensive simulation study with three settings to compare the performance of various models. In Section 6, we apply the proposed model to the motivating clinical trial. Concluding remarks and discussions are given in Section 7.

2 A motivating clinical trial

This methodological development is motivated by the Parkinson’s Disease (PD) Long-term Study-1 (LS-1 study, n=1741), developed by The National Institute of Neurological Disorders and Stroke Exploratory Trials in Parkinson’s Disease (NINDS NET-PD) network. The LS-1 study is a multi-center, double-blind, phase III study of creatine in patients with early treated PD to assess whether creatine slows PD clinical decline defined by a combination of cognitive, psysical, and quality of life measures. A total of 1741 patients with early PD were randomly assigned to receive either placebo or creatine. Participants were followed until the last enrolled participant has completed 5 years of observation. Thus, many participants had extended follow-up, to a maximum of 6 years. In-person evaluations were conducted at baseline and then annually beginning at 12 months. The LS-1 study represents the largest cohort of patients with early treated PD ever enrolled in a clinical trial (Elm, 2012; Kieburtz et al., 2015). The detailed description of the design of the LS-1 study can be found in Elm (2012).

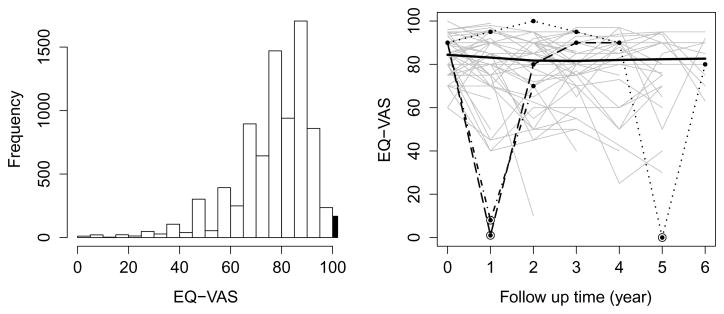
The primary outcome of interest in this article is standardized generic instrument EuroQol vertical visual analog scale (EQ-VAS), which is widely used in PD related research (Kieburtz et al., 2015). EQ-VAS is a patient-reported outcome (PRO) which takes values between 100 (best imaginable health) and 0 (worst imaginable health), on which patients provide a global assessment of their health. Participants of LS-1 study are early PD patients with diagnosis within 2 years. Because PD is a slow progression disease, it is likely that early PD patients in the LS-1 study were still in a very good health condition and they considered themselves as in best imaginable health. Each patient contributed between 1 to 7 (mean=4.73, sd=1.70) EQ-VAS measurements. There are 24 intermittent missing values observed in EQ-VAS and during the follow-up, 78 and 323 individuals died and dropped out the study, respectively. The intermittent missing data and the missing data after loss of follow-up or death are assumed to be missing at random (MAR) in this article. Figure 1 (left panel) displays the histogram based on all EQ-VAS observations. Because there is only one patient reporting zero value for EQ-VAS, we add 0.1 to that observation. However, the presence of a substantial number of 100’s (168 out of 8,227 observations, 2.04%), if unaccounted for, is a potential issue for Beta or Beta rectangular regression models.

Figure 1.

Histogram of the EQ-VAS scores (left panel) and the longitudinal profiles (right panel) of the EQ-VAS scores of 50 randomly selected subjects (grey lines) and 3 subjects with outlying observations (black dashed, dotdashed and dotted lines) from the LS-1 study and the lowess smooth curve (black solid line).

Figure 1 (right panel) displays the longitudinal profiles of the EQ-VAS scores of 50 randomly selected subjects. Because PD is a slow progression disease, it is unexpected to observe sudden value change in the outcome variables such as EQ-VAS, as indicated by the nearly-horizontal lowess smooth curve (black solid line) (Cleveland, 1979). However, compared to baseline measurements, two patients (denoted by dashed and dotdashed lines) have a sudden value drop at their year 1 follow-up visit, and return to a higher level at their year 2 visit. Similarly, another patient’s EQ-VAS score (denoted by dotted line) at the fifth year is significantly lower than the two adjacent years. Hence, these three observations are potential outliers. We divide the EQ-VAS variable by 100 to rescale it to the interval (0, 1]. We are interested in examining the effect of outliers, as well as the boundary values of 1, on the inference of regression models based on the Beta and Beta rectangular distributions.

3 Model and estimation

3.1 Beta distribution

In this section, we briefly review the reparameterization of Beta distribution (Ferrari & Cribari-Neto, 2004). A random variable Y follows a Beta distribution if the probability density function (pdf) in terms of its mean μ and precision parameter ϕ is given by,

$$f_B(Y=y\mid \mu ,\varphi )=\frac{\mathrm{\Gamma }(\varphi )}{\mathrm{\Gamma }(\mu \varphi )\mathrm{\Gamma }((1-\mu )\varphi )}{y}^{\mu \varphi -1}{(1-y)}^{(1-\mu )\varphi -1},$$ (1)

where 0 < y < 1, 0 < μ < 1, and ϕ > 0. Then we have E(Y) = μ and Var(Y) = μ(1 −μ)/(1 + ϕ). We adopt the notation Y ~ Beta(μ, ϕ).

The Beta regression model can be defined by linking the mean and covariates of interest under a GLM framework as logit(μ_i) = X_iβ, where X_i is the covariates vector of interest for subject i. The precision parameter ϕ can be either regressed on covariates after logarithm transformation or considered as a constant among different subjects. By specifying different values of μ and ϕ, the Beta distribution is flexible to allow different shapes and skewness.

3.2 Beta Rectangular Distribution

The Beta rectangular (BR) distribution is a mixture distribution consisting of a Beta distribution and a uniform (rectangular) distribution between 0 and 1. Its probability density function with support (0, 1) is given by

$$f_{BR}(Y=y\mid \mu ,\varphi ,q)=q+(1-q)f_B(y\mid \mu ,\varphi ),$$

where 0 ≤ q ≤ 1 is the mixture probability, and f_B(y|μ, ϕ) is the pdf of the Beta distribution as in (1). We denote the BR distribution as Y ~ BR(μ, ϕ, q). Obviously, if q = 1, the BR distribution reduces to the uniform (rectangular) distribution between 0 and 1 and if q = 0, it reduces to the Beta distribution f_B(y|μ, ϕ). The mean and variance of the BR distribution are $E(Y)=(1-q)\mu +\frac{q}{2}=\gamma$ and $\text{Var}(Y)=\frac{\mu (1-\mu )}{1+\varphi }(1-q)[1+q(1+\varphi )]+\frac{q}{12}(4-3q)$.

However, a regression analysis typically models the mean of the response (Ferrari & Cribari-Neto, 2004). To obtain a more appropriate regression structure for the mean of the BR distribution, Bayes et al. (2012) let $\gamma =\frac{q}{2}+(1-q)\mu$ and $\alpha =\frac{q}{1-(1-q)\mid 2\mu -1\mid }$, whose parameter space is {0 ≤ γ ≤ 1, 0 ≤ α ≤ 1}. Under this reparameterization, the pdf of the BR distribution is

$$f_{BR}(Y=y\mid \gamma ,\varphi ,\alpha )=\alpha (1-\mid 2\gamma -1\mid )+(1-\alpha (1-\mid 2\gamma -1\mid ))\times f_B\left(y|\frac{\gamma -0.5\alpha (1-\mid 2\gamma -1\mid )}{1-\alpha (1-\mid 2\gamma -1\mid )},\varphi \mid \right).$$ (2)

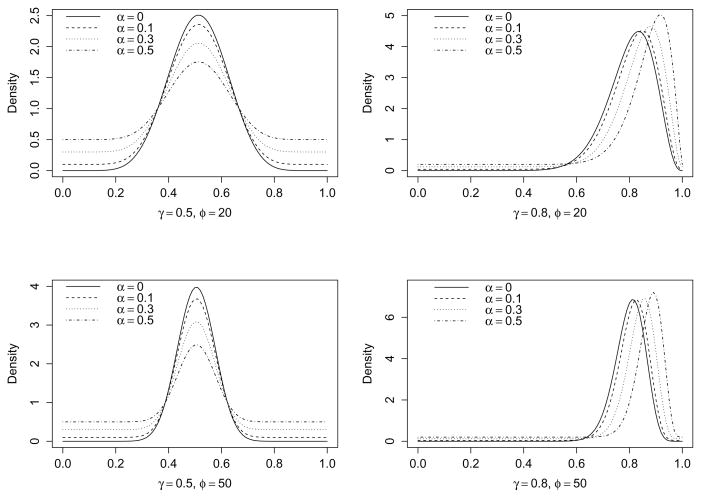
We denote the reparameterized BR distribution as Y ~ BR(γ, ϕ, α), where γ is the mean, ϕ is the precision parameter, and α is a shape parameter controlling the thickness of the tails. When the mixture probability q = 1, then α = 1 and γ = 0.5, the BR distribution reduces to the uniform (rectangular) distribution between 0 and 1. When q = 0, then α = 0 and γ = μ, the BR distribution reduces to the Beta distribution. In general, when 0 < q < 1, then 0 < α < 1, the BR distribution has heavier tails than its Beta distribution counterpart. To visualize this, Figure 2 displays the density functions of various BR distributions with different values of γ, ϕ, and α. It suggests that when α > 0, the BR distribution has a heavier tail than the corresponding Beta distribution.

Figure 2.

The density functions of various Beta rectangular distributions with different values of γ, ϕ, and α. α = 0 (solid line), α = 0.1 (dashed line), α = 0.3 (dotted line), α = 0.5 (dotdash line).

Similar to the Beta regression model, the Beta rectangular regression model can be defined as logit(γ_i) = X_iβ and the precision parameter ϕ can be either regressed on covariates or considered as a constant among different subjects.

3.3 One-augmented Beta rectangular random effects model

In this section, we generalize the Beta rectangular regression model to account for the longitudinal data structure and the boundary values zero and one. For the ease of illustration, we only consider the boundary value of one (rescaled from 100, as in Figure 1 left panel), we illustrate how to extend the model to account for both zero and one in Web Section 2. Let y_ij be the observed outcome (e.g., EQ-VAS) at visit j (j = 1, …, J_i, where j = 1 is baseline and J_i is the number of visits for subject i) from subject i (i = 1, …, I, where I is the number of subjects). Let y_i = (y_i1, …, y_iJi)′ be the outcome vector for subject i and let y = (y₁, …, y_I)′ be the observed outcome matrix. We then propose a one-augmented BR (OABR) model, denoted by Y ~ OABR(p_1ij, γ_ij, ϕ_ij, α), whose probability density function follows:

$$f(Y_{ij}=y_{ij}\mid p_{1ij},{\gamma }_{ij},{\varphi }_{ij},\alpha )=\{\begin{array}{ll}{p}_{1ij}\hfill & \text{if}{y}_{ij}=1\hfill \\ (1-p_{1ij})f_{BR}(Y_{ij}=y_{ij}\mid {\gamma }_{ij},{\varphi }_{ij},\alpha )\hfill & \text{if}{y}_{ij}\in (0,1),\hfill \end{array}$$ (3)

where p_1ij = P(Y_ij = 1), f_BR(Y_ij = y_ij |γ_ij, ϕ_ij, α) is the reparameterized BR density function given in (2), γ_ij = E[Y_ij], and ϕ_ij is the precision parameter of subject i at visit j. Next we propose the OABR regression model by regressing the covariates onto p_1ij, γ_ij, and ϕ_ij, which are transformed by some link functions:

$$\begin{array}{l}\text{logit}[p_{1ij}=P(y_{ij}=1\mid u_{i0})]={\mathit{X}}_{i0}\mathit{\omega }+u_{i0}\\ \text{logit}({\gamma }_{ij}\mid u_{i1})={\mathit{X}}_{i1}\mathit{\beta }+u_{i1}\\ \text{logit}({\varphi }_{ij}\mid u_{i2})={\mathit{X}}_{i2}\mathit{\eta }+u_{i2},\end{array}$$ (4)

where the covariate vectors X_i0, X_i1 and X_i2 can be identical or different and they include covariates of interest (e.g., treatment assignment) and potential confounding variables (e.g., subjects characteristics and socioeconomic status) from subject i. We adopt the logit link function for both p_1ij and γ_ij, while other link functions (e.g., probit and complementary log-log) can also be used. We assume that the random effects vector u_i = (u_i0, u_i1, u_i2)′ follows a multivariate normal distribution N₃(0, Σ), where

$$\mathbf{\sum }=\left\{\begin{array}{ccc}{\sigma }_1^2& {\rho }_{12}{\sigma }_1{\sigma }_2& {\rho }_{13}{\sigma }_1{\sigma }_3\\ {\rho }_{12}{\sigma }_1{\sigma }_2& {\sigma }_2^2& {\rho }_{23}{\sigma }_2{\sigma }_3\\ {\rho }_{13}{\sigma }_1{\sigma }_3& {\rho }_{23}{\sigma }_2{\sigma }_3& {\sigma }_3^2\end{array}\right\}.$$ (5)

The proposed OABR regression model can be modified to accommodate various features in the data. For example, the one-inflated Beta regression model (BEOI) in the GAMLSS family can be obtained by replacing the BR density f_BR(Y_ij = y_ij |γ_ij, ϕ_ij, α) with the Beta density in (1) or equivalently by setting α = 0. If the outcome matrix y contains both zeros and ones, the OABR regression model can be generalized to the zero-one augmented BR (ZOABR) regression model by adding the probability p_0ij = P(Y_ij = 0) to model (3) representing the probability of observing 0 and regressing covariates onto p_0ij transformed by some link function. Note that the ZOABR regression model requires an additional constraint: 0 < p_0ij +p_1ij < 1 and we illustrate in details how to impose this constraint in Web Section 2. On the other hand, if there are no zeros or ones observed, we can let p_0ij = p_1ij ≡ 0, then the OABR regression model reduces to the mixed effects BR regression model. Moreover, we only include random intercepts in model (4) for simplicity, more random effects (e.g., random slope) can be easily included in the model.

Let the parameter vector Θ = (ω, β, η, Σ, α). Conditional on the random effects u_i, all measurements of each subject are assumed to be independent. We have the full likelihood of subject i as follows:

$$L(\mathbf{\Theta },{\mathit{u}}_i;{\mathit{y}}_i)=\left[\prod _{j=1}^{J_i}p(y_{ij}\mid {\mathit{u}}_i)\right]p({\mathit{u}}_i)=\left[\prod _{j=1}^{J_i}{p}_{1ij}^{I(y_{ij}=1)}{\{(1-p_{1ij})f_{BR}(y_{ij}\mid {\gamma }_{ij},{\varphi }_{ij},\alpha )\}}^{1-I(y_{ij}=1)}\right]p({\mathit{u}}_i),$$ (6)

where I(·) denotes the indicator function, f_BR(y_ij |γ_ij, ϕ_ij, α) is the density function of the BR distribution, and p(u_i) is the density function of the random effects u_i.

4 Bayesian inference

We adopt Bayesian methods based on Markov chain Monte Carlo (MCMC) algorithms to obtain statistical inference. The fully Bayesian inference has many advantages. First, MCMC algorithms can be used to estimate exact posterior distributions of the parameters, while likelihood-based estimation only produces a point estimate of the parameters, with asymptotic standard errors (Dunson, 2007). Second, Bayesian inference provides better performance in small samples compared to likelihood-based estimation (Lee & Song, 2004). In addition, it is more straightforward to deal with more complicated models using Bayesian inference via MCMC.

4.1 Prior specification

To make inference on the unknown parameter vector Θ, we use Bayesian inference based on Markov Chain Monte Carlo (MCMC) posterior simulations. We use vague prior distributions on all elements in the parameter vector Θ. The prior distributions of all elements in ω, β and η are N(0, τ²). We use the prior distribution Inverse-Gamma(λ₁, λ₂) for σ’s to ensure positivity. Specifically, we let τ = 10 and λ₁ = λ₂ = 0.001. The prior distribution for ρ’s is ρ ~ Uniform(−1, 1). We have investigated other selections of vague prior distributions with various hyper-parameters (e.g., τ, λ’s) and obtained very similar results. Please refer to Web Section 3 for details of the sensitivity analysis results. The posterior samples are obtained from the full conditional of each unknown parameter using Hamiltonian Monte Carlo (HMC) (Duane et al., 1987; Neal, 1994) and No-U-Turn Sampler (NUTS) (Hoffman & Gelman, 2013). The HMC and NUTS samplers are implemented in Stan (Stan Development Team, 2014, version 2.6.0), which is a probabilistic programming language implementing statistical inference with HMC and NUTS samplers. The model fitting is performed in Stan by specifying the full likelihood function and the prior distributions of all unknown parameters. For large datasets, Stan may be more efficient than BUGS language in achieving faster convergence and requiring less number of samples. To facilitate easy reading and implementation of the proposed OABR regression model, the Stan codes have been posted in the Web Supplement.

To monitor Markov chain convergence, we use history plots and view the absence of apparent trend in the plots as evidence of convergence. We run multiple chains with diffuse initial values and ensure the scale reduction R̂ of all parameters are smaller than 1.1 (Gelman et al., 2013).

4.2 Bayesian model selection and influence diagnostics

There are a variety of model selection criteria in Bayesian inference. The widely used criteria conditional predictive ordinate (CPO) (Geisser, 1993; Dey et al., 1997; Sinha & Dey, 1997; Carlin & Louis, 2009; Ghosh & Hanson, 2010) is adopted to assess model fit and selection. The CPO for the (ij)th observation (observation j from subject i) is defined as

$${\text{CPO}}_{ij}=p(y_{ij}\mid y_{(ij)})=\int p(y_{ij}\mid \mathbf{\Theta })p(\mathbf{\Theta }\mid y_{(ij)})d\mathbf{\Theta },$$ (7)

where y_ij denotes the full data and y_(ij) denotes the data after deleting the (ij)th observation. CPO is a form of cross-validation with high value indicating that the data for observation (ij) can be accurately predicted by a model based on the data from all other observations. Hence, a model with larger CPO_ij for all observations suggests a better fit. Although the close form of CPO_ij is not available for our proposed model, a Monte Carlo estimator of CPO_ij can be obtained by MCMC samples ${\left\{{\mathbf{\Theta }}^{(t)}\right\}}_{t=1}^M$ from posterior distribution p(Θ|y), with M being the total number of post burn-in samples. Because p(y_ij|y_(ij)) = p(y)/p(y_(ij)) = 1/∫ p(Θ|y)/p(y_ij|y_(ij), Θ)dΘ, a harmonic-mean approximation of CPO_ij is ${\widehat{\text{CPO}}}_{ij}={(\frac{1}{M}{\sum }_{t=1}^M\frac{1}{p(y_{ij}\mid y_{(ij)},{\mathbf{\Theta }}^{(t)})})}^{-1}={(\frac{1}{M}{\sum }_{t=1}^M\frac{1}{p(y_{ij}\mid {\mathbf{\Theta }}^{(t)})})}^{-1}$ (Dey et al., 1997). A summary statistics of ${\widehat{\text{CPO}}}_{ij}$ for all individuals is the log pseudo-marginal likelihood (LPML) defined as $\text{LPML}={\sum }_{i=1}^I{\sum }_{j=1}^{J_i}log({\widehat{\text{CPO}}}_{ij})$. A larger value of LPML indicates better fit of the model. Moreover, we adopt a pseudo-Bayes factor for comparing two models defined as PBF₂₁ = exp(LPML₂ − LPML₁) (Ghosh & Hanson, 2010).

To detect the occurrence of outliers and extremal events around the tail-area, we consider the Kullback-Leibler (K-L) divergence defined as $K\{p(\mathbf{\Theta }\mid \mathit{y}),p(\mathbf{\Theta }\mid y_{(ij)})\}=\int p(\mathbf{\Theta }\mid \mathit{y})log\left(\frac{p(\mathbf{\Theta }\mid \mathit{y})}{p(\mathbf{\Theta }\mid y_{(ij)})}\right)d\mathbf{\Theta }$. Peng & Dey (1995) pointed out that K{p(Θ|y), p(Θ|y_(ij))} = log E_Θ|Y[{p(y_ij|Θ)}⁻¹]+E_Θ|Y[log{p(y_ij|Θ)}] = −log(CPO_ij) + E_Θ|Y[log{p(y_ij|Θ)}], where E_Θ|Y(·) denotes the expectation with respect to the joint posterior distribution p(Θ|y). Cancho et al. (2011) proposed the Monte Carlo estimate of the K-L divergence as

$$K\{\widehat{p(\mathbf{\Theta }\mid \mathit{y}),p(\mathbf{\Theta }\mid y_{(ij)})}\}=-log({\widehat{\text{CPO}}}_{ij})+\frac{1}{M}\sum _{t=1}^{M}log\{p(y_{ij}\mid {\mathbf{\Theta }}^{(t)})\}.$$ (8)

5 Simulation studies

In this section, we conduct an extensive simulation study with three settings to compare the performance of the one-inflated Beta (BEOI) regression model in the GAMLSS family and the proposed OABR regression model. In all three settings, we generate 200 datasets with sample size N = 1200 subjects and seven visits (baseline and six follow-up visits, J_i = 7) for each subject. The data structure is similar to the motivating LS-1 study and the continuous proportional outcome is restricted in the interval (0, 1]. We consider one covariate x_i taking value 0 or 1 each with probability 1/2 to mimic the treatment assignment. The time vector t_i = (t_i1, t_i2, …, t_i7)′ = (0, 1, 2, 3, 4, 5, 6)′, which is the same as the motivating LS-1 study.

5.1 Simulation Settings I and II: Data simulated from either the BEOI or the OABR regression model

The aims of simulation Settings I and II are to demonstrate that under model overparameterization, the OABR regression model can reduce to the BEOI regression model, while the BEOI regression model does not perform well when data are generated from the OABR regression model. In these two simulation settings, we assume that there are boundary value ones and generate the datasets from the models

$$\begin{array}{l}\text{logit}[p_{1ij}=P(y_{ij}=1\mid u_{i0})]={\omega }_0+{\omega }_1{x}_i+u_{i0}\\ \text{logit}({\gamma }_{ij}\mid u_{i1})={\beta }_0+{\beta }_1{x}_i+{\beta }_2{t}_{ij}+{\beta }_3{x}_i{t}_{ij}+u_{i1}\\ log({\varphi }_{ij}\mid u_{i2})={\eta }_0+{\eta }_1{x}_i+{\eta }_2{t}_{ij}+{\eta }_3{x}_i{t}_{ij}+u_{i2},\end{array}$$ (9)

where the random effects (u_i0, u_i1, u_i2)′ ~ N₃(0, Σ), with σ₁ = 1.2, σ₂ = 0.6, σ₃ = 0.4 and ρ₁₂ = 0.4, ρ₁₃ = 0.1, ρ₂₃ = 0.4 as the components of the covariance matrix Σ shown in (5). We set the regression coefficients ω = (ω₀, ω₁)′ = (−1.5, −0.5)′, β = (β₀, β₁, β₂, β₃)′ = (1.5, −0.5, −0.1, 0.2)′, and η = (η₀, η₁, η₂, η₃)′ = (2.5, 0.2, 0.1, 0.1)′. We set either α = 0 (Setting I) or α = 0.2 (Setting II), then the data are simulated from either the BEOI (Setting I) or the OABR (Setting II) regression models. We fit the BEOI and OABR regression models to the simulated datasets in both settings. Web Tables 1 and 2 display bias (the average of the posterior means minus the true values), standard deviation (SD, the standard deviation of the posterior means), coverage probabilities (CP) of 95% equal-tail credible intervals, and root mean squared error (RMSE) from the BEOI and OABR regression models in Settings I and II respectively. The results suggest that when data are simulated from BEOI regression model as in Setting I, both the BEOI and OABR regression models generate comparable results with very small bias, RMSE close to SD, and the coverage probability being reasonably close to 0.95. Under model overparameterization, the estimate of the shape parameter α from the OABR regression model is correctly close to zero, suggesting that it is still a reasonable model in this simulation setting. When the data are simulated from the OABR regression model in Setting II (α = 0.2), the OABR regression model can successfully recover all parameters, including α. In contrast, the BEOI regression model gives biased estimates and poor coverage probabilities for most parameters.

5.2 Simulation Settings III: Data simulated from the BEOI regression model with outliers

The aims of simulation Setting III is to compare the performance of the BEOI and OABR regression models while data are simulated from the BEOI model but contaminated with outliers, in order to evaluate the influence of outliers and extremal events around the tail-area. Setting III are similar to Setting I, but we contaminate 1% of the randomly selected observations with high scores (between 0.9 and 1) by decreasing Δ units ( $y_{ij}^{\ast }=y_{ij}-\mathrm{\Delta }$, and Δ = 0.8). To visualize the outliers, we randomly select one dataset in Setting III and plot it in Figure 3. Figure 3 displays the longitudinal profiles (upper panels) of 50 randomly selected subjects and 3 contaminated subjects (denoted by black dashed, dotted, and dotdash lines), in addition to the boxplots of all subjects (lower panels) before (left panels) and after (right panels) the outlier contamination. Some observations from the three highlighted subjects are contaminated and have some potential outliers represented by the sudden value drops. After contamination by outliers, the lower tails of the data become heavier and include more extremal values.

Figure 3.

The longitudinal profiles (upper panels) of 50 randomly selected subjects and 3 contaminated subjects (black dashed, dotted, and dotdash lines), in addition to the boxplots of all subjects (lower panels) before (left panels) and after (right panels) the outlier contamination.

We then fit the BEOI and OABR regression models in Setting III. Table 1 displays the simulation results. In comparison to the BEOI regression model, the OABR regression model provides similar estimates for parameters β and ω, but much smaller bias (e.g., −0.170 v.s. 0.041 for η₀ and 0.090 v.s. 0.035 for η₁) and much smaller RMSE (e.g., 0.180 v.s. 0.073 for η₀ and 0.123 v.s. 0.089 for η₁) for parameters η, σ’s and ρ’s. The estimates of the regression parameter vector ω from both models have small bias because the probability of being 1 is not contaminated. The estimate of the shape parameter α is 0.074 in the OABR regression model, assigning some probability to the occurrences of outliers and extremal events.

Table 1.

Simulation results when data are simulated from the BEOI (Setting III) regression models and are contaminated by 1% outliers.

	BEOI regression model				OABR regression model
	Bias	SD	SE	RMSE	Bias	SD	SE	RMSE
Setting III: Data simulated from the BEOI regression model with outliers
ω0 = −1.5	−0.001	0.071	0.068	0.071	−0.007	0.070	0.068	0.070
ω1 = −0.5	0.005	0.102	0.095	0.102	0.005	0.099	0.096	0.098
β0 = 1.5	−0.103	0.033	0.032	0.108	−0.063	0.034	0.032	0.072
β1 = −0.5	0.015	0.044	0.043	0.047	0.019	0.045	0.043	0.049
β2 = −0.1	0.007	0.006	0.005	0.009	0.004	0.006	0.005	0.007
β3 = 0.2	−0.010	0.008	0.007	0.012	−0.008	0.008	0.007	0.011
η0 = 2.5	−0.170	0.059	0.063	0.180	0.041	0.061	0.058	0.073
η1 = 0.2	0.090	0.084	0.088	0.123	0.035	0.082	0.080	0.089
η2 = 0.1	0.011	0.017	0.015	0.020	0.009	0.017	0.016	0.019
η3 = 0.1	−0.058	0.024	0.021	0.063	−0.014	0.023	0.022	0.028
σ1 = 1.2	0.000	0.057	0.055	0.057	0.003	0.055	0.055	0.055
σ2 = 0.6	−0.043	0.016	0.015	0.045	−0.029	0.015	0.014	0.032
σ3 = 0.4	0.420	0.017	0.027	0.420	−0.069	0.042	0.042	0.081
ρ12 = 0.4	−0.024	0.046	0.044	0.052	−0.006	0.042	0.042	0.042
ρ13 = 0.1	−0.133	0.065	0.060	0.148	−0.025	0.124	0.123	0.126
ρ23 = 0.4	−0.046	0.034	0.041	0.057	−0.058	0.079	0.078	0.098
α = 0					0.074	0.003	0.007	0.074

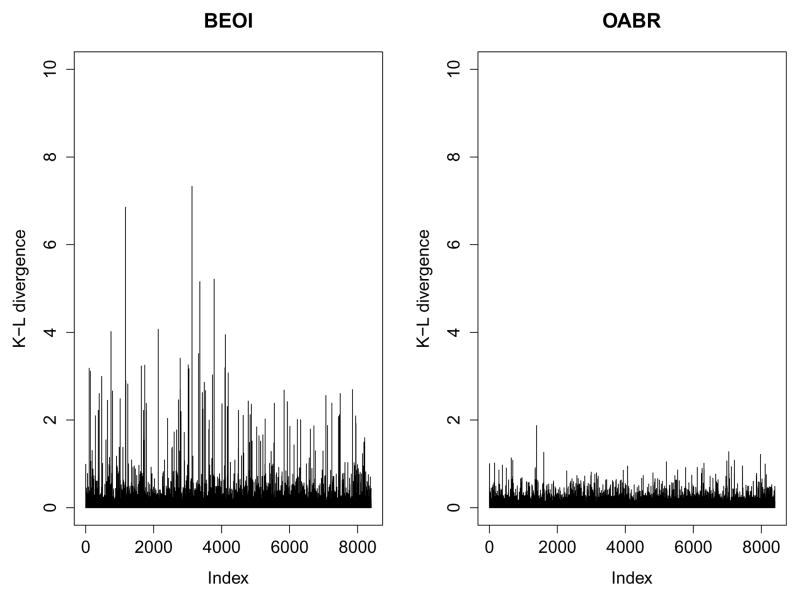
Figure 4 displays the K-L divergence measures of all observations from a randomly selected simulation dataset, estimated by the BEOI (left panel) and OABR (right panel) regression models. The BEOI regression model identifies many observations as potential outliers indicated by K-L divergence measures being larger than 3. However, using the OABR regression model, there seems to be no in-fluential observations with all K-L divergence measures smaller than 2. This figure suggests that in comparison to the BEOI model, the OABR regression model can effectively control the potential outlying observations.

Figure 4.

Estimated K-L divergence measures from the BEOI (left panel) and OABR (right panel) regression models for a randomly selected simulation dataset in Setting III.

In conclusion, the simulation results suggest that when the data are simulated from the BEOI regression model, the overparameterized OABR regression model generates results comparable to the true BEOI regression model. However, when the data are simulated from the OABR regression model, the BEOI regression model provides parameter estimates with large bias and RMSE and poor coverage probabilities. When the data are simulated from the BEOI regression model, but are contaminated by some outliers, the OABR regression model provides parameter estimates with much smaller bias and RMSE, comparing to the BEOI regression model.

6 Application to the LS-1 study

In this section, we apply the BEOI and proposed OABR regression models and the Bayesian inference framework to the motivating LS-1 study. For all results in this section, we run two parallel MCMC chains with overdispersed initial values and run each chain for 2, 000 iterations. The first 1, 000 iterations are discarded as burn-in and the inference is based on the remaining 1, 000 iterations from each chain. Good mixing properties of the MCMC chains for all model parameters are observed in the trace plots. The scale reduction R̂ of all parameters are smaller than 1.1.

In the data analysis, we consider the following covariates: the treatment assignment variable x_i (1 for treatment, and 0 for placebo), time t_ij, and time and treatment interaction. In model (4), we let X_i0 = (1, x_i), X_i1 = (1, x_i, t_i, x_i × t_i) and X_i2 = (1, x_i, t_i, x_i × t_i). We divide the EQ-VAS variable by 100 to rescale it to the interval (0, 1]. Table 2 compares the BEOI and OABR regression models using the model selection criteria discussed in Section 4.2. The OABR regression model performs better than the BEOI regression model with larger LPML. The PBF in favor of the OABR over the BEOI regression model is much greater than 100, indicating decisive evidence of choosing the OABR regression model as the final model.

Table 2.

Model comparison statistics for the LS-1 dataset. LPML: log pseudo-marginal likelihood; PBF: pseudo-Bayes factor.

	LPML	PBF
BEOI	7494.85	Ref
OABR	7504.75	≫ 100

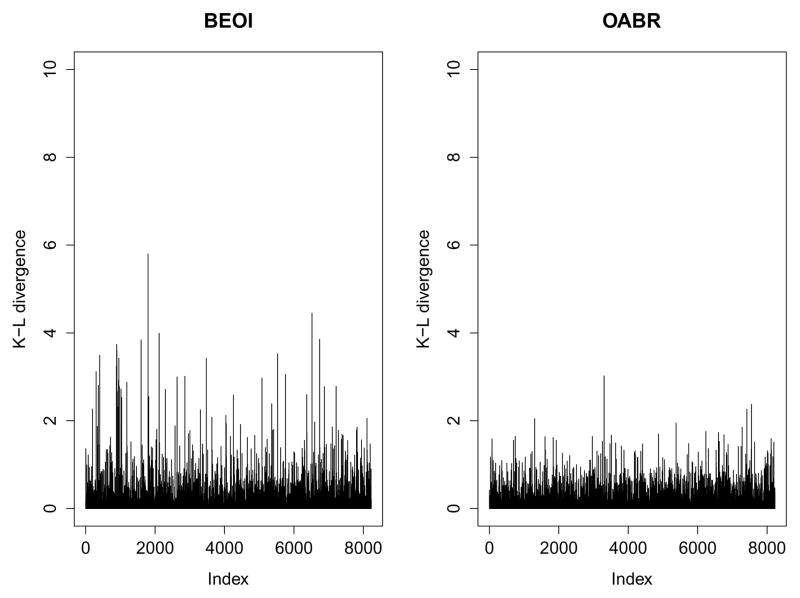
To determine the presence of possible outlying observations, Figure 5 displays the K-L divergence measures of all observations estimated from the BEOI (left panel) and OABR (right panel) regression models. The BEOI regression model identifies many observations as potential outliers indicated by the K-L divergence larger than 3. However, using the OABR regression model, there seems to be only one influential observation while all other observations have K-L divergence measures smaller than 3. This figure suggests that the OABR regression model can effectively control the potential outlying observations.

Figure 5.

Estimated K-L divergence measures from the BEOI (left panel) and OABR (right panel) regression models for the LS-1 dataset.

Table 3 displays the posterior mean, standard deviation (SD), and 95% equal-tail credible intervals from the BEOI and OABR regression models. Parameter estimates are noticeably different from two models. For creatine patients, the odds ratio of reporting 100 in EQ-VAS score is 0.604 (exp(−0.505), 95% CI: [0.348, 0.970]) comparing to the placebo patients, in the BEOI regression model, v.s. 0.607 (exp(−0.500), 95% CI: [0.361, 1.065]) in the OABR regression model. The parameters in the second part of Table 3 represent the covariates effects on the mean EQ-VAS score conditional on not being one. Thus, negative parameters suggest deterioration in patients’ global assessment of their health represented by EQ-VAS score. Conditional on other covariates and the random effects, parameter interpretation can be expressed in terms of the covariate effect on the odds $\frac{{\gamma }_{ij}}{1-{\gamma }_{ij}}$ (rescale) or $\frac{100{\gamma }_{ij}}{100-100{\gamma }_{ij}}$ in the original scale for the OABR regression model. Specifically, for creatine patients, the ratio between the expected EQ-VAS score γ_ij and the difference to perfect health (1 − γ_ij) is 0.941 (exp(−0.061), 95% CI: [0.872, 1.012]) times the ratio of placebo patients. For one year increase in time, the ratio between the expected EQ-VAS score and the difference to perfect health decreases by 7.5% (1 − exp(−0.078), 95% CI: [0.066, 0.085]). The regression parameters in the BEOI regression model can be interpreted in a similar way. The parameters in the third part of Table 3 represent the covariates effects on the precision parameter ϕ_ij. The results suggest that the precision parameter is not affected by treatment, but changes over time.

Table 3.

Results of fitting the BEOI and OABR regression models in the LS-1 dataset.

	BEOI regression model				OABR regression model
	Mean	SD	95%	CI	Mean	SD	95%	CI
For probability of being one
Int	−6.237	0.388	−7.053	−5.587	−6.367	0.369	−7.122	−5.687
Trt	−0.505	0.255	−1.056	−0.030	−0.500	0.273	−1.019	0.063
For conditional mean
Int	1.573	0.036	1.508	1.635	1.599	0.026	1.547	1.649
Trt	−0.041	0.040	−0.121	0.024	−0.061	0.037	−0.137	0.012
Time	−0.076	0.005	−0.087	−0.066	−0.078	0.005	−0.089	−0.068
Time:Trt	0.001	0.008	−0.014	0.015	0.002	0.008	−0.013	0.017
For precision parameter
Int	3.133	0.068	3.024	3.251	3.338	0.055	3.227	3.441
Trt	−0.018	0.077	−0.179	0.143	−0.075	0.076	−0.231	0.068
Time	−0.044	0.018	−0.081	−0.012	−0.057	0.019	−0.095	−0.019
Time:Trt	−0.004	0.023	−0.054	0.041	0.004	0.027	−0.049	0.056
σ1	2.555	0.241	2.084	3.081	2.632	0.225	2.212	3.086
σ2	0.670	0.013	0.646	0.697	0.654	0.014	0.627	0.681
σ3	0.802	0.025	0.759	0.853	0.588	0.031	0.524	0.648
ρ12	0.610	0.051	0.522	0.705	0.646	0.053	0.542	0.742
ρ13	−0.118	0.092	−0.258	0.068	−0.041	0.096	−0.226	0.153
ρ23	0.657	0.026	0.603	0.706	0.643	0.037	0.569	0.717
α					0.053	0.008	0.039	0.068

Note that the estimate of the correlation coeffcient ρ₁₂ between two random effects υ_i0 and υ_i1 is 0.646 (95% CI: [0.542, 0.742]). The significant positive correlation coeffcient indicates that the patients with better global assessment of their health (higher &upsi;_i1) are more likely to report perfect health (higher &upsi;_i0). The facts that the estimate of the shape parameter α is 0.053 (95% CI: [0.039, 0.068]) and the PBF in favor of the OABR regression model over the BEOI regression model is much larger than 100 (as in Table 2) suggest the existence of potential outliers and heavier tails than what the Beta distributions can model.

7 Discussion

In this article, we propose the one-augmented Beta rectangular (OABR) regression model for responses measured in the interval (0, 1], which is extended to data in the closed unit interval [0, 1]. This model accounts for not only the within-subject correlation and the occurrence of boundary values, but also the over-occurrence of tail-area events including heavy tails and outlying observations. We adopt Bayesian inference framework based on Markov Chain Monte Carlo (MCMC) simulation for parameter estimation. The extensive simulation study suggests that the proposed OABR regression model improves the accuracy of parameter estimates when outliers and heavy tails exist. In comparison, the regression model based on the Beta distribution (BEOI regression model in the GAMLSS family) provides parameter estimates with large bias and RMSE and poor coverage probabilities in the presence of heavy tails or outliers. We apply the proposed model to the motivating LS-1 study dataset. The OABR regression model has better fit than the BEOI regression model. The treatment creatine has insignificant effects in either the probability of reporting perfect health (100 in the EQ-VAS score) or the mean EQ-VAS score. This finding is not surprising because the LS-1 study was terminated early for futility based on results of a planned interim analysis (Kieburtz et al., 2015). However, the patient-reported global health assessment deteriorates along with time. The proposed model and Bayesian inference can be easily implemented by the publicly available software packages such as BUGS and Stan, and be easily accessible to by applied researchers.

There are some limitations in our proposed OABR regression model that we will address in our future study. First, the parameters of the augmented Beta rectangular distribution (e.g. p_1ij, γ_ij, and ϕ_ij) are modeled as linear functions of covariates. However, the linear assumption may not be realistic in some scenarios. As pointed out by one reviewer, the GAMLSS family allows non-linear or smooth functions in the regression models and it can handle smooth effects of covariates. In our future research, we would like to investigate a class of varying-coefficient models (Sun & Wu, 2005) that incorporate the time-dependent covariate effects via penalized splines with a truncated polynomial basis and a fixed number of knots (Ruppert, 2002). Second, both the monotone (e.g., dropout) and non-monotone (e.g., missed visit) missing exist in the LS-1 study. In this article, we assume they are all missing at random (MAR). However, monotone missing is likely to be caused by some terminal events such as dropout or death. The terminal events are often correlated with the health outcomes such as EQ-VAS and they create the issue of informative censoring. How to address the informative censoring issue in the proposed augmented Beta rectangular regression model is an interesting direction of future research. Moreover, when the non-monotone missingness due to missed visit is associated with either the unobserved value or the underlying health status (e.g., sicker patients are more likely to miss visits), the non-monotone missing data are missing not at random (MNAR) (Little & Rubin, 2002). Under the MNAR assumption, the missing data mechanism needs to be modeled simultaneously with the outcome variable to avoid biased parameter estimates (Diggle et al., 2002). In addition, we have chosen a multivariate normal distribution for the random effects vector because it is flexible in modeling the covariance structure within and between various types of recurrent events and it has meaningful interpretation on correlation. In generalized linear mixed models, misspecification of random effects distribution has little impact on the parameters that are not associated with the random effects (Jacqmin-Gadda et al., 2007; Rizopoulos et al., 2008; McCulloch et al., 2011). The impact of random effects misspecification in the proposed modeling framework warrants further investigation. We will also investigate the effect of random effects misspecification and relax the normality assumption by considering Bayesian non-parametric (BNP) framework based on Dirichlet process mixture (Escobar, 1994).