The propensity for tropomyosin twisting in the presence and absence of F-actin

Abstract

A canonical model of muscle α-tropomyosin (Tpm1.1), based on molecular-mechanics and electron microscopy of different contractile states, shows that the two-stranded coiled-coiled is pre-bent to present a specific molecular-face to the F-actin filament. This conformation is thought to facilitate both filament assembly and tropomyosin sliding across actin to modulate myosin-binding. However, to bind effectively to actin filaments, the 42 nm-long tropomyosin coiled-coil is not strictly canonical. Here, the mid-region of tropomyosin twists an additional ~20° in order to b etter match the F-actin helix. In addition, the N- and C-terminal regions of tropomyosin polymerize head-to-tail to form continuous super-helical cables. In this case, 9 to 10 residue-long overlapping domains between adjacent molecules untwist relative to each other to accommodate orthogonal interactions between chains in the junctional four-helix nexus. Extensive molecular dynamics simulations show that the twisting and untwisting motions of tropomyosin vary appreciably along tropomyosin length, and in particular that substantial terminal domain winding and unwinding occurs whether tropomyosin is bound to F-actin or not. The local and regional twisting and untwisting do not appear to proceed in a concerted fashion, resembling more of a “wringing-type” behavior rather than a rotation.

Graphical abstract

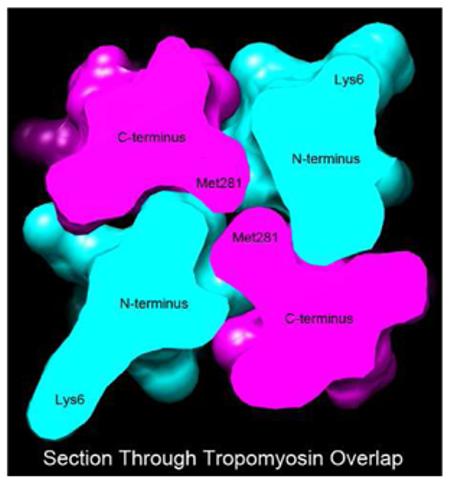
Graphical Highlight – Thick section through the center of the tropomyosin overlap domain model studied, showing the orthogonal arrangement of α-helical chains; selected residues indicated.

Introduction

The changing position of thin filament-linked tropomyosin over actin is responsible for regulating the binding of the myosin crossbridge head and consequently myosin crossbridge movement along the actin filaments that drives muscle contractility [1-6 and reviewed in 7-12]. 40 nm-long coiled-coil tropomyosin molecules link together head-to tail to form a continuous cable that follows the helical track of actin subunits along the thin filament surface [13]. Tropomyosin hovers loosely over the filament to occupy one of three average positions controlled by Ca²⁺-binding to troponin and myosin-binding to actin [5,6,14]. In the absence of Ca²⁺, troponin constrains tropomyosin in a blocking B- state position that obstructs myosin-binding. Ca²⁺ releases the troponin constraint, leading to azimuthal movement of tropomyosin some 15 to 20 Å to a “closed”, C-state position that partially uncovers the myosin-binding site, allowing weak myosin interactions to occur. The subsequent association of myosin heads activates the filament by moving semi-rigid tropomyosin [15] ~10 Å further away from the inhibitory positions on actin (the M-state), fully opening the myosin site on the thin filament, and thereby promoting strong myosin-binding and productive crossbridge cycling associated with contraction [5,6,14]. Thus, myosin binding to the thin filament alters the position of tropomyosin, while full activation of the thin filament requires binding of both calcium and myosin [16]. Further analysis of the kinetics of this three-state model (i.e. involving B-, C-, M-states) largely explains the cooperativity of the actomyosin on-off switching mechanism [17], and its various formulations as currently envisioned are thoughtfully reviewed in [18].

To operate effectively, tropomyosin molecules polymerize head-to-tail to form a seamless cable along F-actin [13,19,20]. Here, a 9 to10 residue-long C-terminal sequence splays open to engulf a more compact N-terminal segment of an adjacent coiled-coil to then generate a four-chained nexus. Previous NMR and x-ray crystallography studies indicate that the four-helix overlap nexus is made possible by the ends of the tropomyosin super-helical chains rotating by up to 90º from their predicted more canonical coiled-coil symmetry [21-23]. Absent such twisting, terminal N- and C-terminal chains of tandem molecules would lie parallel to each other, contrary to observation [19,20]. In our own studies [19,20], we measured the amount of coiled-coil twisting and untwisting occurring during MD simulations when tropomyosin was associated with the F-actin surface. Here, significant untwisting motions were observed at the N- and C-terminal ends of the molecule, but twisting and untwisting was negligible over the central two-thirds of the protein, possibly because they were dampened out by electrostatic links to oppositely charged regions of actin. In the present work, we have now examined the intrinsic capacity of tropomyosin to twist and untwist during MD when tropomyosin is free of F-actin interaction. We find that isolated tropomyosin still displays considerable twisting motions about the average supercoil configurations. Again, rotation is greatest at the molecule’s termini. In fact, even in isolation the component chains abutting the overlap nexus retain much the same propensity to diverge from the canonical twist, supporting the view that terminal domains themselves contribute to the overlap region conformation. In addition, our investigation of tropomyosin twisting raises intriguing questions about possible requirements for tropomyosin rolling behavior on the F-actin surface.

Methods

Molecular Dynamics simulation is a method of choice to study the flexural and torsional flexibility of tropomyosin [24], since it provides dynamic 3D structural data not easily obtained experimentally, for example from comparatively low resolution, 2D projections of tropomyosin recorded by electron or atomic force microscopy [15,24,25,26]. Our previous results on tropomyosin’s flexural motions were based on both experimental and in silico evidence, which were mutually supportive [15,24]. Torsional motions of tropomyosin are not easily measured experimentally, and therefore here we have relied solely on an in silico approach. In the current work, MD calculations on the blocked state tropomyosin model [20] were performed as previously described on α-striated muscle tropomyosin (Tpm1.1). MD simulations were generally run to complete 30 ns of dynamics at 300K in implicit solvent [15] using the program CHARMM c35b1 as described previously [15,27]. The implicit solvent system has the advantage that more conformational space can be explored per unit time than if simulations were carried out in explicit solvent. For example here, a 30 ns MD exploration can survey as much structural information as a 3000 ns simulation done in explicit solvent [15,28]. In contrast, MD on tropomyosin bound to F-actin was performed in explicit solvent using the program NAMD (version 2.6) [29] and the CHARMM 27 [26] force field as first carried out on actin-tropomyosin by Li et al. [30] (also see [31]). In this instance, a cushion of water molecules between actin and tropomyosin is needed to prevent tropomyosin from taking inappropriate close contacts with the F-actin surface.

The following two modifications were added to the system when MD was performed on “length-constrained” models of isolated tropomyosin. First, the centers of mass of residues 1-22 and 263-284 were constrained to their starting coordinates. This constraint preserves the end-to-end length of tropomyosin close to the starting 385 Å value over the course of the simulation. Second, the tropomyosin was modeled as if on F-actin by constraining the centers of mass of every 20-residue segment of tropomyosin to restrict a minimum distance to the z-axis (equivalent to the F-actin filament axis) of 36 Å, while maintaining an average radial distance of 39 Å. Coulombic and van der Waals interactions were monitored and quantified by CHARMM sub-routines.

Pseudo-rotated tropomyosins were generated computationally [32] and minimized [33] using previously published methods [15,30]. The program TWISTER [34] was run on MD frames and the resulting coiled-coil twist (phase) angles were compared to those obtained on the Li et al. canonical structure [15,32] over a given segmental stretch of the coiled-coil.

Results

Molecular Dynamics simulations of isolated tropomyosin in the presence and absence of F-actin

Molecular Dynamics was initiated on the Li model of tropomyosin (see Rynkiewicz et al. [33] modifications of Li et al. [15] structure). This model of tropomyosin displays canonical super-helical coiled-coil shape needed for binding F-actin and has been optimized to maximize potential electrostatic interactions between the two structures. The Li model is a refined version of a canonical structure originally developed by Holmes and Lorenz [32], but now with residue orientations and amino acid side-chain placement specified by their positions in crystal structures [15,33], in which the resulting structure was subjected to extensive energy minimization and MD analysis [33]. Experimental verification of the model is provided by the near perfect docking into reconstructed EM volumes of actin-tropomyosin generated by Li et al. [30] and by Behrmann et al. [35]. Here the model is shaped to lie at a 39 Å radius relative to the central axis of F-actin, as in cryo-EM structures of actin-tropomyosin [35,36] and as critically defined by diffraction of oriented actin-tropomyosin gels [32]. The model shows that tropomyosin is primarily linked to actin by numerous weak electrostatic interactions that provide about 8-fold greater binding energy than even weaker van der Waals forces [30,33]. While the Li et al. model displays perfect helical symmetry to match the F-actin helix, neither it nor earlier models [32] provided information on head-to-tail linkages needed to form the tropomyosin polymeric cable on F-actin.

Twisting and untwisting of single tropomyosin molecules linked to and free of F-actin

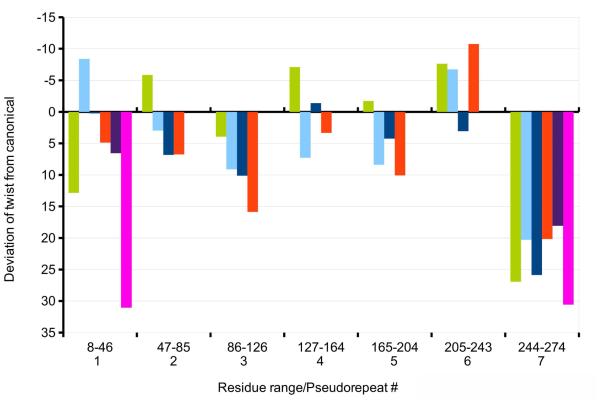
Using the program TWISTER, we previously showed [19] that twisting variance of tropomyosin throughout MD is limited when the coiled-coil is bound to F-actin. However, whereas the most of the molecule maintains near canonical conformation, its ends twist relative to each other by up to ~90°during MD. We have now extended this study to determine the average cumulative twisting and/or untwisting over each pseudo-repeat domain. The approach confirmed that only the ends of tropomyosin, and in particular the C-terminal pseudo-repeat, twist or untwist in a way to diverge appreciably from the canonical shape (Fig. 1, green bar, Table 1).

Figure 1.

Average twisting deviations diverging from canonical values for tropomyosin pseudo-repeats, taken from Table 1. The values are shown for molecular dynamics simulations of tropomyosin present on and linked to F-actin (green), as well as for isolated unconstrained tropomyosin in the blocked conformation (light blue), isolated constrained tropomyosin in the blocked conformation (dark blue) and pseudo-rotated 70°(red), the F-actin-free overlap nexus of tropom yosin (purple), and tropomyosin in the blocked state linked to F-actin (magenta). Note that the y-axis is inverted, so that positive values (facing down) represent untwisting and negative values (facing up) increases in twist. All differences are significant (n ≥ 1000 frames were averaged).

Table 1.

Twisting and untwisting of tropomyosin away from the canonical structure. Twisting values (in degrees) for indicated structures over each of the tropomyosin pseudo-repeats. Using structures sampled 20 ps apart in the molecular dynamics simulations, coiled-coil phase angles output from TWISTER were used to calculate the net twist over each pseudo-repeat, and the difference from the net twist of the canonical structure determined. These differences were then measured over a 10 to 30 ns timescale during the simulations, i.e. once the various structures equilibrated, and average and standard deviation values tabulated. N.B. that TWISTER defines the left-handed twist characterizing the tropomyosin coiled-coil as a negative phase angle, so that a positive value represents an untwisting, viz. straightening, of the coiled-coil, whereas a negative value represents an increase in left-handed twist. Note that when compared to the canonical structure, pseudo-repeat 7 (including residues 244-274) twist away from the canonical structure the most, while variance is much the same in all segments measured. Also note, when full-length tropomyosin is bound to F-actin, the N-terminal twist of the head-to-tail linked N-terminus is influenced by its neighbor’s C-terminal twist. Thus, the N-terminus is more twisted than it is in isolation, but it is not necessarily more dynamic. Standard deviations determined for the twisting values of pseudo-repeat 1 of the isolated tropomyosin overlap complex and those of the non-overlapping complexes are not greatly different; this provides additional evidence that the N-terminus is not distinctively dynamic.

Pseudo-repeat # Residue range	1 8-46	2 47-85	3 86-126	4 127-164	5 165-204	6 205-243	7 244-274	Chains across 4-helix junction
Tpm on F-actin	12.8 ± 8.4	−5.8 ± 8.4	3.9 ± 7.0	−7.1 ± 8.1	−1.7 ± 8.7	−7.6 ± 9.3	27.0 ± 8.8
Unconstrained isolated Tpm	−8.4 ± 6.6	3.0 ± 7.4	9.1 ± 9.4	7.3 ± 7.1	8.4 ± 7.7	−6.7 ± 10.6	20.3 ± 6.5
Constrained isolated Tpm	0.3 ± 8.6	6.8 ± 8.7	10.1 ± 8.7	−1.4 ± 9.3	4.2 ± 8.7	3.1 ± 8.5	25.9 ± 8.0
70° Pseudo- rotated isolated Tpm	4.9 ± 6.8	6.8 ± 8.5	15.9 ± 10.4	3.3 ± 7.7	10.1 ± 6.8	−10.8 ± 8.7	21.2 ± 8.3
Isolated N-/C- Overlap Domain*	6.6 ± 8.2						18.1 ± 8.7	90.6 ± 2.5**
Overlap Domain on F-actin***	31						31	86

^*MD run over a 300 ns timescale.

^**data from Li et al. [23] for the relative twist of C- and N-terminal chains.

^***variance not meaningful.

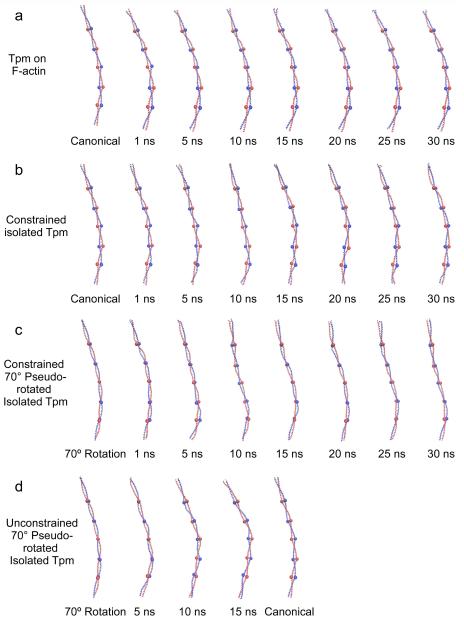
The distinctive twisting and untwisting of tropomyosin can be easily appreciated by examining individual snapshots of tropomyosin conformations during MD simulations. Relative to the starting canonical model, the ends clearly have untwisted, particularly over the C-terminal region (Figs.1, 2a, 3a). However, the rest of the molecule is relatively static without showing evidence of collective rolling over the actin substrate during MD (Figs.1, 2a).

Figure 2.

Twisting of tropomyosin during molecular dynamics simulations. Snapshots of tropomyosin coiled-coils sampled during MD, shown with the C-terminal end facing up. In the case where tropomyosin motions were associated with F-actin, only tropomyosin is shown for comparison but the underlying F-actin is not shown. In each case shown, ribbon diagrams of tropomyosin of one representative structure during the indicated time of simulation is displayed. The structure chosen had the lowest root mean square deviation of backbone atoms to the calculated average structure for the indicated time period. To visualize the changes in orientation of tropomyosin, residues 48, 90, 139, 184, and 233 have been highlighted with large spheres. Note, that in the canonical structure, the spheres lie in the plane of the page, while in the 70°rotation the spheres lie on top of one another. Also note, the twisting during MD that characterizes the tropomyosin ends, particularly at the C-terminal region, and the general lack of substantial twisting in the central domains. While localized twisting can be observed during the simulations, no concerted rotations of the entire tropomyosin chain are seen with the exception of those in panel (d), where a concerted rotation from 70°back to the canonical structure occurs.

Figure 3.

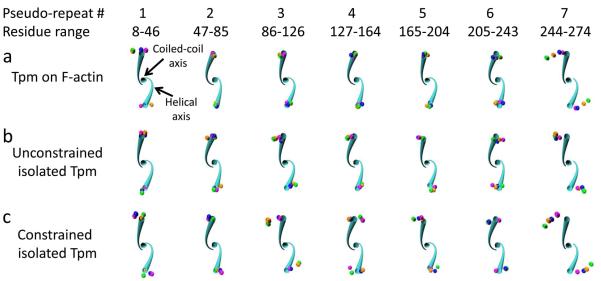
Twisting by pseudo-repeat. Twisting deviation is shown for each tropomyosin pseudo-repeat over time (colored spheres) relative to the canonical tropomyosin structure (cyan tube). The helical axes and coiled-coil axis are displayed for the canonical structure (cyan) for the indicated residue ranges. The view is oriented down the coiled-coil axis looking toward the N-terminus, so that the canonical left-handed rotation proceeds in a clockwise fashion. The pseudo-repeats of each representative structure from the indicated simulations in each panel were aligned to the canonical structure by superposition of four coordinates in the residue range: the two N-terminal helical axes coordinates and the N- and C-terminal coiled-coil axis coordinates. Spheres at the location of the C-terminal residue helical axes for 1 ns (magenta), 10 ns (orange), 20 ns (green), and 30 ns (blue) of the representative structures are shown, displaying the cumulative twist difference over the residue range. Note that pseudo-repeat 7 shows a pronounced counter-clockwise (untwisting) deviation of the representative structure compared to the canonical structure (i.e. the spheres are furthest from the cyan tube), whereas the other pseudo-repeats show little change in twist. All axes positions were calculated with TWISTER.

In order to assess the inherent tendency of the tropomyosin molecule to twist and untwist, we simulated and have now analyzed the behavior of unconstrained single tropomyosin molecules in the absence of actin. Since here isolated tropomyosin was studied, motions of tropomyosin were not dampened by interactions with actin. Snapshots taken during MD again clearly show that the C-terminal end of the molecule untwists relative to the starting canonical model (Figs. 3b). Quantitative differences in twisting of the unbound and bound molecules of the rest of the molecule are not obvious by direct inspection, particularly since the unconstrained molecule bends over time. However, twisting can be revealed quantitatively using TWISTER. When compared to the tropomyosin model bound to F-actin, the average end-to-end rotation in the mid-region of the unconstrained tropomyosin coiled-coil untwists modestly by ~20°relative to the canonical model as the free molecule relaxes from constraints imposed by the binding of the molecule to the helical F-actin substrate. (N.B., the canonical model was in fact constructed to match the F-actin helix using sub-routines developed by Lorenz et al. [32].) Interestingly, measurements of both free and bound tropomyosin indicate that the average magnitude of twisting over individual pseudo-repeats differ from each other as does the direction of their twisting (viz. some repeats show net twisting, others untwisting) (Fig. 1, cf. cyan and green bars). In both cases, the greatest torsional motions occur in the C-terminal repeat and are lowest in pseudo-repeats found in the middle of the molecule (Figs. 1-3). In general, untwisting rotations characterize these motions. No obvious concerted twisting of successive pseudo-repeats is observed in either case (bound or free) (Figs. 1, 2).

Twisting of isolated tropomyosin constrained to mimic F-actin helical geometry

In the above studies on unconstrained, F-actin-free tropomyosin, tropomyosin was able to bend and twist freely in all directions, as if in solution. Additional simulations were performed on isolated tropomyosin where its end-to-end length was constrained in order to restrict motions during MD to ones more likely to be encountered on F-actin. Here, the native 385 Å end-to-end length was maintained during MD (see Methods) as if super-helical tropomyosin was wrapped around and locked to the helical geometry of an invisible F-actin ghost filament. Thus in these simulations, tropomyosin’s longitudinal dimensions were confined within a more narrow range to simulate the regular and periodic head-to-tail packing of the molecule on thin filaments in situ and thereby restrict any tendency to lengthen nor shorten significantly (> 1 Å) from its native 385 Å repeat periodicity [6,14,32]. While this arrangement maintained the overall super-helical shape of F-actin-associated tropomyosin, the molecule otherwise was free to twist and bend locally during the simulation without the constraints of electrostatic interactions with F-actin residues. In fact, during the simulation, the tropomyosin maintained an average radius of 39 ± 2.5 Å from the center of the coiled-coil’s super-helix, consistent with experimental work [32,35,36]. Our analysis here again showed significant untwisting at the C-terminal domain, and a small degree of twisting in the middle periods (Figs. 1 (dark blue bar), 2b, 3c; Table 1). These results confirmed that the torsional behavior observed is an innate feature of tropomyosin, whether or not constrained to F-actin helical symmetry.

Time-dependent twisting

Net twisting of different pseudo-repeat regions of isolated tropomyosin (constrained and unconstrained) was also monitored as a function of time. In all cases, pseudo-repeats 2 to 6 showed relatively small deviations over time from the canonical model, with collective twist values ranging about the baseline canonical twist by ~ 20 to 25°. Back and forth twisting and untwisting (i.e. twist variance) over time relative to the reference canonical model was small (s.d. is ~ 8°). Because of the regional differences in twist, twist direction and twist variance, tropomyosin motions over time resemble a “wringing-like” action and not a pure rotation (Fig. 2).

Twisting of head-to-tail bonded tropomyosin molecules

So far, torsional motions on single unpolymerized tropomyosin models have been presented here. The behavior of the head-to-tail junctional complex was examined previously by MD to assess possible twisting of the coiled-coil chains as they approach an assembled tropomyosin overlap domain. Simulations of tropomyosin head-to-tail molecular linkages were performed in the absence and presence of F-actin by Li et al. [23] and Orzechowski et al. [20]. The TWISTER routine carried out here again revealed marked twisting at terminal pseudo-repeats, required to generate the orthogonal chain interactions (Fig. 2, purple, magenta bars), but low twist variance. Once assembled onto F-actin, as in Orzechowski et al. [20], the twist of C- and N-terminal domains becomes coupled (Fig. 1). In fact, the twist variance across the 4-helix bundle itself is comparable to that of the peripheral 2-chained coiled-coils that lead to the junctional complex (s.d. ~ 2.5°over 10 a residue distance vs. ~ 8.5°over 35 residues) (Table 1).

MD of a 70°pseudo-rotated tropomyosin model

A test model was constructed in silico in which the canonical model was pseudo-rotated by 70°degrees using the method of Lorenz et al. [32], resulting in a structure with the same global super-helical shape as in the Li model [15]. Such a model of isolated tropomyosin still can wrap around F-actin with perfect helical symmetry, but now the pseudo-rotational twisting reoriented residues facing a notional actin ghost filament, such that residues on the concave, actin-facing surface of tropomyosin in the Li model are rotated toward the convex side of the coiled coil away from actin, while other residues on the convex side in the Li model rotate to the concave side pointing toward actin (Fig. 2c). A 70°pseudo-rotation was chosen t o study, since it mirrors the overall structure of tropomyosin proposed by von der Ecken et al. [36] to have rolled around the actin filament. (N.B., as may already be evident from the above description, pseudo-rotation is defined by IUPAC as a “stereoisomerization resulting in a structure that appears to have been produced by rotation of the entire initial molecule and is superposable on the initial one” [37].)

The 70°pseudo-rotated model was constrained to a native 385 Å end-to-end length and MD then carried out on the isolated (actin-free) structure as above. On average, the new model maintained its initially imposed pseudo-rotation, with some sporadic localized back and forth twisting and pronounced twisting of terminal domains (Fig. 1, 2c). The constrained model did not converge on the canonical or any alternative conformation. Thus, during the course of the MD, the model maintained the 70°overall rotation without substantial change, while innate twisting of the C-terminal end still was evident.

However, when the length constraint was removed after 30 ns of MD and MD allowed to then progress, the model twisted to converge on the Li canonical conformation (Fig. 2d). Thus, the pseudo-rotated model no longer displayed a relatively fixed conformation: rather, the C-terminal region of the pseudo-rotated tropomyosin straightened and rotated, and then this behavior propagated towards N-terminal domains, until the new conformation was established, with bending configuration and pseudo-rotation very close to that in the original Li configuration (see Figs. 2d and Movie Supplementary Item 1). The fact that extra flexural freedom may have allowed the unconstrained tropomyosin to twist and essentially “snap” back to the control configuration reinforces the view that Li conformation is an energetically favored tropomyosin structure [15,30]. The behavior noted also supports the observation that isolated tropomyosin is biased to a unique conformation designed to bind F-actin; thereby facilitating interactions of free tropomyosin with the filament [30]. In contrast, when the 70°model was first constrained to a 385 Å end-to-end length to mimic the shape of filament-bound tropomyosin, it was unable to extend and straighten and hence pseudo-rotate during the time course of the MD.

Pseudo-rotation diminishes electrostatic interactions between tropomyosin and F-actin

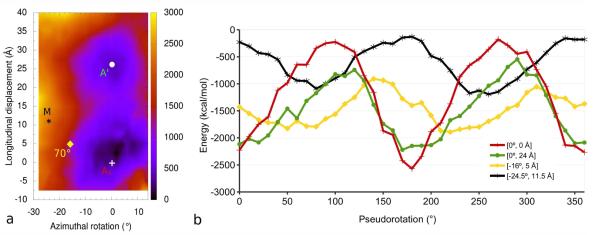
Energy landscape measurement provides a convenient way to assess the likely energy costs of sliding (or rolling) tropomyosin around F-actin [30,32,33,38]. By translating the canonical tropomyosin model over the surface of F-actin in silico, we previously showed that interaction energetics of the actin-tropomyosin complex are defined by two broad energy minima [33]. However, in these and related studies, the effect of tropomyosin pseudo-rotation was assessed only over the deepest minimum on the landscape [30,32]. We now have extended this approach by comparing the effect of tropomyosin pseudo-rotation over both energy minima regions of the landscape (Fig. 4). The procedure demonstrates that the canonical model conformation has favorable energetics over both the primary and the secondary minima, whereas pseudo-rotation of the model yields progressively less favorable interaction energetics at each of the positions. Since the two minima favor the same rotational state of tropomyosin, pseudo-rotation would be highly unlikely during possible tropomyosin movement between the two minima (Fig. 4b). Moreover, when tropomyosin is pseudo-rotated over other considerably less energetically optimal actin-tropomyosin interaction sites on the landscape, for example over the position occupied by tropomyosin in the myosin-induced M-state [35] or that chosen for a 70°rotat ed model in von der Ecken et al. [36], the corresponding change in interaction energy is not pronounced, viz. distinctive energy minima are not observed, as was previously recognized by Lorenz et al. [32] using less robust models. Thus, pseudo-rotation at these sites did not improve interaction energetics, which remained comparatively unfavorable (Fig. 4b).

Figure 4.

The effect of pseudo-rotation on Coulombic interaction energy between tropomyosin and F-actin. Four positions of tropomyosin on actin (a) were selected for analysis from the previous energy landscape [33]: primary (+) and secondary (○) energy minima, M-state (✱), and the position chosen by von der Ecken [36] (◊). Canonical tropomyosin was pseudo-rotated in 10°inc rements on F-actin, the structures minimized, and the Coulombic interaction energy calculated (b) for the primary (red) and secondary (green) energy minima in the energy landscape, as well as the M-state position [35] (black), and the von der Ecken et al. position (yellow). Note the energy minimum for unrotated canonical tropomyosin at both the primary and secondary positions on F-actin in (b) (i.e. for A_i [0,0] and A’ [0,24] positions in the landscape, red and green tracing in the graph). Note also that 0° and 180°rotations are redundant, with one of the two chains in the tropomyosin coiled-coil replacing the other. Pseudo-rotation of tropomyosin in the M-state or in the von der Ecken positions, for example by 70°, does not improve interaction energetics, which remain unfavorable relative to those of canonical tropomyosin located over the primary and secondary minima.

Discussion

The elastic modulus and flexural and torsional stiffness define the mechanical properties of a rod-like material such as tropomyosin. We previously characterized the anisotropic flexural mobility [15, 24] displayed by isolated tropomyosin and its elasticity when on F-actin [19]. We have now quantified the trajectory of tropomyosin twisting during MD on our atomic model of tropomyosin [15,33]. Our MD simulations demonstrate that terminal pseudo-repeats untwist considerably from the canonical model while relatively minor twisting and untwisting characterizes the central five periods of the molecule. The divergence observed at the ends of tropomyosin are conducive to forming orthogonally oriented head-to-tail interactions, as previously concluded [23]. This conformational adjustment at the C- and N-termini allows the tightly coiled N-terminal residues of one tropomyosin to insert into rotated and splayed C-terminal chains of an adjacent molecule [20-23]. This process promotes tropomyosin polymerization during filament assembly, while trapping the N- and C-terminal α-helices in a four-chained overlap junction in the assembled filament [39]. The work performed here indicates that the ability of the ends of tropomyosin to be twisted relative to each other by up to 90°is an intrinsic property of the tropomyosin molecule and not induced by actin-binding. MD and electron microscopy demonstrate that, once formed, the overlap nexus develops comparable stiffness to the rest of the molecule; it does not confer extra flexural or torsional freedom onto the tropomyosin cable [20,23,40] to promote further tropomyosin cable rotation. Thus, the overlapping nexus does not act as a molecular universal joint. In fact, residue-residue axial and rotational shifts or Crick-angles along the nexus, when calculated by the program samCC [41] (data not shown), showed only small deviations from stereotypical, hence very stable, four-helix bundles, a protein motif not expected to enhance the flexural or torsional flexibility of the tropomyosin cable [42].

Flexural and torsional stiffness variation and tropomyosin assembly on F-actin

The binding of single tropomyosin molecules onto actin is exceedingly weak [43]. Still the molecule is biased to form periodic Coulombic interactions with the actin surface, while at the same time assuming an average pre-shaped contour to virtually match helical actin, thus facilitating favorable interaction dynamics during thin filament assembly [14,15,30]. We have argued [39] that the weak binding is responsible for linear diffusion of coiled-coil tropomyosin on actin filaments during the assembly process. It follows that as “shuttling” tropomyosin molecules encounter each other, head-to-tail interactions will readily occur and tropomyosin will form continuous gap-free cables along thin filaments. However, experimental verification is lacking since the resolution currently achieved in otherwise very elegant light microscopy studies was not sufficient to follow gap-closure definitively [44-46].

If elongated single tropomyosin molecules were completely rigid super-helices, docking the protein onto the surface of 7 successive actin subunits would require near-perfect alignment over a 40 nm regulatory-unit span. Since such binding events would be improbable, we propose that the molecule must retain some plasticity to conform to the filament surface effectively. In fact, the high persistence length of isolated tropomyosin, limiting end-to-end curvature variation to about ± 30°, does not preclude limited local flexural motion (or twisting) during filament assembly despite tropomyosin being semi-rigid [24]. Nevertheless, as thin filament assembly progresses and the tropomyosin head-to-tail polymer grows, the structural mechanics of tropomyosin necessarily become increasingly restrictive [19,23,39], with flexural motions dampened by actin-binding overlap domain formation. Clearly, the challenge is to define the mechano-chemical rules that govern tropomyosin assembly and distinguish them from those that characterize tropomyosin in the assembled filament (see commentary in [39]). At the same time, one must guard against conflating tropomyosin thermal stability, residue-residue vibrations, average curvature and twist together with flexural and torsional flexibility (i.e. curvature and twist variance).

The collective interactions of the polymerized tropomyosin cable bound to F-actin are transformative with the apparent affinity of tropomyosin rising at least 1000-fold between the initial binding events of single molecules and cable completion [43]. Yet even after full assembly of the thin filament, tropomyosin binding to actin at a local level remains weak. Hence, tropomyosin position over the charged actin surface can be readily perturbed by the additional effects of troponin, and either nucleotide-free myosin, myosin-ADP or myosin-ADP·P_i – binding during thin filament regulatory transitions [5,6] (or by interactions dependent on ancillary actin-binding proteins such as caldesmon, calponin [47,48] or myosin-binding protein-C [49]). This dichotomy, strong overall interaction that maintains filament integrity, but weak local binding that enables tropomyosin-based regulation, is an inherent characteristic of thin filament interactions.

Pseudo-rotational preferences

MD shows that tropomyosin’s overall torsional stiffness increases modestly once bound to F-actin (end-to-end twisting deviation drops from ± 15-20°[23] to about ± 12°once bound to actin [19]). The low value for composite torsional freedom, and the corresponding low values for more localized twisting determined here, appear unlikely to support a 70 to 90°rolling mechanism proposed f or tropomyosin [36,50] on F-actin. However, while canonical tropomyosin models appear to retain their average super-helical shape and initial pseudo-rotation during MD, tropomyosin models that have been straightened [15] or, as now demonstrated, pseudo-rotated by 70°, snap back to the canonical model during MD. In the case of the pseudo-rotated model examined here, a 110°convergence to the canonical model is stepwise : C-terminal regions of the structures first straighten out and then twist and bend locally, with the process propagating along the molecule (Fig. 3; see Movie, Supplementary item 1). On the other hand, when constrained to a 385 Å end-to-end length, as if on F-actin, and thereby restricted from straightening out, the 70°model di d not reconfigure into the canonical ground-state Li-Rynkiewicz structure during a 30 ns MD. Thus, when straightening is proscribed, as is the case on filaments in situ or when prevented here in silico, spontaneous pseudo-rotational rolling of filament-bound tropomyosin appears to be improbable.

Energy landscapes show that the convergence of the 70° pseudo-rotated model to the canonical structure would be favored energetically when tropomyosin is bound to F-actin. Thus, it follows that pseudo-rotational rolling of ground-state canonical tropomyosin to the 70° model may only be likely if an external energy load has first been applied to the tropomyosin coiled-coil, as we mimicked in silico. Whether or not troponin and/or myosin binding to F-actin-tropomyosin can impose such a pseudo-rotational change in conformation remains unproven. Thus, an important goal is to determine how the binding of troponin and myosin modify the actin-tropomyosin energy landscape. We await high resolution structural solutions of the thin filament in all regulatory states to help to define the nuances of tropomyosin movement on actin.

Highlights.

• Tropomyosin pseudo-domains do not twist or untwist in concert.

• C- and N-terminal domains are oriented at ~90°to form 4-helix overlap connections.

• C- and N-terminal rotation is intrinsic to tropomyosin and not induced by F-actin.

• Central domains of tropomyosin untwist by an average of ~20°when free of F-actin.

• Tropomyosin pseudo-rotated by 70°reverts to a canonical conformation.