Task-specific feature extraction and classification of fMRI volumes using a deep neural network initialized with a deep belief network: Evaluation using sensorimotor tasks

Abstract

Feedforward deep neural networks (DNN), artificial neural networks with multiple hidden layers, have recently demonstrated a record-breaking performance in multiple areas of applications in computer vision and speech processing. Following the success, DNNs have been applied to neuroimaging modalities including functional/structural magnetic resonance imaging (MRI) and positron-emission tomography data. However, no study has explicitly applied DNNs to 3D whole-brain fMRI volumes and thereby extracted hidden volumetric representations of fMRI that are discriminative for a task performed as the fMRI volume was acquired. Our study applied fully connected feedforward DNN to fMRI volumes collected in four sensorimotor tasks (i.e., left-hand clenching, right-hand clenching, auditory attention, and visual stimulus) undertaken by 12 healthy participants. Using a leave-one-subject-out cross-validation scheme, a restricted Boltzmann machine-based deep belief network was pretrained and used to initialize weights of the DNN. The pretrained DNN was fine-tuned while systematically controlling weight-sparsity levels across hidden layers. Optimal weight-sparsity levels were determined from a minimum validation error rate of fMRI volume classification. Minimum error rates (mean ± standard deviation; %) of 6.9 (± 3.8) were obtained from the three-layer DNN with the sparsest condition of weights across the three hidden layers. These error rates were even lower than the error rates from the single-layer network (9.4 ± 4.6) and the two-layer network (7.4 ± 4.1). The estimated DNN weights showed spatial patterns that are remarkably task-specific, particularly in the higher layers. The output values of the third hidden layer represented distinct patterns/codes of the 3D whole-brain fMRI volume and encoded the information of the tasks as evaluated from representational similarity analysis. Our reported findings show the ability of the DNN to classify a single fMRI volume based on the extraction of hidden representations of fMRI volumes associated with tasks across multiple hidden layers. Our study may be beneficial to the automatic classification/diagnosis of neuropsychiatric and neurological diseases and prediction of disease severity and recovery in (pre-) clinical settings using fMRI volumes without requiring an estimation of activation patterns or ad hoc statistical evaluation.

Introduction

Since the development of an efficient weight initialization scheme for a deep belief network (DBN) using the restricted Boltzmann machine (RBM) (Hinton, 2002; Hinton and Salakhutdinov, 2006) and the stacked auto-encoder (SAE) (Bengio et al., 2007), artificial deep neural networks (DNNs) have been gainfully utilized for the feature extraction and/or classification of multimedia data, such as image (Krizhevsky et al., 2012) and speech (Hinton et al., 2012a) data, and have shown unprecedented classification performance. Recently, the convolutional variants (convolutional neural networks or CNNs) trained on millions of natural images have been used to model internal representations of human visual cortices along the ventral pathway (Güçlü and van Gerven, 2015; Khaligh-Razavi and Kriegeskorte, 2014). The biological plausibility of the hidden representations of the trained CNNs has been shown using a linear mapping function between the hidden representations and fMRI brain activity (Güçlü and van Gerven, 2015; Van Gerven et al., 2010) and using representational similarity/dissimilarity analysis (Khaligh-Razavi and Kriegeskorte, 2014).

Using an RBM as a building block of the DBN, Hjelm et al. (2014) presented a comprehensive picture of the RBM application to fMRI data, in which the RBM was applied to both simulated and real auditory odd-ball task fMRI and compared the RBM to conventional single-matrix factorization methods, including independent component analysis (ICA). The results showed the RBM’s ability to extract both temporal and spatial patterns from the 4-D fMRI volumes and to obtain slightly superior temporal features than the ICA (Hjelm et al., 2014). More recently, DNNs have directly been applied to neuroimaging data to obtain efficient feature representations (Kim et al., 2016; Plis et al., 2014; Suk et al., 2014; Zhang et al., 2015b). Zhang et al. (2015) employed CNNs to extract hidden feature representations from anatomical MRI data, such as T1 and T2 images, and a fractional anisotropy map from the diffusion-weighted images. The gray matter, white matter, and cerebrospinal fluid regions were automatically segmented using the data from infants with an isointense phase (i.e., almost identical gray and white matter intensities) (Zhang et al., 2015b). In another recent study, Plis et al. (2014) used structural MRI data as the input for a DBN that consisted of RBMs as building blocks. The authors performed (1) classification to discriminate schizophrenia patients from healthy controls and (2) the prediction of the disease severity of patients with Huntington’s disease. The resulting classification accuracy and prediction capacity were substantially increased when the three-layer DBN, rather than one-layer or two-layer DBNs, was used for classification and prediction (Plis et al., 2014). More recently deep learning has also been used to implement non-linear ICA applied to structural brain imaging data (Castro et al., 2015) and even to perform multimodal data fusion of brain structure and function (Amin et al., 2015).

Despite these recent investigations of the feature extraction and classification of MRI/fMRI data using deep networks, no study has explicitly employed whole-brain fMRI volume as an input for the DNN and blindly extracted hidden features from the fMRI data. Schmah et al. (2008) developed an RBM model-based classifier and applied them to fMRI data to classify (1) either finger or wrist movement and (2) either the early or the late post-stroke period for stroke-recovery patients. However, the input fMRI data were not from the whole brain but, rather, one slice or a few slices due to the small number of samples compared to input dimensions, and the classifier consisted of a single-layer RBM rather than a multiple-layer DBN (Schmah et al., 2008). In our study, we were motivated to deploy the DBN to initialize the hidden features of whole-brain fMRI volumes via the representation of non-linear hidden layers. Consequently, classification of a single fMRI volume would be enabled using the fully connected feedforward DNN (denoted by DNN) initialized with the same number of hidden layers as the pretrained DBN but with the addition of an output layer with class indices in the fine-tuning phase (Kim et al., 2016; Plis et al., 2014). We anticipated that the representations of the non-linear hidden layers from the trained DNN would provide significantly task-specific feature representations. Using hidden representations, the classification performance was evaluated by deploying classifiers such as a softmax and a support vector machine (SVM) (Cortes and Vapnik, 1995; Lee et al., 2009).

The curse of dimensionality was evident when the DNN with tens of thousands of input nodes (i.e., number of voxels; more than approximately 70,000 voxels within a whole brain with a 3-mm isotropic voxel size from a single fMRI volume) was trained on a limited number of input samples. For example, single subject fMRI collection at 2 seconds TR (time of repetition) for one hour results merely in 1,800 fMRI volumes, which is significantly smaller than the number of voxels per volume. To address this issue, explicit control of the weight-sparsity level via L1-norm regularization of the DNN weights has been shown to be beneficial (Kim et al., 2016). In the current study, the DBN was adopted for greedy layer-wise pretraining of the DNN. In the fine-tuning phase of the training the sparsity levels of the weight parameters for each of the hidden layers were automatically adapted to maintain the desired percentage of active (non-zero) weights (Kim et al., 2016). The efficacy of our proposed approach to classifying a single fMRI volume using the DBN pretrained DNN with an explicit weight-sparsity control scheme is presented using the fMRI data acquired from four sensorimotor tasks.

Materials and Methods

Overview

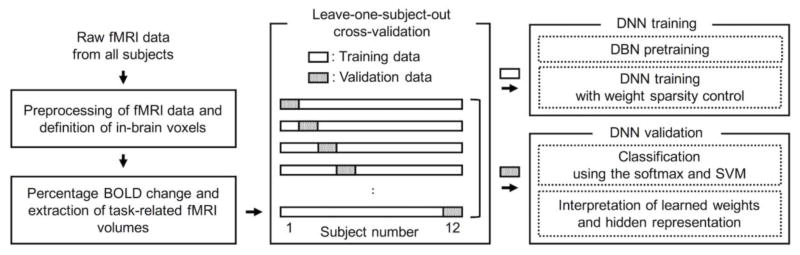
Figure 1 illustrates a flow diagram of our overall study. Raw blood-oxygenation-level-dependent (BOLD) fMRI data were preprocessed, and in-brain voxels were included in subsequent analyses. The percentage signal change with respect to baseline BOLD intensity was calculated, and task-related fMRI volumes were considered as input to the DNN. Based on a leave-one-subject-out cross-validation scheme from a total of 12 subjects, training data (i.e., data from 11 training subjects) were used for the DBN pre-training followed by the DNN fine-tuning across all combinatorial scenarios of weight-sparsity levels across all hidden layers. The trained DNN was validated using the data from one remaining validation subject by calculating the classification error of the softmax output layer or of the SVM classifier using the top hidden layer output. Based on the DNN with a minimum error rate, the learned weights and representation of hidden layer output were interpreted. A nested cross-validation framework was also employed to optimize the target percentage of non-zero weights in the three-layer DNN.

Figure 1.

Flow diagram of our overall study. fMRI, functional magnetic resonance imaging; BOLD, blood-oxygenation-level-dependent; DNN, deep neural network; DBN, deep belief network; SVM, support vector machine.

Participants and fMRI data acquisition/preprocessing

An institutional review board (IRB) at Korea University approved the study protocol. Participants provided written consent forms and were compensated for their participation as denoted in the IRB documents. Twelve right-handed, young, and healthy volunteers without any neuropsychiatric or neurologic problems participated (age = 25.0 ± 2.0 years; handedness = 88.3 ± 10.8 using the Edinburgh handedness inventory (Oldfield, 1971)). Participants performed each of the four sensorimotor tasks, including left-hand clenching (LH), right-hand clenching (RH), auditory attention (AD), and visual stimulus (VS) tasks, and one fMRI run per task was acquired (Kim et al., 2012). Each fMRI run (150 s) included a rest period (30 s) in the beginning and three blocks of task periods (20 s per block) alternating with a rest period (20 s). In the LH and RH tasks, participants clenched their left or right hand approximately twice per second. In the AD task, the participants listened to sounds of 1 kHz during the task period and 900 Hz during the rest period. In the VS task, the participants watched an alternating black and white checkerboard with 8 Hz during the task period and watched a black screen during the rest period. Task instructions were delivered to participants during the task period via MR-compatible goggles (NordicNeuroLab Inc., Bergen, Norway).

BOLD fMRI data were acquired using a standard gradient-echo echo-planar imaging pulse sequence (TR/TE = 2000/30 ms; flip angle = 90°; in-plane voxels = 64×64; field-of-view = 240×240 mm²; 36 axial slices; 4 mm slice thickness without a gap; voxel size = 3.75×3.75×4.0 mm³) and a 3-T Tim Trio MRI scanner with a 12-channel head coil (Siemens, Erlangen, Germany). For each fMRI run, the first five volumes (10 s) were discarded to equilibrate the T1 effect. The remaining 70 fMRI volumes (i.e., 140 s) were preprocessed using the SPM8 software toolbox (www.fil.ion.ucl.ac.uk/spm) with standard options, including slice timing correction, motion correction, spatial normalization to the Montreal Neurological Institute space with a 3-mm isotropic voxel size, and spatial smoothing using an 8-mm full-width at half-maximum Gaussian kernel. To evaluate the quality of the acquired fMRI data and preprocessing, an individual activation map from a general linear model (GLM) was obtained using the onset and duration of the task paradigm convolved with a canonical hemodynamic response function, as implemented in SPM8. Then, a one-sample t-test was performed to calculate the group inference of the GLM activation maps across the 12 subjects. Multiple comparisons were addressed using a family-wise-error (FWE) corrected p-value estimated from a random field theory as implemented in SPM8 if applicable.

Preparation of fMRI volumes as input to the DNN

The voxels whose BOLD intensities were greater than 20% of the maximum BOLD intensity for each preprocessed fMRI volume were defined as an in-brain mask from the fMRI volume. Then, the in-brain mask that overlapped across all fMRI volumes and all subjects was used to define the final set of input voxels (Kim et al., 2013; Kim and Lee, 2013), resulting in a total of 74,484 in-brain voxels. The BOLD intensities of the fMRI volumes within a task-related period (i.e., three blocks of 20-s task periods after a 6-s delay from the task onset for each fMRI run) were normalized to percent signal change relative to the average BOLD signal with the 80-s baseline period. The 30 task-related fMRI volumes (i.e., 60-s task-related period across the three task blocks with 2-s TR) for each fMRI run were used as the input of the DBN and DNN (dimension of one input sample = 74,484×1). A total of 1,440 fMRI volumes (i.e., 30 volumes/run × 4 runs/subject × 12 subjects) were available across all tasks and all subjects.

Pretraining of the DNN using DBN

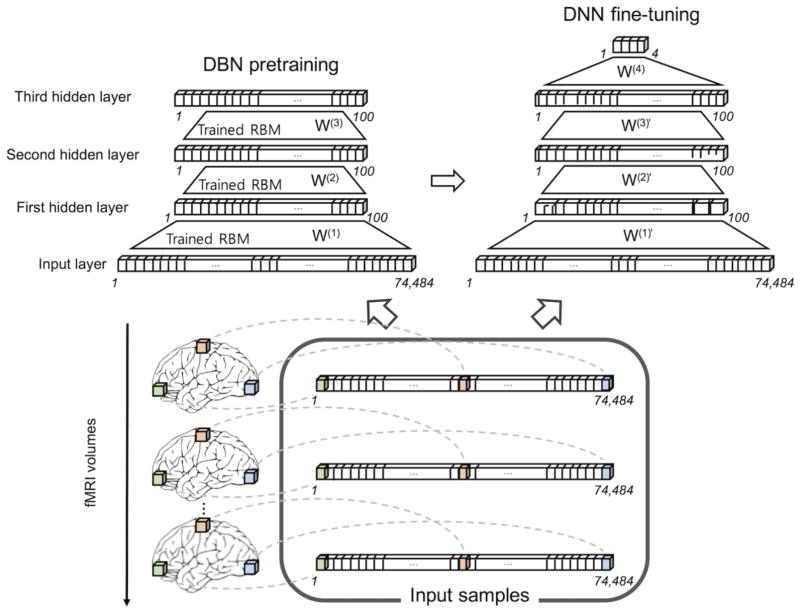
A DBN is a multi-layer directed network whose layers were greedy layer-wise trained using the unsupervised undirected RBM ((Hinton et al., 2006); see Appendix A for details of the DBN training algorithms). The DBN was used to initialize/pretrain the DNN as shown in Fig. 2 since it has been reported that pretraining the DNN using the DBN facilitates the convergence of the DNN during fine-tuning (Erhan et al., 2010). The weights of the RBM were initialized using random values within the range of $\pm 2\sqrt{6/(n_{in}+n_{\mathit{out}})}$, where n_in and n_out are the numbers of nodes in the visible and hidden layers (Kim et al., 2016). The biases were initially zero. The weights and biases were trained over 300 epochs. The learning rates were set to 10⁻⁵, 10⁻², and 10⁻² for the first, second, and third layers, respectively. The momentum factor was 0.5 and the mini-batch size was 10. Once the Gaussian-Bernoulli RBM between the input layer and the first hidden layer was trained, the weight parameter, W⁽¹⁾, was fixed and the output of the first hidden layer was used as the input (i.e., visible nodes) to a Bernoulli-Bernoulli RBM between the first and second hidden layers, after which the stacking of the Bernoulli-Bernoulli RBMs continued to all hidden layers of the DBN (Fig. 2). The hyperbolic tangent (tanh, (Hjelm et al., 2014)) and rectified linear unit (ReLU, (Dahl et al., 2013); see “Appendix C. Rectified linear unit” for details) were used as node functions.

Figure 2.

Schematics of the DBN pretraining followed by the DNN fine-tuning exemplified for three hidden layers. The input layer consisted of 74,484 in-brain voxels of an fMRI volume, each hidden layer consisted of 100 hidden nodes, and the output layer consisted of four nodes to assign each of the four tasks (i.e., LH, RH, AD, and VS). The DBN and DNN were trained using 1,320 fMRI volumes of input samples across 11 training subjects (i.e., 30 volumes per task for each subject), and the trained DNN was validated using 120 fMRI volumes from one remaining validation subject. LH, left-hand clenching; RH, right-hand clenching; AD, auditory attention; VS, visual stimulus.

Fine-tuning of the DNN with weight-sparsity control

The pretrained DBN weights were used as the initial values of the DNN (Fig. 2). An output layer with four nodes for the four tasks was added to the top hidden layer. Then, the DNN was fine-tuned using a back-propagation algorithm by minimizing the mean-squared error (MSE) between the four actual output values and the desired ones (see Appendix B for mathematical details). At each layer four target percentages of non-zero values of weights (i.e., ρ= 0.2, 0.4, 0.6, and 0.8) were used as candidate weight-sparsity levels. All combinatorial scenarios of these percentages of non-zero weights across the hidden layers were used to set the weight-sparsity levels of the DNN, and the corresponding classification accuracies were obtained. The overall learning rate α(t) was initially 10⁻³ and was gradually reduced after 100 epochs to 10⁻⁶, μ was 10⁻³, and ε was 10⁻³. The momentum factor was set to 0.1. The DBN and DNN algorithms, including functions to implement feed-forward neural networks, were adopted from the DeepLearnToolbox implemented in the MATLAB environment (github.com/rasmusbergpalm/DeepLearnToolbox) and were modified to apply our proposed weight-sparsity control scheme. DNNs and DBNs with one, two, and three hidden layers were used. The number of hidden nodes at each hidden layer was 100 and the mini-batch size was 10. Tanh and ReLU functions were used as activation functions of hidden nodes by matching the activation function of the DBN pretraining.

Training the DNN and classification via a leave-one-subject-out cross-validation

Based on a leave-one-subject-out cross-validation scheme, 1,320 fMRI volumes from 11 subjects were used to train the DBN and DNN, and then 120 fMRI volumes from one remaining validation subject were used to evaluate the classification performance using the trained DNN (Figs. 1 and 2). The softmax and SVM classifiers, applied to the output layer of the DNN and to the top hidden layer, respectively, were used to determine the target class label of the input fMRI volume from the validation subject. A linear SVM was adopted to classify the representations of the hidden layer of the trained DNN without an additional non-linear transformation (essentially, treating DNN as a data-driven feature-space projection method). The soft margin parameter C was selected by cross validating grid search on the interval 2⁻⁵, …, 2¹⁵ with step of 2² in the leave-one-subject-out cross-validation. The SVM classifier implemented in the LIBSVM software toolbox in the MATLAB environment (www.csie.ntu.edu.tw/~cjlin/libsvm) was used. The error rates obtained across the four target percentages of non-zero weights for each layer were evaluated using one-way analysis-of-variance (ANOVA) and then an ad hoc paired t-test. A Bonferroni-corrected p-value was used for multiple comparison correction.

To impose further sparsity to the weight parameters between the input layer and the first hidden layer (i.e., the receptive fields of the voxels to the first hidden layer), additional target percentage of non-zero weights of 0.1 and 0.05 were adopted when the three-layer DNN was fine-tuned, and the classification performance was evaluated. For visualization, the representations of the hidden node output (100×1 vector) in the top hidden layer of the fine-tuned DNN were transformed into 2-D representations (2×1 vector) using the t-distributed stochastic neighbor embedding (t-SNE) method (Hinton and Salakhutdinov, 2006; Van der Maaten and Hinton, 2008).

Interpretation of weight parameters of the DNN

Performance of the DNN classifier is often attributed to the efficiency of data (in our case fMRI volumes) representation obtained at the top hidden layer. This representation is completely determined by the value of free parameters-also called receptive fields or features. In this work, high level features at level l (i.e., the l^th hidden layer) were computed as a linear composition of weight-feature matrices from all lower layers as follows (Erhan et al., 2009):

$${\mathbf{F}}_{\mathbf{W}}^{(l)}={\widehat{\mathbf{W}}}^{(l)}{\widehat{\mathbf{W}}}^{(l-1)}\cdots {\widehat{\mathbf{W}}}^{(1)},$$ (1)

$${\widehat{\mathbf{W}}}^{(m)}=\left[\begin{array}{ccc}{\widehat{\mathbf{w}}}_1^{(m),T};& \cdots ;& {\widehat{\mathbf{w}}}_n^{(m),T}\end{array}\right],\text{and}{\widehat{w}}_{ij}^{(m)}=\{\begin{array}{cc}{w}_{ij}^{(m)},& \text{if}\mid w_{ij}^{(m)}\mid \ge c_j^{(m)}\\ 0,& \text{otherwise}\end{array},$$ (2)

where the superscript and subscript denote the hidden layer index and node index, respectively; $c_j^{(m)}$ is the threshold value among the elements of $\mid {\mathbf{w}}_j^{(m)}\mid$ to include a subset of the elements of ${\mathbf{w}}_j^{(m)}$ with the largest magnitude. A subset of the elements (i.e., 5, 10, 20, 50, and 80) as well as all 100 elements for each weight vector ${\mathbf{w}}_j^{(m)}$ (i.e., the weight vector from the nodes at the (m-1)^th layer to the j^th node at the m^th layer) were used to calculate the weight-feature representation. Thus, the robustness of the reconstructed weight-feature representation was evaluated when the elements with lower magnitude in the weight vectors were ignored.

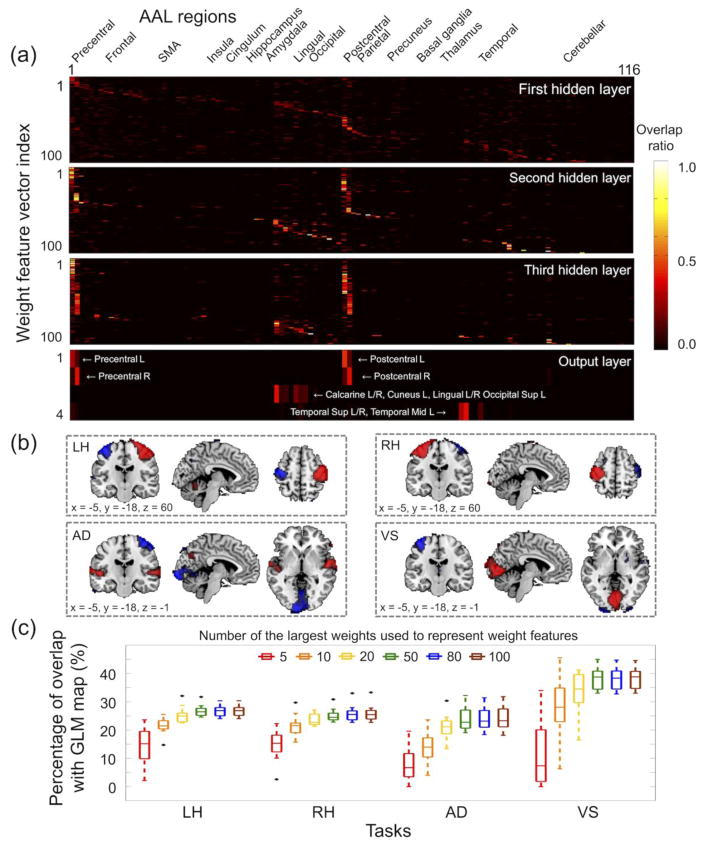
Each column vector of ${\mathbf{F}}_{\mathbf{W}}^{(l)}$ represents the spatial pattern/filter obtained from the weight parameters in the l^th layer (M×N; N is the input dimension, i.e., 74,484; M is the number of hidden nodes, i.e., 100). The anatomical locations of each of the spatial patterns/filters were defined by the automated anatomical labeling (AAL) map (Tzourio-Mazoyer et al., 2002). More specifically, for each of the column vectors of weight-feature representations ${\mathbf{F}}_{\mathbf{W}}^{(l)}$, the corresponding elements were z-scored and the voxel locations of the elements that represented statistically significant intensities (uncorrected p < 10⁻³ with a minimum of 5 connected voxels) were quantitatively evaluated using an overlap ratio with each of the AAL regions. For example, if the voxels fully occupied any of the AAL regions, the overlap ratio with the corresponding AAL region was 1. The overlap ratios across all 116 AAL regions were visualized as a 2-D image plot (Lee et al., 2012a).

The output layer extracts predominantly task-specific features to assure that the values at the output layer could be used to discriminate the class information of the input sample. Exploiting this, we quantified the degree of the task specificity by the overlap ratio between the voxels that represented the top 5 percentile intensities (1) from the group inference of the GLM activation maps from the 11 training subjects for each of the four tasks and (2) from the weight-feature representations at the output layer was calculated.

Interpretation of hidden node outputs of the DNN

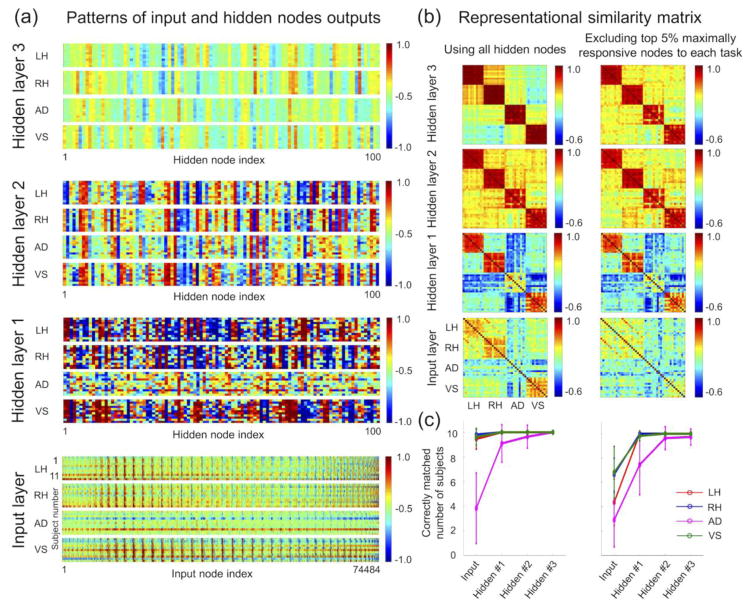
The output of the hidden nodes in each hidden layer (i.e., activations with applied nonlinearities) provided hidden representations of the input fMRI volumes. Consequently, the hidden representations of the optimal DNN with the lowest validation error rate were used to interpret the DNN and to investigate an association with each of the tasks in the corresponding hidden layer. Specifically, the hidden layer output representations were calculated for each of the hidden layers for all fMRI volumes (n = 1,440), that is, those of the 11 training subjects and the validation subject. For each task and for each subject, the average hidden layer output representation was obtained from 30 hidden representations of 30 input fMRI volumes. Then, for each subject, there were four average hidden output representations across the four tasks at each hidden layer, and a representational similarity analysis (RSA) (Kriegeskorte et al., 2008) was conducted using the hidden representations (100×1 vector for each hidden representation) across all four tasks and all 11 training subjects. Several significantly active nodes of the hidden layer or voxels of the input layer could dominate the overall patterns of the RSA matrices. Thus, the significantly active hidden or input nodes with values in the top 5 percentile for each task were excluded, when the corresponding RSA matrices were calculated.

In addition to the RSA, the average hidden representations or average input patterns from each of the four tasks were evaluated on training subjects. In detail, for each training subject, an average hidden representation pattern or input pattern of one of four tasks was selected and the closely matched average hidden representation or input pattern obtained from each of the 10 remaining subjects was identified among the four tasks by calculating Pearson’s correlation coefficients. If the associated task labels of the two matched patterns were identical, they were considered to be correctly matched subjects (i.e., a maximum of 10 would be counted from the 11 training subjects for each task). Similarly, the hidden representations and input patterns from one validation subject were evaluated using those from the 11 training subjects (in this case, the maximum number of matched subjects would be 11). The numbers of correctly matched subjects were also calculated when significantly active hidden or input nodes with values in the top 5 percentile were excluded for each task.

Classification performance under various scenarios of hidden layer output from the DBN/DNN

To evaluate the efficacy of (a) the DNN fine-tuning and (b) the DBN pretraining, the hidden layer output of (1) the pretrained DBN and (2) the fine-tuned DNN with/without DBN pretraining were used as inputs to the softmax and SVM classifiers. In this way classification performance was measured under various scenarios of the DBN without DNN fine-tuning and of the DNN with/without DBN pretraining.

Classification test using the DBN-pretrained DNN from a nested cross-validation framework

To apply the DNN in real situation and obtain the classification performance of a test subject, a nested cross-validation needs to be performed to optimize target percentage of non-zero weights. To ascertain the classification performance with one test subject via a nested cross-validation, 11 sets of leave-one-subject-out cross-validation were performed using the data from the remaining 11 subjects for training/validation. For each of the 11 sets, the 1,200 fMRI volumes of 10 out of the 11 subjects were used to train the DBN and DNN with candidate target percentages of non-zero weights across all the hidden layers. The 120 fMRI volumes of the validation subject were used to validate the classification performance of the trained DNN with each candidate target percentage of non-zero weights. This training and validation of the DNN with the candidate target percentage of non-zero weights was repeated for all 11 sets of 10 training subjects and one validation subject to obtain the average validation accuracy. The lowest average validation error rate was determined to identify the optimal target percentage of non-zero weights. The DNN was then re-trained using the optimal target percentage and the 1,320 fMRI volumes from the 11 training/validation subjects and tested using the 120 fMRI volumes from the one remaining test subject to obtain test accuracy. The softmax and linear SVM classifiers were applied to the output of the output layer and to the output of the top hidden layer of the DNN. The three-layer DNN was used, and one subject whose error rate from a leave-one-subject-out cross-validation scheme was in the vicinity of the average error rate across all subjects was selected as the test subject.

Results

Group-level GLM activation maps of the four tasks

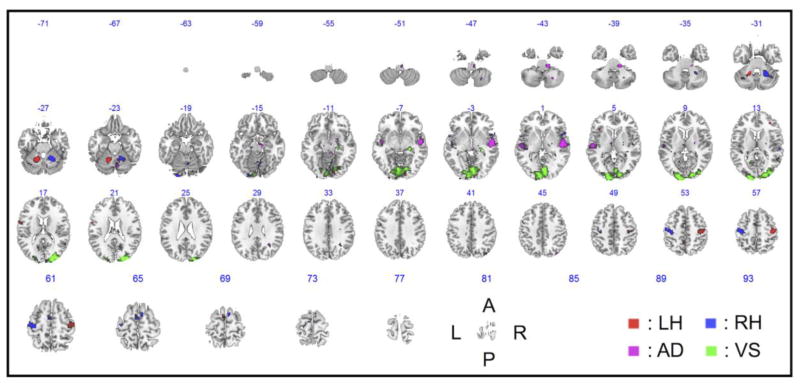
Figure 3 shows the group inference of the GLM activation maps across all subjects for each of the four tasks. Note that the highly task-specific brain regions—such as the contralateral precentral gyri and ipsilateral cerebellum areas (for the LH and RH tasks); the superior temporal cortex, including the planum temporale/Heschl’s gyri (for the AD task); and the lingual gyri and calcarine cortices (for the VS task)—showed activations at an FWE-corrected thresholds of p < 10⁻² for the LH, RH, and VS tasks and an uncorrected threshold of p < 10⁻⁴ for the AD task. Table 1 summarizes the detailed information.

Figure 3.

Group inference of the GLM activation maps for each of the four tasks across all 12 subjects (uncorrected p < 10⁻³). The number above an axial image denotes the z-coordinate (mm) in the MNI space. L, left; R, right; A, anterior; P, posterior; MNI, Montreal Neurological Institute.

Table 1.

Brain regions that presented significant activation patterns for each task (FWE-corrected p < 10⁻² for the LH, RH, and VS tasks; uncorrected p < 10⁻⁴ for the AD task).

Task	Automated anatomical labeling (AAL) / Brodmann’s area (BA)	Size	Foci (x/y/z) in mm	Peak t-score
LH	Cerebellum (L), Culmen, Dentate	48	−15/−51/−27	23.21
	PrCG (R), PoCG (R) / BA3, 4, 6	48	45/−18/57	15.25
RH	Cerebellum (R), vermis, dentate	73	24/−48/−30	25.48
	PrCG (L), PoCG (L) / BA3, 4, 6	74	−36/−21/60	22.56
	SMA (L/R), SFG, MFG, Cerebellum (L/R) / BA 6	11	9/3/66	14.63
	Cerebellum (L/R), Lingual (L), IOG, FG / BA 18	11	−21/−93/−18	14.30
	Cerebellum (R)	13	6/−63/−21	13.03
	SMA (L)	13	−3/−6/63	12.99
AD	STG, MTG / BA 21, 22	11	54/−12/−3	6.93
VS	Cerebellum (L/R), Lingual (L/R), Cuneus(L/R), Calcarine (LR) MOG(L/R) / BA 18	456	24/−90/18	25.15

Size denotes a number of voxels; L, left; R, right; LH, left-hand clenching; RH, right-hand clenching; AD, auditory attention; VS, visual stimulus; PrCG, precentral gyrus; PoCG, postcentral gyrus; SMA, supplementary motor area; SFG, superior frontal gyrus; MFG, medial frontal gyrus; IOG, inferior occipital gyrus; FG, fusiform gyrus; STG, superior temporal gyrus; MTG, middle temporal gyrus; MOG, middle occipital gyrus.

Brain regions of the clusters were identified using the xjView (www.alivelearn.net/xjview8).

Classification results of DNN from leave-out-subject-out cross-validation

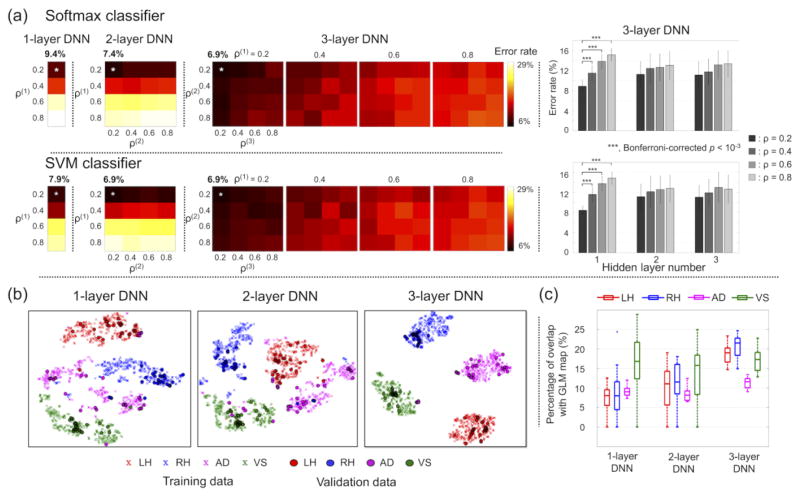
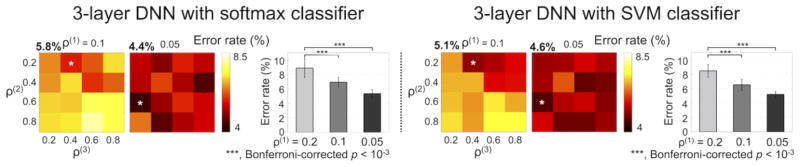
Figure 4 shows the average error rates across all 12 validations for each of the combinatorial scenarios of the target percentages of non-zero weights and for each of the one-layer, two-layer, and three-layer DNNs. The softmax classifier of the fine-tuned DNNs produced minimum average error rates (± standard deviation; %) of 9.4 (± 4.6), 7.4 (± 4.1), and 6.9 (± 3.8) with the one-layer, two-layer, and three-layer DNNs, respectively. The corresponding target percentages of non-zero weights were 0.2 for the one-layer DNN, 0.2 and 0.2 for the two-layer DNN, and 0.2, 0.2, and 0.2 for the three-layer DNN. The error rates across the four target percentages of non-zero weights were significantly different only in the first hidden layer of the three-layer DNN (one-way ANOVA; d.f. = 15, Bonferroni-corrected p < 10⁻⁵). In the first hidden layer, ad hoc paired t-tests revealed that the error rates from the target percentage of non-zero weights of 0.2 were significantly lower than the error rates from the remaining target percentages of non-zero weights (i.e., 0.4, 0.6, and 0.8). The linear SVM classifier produced minimum average error rates of 7.9 (± 5.0), 6.9 (± 4.0), and 6.9 (± 3.4) with the one-layer, two-layer, and three-layer DNNs, respectively, and the corresponding target percentages of the non-zero weights were 0.2 across all hidden layers. Further investigation revealed that the misclassified fMRI volumes were mainly from the AD task (22.2 ± 11.7 %), in contrast to the LH (3.1 ± 6.3 %), RH (1.4 ± 2.7 %), and VS (0.8 ± 2.1 %) tasks using the three-layer DNN. In the one-layer and two-layer DNNs, the error rates were slightly lower when using the linear SVM classifier than when using the softmax classifier. Figure 4b illustrates the t-SNE plots of the representation of the hidden layer output from the top hidden layer of the one-layer, two-layer, and three-layer DNNs, in which the exclusively task-specific feature representations were obtained in the top hidden layer of the three-layer DNN compared to the one-layer DNN. The weight-feature vector representations at the output layer showed an increased overlap with the group inference of the GLM activation maps as the number of hidden layers of the DNN increased (Fig. 4c). This finding is in line with the superior classification performance of the three-layer DNN compared to the one-layer and two-layer DNNs. Figure 5 shows the classification performance from the sparser (i.e., target percentage of non-zero weights = 0.1 or 0.05) weight parameters between the input layer and the first hidden layer. The minimum error rates were significantly reduced (one-way ANOVA; d.f. = 15, Bonferroni-corrected p < 10⁻³) when the degree of weight sparsity was strengthened.

Figure 4.

(a) Classification performance of the 1-, 2-, and 3-layer DNNs from the softmax (top) or SVM (bottom) classifiers across all combinatorial scenarios of four target percentages of non-zero weights (i.e., 0.2, 0.4, 0.6, and 0.8) across the hidden layers to systematically control the weight-sparsity level in each of the hidden layers. ρ^(l) denotes the target percentage of non-zero values of weight parameters between the (l-1)^th and l^th hidden layers (the input layer is equivalent to the 0^th hidden layer). Error rates across the four target percentages of non-zero weights are shown as boxplots for each of the three hidden layers of the three-layer DNN. The statistical significance was evaluated using one-way ANOVA followed by ad hoc paired t-tests. (b) The t-SNE representations of the top hidden layer output (100-dimensional space) of the three DNNs on a 2D plane. All 1,320 training data samples (cross) and 120 validation data samples (circle) are presented. (c) Box-whisker plots of the percentage overlap between (1) the voxels corresponding to the top 5 percentile values of the z-scored weights in the output layer for each task and (2) the voxels corresponding to the top 5 percentile values of the group inference of the GLM activation maps of the task across 11 training subjects. ANOVA, analysis of variance; t-SNE, t-distributed stochastic neighbor embedding; LH, left-hand clenching; RH, right-hand clenching; AD, auditory attention; VS, visual stimulus; GLM, general linear model.

Figure 5.

Error rates of the three-layer DNN when the percentage of non-zero values of weights between the input and hidden layers (i.e., ρ⁽¹⁾) was 0.1 or 0.05. ρ⁽²⁾ and ρ⁽³⁾ values were selected to be 0.2, 0.4, 0.6, or 0.8. Error rates (mean ± standard deviation) when ρ⁽¹⁾ = 0.2, 0.1, and 0.05 are shown as bar plots.

Interpretation of learned weight-feature representation

Figure 6 shows the overlap ratio between (1) the weight-feature vector associated with each hidden node in each hidden layer and (2) each of the 116 AAL regions using the three-layer DNN with 0.2-0.2-0.2 weight-sparsity levels across the hidden layers. In the first hidden layer, each of the weight-feature vectors showed a moderate level of overlap with each of the 116 AAL regions. However, in the top hidden layer, the weight-feature vectors were highly task specific, with each weight-feature vector showing a substantial overlap with either (1) the left precentral/postcentral regions; (2) the right precentral/postcentral regions; (3) the bilateral superior/middle temporal regions; or (4) the bilateral calcarine, lingual, and superior occipital regions. The four weight-feature vectors in the output layer were extremely task specific (Fig. 6b), and the overlap ratios with the highly task-related AAL regions were markedly increased (bottom of Fig. 6a). Figure 6c shows the overlap ratios between (1) the group inference of the GLM activation maps from training subjects and (2) the weight-feature representation at the output layer for several options to include a subset of weight values to calculate the weight-feature representation using Eqs. (1) and (2). The overlap ratios increased as more elements of weights were used to calculate the weight-feature representation, and the overlap ratios were saturated at approximately 50 elements of weights that were used to calculate the feature representation. Overall, the overlap ratios were greater in the VS task than in the LH, RH, and AD tasks, which is consistent with the corresponding classification performance.

Figure 6.

Interpretation of weight parameters learned from the three-layer DNN with the percentage of non-zero weights of 0.2, 0.2, and 0.2 in the first, second, and third layers, respectively. (a) Overlap ratios between each of the weight feature vectors in each layer and each of the 116 AAL regions (see the labels of the 116 AAL regions at http://neuro.imm.dtu.dk/wiki/Automated_Anatomical_Labeling). (b) Four weight-feature vectors in the output layer were pseudo z-scored to have a zero-mean and unit-variance for visualization (absolute z-score > 3.29 or p < 0.001; positive values in red and negative values in blue). (c) Box-whisker plots illustrate the overlap ratios between the weight-feature vector representations in the output layer and the group inference of the GLM activation maps for each task (uncorrected p < 0.001). Weight-feature vector representations in the output layer were calculated for varying numbers of large values from the weight vector representation in each of the hidden layers using Eqs. (1) and (2). AAL, automated anatomical labeling; Sup, superior; Mid, middle.

Interpretation of hidden layer output

Figure 7a shows the 2-D plots of the average pattern of the hidden layer output or the input layer for each task (i.e., average of patterns from 30 volumes for each task and for each subject) obtained from the three-layer DNN with 0.2-0.2-0.2 weight-sparsity levels across hidden layers. The average BOLD intensities of in-brain voxels in the input layer appeared to be similar across tasks and across subjects. The average pattern representations of the first hidden layer output were noisy, and it seemed that there was no clear distinction in these patterns across subjects within a task. However, the average pattern representations of the third hidden layer output clearly demonstrated the similarity structures across the subjects within a task and the dissimilarity structure across the four tasks. These similarity and dissimilarity structures of the input layer and each of the three hidden layers were clearly shown in the RSA matrices, as shown in Figure 7b. Figure 7c shows that the number of correctly determined tasks among subjects increased from the lower to the top hidden layers. The performance of the AD task was inferior to that of the remaining three tasks.

Figure 7.

(a) Hidden layer output patterns and the input sample patterns for each task and for each training subject from the three-layer DNN with percentage of non-zero weights of 0.2, 0.2, and 0.2 in the first, second, and third layers, respectively. The hidden layer output and input sample patterns across the 30 volumes for each task and for each subject were averaged. (b) The RSA matrices using these patterns revealed a markedly enhanced similarity structure across subjects within a task and a dissimilarity structure among the four tasks. These RSA matrices were not substantially altered when the top 5% of the hidden or input nodes per task that showed greater values than the remaining nodes were excluded (right column). (c) The correctly matched numbers of subjects in the training data were calculated by comparing the hidden representation pattern from one subject with the patterns from the 10 remaining subjects in the training set and are visualized for each of the four tasks. RSA, representational similarity analysis; Hidden #1, the first hidden layer; Hidden #2, the second hidden layer; Hidden #3, the third hidden layer.

Figure 8a shows the average pattern representations from one validation subject, which is similar to the representations of the 11 training subjects in Figure 7a. Figure 8b shows that the distinctness of the pattern representations is increased from lower to higher layers. At the 3^rd hidden layer of the three-layer DNN, the hidden layer representations of each of the four tasks were perfectly distinguished despite the top 5 percentile values of the hidden node outputs of each task being excluded (Fig. 8b right).

Figure 8.

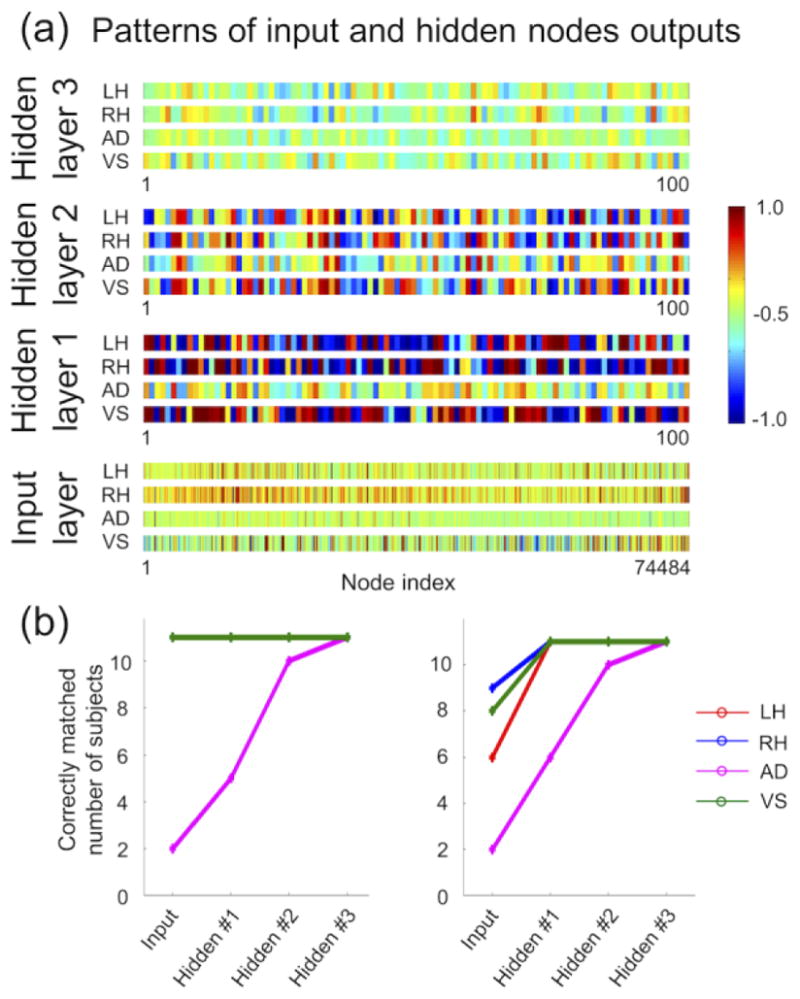
(a) Hidden layer output patterns and input sample patterns from one validation subject and (b) the correctly matched numbers of subjects in the training sets were calculated by comparing hidden representation patterns from the training subjects with those of the validation subject for each of the four tasks. In the right graph the top 5 percentile values of the hidden node outputs for each task were excluded. Please refer to the legend of Fig. 7 for more detailed information.

Classification from DBN without DNN fine-tuning and DNN with/without DBN pretraining

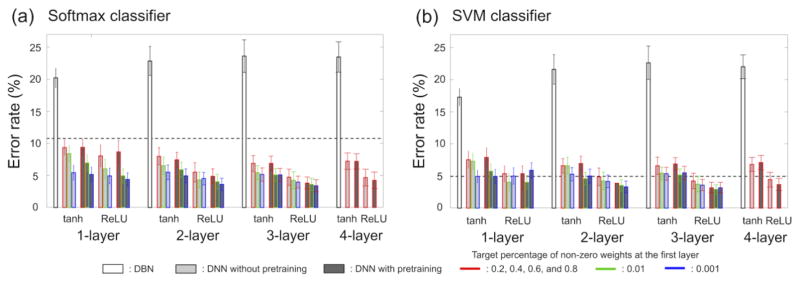
Figure 9 shows the error rates obtained by varying the inputs to the softmax/SVM classifiers. First, the hidden layer output from the DBN pretraining (white bars) shows the highest error rates across all conditions and these error rates were greater than the error rates from the BOLD intensities across the whole brain as input to the classifiers (dotted lines; baseline performance). Second, the error rates, particularly of the two-/three-layer DNNs, decreased when DBN pretraining was used to initialize the weights of the DNNs. Error rates were further reduced by using the ReLU function rather than the tanh function. Table 2 summarizes the performance improvement obtained by using the hidden representations of the DNNs with the ReLU activation function rather than the BOLD intensities as input.

Figure 9.

Classification errors (%) from the (a) softmax and (b) SVM classifiers using the hidden layer output of the DBN without DNN fine-tuning (white box), DNN without DBN pretraining (light gray box), and DNN with DBN pretraining (dark gray box). The performance of the hidden activation function using tanh and ReLU is also compared. The dashed lines indicate the classification performance using fMRI volume (from the input layer) as an input to each classifier. tanh, hyperbolic tangent; ReLU, rectified linear unit; SVM, support vector machine; DBN, deep belief network; DNN, deep neural network.

Table 2.

Improvement of classification performance at different network depths using the ReLU activation function when the target percentage of non-zero weights was 0.001 at the first layer (i.e., this condition showed the lowest error rate). The percentage improvement in classification error of the one- to three-layer DNNs over the classification performance achieved with the zero-layer DNN (i.e., with the input layer only) are given in parentheses.

Classifier	0-layer	Pretraining	1-layer	2-layer	3-layer
Softmax	10.8	without	4.9 (+54.6%)	4.5 (+58.3%)	4.0 (+63.0%)
		with	4.4 (+59.3%)	3.6 (+66.7%)	3.4 (+68.5%)
SVM	4.9	without	5.0 (−2.0%)	4.2 (+14.3%)	3.6 (+26.5%)
		with	5.9 (−20.0%)	3.3 (+32.7%)	3.2 (+34.7%)

DNN, deep neural network; ReLU, rectified linear unit; SVM, support vector machine.

Classification using the DBN-pretrained DNN from a nested cross-validation framework

Using the nested cross-validation scheme, the classification errors of the test subject were 7.5% using the softmax classifier and 5.8% using the SVM classifier. The corresponding optimal percentages of non-zero weights were 0.2, 0.2, and 0.4 across the first, second, and third hidden layers. Note that the error rates of this subject from a leave-one-subject-out cross-validation scheme were 6.7% for both the softmax and SVM classifiers and that the corresponding percentages of non-zero weights were 0.2, 0.2, and 0.2 across the first, second, and third hidden layers.

Discussion

Summary of the study

In this study, we presented the utility of the deep neural network for the classification of a single fMRI volume. The restricted Boltzmann machine was used as a building block to initialize the weight parameters of each layer of the DNN, and the DNN was fine-tuned for the classification of fMRI volumes obtained from the four overt sensorimotor task paradigms. To circumvent the paucity of input samples available to train the DNN, an explicit control of the weight-sparsity level of each hidden layer of the DNN was adopted. The adaptive control of L1 regularization strength facilitated obtaining distinct sparsity levels of weights depending on the target percentages of non-zero values of weights (Fig. S2a). The fixed L1 regularization strength was unable to achieve distinct levels of weight sparsity as exemplified in Fig. S2b; an L1 regularization strength of 0.01 and 0.001 reached approximately the same levels of weight sparsity for both the kurtosis and Hoyer’s sparseness measure (Hoyer, 2004). Weight sparsity levels insensitive to the learning rate can be achieved using sparseness measures such as kurtosis and/or Hoyer’s sparseness as target weight sparsity levels instead of the computationally efficient percentage of non-zero weights.

The classification accuracies were evaluated across all combinatorial scenarios of weight-sparsity levels across all hidden layers via a leave-one-subject-out cross-validation scheme. The lower error rates were obtained from the linear SVM than from the softmax classifier, which was used for DNN fine-tuning and this may be explained by the superior optimization/generalization capability of the SVM classifier based on maximization of the margin between support vectors (a subset of training samples) and the hyperplane when compared to that of the softmax classifier based on cross-entropy minimization using all the samples (Tang, 2013; Zhang et al., 2015a). For example, (a) the lower cross-entropy value obtained by the softmax classifier training led to a higher classification error and (b) the deep network that was initialized using the weights of the trained deep network with the SVM output layer (11.9% error) showed an increased classification error (14%) when the network was fine-tuned using a softmax output layer (Tang, 2013). This limited evidence suggests that the linear SVM may have better optimization and generalization capability than the softmax classifier. The weight-feature representations and hidden layer output explained well the trained DNN and the corresponding classification performance.

Current methods used for fMRI data analysis

In conventional fMRI data analysis, a model-based general linear model (GLM, (Worsley and Friston, 1995)) and a data-driven independent component analysis (ICA, (Calhoun et al., 2001; McKeown and Sejnowski, 1998)) have gainfully been applied to estimate neuronal activations from fMRI measurements. In the context of fMRI data classification using estimated neuronal activations, multivoxel/multivariate pattern analysis (Davis et al., 2014; Haynes and Rees, 2006; Kriegeskorte et al., 2006) has been widely appreciated as a promising approach due to its representational capability in high-dimensional space when compared to the voxel-wise mass-univariate approach. Our presented method is advantageous compared to the searchlight-based MVPA approach because it enables (1) the use of raw BOLD intensities from a single fMRI volume rather than the activation patterns from the GLM/ICA that utilize all the fMRI volumes during the task-period, and (2) extraction of the hierarchical features of the neuronal activations of the whole-brain across multiple hidden layers of the DNN. The classification error obtained over 48 runs (i.e. 12 subjects with four tasks/runs each) with the softmax classifier was 4.2% using the activation patterns of the GLM due to two miss-classified AD runs and 2.1% using those of the ICA due to one miss-classified AD run and with the SVM classifier was 0% using the activation patterns of the GLM and 6.3% using those of the ICA due to three miss-classified AD runs. These results are described in the supplementary material (“Classification of activation patterns from GLM/ICA”). All miss-classified runs were AD task runs due to the aberrant time courses of the auditory areas from the experimental paradigm as shown in Fig. S3b. It is worth noting that our presented method is based on an fMRI volume-by-volume classification and thus the variability of fMRI volumes must be predominantly greater than that of the estimated spatial patterns from the GLM/ICA.

A single fMRI volume classification from the adopted tasks

The error rates from the AD task using the DNNs were greater than the error rates of each of the remaining three tasks. This difference may have arisen because the subjects found it difficult to concentrate on the sinusoidal sounds that distracted them from the background noises, such as MR gradient switching and a cryogenic pump artifact (Kim et al., 2015), during fMRI data acquisition. The fact that the time course of the IC spatial pattern of the auditory area deviated from the experimental paradigm would also support this distraction during the AD task (Fig. S3b). Consistent with this, the statistical significance of the group inference of the GLM activation maps was relatively lower for the AD task than for the other tasks. Notably, the weight parameters of the output node associated with the AD task assigned negative values to the brain regions related to the LH and VS tasks (Fig. 6b), which enhanced the classification performance of the AD task. These negative values of weight parameters were also observed from the weight vectors of the output nodes associated with the LH and RH tasks (Fig. 6b). In our study, overt sensorimotor tasks were used to evaluate the capacity of the DNN toward a single fMRI volume classification. The efficacy of the DNN for the fMRI volume classification acquired from covert/imagery tasks (Boccia et al., 2015; Lee et al., 2009) is important because it can be extended to brain decoding without any overt task paradigm (Boccia et al., 2015; Haynes and Rees, 2006; Lee et al., 2012b).

Classification performance depending on hidden node function

The hyperbolic tangent (tanh) function rather than a sigmoid function was used as a node function of the hidden layer in our reported findings since the error rates were slightly elevated when the sigmoid node function was used (data not shown). The fact that the tanh function was symmetrical to zero and provided a broader dynamic range than the sigmoid function (Hjelm et al., 2014) may have affected classification performance. The performance was substantially improved using the ReLU activation function instead of the tanh function and this is possibly due to the ReLU function preventing the vanishing gradient problem of the stochastic gradient descent learning algorithm (Maas et al., 2013; Nair and Hinton, 2010).

Classification performance depending on the depth of the DNN and corresponding sparsity levels

Error rates decreased as the number of hidden layers of the DNN increased, and the representations at the top hidden layer were more distinct and specific to the tasks from the three-layer DNN compared to the one-layer or two-layer DNNs. Using the four candidate target percentages of non-zero weights (i.e., 0.2, 0.4, 0.6, and 0.8), the sparsest set (i.e., 0.2-0.2-0.2) of the three-layer DNN showed the lowest error rate (i.e., 6.9 %) across the 12 validation subjects using the linear SVM classifier. Further analysis using the error rates obtained from all combinatorial scenarios of target percentages of nonzero weights revealed that the sparse weight parameters reduced the error rates in only the first hidden layer. The error rates (%) were further reduced when the target percentages of non-zero weights at the first hidden layer were 0.1 (6.9 ± 0.7 and 6.5 ± 0.8 from the softmax and SVM classifiers, respectively) and 0.05 (5.4 ± 0.5 and 5.2 ± 0.4) compared to the 0.2 target percentage of non-zero weights (8.9 ± 1.3 and 8.4 ± 0.9) across all four (0.2, 0.4, 0.6, and 0.8) target percentages of non-zero weights in the second and third hidden layers of the three-layer DNN. The massive number of input nodes (i.e., the number of in-brain voxels) caused the substantial number of elements of weight parameters between the input and the first hidden layers. Thus, the corresponding weight parameters would have achieved successful training using a limited number of samples with the help of a sparsity constraint and consequently the stringent sparsity level at the first layer (i.e., 0.01 or 0.001 target percentage) further reduced the error rates (Figs. 5 and 9). It appears that the error rates were also reduced as the sparsity of weight parameters in the second and third hidden layers increased. However, the error rates across the four target percentages of non-zero weights of weights parameters were not statistically significant (uncorrected p = 0.3 for the second hidden layer and uncorrected p = 0.053 for the third hidden layer). The error rates (%) from the four-layer DNN by adding one more layer to the three-layer DNN (with 0.2, 0.2, and 0.2 target percentages of non-zero weights from the first to third hidden layers) were 7.4 (± 3.9), 7.2 (± 4.1), 7.2 (± 4.2), and 7.8 (± 3.8) using the softmax classifier and 7.1 (± 3.9), 7.2 (± 4.4), 7.5 (± 4.5), and 7.7 (± 3.6) using the SVM classifier when the target percentages of non-zero weights were 0.2, 0.4, 0.6, and 0.8 in the fourth hidden layer, respectively. The lower performance of the four-layer DNN compared to the three-layer DNN may be due to the limited number of samples in our study, which could have led to the overfitting of the training data.

Spatial features/filters learned from weight parameters across the hidden layers of the DNN

The greater intensities of the learned weight parameters in the first layer were localized in brain regions across the whole brain (i.e., overlapping with most of the AAL regions), and the weight parameters in the output layer showed greater intensities within brain regions highly specific for each of the four tasks (i.e., overlapping with the motor, auditory, and visual areas). This finding is analogous to our earlier report, in which we observed the hierarchy of the learned weight parameters of the DNN using the whole-brain functional connectivity (FC) of resting-state fMRI data acquired from schizophrenic patients and healthy controls (Kim et al., 2016). In that study, abnormal FC patterns from pairs of brain regions were extracted from the weight parameters in the lower layer, whereas abnormal FC patterns across the whole brain distinguishing the schizophrenic patients from the healthy controls were learned from the weight parameters in the higher hidden layer (Kim et al., 2016). These results may indicate that the weight parameters of the multi-layer DNN would capture low-level features (i.e., localized and distributed brain regions across a brain area defined in the input nodes or FC patterns from pairs of brain regions) in the lower hidden layer and high-level features (i.e., highly task-specific brain regions or FC patterns across a whole brain) in the higher hidden layer. For example, using the BOLD intensities of in-brain voxels of fMRI volumes collected during face and place recognition tasks (Haxby et al., 2001; Kanwisher, 2010) as input samples, the multi-layer DNN may learn the spatial features/filters that are significantly more active in the primary visual areas in the lower hidden layer. The spatial features/filters in the higher hidden layer may primarily be active in the ventral temporal regions, such as the fusiform gyri and parahippocampal place areas, in which the multi-layer DNNs may ultimately be applicable to decode visual stimuli using only brain fMRI activity (Kay et al., 2008; Miyawaki et al., 2008; Naselaris et al., 2009; Schoenmakers et al., 2013; Thirion et al., 2006).

It is worth noting that the estimation of input patterns via the maximization and/or minimization of output/hidden nodes of the trained multi-layer DNNs (Erhan et al., 2009; Simonyan et al., 2013) would be a useful alternative way to characterize the trained DNN (Erhan et al., 2009; Lee et al., 2008). For example, in the activation maximization method, the estimated input pattern x^* is obtained by maximizing the activation of output and/or hidden node: ${\mathbf{x}}^{\ast }=\underset{\mathbf{x}}{\text{argmax}}\left\{h_k^{(l)}\left(\theta ,\mathbf{x}\right)\right\}$, where x is the input pattern and θ are the DNN parameters. This activation maximization method would be particularly useful for characterizing the learned features of deep convolutional neural networks which consist of several pooling layers (Simonyan et al., 2013) which would not be straightforward using the linear combination of weight matrices. When the DNN is trained to predict the target value of an output node in the regression framework, the trained DNN features that increase/decrease an output value can be obtained from estimated input patterns by maximizing/minimizing an output value.

Hidden representations in the hidden layers of the DNN

From the three-layer DNN, the error rates obtained from the softmax and SVM classifiers were comparable. This finding indicates that the representations of the third hidden layer were readily distinct and separable when the three-layer DNN was fine-tuned. The RSA using the hidden node outputs also showed that the patterns in the top hidden layer output were remarkably task specific; the similarity was higher within a task, whereas the dissimilarity was higher between pairs of the four tasks. The RSA using the hidden node outputs were comparable (1) when all nodes were used and (2) when highly task-specific nodes with values in the top 5 percentile were excluded (Fig. 7b). This finding indicates that the hidden layer representations can be treated as patterns and that several maximally active hidden nodes to the task would not critically alter the structure of the patterns, as similarly shown by Haxby et al. (2001) for the multivoxel-pattern analysis of visual object recognition using BOLD fMRI activity. It would be worth investigating whether techniques such as the random zeroing of input nodes adopted in a denoising auto-encoder (Vincent et al., 2008) and the dropout of hidden nodes (Hinton et al., 2012b; Srivastava et al., 2014) would facilitate the learning of the robust representation of the hidden layers against confounding artifacts of fMRI data such as head motion and physiological noises such as cardiac and respiratory signals (Allen et al., 2012; Power et al., 2015) and thus would further enhance the classification performance.

Classification performance with/without the DBN pretraining

Our results showed that the pretraining improved the classification performance of the DNN particularly when the stringent weight sparsity level was used in the first layer (i.e., 0.01 or 0.001 percentage of non-zero weights). The feature representations obtained from the DBN were not distinct to the target task, as evidenced by the classification performance shown in Fig. 9. The DNN with DBN pretraining showed better classification performance than the DNN without the DBN pretraining for both the tanh and ReLU activation functions. Unsupervised pretraining using the DBN has been interpreted as a network regularizer of the DNN and has enhanced classification performance when the network is deep and the number of hidden nodes is large, in which case the pretraining helps to prevent settling on a poor local minimum of the complex network (Erhan et al., 2010). Our finding that the pretraining enhanced both the convergence speed and classification performance of the three-layer DNN for both the training and validation phases (Fig. S1) also indicate that the pretraining helped find a good local minimum of the DNN with the adopted numbers of hidden nodes. Note, however, that purely supervised training without pretraining has also proved successful when using a large quantity of labeled training data with proper initialization and a choice of activation function (Bengio et al., 2013).

Potential issues of the DNN and application of convolutional NN

The training of the DBN and the DNN is computationally expensive. In our study, a nested cross-validation was performed on one test subject using three-layer DNN trained/optimized from 11 training/validation subjects. The resulting error rates and optimally chosen percentage of non-zero weights were comparable to these from the leave-one-subject-out cross-validation scheme. Using this nested cross-validation scheme, the training/optimization of the three-layer DNN took approximately 8 days since one of the 11 sets of training/validation from the 11 training/validation subjects took approximately 17 hours to complete. Graphic processing unit (GPU) installed hardware running a MATLAB environment (Intel i7-4790 3.6 GHz; Nvidia GeForce GTX980; 32 GB RAM; Fedora version 20) was used. The error rate was obtained using the one remaining test subject. The classification performance under the nested cross-validation scheme with the remaining test subjects could have been obtained at a computational cost. The built-in commands to utilize the GPU cores (i.e., ‘gpuArray.m’ and ‘gather.m’) during computation in the MATLAB environment were used to minimize the effort to transform the MATLAB codes of the DeepLearnToolbox into the Compute Unified Device Architecture (CUDA) programing (www.nvidia.com/cuda). This CUDA implementation, the Python based DNN toolboxes such as TensorFlow (tensorflow.org) and Theano (deeplearning.net/software/theano), and Torch (torch7.org) would be of benefit to optimization of DNNs, including weight-sparsity control across the hidden layers with fine-grained intervals and much deeper DNN architectures than the three-layer or four-layer DNNs used in this study.

In addition, the convolutional DNN (Krizhevsky et al., 2012) can be gainfully utilized to learn shift-invariant features from the fMRI volumes when voxel locations are distorted due to spatial misalignment during the spatial normalization step of the fMRI volume preprocessing. The shift-invariant features can be learned from convolutional kernel weights followed by a pooling layer rather than fully connected weights between the input and the first hidden layer. A 3D convolutional kernel that was developed to extract the temporal dynamics of a video sequence (Ji et al., 2013) can be modified for application to the fMRI volume and to implement a dependence of voxels across the whole brain. Additionally, the sparsity constraint to the convolutional kernel weight parameters could be deployed to reduce a number of parameters to train, which would reduce hardware resources while maintaining performance (Collins and Kohli, 2014).

Conclusion

To our knowledge, our study is the first to show the training of multi-layer DNNs that are pretrained using the DBN with BOLD intensities of in-brain voxels of fMRI volumes and the consequent classification of a single fMRI volume within a cross-validation scheme. The presented method can classify a label of the task using input fMRI volumes obtained from more challenging tasks, such as covert/imagery tasks, than the presented overt sensorimotor tasks. Our adopted explicit control of weight-sparsity levels can be gainfully utilized to learn weight parameters from a limited number of available input samples for training and can be optimized using a cross-validation scheme. Abundant neuroimaging data from data-sharing initiatives (Calhoun, 2015) and from the generation of realistic synthetic neuroimaging data (Castro et al., 2015) would tremendously benefit the application of the DNN to neuroimaging data while minimizing potential overfitting. A development of the DNN algorithms, including a pretraining algorithm such as the DBN, into a software toolbox implemented using the CUDA and/or Python codes with a user-friendly interface would drastically extend the utility of the DNN to fMRI data analysis and applications.

Highlights.

• Deep neural network (DNN) was proposed to classify fMRI volume of sensorimotor tasks.

• DNN weights were optimized via non-zero value percentage in cross-validation (CV) framework.

• Classification performance was superior from three-layer DNN than one-/two-/four-layer DNNs.

• Weight/hidden representations were highly task-specific from higher than lower hidden layers.

• Sparsity of weights between the input and first hidden layer enhanced the performance.

Appendix

Appendix A. Deep belief network (DBN) pretraining

As a building block of the DBN (Fig. 2; left), the RBM is a single-layer bipartite network model with visible nodes, v ∈ {0,1}^N_v, and hidden nodes, h ∈ {0,1}^N_h, where N_v and N_h are the numbers of visible and hidden nodes, respectively. For example, in the RBM, to link the input and the first hidden layer of a DBN, the input nodes are the visible nodes and the nodes at the first hidden layer are hidden nodes. The visible and hidden nodes of the RBM have undirected connections, and there is no connection either between the visible nodes or between the hidden nodes (Hinton, 2002). The likelihood that the RBM assigns values in the visible nodes using network parameters is represented using the joint probability of the visible and hidden nodes (i.e., p(v, h)) and its energy function (i.e., E(v, h)):

$$p(\mathbf{v})={\sum }_{\mathbf{h}}p(\mathbf{v},\mathbf{h})={\sum }_{\mathbf{h}}\frac{1}{Z}{e}^{-E(\mathbf{v},\mathbf{h})}=\frac{1}{Z}{\sum }_{\mathbf{h}}{e}^{-{\mathbf{v}}^T\mathbf{b}-{\mathbf{h}}^T\mathbf{c}-{\mathbf{v}}^T\mathbf{Wh}}$$ (A.1)

where Z = Σ _v′,h′e^{−E(v′h′W)} is the partition function; W ∈ R^N_v×N_h is the weight matrix of network, and b ∈R^N_v and c∈ R^N_hare visible and hidden node biases, respectively (Hinton, 2002; Hinton et al., 2012a). The gradient descent scheme to the negative log-likelihood of visible nodes with respect to weight parameters can be used to derive a learning rule as follows:

$$\mathrm{\Delta }{w}_{ji}\propto \frac{1}{N}\sum _{n=1}^N\frac{\partial \text{log}p\left({\mathbf{v}}^n\right)}{\partial w_{ji}}={\langle v_i{h}_j\rangle }_{\text{data}}-{\langle v_i{h}_j\rangle }_{\text{model}},$$ (A.2)

where w_ji is the weight value between the i^th visible node v_i and the j^th hidden node h_j, N is the number of training samples and 〈·〉 is an expectation operator under the distribution specified by the subscript (Hinton, 2002; Hinton et al., 2012a). Due to the absence of direct connections either between hidden nodes or between visible nodes in this Bernoulli-Bernoulli RBM, the calculation of unbiased samples of 〉v_ih_j〈_data is straightforward:

$$p\left(h_j=1\mid \mathbf{v}\right)=f\left(c_j+\sum _i{w}_{ji}{v}_i\right),\text{and}p\left(v_i=1\mid \mathbf{h}\right)=f\left(b_i+\sum _j{h}_j{w}_{ji}\right),$$ (A.3)

where f(·) is a node function. To obtain an unbiased sample of 〈v_ih_j〉_model, a contrastive divergence (CD) scheme was adopted to estimate the reconstructed hidden and visible values with the probability given by Eq. (A.3). The CD-1 is a single step of full Gibbs sampling to update all visible nodes in parallel after an initial update of the hidden nodes and, consequently, to update all the hidden nodes in parallel (Hinton, 2002; Hinton et al., 2012a). As a result, the learning rules of the parameters when using the CD-1 scheme are given as:

$$\begin{array}{l}\mathrm{\Delta }{w}_{ji}\propto \frac{\partial \text{log}p(\mathbf{v})}{\partial w_{ji}}=v_i^0{h}_j^0-v_i^1{h}_j^1,\\ \mathrm{\Delta }{b}_i\propto \frac{\partial \text{log}p(\mathbf{v})}{\partial b_i}=v_i^0-v_i^1,\\ \mathrm{\Delta }{c}_j\propto \frac{\partial \text{log}p(\mathbf{v})}{\partial c_j}=h_j^0-h_j^1,\end{array}$$ (A.4)

where the superscript of visible or hidden nodes indicates the number of steps of the Gibbs sampling chain (Hinton, 2002; Hjelm et al., 2014). For real-valued input, such as fMRI data, the energy function was modified as (Hinton et al., 2012a):

$$E(\mathbf{v},\mathbf{h})=\sum _i\frac{{\left(v_i-b_i\right)}^2}{2{\sigma }_i^2}-\sum _j{c}_j{h}_j-\sum _{i,j}\frac{h_j{w}_{ji}{v}_i}{{\sigma }_i},$$ (A.5)

where σ_i is the standard deviation of the Gaussian noise for the visible node v_i. In this Gaussian-Bernoulli RBM, the conditional distributions for CD-1 are as follows (Hinton et al., 2012a; Hjelm et al., 2014):

$$p\left(h_j\mid \mathbf{v}\right)=f\left(c_j+{\sum }_i\frac{w_{ji}{v}_i}{{\sigma }_i}\right),\text{and}p\left(v_i\mid \mathbf{h}\right)=N\left(b_i+{\sigma }_i{\sum }_j{h}_j{w}_{ji},{\sigma }_i^2\right).$$ (A.6)

The update rules for the real-value parameters are as follows:

$$\begin{array}{l}\mathrm{\Delta }{w}_{ji}\propto \frac{1}{{\sigma }_i^2}{v}_i^0{h}_j^0-\frac{1}{{\sigma }_i^2}{v}_i^1{h}_j^1,\\ \mathrm{\Delta }{b}_i\propto \frac{1}{{\sigma }_i^2}{v}_i^0-\frac{1}{{\sigma }_i^2}{v}_i^1,\\ \mathrm{\Delta }{c}_j\propto h_j^0-h_j^1,\end{array}$$ (A.7)

Appendix B. DNN fine-tuning with weight-sparsity control

A back-propagation algorithm was adopted to fine-tune the DNN by minimizing the mean-squared error (MSE) between the four actual output values (i.e., y) and desired output values (i.e., d) in Fig. 2 (right). A non-zero value 1 was assigned as desired output value only for an output node when the input fMRI volume was associated with the task assigned to the corresponding output node. The dimension of the input sample was substantially greater than the available number of input samples. Thus, the sparsity of the weight parameters via L1-norm regularization was added to the MSE cost function of an ordinary back-propagation algorithm as follows:

$$J=\underset{\mathbf{W}}{\text{argmin}}\left\{(1-\beta ){\Vert \mathbf{d}-\mathbf{y}\Vert }_2^2+\beta {\Vert \mathbf{W}\Vert }_1\right\},$$ (A.8)

where β is an L1-norm regularization parameter of weights, which was auto-tuned based on the percentage of non-zero values of weights, and ||·||₂ and ||·||₁ are the L2- and L1-norms, respectively. Then, the weight update term was derived using a gradient descent scheme to minimize the cost function, J:

$$\mathrm{\Delta }\mathbf{W}\left(t\right)=\alpha \left(t\right)\left(\left(1-\beta \left(t\right)\right){\mathrm{\Delta }}_{BP}\mathbf{W}\left(t\right)+\beta \left(t\right)\text{sign}\left(\mathbf{W}\left(t\right)\right)\right),$$ (A.9)

where Δ_BP W(t) is the weight update term of an ordinary back-propagation algorithm and is defined as the first-order derivative of the MSE between d and y; i.e., the first term of Eq. (A.8), t is the epoch number, α(t) is the overall learning rate, β(t) is the L1-norm regularization parameter to control weight sparsity to the target percentage of non-zero weights at the t^th epoch, and 1−β(t) is multiplied by Δ_BP W(t) to control the relative contribution of the MSE and the weight sparsity. A momentum factor can also be applied to accelerate the gradient descent learning (Bishop, 1995; Kim et al., 2016).

To explicitly control the level of weight sparsity, the degree of the L1-norm regularization parameter was adjusted to achieve the target percentage (0–1) of non-zero values of weights:

$$\mathrm{\Delta }\beta \left(t\right)=\mu \text{sign}\left(\mathit{pnz}\left(\mathbf{W}\left(t\right)\right)-\rho \right),$$ (A.10)

where μ is the learning rate of β (t), ρ is the target percentage of non-zero values of weights, and pnz(·) is a function that accounts for the percentage of non-zero values whose absolute values are greater than threshold ε. β(t) increases when the percentage of non-zero values of current weights W(t) is above the target percentage level; thus, L1-norm regularization is strengthened, leading to sparser weights (Kim et al., 2016). In contrast to our earlier study (Kim et al., 2016), the sign function was applied to Eq. (A.10) to facilitate the L1-norm regularization of weights to a target percentage of non-zero weights even when the difference between the target percentage and the percentage of nonzero values of current weights was negligible.

Appendix C. Rectified linear unit activation function

The rectified linear unit (ReLU) activation function is defined as:

$$h_k^{(l)}=max\left({\mathbf{w}}_k^{(l),T}{\mathbf{h}}^{(l,1)},0\right),$$ (A.11)

where $h_k^{(l)}$ is the k^th hidden node output at the l^th hidden layer, ${\mathbf{w}}_k^{(l)}$ is the weight vector of the k^th hidden node at the l^th hidden layer from the (l-1)^th hidden layer, and h^(l-1) is the node output at the (l-1)^th hidden layer. The advantage of the ReLU function over the tanh and sigmoid activation functions is that it can minimize the potential vanishing gradient problem of the stochastic gradient descent learning algorithm (Maas et al., 2013).

To apply the ReLU function to the RBM model, the noisy rectified linear unit (NReLU) was introduced as follows (Dahl et al., 2013; Nair and Hinton, 2010):

$$h_k^{(l)}=max\left({\mathbf{w}}_k^{(l),T}{\mathbf{h}}^{(l-1)}+{\epsilon }_k^{(l)},0\right),$$ (A.12)

where ${\epsilon }_k^{(l)}$ is drawn from a normal distribution, $N\left(0,{\left(1+e^{-{\mathbf{w}}_k^{(l),T}{\mathbf{h}}^{(l-1)}}\right)}^{-1}\right)$. During the DNN fine-tuning phase, the ordinary ReLU in Eq. (A.11) was used (Dahl et al., 2013).